Redes neurais profundas:
aspectos matemáticos e estatísticos
Roberto
Imbuzeiro
Oliveira

O que faz uma rede neural profunda?
Identifica imagens
Faz tradução automática

Joga xadrez e outros jogos

Dirige carros (?)

Uma família de algoritmos por trás de tudo.
Rede neural profunda
- Entrada
- Saída
- "Neurônios": lugares onde computações são feitas
- "Pesos sinápticos": parâmetros do modelo.
Perceptron = 1 neurônio
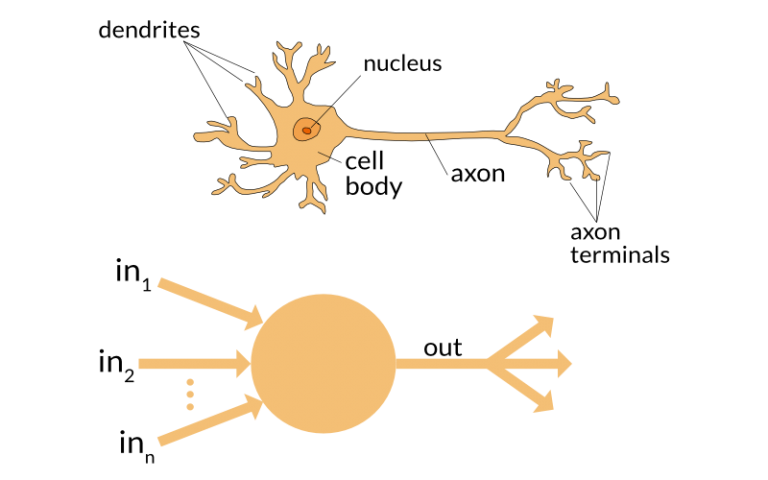
Perceptron (Rosenblatt'58)
\[ \sigma(x;w,a,b) = a \phi(w.x + b) \]
onde \(x\in\R^d\) é a entrada (vetor),
\(\phi:\R\to\R\) é função não-afim fixa
e \(w\in\R^d\), \(a\in\R\) , \(b\in \R\) são pesos.
Perceptron (Rosenblatt'58)
\[ \sigma(x;w,a,b) = a \phi(w.x + b) \]
Exemplos de \(\phi\):
- \(\phi(t) = \frac{e^t}{1+e^t}\) sigmóide
- \(\phi(t) = \max\{t,0\}\) ReLU
Treinando o perceptron
- Exemplos: pares \((X_i,Y_i)\in\R^d\times \R,\,i=1,2,3,4,\dots\)
- Aprendizado: ajuste dos pesos \(w, a, b\) de modo a minimizar o erro
\[\widehat{L}_n(w,a,b):=\frac{1}{n}\sum_{i=1}^n (Y_i - \sigma(X_i;w,a,b))^2.\]
Rede de 1 camada interna

Camada cinza = vetor de perceptrons.
\(\vec{h}=(a_i\phi(x.w_i+b_i))_{i=1}^N.\)
Saída= perceptron a partir do cinza.
\(\widehat{y}=a\phi(w.\vec{h}+b).\)
Rede profunda (DNN)

Tipos de neurônios
- Conexões completas com neurônios anteriores.
- Convoluções com pedaços da entrada/imagem, seguidas de funções não lineares (ConvNet).
- "Pooling" de janelas pequenas...
Literatura empírica é IMENSA
Aprendender pesos?
- Rede calcula função a partir da entrada com pesos como parâmetros: \[(x,\theta)\in\R^d\times \R^N\mapsto \widehat{y}(x;\theta).\]
- Perda: \[\widehat{L}(\theta):=\frac{1}{n}\sum_{i=1}^n(Y_i - \widehat{y}(X_i;\theta))^2.\]
- Como escolher \(\theta\) para minimizar perda?
Descida de gradiente
\[\theta^{(k+1)} = \theta^{(k)} - \alpha(k)\nabla\widehat{L}(\theta^{(k)})\]
Porque parece boa ideia: \(-\nabla\widehat{L}(\theta)\) é a direção em que \(\widehat{L}\) diminui mais depressa.
"Backpropagation" (Hinton): regra da cadeia compacta para calcular o gradiente.
Funciona?
Tudo indica que sim.
Redes com \(O(10^1)\) - \(O(10^2)\) camadas.
\(O(10^7)\) ou + neurônios por camada.
Bases de dados: ImageNet tem \(O(10^9)\) imagens.
Método exige potência computacional e muitos ajustes.
Por quê?
Ninguém sabe.
Descobrir isso é um objetivo de pesquisa de muitos.
Aplicações potenciais?
Performance no CIFAR-10

Taxa de erro desceu de 21% para 1%.
E agora?
- Principais conferências dobram de tamanho a cada ano.
- Indícios de que Inteligência computacional substituirá humanos em várias tarefas.
- Pouquíssima compreensão teórica.
Teoria para quê?
- Para entender melhor
- Para melhorar os métodos (?)
Como formular o problema?
Aprendizado Estatístico
Artigo relevante: Leo Breiman.
"Statistical Modeling: The Two Cultures"
Statistical Science v. 16, issue 3 (2001), 199 -231
Aprendizado supervisionado (regressão)
- É dada uma função \(f:\R^d\times \Theta\to\R\).
- Objetivo é escolher \(\theta\in \Theta\) de modo a minimizar o erro médio quadrático:
\[L(\theta):= \mathbb{E}_{(X,Y)\sim P}(Y-f(X;\theta))^2.\]
- Aprendizado "estatístico" porque \((X,Y)\in\R^d\times \R\) são aleatórios.
Dados e erro empírico
Na prática, não se sabe calcular a esperança, mas temos dados independentes e identicamente distribuídos.
\[(X_1,Y_1),(X_2,Y_2),\dots,(X_n,Y_n)\sim P.\]
Problema: como e o quanto o quanto podemos nos aproximar de um \(\theta\) ótimo? Quando isso é bom o suficiente?
Dados e erro empírico
Ideia: trocar a minimização do valor esperado pela minimização do "erro empírico".
\[\widehat{L}_n(\theta):= \frac{1}{n}\sum_{i=1}^n(Y_i-f(X_i;\theta))^2.\]
Chame de \(\widehat{\theta}_n\) o minimizador deste erro.
Por que pode dar certo?
Lei dos grandes números: se \(n\) é grande,
\[ \frac{1}{n}\sum_{i=1}^n(Y_i-f(X_i;\theta))^2 \approx \mathbb{E}_{(X,Y)\sim P}(Y-f(X;\theta))^2 \]
\[\Rightarrow \widehat{L}_n(\theta)\approx L(\theta).\]
Minimizar erro empírico parece com minimizar erro médio quadrático (na "população")?
O que pode dar errado?
Precisamos de convergência sobre todos os \(\theta\in \Theta\) ao mesmo tempo.
Lei uniforme dos grandes números.
Vapnik, Chervonenkis, Dudley, ... .
Viés e variância
Viés: se \(\Theta\) é "pequeno", pode ser que todas as escolhas de parâmetro tenham erro \(\mathbb{E}(Y-f(X;\theta))^2\) grande.
Variância: se \(\Theta\) é "muito grande", o erro na lei dos grandes números pode ser grande e isso complica a vida.
Underfitting e overfitting

Visão tradicional: overfitting \(\approx\) interpolação
Como medir a variância
Complexidade de Rademacher (Bartlett, Mendelson, Koltchinskii):
\[\mathcal{R}_n(\Theta):= \sup_{\theta\in\Theta}\frac{1}{n}\sum_{i=1}^n \epsilon_if(X_i;\theta),\]
onde os \(\epsilon_i\) são sinais \(\pm 1\) independentes entre si e dos \(X_i\).
"Variância alta \(\Leftrightarrow\) quase-interpolação \(\Leftrightarrow \mathcal{R}_n(\Theta)\) grande"
Teoria dá errado nas DNN
Viés pequeno
Suponha \[Y=f_*(X) + \text{ruído}\] com \(f_*\) contínua, então redes neurais com 1 camada interna com \(N\to +\infty\) neurônios têm viés \(\to 0\).
Kurt Hornik (1991) "Approximation Capabilities of Multilayer Feedforward Networks", Neural Networks, 4(2), 251–257
Problemas
- Quem disse que calculamos o minimizador do erro empírico?
- Quem disse que a variância é pequena?
- Quem disse que uma rede não é capaz de interpolar os dados?
Descida de gradiente?

Erro empírico?
Teoria tradicional foi pensada para problemas convexos.
DNNs estão longe de serem convexas.
Não há garantias de que descida de gradiente converge para um mínimo global.
Mínimos locais podem ou não ser bons.
Interpolação
Teoria tradicional diz que variância vem capacidade de interpolar.
DNNs são capazes de interpolar quando têm muitos parâmetros.
Logo, a teoria de Complexidade de Rademacher não se aplica a elas.
Zhang et al, "Understanding deep learning requires rethinking generalization." ICLR 2017
Não otimiza
Não adianta aplicar uma teoria baseada na minimização do erro empírico.
Falta de convexidade é a razão.
O que parece garantir convergência na prática?
Interpola
Complexidades de Rademacher e outras medidas tradicionais de variância são inúteis.
Como medir variância?
Por que o "overfitting" não parece ser sempre um problema?
Min local
Teoria para métodos/estimadores que convergem para mínimos locais.
(Arora, Ge, Jordan, Ma, Loh, Wainwright, etc)
Interpolação
É possível encontrar métodos muito simples (não DNN) que interpolam e têm bons resultados em alguns casos.
(Rakhlin, Belkin, Montanari, Mei, etc)
Problema: nada disso é sobre redes neurais.
DNNs: algum progresso?
Hipóteses de trabalho
- Devemos pensar em DNNs com infinitos parâmetros ("tamanho não importa").
- No limite de infinitos parâmetros, problema é "otimizável"
- O próprio método de descida de gradiente está ajudando para que tudo funcione.
Evidências: Zhang et al ICLR 2017.
Controle de complexidade

Uma camada interna
Próximos slides: relato sobre trabalhos de Mei, Montanari e Nguyen; Rotskoff e Vanden Eijden; Sirignano e Spiliopoulos (todos no ArXiv em 2018).
O problema
Dados iid: \((X_i,Y_i)\in\R^d\times \R\) com distribuição \(P\)
Rede com uma camada interna:
\[\widehat{y}_N(x;\theta_N) = \frac{1}{N}\sum_{i=1}^N\sigma(x;\theta^{(i)}_{N}).\]
Resíduo: \({\rm res}_k(\theta):= Y_{k+1} - \widehat{y}_N(X_{k+1};\theta)\)
Descida estocástica de gradiente:
\[\theta_N(k+1) -\theta_N(k) = -\varepsilon\alpha(k)\,{\rm res}_k(\theta_N(k))\,\nabla\widehat{y}_N(X_{k+1},\theta_N(k))\]
O problema
Medida empírica dos pesos:
\(\widehat{\mu}_N(k):= \frac{1}{N}\sum_{i=1}^N\delta_{\theta_N^{(i)}(k)}\)
Dinâmica para cada peso:
\[\theta^{(i)}_N(k+1) - \theta^{(i)}_N(k) = \varepsilon b(\theta^{(i)}_N(k),\widehat{\mu}_N(k),X_{k+1},Y_{k+1}).\]
Direção média: \[b_P(\theta,\mu) = \int_{\R^d\times \R}b(\theta,\mu,x,y)\,dP(x,y).\]
Teorema
Quando \(N\to +\infty\), \(\varepsilon\to 0\) e os pesos iniciais são iid \(\mu(0)\), temos a convergência:
\[\widehat{\mu}_N(t/\epsilon)\Rightarrow \mu(t),\]
e os pesos são assintoticamente iid. \(\mu(t)\).
Lei \(\mu(t)\) resolve problema de McKean-Vlasov:
Há um processo \(t\geq 0\mapsto \bar{\theta}(t)\) com trajetórias contínuas tal que \(\theta(t)\sim \mu(t)\) para todo \(t\geq 0\) e além disso:
\[\frac{d\bar{\theta}}{dt}(t) = b_P(\bar{\theta}(t),\mu(t)).\]
Heurística
Supondo pesos i.i.d. no tempo \(0\) e LGN
\(\widehat{\mu}_N(t/\epsilon)\Rightarrow \mu(t)\) (para alguma \(\mu(t)\)) então:
- Os pesos são assintoticamente iid em todos os tempos, pois \[\theta_N^{(i)}(k+1) - \theta_N(k) \approx \varepsilon b_P(\theta_N^{(i)}(k),\mu(\epsilon k)).\]
- Quando \(\varepsilon\to 0\), aproxima solução de EDO: \[\frac{d\theta_N^{(i)}}{dt}(t) =b_P(\theta_N^{(i)}(t),\mu(t)).\]
- Auto-consistência: \(\theta_N^{(i)}(t)\sim \widehat{\mu}_N(t) \approx \mu(t),\) logo solução de McKean-Vlasov.
Consequências
Evolução de \(\mu(t)\): fluxo de tipo gradiente com potencial convexo no espaço de medidas de prob. sobre \(\R^D\).
Tipo de EDP estudado por Ambrosio, Gigli, Savaré; Villani; Otto; etc.
\(\Rightarrow\) convexidade no limite.
Redes neurais com uma camada interna são um método não-paramétrico baseado em otimização convexa.
Nosso trabalho
Como isso se estende para redes com várias camadas internas?
Trabalho com Dyego Araújo (IMPA) e Daniel Yukimura (IMPA/NYU).
"A mean field model for certain deep neural networks"
https://arxiv.org/abs/1906.00193
Nosso trabalho
Desafio: provar que há um limite.
Não sabemos nada sobre a EDP descrevendo a medida.
As redes que estudamos
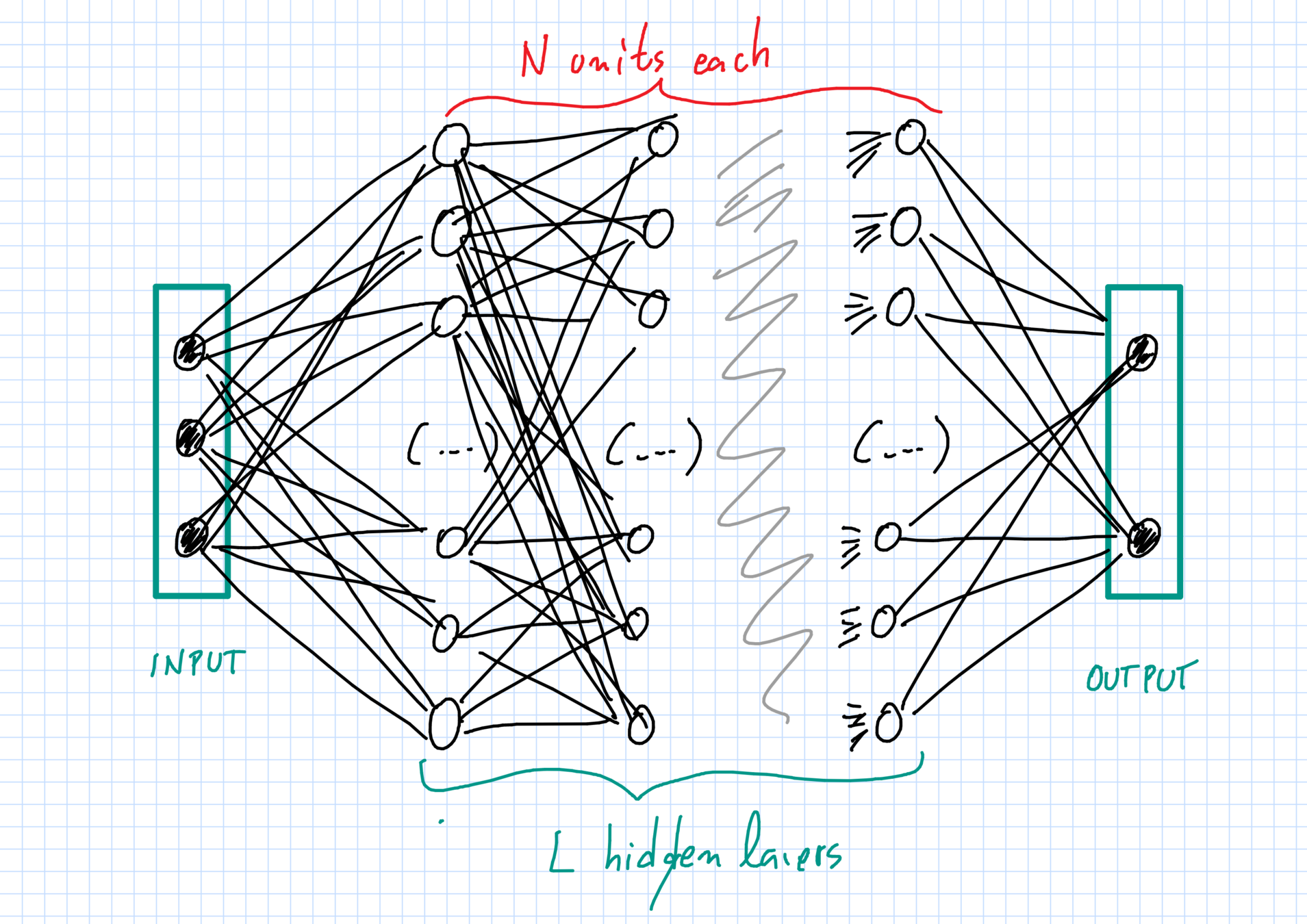
Evolução limite dos pesos
- A forma da EDO depende apenas da camada.
- Envolve o peso, as densidades de pesos vizinhos e (para camadas perto da entrada e da saída \(\ell=1,L\)) outros pesos.
LGN + "backpropagation"
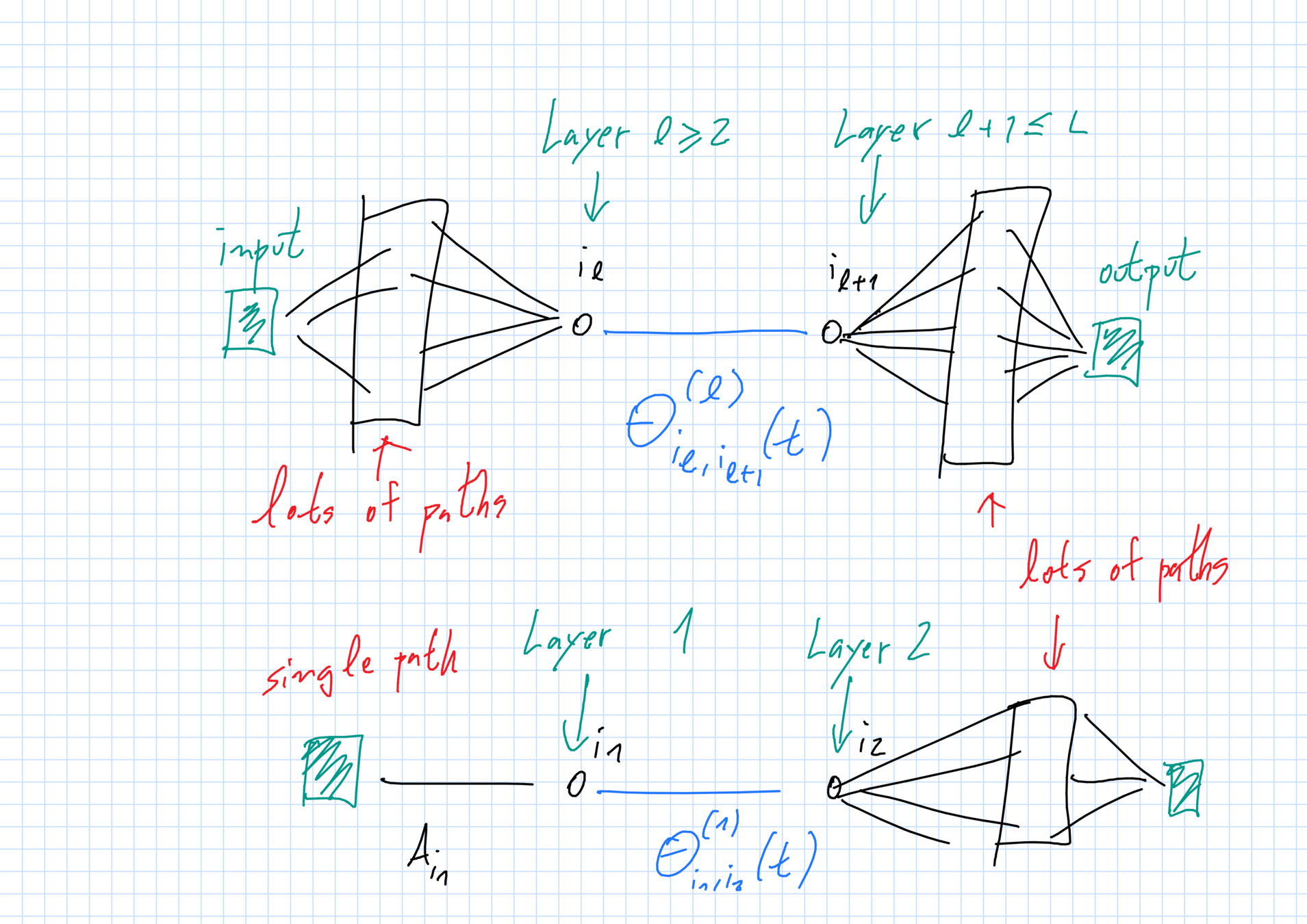
McKean-Vlasov
Ansatz:
- Termos envolvendo somas com muitos pesos aleatórios viram integrais no limite
- Distribuição do peso só depende da camada em que ele está.
\(\Rightarrow\) McKean-Vlasov
Diferenças
Antes: as "partículas" eram os pesos, que se mantinham i.i.d. todo o tempo \(N\gg 1\). Problema clássico.
Agora: unidades básicas são caminhos na rede. Alguns pesos perto da entrada e da saída permanecem dependentes no limite.
Problemas técnicos porque problema-limite é descontínuo.

Por que funciona?
Porque as dependências no limite são compreensíveis.
Como é a prova
Existência e unicidade do processo McK-V \((\mu_t)_{t\geq 0}\) que deve corresponder à distribuição limite de pesos ao longo de um caminho.
Provar que esta medida tem a estrutura certa de independência.
\[\mu_{[0,T]} = \mu^{(0,1)}_{[0,T]}\otimes \mu^{(2)}_{[0,T]} \otimes \mu_{[0,T]}^{(L-1)}\otimes \mu_{[0,T]}^{(L,L+1)}.\]
Usar essa estrutura
Dá para comparar os pesos reais e "partículas ideias" derivadas de \(\mu(t)\) através de argumentos de acoplamento.
A estrutura de dependências é fundamental neste passo.
A EDP limite é mais ou menos assim
[Public domain/Wikipedia]

Uma direção de pesquisa
No limite, o que uma DNN do nosso tipo faz é calcular composições de funções:
\(x\mapsto h(x;Q):= \int\,h(x,\xi)\,dQ(\xi)\) onde \(Q\in M_1(\mathbb{R}^{D})\).
- Tomando as medidas \(Q\) como parâmetros, como é o problema de aprendizado/regressão neste espaço?
- Qual é o melhor que dá para fazer?
- DNNs são discretização disso. Há outras? Qual a melhor?