Correct by Construction:

Let the compiler prove itself to you.

What does it mean for software to be “correct”?

There are three main criteria:

There must be very strong evidence that the properties under question are true and the evidence for this must be independently verifiable.
It must continue to function as required for all possible inputs.
It must carry out these functions and do nothing else.

Make it work for real world effects: exceptions, contracts, loops.
These things are still needed..

A convincing demonstration of correctness being impossible as long as the mechanism is regarded as a black box, our only hope lies in not regarding the mechanism as a black box.

Dijkstra (1970) "Notes On Structured Programming"

The compiler is a actually a proof assistant; so you can leverage types as propositions.

Word on the Street

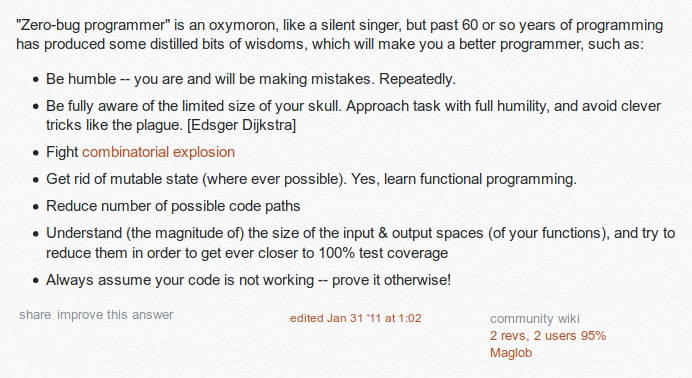
... Prove it otherwise ...

Types ≃ Propositions ≃ Objects

Terms ≃ Proofs ≃ Morphisms

Curry-Howard(-Lambek) Correspondance.

//In other words:
def true: Unit = () // not true: Boolean
def false: Nothing = ??? // not false: Boolean

... and these ideas are shaping new foundations for mathematics ...

We can prove logical statements by constructing elements of types

Proofs, or code paths, like any good story, or program run have a beginning, a middle and an end:

What's a Proof?

Assumptions.
Our domain types.
Statements in order.
Functions.
The goal.
A value.

Types ≃ Propositions

If you can define the method, you found the proof...

// implication: A => B
def implication[A, B](a: A): B = ???

so what?

// f: If A then B is carried along (provided)
def implication[A, B](a: A)(f: A => B): B = f(a)

Terms ≃ Proofs

Truth is type inhabitance...

def possible[A, B](a: A)(implicit proof: A => B): B = 
  proof(a)

// or:

def possible[A, B](implicit proof: A => B): A => B = 
  proof(_)

Logic

Constructive Logic as types...


// Constructive Connectives
type False = Nothing

type And[A, B] = (A, B)
type Or[A, B] = Either[A, B]
type Implication[A, B] = A => B

type Not[A] = A => Nothing

Ingredients for Correctness

It must carry out the functions that are required and do nothing else.
It must continue to function as required for all possible inputs.
There must be very strong evidence that these properties are true and the evidence for this must be independently verifiable.

... can constructivism be practical? ...

In terms of Computation

Total Functions
Referential Transparency
Termination

Referential Transparency

Avoid mutation

var x = 5 = 3
val x = 5 = 3 // Exception

if (x = 1) // Oops

r = open("w")
r = open("y") // Oops

Referential Transparency

Decouple evaluation

def systemTime: IO[Timestamp] = ...

systemTime()
doSomething()
sleep(1)
systemTime()
doSomethingElse()

Total Functions

Avoid exceptions

def decode[A](s: String): A
def decode[A](s: String): Either[Error, A]

Total Functions

Restrict input values

def rational(a: Int, 
             b: Int Refined NonZero): Rational = ...

Termination

Avoid recursion

//hmmm: http://stainless.epfl.ch/doc/intro.html
def use[A](a: A): A = use(a) 

def sum(l: List[Int]): Int = l.fold(0)(_ + _)

Turing's Halting Problem ≃ Gödel's Incompleteness Theorems

Termination

Turing's Halting Problem ≃ Gödel's Incompleteness Theorems

Avoid loops

def use[A](a: A): A = while (true) { ... }; a

val fib = 0 #:: fib.scanLeft(1)(_ + _)

Is it really that simple?

Yes.

But we want to build a giant system!

Category Theory is the study of composition.

Constructive programming is a (family) of Proof calculi aligned with software development.

Start with constructive logic.


type And[A, B] = (A, B)

type Or[A, B] = Either[A, B]

type Implication[A, B] = A => B

Quantify.


trait Exists { type A; val witness: A }

trait ForAll[F[_]] { apply[A]: F[A] }

def boundedUse[A: F]: F[A] = implicitly[F[A]]

Use category theory for composition.

Quantification is just a specific adjoint functor.

We have at our disposal all of the structures identified in category theory for program composition.

Real world Examples

TravelParty

sealed trait TravelParty

case class SimpleTravelParty(
  adults: Int Refined Positive, 
  children: Int Refined NonNegative, 
  babies: Int Refined NonNegative
) extends TravelParty

case class DatedTravelParty(
  adults: Int Refined Positive, 
  childrenAges: Seq[LocalDate]
) extends TravelParty

@ val s = SimpleTravelParty(1, 0, 0)
s: SimpleTravelParty = SimpleTravelParty(1, 0, 0)

@ val s = SimpleTravelParty(0, 0, 0)
cmd56.sc:1: Predicate failed: (0 > 0).
val s = SimpleTravelParty(0, 0, 0)
                          ^
Compilation Failed

Real world Examples

TravelParty

object SimpleTravelParty {
  implicit val semigroup: Semigroup[SimpleTravelParty] = new Semigroup[SimpleTravelParty] {
    def combine(x: SimpleTravelParty, y: SimpleTravelParty): SimpleTravelParty = 
      new SimpleTravelParty(PosInt.unsafeFrom(x.adults.value + y.adults.value), 
                            PosInt.unsafeFrom(x.children.value + y.children.value), 
                            PosInt.unsafeFrom(x.babies.value + y.babies.value))
  }
}

val stp0 = SimpleTravelParty(1, 0, 0)
val stp1 = SimpleTravelParty(1, 0, 1) 
stp0 ++ stp1

class SimpleTravelPartyTest extends CatsSuite {

  implicit val arbSimpleTravelParty: Arbitrary[SimpleTravelParty] =
    Arbitrary(SimpleTravelPartyGenerators.simpleTravelPartyGen)


    checkAll("SimpleTravelParty", SemigroupTests[SimpleTravelParty].semigroup)
}

Real world Examples

Conflict-free Replicated Data Types

//GSet Grow Only Set

val counter = Monoid[GSet[Int]].empty // empty G-Set
val firstReplica = counter + 1 // add element
val secondReplica = counter + 2 // add element
val firstReplicacombined = firstReplica |+| secondReplica // combine
val secondReplicacombined = secondReplica |+| firstReplica // combine

firstReplicacombined == secondReplicacombined // the result is independent of combine order

class GSet[E](val state: Set[E]) {
  def +(element: E) = 
    new GSet[E](state + element)

  def value: Set[E] = state
}

object GSet {
  implicit def monoid[E] = 
    new Monoid[GSet[E]] {
      override def empty = apply[E]()
      override def combine(x: GSet[E], 
                           y: GSet[E]) =
      new GSet[E](x.value ++ y.value)
  }

  implicit def partialOrder[E] = 
    PartialOrder.byLteqv[GSet[E]] { 
      (x, y) => x.state subsetOf y.state
    }
}

Implicit parameters (terms) are antecedant proofs or theorems:

def foldMap[A, B: Semigroup](as: NonEmptyList[A])(f: A => B) = 
  as.map(f).reduce(_ ++ _)
  
def foldMap[A, B: Monoid](as: List[A])(f: A => B) = 
  as.foldLeft(Monoid[B].empty)((b, a) => b ++ f(a))

The later carries proof of the proposition (implication):

If B forms a Monoid then it has a zero.

def zero[B: Monoid] = Monoid[B].empty

Real world Examples

Proof Requirements.

Generalizing implication

/**
  * `FunctionK[F[_], G[_]]` is a functor transformation from `F` to `G`
  * in the same manner that function `A => B` is a morphism from values
  * of type `A` to `B`.
  * They are higher order implications. and can also be viewed as a
  * less general (bounded) ForAll proposition. 
  * for all 
  */
trait FunctionK[F[_], G[_]] { ... }

trait ArrowChoice[F[_, _]] extends Arrow[F] with Choice[F] { ... }

ArrowChoice?

sealed trait Person
case class Teacher(name: String, students: List[Person]) extends Person
case class Student(name: String, teacher: Teacher) extends Person
type Pay = Double
type Fee = Double

def findPerson(name: String): Option[Either[Student, Teacher]] = ???

def payCalc: Teacher => Pay = _.students.foldLeft(0.0){
  case (pay, t:Teacher) => pay + 0.1 * payCalc(t)
  case (pay, s:Student) => pay + 2.5
}
def feeCalc: Student => Fee = _ match {
  case Student(_, t) => 1.10 * payCalc(t) / t.students.length
}

val calc: Either[Student, Teacher] => Either[Fee, Pay] = 
  feeCalc +++ payCalc

val names: List[String] = List.empty

val feesAndPayments: List[Either[Fee, Pay]] = 
  names flatMap findPerson map calc

val profit: Double = 
  feesAndPayments foldMap identity(_).choice(- _)

Real world Examples

Correct by Construction:

Let the compiler prove itself to you.

What does it mean for software to be “correct”?

Dijkstra (1970) "Notes On Structured Programming"

Word on the Street

Curry-Howard(-Lambek) Correspondance.

What's a Proof?

Types ≃ Propositions

Terms ≃ Proofs

Logic

Ingredients for Correctness

In terms of Computation

Referential Transparency

Avoid mutation

Referential Transparency

Decouple evaluation

Total Functions

Avoid exceptions

Total Functions

Restrict input values

Termination

Termination

Is it really that simple?

But we want to build a giant system!

Start with constructive logic.

Quantify.

Use category theory for composition.

Real world Examples

TravelParty

Real world Examples

TravelParty

Real world Examples

Conflict-free Replicated Data Types

Real world Examples

Proof Requirements.

Generalizing implication

ArrowChoice?

Further Reading (References)