Logic in your Programs:
Use the compiler to prove your business logic.
"Correct Software"
What does it mean for software to be “correct”?
There are three main criteria:
- There must be very strong evidence that the properties under question are true and the evidence for this must be independently verifiable.
- It must continue to function as required for all possible inputs.
- It must carry out these functions and do nothing else.
How to make it practical: exceptions, contracts, loops.
These things are still needed..
A convincing demonstration of correctness being impossible as long as the mechanism is regarded as a black box, our only hope lies in not regarding the mechanism as a black box.
Dijkstra (1970) "Notes On Structured Programming"
By using types to shed light into your assertions and invariants your compiler is then a proof assistant.
Word on the Street
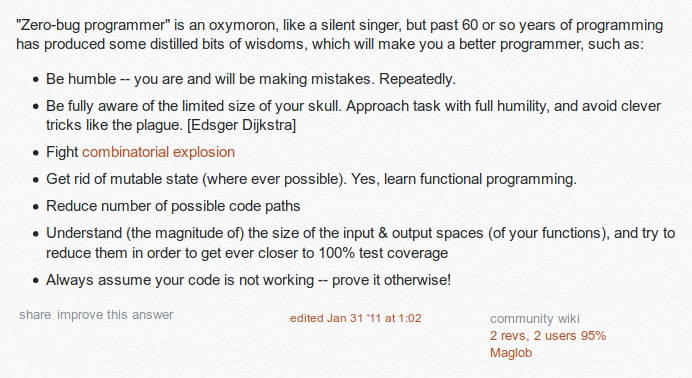
... Prove it otherwise ...
Can Existence be Truth?
Let's define a TYPE to be True if it has values, and False if it has no values.
A Type's inhabitence can also be unknown, and it's truth value is undecidable.
Let's choose to only work with types that are True.
... Prove it otherwise ...
Logic in the Types.
//In other words:
def true: Unit = () // not true: Boolean
def false: Nothing = ??? // not false: Boolean... and these ideas are shaping new foundations for mathematics ...
We can prove logical statements by constructing elements of types
def intToString: Int => String = _.toString
def times2: Int => Int = a => a * a
def always[A]: A => Option[A] = Some(_)Logic
Constructive Logic as types...
// Constructive Connectives
type False = Nothing
type And[A, B] = (A, B)
type Or[A, B] = Either[A, B]
type Implication[A, B] = A => B
Proofs, or code paths, like any good story, or program run have a beginning, a middle and an end:
What's a Proof?
-
Assumptions.
Our domain types. -
Statements in order.
Functions. -
The goal.
A value.
Let's write some proofs code.
Ingredients for Correctness
- It must carry out the functions that are required and do nothing else.
- It must continue to function as required for all possible inputs.
- There must be very strong evidence that these properties are true and the evidence for this must be independently verifiable.
... can constructivism be practical? ...
In terms of Computation
- Total Functions (e.g. don't throw exceptions)
- Referential Transparency (e.g. avoid side effects)
- Termination (e.g. avoid loops)
Total Functions
Expand the Output.
def decode[A](s: String): A
def decode[A](s: String): Either[Error, A]Excercises: http://bit.ly/cp-total-exercises
Total Functions
Restrict input values.
def squareRoot(a: Int): Int = ...
def squareRoot(a: UnsignedInt): UnisignedInt = ...Excercises: http://bit.ly/cp-total-exercises
Referential Transparency
Avoid mutation
var x = 5 = 3
val x = 5 = 3 // Exception
if (x = 1) // Oops
r = open("w")
r = open("y") // OopsExercises: http://bit.ly/cp-transparency-excercises
Referential Transparency
Decouple evaluation
def cpsSystemTime: () => Timestamp = ...
def systemTime: IO[Timestamp] = ...
systemTime()
doSomething()
sleep(1)
systemTime()
doSomethingElse()Exercises: http://bit.ly/cp-transparency-excercises
Termination
Avoid recursion
//hmmm: http://stainless.epfl.ch/doc/intro.html
def use[A](a: A): A = use(a)
def sum(l: List[Int]): Int = l.fold(0)(_ + _)Turing's Halting Problem ≃ Gödel's Incompleteness Theorems
Excercises: http://bit.ly/cp-termination-excercises
Termination
Avoid loops
def use[A](a: A): A = while (true) { ... }; a
val fib = 0 #:: fib.scanLeft(1)(_ + _)Excercises: http://bit.ly/cp-termination-excercises
Is it really that simple?
Yes.
But we want to build a giant system!
Category Theory is the study of composition.
Constructive programming is a family of of Proof calculi aligned with goal of productive software development.
State some initial propostions.
sealed trait Person
case class Teacher(name: String, students: List[Person])
extends Person
case class Student(name: String, teacher: Teacher)
extends Person
type Pay = Double
type Fee = Double
type Balance = DoubleProvide evidence for further statements.
def payCalc: Teacher => Pay = _.students.foldLeft(0.0){
case (pay, t:Teacher) => pay + 0.1 * payCalc(t)
case (pay, s:Student) => pay + 2.5
}
def feeCalc: Student => Fee = _ match {
case Student(_, t) => 1.10 * payCalc(t) / t.students.length
}
def feeBalance: Fee => Balance = identity
def payBalance: Pay => Balance = - _Quantify the
boundaries as necesary.
def findPerson(name: String):
Option[Either[Student, Teacher]] = ???Use category theory for composition.
def findPerson(name: String):
Option[Either[Student, Teacher]] = ???val names: List[String] = ???
val schoolBalance: Balance = names
.flatMap(findPerson)
.map(feeCalc.choose(payCalc))
.foldMap(feeBalance.choice(payBalance))
// res: Balance = 0.0Reference Material
- Constructive Programming Portal:
https://constructive.dev - Exercises:
http://bit.ly/cp-logic-exercises - Proposed solutions:
http://bit.ly/cp-logic-answers - These slides:
http://bit.ly/cp-logic-slides
Further Reading (References)
-
http://cheng.staff.shef.ac.uk/proofguide/proofguide.pdf
-
http://math.andrej.com/wp-content/uploads/2017/12/Spartan-Type-Theory.pdf
-
http://ecee.colorado.edu/ecen5533/fall11/reading/free.pdf
-
http://tesi.cab.unipd.it/56555/1/tesi_Mengato_def.pdf
-
http://www.lix.polytechnique.fr/~lengrand/Work/Teaching/MPRI/Notes.pdf
-
https://en.m.wikipedia.org/wiki/Curry%E2%80%93Howard_correspondence
-
https://www.youtube.com/watch?v=IOiZatlZtGU
-
http://math.andrej.com/2016/08/09/what-is-a-formal-proof/
-
https://github.com/Chymyst/curryhoward