Algorithmique: Les Arbres Rouges-Noirs

1. Arbres binaires de recherche

Un arbre binaire de recherche est un arbre binaire dans lequel chaque nœud possède une clé.

Chaque nœud du sous-arbre gauche a une clé inférieure ou égale à celle du nœud considéré, et chaque nœud du sous-arbre droit possède une clé supérieure à celle-ci.

Les nœuds que l'on ajoute deviennent des feuilles de l'arbre.

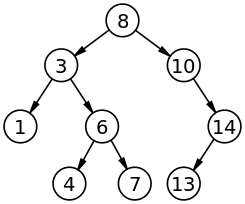
2. Arbres dégénérés

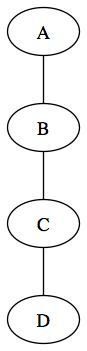
Que se passe t-il si l'arbre ressemble à l'image ci-dessous ?

On appelle ce type d'arbres des arbres dégénérés.

Un arbre dégénéré (appelé aussi filiforme) est un arbre dont les noeuds ne possèdent qu'un et un seul fils. Cet arbre est donc tout simplement une liste chaînée. Ce type d'arbre est donc à éviter, puisqu'il n'apportera aucun avantage par rapport à une liste chaînée simple !

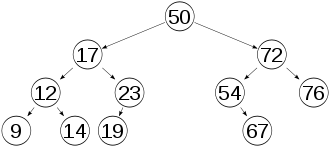
3. Arbres équilibrés

Un arbre équilibré est un arbre qui maintient une profondeur équilibrée entre ses branches. Cela a l'avantage que le nombre de pas pour accéder à la donnée d'une clé est en moyenne minimisé.

Le but est d'éviter de construire des arbres dits dégénérés dans lesquels certains chemins d'accès aux données sont d'une longueur disproportionnée. Utiliser un arbre équilibré permet d'avoir un temps de recherche de complexité logarithmique dans le pire des cas au lieu d'une complexité linéaire, comme c'est parfois le cas pour des arbres dégénérés.

4. Equilibre des arbres binaires de recherche

Les arbres binaires de recherche présentent des cas de dégénérescence les rendant trop lents dans beaucoup de cas.

Une amélioration consiste à ajouter à leurs spécifications un critère d'équilibre imposant des restrictions sur le sous-arbre droit (SAD) et gauche (SAG).

5. A.V-L

Dans un arbre AVL, la hauteur du SAG et celle du SAD diffèrent au plus de un. Le nombre maximal de réorganisations est en O(log2 N), c'est-à-dire la hauteur de l'arbre.

L'insertion, la recherche et la suppression sont en O(log2 N).

6. Arbres Rouges Noirs : intro

Même si les arbres A.V-L et les B-arbres possèdent des propriétés intéressantes, ils ont aussi des désavantages.

Les arbres A.V-L peuvent nécessiter plusieurs rotations après une suppression; les B-arbres quant à eux peuvent nécessiter plusieurs opérations de regroupements ou d'éclatements après une insertion ou un suppression...

On introduit donc une nouvelle structure de donnée pour représenter les arbres binaires équilibrés. Les arbres rouges noirs.

7. Arbres Rouges Noirs : Définition

Un arbre rouge et noir est un arbre binaire de recherche où chaque nœud est de couleur rouge ou noire de telle sorte que :

Les noeuds sont soit rouges, soit noirs.
La racine et les feuilles sont noires
Les enfants d'un nœud rouge sont noirs.
Le chemin de la racine à n'importe quelle feuille contient le même nombre de nœuds noirs. On peut appeler ce nombre de nœuds noirs la hauteur noire

8. Arbres Rouges Noirs : Exemple

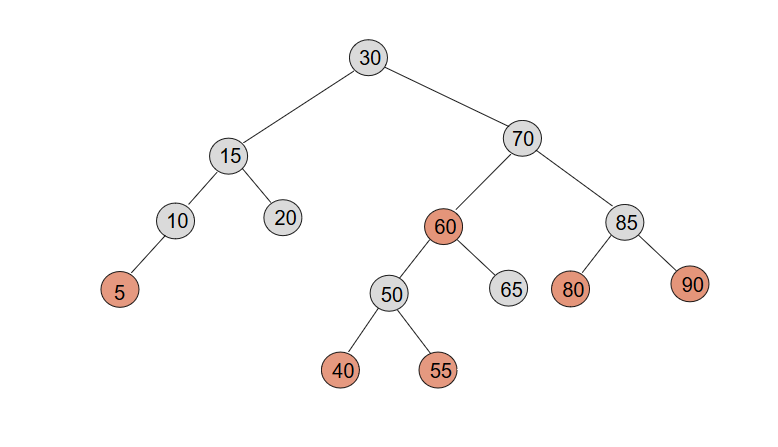
Les feuilles sont toujours de couleur noires et n'influent pas sur les propriétés de l'arbre. Donc on ne les représente pas.

9. Arbres Rouges Noirs : contre-exemple

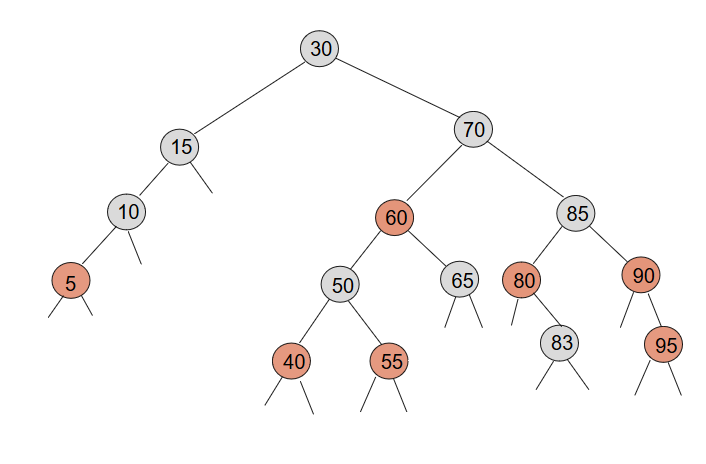
9. Arbres Rouges Noirs : contre-exemple (2)

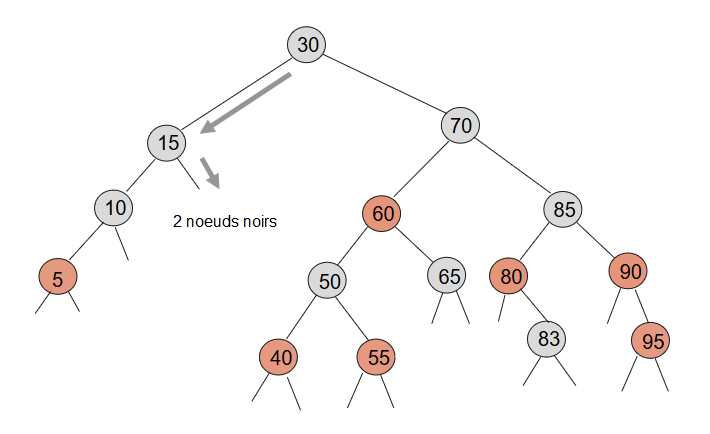
9. Arbres Rouges Noirs : contre-exemple (3)

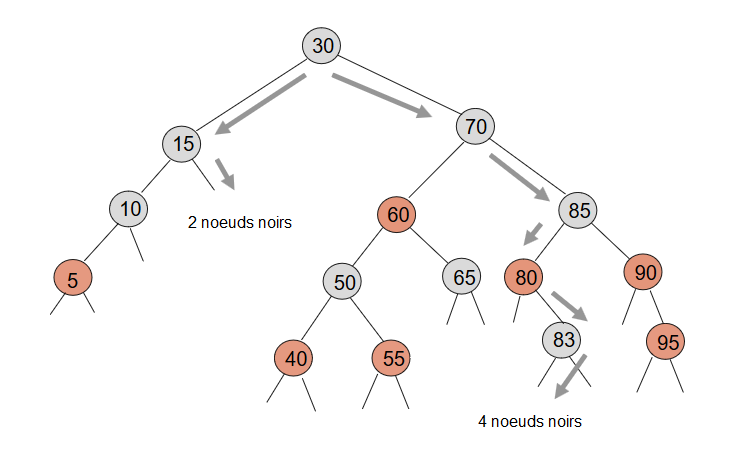
9. Arbres Rouges Noirs : contre-exemple (4)

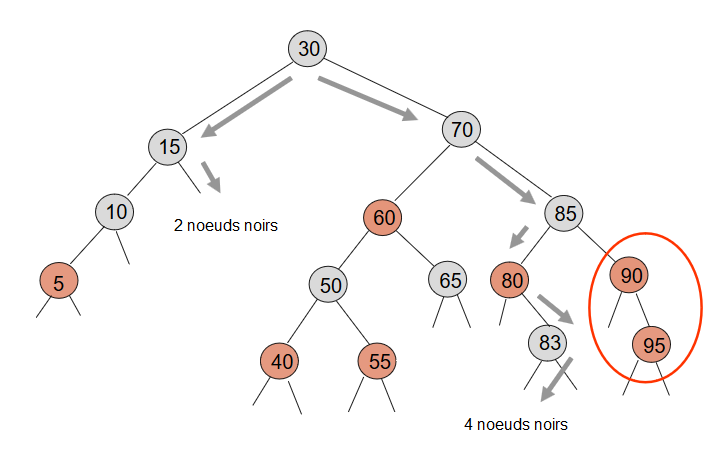
Remarques

Un arbre rouge-noir ayant n noeuds interne a une hauteur au plus égale à 2lg(n+1).

La conséquence immédiate c'est que les opérations: Rechercher, Minimum, Maximum, Prédécesseur, Successeur peuvent être implémentées en O(lg(n)), vu qu'elles dépendent de la hauteur de l'arbre...

Le plus long chemin de l'arbre (branche qui va de la racine à la feuille la plus éloignée) ne peut pas être plus deux fois plus long que le plus court.

Cela nous garantit d'avoir un arbre à peu près équilibré.

10. Opérations

Les opérations classiques sur les arbres sont: l'insertion, la suppression, la recherche.

Nous verrons plus tard qu'à l'instar de la recherche, la suppression et l'insertion se font en O(lg(n)); cependant l'insertion et la suppression nécessitent qu'on effectue des manipulations pour préserver l'arbre en tant que arbre rouge-noir...

Ces manipulations ce sont les rotations.

11. Rotations

Les rotations modifient la structure de l'arbre en arrangeant les sous-arbres.

Le but c'est de baisser la hauteur de certains sous-arbres:

Pour avoir un arbre équilibré (avec les A-V.L)
Pour maintenir la structure de l'arbre ( avec les arbres rouges-noirs)

12. Rotations (2)

Les rotations n'affectent pas l'ordre des éléments. On est donc certains que l'arbre restera un arbre binaire de recherche après elles.

Les arbres rouges-noirs sont relativement équilibrés et ce, de manière naturelle (grâce à leurs propriétés).

13. Rotations gauche

On fait une rotation gauche autour du noeud 5 (le bleu).

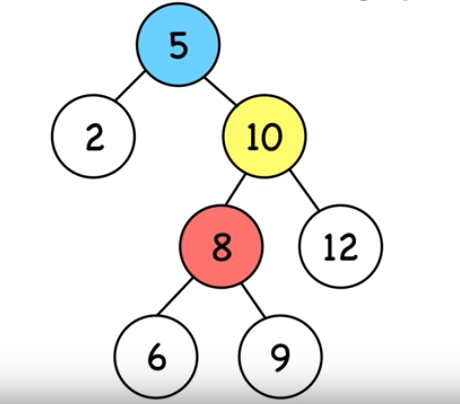
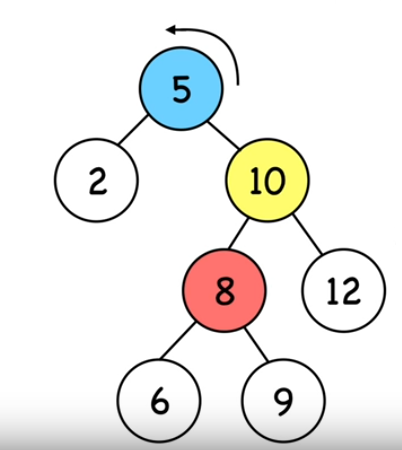
13. Rotations gauche (2)

Le noeud qui était enfant du noeud 5 devient son parent.

Nous appellerons le noeud qui passe de enfant à parent (10) le noeud "promu", tandis que celui qui passe de parent à enfant (5) est le noeud "déchu".

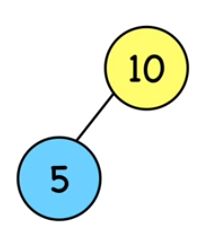
13. Rotations gauche (3)

Dans la rotation gauche le noeud promu greffe son sous-arbre gauche au noeud déchu. Par exemple, le noeud (8) était le fils gauche du noeud (10), il est à présent fils droit du noeud (5).

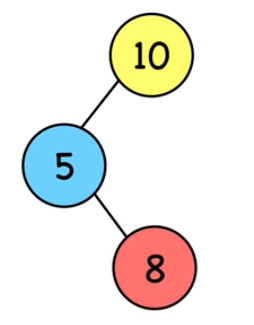
13. Rotations gauche (3)

Le noeud promu greffe son sous-arbre gauche au noeud déchu. Par conséquent le noeud (8) est greffé avec tout ses descendants (enfants, petits-enfants, etc...).

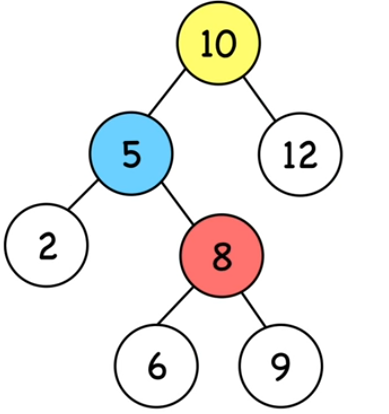
13. Rotations droite

Cette fois faisons une rotation droite autour du noeud 10.

13. Rotations droite (2)

Cette fois le noeud promu transmet son sous-arbre droit au noeud déchu. C'est pourquoi le noeud (8) devient le fils gauche du noeud (10).

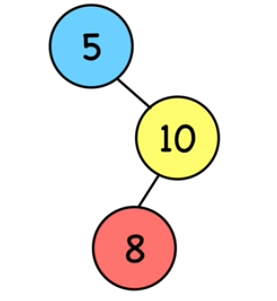
13. Rotations droite (3)

Le principe est le miroir du principe précédent. Le noeud parent (10) devient le noeud enfant et le noeud enfant (5) devient le noeud parent.

13. Rotations droite (4)

Lorsque le noeud (8) est greffé au noeud (10), il est greffé avec tous ces descendants (enfants, petits-enfants, etc...).

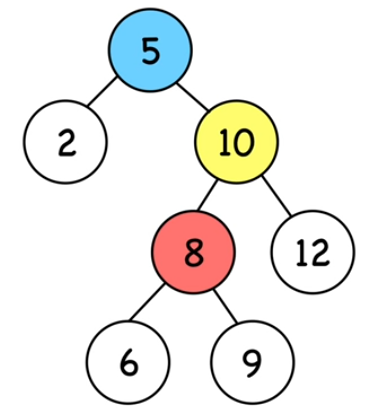
14. Arbres Rouges Noirs : Rappel

Un arbre rouge et noir est un arbre binaire de recherche qui vérifie :

Les noeuds sont soit rouges, soit noirs.
La racine et les feuilles sont noires
Les enfants d'un nœud rouge sont noirs.
Le chemin de la racine à n'importe quelle feuille contient le même nombre de nœuds noirs. On peut appeler ce nombre de nœuds noirs la hauteur noire

15. Arbres rouges noirs: insertion

Voici les principes d'insertion dans un arbre rouge noir:

Un noeud inséré est toujours une feuille.
On insère toujours en couleur rouge.
Si le père est un noeud noir, pas de problème.
Si le père est un noeud rouge, on viole la condition 3. Dans ce cas, on ajuste l'équilibre de l'arbre avec des changements de couleur et de rotations.

16. Arbres rouges noirs: insertion (2)

Etant donné un noeud z inséré dans un arbre rouge noir, il y'a quatre scénarios possibles :

Cas 0: z est inséré en racine.
Cas 1: L'oncle de z est rouge.
Cas 2a: L'oncle de z est noir (mode triangle).
Cas 2b: L'oncle de z est noir (mode ligne).

17. Insertion cas 0: Racine

Ce cas est simple. On insère le noeud on le colore en noir.

19. Insertion cas 1: Oncle rouge

Si l'oncle du noeud à insérer est rouge il y'a violation de la règle 3. Dans ce cas on colore son parent et son oncle en noir.

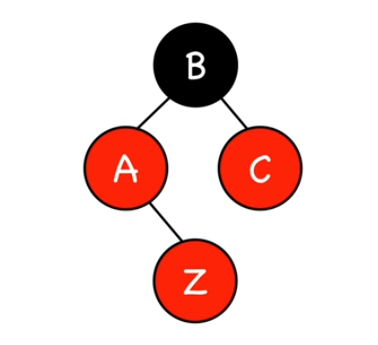
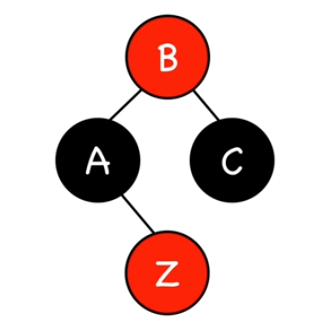
Il faut voir l'arbre de droite comme un sous-arbre. Il ne faut donc pas s'inquiéter qu'il soit de couleur rouge. B n'est pas forcément une racine...

20. Insertion cas 2a: Oncle noir

Si l'oncle du noeud à insérer est noir, il y'a deux cas possibles. Le premier a lieu quand le noeud à insérer (Z) , son parent (A) et son grand-parent (B) forment un triangle.

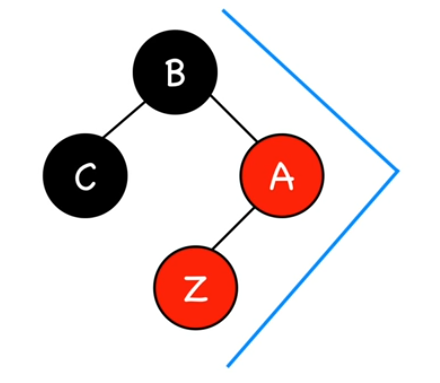
Le noeud (Z) est fils gauche de (A) tandis que le noeud (A) est fils droit de (B). Le triangle est donc présent.

20. Insertion cas 2a: Oncle noir (2)

Le raisonnement est le même en cas de situation symétrique.

20. Insertion cas 2a: Oncle noir (3)

On fait une rotation autour du parent de (Z).

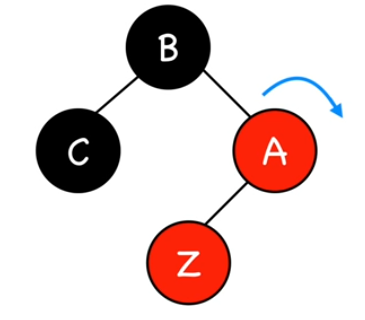
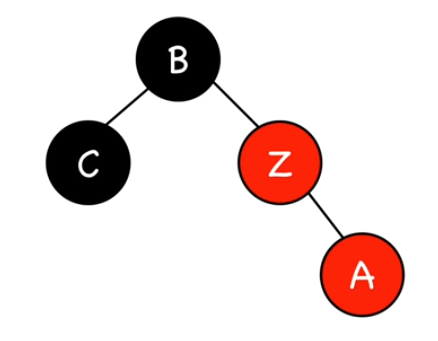
C'est pas encore fini mais la configuration obtenue nous rapproche du cas suivant...

21. Insertion cas 2b: Oncle noir (2)

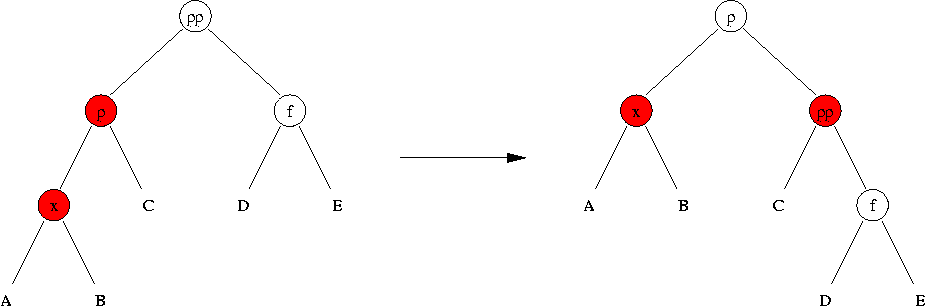
Si l'oncle du noeud (x) à insérer est noir, il y'a deux cas possibles. Le deuxième a lieu quand le noeud à insérer (x) , son parent (p) et son grand-parent (pp) forment une ligne.

Dans ce cas, on fait une rotation autour du grand parent et on recolore le parent en noir et les deux enfants en rouge.

22. Récapitulatif

Si on veut insérer un nouvel élément dans un arbre rouge noir, il y' a plusieurs cas de figures:

Si on veut insérer en racine, on insère puis on colore en noir.
Si on veut insérer un élément et que son oncle est rouge. On recolore son parent et son oncle en noir et le grand-parent en rouge.
Si on veut insérer un élément et que son oncle est noir:
- Soit l'élément forme un triangle avec son parent et son grand-parent, dans ce cas on fait une rotation autour du parent, ce qui nous amène au cas en-dessous...
- Soit l'élément forme une ligne avec son parent et son grand-parent, dans ce cas rotation autour du grand-parent , coloration du parent en noir, coloration des deux fils en rouge.
- Ces rotations lorsqu'elles sont cumulées s'apparentent à une rotation double...

23. Rotation double

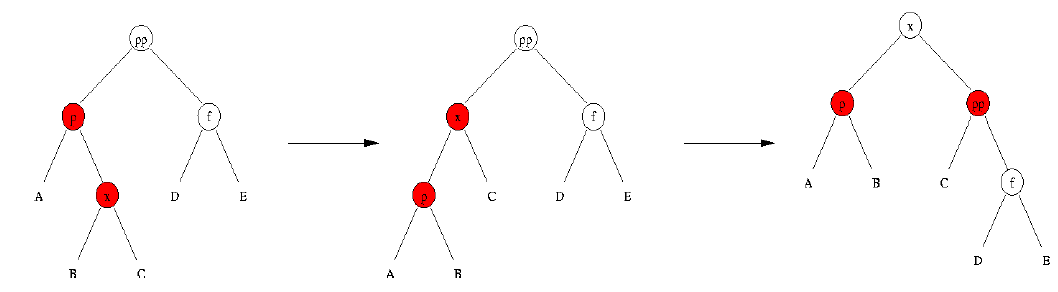
Si l'élément que l'on cherche à insérer, a un oncle noir et qu'il est dans une "configuration de triangle" avec son parent et son grand-parent, on fait d'abord une rotation autour du parent puis une rotation en sens inverse autour du grand-parent.

Cela revient à faire une rotation double (gauche-droite dans l'exemple, car gauche d' abord puis droite ensuite)

23. Rotation double (2)

Le cas symétrique est par ailleurs tout autant valable. On aurait fait une rotation droite autour du parent et une rotation gauche autour du grand-parent, ce qui aurait donné une rotation droite-gauche...

En fait le principe de la rotation double est facile. Le noeud qui est le plus bas est "promu" au plus haut niveau. Celui qui est à sa gauche se déporte à gauche. Celui qui est à a droite se déporte à droite.

Le noeud promu lègue son sous-arbre gauche au noeud qui est à sa gauche et lègue son sous-arbre droit au noeud qui est à sa droite.

23. Rotation double : exemple

Le noeud promu (8) lègue son sous-arbre gauche au noeud qui est à sa gauche et lègue son sous-arbre droit au noeud qui est à sa droite. Si (8) avait eu des enfants son fils gauche serait allé à (5), son fils droit serait allé à (10).

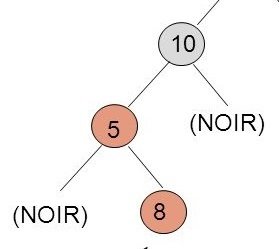
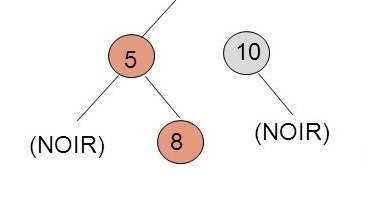
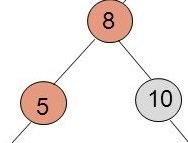
Le noeud qui est le plus bas (8) est promu tout en haut. Celui qui est à sa gauche (5) se déporte à gauche. Celui qui est à a droite (10) se déporte à droite.

24. En résumé

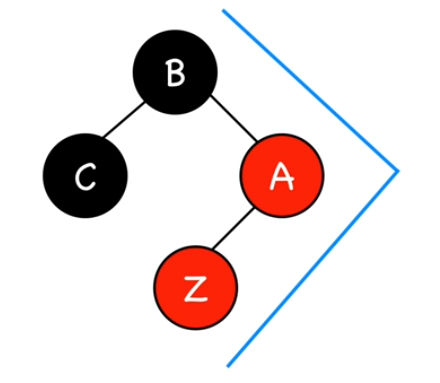
En résumé, si on tombe dans le cas 2b, à savoir qu'on veut insérer un noeud z dont l'oncle est un noeud noir...

Si on tombe sur une configuration triangle, c'est-à-dire que le noeud z, son père et son grand-père forment un triangle, on peut soit:

Faire une rotation simple autour du parent (pour retrouver une configuration ligne). Puis une rotation simple de sens contraire autour du grand-parent et recolorer.
Faire une rotation double et recolorer.

Les deux choix reviennent au même.

24. Stratégie Top - Down

Pour éviter d'enchaîner les rotations on peut choisir de pratiquer une stratégie "top-down".

L'idée c'est de garantir que lorsqu'on arrive à l'endroit où on veut insérer un nouveau noeud, on ne tombe pas sur un noeud rouge (car c'est là que le problèmes commencent en général, par exemple quand vous ajoutez un noeud rouge après un autre noeud rouge).

Si on tombe sur un noeud noir, tout ce qu'on a à faire d'est d'insérer notre noeud, aucune propriété n'est mise en danger.

24. Stratégie Top - Down (2)

En descendant depuis la racine de l'arbre, lorsqu'on tombe sur un noeud qui a deux fils rouge, on colorie ses deux fils en noir et le père en rouge.

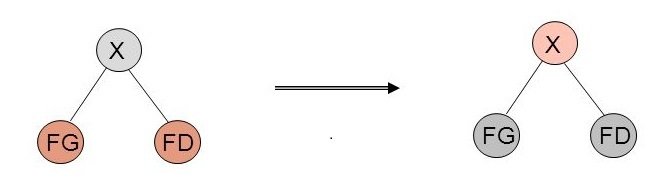
Ainsi, le nombre de noeuds noirs dans un chemin restent inchangés.

Ceci dit, cela peut poser problème si le parent de x est rouge dans ce cas ça nous oblige à une rotation.

Il faut aussi s'assurer que la racine reste noire.

25. Exemple détaillé

Illustrons l'insertion dans un arbre rouge noir à travers un exemple concret. On désire insérer la suite de noeuds suivants (dans cet ordre):

10, 85, 15, 70, 20, 60, 30, 50, 65, 80, 90, 40, 5, 55

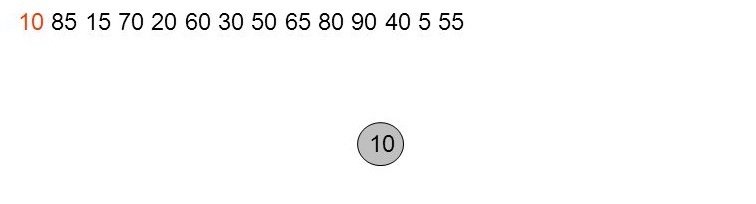
On est dans le cas 0. Insertion en racine, dans ce cas on colore en noir.

25. Exemple détaillé (2)

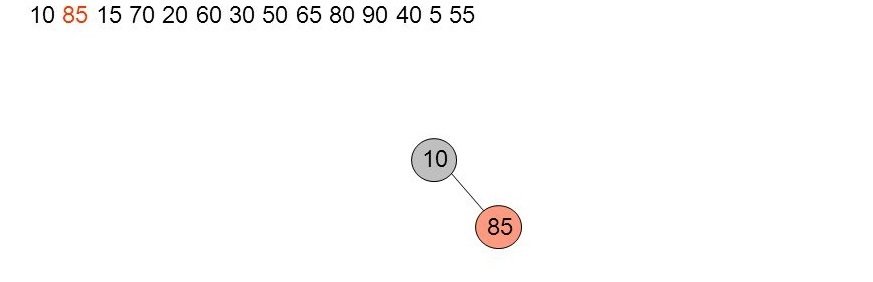
On insère 85 à droite du noeud 10 (on rappelle que les arbres rouges noirs sont des arbres binaires de recherche). Pas de problèmes particuliers.

25. Exemple détaillé (3)

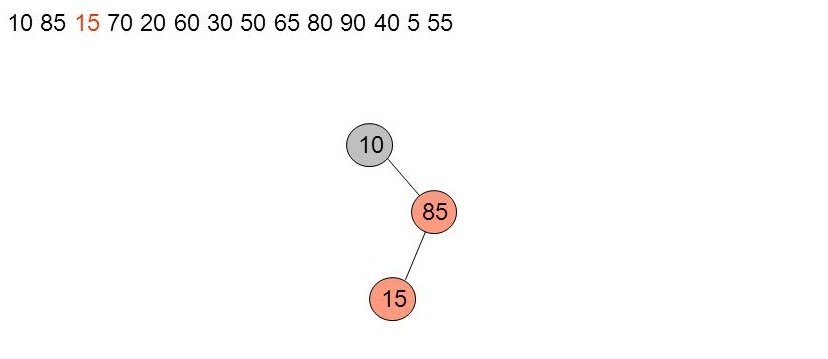
Insertion de 15

Ici il y'a violation de la règle (3) qui dit que les noeuds rouges ne peuvent générer que des noeuds noirs. Il faut corriger.

25. Exemple détaillé (4)

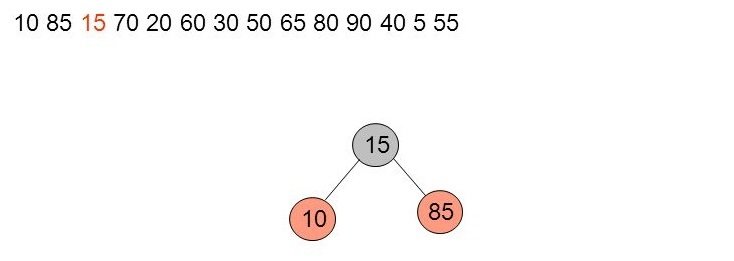
On était dans la cas oncle noir avec structure en triangle entre le fils, le père et le grand-père (cas 2b). Nous rappelons que les feuilles sont toujours de couleur noires et ne sont pas représentées.

Pour corriger on fait une rotation double et on recolore le parent en noir tandis que les enfants sont en rouge.

25. Exemple détaillé (5)

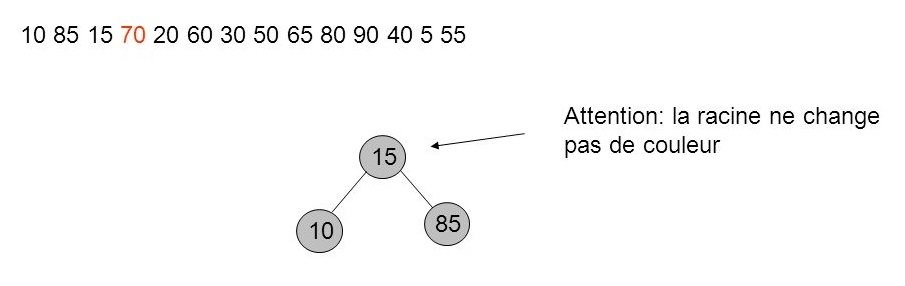
On applique la stratégie top-down à l'arbre précédent pour déporter les noeuds noirs vers le bas.
On recolore la racine en noir pour respecter la règle 2.

25. Exemple détaillé (6)

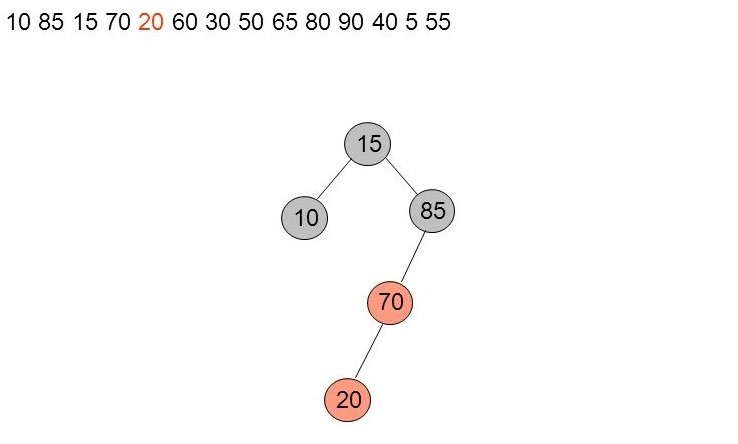
Insertion de 20

Il y' a violation de la règle 3. On est dans le cas 2a (oncle noir, ici une feuille non visible) et structure en ligne entre le nœud inséré, son père et son grand-père. On fait donc une rotation autour du grand-père.

25. Exemple détaillé (7)

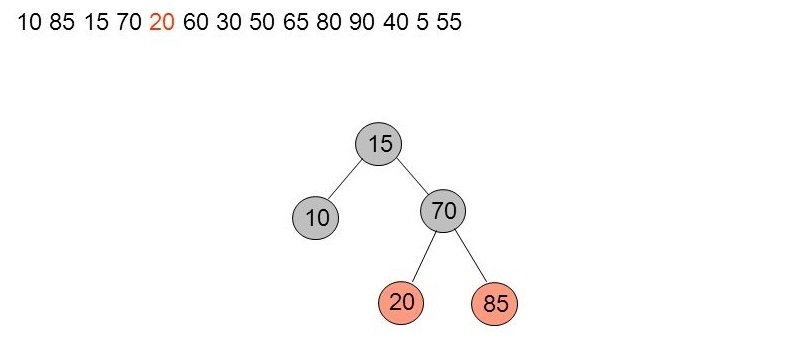
Rotation simple autour du grand-père (85)

25. Exemple détaillé (8)

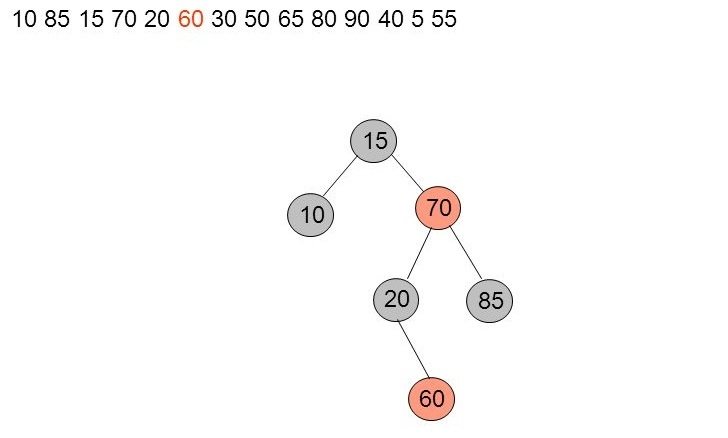
Insertion de 60

Pas de problème.

25. Exemple détaillé (9)

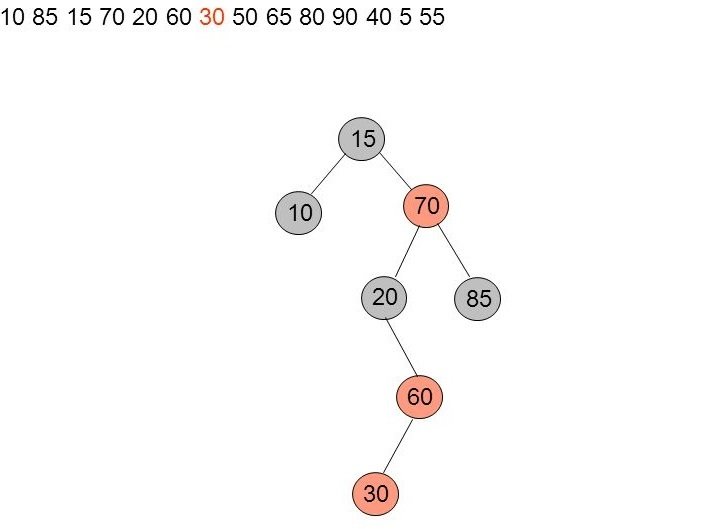
Insertion de 30

Il y'a violation de la règle 3. La configuration est en triangle (30,60,20) c'est le cas 2b. On fait une rotation double et on recolore le parent en noir et les deux enfants en rouge.

25. Exemple détaillé (10)

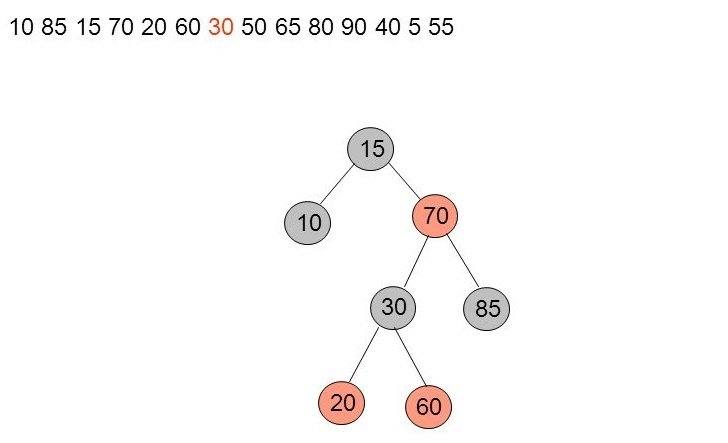
Rotation double et recoloration

Le nœud le plus haut est coloré en noir, ses deux enfants en rouge.

25. Exemple détaillé (11)

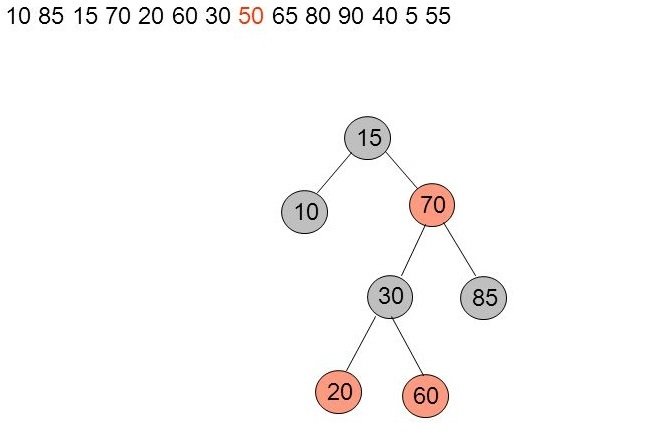
Insertion de 50

Comme le nœud 30 se trouve dans le chemin d'insertion du nouveau nœud (50), on peut lui appliquer au passage une stratégie top-down.

25. Exemple détaillé (12)

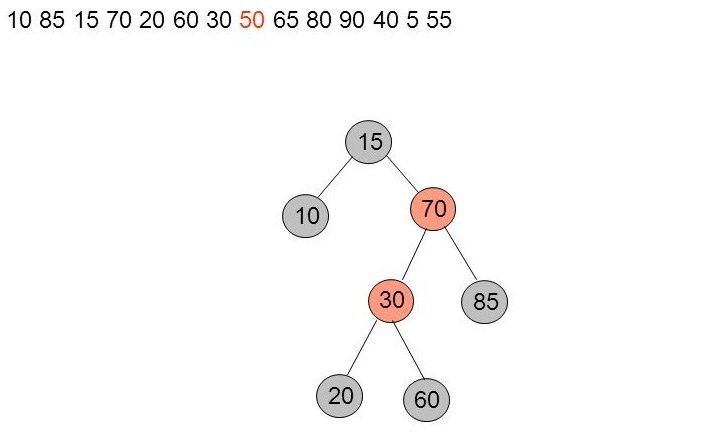
Insertion de 50 - stratégie top-down

On inverse les colorations entre le parent (30) et les enfants (20, 60) en déportant les noirs vers le bas. Cela nous permettra d'ajouter tranquillement le 50...

25. Exemple détaillé (13)

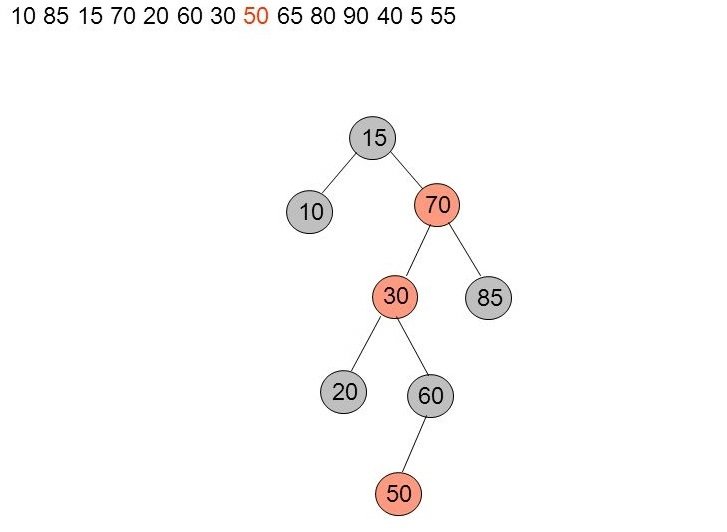
Insertion de 50

Notre stratégie a crée une violation de la règle 3. On est dans une configuration triangle (30,70,15) avec oncle noir (cas 2b). On fait donc une rotation double + recoloration.

25. Exemple détaillé (14)

Rotation double: principe

Le noeud promu (30) est coloré en noir et ses deux enfants en rouge. De plus, le noeud promu cède son sous-arbre gauche à sa gauche et son sous-arbre droit à sa droite.

25. Exemple détaillé (15)

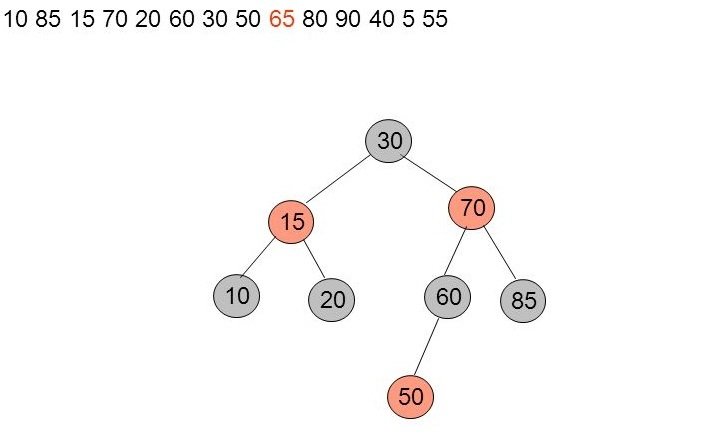
Insertion de 65 - Stratégie top-down

Sur le chemin pour aller insérer 65, on passe par la racine sur laquelle on applique une stratégie top-down. Elle est donc colorée en rouge et ses deux enfants en noirs.

Puis, on recolore la racine en noir pour respecter la règle 2.

25. Exemple détaillé (16)

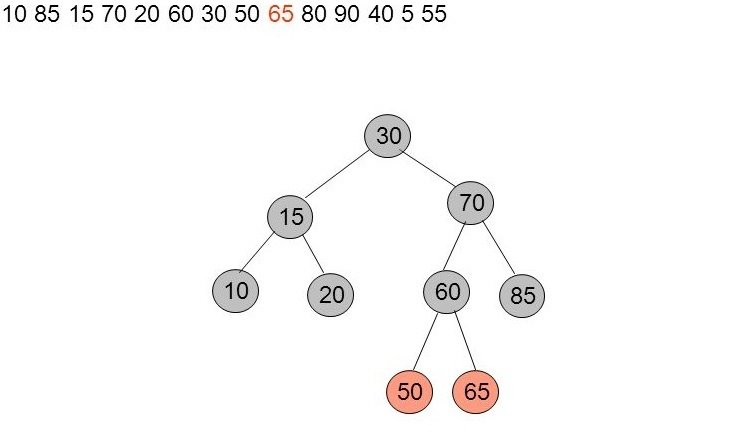
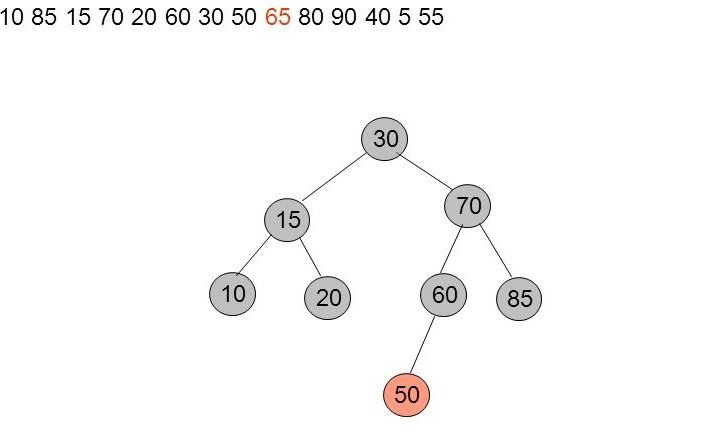
Insertion de 65

L'insertion de 65 ne pose pas de problèmes.

25. Exemple détaillé (17)

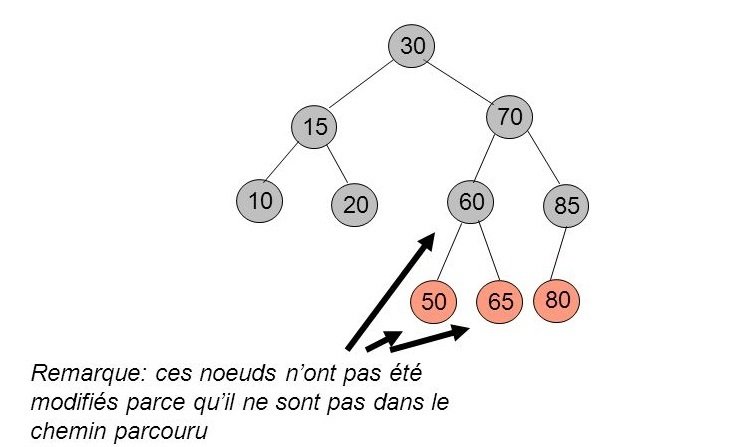
Insertion de 80 - limites de la stratégie top-down

L'insertion de 80 ne pose pas de problèmes. Au passage, vous constatez qu'on a pas appliqué de stratégie top-down sur 60, 50 et 65. La stratégie top-down ne peut s'appliquer que sur les noeuds présents dans le parcours d'insertion. Et pour insérer 80 on ne passe pas par 60 (mais par 70 et 85).

25. Exemple détaillé (19)

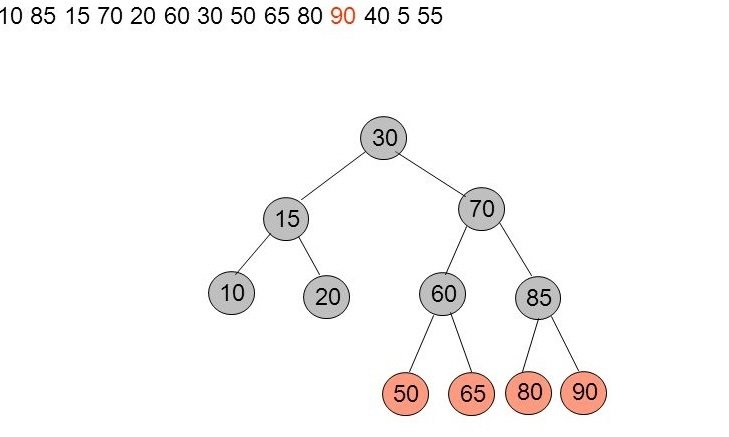
Insertion de 90

L'insertion de 90 ne pose pas de problèmes.

25. Exemple détaillé (20)

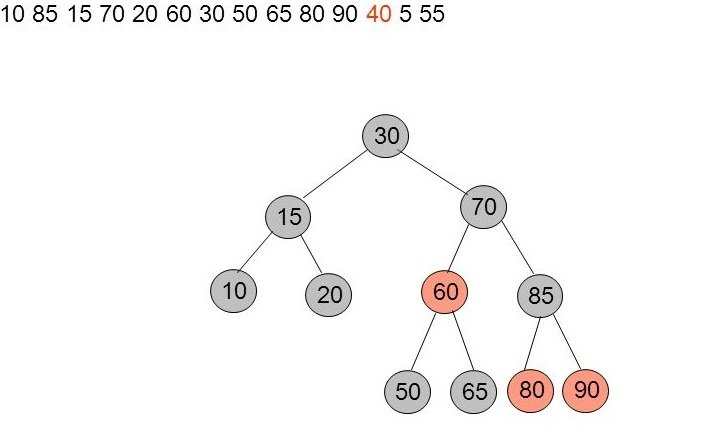
Insertion de 40 - stratégie top-down

Le chemin d'insertion de 40 passe par (30,70,60 et 50). Au passage, on constate alors que 60 est éligible pour une stratégie top-down (père noir, enfants rouges). On applique donc cette stratégie en inversant sa coloration et celle de ses fils (il devient rouge, ils deviennent noirs).

25. Exemple détaillé (21)

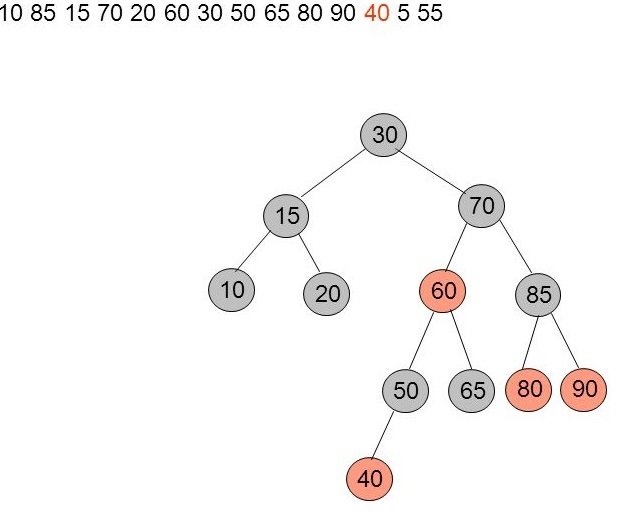
Insertion de 40

Le noeud 40 peut ensuite être inséré sans soucis.

25. Exemple détaillé (22)

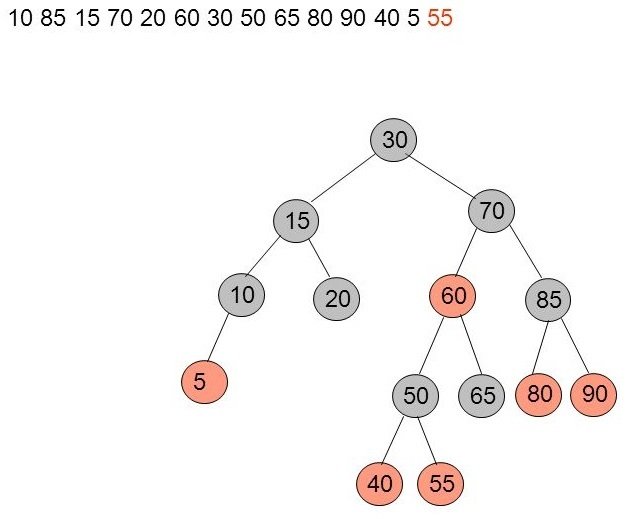
Insertion de 55

L'insertion du noeud 55 ne pose pas de problèmes. FIN