Algorithmique: Les tables de hachage
II
Table de Hachage
Soit U l’ensemble des valeurs possibles correspondant à un univers de clés et soit K, un sous ensemble de U, représentant l’ensemble des valeurs effectivement utilisées.
Une table de hachage est une table (tableau) dont :
- Les éléments sont placés dans des cases (alvéoles).
- Le choix de case est effectué en appliquant une fonction sur une valeur : c'est la fonction de hachage.
Fonction de hachage, valeur de hachage
Une fonction de hachage h établit une relation entre U (univers des valeurs) et un sous-ensemble fini :
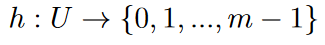
h(k) est appelée valeur de hachage de k.
- On place notre élément dans la case h(k).
- Bonne nouvelle: on doit gérer m valeurs au lieu de |U|.
- Mauvaise nouvelle: Plusieurs valeurs peuvent avoir la même valeur de hachage, c'est la collision.
Fonction de hachage uniforme
Si chaque élément a la même chance d'être haché dans n'importe laquelle des alvéoles, indépendamment des éléments précédents, la fonction de hachage est dite uniforme.
Collision
Il y'a collision si deux valeurs (ou plus) ont la même valeur de hachage, c'est-à-dire :
h(k1) = h(k2)
Exemple
Prenons une table de capacité 10, pour y stocker des éléments déterminés par des clés à valeurs entières.
La fonction de hachage est h(x) =x mod 10 + 1. Si les valeurs des clés à introduire dans la table sont 12, 17, 29 et 33 on aura la configuration suivante :

Exemple
Prenons une table de capacité 10, pour y stocker des éléments déterminés par des clés à valeurs entières.
La fonction de hachage est h(x) =x mod 10 + 1. Si les valeurs des clés à introduire dans la table sont 12, 17, 29 et 33 on aura la configuration suivante :

Que se passerait-il si on voulait introduire la valeur 42 ?
Exemple
Prenons une table de capacité 10, pour y stocker des éléments déterminés par des clés à valeurs entières.
La fonction de hachage est h(x) =x mod 10 + 1. Si les valeurs des clés à introduire dans la table sont 12, 17, 29 et 33 on aura la configuration suivante :

Que se passerait-il si on voulait introduire la valeur 42 ?
Elle devrait occuper la même case que 12... collision !
Suite
Pour résoudre les collisions on envisage deux solutions:
- Le chaînage (méthode indirecte)
- Le calcul ou l'adressage ouvert (méthode directe)
Le chaînage
Résolution des collisions par chaînage
Avec cette technique on place dans une liste tous les éléments ayant la même valeur de hachage.
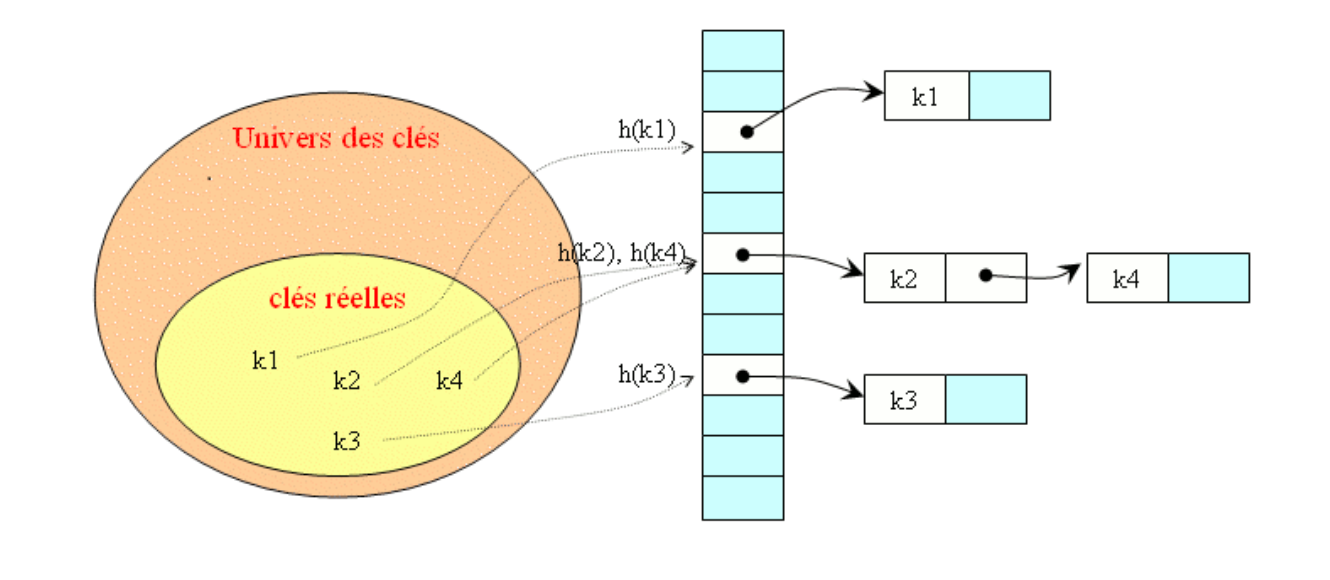
Le chaînage (2)
Pour rechercher un élément, il suffit de parcourir la liste dont l’accès se trouve dans la case d’indice h(x). L’avantage c'est que c'est plus facile à programmer.
Il n’y a pas de limitation (théorique) du nombre de clés. Toutefois, il faut veiller à prendre un tableau assez grand pour que la taille des listes reste réduite, le but étant de minimiser les parcours.
Exemple
En reprenant la fonction de hachage h(x) = x mod 10 + 1
Supposons qu'on introduise les valeurs 12, 17, 29, 33, 42 et 39.
On obtiendra le tableau suivant (les nouveaux ajouts se font en début de liste).

Différents types de chaînages
Dans les méthodes de résolution des collisions par chaînage, les éléments en collision sont chaînés entre eux.
- Ils peuvent être reliés à l'extérieur du tableau (hachage avec chaînage séparé).
- Ils peuvent être dans une zone de débordement (hachage coalescent) .
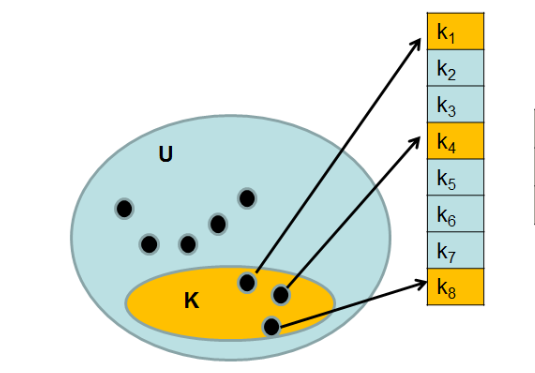
Hachage avec chaînage séparé
Comme nous l'avions dit, cette méthode chaîne les éléments entre eux à l'extérieur du tableau de hachage.
Pour les valeurs d'exemple suivantes :

Hachage avec chaînage séparé (2)
Et si les éléments en collision devenaient si nombreux qu'ils constituent une liste classique ? Y rechercher un élément aurait une complexité en O(n) et on perdrait tous les avantages des tables de hachage...
Si la fonction de répartition est uniforme et adaptée (notre postulat de départ) à la collection de données, le nombre de collision ne devrait pas atteindre un nombre trop élevé.
En terme de recherche (même séquentielle) c'est tout à fait "tolérable/acceptable".
Chaînage séparé et opérations (1)
Recherche
La recherche est simple à implémenter, il suffit pour l'élément de déterminer sa valeur de hachage. En cas de collision, on compare chaque élément de la liste des éléments en collision à notre valeur pour déterminer si la valeur qu'on cherche existe ou non.
Chaînage séparé et opérations (2)
Ajout
Pour l'ajout, il y a deux possibilités :
- Recherche d'appartenance de l'élément à ajouter, et s'il n'existe pas, ajout de celui-ci en fin de liste de collision (nous y sommes déjà après la recherche). L'intérêt est de maintenir des listes courtes.
- Ajout en première place de la liste de collision. L'avantage est qu'il n'y a pas de recherche préalable, donc gain de temps. L'inconvénient est de rallonger les listes de collision (doublons éventuels).
Chaînage séparé et opérations (3)
Suppression
Comme pour l'ajout, il y a deux possibilités dont le choix dépend de celle choisie pour l'ajout :
- Recherche de l'élément à supprimer et s'il existe, suppression.
- Recherche de toutes les occurrences possibles de l'élément à supprimer et, le cas échéant, suppression. Le principal inconvénient est de devoir systématiquement parcourir toute la liste de collision.
Hachage coalescent
Si l'allocation dynamique de la mémoire n'est pas possible, il est alors nécessaire de chaîner les éléments entre eux à l'intérieur du tableau de hachage.
Chaque indice référence deux champs : un élément et un lien (généralement entier) représentant l'indice du tableau où se trouve l'éventuel élément en collision primaire avec celui-ci.
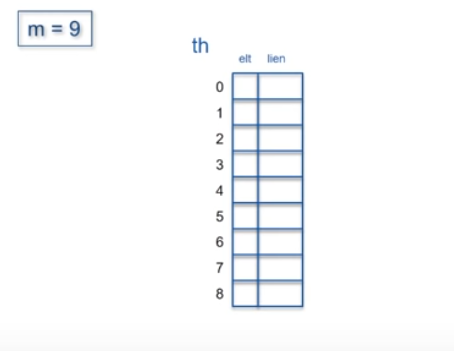
Hachage coalescent
Le principe est de séparer le tableau de hachage (de taille m) en deux zones :
- une zone de hachage primaire de p éléments,
- une zone de réserve de r éléments permettant de gérer les collisions.
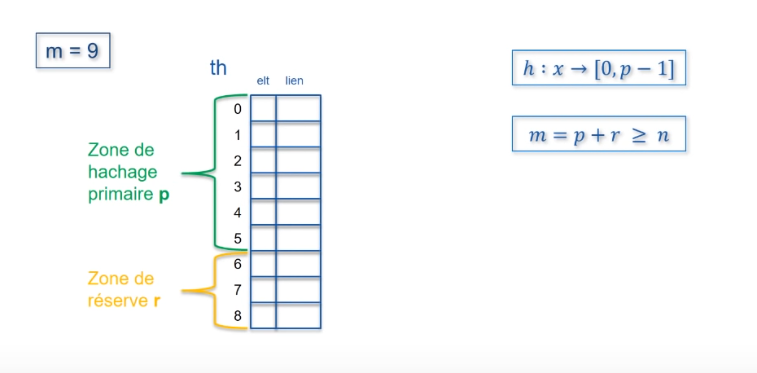
Hachage coalescent
Les contraintes sont d'avoir m=p+r supérieur ou égal au nombre d'éléments de la collection à "hacher" et un élément de lien, pour chaque valeur d'indice à l'intérieur du tableau de hachage.
Lorsqu'un élément est à placer et que sa valeur de hachage primaire atteint une case vide de la zone principale, il est placé là, sinon, il est placé dans la zone de réserve et le lien de collision est mis à jour.
Remarque : La zone de réserve est toujours utilisée en ordre décroissant d'indices (de bas en haut).
Hachage coalescent: exemple
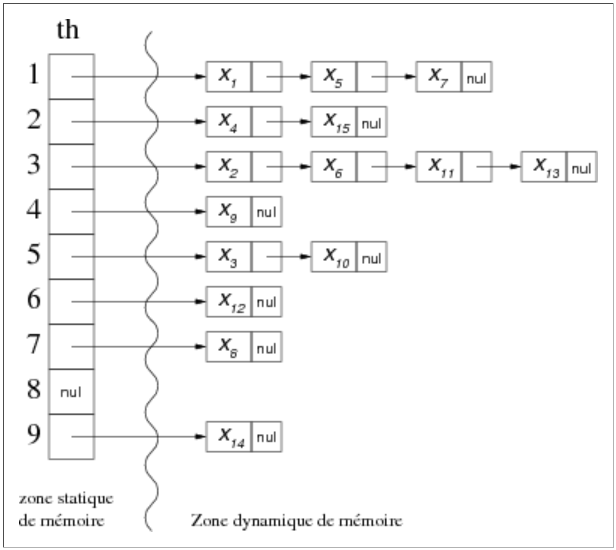
Avec p=6 et r=3, pour les valeurs d'exemple suivantes :

Nous aurions le tableau th suivant :
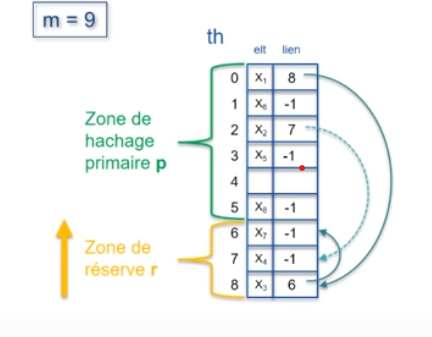
Hachage coalescent: exemple (2)
Comme nous pouvons le constater, la difficulté réside dans le choix de la taille de la réserve.
Sur l'exemple précédent, si nous voulions ajouter un élément dont la valeur de hachage primaire est 0, 1, 2, 3, 4 ou 5, il serait en collision avec un autre élément déjà présent dans le tableau et nous serions dans l'impossibilité de lui trouver une place dans la mesure où la réserve est déjà pleine.
Hachage coalescent: exemple (3)
Le problème est le suivant :
- Si la réserve est trop petite, elle se remplit trop vite et l'utilisation du tableau est incomplète,
- Si la réserve est trop grande, l'effet de dispersion est perdu et une extrapolation donnerait une liste chaînée (ce qui ne présente aucun intérêt).
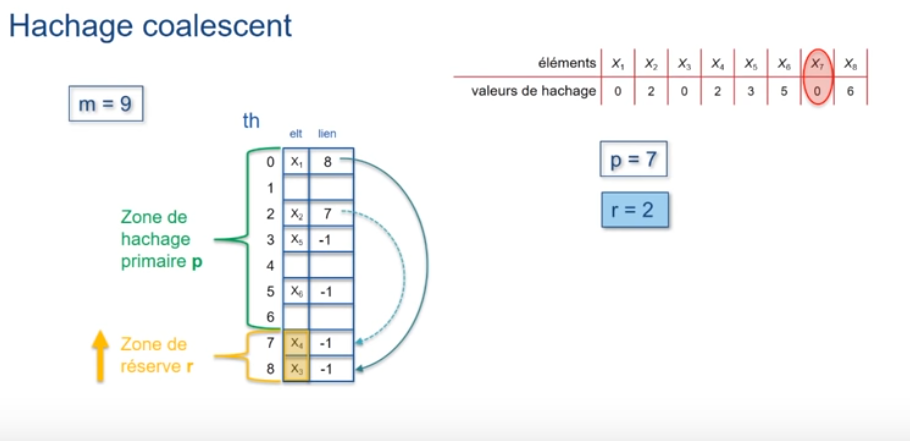
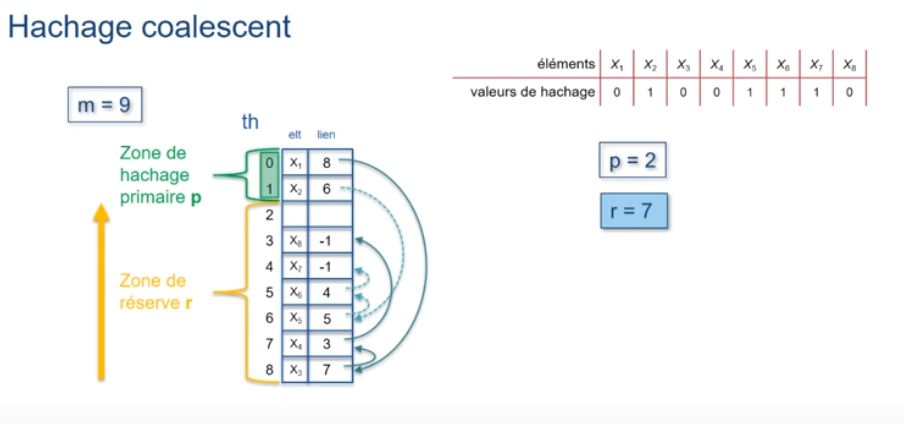
Hachage coalescent: exemple (4)
Dans ce cas, une solution est de fusionner la zone de hachage primaire p et la zone de réserve r sur toute la longueur de m.
On remplit p en respectant la valeur de hachage.
On remplit r en décroissant à partir de l'indice m-1 (si collision).
L'inconvénient, c'est que cela crée des collisions qui ne sont pas dues à la coïncidence des valeurs de hachage primaire. On les appelle des collisions secondaires.
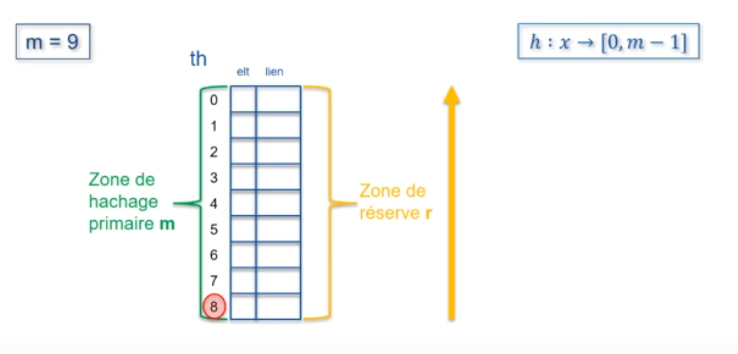
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :

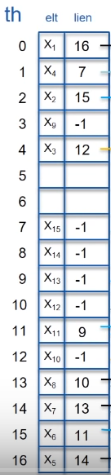
Ce qui nous donne la répartition suivante -->
Culture : Coalescent; Qui est soudé, réuni à un élément proche mais distinct (Petit larousse) :D
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Ce qui nous donne la répartition suivante -->
Question : Comment en est-on arrivé là ?
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


- Ajout de X1 en 0.
- Ajout de X2 en 2.
- Ajout de X3 en 4.
- Ajout de X4 en 1.
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision primaire
Ajout de X5 en 0.. déjà pris on le met en 16
Sans oublier de mettre à jour son prédécesseur dans la liste de collision.
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision primaire
Ajout de X6 en 2.. déjà pris on le met en 15
On met à jour le lien de son prédécesseur dans la liste de collision.
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision primaire
Ajout de X7 en 0. En collision avec X5 lui-même en collision avec X1. On le met en 14.
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision secondaire
Arrive X8 qui est censé être stocké en 16. Or cette place est déjà prise par X5. X5 n'a pas la valeur de hachage adéquate pour occuper cette place, c'est donc une collision secondaire.
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Ajout de X9 en 3, pas de soucis.
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision primaire
Ajout de X10 en 4. Collision avec X3 on le met donc en 12 sans oublier de mettre à jour le lien de X3, son prédecesseur dans la liste de collisions.
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision primaire
Ajout de X11
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision secondaire
Ajout de X12
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision primaire
Ajout de X13
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Ajout de X14
Hachage coalescent: exemple (5)
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :


Collision primaire
Ajout de X15
Hachage coalescent: recherche
La recherche est simple à implémenter, il suffit pour l'élément de déterminer sa valeur de hachage, et ensuite de comparer chaque élément en parcourant la liste, à l'aide du lien, jusqu'à trouver l'élément recherché (recherche positive) ou trouver un lien égal à -1 (recherche négative).
Remarque : Nous ne perdons pas beaucoup de temps, puisque parcourons la liste fusionnée de collisions depuis l'indice de valeur de hachage primaire de la valeur que l'on cherche.
Hachage coalescent: recherche (2)
Simulons la recherche de l'élément X8:

On calcule la valeur de hachage de X8. On trouve
16.
On regarde la valeur comprise à l'indice 16 c'est...X5.
Le lien de X5 n'est pas égal à -1, on le suit donc pour atterrir à l'indice 14.
L'élément présent en 14 n'est toujours pas X8 et le lien n'est pas -1, on continue donc en 13.
La valeur à l'indice 13 est bien X8. On arrête donc la recherche de manière positive.