Algorithmique: Tri Par Fusion

Tri Fusion : Principe

Le principe du tri par fusion suit le paradigme « diviser pour régner » dont le principe est le suivant :

On divise en deux moitiés la liste à trier.

On trie chacune d'entre elles.
On fusionne les deux moitiés obtenues pour obtenir la liste triée.

Tri Fusion : Exemple

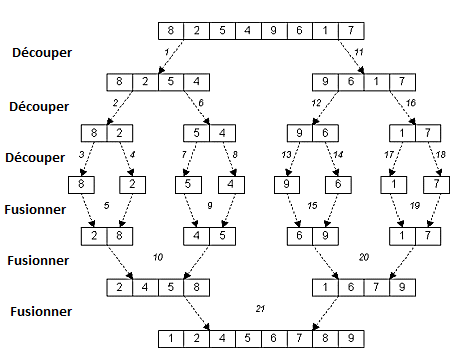
Voici un exemple explicatif du tri par fusion sur la liste
L=[ 8 , 2 , 5 , 4 , 9 , 6 , 1 , 7] :

Tri Fusion : Détail

Rappel:

On divise en deux moitiés la liste à trier.

On trie chacune d'entre elles.
On fusionne les deux moitiés obtenues pour obtenir la liste triée.

Tri Fusion : Détail

Rappel:

On divise en deux moitiés la liste à trier (diviser).

On trie chacune d'entre elles (régner).
On fusionne les deux moitiés obtenues pour obtenir la liste triée (fusionner).
...Chacune de ces opérations va correspondre à une fonction qui sera utilisée pour écrire l'algorithme de tri final.

Tri Fusion : Détail (2)

La difficulté de l'algorithme de tri par fusion repose sur la fusion des deux liste triées. Pour illustrer ce principe on va utiliser la métaphore d'un jeu de cartes.

Supposons qu'on ait deux tas de cartes comme dans le jeu de la bataille. A chaque tour on compare les cartes des deux tas et c'est la plus faible qu'on place dans la pioche finale.

Un moment donné l'un des deux tas sera vide. A ce moment là plus besoin de comparer, il suffira de placer toutes les cartes restantes dans la pioche résultat.

Le tri par fusion fait exactement la même chose.

Première étape : diviser

# Divise la liste en deux parts. Retourne chacune des parts

def diviser(l):
    n = len(l)
    return l[0:n//2] , l[n//2:n]

Dernière étape : fusionner

# Fusionne les listes en tenant compte de l'ordre ascendant

def fusion(l1,l2):
    resultat = []
    longueur1, longueur2 = len(l1), len(l2)
    index1, index2 = 0, 0
    # Tant qu'on a pas parcouru complètement une des deux listes
    while index1 < longueur1 and index2 < longueur2:    
        if l1[index1] < l2[index2]:    
            resultat.append(l1[index1])    # On ajoute l'élément le plus petit au résultat
            index1 = index1 + 1    # On étudie l'élément placé à l'indice suivant
        else:
            resultat.append(l2[index2])
            index2 = index2 + 1
    # On est arrivé au bout de index1 mais pas de index2
    if index1 == longueur1 and index2 != longueur2:    
        resultat.extend(l2[index2:])    # On ajoute d'un coup tous les éléments restants de l2
    else:
        resultat.extend(l1[index1:])    # On ajoute d'un coup tous les éléments restants de l1
    return resultat

Tri fusion

# Tri Fusion

def triFusion(l):
    n = len(l)
    if n == 0 or n == 1:
        return l
    else:
        l1, l2 = diviser(l)
        l1 = triFusion(l1)
        l2 = triFusion(l2)
        return fusion(l1,l2)

Complexité du tri par fusion

La complexité d'un algorithme est le nombre d'étapes nécessaires à son accomplissement en fonction de la taille des données qu'on lui a donné en paramètres.

La complexité du tri par fusion est en O(nlg(n)).