Обучение без учителя. Кластеризация
Нейросети
Метод главных компонент (PCA)

Представим выборку в ортогональном базисе
Метод главных компонент (PCA)

Как отобразить хренову тучу признаков в небольшое число?
Метод главных компонент (PCA)
Ковариация признаков:
Матрица ковариации:
Матрица ковариации представляет собой симметричную матрицу, где на диагонали лежат дисперсии соответствующих признаков, а вне диагонали — ковариации соответствующих пар признаков
Главные компоненты - собственные вектора матрицы (\(M w_i = \lambda_i w_i\))
Метод главных компонент (PCA)
Подпространство исходных признаков
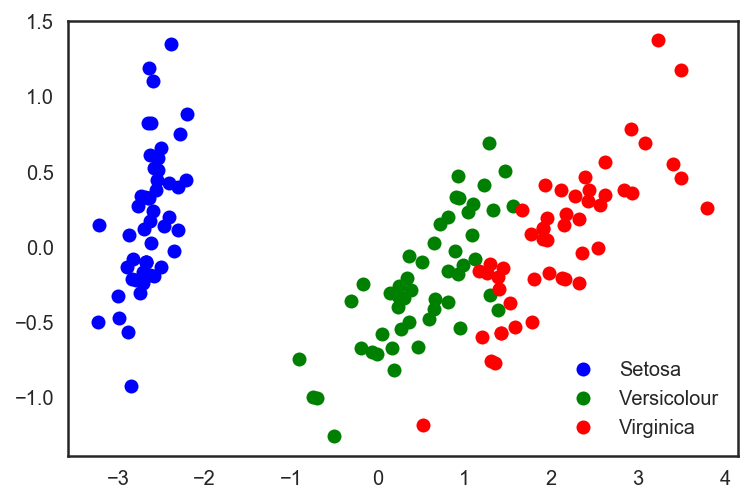
Метод главных компонент (пример)
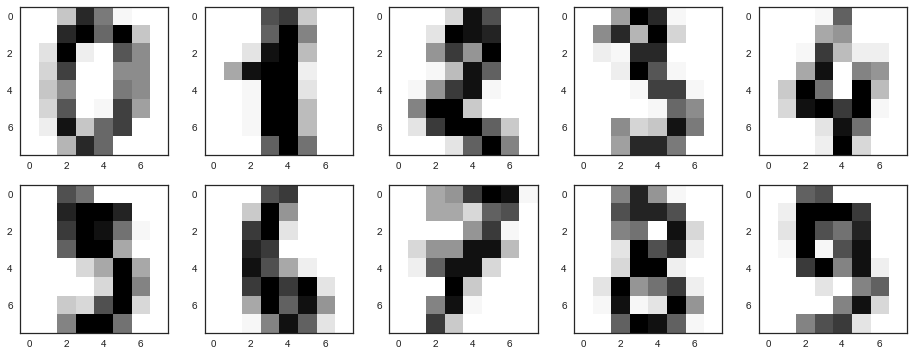
Метод главных компонент (пример)
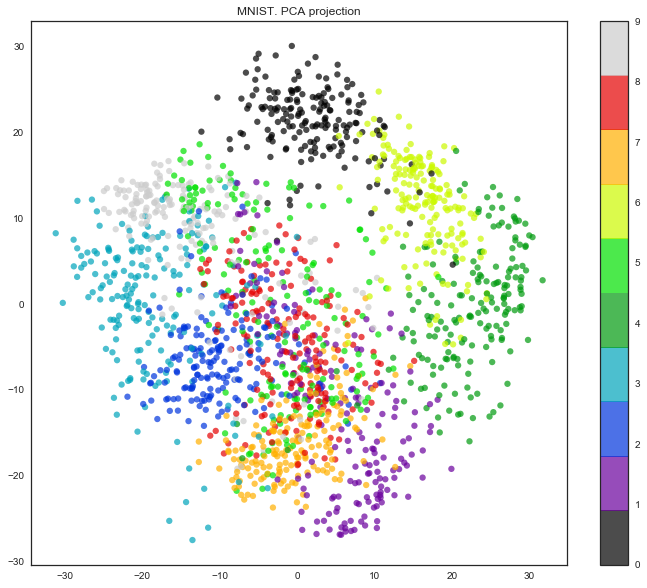
Метод главных компонент (пример)

Метод главных компонент (когда остановиться?)
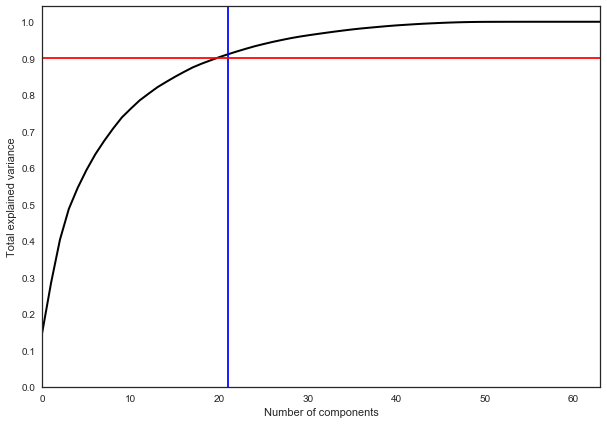
Обучение без учителя

Кластеризация
\(X\) - пространство признаков;
\(X^l = \{x_i\}_{i = 1}^l \) - обучающая выборка;
\(\rho(x_i, x_j) \rightarrow [0, +\infty) \) - функция расстояния между объектами
Ищем метки кластеров:
\(y_i \in Y\)
- каждый кластер состоит из близких объектов
- объекты разных классов существенно различаются
Постановка задачи
Кластеризация
\(X\) - пространство признаков;
\(X^l = \{x_i\}_{i = 1}^l \) - обучающая выборка;
\(\rho(x_i, x_j) \rightarrow [0, +\infty) \) - функция расстояния между объектами
Ищем метки кластеров:
\(y_i \in Y\)
- каждый кластер состоит из близких объектов
- объекты разных классов существенно различаются
Постановка задачи
Kmeans
- Выбрать количество кластеров \(k\), которое нам кажется оптимальным для наших данных.
- Высыпать случайным образом в пространство наших данных \(k\) точек (центроидов).
- Для каждой точки нашего набора данных посчитать, к какому центроиду она ближе.
- Переместить каждый центроид в центр выборки, которую мы отнесли к этому центроиду.
- Повторять последние два шага фиксированное число раз, либо до тех пор пока центроиды не "сойдутся" (обычно это значит, что их смещение относительно предыдущего положения не превышает какого-то заранее заданного небольшого значения).
Kmeans

Kmeans

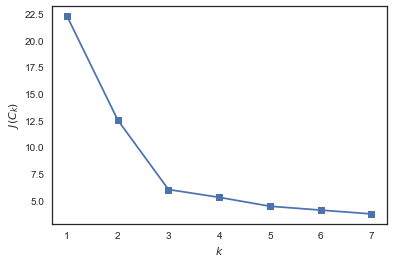
Kmeans - оптимальное число кластеров
Kmeans - проблемы
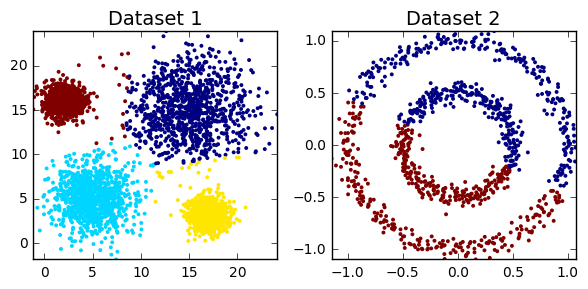
Спектральная кластеризация
- Полный граф с вершинами в наших наблюдениях и рёбрами между каждой парой наблюдений с весом, соответствующим степени похожести этих вершин
Агломеративная кластеризация
- Начинаем с того, что высыпаем на каждую точку свой кластер
- Сортируем попарные расстояния между центрами кластеров по возрастанию
- Берём пару ближайших кластеров, склеиваем их в один и пересчитываем центр кластера
- Повторяем п. 2 и 3 до тех пор, пока все данные не склеятся в один кластер
Агломеративная кластеризация
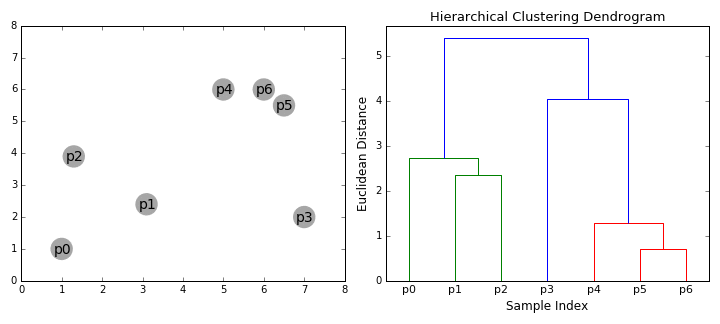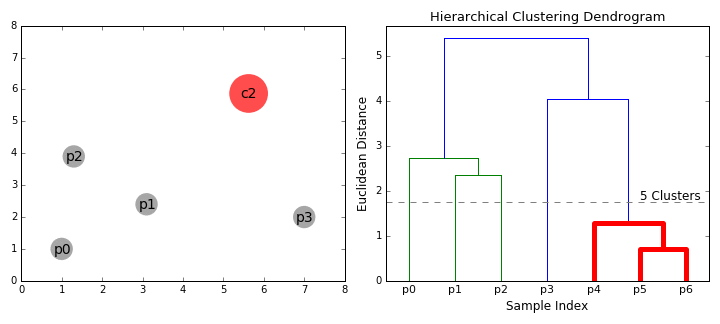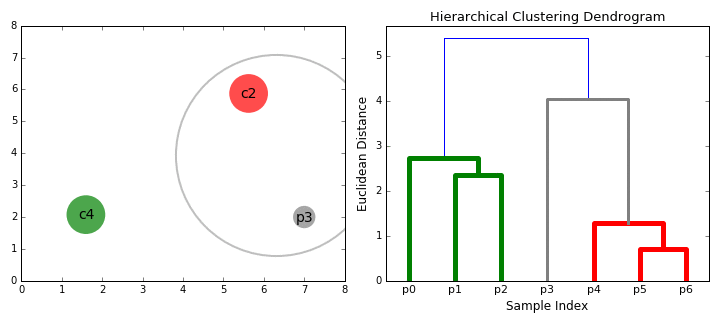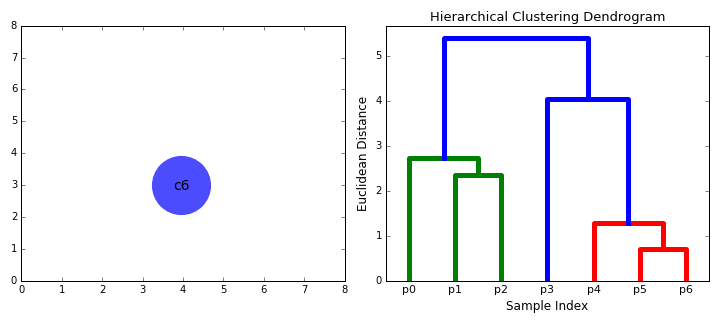
Агломеративная кластеризация
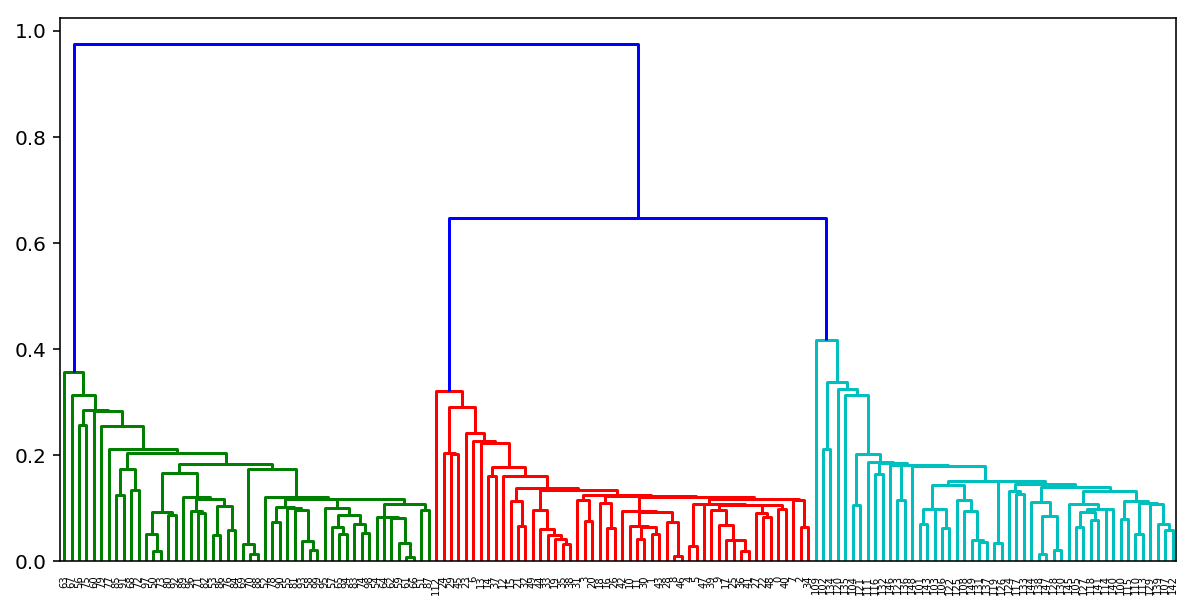
Агломеративная кластеризация
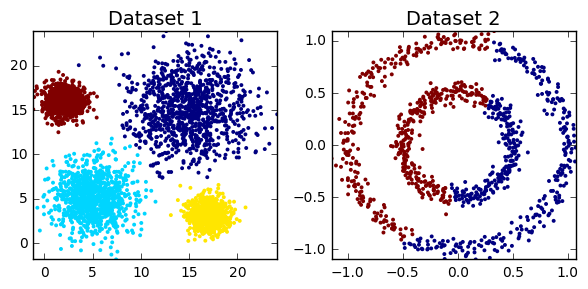
Метрики качества
Rand Index: \(RI = \frac{2(a + b)}{n(n-1)} \)
а - число пар элементов из одного класса, b - число пар элементов из разных классов, n - число объектов
Нормируем: \(ARI = \frac{RI - E[RI]}{\max(RI) - E[RI]}\)
\(ARI \in [-1, 1]\), отрицательные значения соответствуют "независимым" разбиениям на кластеры, значения, близкие к нулю, — случайным разбиениям, и положительные значения - схожим

Mutual information

Метрики качества
Гомогенность, полнота:
\(h = 1 - \frac{H(C\mid K)}{H(C)}, c = 1 - \frac{H(K\mid C)}{H(K)}\)
K — результат кластеризации, C — истинное разбиение выборки на классы. Таким образом, h измеряет, насколько каждый кластер состоит из объектов одного класса, а — c насколько объекты одного класса относятся к одному кластеру.
V-мера: \(v = 2\frac{hc}{h+c}\)
Силуэт: \(s = \frac{b - a}{\max(a, b)}\)
Обозначим через а среднее расстояние от данного объекта до объектов из того же кластера, через b — среднее расстояние от данного объекта до объектов из ближайшего кластера (отличного от того, в котором лежит сам объект)
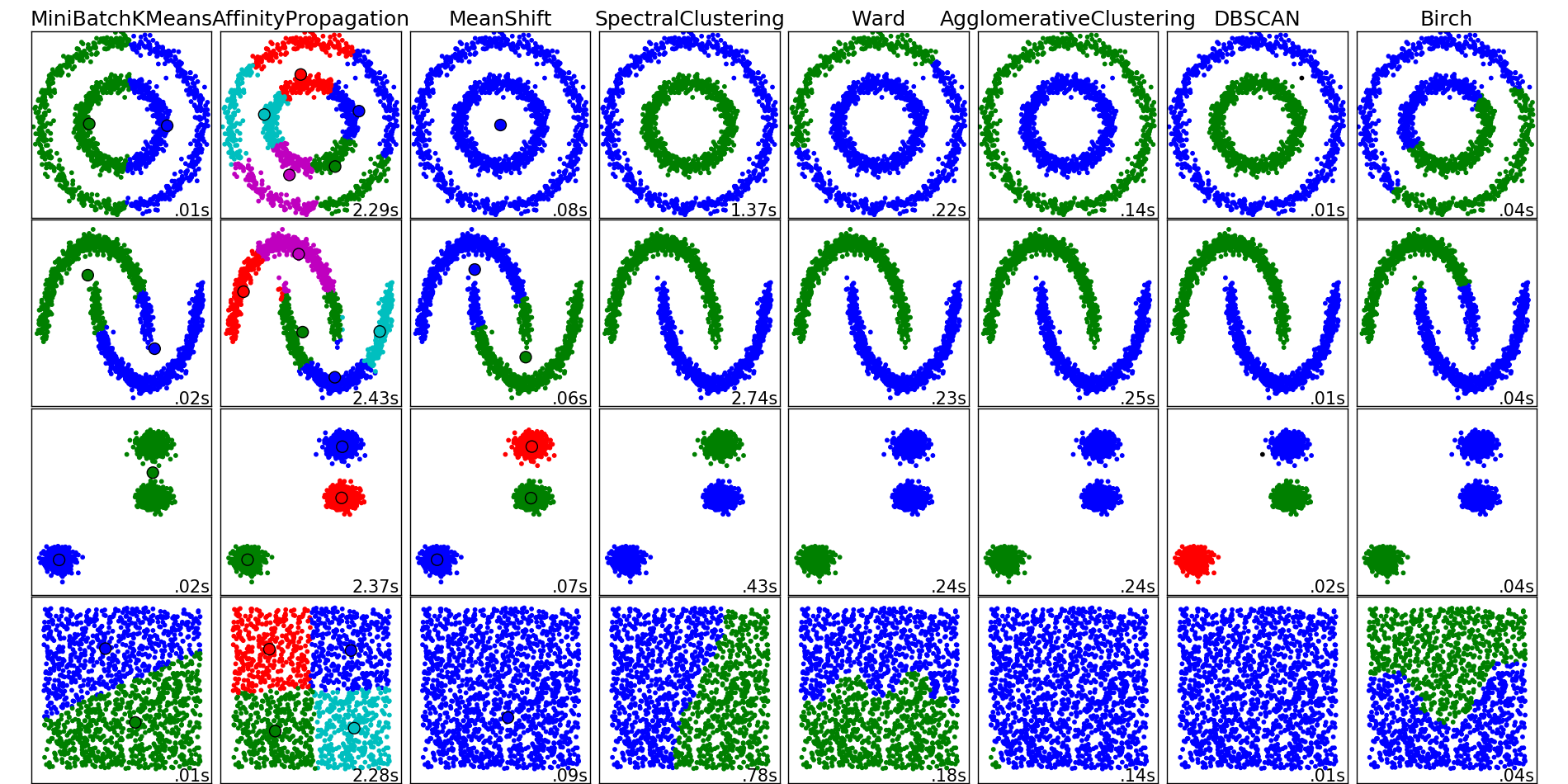
Кластеризация


Кластеризация
Нейросети
Линейная модель МакКаллока-Питтса
\(f_j: X \rightarrow \mathbb{R}, j = 1, ..., n,\) - числовые признаки, \(x^j = f_j(x)\)
\(a(x, w) = \sigma(<w, x>) = \sigma(\sum\limits_{j=1}^n w_j f_j(x) - w_0) \),
где \(w_0, ..., w_n \in \mathbb{R}\) - веса признаков, \(\sigma(s)\) - функция активации (например, sign)
Линейная модель МакКаллока-Питтса

Функция активации

Нейронная реализация логических функций
\(x^1 \land x^2 = [x^1 + x^2 - \frac{3}{2} > 0]\)
\(x^1 \vee x^2 = [x^1 + x^2 - \frac{1}{2} > 0]\)
\(\neg x^1 = [-x^1 + \frac{1}{2} > 0]\)

Нейронная реализация логических функций
\(x^1 \oplus x^2 = [x^1 + x^2 - 2 x^1 x^2 - \frac{1}{2} < 0\)
\(x^1 \oplus x^2 = [(x^1 \vee x^2) - (x^1 \land x^2) - \frac{1}{2} > 0]\)

Многослойная нейросеть


Ошибка на скрытом слое вычисляется по ошибке на выходе
Задание
по кластеризации: про попугаев. Картинка с попугаями
Задание по печатному почерку. Требуется ввести текст (см. по ссылке). Дать предположение о том, какие признаки можно выделить из данных (см. файлы, ссылки на которые будут после набора текста). В идеальном случае - провести кластеризацию по этим файлам, исключив шумы.
по нейронке - АКЦИЯ: кто сдаст все лабы до того, как появится задание по нейронке, может не делать нейронку