Машинное обучение

Задача машинного обучения

  • классификация – отнесение объекта к одной из категорий на основании его признаков;
  • регрессия – прогнозирование количественного признака объекта на основании прочих его признаков;
  • кластеризация – разбиение множества объектов на группы на основании признаков этих объектов так, чтобы внутри групп объекты были похожи между собой, а вне одной группы – менее похожи;
  • рекомендации
  • и много других.

Задача машинного обучения

Признаки

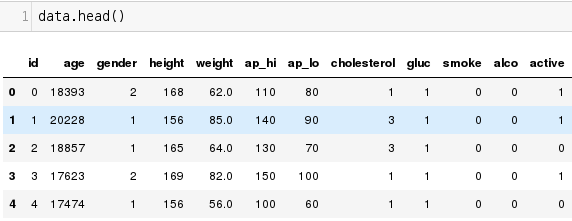
Целевая переменная

Объекты

X_i = \{x_{i1}, x_{i2}, ..., x_{in}\} \\ y_i = y(X_i) \\ y_i \approx a(X_i) \\ y \approx a(X)

Классификация

  • \(x_1, x_2, ..., x_l\) - объекты, для которых известны классы \(y_1, y_2, ..., y_l\)
  • Строим алгоритм \(y_i = a(x_i)\)
  • Иногда он ошибается:

\( \sum\limits_{i=1}^l[y_i \ne a(x_i)] \rightarrow min \)

Регрессия

  • \(x_1, x_2, ..., x_l\) - точки, в которых известны значения некоторой переменной \(y_1, y_2, ..., y_l\)
  • Строим алгоритм \(y_i \approx a(x_i)\)
  • Иногда он ошибается:

\( \sum\limits_{i=1}^l(y_i - a(x_i))^2 \rightarrow min \)

\( \sum\limits_{i=1}^l \mathscr{L} (y_i, a(x_i)) \rightarrow min \)

Работа с данными

Anaconda и Jupyter Notebook

https://www.anaconda.com/download/

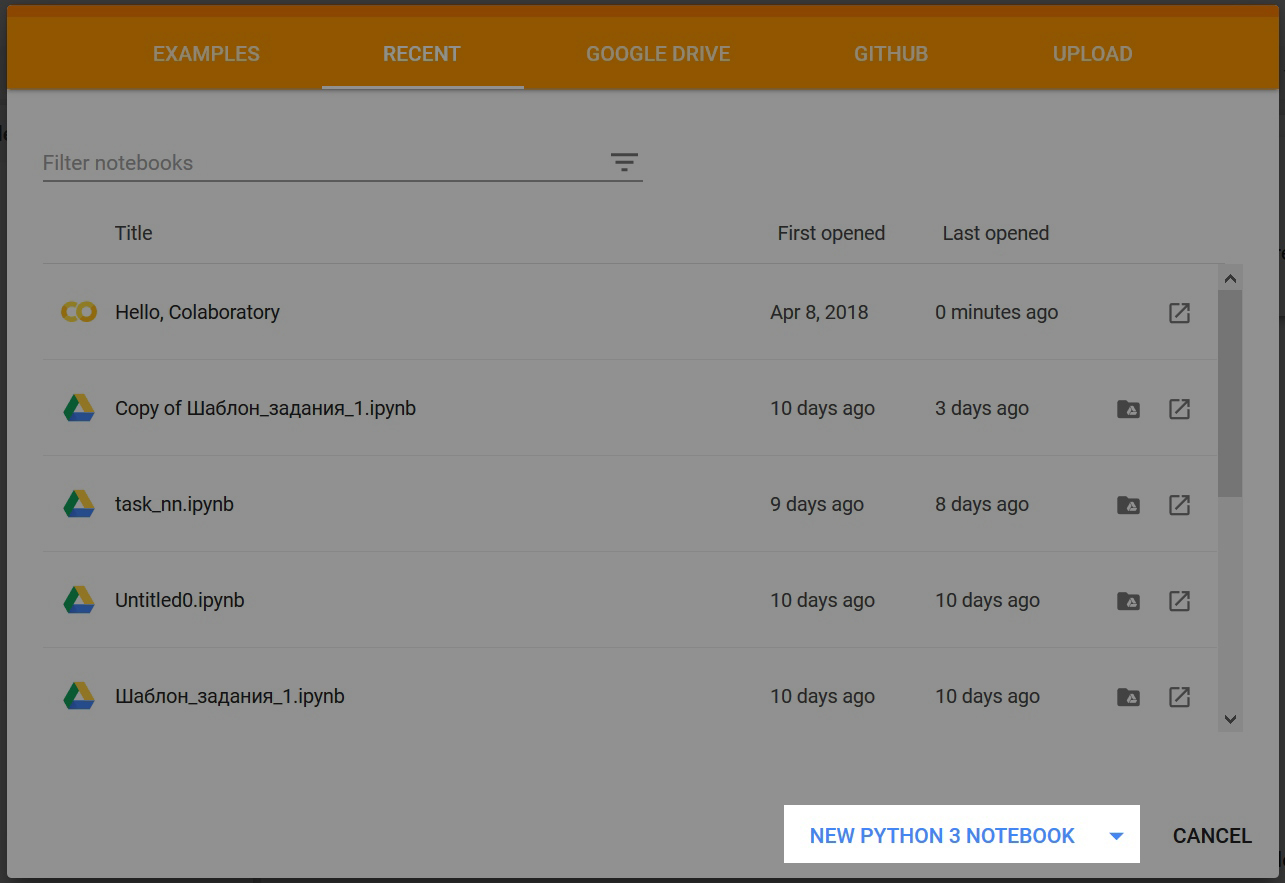
Google Colab

https://colab.research.google.com/

  • модифицированный Jupyter Notebook
  • онлайн - ничего устанавливать не надо
  • 12 часов бесплатного использования GPU
  • использование нескольких ЯП "из коробки"
  • интеграция с github.com и google drive:
import os
os.listdir("/drive")

Google Colab

Будем использовать Python 3

Синтаксис Python

Ссылка на Google Colab Notebook

Главное:

  • отступы в блоках;
  • всё является объектами;
  • динамически типизированный язык (т.е. в одну переменную в разное время можно записать объекты разных типов)

Метрические методы в машинном обучении

Понятие расстояния

\rho (x, y) \ge 0 \\ \rho (x, y) = \rho (y, x) \\ \rho (x, y) \le \rho(x, z) + \rho(z, y)

Например, метрика Минковского - общий случай Евклидова расстояния:

( \sum_{i=1}^n (|x_i - y_i|)^q ) ^ { 1 / q }

Метод ближайших соседей

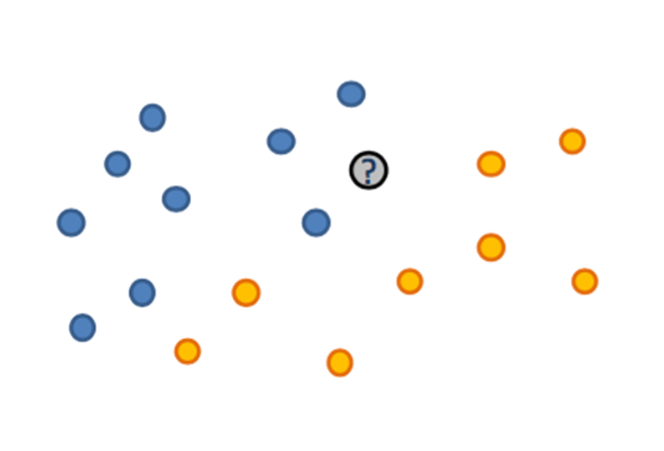
К какому классу относится серый кружок?

Метод ближайших соседей

Попробуем отнести его к классу ближайшего соседа - но никто не защищен от выбросов

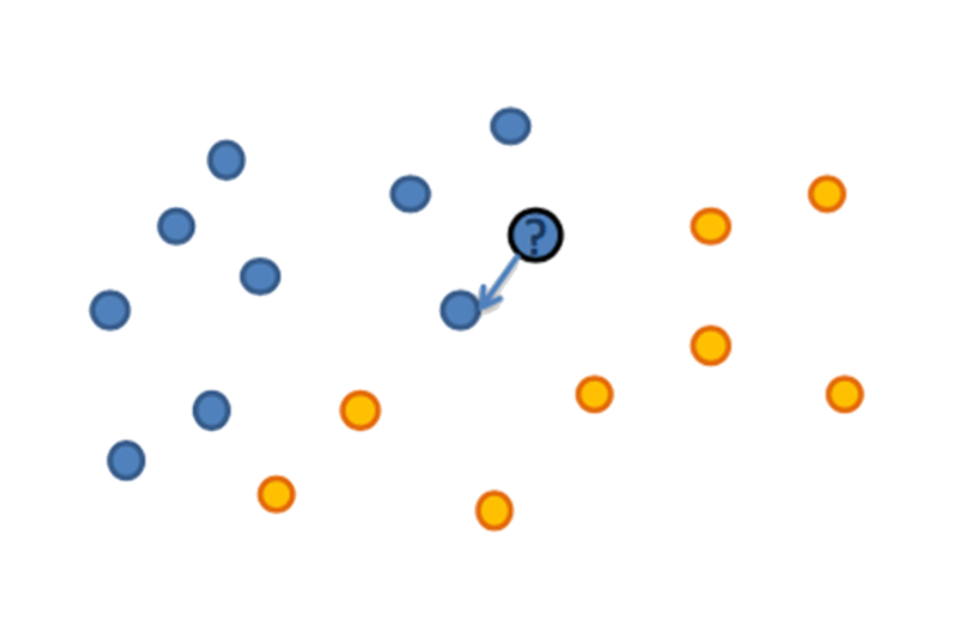
Метод ближайших соседей

Возьмем больше соседей, например, 5. В этом конкретном случае всё однозначно

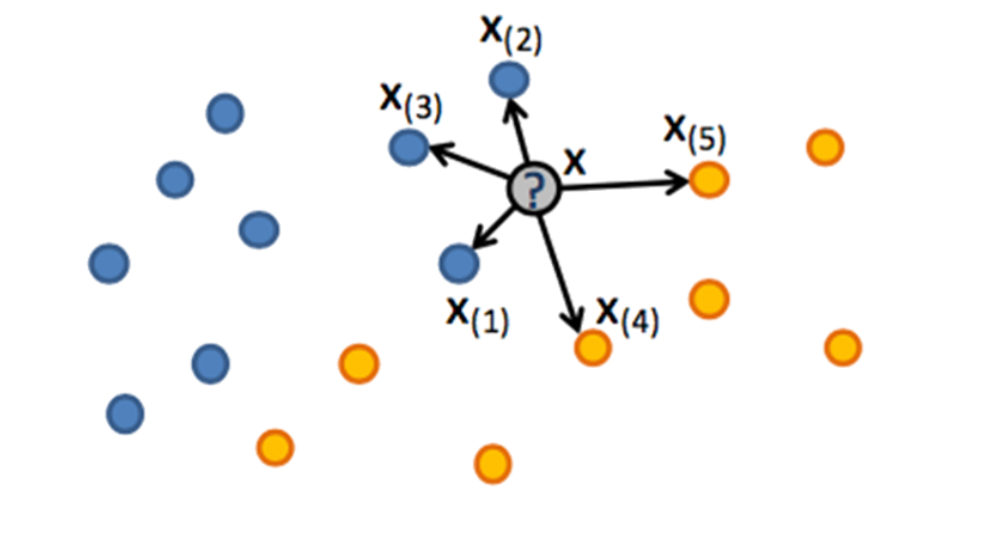
Метод ближайших соседей

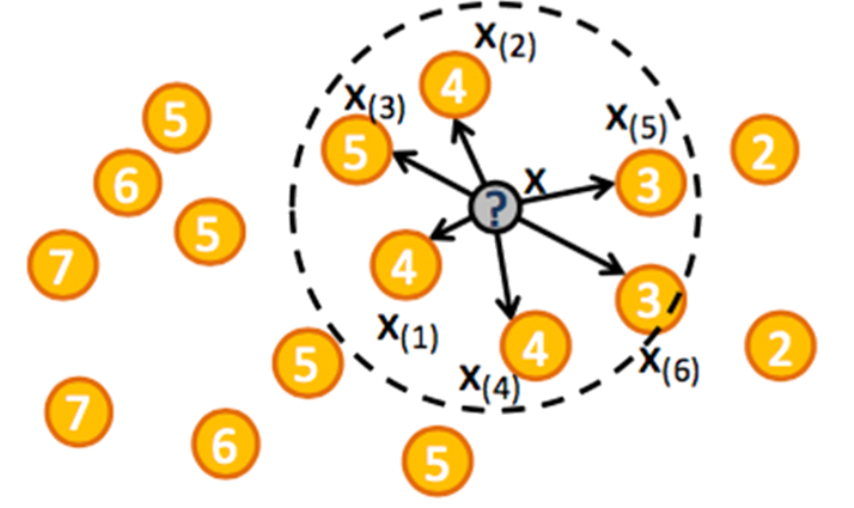
Попробуем 6 соседей. Что-то пошло не так.

Метод ближайших соседей

Попробуем 6 соседей. Что-то пошло не так

Введем веса объектов, например, в виде функции от расстояния:

\(w(x_{(i)}) = w(i) \)

\(w(x_{(i)}) = d(x, x_{(i)}) \)

Тогда степень принадлежности к каждому из классов определится просто суммой весов соседей, принадлежащих классу:

\(Z_{желтый} = w(x_{(4)}) + w(x_{(5)}) + w(x_{(6)}) \)

\(Z_{синий} = w(x_{(1)}) + w(x_{(2)}) + w(x_{(3)}) \)

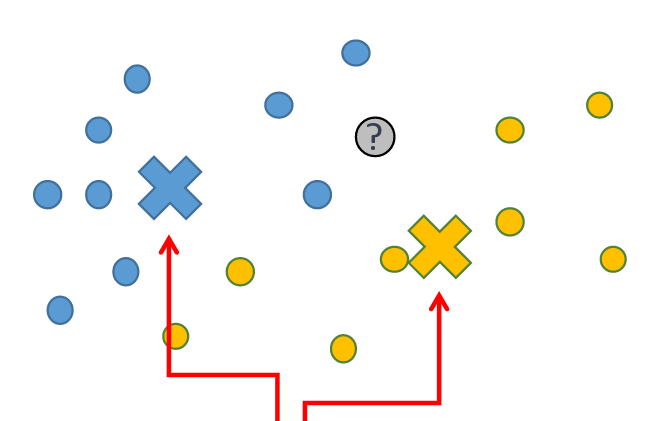
Метод ближайших соседей

Другой вариант - центроидный классификатор

Метод ближайших соседей для задачи регрессии

a(x_{(?)}) = \frac {\sum_{j=1}^{l}y_{(j)} w(x_{(j)})} {\sum_{j=1}^{l} w(x_{(j)})}

Машинное обучение в Python

Используемые библиотеки

  • numpy - библиотека для работы с матрицами и многомерными массивами
  • pandas - для работы с данными: объектами, признаками, ответами и т.д.
  • sklearn (scikit-learn) - содержит реализацию всех популярных методов машинного обучения
  • matplotlib (pyplot), seaborn - визуализация данных
# Импорт библиотеки:
import numpy as np     # можем обращаться к библиотеке по имени np
import matplotlib      # обращаемся к библиотеке по изначальному имени

# Импорт отдельных модулей из библиотеки:
from sklearn.neighbors import KNNClassfier

Отложенная выборка и кросс-валидация

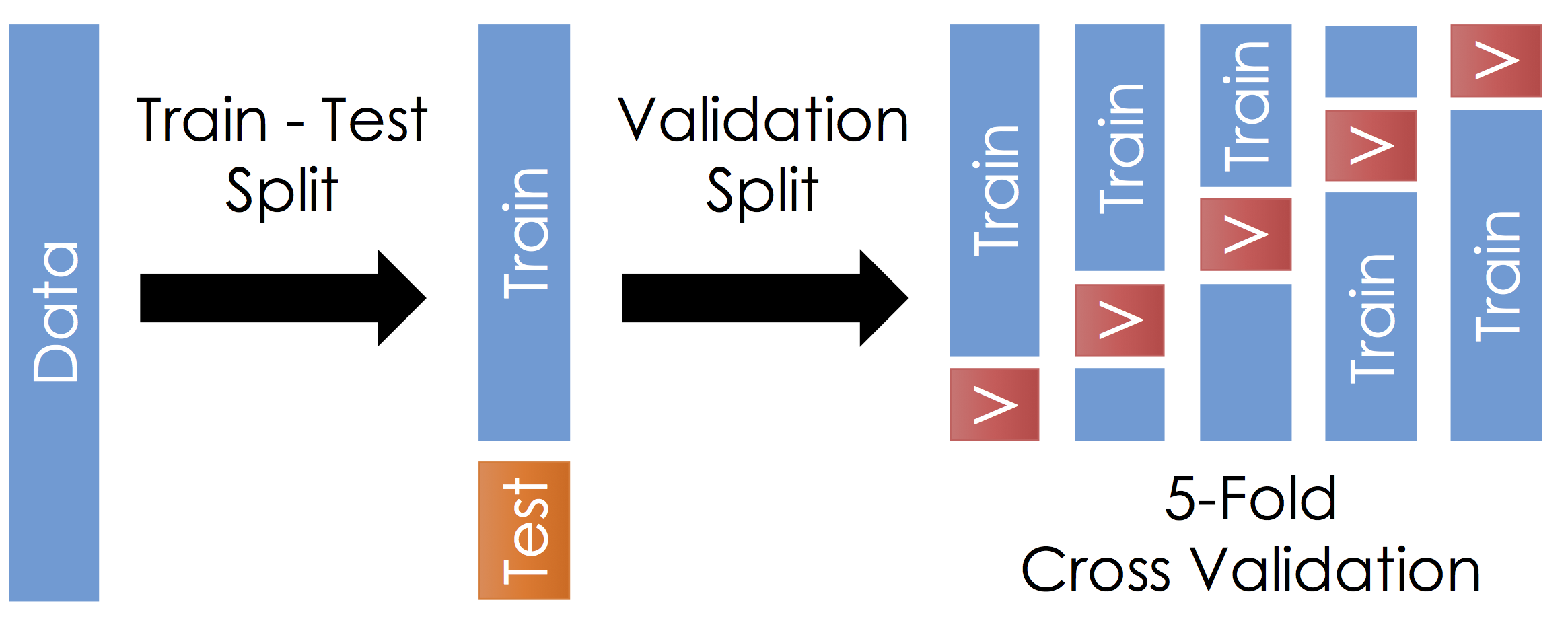
Работа с данными

Блокнот

Данные

Категориальные переменные

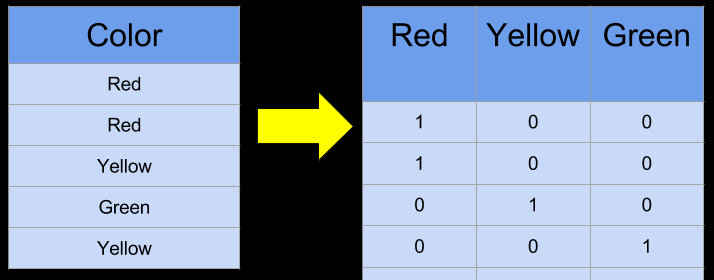
One-hot encoding

Категориальные переменные

  • One-hot encoding
  • Hash-based encoding
  • Замена частотой встречаемости
  • Замена на индикатор больших групп

Обработка пропусков

  • Если признак бинарный - можно ввести еще одно значение, равноудаленное по метрике расстояния от 0 и 1.
  • Популярны способы кодирования пропусков нулями, но это не подойдет для метрических методов.
  • Можно кодировать пропуски средним значением признака
  • Если пропусков слишком много или слишком   мало - стоит убрать либо строки таблицы, либо колонки

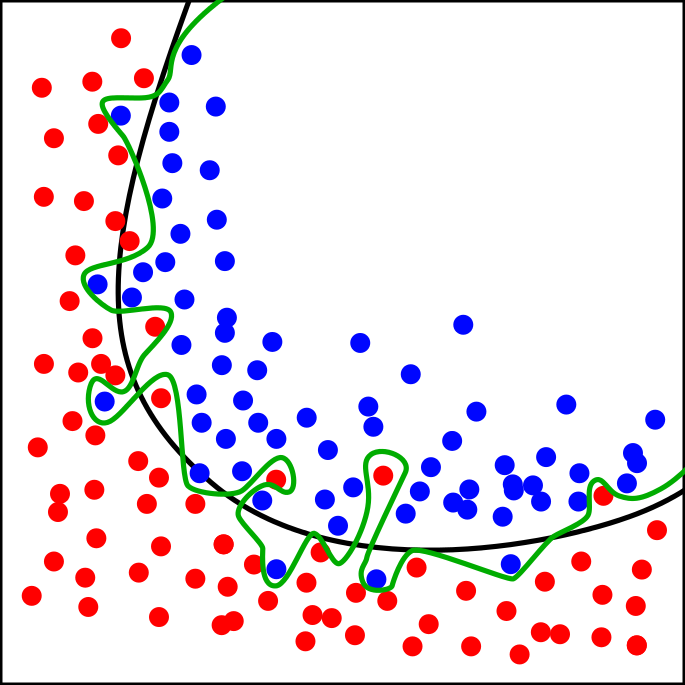
Переобучение

Чрезмерная подстройка алгоритма под обучающую выборку

Переобучение

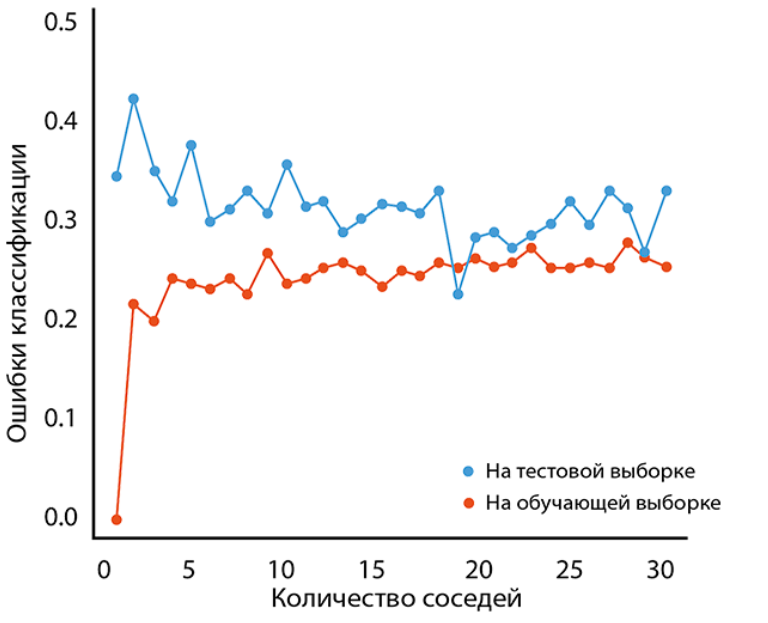
Гиперпараметры алгоритма

Гиперпараметры алгоритма

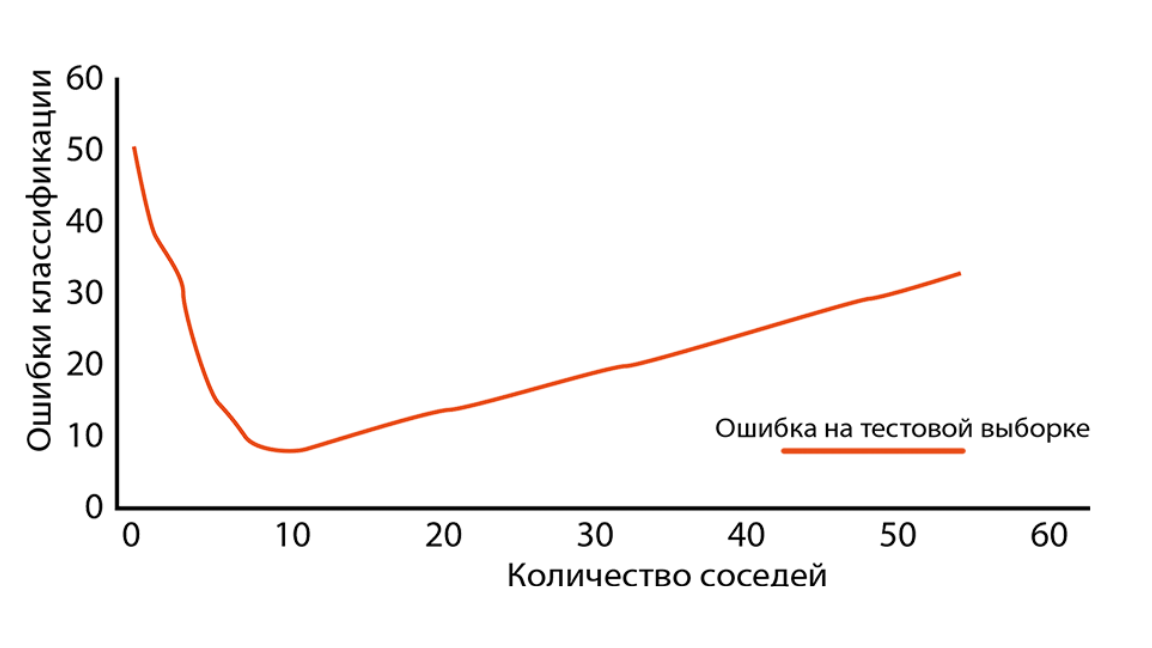
Плюсы kNN

  • Простая реализация;
  • Можно адаптировать под нужную задачу выбором метрики или ядра (функции сходства объектов);
  • Неплохая интерпретация.

Минусы kNN

  • Если число соседей, используемых для классификации, будет большим (100-150), и в таком случае алгоритм будет работать не так быстро, как дерево решений;
  • Среди множества признаков трудно подобрать подходящие веса и определить, какие признаки не важны;
  • Зависимость от выбранной метрики расстояния между примерами.
  • Нет теоретических оснований выбора определенного числа соседей — только перебор. В случае малого числа соседей метод чувствителен к выбросам, то есть склонен переобучаться;
  • Как правило, плохо работает, когда признаков много.

Задание на лабораторную

  • Есть сайт с огромным количеством разных наборов данных: https://www.kaggle.com/
  • Нужно найти интересный для себя набор данных:
    • количество признаков и сам размер файла не должны быть большими, чтобы самим было легче
    • набор данных должен быть подобран под задачу классификации
  • Провести манипуляции со своим набором данных по аналогии с рассмотренными: предобработка данных, предсказания с помощью метода ближайших соседей.
  • Отчет в формате ipynb, лучше всего ссылкой на файл в google colab. В отчете: код, пояснения, выводы, графики.

Обратная связь

https://goo.gl/forms/gxwj76vMuaOTi8ea2

(анонимно)

Made with Slides.com