Разведочный анализ данных

Зима близко! Пора делать лабы!

Как вообще подступиться к данным?

Блокнот с графиками

Метрики качества моделей

Метрики в задаче регрессии

MAE - Mean Absolute Error

MAE(a, X) = \frac{1}{l} \sum_{i=1}^{l}{|a(x_i) - y_i|}

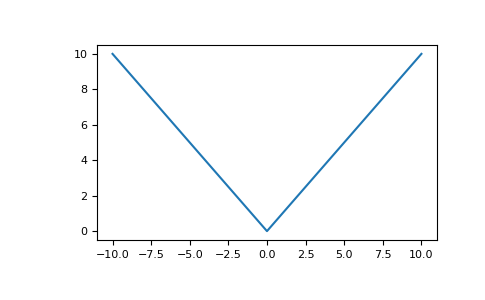
\(a(x_i)-y_i\)

\(MAE\)

MSE - Mean Squared Error

MSE(a, X) = \frac{1}{l} \sum_{i=1}^{l}{(a(x_i) - y_i)^2}

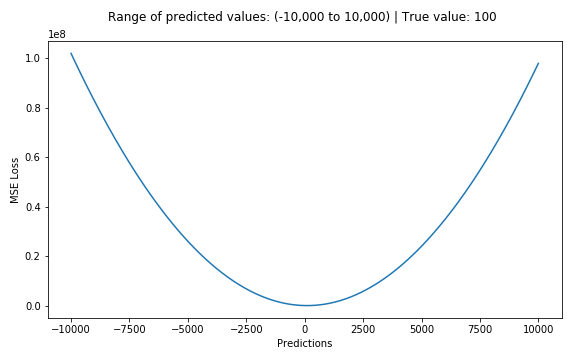
MSE vs. MAE

Больше настраивается на выбросы. Оптимальный прогноз - среднее

Недифференцируема - сложнее минимизировать. Оптимальный прогноз - медиана

Несимметричные функции потерь. Квантильная функция

Оптимальный прогноз - квантиль \(\tau\)

Метрики качества моделей

Метрики в задаче классификации

Accuracy

accuracy(a, X) = \frac{1}{l} \sum_{i=1}^{l}{[a(x_i)=y_i]}

Огромный недостаток:

Пусть \(q_0\) - доля самого крупного класса, тогда:

\(accuracy \in [q_0, 1]\)

могут быть проблемы на несбалансированных выборках
не учитывается цена ошибки

	y = True	y = False
a(x) = True	True Positive (TP)	False Positive (FP)
a(x) = False	False Negative (FN)	True Negative (TN)

Ошибки 1 и 2 рода

Precision & recall

Accuracy

\(\large accuracy = \frac{TP + TN}{TP + TN + FP + FN}\)

Precision и recall

\(\large precision = \frac{TP}{TP + FP}\)

\(\large recall = \frac{TP}{TP + FN}\)

F-мера

F = \(\frac{2*precision*recall}{precision+recall}\)

F\(_\beta = (1+{\beta}^2)\frac{2*precision*recall}{\beta^2precision+recall}\)

Precision & recall

Кредитный скоринг:

неудачный кредитов должно быть не больше 3%
\(precision(a, X) \ge 0.97\)
задача оптимизации: максимизация полноты

Медицинская диагностика:

найти не менее 90% больных;
\(recall(a, X) \ge 0.9 \)
задача оптимизации: максимизация точности

Что есть что?

\(precision\): какова вероятность того, что предсказание

\(a(x) = 1\) - точное?

\(recall\): какую долю истинно положительных объектов находит алгоритм?

Оценка вероятности принадлежности классу

\(a(x) = [b(x) > t] \), \(b(x)\) - оценка принадлежности классу +1

как оценить качество работы алгоритма b(x)?
порог вероятности классификации выбирается позже
порог зависит от ограничений на точность и полноту
пример - биометрия

PR curve

Видео на курсере про PR кривую

b(x)	0.14	0.23	0.39	0.52	0.73	0.90
y	0	1	0	0	1	1

Левая точка: (0, 0)
Правая точка: (1, r), r - доля положительных объектов
Идеальный классификатор: проходит через (1, 1)
Задача максимизации AUC-PRC

Receiving operating characteristic

FPR = \frac{FP}{FP + TN} = \frac{FP}{N} \\ \\ TPR = \frac{TP}{TP+FN} = \frac{TP}{P}

Ось Х: FPR - доля ошибочных положительных классификаций
Ось Y: TPR - доля правильных положительных классификаций

ROC AUC

Видео на курсере про ROC кривую

b(x)	0.14	0.23	0.39	0.52	0.73	0.90
y	0	1	0	0	1	1

Левая точка: (0, 0)
Правая точка: (1, 1)
Идеальный классификатор: проходит через (0, 1)
Площадь от 0,5 до 1
Задача максимизации AUC-ROC

ROC AUC vs. PRC AUC

ROC AUC:

не зависит от соотношения классов
вероятность того, что случайно взятый объект класса 1 получит оценку выше, чем случайный объект из класса 0
неточна при сильном дисбалансе классов (т.к. нормируется на их размеры)

PRC AUC:

нормируется на количество положительных прогнозов, изменится с изменением баланса классов
максимальная ROC AUC зависит от соотношения классов
подходит при сильном дисбалансе классов

ROC AUC vs. PRC AUC

Пример

50 000 объектов класса 0

100 объектов класса 1

950 000 объектов класса 0

порог отнесения к классу 1

\(a(x) = 1\) - 50095 объектов

\(FP = 50000, TP = 95\)

\(TPR = 0.95, FPR = 0.05\)

\(precision = 0.0019, recall = 0.95\)

\(b(x) = 0\)

\(b(x) = 1\)

Задача оптимизации

Минимум функции - частные производные равны нулю

Градиентный спуск

\vec{x}^{[j+1]} = \vec{x}^{[j]} - \gamma^{[j]} \nabla F(\vec{x}^{[j]})

Напоминание: оператор Набла

\nabla

Градиентный спуск

Проблема локальных минимумов

Сохранение модели

Обертка над моделью и препроцессингом признаков - sklearn Pipeline
Формат хранения любых питоновских объектов - pickle

Блокнот

Задание на лабораторку

Провести визуальный анализ своего набора данных
Выбрать и обосновать метрику качества. Попробовать несколько методов машинного обучения из sklearn, посмотреть, какой метод лучше всего подойдет в контексте выбранной метрики (пока без подбора гиперпараметров). Оптимизировать KNN в соответствии с метрикой
Обернуть все предыдущие действия с данными (преобразование, нормализацию и т.д. - из первой и второй лабы) в Pipeline и сохранить получившуюся модель в pickle