Деревья решений и композиции алгоритмов

Решающее дерево

Критерий информативности
Для регрессии: \( H(X) = \frac{1}{|X|} \sum \limits_{i \in X} (y_i - \overline{y}(X))^2 \)
Для классификации:
- Доля объектов класса k в выборке X: \(p_k = \frac{1}{|X|} \sum \limits_{i \in X} [y_i = k] \)
- Критерий Джини: \( H(X) = \sum\limits_{k=1}^{K}p_k(1-p_k)\)
- Энтропийный критерий (по Шеннону): \(H(X) = -\sum_{k=1}^{K}p_k \ln{p_k}\)

Критерий ошибки
Разброс ответов в правом листе
Разброс ответов в левом листе
Доля объектов в левом листе относительно всех объектов родительского узла
Доля объектов в правом листе относительно всех объектов родительского узла

Решающее дерево
s0 = вычисляем энтропию исходного множества
Если s0 == 0 значит:
Все объекты исходного набора, принадлежат к одному классу
Сохраняем этот класс в качестве листа дерева
Если s0 != 0 значит:
Перебираем все элементы исходного множества:
Для каждого элемента перебираем все его атрибуты:
На основе каждого атрибута генерируем предикат,
который разбивает исходное множество на два подмножества
Рассчитываем среднее значение энтропии
Вычисляем ∆S
Нас интересует предикат с наибольшим значением ∆S
Найденный предикат является частью дерева принятия решений, сохраняем его
Разбиваем исходное множество на подмножества, согласно предикату
Повторяем данную процедуру рекурсивно для каждого подмножества
Критерий останова
- Все объекты в вершине принадлежат к одному классу;
- В вершину попало \(\le n\) объектов;
- Ограничение на глубину;
- Ограничение на количество листьев.
При каком n дерево получится максимально переобученным?
Борьба с переобучением
- Строим максимально переобученное дерево;
- Удаляем листья по некоторому критерию;
- (например, пока улучшается качество модели на валидации)
- Профит
Тем не менее, это достаточно трудоемкая процедура, и она имеет смысл только при использовании одиночного дерева
Категориальные признаки

Границы значений признаков

Есть ли смысл ставить границу по возрасту 17,5?
Практика
Плюсы деревьев
- Порождение четких правил классификации, понятных человеку (интерпретируемость модели);
- Деревья решений могут легко визуализироваться;
- Быстрые процессы обучения и прогнозирования;
- Малое число параметров модели;
- Поддержка и числовых, и категориальных признаков.
Минусы деревьев
- Очень чувствительны к шумам во входных данных;
- Разделяющая граница, построенная деревом решений, имеет свои ограничения;
- Необходимость отсекать ветви дерева (pruning) или устанавливать минимальное число элементов в листьях (переобучение);
- Нестабильность;
- Проблема поиска оптимального дерева решений (минимального по размеру и способного без ошибок классифицировать выборку);
- Сложно поддерживаются пропуски в данных;
- Модель умеет только интерполировать, но не экстраполировать.
Композиции алгоритмов
- обучим много алгоритмов
- усредним ответы

Но как получить разные результаты, используя однотипные алгоритмы?
Бутстрэп выборки

- выбираем из обучающей выборки \(l\) объектов с возвратом
- \(0,632l\) различных объектов
- можно также выбирать случайные подпространства признаков
Бутстрэп выборки

Теперь мы можем более объективно рассматривать статистики выборок (здесь мы имеем некоторое представление центральной предельной теоремы)
Центральная предельная теорема
- Имеем n распределений величины
- Величина распределена по одному и тому же закону \(y \sim F(X)\) с математическим ожиданием \(\mathbb{E}y\) и дисперсией \(\sigma^2 \)
- Сформируем новое распределение из выборочных средних: \(\overline{y}_n = \frac{1}{n}\sum\limits_{i=1}^{n}y_i \)
- Математическое ожидание нового распределения: \(\mathbb{E}y\)
- Дисперсия нового распределения: \(\frac{\sigma^2}{n} \)
Бэггинг
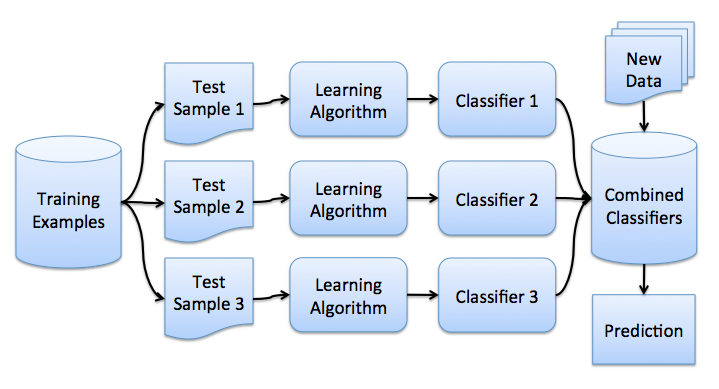
Составляющие ошибки
Случайный лес
- Для \(n = 1, ..., N:\)
- Сгенерировать выборку \(\widetilde X\) с помощью бутстрапа и метода случайных подпространств
- Построить решающее дерево \(b_n(x)\) по выборке \(\widetilde X\)
- Дерево строится, пока в каждом листе не окажется не более \(n_{min}\) объектов
- Регрессия:
\(a(x) = \frac{1}{N}\sum\limits_{n=1}^Nb_n(x) \)
- Классификация:
\(a(x) = sign\frac{1}{N}\sum\limits_{n=1}{N}b_n(x) \)
Случайный лес
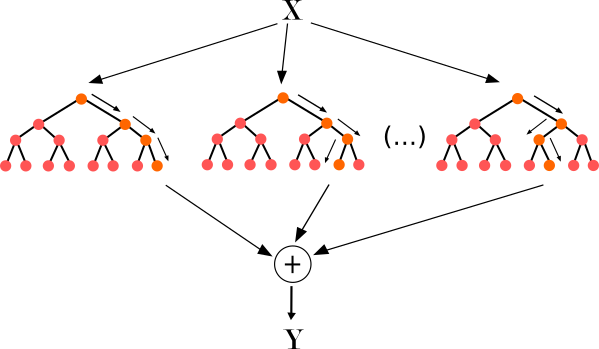
Основные параметры:
- количество деревьев
- глубина построения деревьев / количество листовых вершин в деревьях
- количество признаков, по которым вычисляется энтропия
Градиентный бустинг
Регрессия
Обучим простой алгоритм:
\(b_1 (x) = \arg \min \limits_{b} \frac{1}{l} \sum\limits_{i=1}^{l} (b(x_i) - y_i)^2\)
Как исправить ошибки \(b_1(x)\)?
\(b_1(x_i) + b_2(x_i) = y_i\)
\(b_2\) - специальная модель, которая предсказывает необходимые исправления ответов модели \(b_1\)
\(b_2(x) = \arg \min \limits_b \frac{1}{l} \sum\limits_{i=1}^l (b(x_i) - (y_i - b_1(x_i)))^2 \)
Бустинг
- направленное построение композиции, в отличие от случайного леса, который строится случайно
- итеративно настраиваемся в сторону меньшей ошибки

Градиентный бустинг
Уже построили N-1 алгоритмов:
\(a_{N-1}(x) = \sum\limits_{n=0}^{N-1}b_n(x) \)
Нужно минимизировать функционал ошибки:
\(\sum\limits_{i=1}^l L(y_i, a_{N-1}(x_i) + b(x_i)) \rightarrow \min\limits_b \)
Ищем оптимальный сдвиг:
\(b(x_i) = s_i \),
\(s = -\nabla F = (-L_z'(y_1, a_{N-1}(x_1)), ..., -L_z'(y_l, a_{N-1}(x_l))\)
Обучение базового алгоритма
\(b_N(x) = \arg\min\limits_b \frac{1}{l} \sum\limits_{i=1}^l(b(x_i) - s_i)^2 \)
- вся информация о функции потерь содержится в сдвигах \(s_i\)
- для новой задачи оптимизации можем использовать среднеквадратичную ошибку независимо от исходной задачи
Алгоритм градиентного бустинга
- Построить начальный алгоритм \(b_0(x)\)
- Для \(n = 1, ..., N\):
- Вычислить сдвиги:
\(s = (-L_z'(y_1, a_{N-1}(x_1)), ..., -L_z'(y_l, a_{N-1}(x_l))\) - Обучить новый базовый алгоритм:
\(b_N(x) = \arg\min\limits_b \frac{1}{l} \sum\limits_{i=1}^l(b(x_i) - s_i)^2 \) - Добавить алгоритм в композицию:
\(a_n(x) = \sum\limits_{m=1}^{m}b_m(x) \)
- Вычислить сдвиги:
Градиентный бустинг
- последовательно строит композицию
- базовый алгоритм приближает антиградиент функции ошибки
- результат - градиентный спуск в пространстве алгоритмов
- возможен также стохастический градиентный бустинг, когда каждый алгоритм обучается по случайной подвыборке
Градиентный бустинг над решающими деревьями
- базовый алгоритм - решающее дерево
- прогнозы в листьях подбираются под исходную функцию потерь
- структура дерева настраивается по MSE
Перенастройка в листьях:
\(\sum\limits_{i=1}^lL(y_i, a_{N-1}(x) + \sum\limits_{j=1}^J[x \in R_{N_j}]b_j) \rightarrow \min\limits_{b_1, ..., b_J} \)
Градиентный бустинг над решающими деревьями в Python
- sklearn - плох для реальных задач
- xgboost
- lightgbm
- catboost от Яндекса
Задание
- Убедиться в нестабильности одиночного дерева на своих данных
- Отобрать самые важные признаки случайным лесом, сравнить результат с отбором признаков линейным методом с \(L_1\)-регуляризацией
- Сравнить качество работы случайного леса без кросс-валидации с кросс-валидацией
- Сравнить качество работы и время обучения (%%time в начале ячейки) леса с градиентным бустингом над решающими деревьями, при подобрав для каждого оптимальные параметры. Особо хорошо будет, если градиентный бустинг обучите на видеокарте