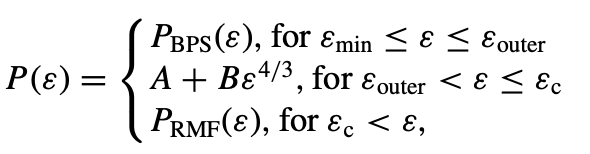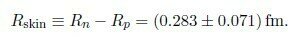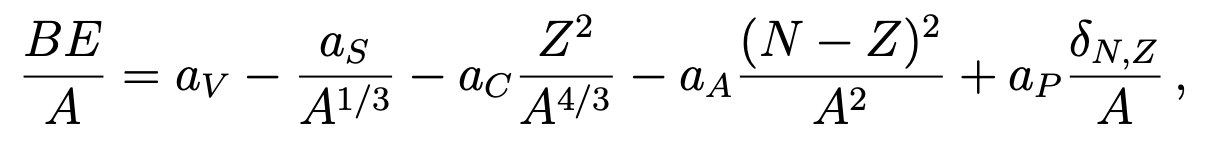Dense nuclear matter in the era of multimensenger astronomy
R. Lisboa
ronai.lisboa@ufrn.br
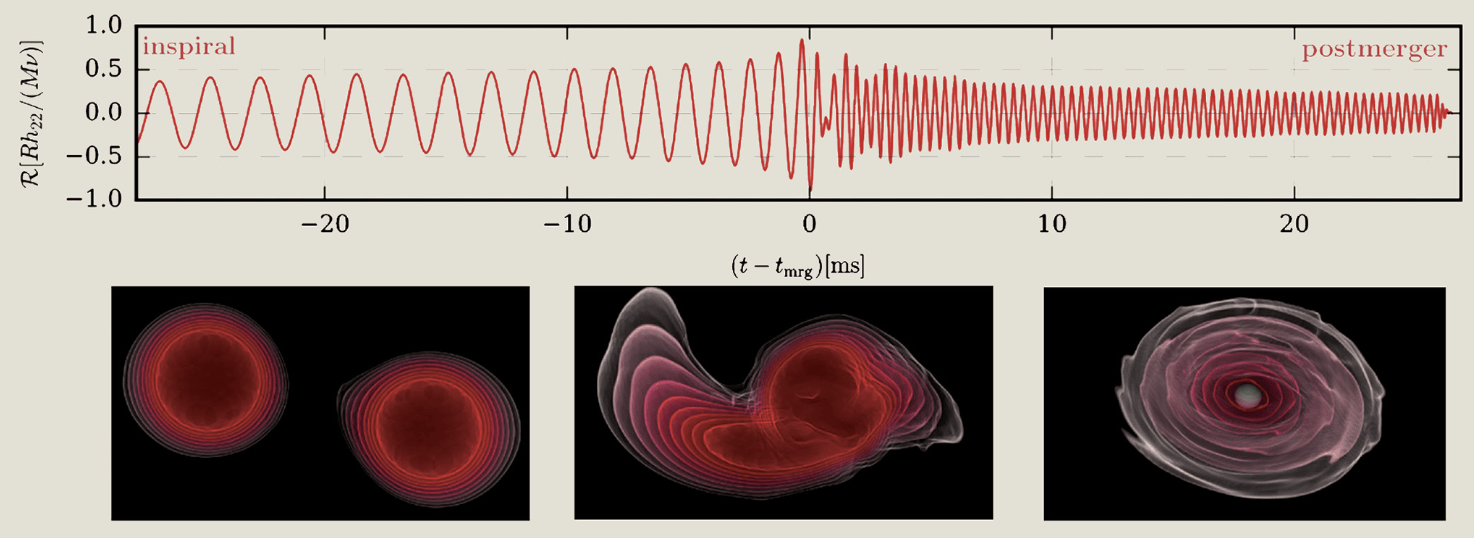
Designed image: T. Dietrich, T. Hinderer, and A. Samajdar: published in General Relativity and Gravitation (2021) 53:27 https://doi.org/10.1007/s10714-020-02751-6 PPGF UNIFAL-MG/UFSJ International Conference on Multimessenger Astrophysics
School of Science and Technology - UFRN - Jul 2024
Overview
- Basic structure of Neutron Stars.
- The equation of state (EoS).
- Astrophysics of Neutron Stars.
- Constrains and measurements of the radii and mass.
- Nuclear physics and Neutron Stars (can be omitted).
- Conclusions
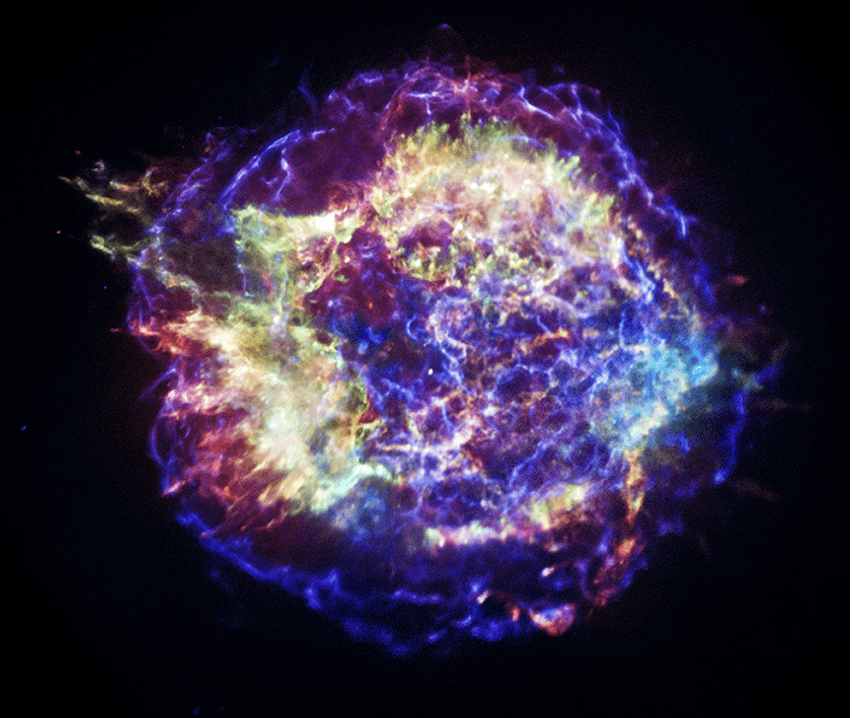
Cassiopeia A is the remnant of a supernovae explosion that was witnessed in the northern sky about 300 years ago.
The image was created using NASA’s Chandra x-ray observatory
https://www.nasa.gov/image-article/exploring-third-dimension-of-cassiopeia/For a star of small mass the white-dwarf stage is an initial step towards complete extinction. A star of large mass cannot pass into the white-dwarf stage and one is left speculating on other possibilities.
-
In 1931, Subramanyan Chandrasekhar realized that as electrons become relativistic, the pressure support weakens and white dwarf stars emerge when the mass is greater than about 1.4 solar masses.
History. Compact stars.
Subramanyan Chandrasekhar
The Maximum Mass of Ideal White Dwarfs
With all reserve we advance the view that supernovae represent the transition from ordinary stars into “neutron stars”, which in their final stages consist of extremely closed packed neutrons.
-
In 1933, Walter Baade and Fritz Zwick coined the name "Neutron Stars":


Walter Baade
Fritz Zwick
Remarks on Super-Novae and Cosmic Rays
History. Compact stars.
-
It is speculated that Lev Landau improvised the concept of neutron stars in a discussion with Bohr and Rosenfeld, in Zurich in February 1931.

-
In 1932, Lev Landau wrote seminal paper:
all stars heavier than 1.5\(\odot\) certainly possess regions in which the laws of quan- tum mechanics (and therefore of qantum statistics) are violated.
On the theory of stars
History. Compact stars.
Lev Landau
-
In 1939, Tolman, Oppenheimer and Volkoff calculated the structure of neutron stars employing Einstein's theory of general relativity.
Richard Tolman
https://en.wikipedia.org/wiki/Richard_C._Tolmanhttps://pt.wikipedia.org/wiki/Robert_Oppenheimerhttps://ahf.nuclearmuseum.org/ahf/profile/george-volkoff/Robert Oppenheimer
George Volkoff
On Massive Neutron Cores
Static Solutions of Einstein's Field Equations for Spheres of Fluid



History. Compact stars.
-
In 1967, Jocelyn Bell discovered “pulsars” identified as rapidly rotating neutron stars.
-
Jocelyn Bell found an extremely stable periodic radio signal with a period of 1.337302088331 seconds.
-
Later, the idea was consolidated that pulsars are magnetized neutron stars, rotating rapidly (PSR B1919+21”).
-
The Caranguejo pulsar, discovered in 1968, has a very short period of 33.09112 milliseconds.

History. Compact stars.
-
Do not burn nuclear fuel in order to thermally withstand gravitational collapse.
-
Mark the end of stellar evolution.
Gravitational collapse is sustained due to repulsive interactions between particles and not exclusively due to neutron degeneracy pressure.
Corona Australis ConstellationRX J1856.6-3754 -- Pulsar
-
The NS are objects with densities above those achieved in research laboratories: \(\rho_{0,nuclear \,matter} = 2.5 \times 10^{14}\text{g.cm}^{-3} \equiv (0.15 \pm 0.01) \text{ fm}^{-3} \).
C. J. Horowitz, J. Piekarewicz, and Brendan Reed Phys. Rev. C 102, 044321 Structure. Neutron stars.
-
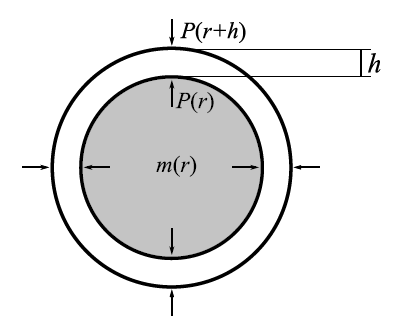
The numerical solution requires only two conditions:
-
Central pressure at the origin: \(P(0)=P_c\);
-
Mass at origin \(M(0) = 0\).
-
The relation \(M-R\) is derived from the Tolman-Oppenheimer-Volkoff (TOV) solution, which for a static and spherically symmetric system are:
-
The radius and mass are determined as the point at which the pressure goes to zero \(P(R)=0\) and the total mass is the value of the mass enclosed in such radius \(M=M(R)\) .
R. F. P. Mendes, Cadernos de Astronomia, vol. 2, n.2, 58-70 (2021).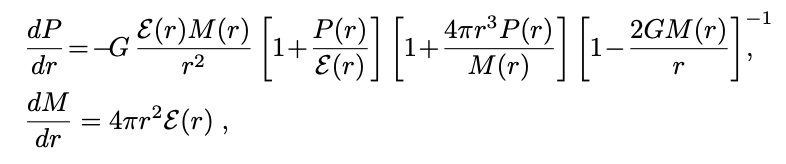
Structure. Neutron stars.
-
For a relativistic neutron gas, the equation of state is given by the pair of equations (toy model):
Equation of state. Neutron stars.
Irina Sager, Eur. J. Phys. 27 (2006) 577–610
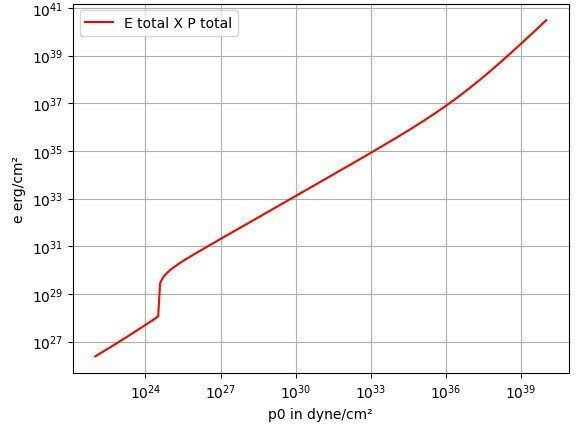
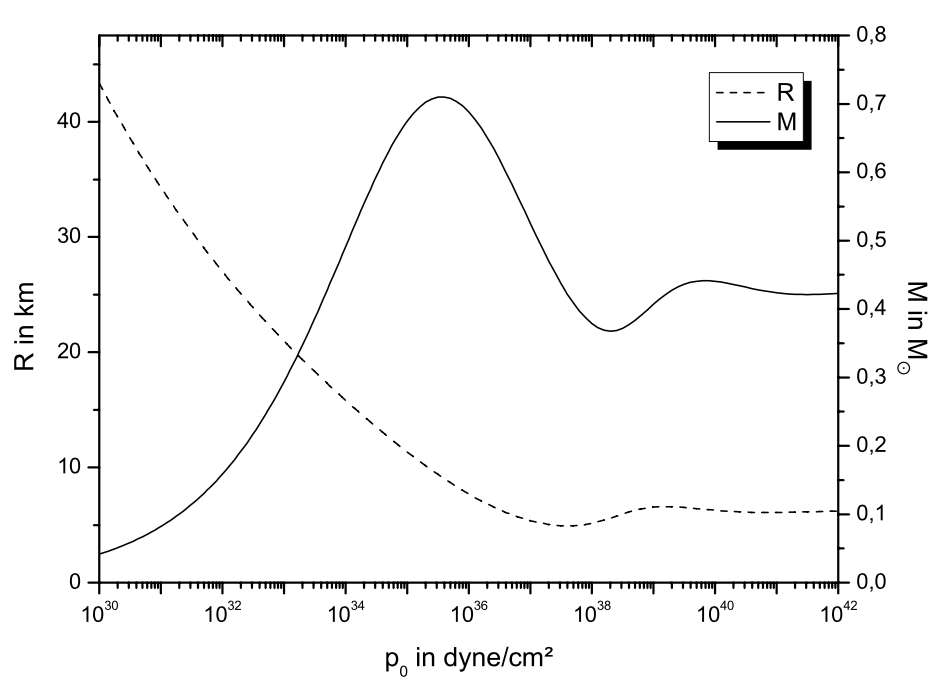
Equation of state. Neutron stars.
-
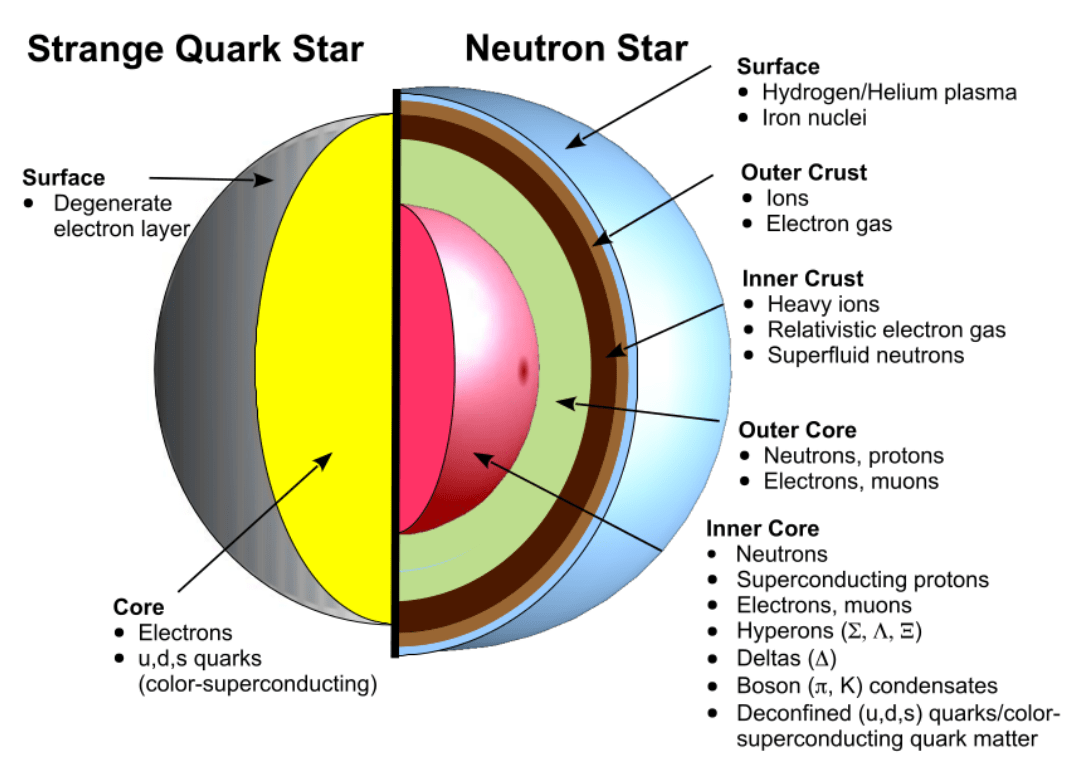
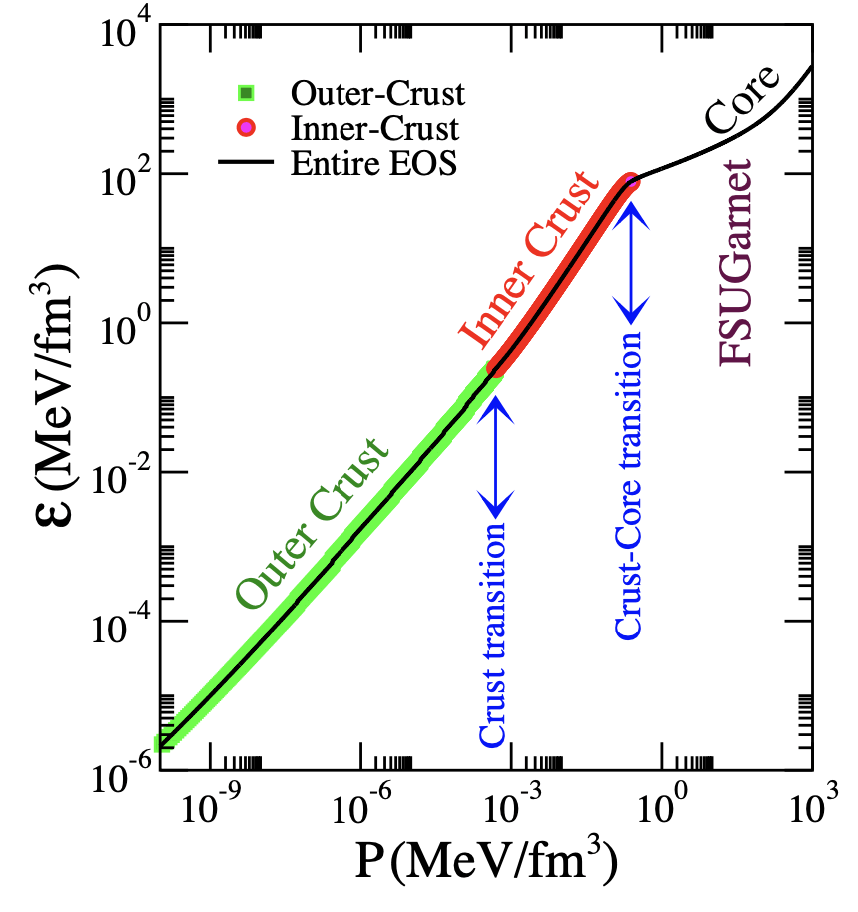
Realistic EOS should match the distinct densities between the neutron star's crust and core:
W.-C. Chen and J. Piekarewicz, Phys. Lett. B748, 284 (2015). Equation of state. Neutron stars.
-
A collection of EoS core within a model of nuclear matter that is based on a relativistic field theory approach:
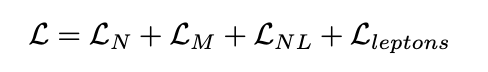
nucleons (Dirac)
mesons (first order interaction)
mesons (superior order interaction)
leptons (Dirac)
-
The energy density of the baryons and leptons are given by the following expressions:
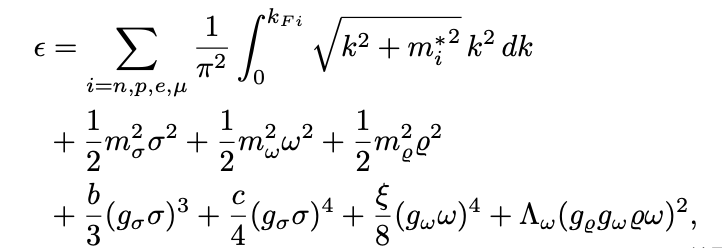
-
The pressure is then determined from the thermodynamic relation:
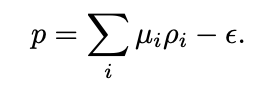
Sk Md Adil Imam et al., arXiv:2401.06018v2 -
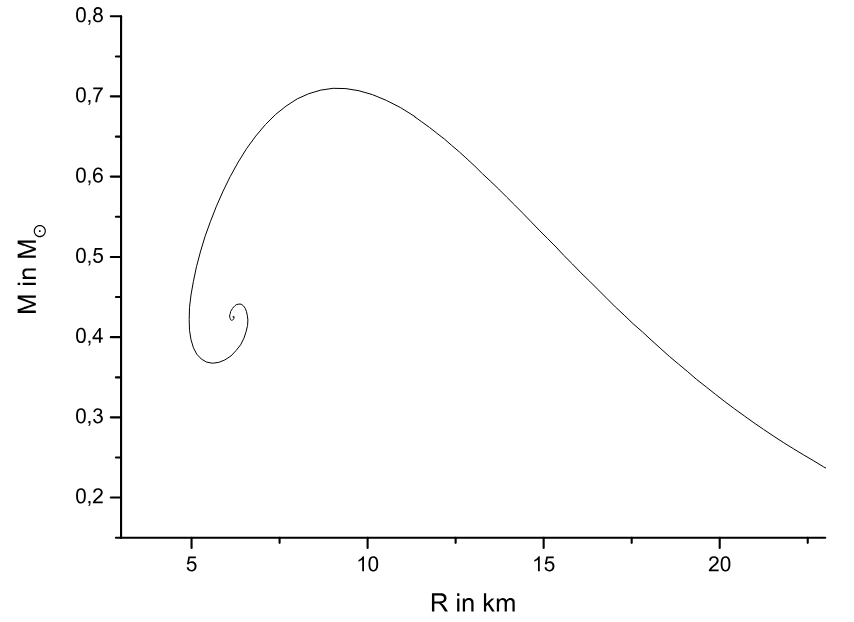
Each EoS model predicts a different curve on the mass x radius diagram. Plot show Mass x Radius (plot before Ligo/Virgo).
P. Demorest, T. Pennucci, S. Ransom, M. Roberts & J. W. T. Hessels, arXiv:1010.5788v1, 2010.Astrophysics. Neutron stars.
J. Antoniadis, P. C. Freire, N. Wex, T. M. Tauris, R. S. Lynch, et al., Science 340, 6131 (2013), arXiv:1304.6875 [astro-ph.HE]. -
The first constraint for the EoS comes from the observation of two-solar-mass \(2M_{\odot}\) stars.
-
The mass-radius curve must support massive enough stars, \(M_{max} \approx\) 2M⊙.
-
This requires that the EoS be stiff enough.
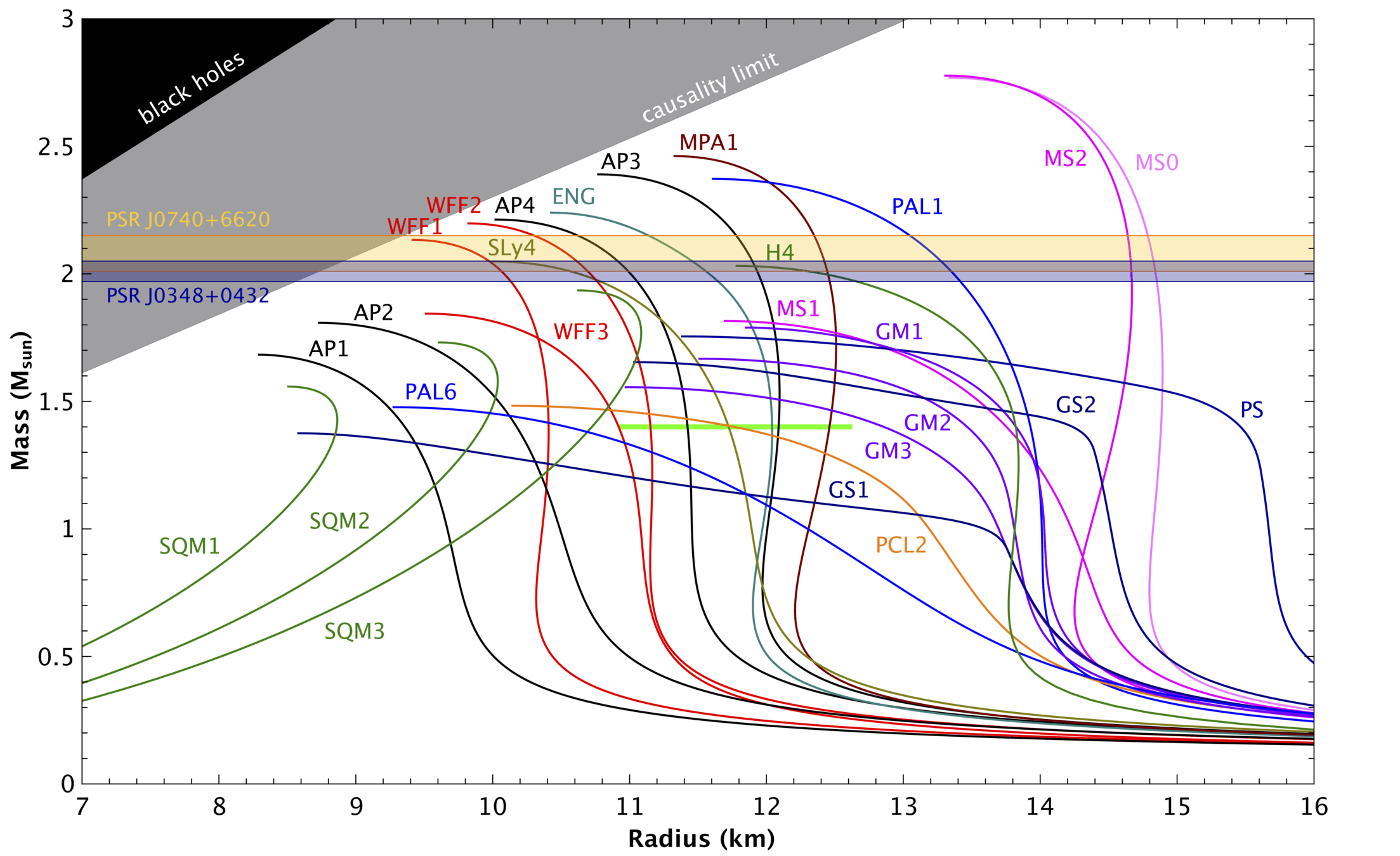
- Currently, thousands of neutron stars have been identified.
P. Freire e V. V. Krishnan, 2024. Pulsar mass measurements and tests of general relativity
- The masses are in a range of 1.2 to 2.1 solar masses.
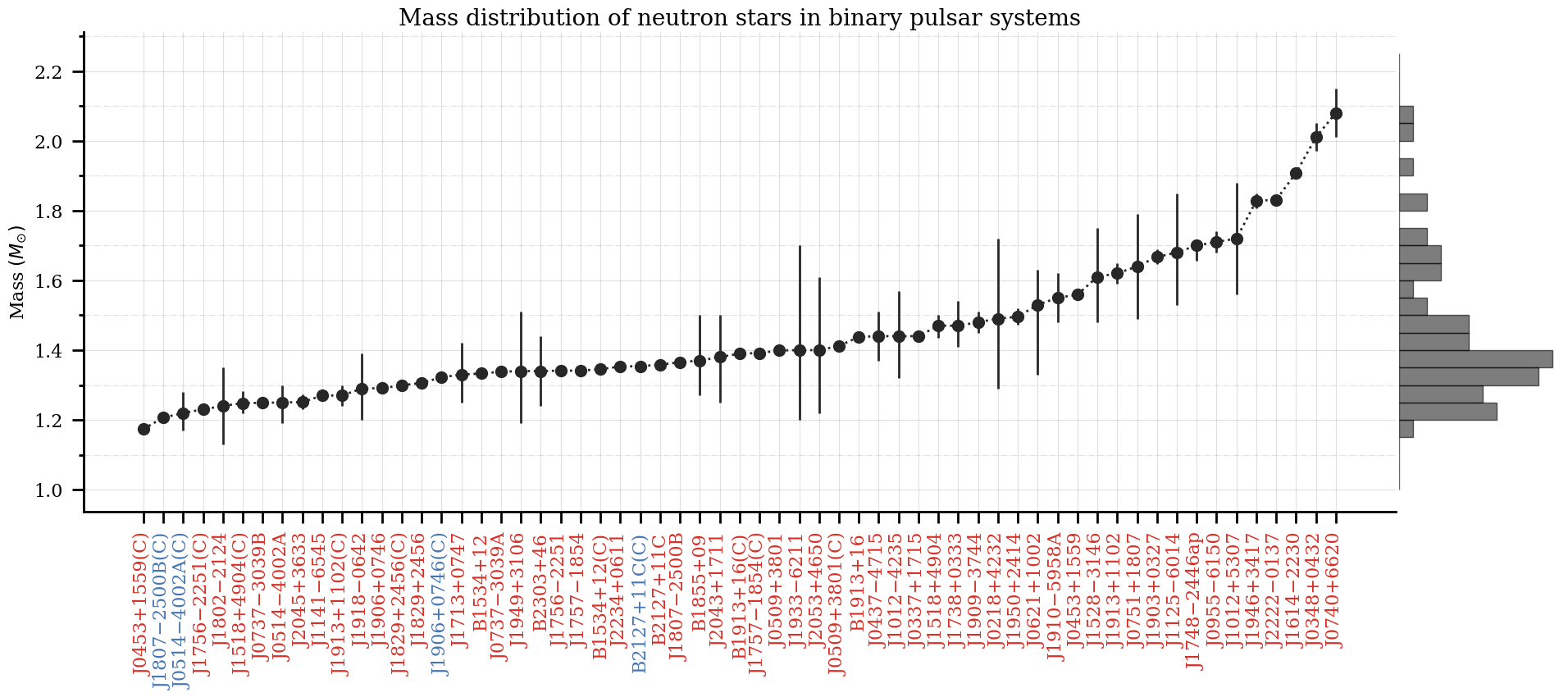
Astrophysics. Neutron stars.
Astrophysics. Neutron stars.
Nils Andersson, J. Astrophys. Astr. (2017) : 38:58
Adapted from J. Read J.S. Read et al, Phys. Rev. D 88, 044042 (2013) - The GW strain is related to the intrinsic properties of the binary source as:
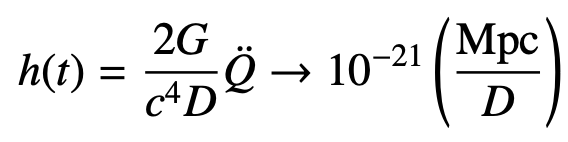
where D is the distance to the source and Q is the induced, time-varying mass quadrupole.
- In the case of GW170817, with the source at a distance of 40 Mpc, the gravitational wave strain is of the \(h\sim 2.5\times 10^{-23}\).

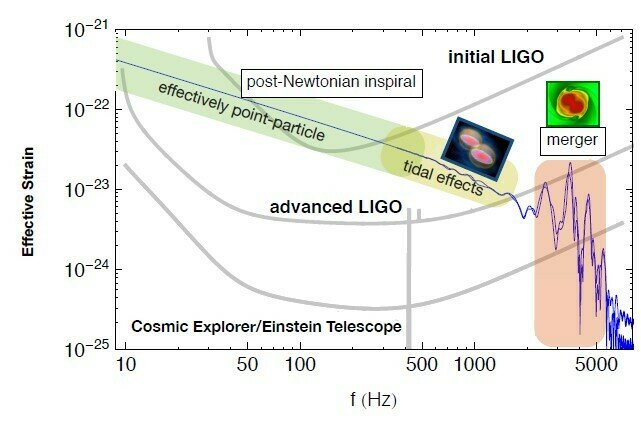
- Encoded in the GW signal are matter effects imprinted in the tidal deformability. In the linear regime the induced mass quadrupole (\(Q\)) is proportional to the tidal field ( \(\mathcal{E}_{ij}\) ) from the companion star :
and \(k_2\) is the dimensionless second Love number, and \(M\) and \(R\) are the stellar mass and radius, respectively. \(R_S\) é o raio de Shwarchild.
where the dimenisonless tidal deformability \(\Lambda\) is given by:
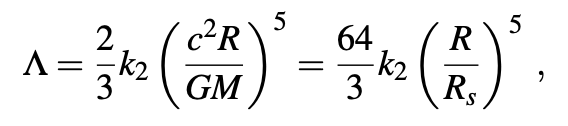
Q_{ij}=-\Lambda \mathcal{E}_{ij}
- The \(\Lambda\) is an intrinsic neutron-star property highly sensitive to the stellar compactness (\(\xi=R/R_S\)) that describes the tendency of a neutron star to develop a mass quadrupole as a response to the tidal field induced by its companion. \(k_2\) encodes the compressibility of the stellar fluid.
Astrophysics. Neutron stars.
Andreas Zacchi, arXiv:2007.00423v1.Bounds on the properties of GW170817 presented in the LIGO original paper are 90% posterior probability intervals that enclose systematic differences from currently available waveform models.
Astrophysics. Neutron stars.

B. P. Abbott et al., PRL 119, 161101 (2017) 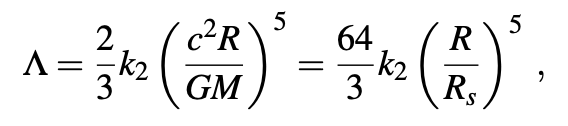
-
Tidal polarizabilities \(\Lambda_1\) and \(\Lambda_2\) associated with the high-mass \(M_1=1.4M_{\odot}\) and low-mass \(M_1=1.33M_{\odot}\) components of GW170817 and 10 relativistic models.
Astrophysics. Neutron stars.
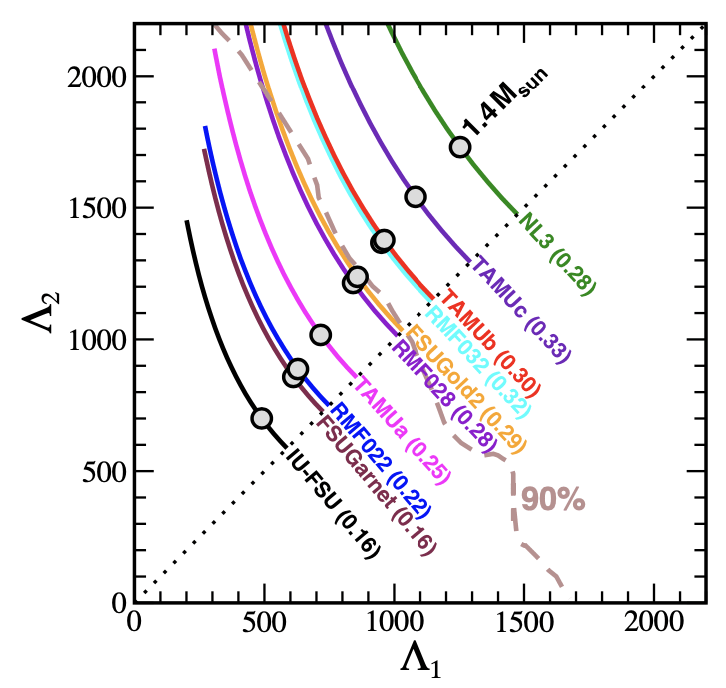
F.J.Fattoyev, Phys. Rev. Lett., vol. 120, no. 17, p. 172702, 2018. -
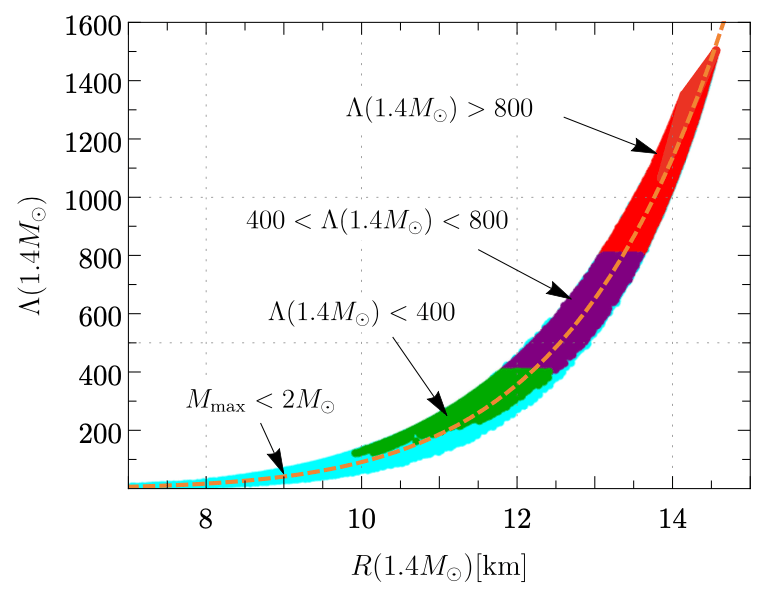
Models to the right side of the 90% probability contour extracted from the low-spin scenario of GW170817 are ruled out because \(R(1.4M_{\odot})\) is too large.
-
The \(\Lambda < 800\) limite require that the EoS be soft enough.
Less compact
More compact
-
For a 1.4 M⊙ neutron star, limits on the tidal polarizability translate into an associated stellar radius of \(R(1.4M_{\odot}) < 13.6\) km.
The mass-radius clouds corresponding to EoS considering data from original paper of the GW170817 where Tidal polarizabilities limit is \(\Lambda_{1.4} < 800\).
Astrophysics. Neutron stars.
E. Annala, T. Gorda, A. Kurkela, and A. Vuorinen, Phys. Rev. Lett., vol. 120, no. 17, p. 172703, 2018. 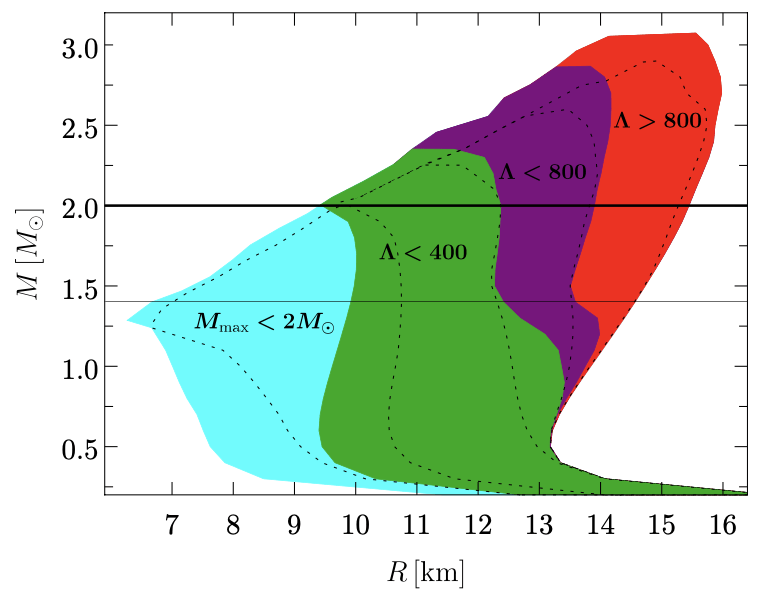
-
As hard EoS lead to stars with large radii and large tidal deformabilities, an upper bound on \(\Lambda\) brackets the EoS from a direction opposite the \(2M_{\odot}\) observation.
-
The \(2M_{\odot}\) constraint implies \(R(1.4M_{\odot})\) > 9.9 km.
The new limit from the \(\Lambda\) measurement reads \(R(1.4M_{\odot})\) < 13.6 km.
-
From follow-up paper of GW170817 event the LIGO/Virgo collaboration reported a tidal deformability of \(\Lambda_{1.4} = 190^{+390}_{-120}\) and the stellar radius of the two coalescing stars suggest a common radius of \(R_{1} = 10.8^{+2.0}_{-1.7}\) km and \(R_{2} = 10.7^{+2.1}_{-1.5}\) km, at the 90% confidence level.
B.P. Abbott et al., Phys. Rev. Lett. 121, 161101 (2018).Astrophysics. Neutron stars.
-
Relatively small value of \(\Lambda_{1.4}\) suggests that neutron stars are fairly compact, thereby favoring a soft equation of state
-
To constrain the EOS, NICER (Neutron star Interior Composition Explorer) relies on the powerful technique of Pulse Profile Modeling to monitor electromagnetic emission from the hot spots located on the surface of the neutron star.
-
As the neutron star spins, the hot spots come in and out of view producing periodic variations in the brightness.
-
The gravitational field around the neutron star is so strong, that x-rays emitted from the back of the star get bent and are eventually detected by NICER's sophisticated instruments.
Astrophysics. Neutron stars.
https://science.nasa.gov/mission/nicer/-
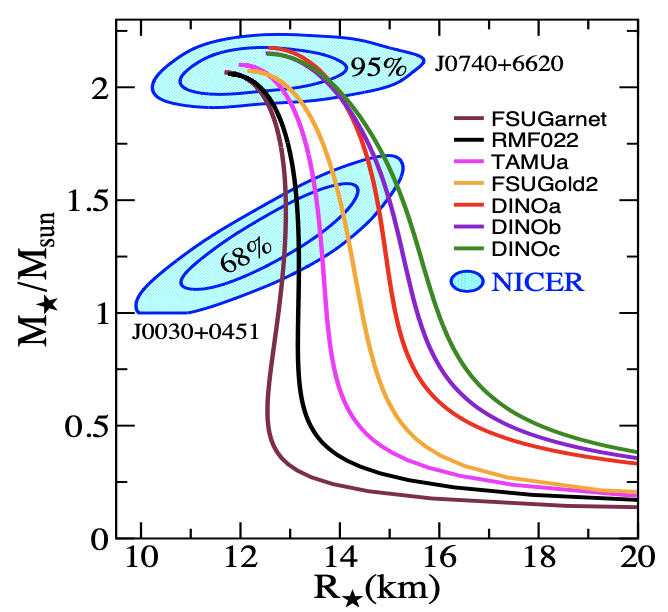
The first mass-radius determination was for the millisecond pulsar PSR J0030+0451 (without independent determination of the mass):
Riley T E et al. 2019 Astrophys. J. Lett. 887 L21Miller M C et al. 2019 Astrophys. J. Lett. 887 L24-
The second mass-radius determination was for the millisecond pulsar PSR J0740+6620 (with independent determination of the mass using Shapiro delay):
-
NICER + tidal deformability from GW170817 data, the radius of 1.4 \(M_{\odot}\):
As it suggests that the equation of state at the highest densities ever probed is not soft.
Astrophysics. Neutron stars.
-
Some RMF models generates an EoS that is sufficiently stiff to support a \(M_{\star}\approx 2M_{\odot}\) neutron star.
J. Piekarewicz,and F.J.Fattoyev, arXiv:1812.09974v1.-
The tidal polarizability extracted from GW170817 allow to infer upper limits on the radius of a \(M_{\star}=1.4 M_{\odot}\) neutron star as \(R_{1.4} < 13.76 \) km.
-
GW170817 provides one of the very few indications that the EOS is soft.
Astrophysics. Neutron stars.
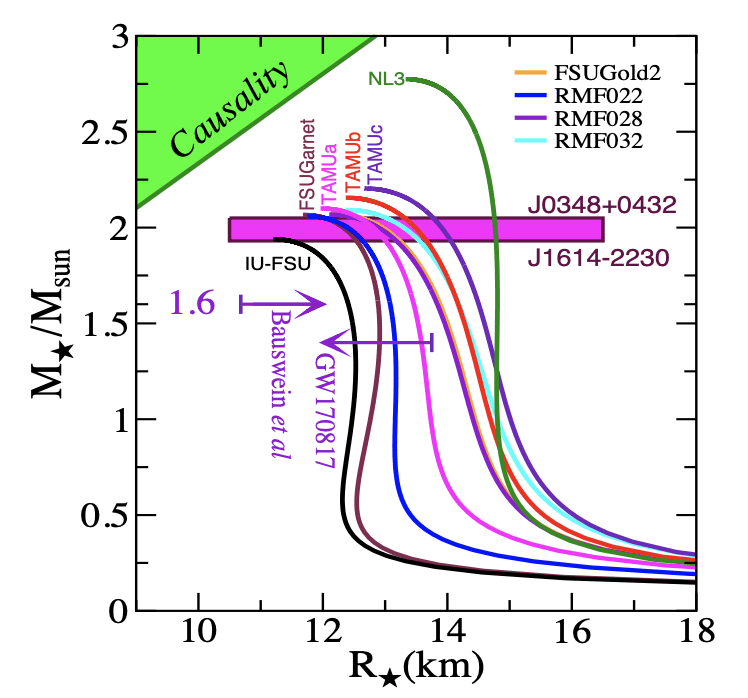
-
Only four models remain consistent with the (\(M_{star}, R_{1.4} \)).
Since then, masses and radii are now available for two-millisecond pulsars: PSR J0030 and PSR J0740.
-
For PSR J0740 the stellar radius is about 12.4 km, suggesting that in the stellar radius-sensitive density regime—about two to three times nuclear saturation—the EOS is not soft.
Jorge Piekarewicz, arXiv:2403.16154v1.
Astrophysics. Neutron stars.
PSR J0740+6620
-
PSR J0030+0451
-
The masses and radii of neutron stars already observed indicate that:
-
The assumption that neutrons behave as a gas of non-interacting fermions does not appear to be realistic.
-
Nuclear interactions can explain the structure, dynamics and composition of neutron stars.
-
BUT different nuclear models are based on distinct specific subsets of free parameters chosen by different experimental calibration methods.
-
Relativistic models should be treated as an effective field theory that can bypass detailed short-distance behavior by calibrating parameters from physical observables.
Conclusions
-
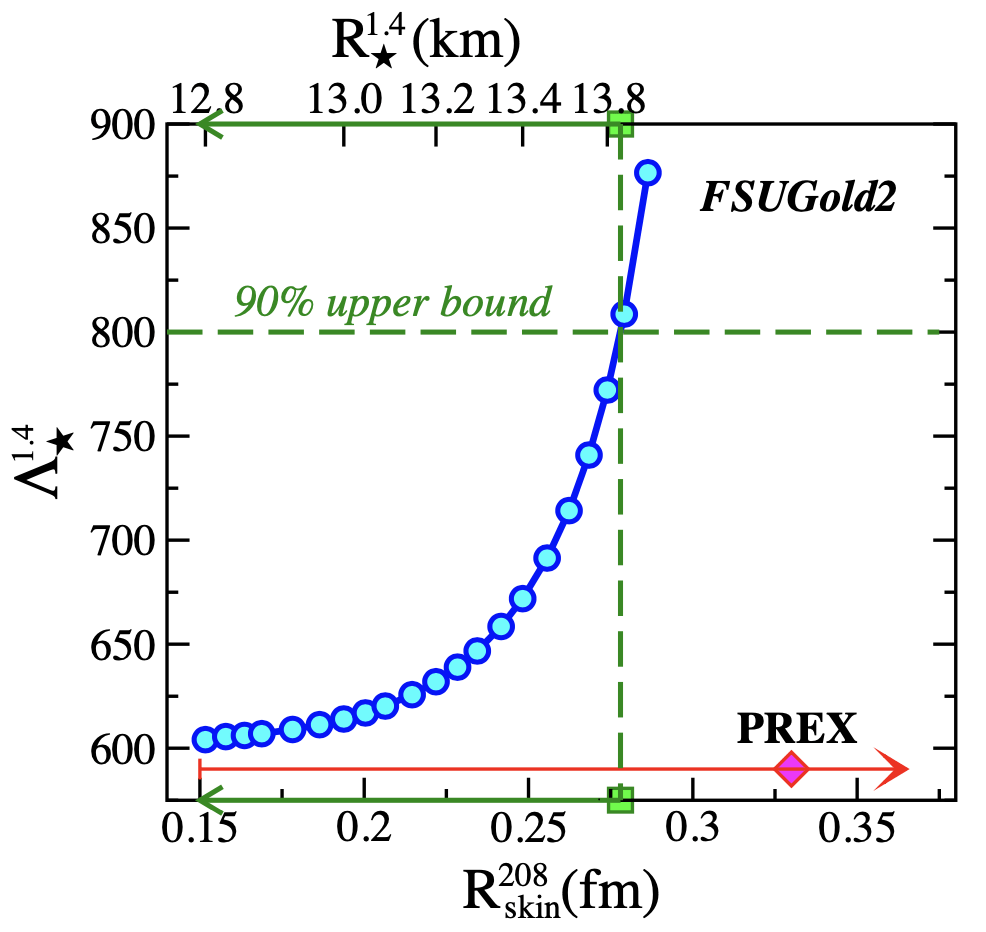
The consequences of the Λ1.4 ≤ 800 limit provided by the LIGO- Virgo collaboration, we deduced a limit on the stellar radius of a 1.4 M neutron star of R1.4 < 13.76 km.
-
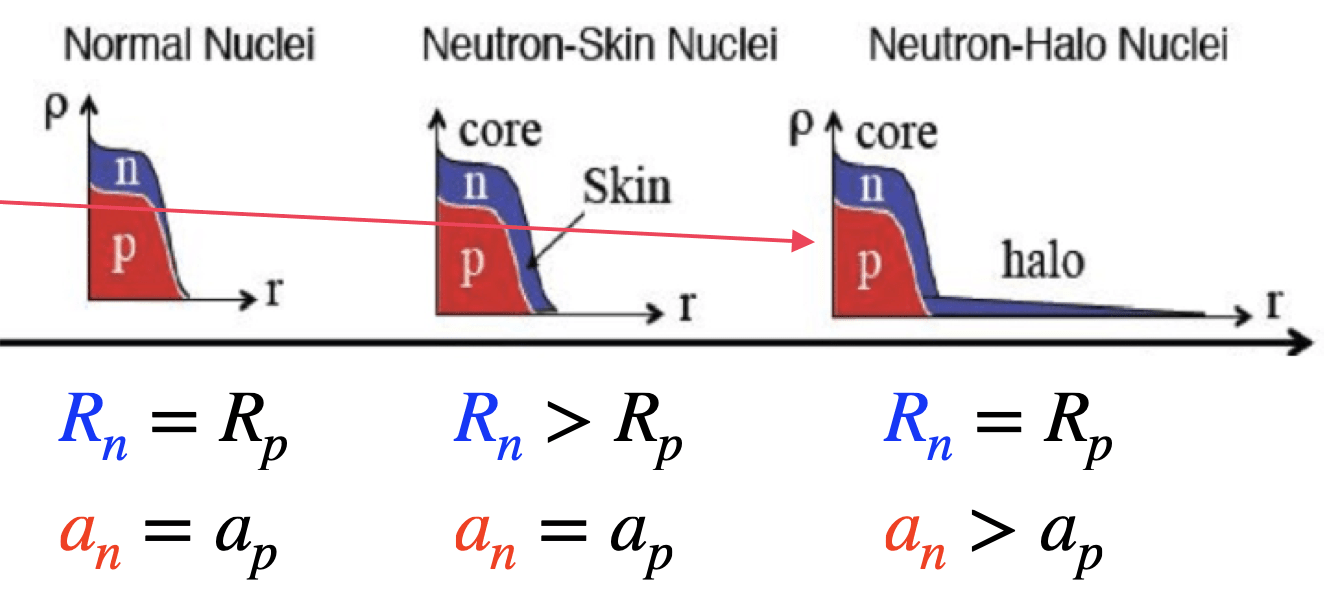
This translates into a neutron-skin thickness of 208Pb of R208 < 0.25 fm, which is well below the upper limit obtained by the PREX collaboration.
-
Relying on PREX lower limit on R208 < 0.33 fm, we were able to provide a lower limit on the tidal polarizability of Λ1.4 > 490.
-
The relatively small neutron-star radii suggested by GW170817 implies that the symmetry energy at higher densities is soft.
The evolution from stiff to soft may be indicative of a phase transition in the neutron-star interior.
Conclusions
EXTRA
-
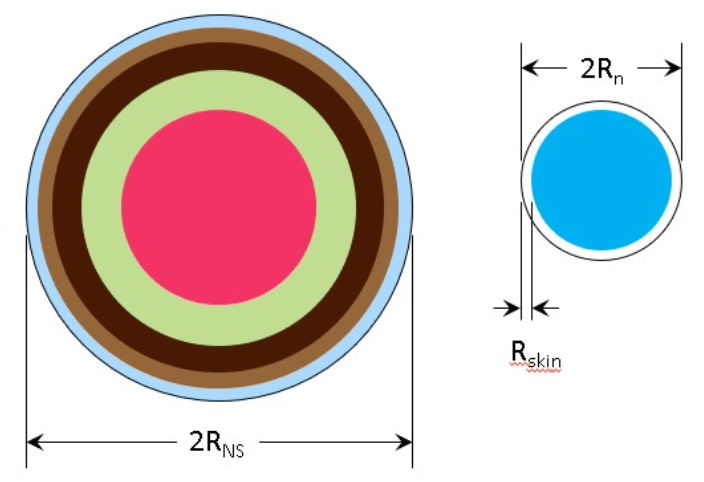
A neutron star (left) is 18 orders of magnitude larger than a Pb nucleus (right, not to scale). However, the star is made of the same neutrons with the same strong interactions and equation of state.
J. M. Mammei, et al. arXiv:2311.06146v1
Nuclear physics experiments. Neutron stars.
-
The difference between these two radii is known as the neutron skin thickness, a dilute region of the nucleus populated primarily by neutrons.
-
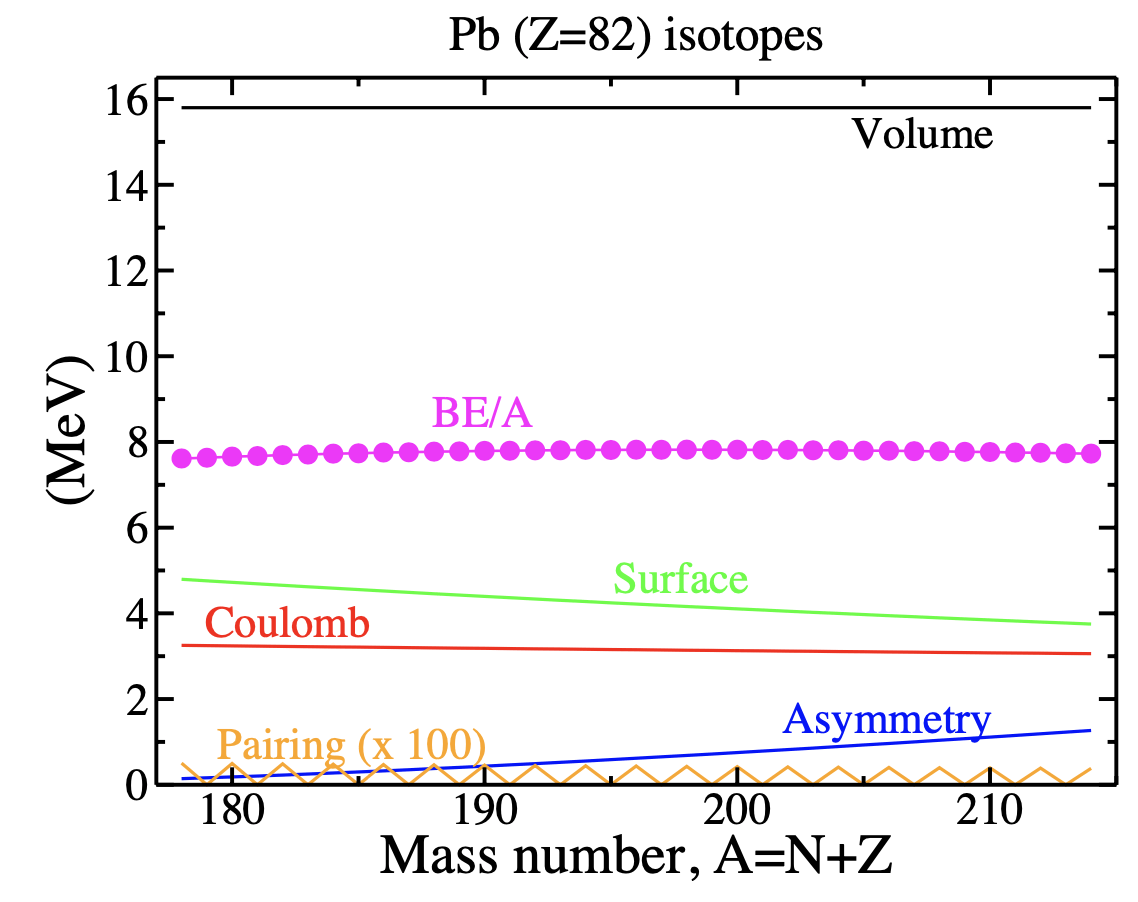
A simple equation based on the Liquid Drop model and used to obtain the well known Bethe-Weizsacker (BW) mass formula:
Nuclear physics experiments. Neutron stars.
where \(Z\) protons and \(N\) neutrons form an incompressible droplet with a relatively sharp surface.
-
Only Neutrons:
Or Neutron-Stars:
A Rios, arXiv:2104.12449v1; A Pastore , arXiv:2007.06872v2.-
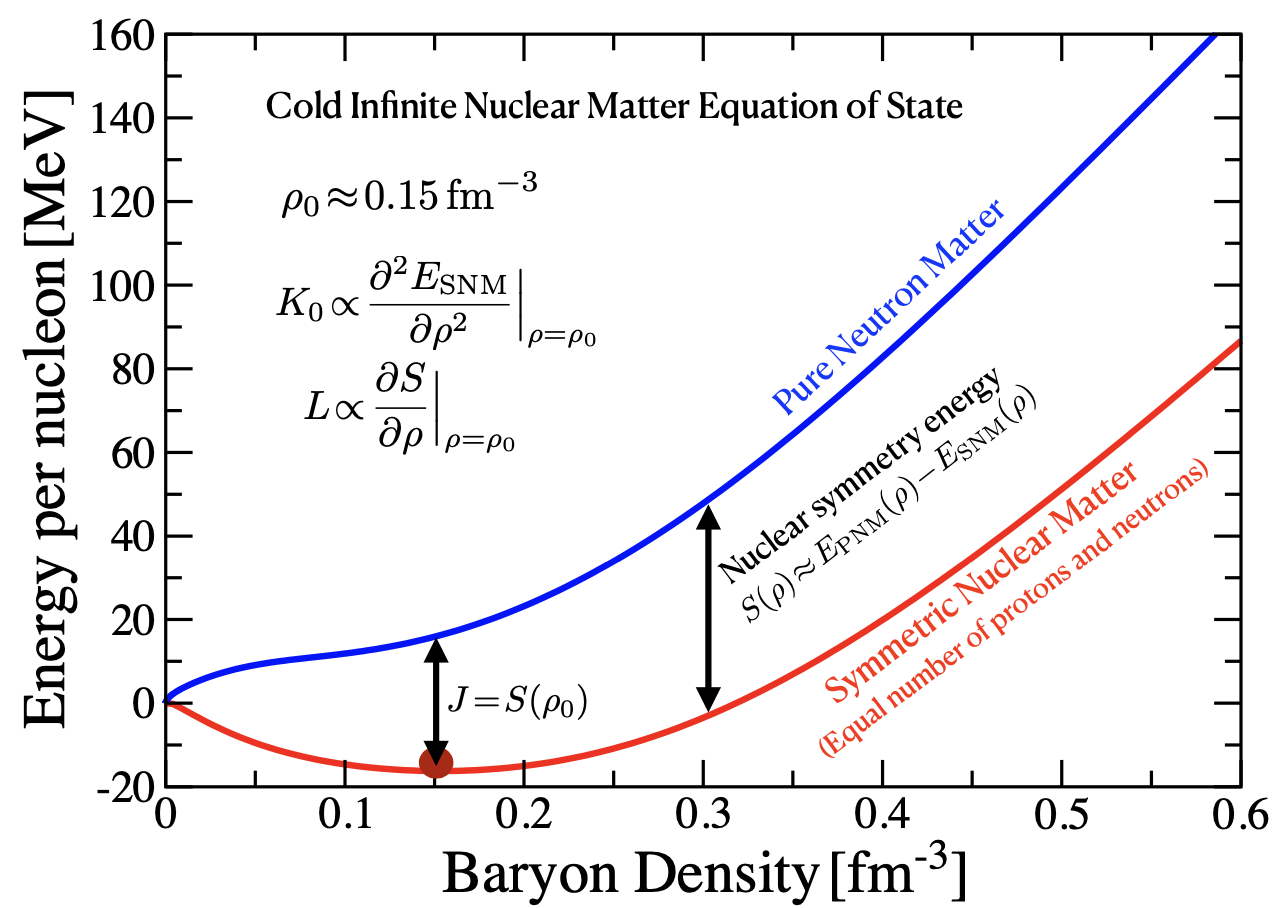
An asymmetric nuclear matter equation of state is obtained:
The energy density of the system is a function of the conserved baryonic density: \(ρ = ρ_n + ρ_p\) and neutron-proton asymmetry: \(α≡(ρ_n−ρ_p)/(ρ_n+ρ_p)\).
-
The equation of state is separated into two contributions:
-
\(\mathcal{E}_{SNM}(\rho) \rightarrow\) Energy per nucleon of symmetric nuclear matter: \(\rho_n=\rho_p\).
-
\(\mathcal{S}(\rho) \rightarrow\) Symmetry energy - the cost required to convert symmetric nuclear matter (\(\alpha = 0\)) in a pure matter of neutrons (\(\alpha = 1)\), that is, to the increase in neutrons:
Nuclear physics experiments. Neutron stars.
-
In the vicinity of the nuclear saturation density, \(\rho_0\), the density dependence of the symmetry energy is parameterized:
-
The slope of the symmetry energy \(L\) is closely related to the pressure of pure neutron matter at the saturation density.
-
\(J\) represents the correction to the binding energy of symmetric nuclear matter; \(L\) dictates how rapidly the symmetry energy increases with density and \(K_{sym}\) represent the incompressibility bulk.
Nuclear physics experiments. Neutron stars.
Symmetric nuclear matter saturates, that is, its pressure disappears at saturation.
-
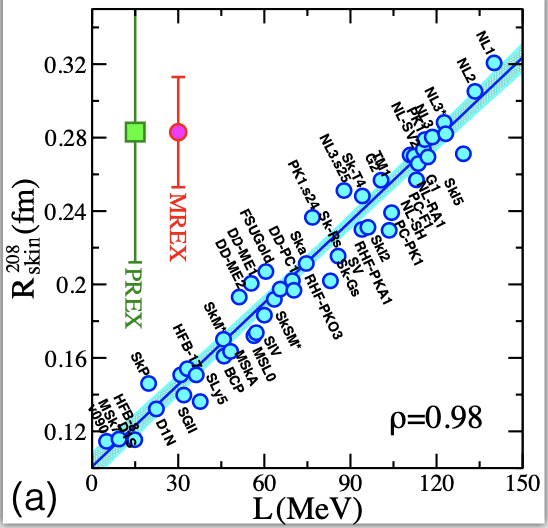
(a) Experiments at PREX and MREX reveal that the neutron thickness of the \(^{208}\)Pb has proven to be an ideal laboratory for constraining EOS.
(b) The neutron radius of a 1.4 M⊙ neutron star versus the slope of the symmetry energy L.
X. Roca-Maza, M. Centelles, X. Viñas, and M. Warda, Phys. Rev. Lett. 106, 252501 (2011).Nuclear physics experiments. Neutron stars.
Nuclear physics experiments. Neutron stars.
F. J. Fattoyev, arXiv:1711.06615v2
-
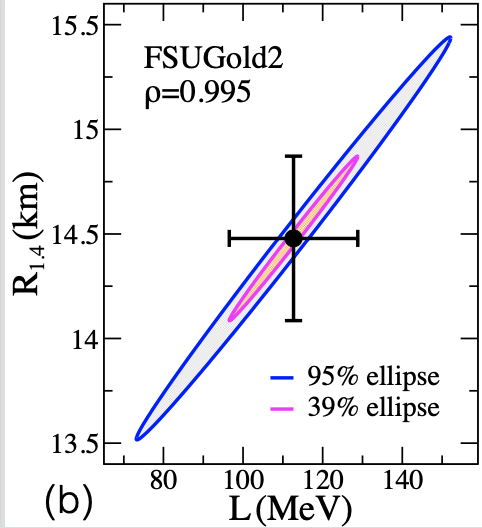
FSUGold2 family to predict the tidal polarizability \(\Lambda_{1.4}\) of a \(1.4M_{\odot}\) neutron star as a function of both \(R^{208}_{skin}\) lead nucleus and \(R_{1.4}\) neutron star.
-
The large value of \(L\) implies a correspondingly large value for the radius of a \(1.4 M_{\odot}\) neutron star of \(13.25 < R_{1.4} < 14.26 \) km suggesting that the symmetry energy is fairly stiff.
These EoSs are further constrained within the Bayesian framework by experimental data and astrophysical observations.
Sk Md Adil Imam, arXiv:2401.06018v2 Nuclear physics experiments. Neutron stars.
These EoSs are further constrained within the Bayesian framework by experimental data and astrophysical observations.
Sk Md Adil Imam, arXiv:2401.06018v2 Nuclear physics experiments. Neutron stars.
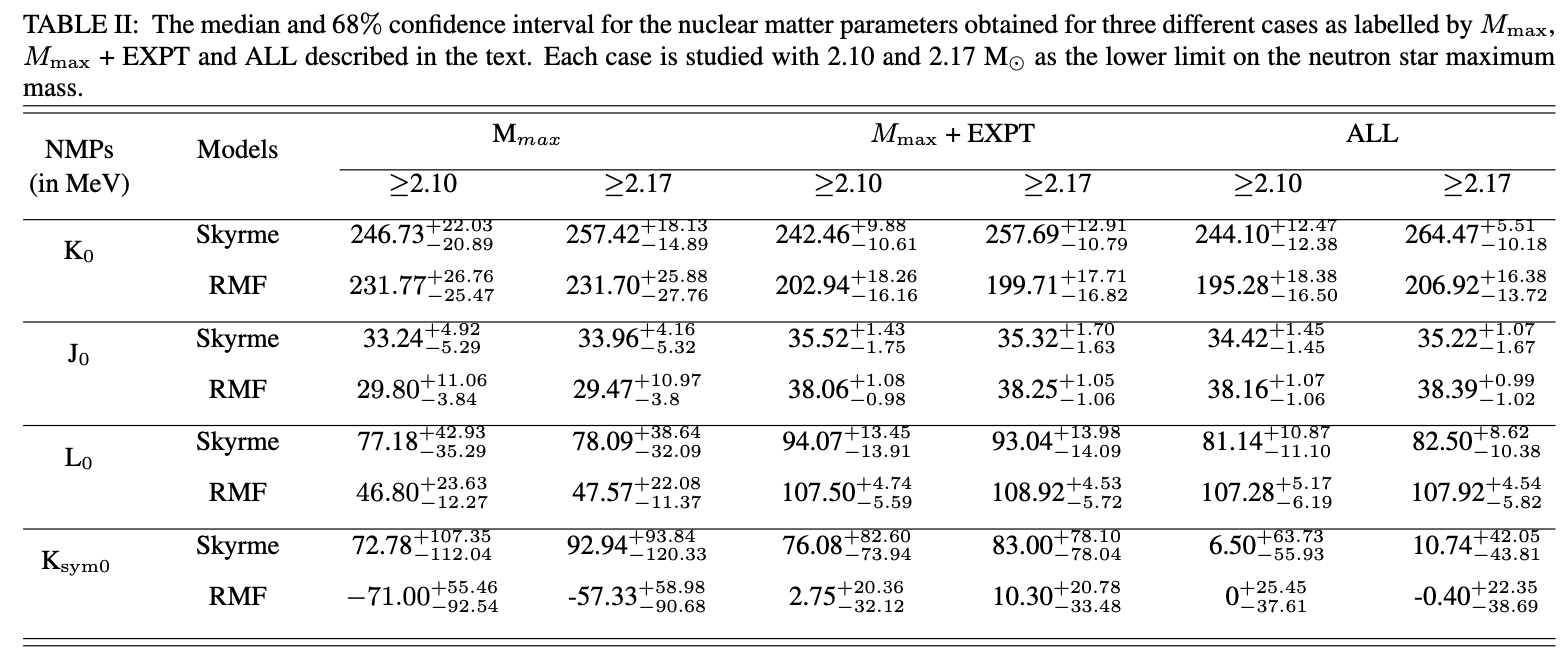
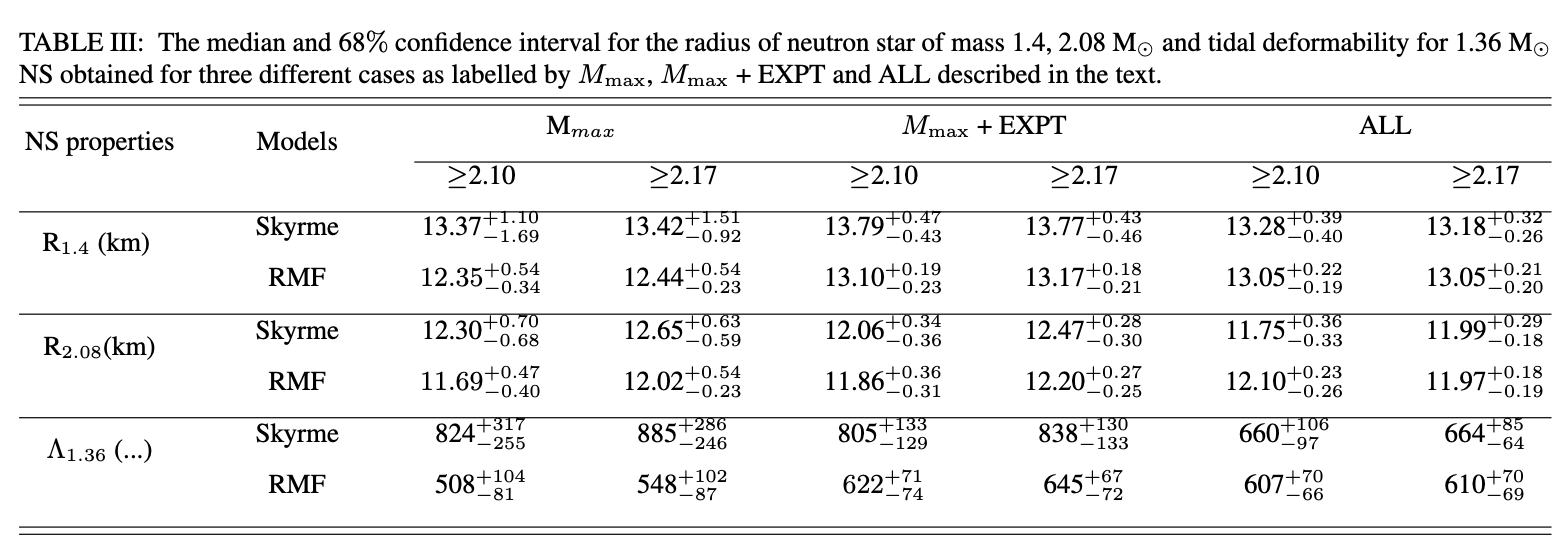
The precise and largely model-independent extraction of the mass of PSR J074 relies on measuring the Shapiro delay.
P.B. Demorest, T. Pennucci, S.M. Ransom, M.S.E. Roberts, and J.W.T. Hessels, Nature 467, 1081 (2010).-
The Shapiro delay amounted to about 20 µs, resulting in a mass determination for PSR J074+6620 of \(M=(2.08\pm 0.07) M_{\odot}\).
Astrophysics. Neutron stars.
Time delay