Pesquisa. Otimizando medidas de aceleração usando um único photogate

Otimizando medidas de aceleração usando um único photogate

Optimizing acceleration measurements using a single photogate

A Bessa, P C Ferreira, R Lisboa. Eur. J. Phys. 42 055003 (2021)

https://docente.ufrn.br/201900340689/perfil

Visão global

Introdução
Medida da aceleração com dois photogates e suas limitações.
Medida da aceleração usando um único photogate
Análise dos efeitos sistemáticos nos sensores
Conclusões

1. Introdução

Entre os conceitos cinemáticos desenvolvidos em um curso introdutório à mecânica, a aceleração é talvez o mais contra-intuitivo para os alunos.

Fonte: https://mundoeducacao.uol.com.br

Normalmente, eles têm problemas para entender o sinal de aceleração, isto é, o sentido da aceleração, nos casos em que há mudanças na direção do movimento e de que a aceleração depende do impulso inicial.

1. Introdução

Apresentamos um método alternativo de medição de aceleração que usa apenas um sensor de tempo, superando parcialmente as limitações de calibração.

Mostramos que este método é consideravelmente mais preciso do que aquele que usa dois sensores de tempo, e seus resultados são menos dependentes do sensor de tempo usado.

1. Introdução

Nosso objetivo é obter melhores medidas de aceleração para laboratórios de mecânica na graduação do Bacharelado em Ciências e Tecnologia (curso de dois ciclos).

A abordagem mais natural para medir a aceleração é, talvez, aquela que deriva da aceleração como a variação na velocidade dividida pelo tempo decorrido correspondente.

a=\frac{\Delta v}{\Delta t}

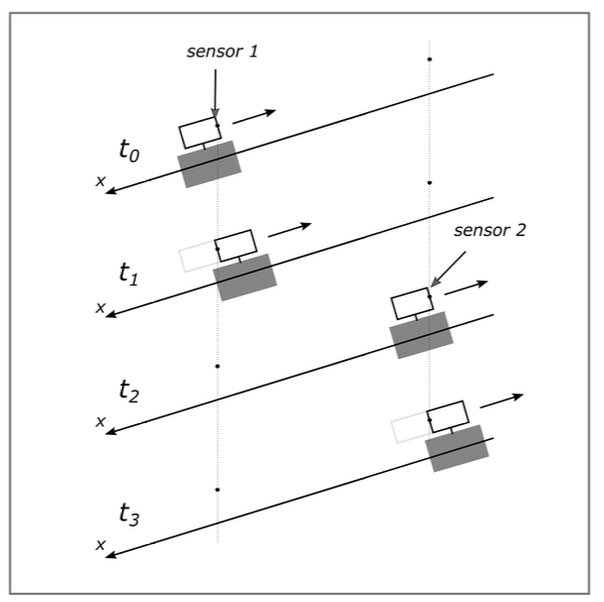
2. Medida da aceleração com dois photogates e suas limitações.

Utilizando um par de sensores de tempo e uma barreira de luz acoplada ao carrinho, é possível medir a aceleração diretamente a partir da equação:

A Bessa, at al 2021 Eur. J. Phys. 42 055003

a_+=\frac{\Delta v}{\Delta t}

=\frac{v_2-v_1}{\Delta t}

v_1=-\frac{L}{\Delta t_1}

v_2=-\frac{L}{\Delta t_2}

\Delta t = \frac{t_2+t_3}{2}-\frac{t_0+t_1}{2}

a_+=\frac{ \left( \frac{L}{\Delta t_1}- \frac{L}{\Delta t_2} \right)}{ \left( \Delta t_{12}+\frac{\Delta t_2}{2}+\frac{\Delta t_1}{2} \right)}

A equação para a aceleração no movimento se subida:

2. Medida da aceleração com dois photogates e suas limitações.

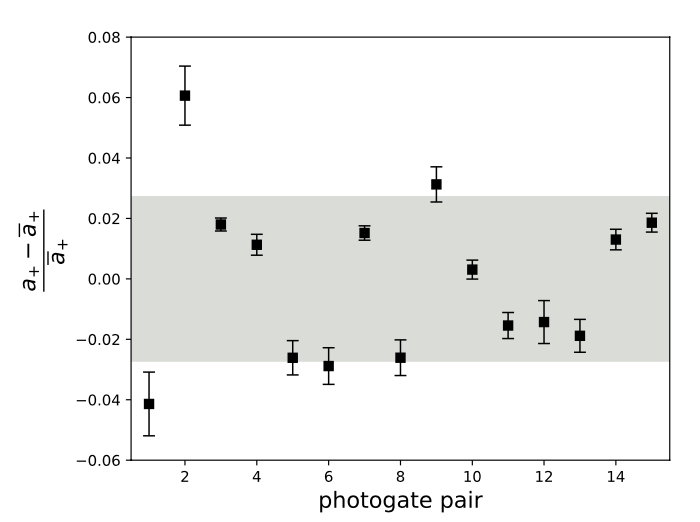
A aceleração média geral foi determinada como:

\overline{a}_+=(0,42\pm0,01)\text{ m/s}^2

uso de 15 pares diferentes de sensores;

10 lançamentos para cada par de sensores;

distância fixa de 20 cm entre os sensores.

Os valores de aceleração oscilam até 6% em torno da média geral, dependendo do par de sensores de tempo utilizado.

A Bessa, at al 2021 Eur. J. Phys. 42 055003

2. Medida da aceleração com dois photogates e suas limitações.

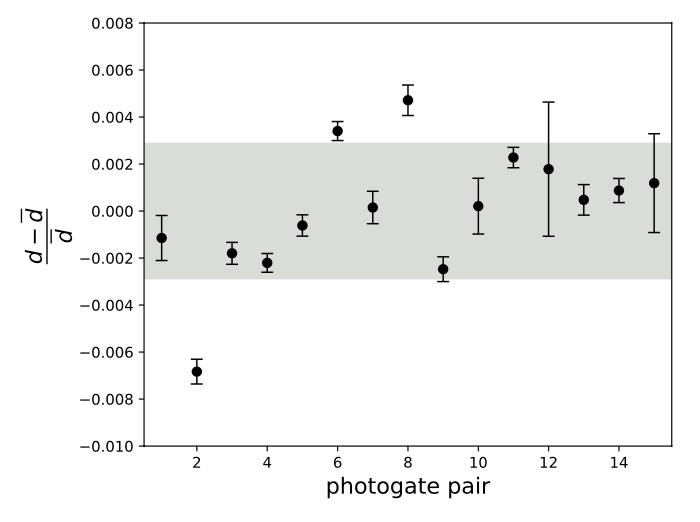
O deslocamento do carrinho, apresenta variações significativamente menores.

d = \frac{v_1^2-v_2^2}{2a_+}=\frac{1}{2} \left( \frac{L}{\Delta t_1}- \frac{L}{\Delta t_2} \right) \left( \Delta t_{12}+\frac{\Delta t_2}{2}+\frac{\Delta t_1}{2} \right)

O deslocamento médio geral foi determinado:

\overline d=(0,1999\pm0,0006)\text{ m/s}^2

Os valores do deslocamento oscilam até 0,7% em torno da média geral, dependendo do par de sensores de tempo utilizados. Cerca de 9 vezes menores do que para as acelerações.

A Bessa, at al 2021 Eur. J. Phys. 42 055003

2. Medida da aceleração com dois photogates e suas limitações.

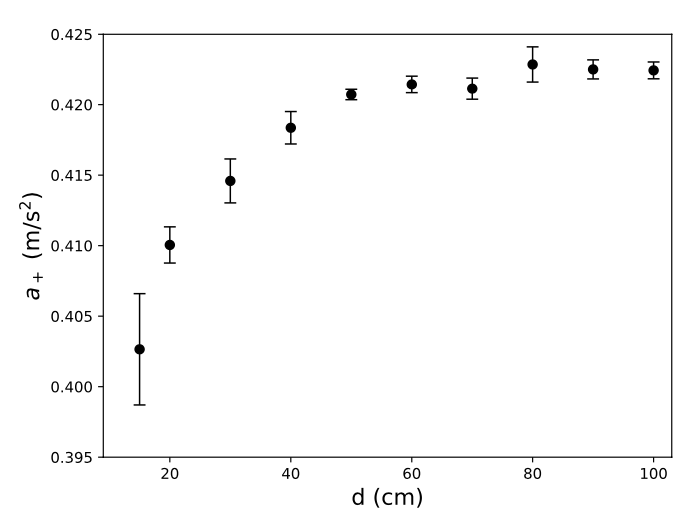
Mostramos a aceleração em função da distância entre os sensores

O gráfico mostra uma variação considerável e inesperada na aceleração quando os sensores são aproximados.

Tais variações significativas invalidam o uso do método de dois sensores para obter e analisar os valores de aceleração.

A Bessa, at al 2021 Eur. J. Phys. 42 055003

3. Medida da aceleração usando um único photogate

A ideia é lançar o carrinho plano acima e realizar as medidas necessárias de intervalos de tempo ao longo do movimento de subida e descida.

\Delta t_{01}=t_1-t_0

\Delta t_{23}=t_3-t_2

\Delta t_{12}=t_2-t_1

(subida)

(descida)

(sobe-desce)

a_{ud}=\frac{\Delta v}{\Delta t}

A aceleração de subida (u) e descida (d) é medida a partir da equação:

a_{ud}=\frac{ \left( \frac{L}{\Delta t_1}+ \frac{L}{\Delta t_2} \right)}{ \left( \Delta t_{12}+\frac{\Delta t_2}{2}+\frac{\Delta t_1}{2} \right)}

A Bessa, at al 2021 Eur. J. Phys. 42 055003

v_1=-\frac{L}{\Delta t_1}

v_2=+\frac{L}{\Delta t_2}

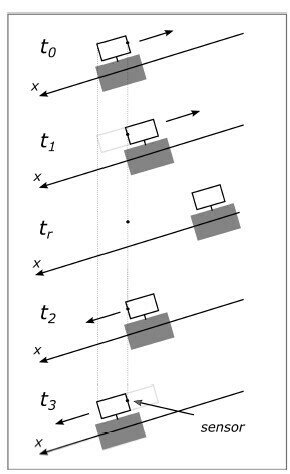
3. Medida da aceleração usando um único photogate

Para explicar o significado da aceleração média medida é necessária uma análise dinâmica do problema, levando em consideração o atrito:

Subida:

a_+=a_0+\delta a

Descida:

a_-=a_0-\delta a

Isso enfatiza que o movimento todo não é um MRUV

a_{\pm}=g\text{sen}\theta\pm\frac{F_a}{m}

Mostramos no nosso trabalho que a aceleração média medida com um único sensor é, com boa aproximação, a aceleração que o carrinho teria se não houvesse atrito:

a_{ud} \simeq a_0

3. Medida da aceleração usando um único photogate

A aceleração média geral foi determinada como:

\overline{a}_{ud}=(0,420\pm0,002)\text{ m/s}^2

uso de 15 pares diferentes de sensores;

10 lançamentos para cada par de sensores;

uma distância fixa de 20 cm entre os sensores.

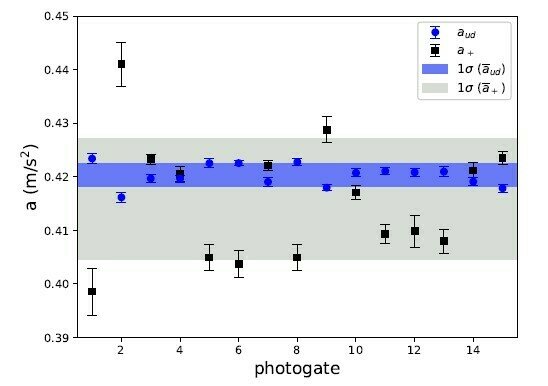
Para medições com um único sensor de tempo, a maior diferença entre sua medição de aceleração e a média geral ocorre para o sensor '2', que é de aproximadamente 1%.

4. Análise dos efeitos sistemáticos nos sensores

Apesar da maior precisão ao usar apenas um sensor de tempo, é importante observar que ainda existem discrepâncias entre as diferentes medições do sensor.

Isso indica que a fonte do erro sistemático persiste.

Os intervalos medidos pelos sensores de tempo estão sujeitos a efeitos indesejados ou inesperados que podem fazer com que um sensor registre sistematicamente intervalos de tempo ligeiramente diferentes de outro.

4. Análise dos efeitos sistemáticos nos sensores

Analisamos o impacto nas grandezas cinemáticas analisadas nas seções 2 e 3 quando há variações de cerca de \(\delta t_2 = 1,3\) ms nas medidas de tempo para o cálculo da aceleração.

Consideramos os valores médios compatíveis com os dados coletados:

v_1=v_2=0,7 \text{ m/s}

a=0,4 \text{ m/s}^2

\left| \frac{a_+ - a_+^{(0)}}{a_+} \right|\approx 45\delta t_2

\left| \frac{d - d^{(0)}}{d} \right|\approx 2\delta t_2

\left| \frac{a_{ud} - a_{ud}^{(0)}}{a_{ud}} \right|\approx 4\delta t_2

Consideramos que apenas o intervalo de tempo \(\Delta t_2 = \Delta t_2^{(0)} +\delta t_2 \) é medido com um efeito sistemático:

5. Conclusões

Mostramos que uma medida simples de aceleração que usa a mudança de velocidade de um carrinho entre dois photogates tem dois problemas:

(i) baixa precisão (aceleração desviada em até 6% do valor médio geral de \(\overline{a}_+\) = (0,42 ± 0,01) m/s\(^2\) , dependendo do par de sensores usado); e

(ii) o valor da aceleração tem uma dependência espúria da distância entre os sensores.

O novo método proposto que usa apenas um sensor de tempo, desviou apenas até 1% da média geral de \(a_{ud}\) = (0,420 ± 0,002) m/s\(^2\), dependendo do sensor usado.

5. Conclusões

Verificamos que medidas de aceleração realizadas com diferentes photogates produzem valores que são estatisticamente incompatíveis entre si, revelando a existência de efeitos sistemáticos.

Mostramos que desvios de calibração de apenas 1,3 ms nos intervalos de tempo registrados podem explicar a sistemática observada.

6. Referências

[1] Bernhard J 2018 Instrum. Sci. 46 819
[2] Liu G and Fang N 2016 Int. J. Eng. Educ. 32 19
[3] Vaara R L and Sasaki D G G 2019 LUMAT: Int. J. Math. Sci. Technol. Educ. 7 1
[4] Martineli F and Pacca J L A 2006 Rev. Bras. Ens. Fís. 28 497
[5] Venable D D, Batra A P and Hubsch T 2001 Phys. Teach. 39 215
[6] Ramirez S A and Ham J S 1990 Phys. Teach. 28 602
[7] Kluk E and Lopez J L 1992 Phys. Teach. 30 48
[8] Schoch F and Winiger W 1991 Phys. Teach. 29 98
[9] PHYWE 2017 PHYWE series of publications, laboratory experiment physics https://repository. curriculab.net/files/versuchsanleitungen/p2130360/p2130360e.pdf (accessed 4 June 2021) [10] Wolbeck J 2010 Phys. Teach. 48 262
[10] Wolbeck J 2010 Phys. Teach. 48 262

6. Referências

[11] Amato J C and Williams R E 2010 Phys. Teach. 48 322
[12] Mosca E P and Ertel J P 1989 Am. J. Phys. 579
[13] Cavalcante M A and Tavolaro C R C 2000 Rev. Bra. Ens. Fís. 22 247

[14] Edmiston M D 2005 https://homepages.bluffton.edu/~edmistonm/double.flag.timing.pdf Unpublished manuscript by Michael D Edmiston at Bluffton University (accessed 4 June 2021)

[15] Hessel R, Canola S R and Vollet D R 2013 Rev. Bra. Ens. Fís. 35 2504
[16] Suwanpayak N, Sutthiyan S, Kulsirirat K, Srisongkram P, Teeka C and Buranasir P 2018 J. Phys.: Conf. Ser. 1144 012001

Obrigado!