Aula 10
Fundamentos da Mecânica
Prof. Ronai Lisbôa
UFRN - ECT - BCT
Objetivos
Estudar sistemas com movimento curvilíneo.
Calcular a aceleração e força centrípetas.
Bibliografia.
Tipler - Cap. 3
Seção 3.3
Tipler - Cap. 5
Seção 5.3
- Refaça alguns exercícios resolvidos.
O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)
Movimento circular é um movimento curvilíneo cuja trajetória é um círculo.
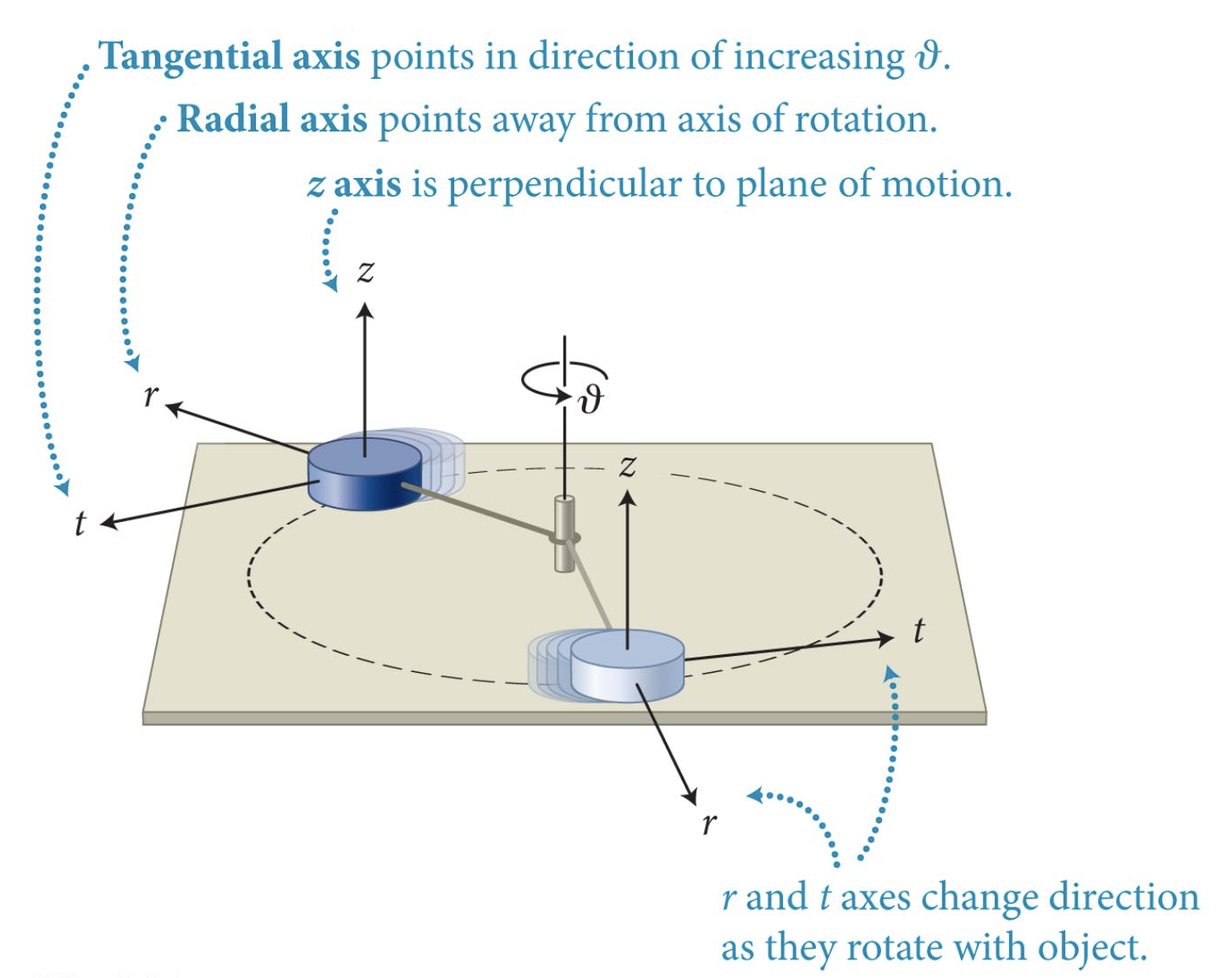
Eixo tangencial e aponta na direção do aumento da coordenada angular.
Eixo radial e aponta para longe do eixo de rotação.
Eixo normal e é perpendicular ao plano de rotação.
Os eixos r e t mudam de direção quando eles giram com o objeto.
Os eixos são perpendiculares e têm a direção dos vetores unitários radial (\(\hat r\)) e tangencial (\(\hat t\)).
Fonte: Eric Mazur
O movimento circular
Mesmo que a velocidade seja constante, uma partícula pode ter aceleração se se mover ao longo de uma trajetória curva, como um círculo.
O movimento circular: Aceleração centrípeta
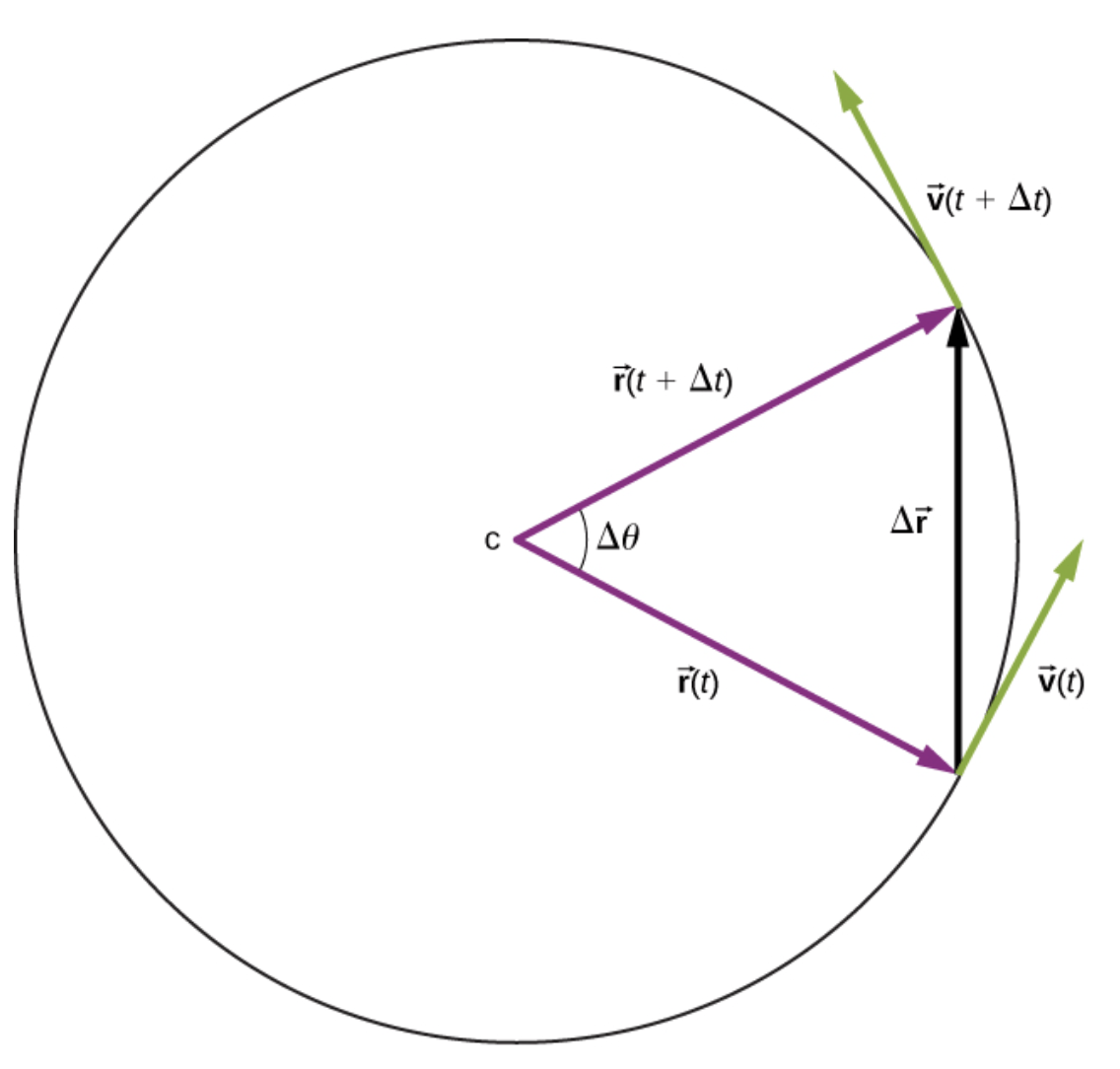
Fonte: Openstax.orgO vetor velocidade tem magnitude constante e é tangente à curva, mas a direção muda num intervalo de tempo, \(\Delta t\):
Como o vetor velocidade \(\vec v(t)\) é perpendicular ao vetor posição \(\vec r(t)\), os triângulos formados pelos vetores posição e \(\Delta \vec r\) , e os vetores velocidade e \(\Delta \vec v\) são semelhantes.
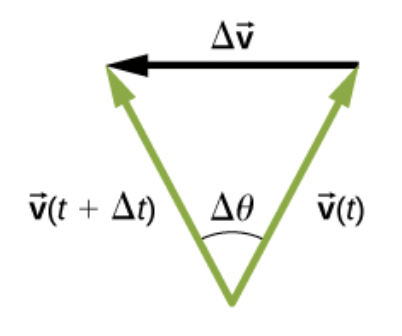
A aceleração centrípeta.
A magnitude da aceleração média:
No limite \(\Delta t \rightarrow 0\), define-se a aceleração centrípeta:
que é direcionada radialmente para dentro da trajetória curvilínea e é perpendicular à velocidade tangente à curva.
A aceleração devido ao movimento circular mantem o objeto se movendo à rapidez \(v_t\) ao longo da circunferência de um círculo de raio \(r\).
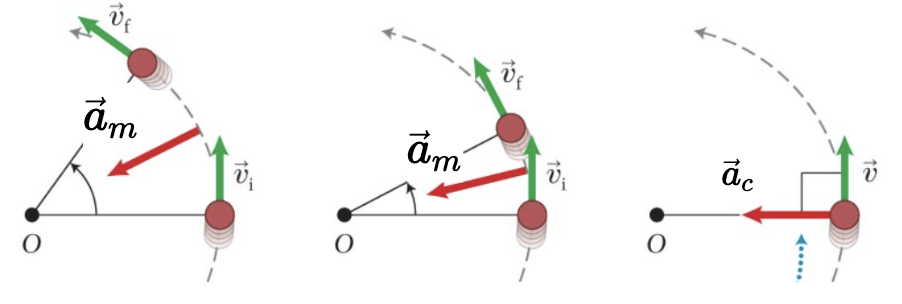
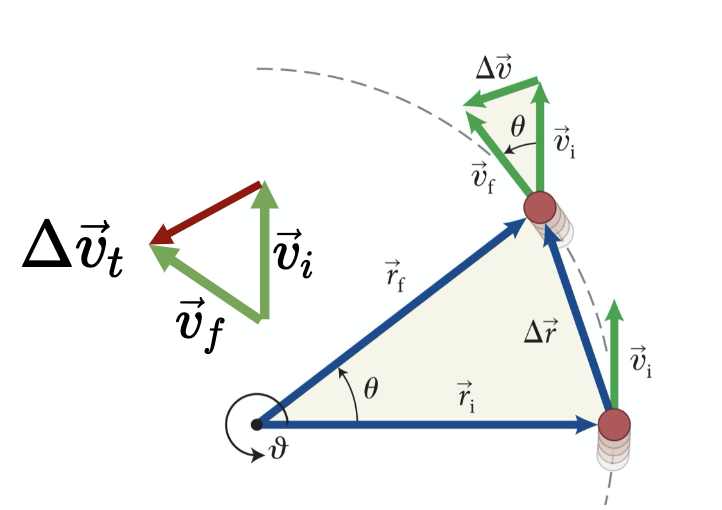
Fonte: Eric Mazur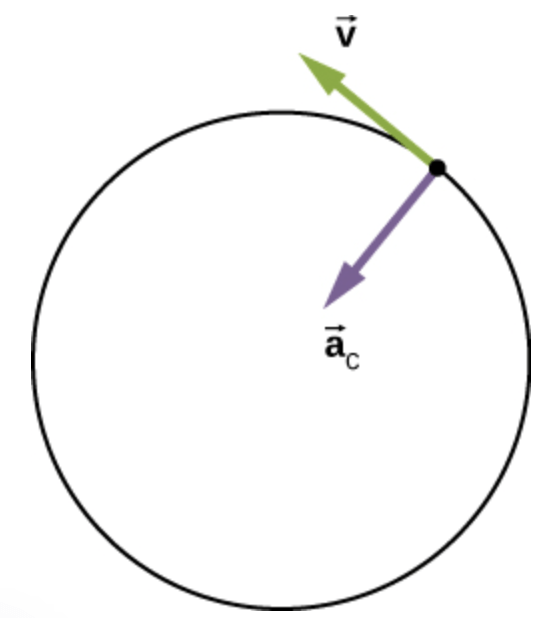
O movimento circular: Aceleração centrípeta



O movimento circular: Aceleração centrípeta
Um jato voa a 134,1 m/s em linha reta e faz uma curva ao longo de uma trajetória circular nivelada com o solo. Qual deve ser o raio do círculo para produzir uma aceleração centrípeta de 1 g no piloto e no jato em direção ao centro da trajetória circular?
Exemplo 1
Quando a rapidez do objeto não é constante temos uma aceleração tangencial.
A aceleração tangencial é uma medida da variação da magnitude da velocidade tangencial.
A aceleração tangencial é tangente à curva e tem a direção da variação da velocidade tangencial:
mas poder ter o mesmo sentido da velocidade tangencial ou sentido oposto.
O movimento circular: Aceleração tangencial
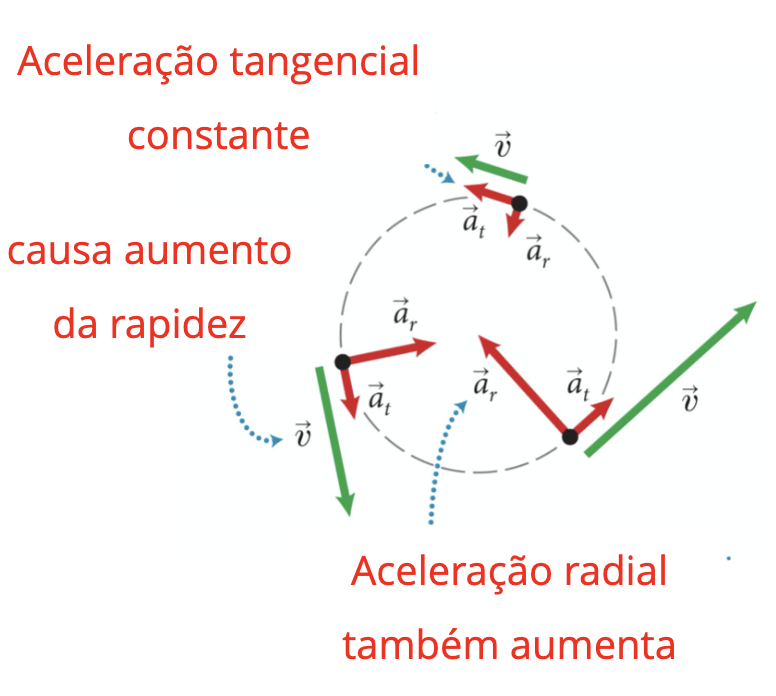
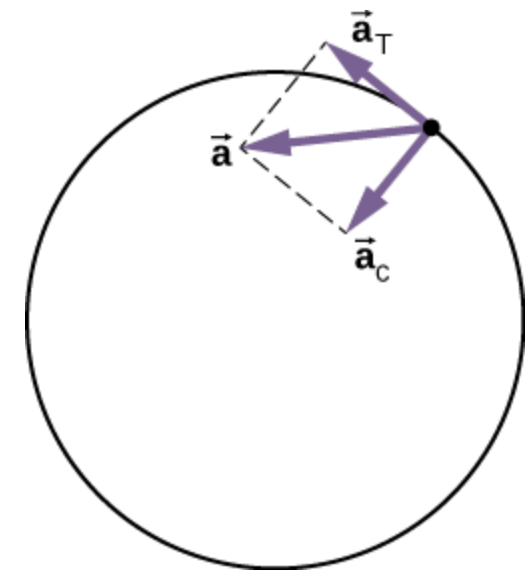

Acelerado
Retardado
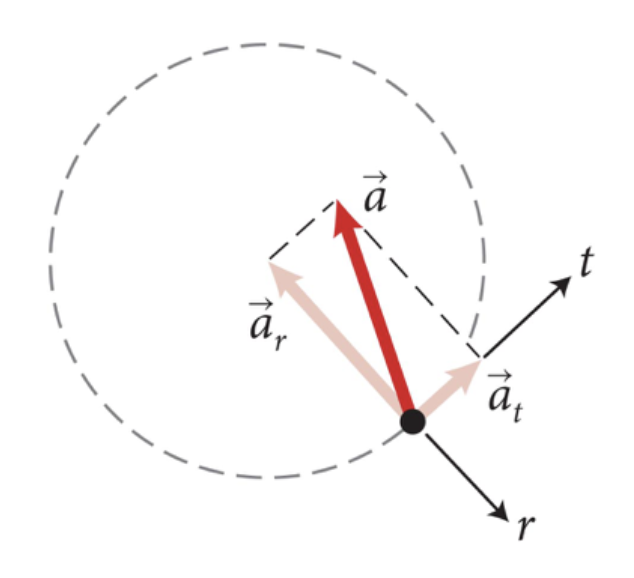
Podemos analisar as aceleração tangencial e centrípeta que estão contidas no plano.
MCU
O movimento circular: Aceleração resultante
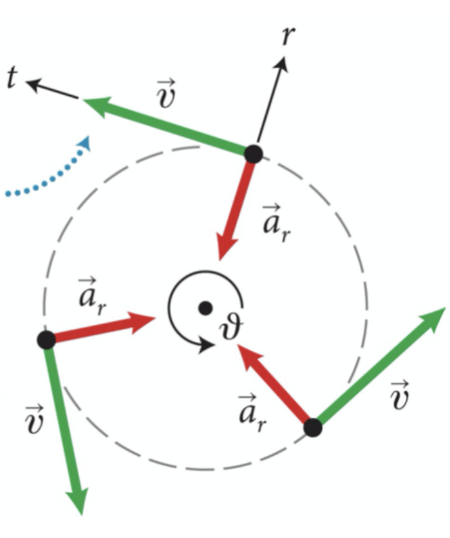
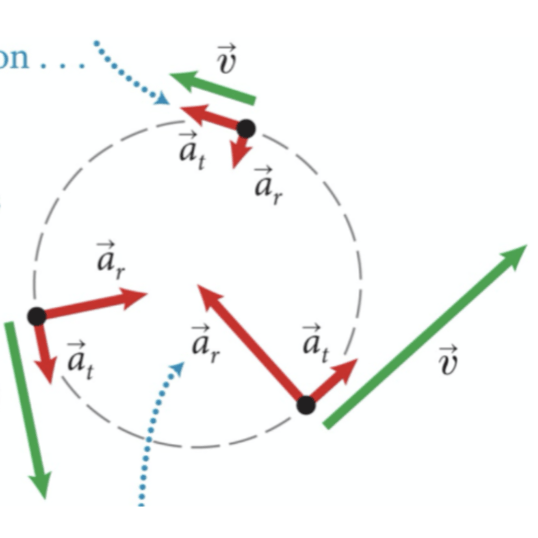
MCUV
Aceleração resultante
Uma partícula movendo-se ao longo da trajetória curva terá acelerações direcionadas como mostrado.
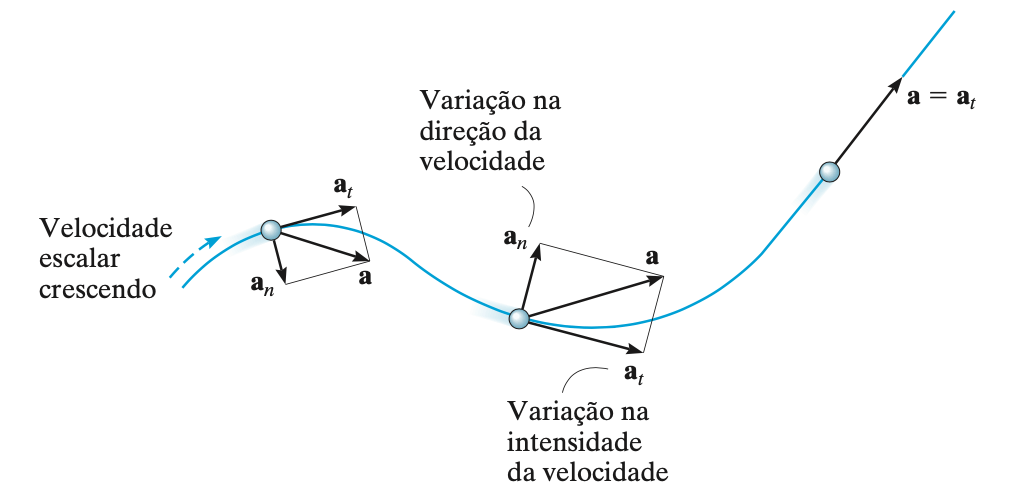
Fonte: Hibbeler
O movimento circular: Aceleração resultante
A aceleração tangencial é sempre tangente à curva, a aceleração centrípeta aponta radialmente para o centro da trajetória. A aceleração resultante aponta para dentro da curva.
Uma partícula move-se num círculo de raio r = 2,0 m. Durante o intervalo de tempo de t = 1,5 s a t = 4,0 s, a sua velocidade varia com o tempo de acordo com:
Exemplo 2
com \(c_1 = 4,0 \text{ m/s}\) e \(c_2 = 6,0 \text{ m.s}\) . Qual é a aceleração total da partícula em t = 2,0 2?
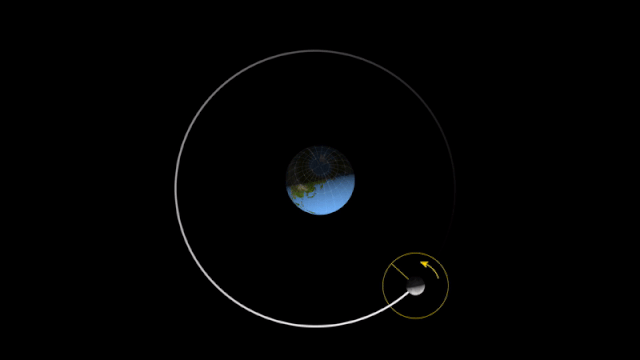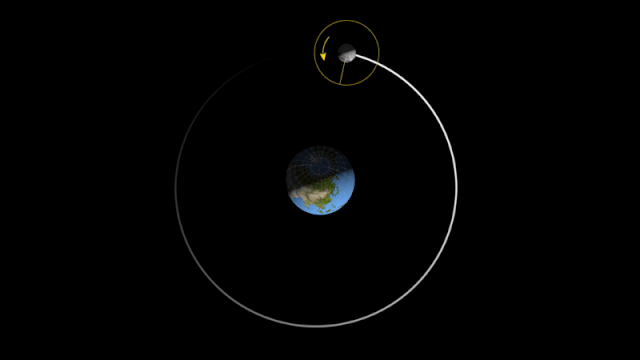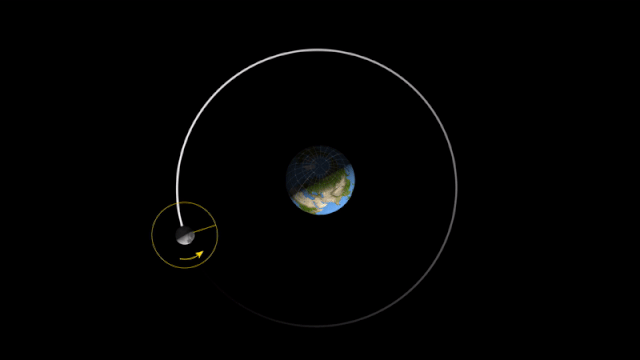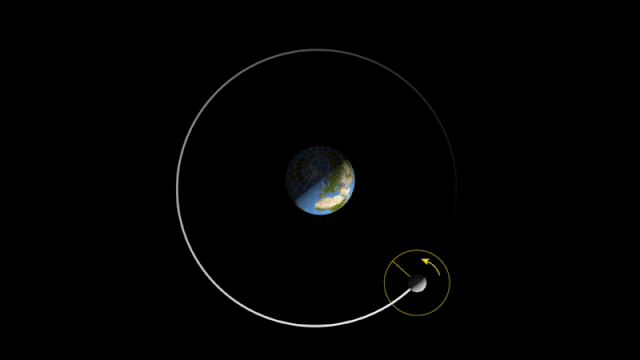
A força centrípeta sobre um objeto em movimento circular à rapidez constante nos diz que a soma vetorial das forças exercidas no objeto deve ser direcionada para o centro do círculo, ajustando continuamente a direção do objeto.

Sem essa soma vetorial de forças apontando para dentro, o objeto se moveria em uma linha reta na direção da velocidade tangencial.
A magnitude da força centrípeta:
A força centrípeta é uma força central que varia a direção da velocidade tangencial instantânea.
A força centrípeta
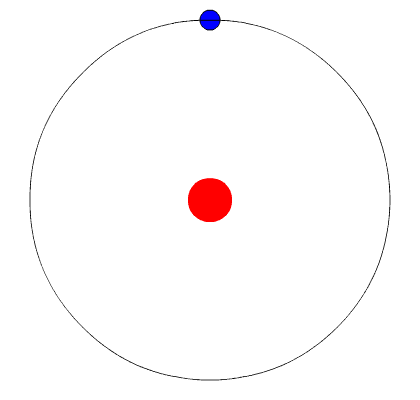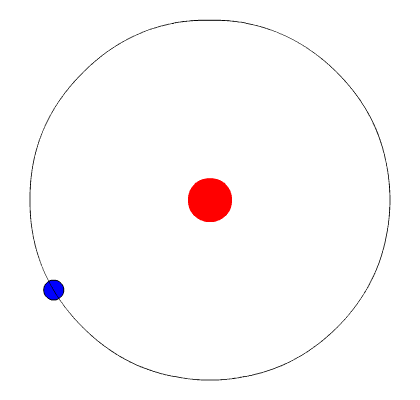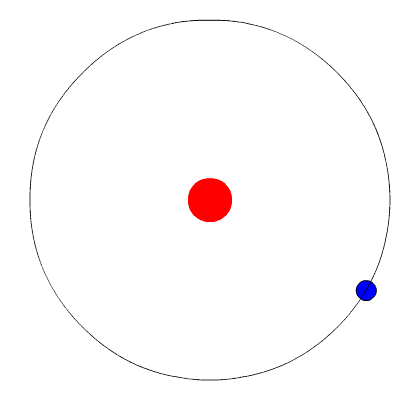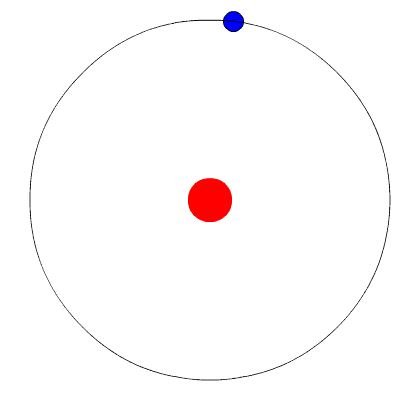
O giro da Terra em torno do Sol está sujeito a uma força central.
A força central não quer dizer que o objeto em movimento circular será atraído para centro.
A força central varia a direção do vetor velocidade tangencial.
Removendo a força centrípeta o objeto vai se mover em linha reta a partir da tangente da trajetória circular e com \(\vec v_t = constante\).
A força centrípeta
Exemplo 3
(a) Calcule a força centrípeta exercida sobre um carro de 900,0 kg que percorre uma curva de raio de 500,0 m a 25,00 m/s. (b) Supondo uma curva sem inclinação, encontre o coeficiente de atrito estático mínimo entre os pneus e a estrada, sendo o atrito estático o motivo que impede o carro de escorregar.
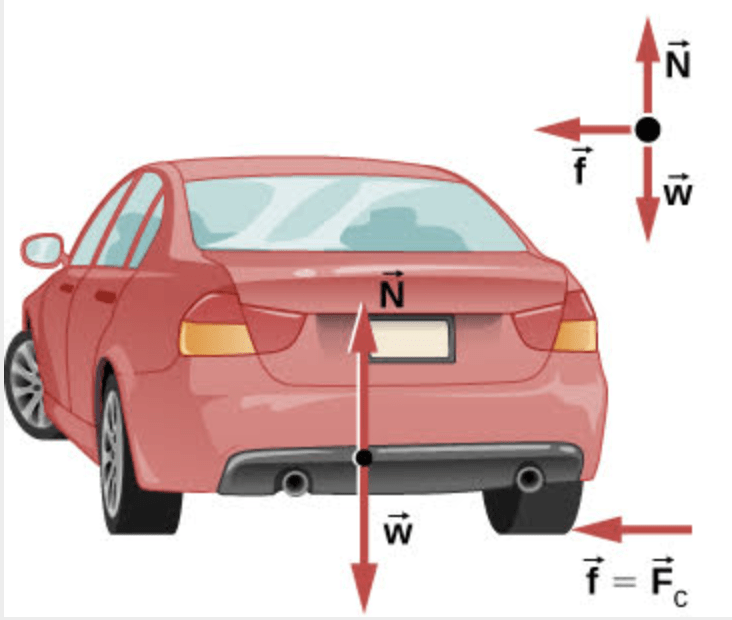
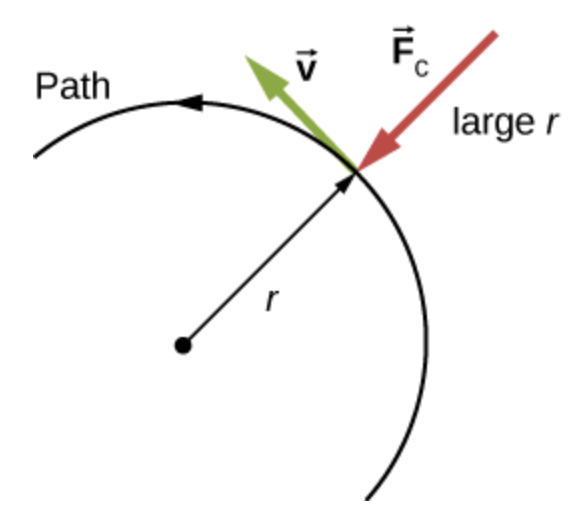
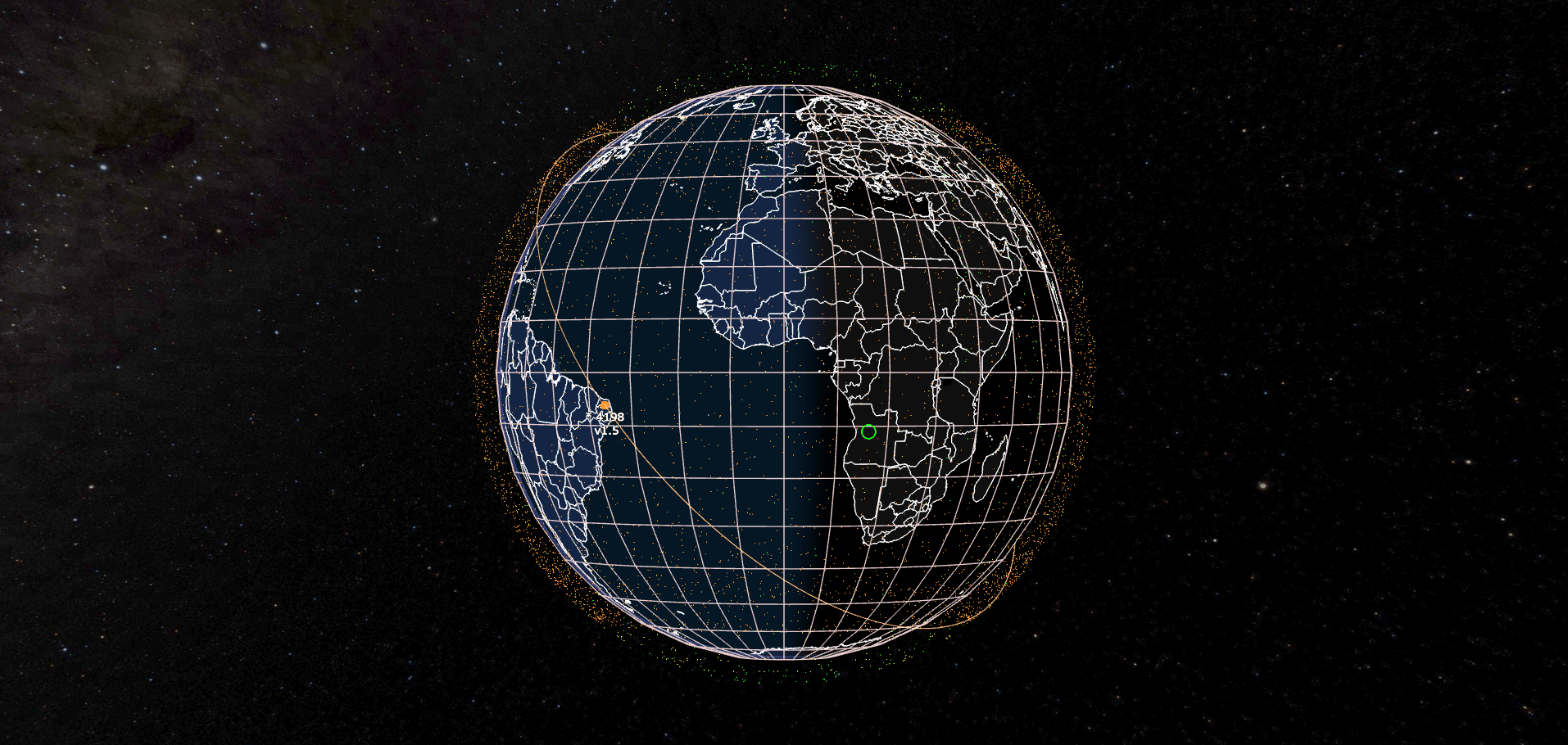
Fonte: Openstax.orgOs pequenos satélites da Starlink, orbitam a Terra em alturas entre 500 a 1200 km acima da superfície da Terra.
O objetivo é estabelecer um serviço mundial de Internet de banda larga confiável e fácil acesso.
Os satélites operam em órbita terrestre baixa (LEO), o que resulta em latência mais baixa e taxas de transferência de dados (20 milisegundos) mais rápidas do que os satélites geoestacionários típicos (600 milisegundos) que orbitam em altas altitudes (36 000 km).

É importante criar mecanismos que controlem a distância entre o satélite e o centro da Terra, pois isso afeta a velocidade e o período do satélite.
A força centrípeta
O que mantém os satélites em órbita é a física newtoniana, em primeira aproximação:
A força centrípeta resultante que atua sobre este satélite em órbita é dada pela relação:
A equação para a velocidade do satélite movendo-se em uma órbita circular em torno da Terra:
A velocidade para completar a órbita circular \(\Delta S=2\pi R\) num período \(T\):
O período \(T\) e a velocidade não dependem da massa do satélite:
Terceira lei de Kepler
A força centrípeta
STARLINK-30856
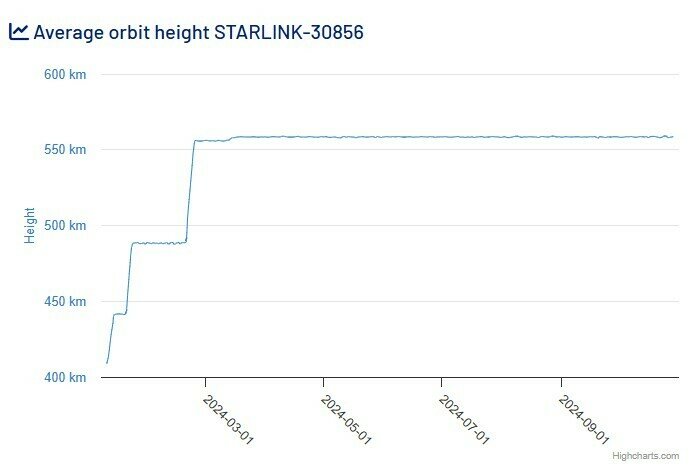
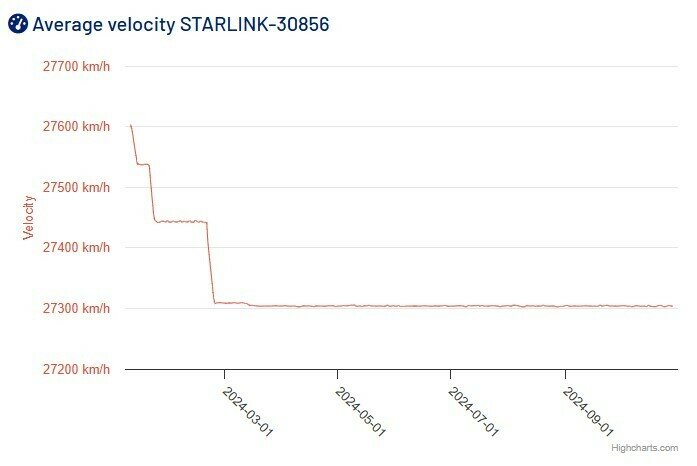
Os satélites estão sujeitos à terceira lei de Kepler
A força centrípeta
Altitude (km)
Velocidade (km\h)
Tempo (dias)
Tempo (dias)
Exemplo 4 (A11.P1-14)
Um carro passa com velocidade constante por uma colina circular e por um vale circular de mesmo raio. No alto da colina, a força normal exercida sobre o motorista pelo assento do carro é zero. A massa do motorista é de 70,0 kg. Qual é o módulo da força normal exercida pelo assento sobre o motorista quando o carro passa pelo fundo do vale?
Fonte: Halliday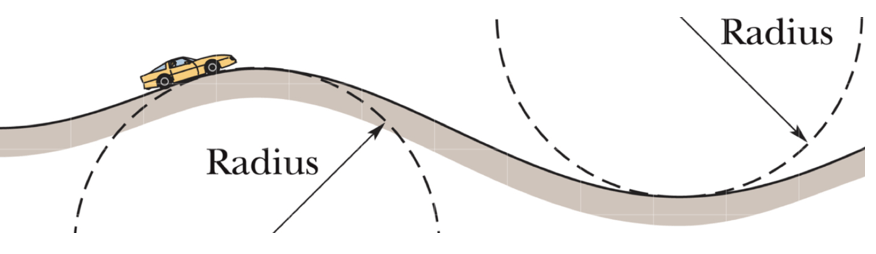
Exemplo 5 (A11.P1-09)
Um cubo está sobre uma plataforma giratória, girando inicialmente a rapidez constante. A rapidez angular da plataforma giratória é aumentada lentamente e, em um instante, o cubo desliza para fora da plataforma giratória. Explique por que isso acontece.
Fonte: Eric Mazur
Exemplo 6 (A11.P1-15)
Uma bola de 50 g oscila em um círculo vertical presa por um barbante de 1,5 m de comprimento. Quando a bola se encontra no fundo da trajetória circular, a tensão no barbante é de 15 N. (a) Quanto vale a velocidade da bola neste ponto? (b) Qual o trabalho realizado pela força resultante?
Fonte: Wolfgang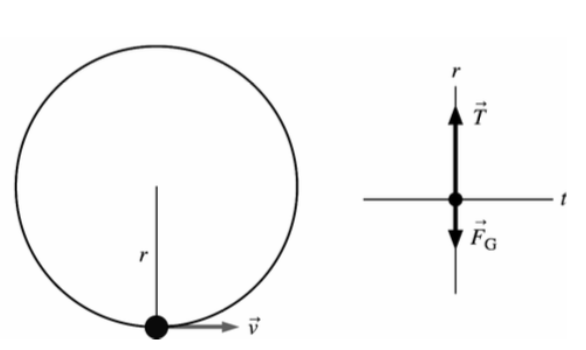
Exemplo 7 (A11.P1-16)
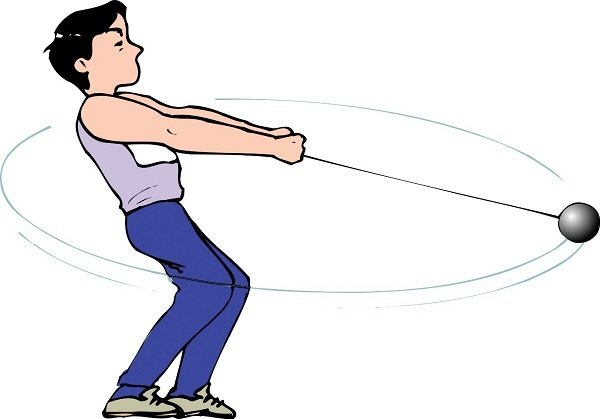
Um estudante amarra uma pedra de 500 g por um barbante de 1,0 m de comprimento e a gira sobre a cabeça em um círculo horizontal. A que valor de velocidade angular, em rpm, o barbante ficará inclinado para baixo em 10°?
Fonte: Wolfgang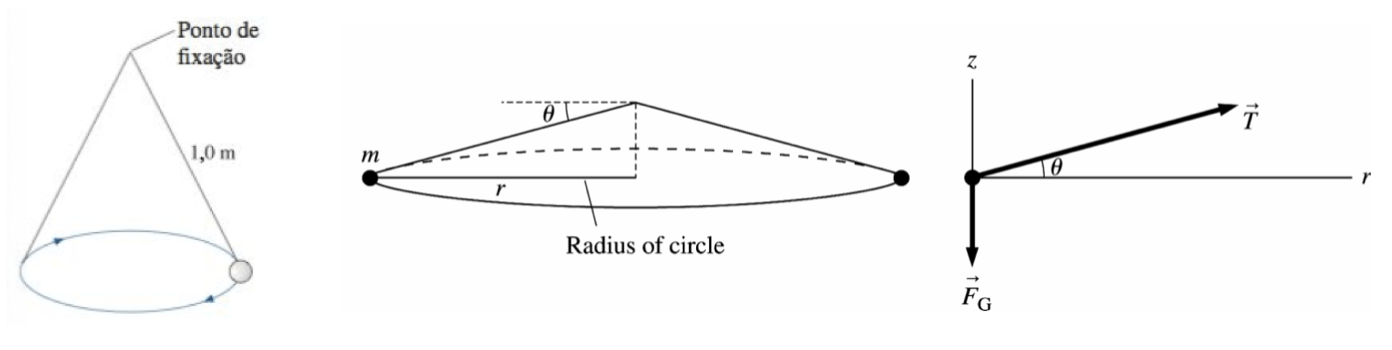
Exemplo 8 (A11.P1-17)
Uma bola de 500 g move-se em um círculo vertical presa por um barbante de 102 cm de comprimento. Se a velocidade no topo vale 4,0 m/s, o valor da velocidade no fundo será 7,5 m/s. (No Capítulo 10 você aprenderá a demonstrar isto.) a. Quanto vale a força gravitacional exercida sobre a bola? b. Quanto vale a tensão no barbante quando a bola se encontra no topo? c. Quanto vale a tensão no barbante quando a bola se encontra no fundo?
Fonte: Wolfgang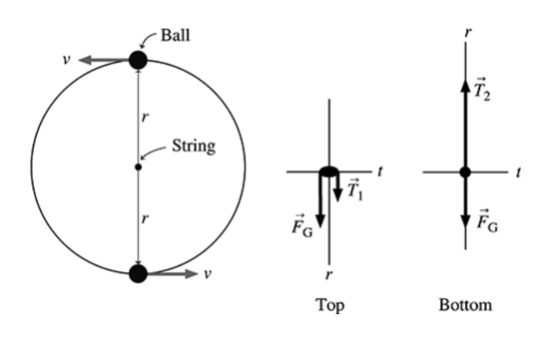
Exemplo 9 (A11.P1-10)
A corda que segura o balde ou uma esfera faz um pequeno ângulo com a horizontal. É possível girar o balde para que a corda fique exatamente na horizontal? Qual a velocidade tangencial?

componente horizontal da tensão
componente vertical da tensão
contato
peso
Exemplo 10 (A11.P1-11)
Uma piloto contorna uma curva a toda velocidade, inclinando-se bruscamente para a curva. Se, durante a volta, ela percorre o arco de um círculo de raio 4,5 m a uma rapidez constante de 5,0 m/s, qual ângulo o corpo deve fazer com a vertical para fazer a curva sem cair
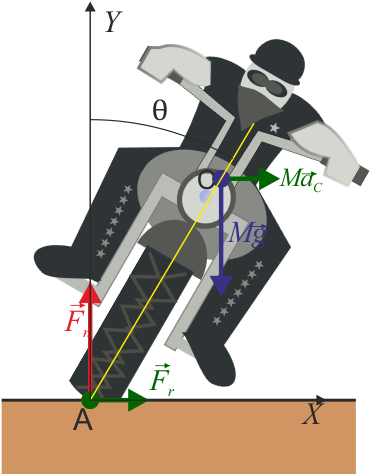
Fonte: https://www.nicepng.com

normal
contato
atrito estático
peso
Exemplo 11
Quando um avião viaja a velocidade (vetorial) constante na horizontal, suas turbinas ou hélices “sentem” uma força horizontal para a frente. A atuação do ar no corpo e nas asas do avião exerce uma força com uma componente horizontal para traz, que é uma força de atrito, e outra componente (E) vertical para cima, que sustenta o avião.
(a) Por que o avião não consegue fazer uma curva na horizontal sem inclinar as asas?
(b) Qual o ângulo que as asas devem ser inclinadas para que o avião realize uma curva na horizontal de raio R?

Exemplo 12 (A11-P1-13):
Uma curva de 30,0 m de raio é inclinada de um ângulo θ. Isto é, a normal da superfície da estrada forma um ângulo com a vertical. Encontre θ para que o carro percorra a curva a 40,0 km/h, mesmo se a estrada está coberta de gelo, o que a torna praticamente sem atrito.
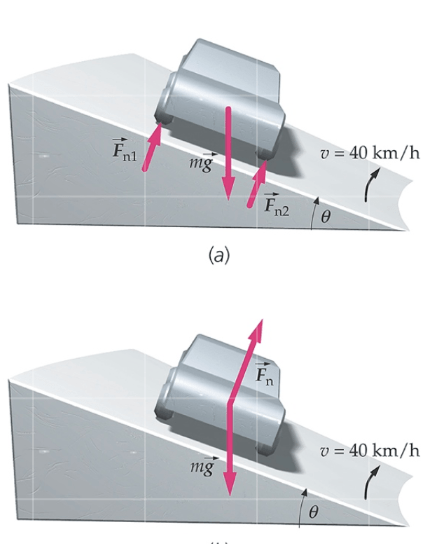
Fonte: Tipler
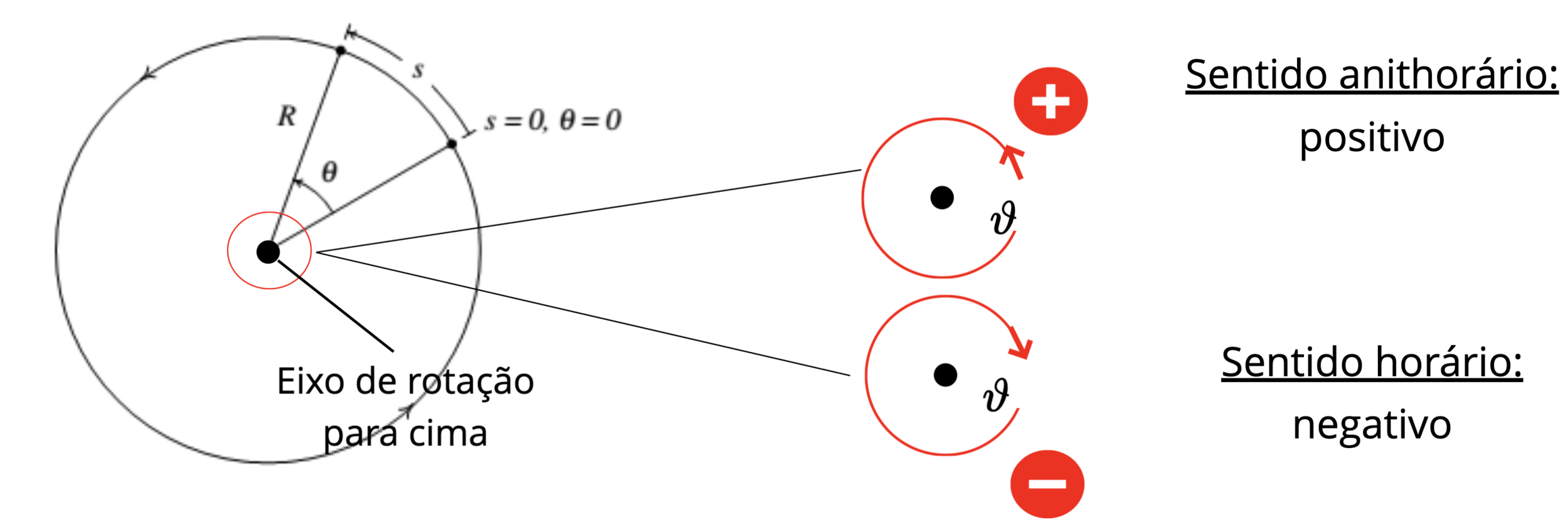
A orientação da rotação em relação ao eixo de rotação é uma convenção.
O ângulo polar, \(\theta\), de um objeto que se move ao longo de um círculo de raio, \(r\), é definido como o comprimento do arco, \(s\), sobre o qual o objeto se moveu dividido pelo raio:
Como as medidas do ângulo polar são feitas em radianos
mesmo que radiano não seja uma unidade.
Ao dividir as grandezas \(s/r\), com dimensões de comprimento, vê-se que \(\theta\) admensional.
arco
raio
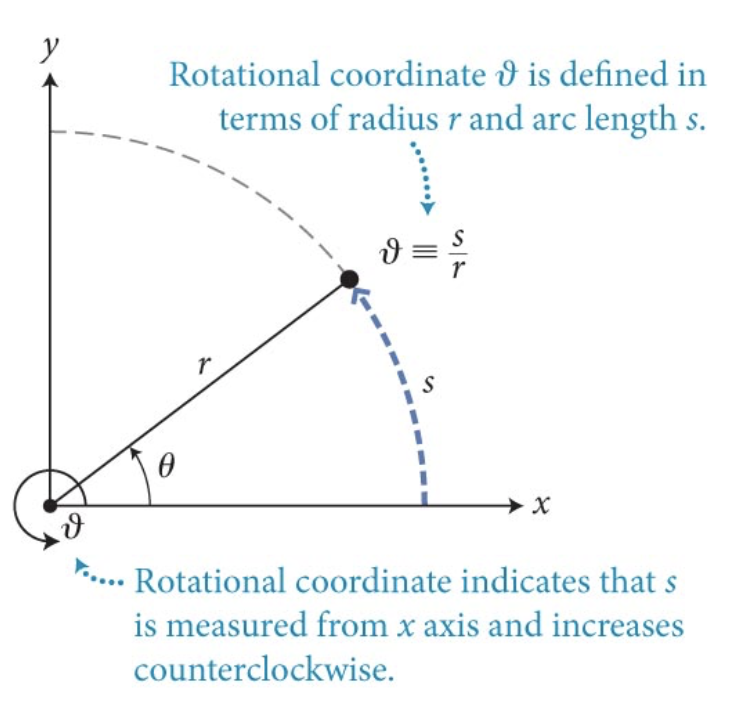
O movimento circular
A variação do ângulo polar, \(\Delta \theta\), é igual ao ângulo polar final menos o ângulo polar inicial, é
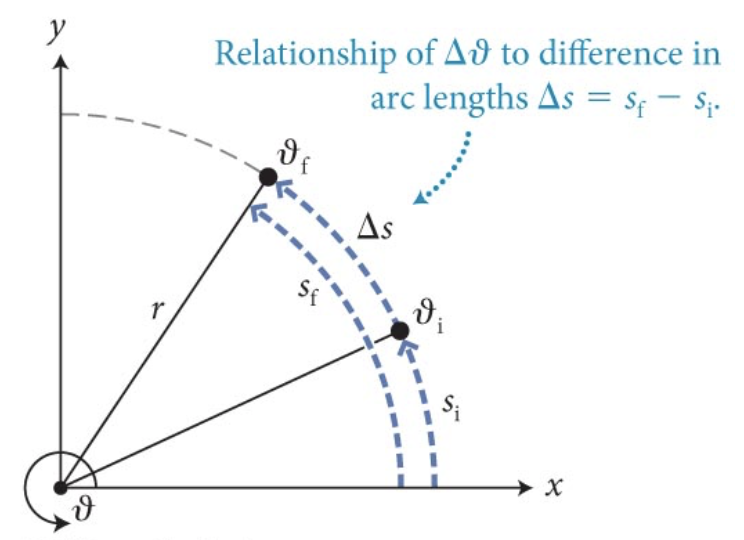
como
A variação do ângulo polar é igual a razão entre a variação do comprimento de arco pelo raio da circunferência:
O movimento circular
A partir da definição de velocidade média:
E o mesmo para a velocidade tangencial instantânea:
e que \(\Delta s = r \Delta \theta\), existe uma relação entre a velocidade média e velocidade angular média, \(\omega_m\).
- \vec v_m
A velocidade angular média é:
- \vec v_t
O movimento circular
O movimento circular
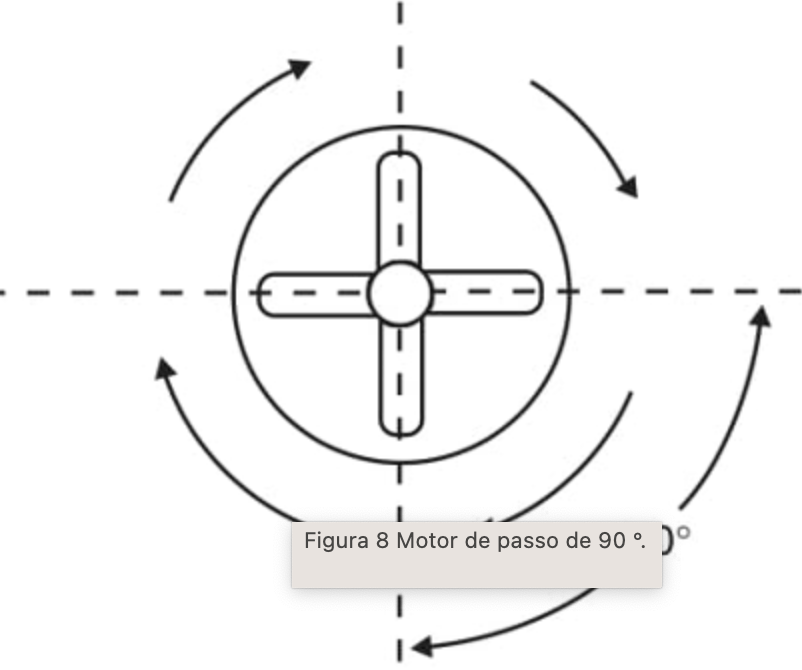
Motor de passo de 90 graus
O motor "para" 4 vezes ao completar uma volta.
Para completar 1 volta é necessário aplicar 4 pulsos.
1 volta =
O motor com ângulo de grau de \(1,8^o\), "para" quantas vezes?
Quantos pulsos são necessários para 1 volta? E se for um motor com redução 1:64?

O movimento circular
Motor de passo de 1,8 graus
O motor com ângulo de grau de \(1,8^o\) "para" 200 vezes.
Ao aplicar 200 pulsos a cada segundo vamos saber a velocidade angular do motor:

A velocidade angular pode ter as seguintes unidades:
A frequência angular pode ter as seguintes unidades:
O movimento circular
Velocidade angular e frequência angular?
A velocidade angular do motor de passo de \(1,8^o\).

De forma geral, para uma volta completa:
O período é o tempo para completar 1 volta.
A frequência angular é o número de voltas por unidade de tempo.
A frequência angular do motor de passo \(f = 1 \text{ rps}\). Portanto, \(\omega_m = (2\pi \text{ rad)} f = 6,28\text{ rad}/\text{s}\).
O movimento circular
Engrenagens
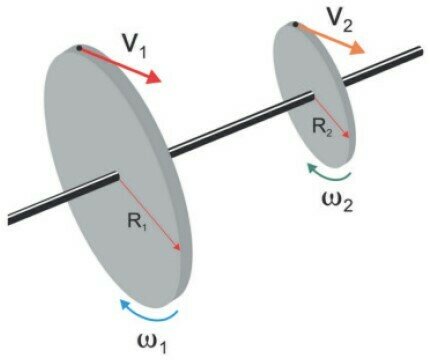
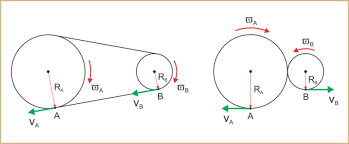
O movimento circular
Engrenagens
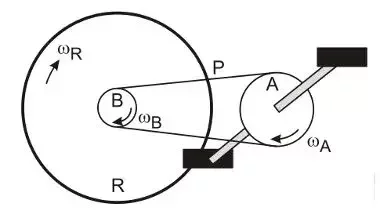
Quais as relações?
Modelando o movimento circular
O vetor velocidade angular é pode ser representada como uma grandez vetorial de direção perpendicular ao plano do movimento e seu sentido é dado pela regra da mão direita.
Crédito: https://www.geogebra.org/m/ugsjfsy5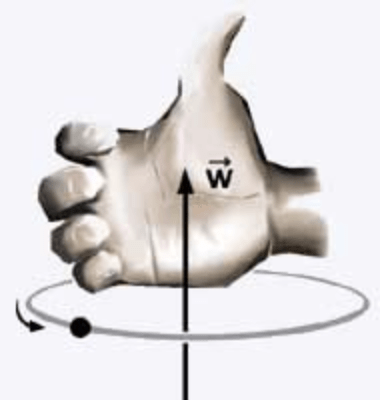
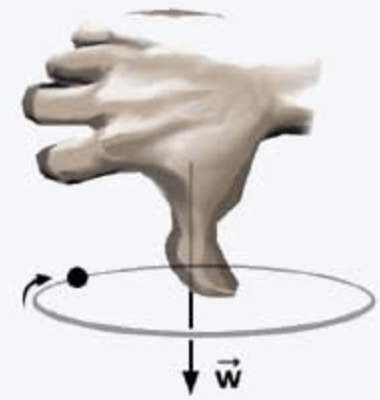
Crédito: http://www.cepa.if.usp.br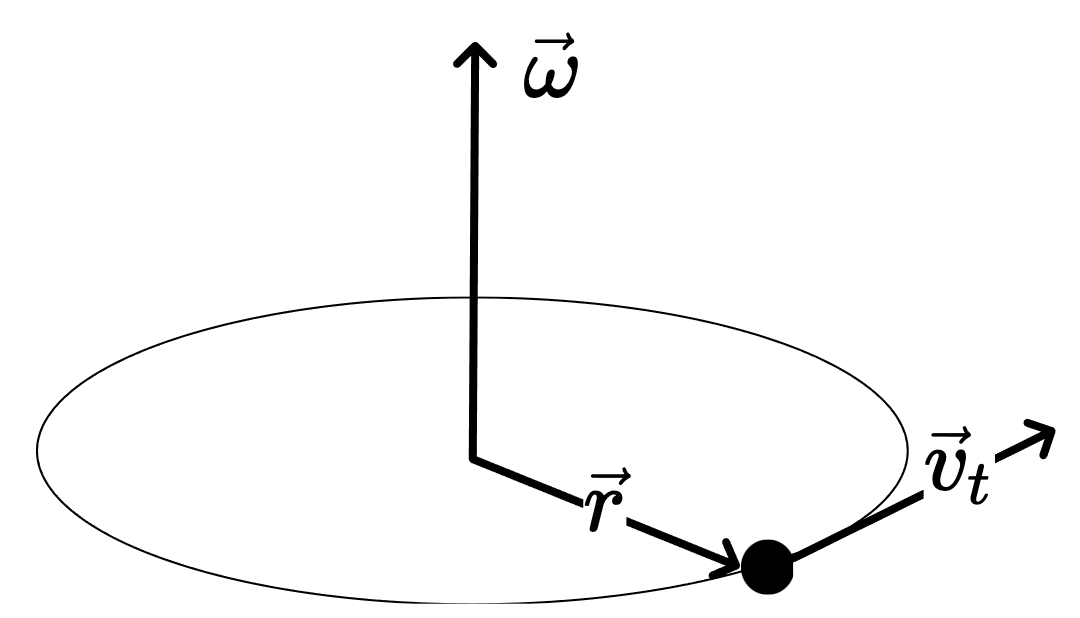
Se \(\theta = 90^o\)
Modelando o movimento circular
Como o vetor velocidade tangencial muda de direção no movimento circular, nós podemos calcular o vetor aceleração
Para um movimento circular uniforme, \(\vec \omega = constante\), a aceleração é centrípeta e perpendicular ao vetor velocidade tangencial:
ou
Se todos os ângulos são retos:
ou
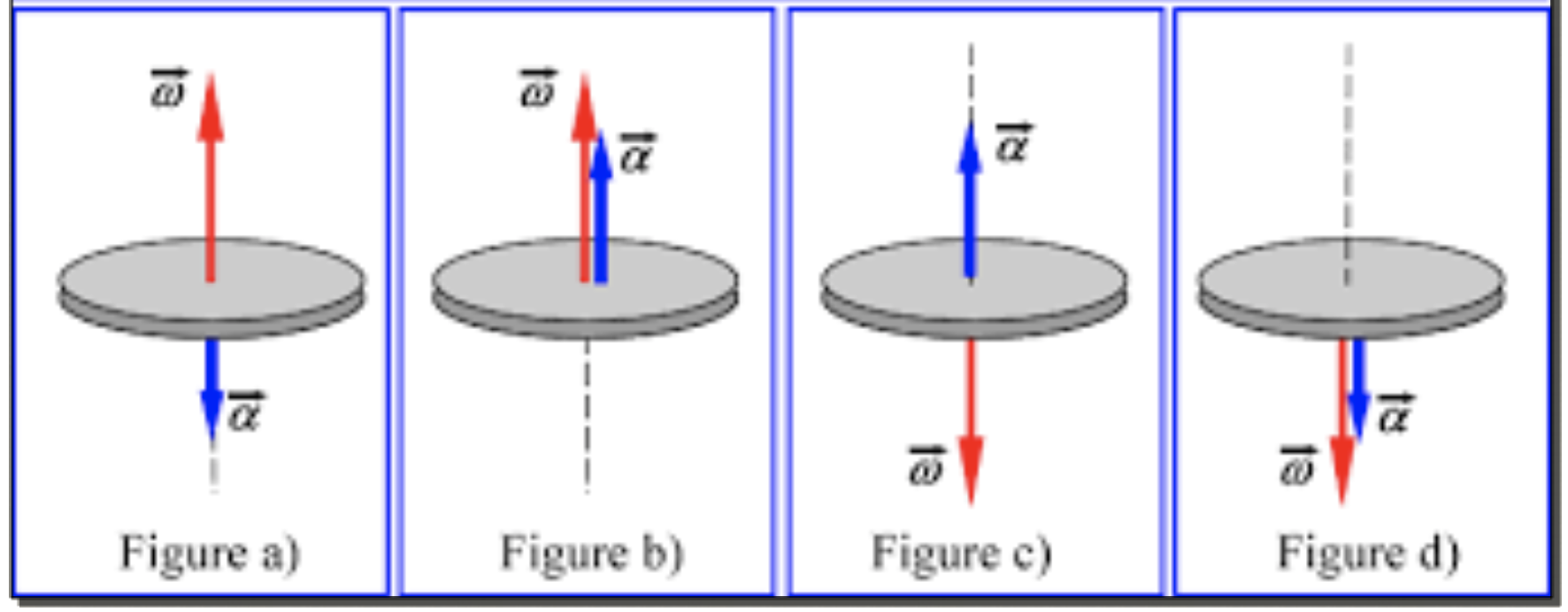
Para um movimento circular não uniforme, a maginute da velocidade tangencial varia,
O movimento pode ser acelerado ou retardado.
Retardado
Retardado
Acelerado
Acelerado
- \vec \omega \cdot \vec \alpha >0
- \vec \omega \cdot \vec \alpha >0
- \vec \omega \cdot \vec \alpha <0
- \vec \omega \cdot \vec \alpha <0
Modelando o movimento circular
A velocidade média angular e a aceleração média angular.
Existe uma relação entre as grandezas de translação e rotação;
Fonte: https://www.compadre.org
E que:
Modelando o movimento circular
Um disco está girando em torno do eixo central como um carrossel. A posição angular é θ(t) de uma reta de referência do disco é dada por
Fonte: https://www.compadre.org
Modelando o movimento circular
com t em segundos, θ em radianos e a posição angular zero indicada na figura.
Analise a cinemática do movimento.