Aula 11

Fundamentos da Mecânica

Prof. Ronai Lisbôa

UFRN - ECT - BCT

Objetivos

Calcular o trabalho realizado em uma única partícula.

Potência de uma força.

Enunciar o teorema trabalho-energia cinética.

Conceituar o trabalho mecânico como um processo de transferência de energia.

O trabalho como o produto de dois vetores.

Bibliografia.

Tipler - Cap. 6

Seções: 6.1, 6.3

- Refaça os exercícios resolvidos.

Conceituar a energia cinética de uma partícula.

O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)

 

Sem utilizar I.A. ou solucionários.

Energia cinética

K=\frac{1}{2}mv^2
\vec v
m

No Sistema Internacional, a unidade da energia é o joule (J).   Sendo 1 J = 1 N.m:

\frac{[M][L]^2}{[T]^2}\equiv\text{kg}\frac{\text{m}^2}{\text{s}^2}\equiv \text{joule}=\text{J}

Se uma partícula apenas se move de um ponto para o outro, podemos considerar apenas sua energia cinética.

Uma energia associada ao movimento que leva em conta a massa inercial, e claro a velocidade.

Uma grandeza extensiva. Isto é, não pode ser criada ou destruída, mas que pode ser alterada pelos processos de entrada e saída de energia do sistema.

Uma partícula livre em movimento tem somente energia cinética!

Energia cinética

A energia cinética tem algumas características:

Está associada a um único objeto de inércia \(m\).

K=\frac{1}{2}mv^2

É sempre positiva. É um escalar.

Está associada ao movimento.

Não depende da direção e sentido do movimento.

\vec v
m
\vec v
m
\vec v
m
K_1=K_2=K_3

Se \(m_1=m_2=m_3\) e \(v_1=v_2=v_3\):

A energia e momento linear de uma única partícula.

Para baixas velocidades e em um processo onde a integridade da partícula não muda, sua energia é apenas cinética.

E=K

Uma partícula livre possui somente energia cinética:

K=\frac{1}{2}mv^2

Quando \(\Delta K =0\)  a partícula é livre. Só existe ela!

Não há variação da energia cinética e momento linear para uma partícula livre.

Energia cinética

Em um processo a variação da energia cinética é

\Delta K = K_f-K_i

Se \(\Delta K > 0\): A rapidez aumenta.

Como \(\Delta K \neq 0\), a partícula não é livre. Ela não está só.

O que alterou a energia cinética  da partícula?

A energia e momento linear de um sistema de partículas únicas.

Se \(\Delta K < 0\) : A rapidez diminui.

Provavelmente alguma outra coisa que fez a partícula variar sua energia cinética.
 Alguma interação fez isso!

Energia cinética

Trabalho

O trabalho equivale a uma transferência de energia de um sistema para o ambiente ou do ambiente para o sistema.

Somente uma interação entre um objeto dentro do sistema (lambreta+piloto ou mola) e um objeto fora dele (amigo ou mão) - uma interação externa - pode transferir energia através dos limites do sistema.

Vizinhança

Sistema

Só há trabalho se o ponto de aplicação da força se deslocar!

Vizinhança

Sistema

Fonte: www.pixbay.com

Fonte: www.pixbay.com

Deformação

Aceleração

Exemplo 1

1) Imagine empurrar contra uma parede de tijolos, como mostra a figura.

(a) Considerando a parede como o sistema, a força que você exerce sobre ela é interna ou externa? (b) A força que você exerce na parede faz trabalho na parede?

\vec F^c_{hp}

Ponto de aplicação da força

Fonte: www.pixbay.com

\Delta \vec r_F = \vec 0

O ponto de aplicação da força não se move. O trabalho é nulo!

Trabalho

As forças externas exercidas em um sistema nem sempre realizam trabalho no sistema.

Para que uma força faça trabalho, o ponto de aplicação da força deve sofrer um deslocamento.

\vec F^c_{hp}
\Delta \vec r_F = \vec 0

Trabalho não nulo \(W \neq 0\)

Trabalho nulo \(W = 0\)

\vec F^c_{pc}
\Delta \vec r_F

Fonte: www.pixbay.com

Deformação

\vec F^c_{pc}
\vec F^c_{pc}
\Delta \vec r_F

Fonte: www.pixbay.com

Aceleração

Exemplo 2

1)  Para qual das seguintes forças o deslocamento de força é zero:

 

(a) a força exercida por uma mão que comprime uma mola.

 

(b) a força exercida pela Terra em uma bola lançada para cima.

 

(c) a força exercida pela terra sobre você no instante em que você pula para cima.

 

(d) a força exercida pelo piso de um elevador sobre você enquanto o elevador se move para

baixo a velocidade constante.

 

Diagramas de energia

A energia do sistema pode variar em situações que envolvam trabalho.

Os diagramas de energia são uma representação gráfica da conservação de energia: mostram que a energia de um sistema pode variar apenas devido à transferência de energia para dentro ou para fora do sistema.

Na mecânica essa transferência de energia para dentro ou para fora do sistema é possível devido ao trabalho mecânico.

É crucial definir o sistema e a vizinhança para a determinação do trabalho e o deslocamento da força.

Diagramas de energia

O trabalho positivo aumenta a energia do sistema.

Trabalho positivo significa que a força externa e o deslocamento da força têm a mesma direção e sentido.

Energia inicial

Trabalho

8\text{ J}
4\text{ J}
12\text{ J}

Energia final

\Delta \vec r_F
\vec F_{ext}
\vec F^c_{pc}
\vec F^c_{pc}
\vec v_f
\Delta \vec r_F

Sistema é o carrinho.

A energia do sistema aumentou.

W>0

Fonte: www.pixbay.com

\vec v_i

Diagramas de energia

O trabalho negativo diminui a energia do sistema.

Energia inicial

Trabalho

8\text{ J}

Energia final

Trabalho negativo significa que a força externa e o deslocamento da força têm a mesma direção e sentidos opostos.

2\text{ J}
-6\text{ J}
\vec F^c_{pc}
\vec F^c_{pc}
\vec v_i
\Delta \vec r_F
\vec v_f
\Delta \vec r_F
\vec F_{ext}

Sistema é o carrinho.

A energia do sistema diminuiu.

W<0

Fonte: www.pixbay.com

O teorema trabalho e energia cinética

Uma força constante dá à partícula uma aceleração constante dada pela equação do movimento:

a = \frac{F_{R}}{m}

Integrando essa equação, obtemos uma expressão para a variação da energia cinética da partícula e o trabalho externo sobre ela.

\frac{dv}{dt} =a
\int_{v_{i}}^{v_{f}}v_xdv_=\int_{x_i}^{x_f}adx
\Rightarrow
\frac{dv}{dx}\frac{dx}{dt} =a
\Rightarrow
\frac{dv}{dx} v =a
\frac{v_{f}^2}{2} - \frac{v_{i}^2}{2} = a(x_f-x_i)
\frac{v_{f}^2}{2} - \frac{v_{i}^2}{2} = \frac{F_{R}}{m}(x_f-x_i)
\frac{mv_{f}^2}{2} - \frac{mv_{i}^2 }{2} = F_{R}\Delta x_F
\Rightarrow
\Rightarrow
\Delta K = W_{ext}
\vec F
\vec F
\Delta \vec r_F
m
m
\vec v_i
\vec v_f

Segunda lei de Newton

Teorema trabalho-energia cinética

Encontramos o resultado:

Para o movimento em uma dimensão, o trabalho realizado por uma força constante exercida sobre uma partícula é igual ao produto dos componentes x da força pelo deslocamento da força.

\vec F
\vec F
\Delta \vec r_F
m
m
\vec v_i
\vec v_f
F_{R} \Delta x_F = \Delta K

Foi possível definir a energia cinética:

\Delta K = W_{ext}=F_{R}\Delta x

Esse é o Teorema Trabalho-Energia Cinética:

W_{ext} =\Delta K
K=\frac{1}{2}mv^2

E verificar que o trabalho da força externa é igual à variação da energia cinética da partícula.

O teorema trabalho e energia cinética

O teorema trabalho e energia cinética

\Delta K = F_{R} \Delta x_F

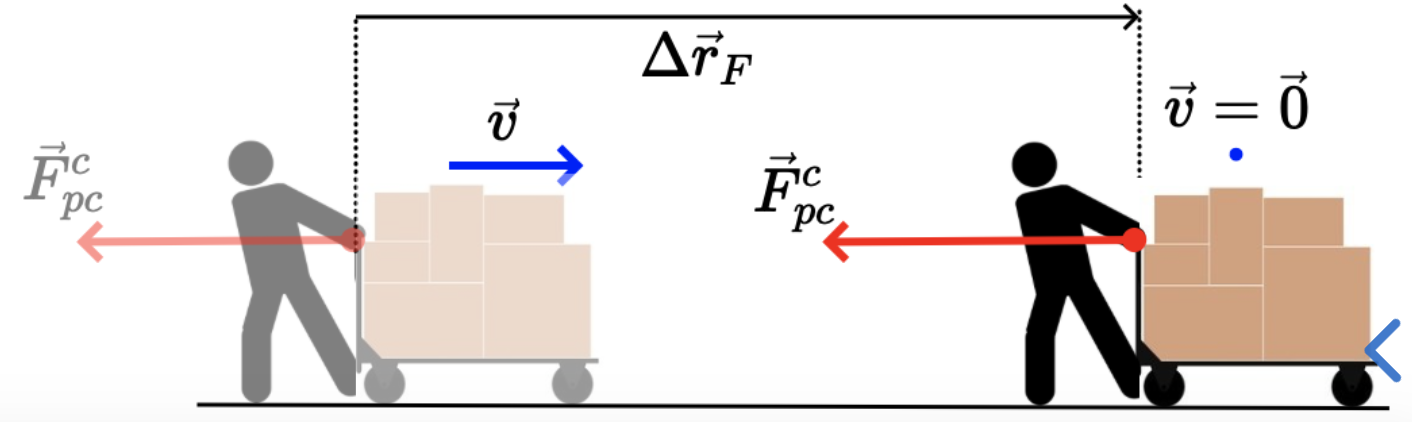
A partir do Teorema Trabalho-Energia Cinética:

Se  \(F_{R}\) e \(\Delta x_F\) são tais que o produto \(F_{R} \Delta x_{F}\) é negativo. A energia cinética diminui e sua variação é negativa.

\Delta \vec r_F
\vec F_{ext}
\Delta K < 0

Fonte: www.pixbay.com

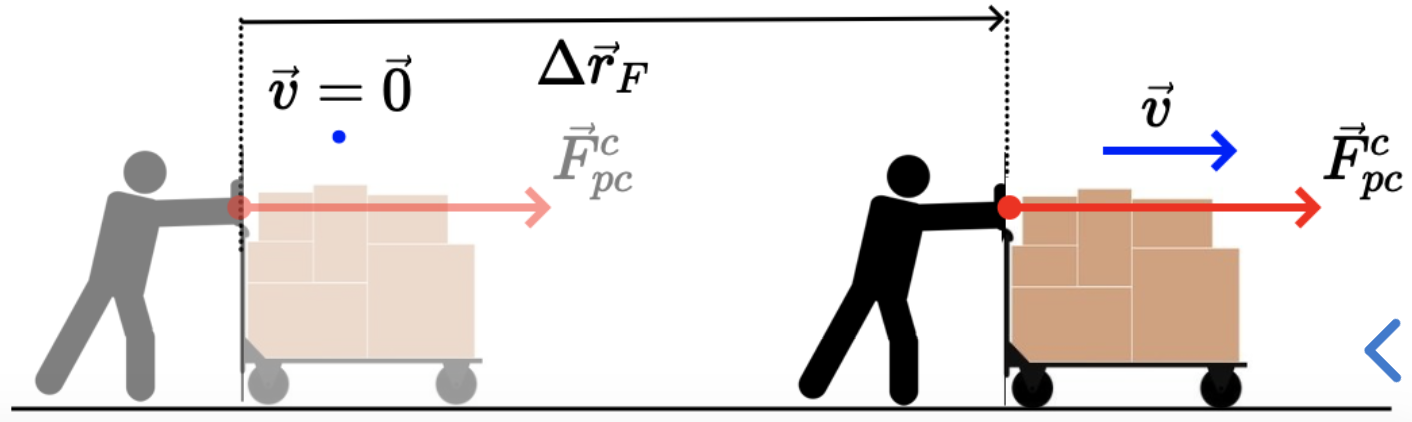
Se  \(F_{R}\) e \(\Delta x_F\) são ambos positivos ou ambos negativos, o produto \(F_{R} \Delta x_{F}\) é positivo. A energia cinética aumenta e sua variação é positiva.

\Delta \vec r_F
\vec F_{ext}
\Delta K > 0

Fonte: www.pixbay.com

Exemplo 3

3) Uma bala tem massa de 2,60 g e velocidade inicial de 335 m/s. Ela pode penetrar oito tábuas de pinho, cada uma com espessura de 1,9 cm. Qual é a força de parada média exercida pela madeira, conforme mostrado na figura?

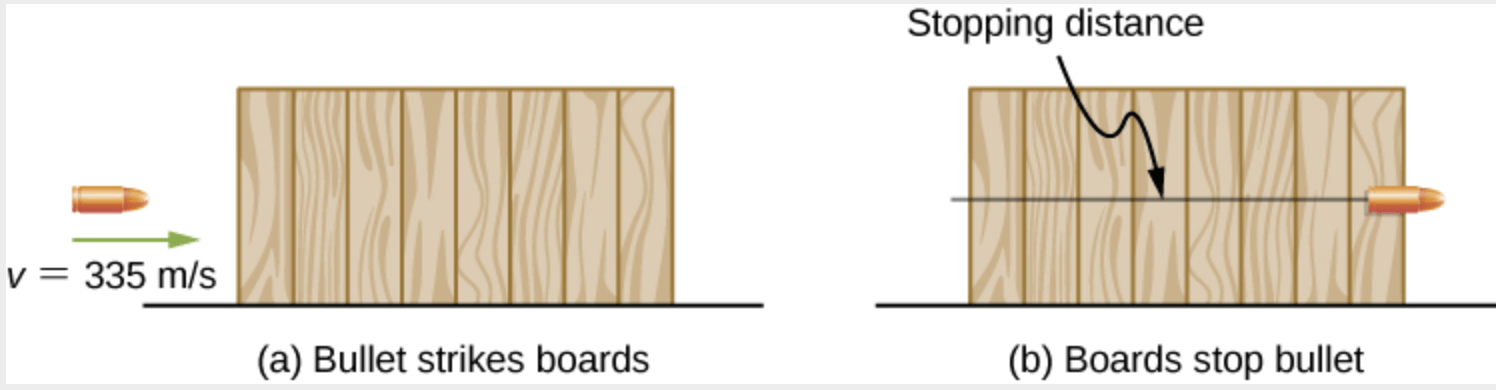
Fonte: OpenStax

O trabalho é um escalar, mas força e deslocamento são vetores.

Em 1 dimensão para uma força constante:

W=F_x\Delta x_F

e pode ser positivo ou negativo ou nulo.

\vec F
\Delta \vec r_F
\vec F
\Delta \vec r_F
W>0
W<0

E se o deslocamento e a força não apontam na mesma direção?

\vec F
\Delta \vec r_F
\vec F
\Delta \vec r_F
\vec F
\Delta \vec r_F

O trabalho como o produto de dois vetores.

O trabalho para uma força constante é calculado a partir do produto escalar entre os vetores força e o vetor deslocamento da força:

W=\vec F\cdot \Delta \vec r

e pode ser nulo, positivo ou negativo.

O trabalho como o produto de dois vetores.

\vec F
\Delta \vec r_F
W=0
\vec F
\Delta \vec r_F
W>0
\vec F
\Delta \vec r_F
W<0
W=|\vec F||\Delta \vec r|\text{cos }\theta

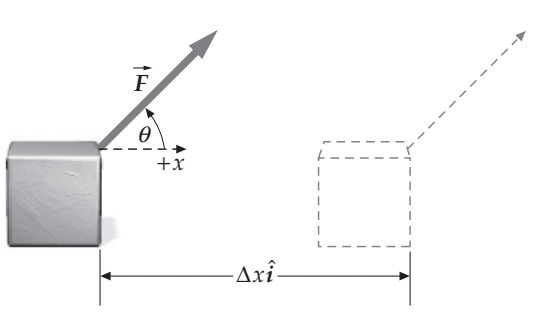
Fonte: Tipler & Mosca

e \(\theta\) é o menor ângulo entre os vetores.

Para uma força resultante constante

O trabalho realizado pela força é

W=\vec F\cdot \Delta \vec r

Somente o componente da força na direção do deslocamento contribui para o trabalho resultante.

O trabalho como o produto de dois vetores.

Esse é o papel do produto escalar.

W=F\Delta r \text{cos}\phi
W = F\Delta r
W = F_{\|}\Delta r
W=(F\text{cos}\phi )\Delta r
W=F_{\|}\Delta r

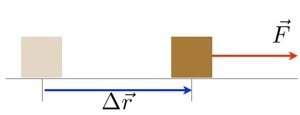
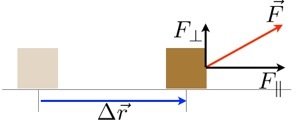
O trabalho é definido a partir de um produto escalar entre dois vetores.

O trabalho como o produto de dois vetores.

Força centrípeta

W=\vec F_{cp}\cdot \Delta \vec r
W=\vec F_{cp}\cdot \Delta \vec r
W=\vec F_{cp}\cdot \vec v_t \Delta t
W = F_{cp}v_t\cos(90^o)\Delta t
W = 0
\vec v_t
\vec F_{cp}

Aplicando o teorema trabalho-energia cinética:

W = \Delta K \Rightarrow 0 = \Delta K \Rightarrow K_f = K_i

A força centrípeta não realiza trabalho; logo, não varia a magnitude da velocidade tangencial.

Para um satélite orbital em torno da Terra, a força gravitacional é a força centrípeta. Portanto, a energia cinética do satélite não muda, em teoria, pois há claro algum arraste residual e outras forças sobre ele.

Potência

A taxa na qual a energia é transferida ou convertida é chamada de potência.

Se a energia de um sistema variar em uma quantidade \(\Delta E\) durante um intervalo de tempo \(\Delta t\), a potência média é definida como:

P_{m}=\frac{\Delta E}{\Delta t}

A unidade SI de potência é o watt (W), que é igual a 1 J de energia por segundo: 1 W =  1 J/s.

A potência instantânea é:

P = \lim_{\Delta t\rightarrow 0}\frac{\Delta E}{\Delta t} =\frac{dE}{dt}

que fornece a taxa na qual a energia de um sistema varia. A potência é um escalar.

De forma geral, o trabalho é o produto escalar de dois vetores:

A potência (W) é a energia por unidade de tempo (J/s). Então:

\vec F\cdot \Delta \vec r =W
\vec F\cdot \vec v\,\Delta t =W
\vec F\cdot \vec v=\frac{W}{\Delta t}
\vec v
\vec F
\vec v
\vec F
P= \vec F\cdot \vec v
P=Fv\cos( \theta)
P=(F\cos( \theta ))v
P=F_{\|}v
\vec F_{\|}

Somente a componente da força na direção da velocidade contribui para a potência.

Potência

Exercício 4 (A9.P12-09)

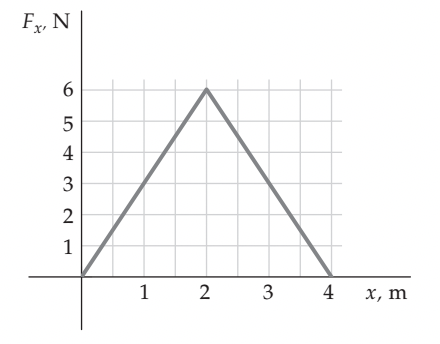
A9.P12-09 Uma partícula de 3,0 kg, que se move ao longo do  eixo x, tem uma velocidade de 2,0 m/s quando passa pela origem. Ela está sujeita a uma força única, Fx, que varia com a posição como mostrada na Figura. (a) Qual é a energia cinética da partícula quando ela passa pela origem? (b) Qual é o trabalho realizado pela força, enquanto a partícula se move de x = 0,0 m até x = 4,0 m? (c) Qual é a rapidez da partícula quando ela está em x = 4,0 m?

Exercício 5 (A9.P12-10)

Uma caixa de 7,5 kg está sendo levantada por uma corda leve que passa por uma única polia, leve e sem atrito, que está presa ao teto.

(a) Se a caixa está sendo levantada com uma rapidez constante de 2,0 m/s, qual é a potência desenvolvida pela pessoa que puxa a corda?

(b) Se a caixa é levantada, com uma aceleração constante, a partir do repouso no chão, até a uma altura de 1,5 m acima do chão, em 0,42 s, qual é a potência média desenvolvida pela pessoa que puxa a corda?

(c) Determine a potência da força de tração.

Exercício 6 (A9.P12-11)

Um canhão colocado na beirada de um penhasco de altura H, dispara uma bala diretamente para cima, com uma rapidez inicial \(v_0\). A bala se eleva, cai de volta (errando o canhão por uma pequena margem) e chega ao pé do penhasco.

Desconsiderando a resistência do ar, calcule a velocidade \(v\) como função do tempo e mostre explicitamente que a integral temporal de \(F_{res}v\) , enquanto a bala está em vôo, é igual à variação da energia cinética da bala no mesmo tempo.

Fonte: https://images.app.goo.gl

Exercício 7 (A10.P2-05)

Uma partícula de 2,0 kg sofre um deslocamento Durante esse deslocamento de

 

 

Durante esse deslocamento, uma força constante

 

 

atua sobre a partícula.

(a) Determine o trabalho realizado por essa força para esse deslocamento.

(b) Determine a componente da força na direção desse deslocamento.

\Delta \vec r = [(3,0\hat i)+(3,0\hat j)+(-2,0\hat k)] \text{m}
\vec F = [(2,0 \hat i) + (-1,0 \hat j) + (1,0 \hat k)]\text{ N}

Exercício 8 (A10.P2-06)

Determine a potência desenvolvida por uma força F que atua sobre uma partícula que se move com velocidade v, onde

 

(a)  

 

(b)

\vec F = [(4,0\hat i) + (3,0\hat k)]\text{ N}
\vec v = (6,0\hat i)\text{ m/s}
\vec F = [(6,0\hat i) + (-5,0\hat j)]\text{ N}
\vec v = [+(-5,0\hat i)+(+4,0\hat j)]\text{ m/s}

Exercício 9 (A10.P2-07)

Uma partícula de massa m se move ao longo do eixo x. Sua posição varia no tempo de acordo com \(x(t) = 2t^3+4t^2\), onde x está em metros e t está em segundos. Determine (a) a velocidade e a aceleração da partícula como funções de t, (b) a potência fornecida à partícula em função de t e (c) o trabalho realizado pela força resultante entre t = 0 e t = t1. T6.65.

Exercício 10 (A10.P2-09)

Uma caixa de massa M está em repouso na base de um plano inclinado sem atrito. A caixa está presa a um fio que a puxa com uma tensão constante T. (a) Determine o trabalho realizado pela tensão T, enquanto a caixa é puxada por uma distância x ao longo do plano. (b) Determine a rapidez da caixa como função de x. (c) Determine a potência desenvolvida pela tensão do fio como função de x. T6.70

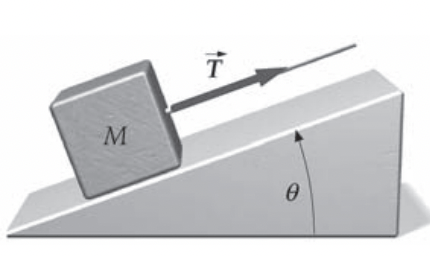
Fonte: Tipler

Exercício 11 (A10.P2-11)

Um bloco de 6,0 kg escorrega 1,5 m abaixo sobre um plano inclinado sem atrito que forma um ângulo de 60° com a horizontal. (a) Desenhe o diagrama de corpo livre para o bloco e encontre o trabalho realizado por cada força, enquanto o bloco escorrega 1,5 m (medidos ao longo do plano inclinado). (b) Qual é o trabalho total realizado sobre o bloco? (c) Qual é a rapidez do bloco após ter escorregado 1,5 m, se ele parte do repouso? T6.32

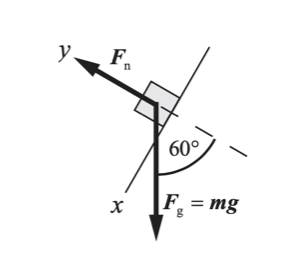
Fonte: Tipler

Made with Slides.com