Aula 12

Fundamentos de Mecânica

Prof. Ronai Lisbôa

UFRN - ECT - BCT

Objetivos

Aplicar o teorema trabalho-energia cinética quando a força é variável.

Força variável (elástica).

Forças constantes (peso, normal, tração)

Bibliografia.

Tipler - Cap. 6

Seções: 6.2 e 6.4

- Refaça os exercícios resolvidos.

Força distribuída (atrito).

O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)

 

Para usar I.A. você deve saber ou ter ideia do que está fazendo. Se não é só informação fugaz.

Força elástica

Crédito: https://youtu.be/JhJzdtzl6KY
Crédito: https://youtu.be/0EEHuh5q2p8

Simulação

Mundo real

É uma força variável porque depende da deformação.

Força elástica

Crédito: https://youtu.be/7eGOnKST6nw?si=lpf7WjX_2xGyoNPF

A força elástica é proporcional à deformação desde que a deformação seja "pequena".

A força elástica é obtida a partir da experimentação.

O gráfico mostra o componente \(x\) do deslocamento da extremidade livre da mola de sua posição relaxada em \(x_0\) versus a força aplicada à mola.

regime elástico

regime plástico

ponto de ruptura

k=\frac{\Delta F}{\Delta x}
k=\frac{25\text{ N}}{0,01\text{m}}
k=2,5\times 10^3\text{ N/m}

Na verdade é uma bola bastante rígida!

Intervalo elástico

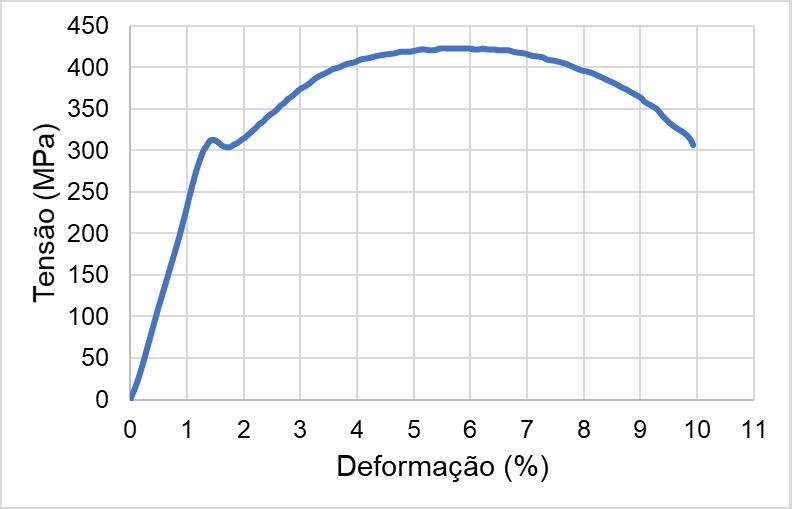
\(x-x_0\) (cm)

\(F_a\) (N)

A força elástica (uma força de contato)

No regime elástico

k=\frac{\Delta F}{\Delta x}

A força elástica é proporcional à deformação desde que a deformação seja "pequena".

F_{\text{elástica}} =- k(x-x_0)

Mola macia

Mola dura

Poste de aço

\vec F^c_{e}
\vec F^c_{e}
\vec F^c_{e}
\vec F^g_{Tt}

Para uma mesma força aplicada (peso) a deformação é maior para a mola macia

Fonte: Eric Mazur

Fonte: Eric Mazur

Podemos modelar qualquer superfície como um conjunto de molas.

Quanto mais rígida a superfície maior o valor da constante elástica e menor será a deformação para uma mesma força aplicada.

F^c_{e}=-k\Delta x
k_{\text{macia}} < k_{\text{dura}} < k_{\text{aço}}
\Delta x_{\text{macia}} > \Delta x_{\text{dura}} > \Delta x_{\text{aço}}

A força elástica (uma força de contato)

\vec P
\vec P
\vec P
\Delta x=-\frac{mg}{k}
F^c_{e}-P=0
-k\Delta x = mg

Exemplo 1

Um livro de inércia de 1,2 kg é colocado no topo da mola na figura. Qual é o deslocamento da extremidade superior da mola da posição relaxada quando o livro está parado em cima da mola de constante de mola \(k = 2,5 \times 10^3\) N/m?

\vec F^c_{ml}=\vec F_e
\vec F^g_{Tl}=\vec P
\cdot \quad\vec a =0
+x
x_0
x
\Delta x

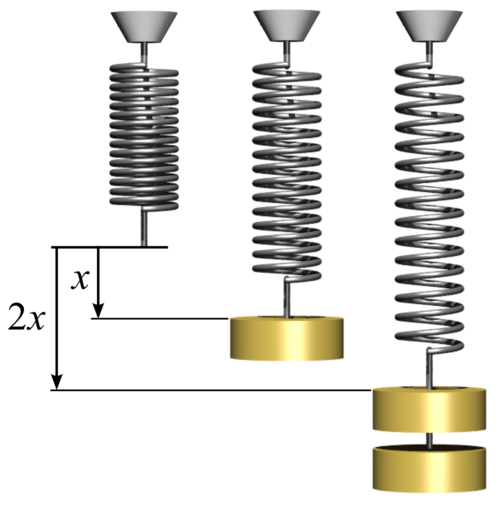
Fonte: Tipler & Mosca

O trabalho de forças variáveis (força elástica)

O trabalho feito por uma força é a integral da força em relação ao deslocamento ao longo do caminho do deslocamento:

W_{AB}=\int_A^B \vec F\cdot d\vec r

O trabalho é calculado via uma integral de caminho (ou integral de linha).

Fonte: OpenStax

Para uma força constante:

W_{AB}=\vec F\cdot \Delta \vec r

Para uma força variável, a função \(\vec F \) deve ser conhecida como função da posição.

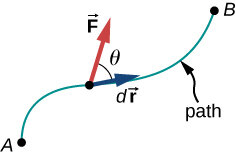
caminho

O trabalho de forças variáveis (força elástica)

A força elástica varia com a compressão ou alongamento do comprimento de um mola.

O trabalho da força elástica vem da integral de caminho. Em uma dimensão:

F_e=-kx
W_e=\int_{x_i}^{x_f}F_x(x)dx
\Rightarrow
W_e=-(\frac{1}{2}kx_f^2-\frac{1}{2}kx_i^2)

Aplicando o teorema trabalho-energia cinética:

Vemos que é possível alterar a energia cinética da massa por meio do trabalho da força elástica.

\Delta K_{bloco}=W_e
F_x<0
F_x>0
F_x=0
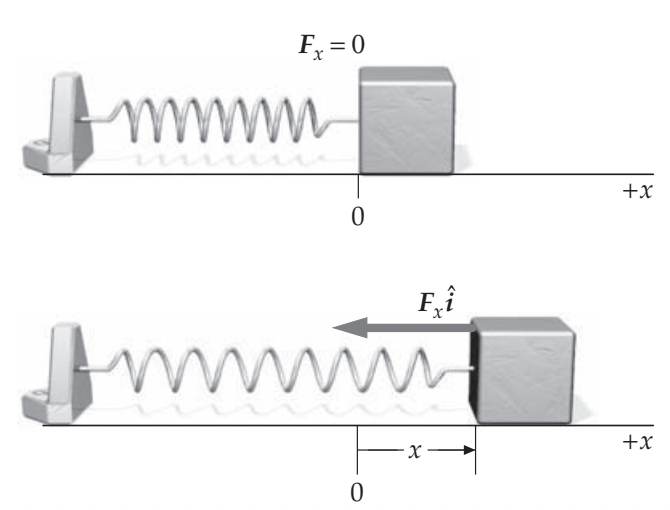
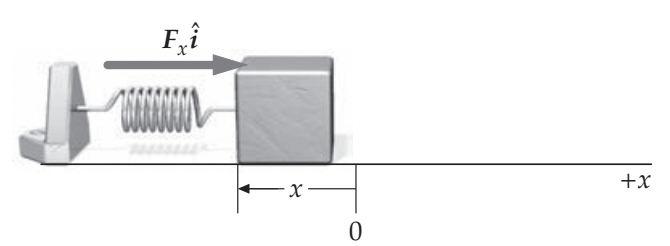
Fonte: Tipler

O trabalho da força elástica depende apenas das posições inicial e final ao longo do caminho.

No gráfico, em que a força é função da deformação, a área é numericamente igual ao trabalho.

W_{n} = F(x_n)\Delta x

Aplicamos a equação do trabalho e somamos para todos os \(n\) retângulos sob a curva:

W \approx \sum_n W_{n}
W = \sum _nF(x_n)\Delta x
\Rightarrow
\Rightarrow

Se permitirmos que o \(\Delta x\) se aproxime de zero (e o número de pequenos deslocamentos se aproximam do infinito \(n\rightarrow \infty\)),

W = \lim_{\Delta x_F \rightarrow 0} \sum _nF(x_n)\Delta x
\Rightarrow
W=\int_{x_i}^{x_f}F(x)dx \equiv \text{Área \,sob\, a\, curva}

O trabalho de forças variáveis (força elástica)

Fonte: Tipler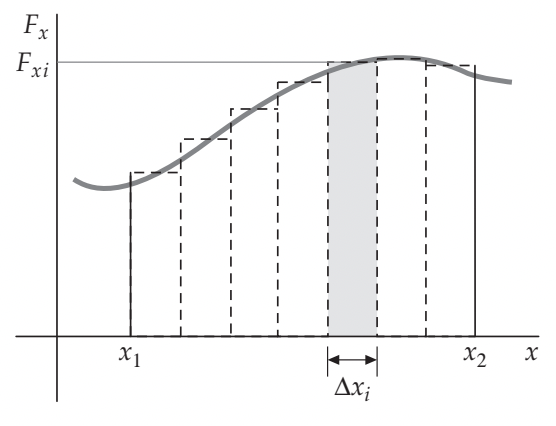

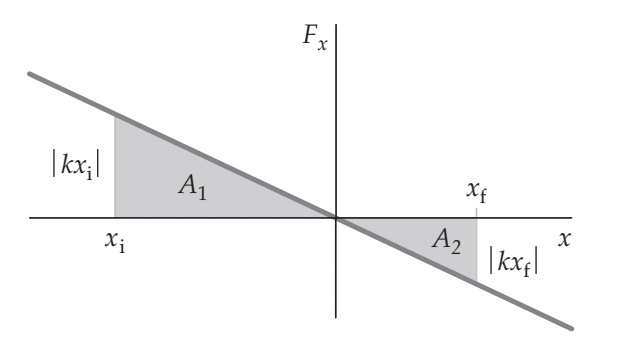
Exemplo 2

Um bloco de 4,0 kg está sobre uma mesa sem atrito e preso a uma mola horizontal com k  400 N/m. A mola é inicialmente comprimida de 5,0 cm. Encontre (a) o trabalho realizado sobre o bloco pela mola enquanto o bloco se move de \(x_1 =-5,0\) cm até sua posição de equilíbrio \(x_2 = 0\) cm, e (b) a rapidez do bloco em \(x_2\).

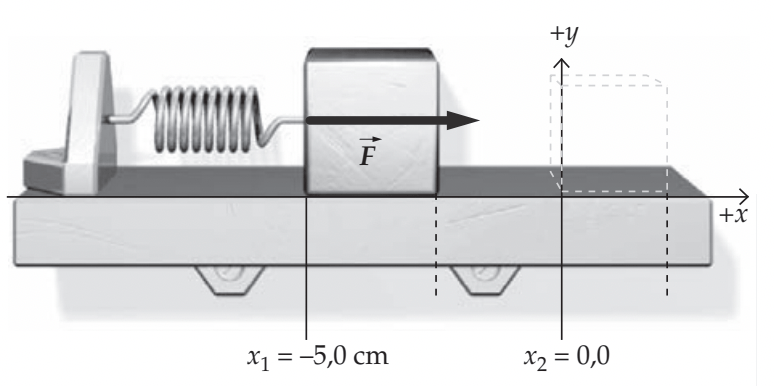
Fonte: Tipler

Exemplo 3

Um objeto move-se ao longo de uma trajetória parabólica de trajetória \(y = 0,5 x^2\), onde \(x\) e \(y\) estão em metros. A origem está em \((x,y)=(0,0)\) m. O ponto final está em \(x,y)=(2,2) \) m. O objeto move-se sob ação de uma força \(\vec F(x,y) = 5,0 y \hat i + 10 x \hat j\), onde a força está em newtons. Calcule o trabalho realizado pela força.

Fonte: OpenStax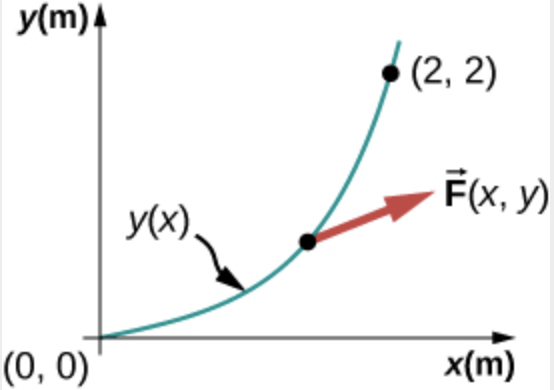

Exercício 4 (A9.P12-08)

Uma partícula, de massa m, está inicialmente posicionada no eixo x positivo, em \(x = x_i\), e sujeita a uma força repulsiva \(F_x\), exercida pela partícula b. A posição da partícula b está fixa, na origem. A força \(F_x\) é inversamente proporcional ao quadrado da distância x entre as partículas. Isto é, \(F_x= A/x^2\), onde \(A\) é uma constante positiva. A partícula a é largada do repouso e fica livre para se mover sob a influência da força. Encontre uma expressão para o trabalho realizado pela força sobre a partícula, como função de x. Encontre a energia cinética e a rapidez de a no limite em que x tende a infinito.

O trabalho pode ser definido a partir de um produto escalar entre dois vetores: \(\vec A\cdot\vec B = AB\text{ cos }\phi\)

O trabalho realizado pela força peso é:

W=\vec P\cdot \Delta \vec r
W=P\Delta x \text{ cos }\phi
W=mg\left( \frac{h}{\text{sen }\theta} \right)\text{cos }\phi

O trabalho da força peso é:

|\Delta r|=\Delta x

pois

W=mgh
x
y
\vec a
\theta
\vec P
\Delta \vec r
\phi

O problema se resumiu ao produto usual da força peso (mg) pelo deslocamento na vertical (h)!

W=mg\left( \frac{h}{\text{sen }\theta} \right)\text{sen }\theta

O trabalho de forças constantes

pois

\phi = \frac{\pi}{2}-\theta

pois

\cos\left(\frac{\pi}{2}-\theta\right)=\text{sen}(\theta)
W=mg(y_f-y_i)
\Rightarrow
h
\Delta x
\theta

No plano inclinado, as componentes da força de contato (\(N\)) e força peso (\(P_y\)) são perpendiculares ao deslocamento da força. Assim, não realizam trabalho.

W_{N}\equiv 0
W_{P_y}\equiv 0

e

O trabalho realizado no bloco realizado pelo componente da força da gravidade ao longo do deslocamento é:

W_{P_x}=P_x\Delta x
W_{P_x}= (+mg\text{sen}\,\theta) \left( \frac{+h}{\text{sen}\,\theta} \right)=mgh

Isso faz sentido, porque é o componente x da força da gravidade que causa o deslocamento do bloco e faz todo o trabalho nele. As forças na direção y não causam deslocamento e, portanto, não realizam trabalho sobre o bloco.

x
y
\Delta \vec x
\theta
\vec P
\vec N
\vec P_y
\vec P_x

O trabalho de forças constantes

W_{P_y}=P_y\Delta x\cos(90^o)
W_{P_y}=0

Exemplo 5

Você move um livro de biblioteca grande, pesando 20 N, cerca 1 m verticalmente para baixo de uma prateleira, e o carrega 3 m horizontalmente até uma mesa.

(a) Quanto trabalho a gravidade faz no livro?

(b) Quando terminar de ler o livro, você move o livro em linha reta de volta ao seu lugar original na prateleira. Qual foi o trabalho total feito contra a gravidade, afastando o livro de sua posição original na prateleira e voltando?

Fonte: OpenStax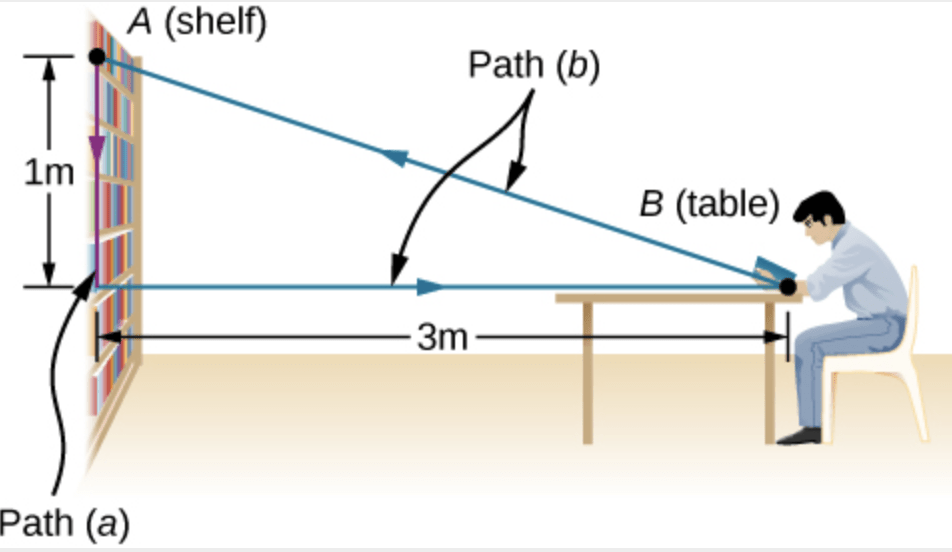

Exemplo 6

Você e uma amiga estão em uma estação de esqui que tem duas pistas, a pista para iniciantes e a pista para veteranos. As duas pistas começam no topo da colina e terminam na base da colina. Seja h a descida vertical para as duas pistas. A pista para iniciantes é mais longa e menos íngreme do que a pista para veteranos. Você e sua amiga, que é muito melhor esquiadora do que você, estão testando esquis experimentais sem atrito. Para tornar as coisas interessantes, você propõe a ela uma aposta: que se ela tomar a pista de veteranos e você tomar a pista de iniciantes, a rapidez dela ao final não será maior do que a sua. Não se dando conta de que você é um estudante de física, ela aceita a aposta. As condições são que vocês dois partam do repouso no topo da colina, deixando que os esquis deslizem sem outra interferência. Quem vence a aposta?

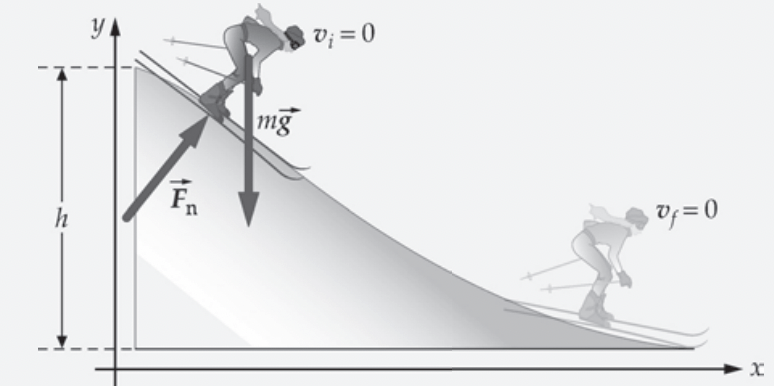
Fonte: Tipler

As forças normal e de atrito estático são forças que provocam deformações elásticas.

As deformações elásticas são reversíveis. O piso não ficará arranhado ao remover a força aplicada antes do bloco iniciar o movimento. A força de atrito estático provoca deformações elásticas.

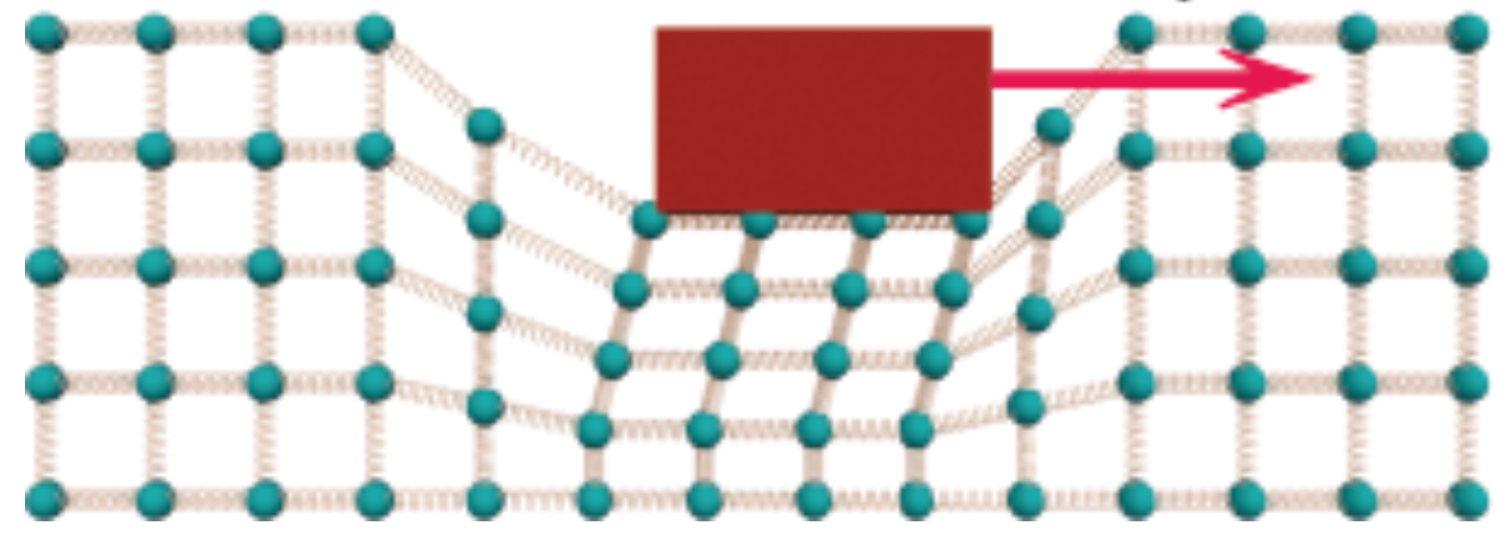
Fonte: Chabay & Sherwood

A força de atrito cinético são forças que provocam deformações permanentes. Está relacionada à energia térmica.

As deformações permanentes são irreversíveis. O piso e o bloco ficarão arranhados por mais cuidadoso que seja o empurrão.

Fonte: Chabay & Sherwood

A força do atrito cinético não é uma força elástica e, portanto, causa dissipação de energia. A força do atrito estático é uma força elástica e, portanto, não causa dissipação de energia.

O trabalho das forças de atrito

O trabalho das forças dissipativas é negativo e leva ao aumento da energia térmica:

\Delta E_{ter}= -W^{nc}_{int}

onde a variação da energia térmica é:

A partir do teorema trabalho-energia cinética, vemos que  trabalho da força de atrito cinético diminui sempre vai diminuir a energia cinética do sistema:

W^{nc}_{int}
\Delta r = d_{efetivo}
\vec F_{at,c}
\vec F_{ap}
\Delta E_{ter}=-\vec F_{at,c}\cdot \Delta \vec r
\Delta E_{ter}=-F_{at,c} d\cos(180^o)=F_{at,c}d>0

Sendo uma variação positiva e, portanto aumenta.

\Delta E_{ter} = -\Delta K < 0

O trabalho das forças de atrito cinético

Fonte: Nikita Golubev

\vec a
\vec a

Fonte: Luiz Felipe

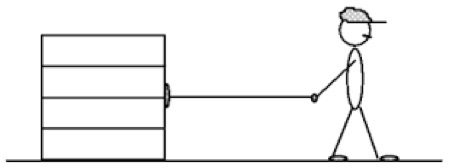
pessoa

pacote

\vec N
\vec F_{at,est}
\vec P
y
x
\vec F^c

Há somente a componente horizontal da aceleração (pessoa ou pacote)

F_{Rp} = m_p a_p\Rightarrow a_p = \frac{F_{at,est}}{m_p}

O deslocamento da força de atrito estático não é nulo para o pacote: \(\Delta r = d\). Daí

W=F_{Rp}d

O deslocamento da força de atrito estático é nulo para a pessoa: \(\Delta r_F = 0\). Daí,

W=F_{Rp}\Delta r\equiv 0
\Delta r = v\Delta t
0
\Delta \vec r_f
v=0
W=(m_pa)_pd

O trabalho das forças de atrito estático

O atrito estático não envolve nenhum movimento das duas superfícies de uma em relação a outra.

Exemplo 7

Você decide mover seu sofá para uma nova posição no chão horizontal da sua sala de estar. A força normal no sofá é de 1 kN e o coeficiente de atrito é de 0,6. (a) Primeiro você empurra o sofá 3 m paralelo a uma parede e depois 1 m perpendicular à parede (A a B na Figura). Quanto trabalho é feito pela força de atrito? (B) Você não gosta da nova posição, então você move o sofá de volta à sua posição original (B para A na Figura 7.4). Qual foi o trabalho total feito contra o atrito movendo o sofá para longe de sua posição original e para trás novamente?

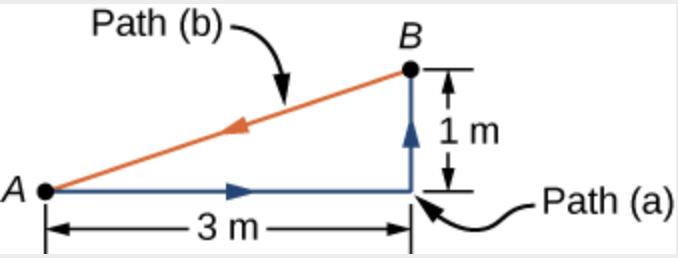
Fonte: OpenStax

Exemplo 8

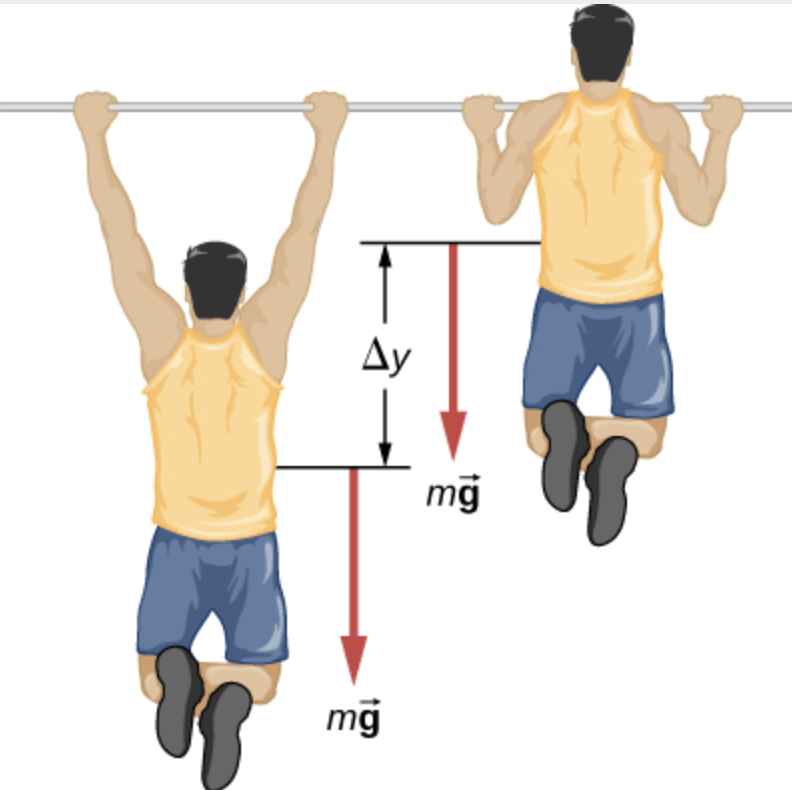
Um estagiário do exército de 80 kg faz flexões em uma barra horizontal (Figura). O estagiário leva 0,8 segundos para elevar o corpo de uma posição mais baixa para onde o queixo está acima da barra. Quanta força os músculos do estagiário fornecem movendo seu corpo da posição inferior para onde o queixo está acima da barra? (Dica: Faça estimativas razoáveis para quaisquer quantidades necessárias.)

Fonte: OpenStax

Exemplo 9 (A9.P1-04 )

Um carro requer 300 kJ de energia para superar a resistência do ar e manter uma velocidade constante de 20 m/s por uma distância de 1,0 km. Qual é a força da resistência do ar exercida no carro?

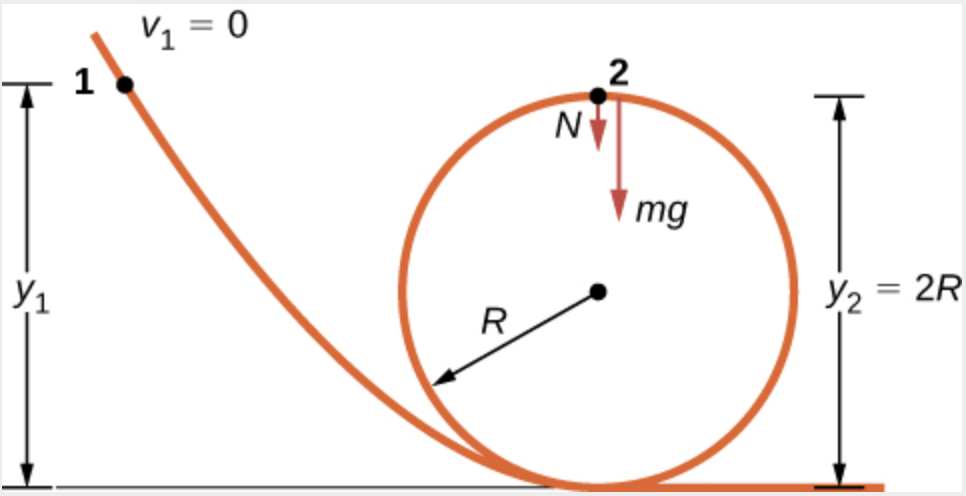
Exemplo 10

A pista sem atrito para um carro de brinquedo inclui um loop-the-loop de raio R. Quão alto, medido a partir da parte inferior do loop, o carro deve ser colocado para começar do repouso na seção de aproximação da pista e contornar todo o loop?

Fonte: OpenStax

Exercício 11

Por um curto período de tempo, o guindaste na figura levanta a viga de 2,50 Mg com uma força de F = (28 + 3y) kN. Determine a rapidez da viga quando ela subiu y = 3 m. Além disso, quanto tempo leva para atingir essa altura a partir do repouso?

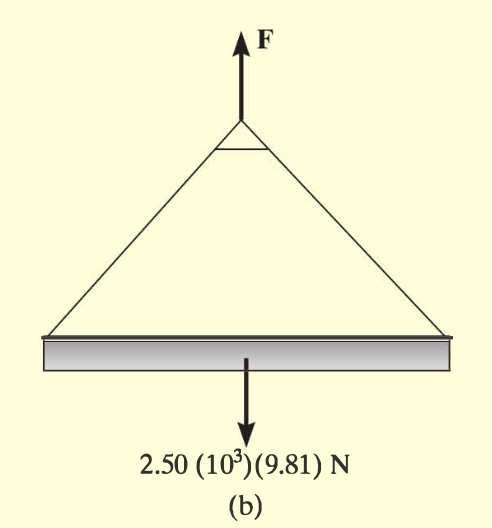
Fonte: Hibeller

Made with Slides.com