Aula 14

Fundamentos de Mecânica

Prof. Ronai Lisbôa

UFRN - ECT - BCT

Em preparação

Objetivos

Enunciar o princípio da energia

Referência: Tipler & Mosca. Capítulo 7

Verifique no SIGAA questões recomendadas

É sempre um pouco complicado definir conceitos fundamentais. Como são a base de tudo o que se segue, eles mesmos parecem não ter base própria. Os físicos têm dificuldade em definir a matéria e a energia, os biólogos, em definir vida, os filósofos, em definir a realidade.

Yuval Noah Harari

Nexus - Uma breve história das redes de informação, da Idade da Pedra à Inteligência Artificial

Dissipação ou degradação da energia

A parte da energia cinética convertida que não reaparece após uma interação inelástica é dissipada ou degradada (em outras palavras, é convertida irreversivelmente).

<= Reversível

Irreversível =>

 Se você remover a mão:

O papel retorna ao formato original.

A deformação ocorre de maneira coerente.

O papel permanece dobrado.

A deformação ocorre de maneira incoerente.

Fonte: http://www.graficaobscura.com

A energia pode ser dissipada:

Em movimentos incoerentes.

 Em deformações incoerentes.

Energia interna \(\neq\) Energia cinética.

Quando uma bola de tênis bate em uma superfície dura, parte da energia cinética da bola é convertida em energia incoerente (irreversível) dos átomos que compõem a bola.

A energia cinética da bola após o salto é menor do que a anterior ao salto e, portanto, a altura do rebote está abaixo da altura original

Dissipação ou degradação da energia

 Fonte: Stroboscopic image of a ball bounce (image courtesy of Professor Andrew Davidhazy, Rochester Institute of Technology)  

Toda energia pode ser dividida em duas classes fundamentais:

  • energia associada ao movimento (cinética);
  • a energia associada à configuração de objetos em interação (interna).

Quando todos os átomos de um objeto se movem de maneira coerente na mesma direção.

Energia Cinética (K)

A energia armazenada em mudanças coerentes na configuração

Energia Potencial (U)

Energia Mecânica = K + U = constante

COERENTE

Dissipação ou degradação da energia

Quando todos os átomos de um objeto se movem de maneira aleatória em todas as direções.

Energia Incoerente: \(E_{termica}\), \(E_{fonte}\), etc.

A energia armazenada em mudanças incoerentes na configuração

Energia interna.

Toda energia pode ser dividida em duas classes fundamentais:

INCOERENTE

Energia interna = \(E_{ter}\) + \(E_{fonte} + U\)

Dissipação ou degradação da energia

  • energia associada ao movimento (cinética);
  • a energia associada à configuração de objetos em interação (interna).

A energia associada ao movimento é a energia cinética (coerente).

A energia associada à configuração do sistema é a energia interna.

A energia interna é a soma das energias térmicas, inelásticas e fontes de energia (incoerentes) e energia potencial (coerente).

A energia mecânica é a soma das energias coerentes: cinética + potencial.

A dissipação de energia corresponde à conversão de energia coerente em energia incoerente.

Dissipação ou degradação da energia

Esse processo é irreversível porque a energia incoerente não pode reverter por si só para uma forma coerente.

Energia interna = \(E_{ter}\) + \(E_{fonte} + U\)

Energia Mecânica = K + U = constante

A dissipação de energia é um processo é irreversível porque a energia incoerente não pode reverter por si só para uma forma coerente.

Se você sacudir a caixa para que todas as bolas se movam descontroladamente, você está armazenando uma certa quantidade de energia incoerente no sistema.

Essa energia incoerente não se transforma espontaneamente em energia cinética coerente da caixa como um todo.

A energia cinética de cada bola também é dissipada no movimento incoerente dos átomos individuais que compõem cada bola.

Fonte: http://astroacademy.org.uk/resources/kinetic-theory/

Dissipação ou degradação da energia

O atrito, que ocorre sempre que dois objetos sólidos se esfregam ou quando um objeto se move através de qualquer fluido  é uma das causas da dissipação de energia.

Vamos assumir que o único tipo de dissipação causada pelo atrito é a dissipação da energia mecânica em energia térmica.

Fonte: https://youtu.be/P2JDNz15ig0

Fonte: https://youtu.be/L4jh6DQc7AU

Dissipação ou degradação da energia

Fontes de energia

Devido à inevitável dissipação da energia mecânica (energia coerente: E\(_{mec}\) = K + U), precisamos de fontes de energia para gerar ou manter a energia mecânica do sistema.

Gasolina é necessária para manter o carro em movimento.

Sem esse suprimento de energia, o carro diminui à medida que sua energia cinética se dissipa por causa do atrito.

Alimento é necessário para correr, brincar e estudar.

Sem esse suprimento de energia, não seremos capazes de executar essas ações à medida que a energia potencial (gravitacional e elástica) se dissipa por causa da energia química.

Fonte: https://pxhere.com/pt/photo/872151

Fonte: https://pxhere.com/pt/photo/518533

Fontes de energia

São várias as fontes de energia:

Combustíveis fósseis e minerais, nuclear, biomassa, solar, eólica, etc.

Existem quatro tipos de fontes de energia:

Energia química (liberada em reações químicas: queima de combustíveis fósseis e minerais)

Energia nuclear (liberada em reações nucleares: quebra do núcleo atômico)

Energia solar (liberada como radiação eletromagnética)

Energia solar armazenada (aquecimento desigual da atmosfera (eólica); células fotovoltaicas; evaporação e condensação da água (hidrelétrica));

Fonte: https://conhecimentocientifico.r7.com

Fonte: https://pxhere.com

Fonte: https://pxhere.com

Fontes de energia

Vamos classificar as energias em quatro categorias:

Energia cinética (K): energia coerente associada com o movimento dos objetos.

Energia potencial (U): energia coerente associada com a configuração dos objetos interagindo (gravitacional e elástica).

Fontes de energia (E\(_f\)): energia incoerente usada para produzir outras formas de energia (química, nuclear, solar, solar armazenada).

Energia térmica (E\(_t\)): energia incoerente associada com o movimento aleatório dos átomos que formam os objetos.

K
U
E_f
E_t
\underbrace{}

Energia Mecânica

(energia coerente)

Fontes de energia

Em um sistema fechado, a soma das quatro categorias de energia é constante.

K
U
E_f
E_t
E = K + U +E_f + E_t
F

Fontes de energia

As energias podem ser convertidas de uma categoria para outra.

Energia cinética pode ser convertida em energia potencial, e vice-versa.

Não dissipativa (reversível)

K
U
E_f
E_t

Dissipativa (irreversível)

Atrito converte energia mecânica irreversivelmente em energia térmica.

K
U
E_f
E_t

Uma fonte de energia é convertida para energia mecânica e alguma energia convertida irreversivelmente para energia térmica.

K
U
E_f
E_t

Uma fonte de energia pode ser convertida completamente e irreversivelmente para energia térmica.

K
U
E_f
E_t

Fontes de energia

O consumo de energia é uma diminuição da quantidade disponível de alguma fonte de energia armazenada na Terra.

Por causa da dissipação, todas as formas de energia acabam sendo convertidas em energia térmica.

Nossa capacidade de recuperar energia mecânica da energia térmica é muito limitada o que torna a energia térmica não tão útil quanto outras formas de energia.

Embora algumas fontes de energia sejam renováveis (solar, eólica, água, biomassa), é improvável que atendam às nossas futuras demandas por energia.

A energia é sempre conservada, mas torna-se menos disponível para o uso quando se converte em energia térmica.

Fontes de energia

Interações irreversíveis variam a energia térmica de um sistema e são chamadas de interações dissipativas;

Interações reversíveis não variam a energia térmica em um sistema e são chamadas de interações não dissipativas ou interações conservativas.

Para determinar se uma interação é ou não dissipativa, tudo o que você precisa fazer é se perguntar se a interação é reversível:

Interações que causam mudanças reversíveis não são dissipativas; aqueles que causam mudanças irreversíveis são dissipativas.

Fontes de energia

Se reproduzisse o vídeo ao contrário, notaria imediatamente que algo não está correto. As bolhas não se formarão a partir das gotículas de água e sabão espontaneamente. Esse processo é irreversível.

Fonte: https://www.youtube.com/embed/blNe2Ae5a2c?enablejsapi=1

Energia cinética: se o lápis estiver parado em sua mesa, sua energia cinética será zero. Se, no entanto, você jogá-lo através da sala, você fornece uma energia cinética de cerca de 1 J.

Energia potencial: para armazenar energia potencial no lápis, você deve alterar sua configuração apertando ou dobrando-o. O lápis, sendo rígido, não se dobra ou aperta com facilidade; portanto, se você tiver sorte, poderá armazenar 0,1 J de energia potencial elástica nele antes que ele se rompa.

Fonte: www.pixbay.com

Fonte: www.pixbay.com

Fontes de energia

Energia coerente - reversível - não dissipativa.

Energia térmica: É impossível converter toda essa energia em outra forma. Vamos imaginar que você carregue um lápis no bolso, para que a temperatura suba da temperatura ambiente para a temperatura corporal. Esse aumento de temperatura aumenta sua energia térmica em 100 J.

Energia química: Se você queimar o lápis, a madeira se transforma em cinzas e a energia de configuração armazenada nas ligações químicas é convertida em energia térmica, que você sente como calor. A energia convertida pela queima do lápis é de 100.000 J.

Energia química quebrada: Se você dobrar o lápis o suficiente, ele quebrará. A energia necessária para quebrar as ligações químicas do lápis é de cerca de 0,001 J.

Fonte: www.pixbay.com

Fontes de energia

Energia incoerente - irreversível - dissipativa.

Primeiro, formas coerentes de energia são insignificantes em comparação com formas incoerentes - a maior parte da energia à nossa volta está na forma de energia incoerente.

Energia incoerente - irreversível - dissipativa.

Segundo, quando a energia é dissipada, praticamente tudo se torna energia térmica; a energia incoerente da configuração associada à deformação, quebra e abrasão é geralmente insignificante em comparação com as energias necessárias para causar essas alterações.

Fontes de energia

Energia coerente - reversível - não dissipativa.

x

A escolha do sistema determina as categorias de energias que precisamos considerar.

A energia do sistema A é:

\Delta K+\Delta E_{int} = W_{ext}

A energia interna pode ter uma contribuição da energia térmica, energia potencial e outras fontes de energia (química):

\Delta K+ \Delta U+ \Delta E_{t}+\Delta E_f=W_{ext}

O princípio da energia

A escolha do sistema

Para uma dada situação, diferentes opções de sistema produzem diferentes diagramas de energia.

Sistema: Cesta + Terra:

\Delta K
\Delta U
\Delta E_f
\Delta E_t
W
\Delta \vec r_F
W<0
\Delta K <0
\Delta U <0
\Delta E_f =0
\Delta E_t =0

Fonte: www.pixbay.com

A escolha do sistema

Para uma dada situação, diferentes opções de sistema produzem diferentes diagramas de energia.

Sistema: Pessoa + Cesta + Terra:

\Delta K
\Delta U
\Delta E_f
\Delta E_t
W
\Delta \vec r_F
F
F
W=0
\Delta K <0
\Delta U <0
\Delta E_f =0
\Delta E_t >0

Fonte: www.pixbay.com

A escolha do sistema

Para uma dada situação, diferentes opções de sistema produzem diferentes diagramas de energia.

Sistema: Pessoa + Cesta + Corda:

\Delta K
\Delta U
\Delta E_f
\Delta E_t
W
\Delta \vec r_F
W>0
\Delta K <0
\Delta U =0
\Delta E_f =0
\Delta E_t >0

Fonte: www.pixbay.com

corrigir: o sistema não inclui a Terra

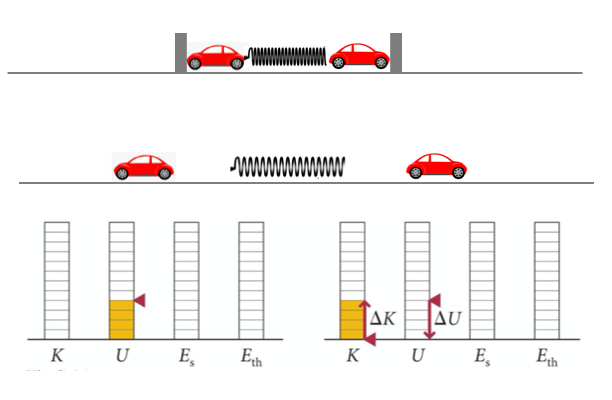
Interações explosivas

A energia cinética de um sistema aumenta em uma separação explosiva.

O aumento da energia cinética (coerente) é devido à energia potencial elástica (coerente):

\Delta K + \Delta U =0

Como a compressão da mola é reversível, essa interação é não dissipativa.

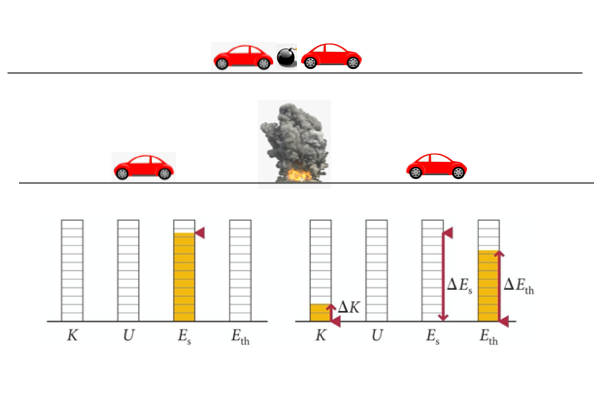
O aumento da energia cinética (coerente) é devido a energia química (incoerente). Mas parte da energia é degradada em energia térmica (incoerente).

\Delta K + \Delta E_{f}+\Delta E_{ter} = 0

Interações dissipativas

Uma interação dissipativa é aquela em que há variações na energia térmica.

Essas interações são irreversíveis.

O vídeo mostra um copo de cerveja deslizando ao longo de uma mesa madeira e diminuindo a velocidade até parar.

O atrito que atua no copo faz com que sua energia cinética seja convertida em energia térmica - seja dissipada. No sistema copo + mesa + Terra é fechado:

\Delta K + \Delta U + \Delta E_f + \Delta E_t = 0
\Rightarrow
\Delta K + \Delta E_t = 0
\Rightarrow
\Delta K =- \Delta E_t

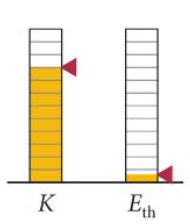
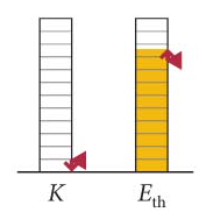
Fonte: www.gifphy.com

Interações dissipativas

Uma interação dissipativa o processo é irreversível.

Você não espera que o copo volte à posição de origem espontaneamente a partir da energia térmica.

Fonte: www.gifphy.com

Existe uma seta do tempo para os eventos. Uma único sentido no tempo!

Para forças não conservativas devemos aplicar o teorema trabalho-energia cinética.

As forças não conservativas são aquelas que dissipam energia.

W = \int \vec F\cdot d\vec r

Forças não conservativas

Forças aplicadas ( necessitam de fontes de energia).

Forças que dependem da velocidade.

Forças de atrito cinético.

Para a força peso no sistema Terra+Cabo+Bondinho:

\Delta K = -\Delta U

Para a força aplicada no sistema Terra+Cabo+Bondinho:

\Delta K = \int\vec F_{ap}\cdot d\vec r

A força de atrito cinético é uma forças distribuída (não possui um ponto de aplicação da força). Assim, não faz muito sentido em falar sobre o trabalho da força de atrito, mas para fins práticos você pode calcular via o teorema trabalho energia cinética

Trabalho e força de atrito

As forças normal e de atrito estático são forças que provocam deformações elásticas.

As deformações elásticas são reversíveis. O piso não ficará arranhado ao remover a força aplicada antes do bloco iniciar o movimento.

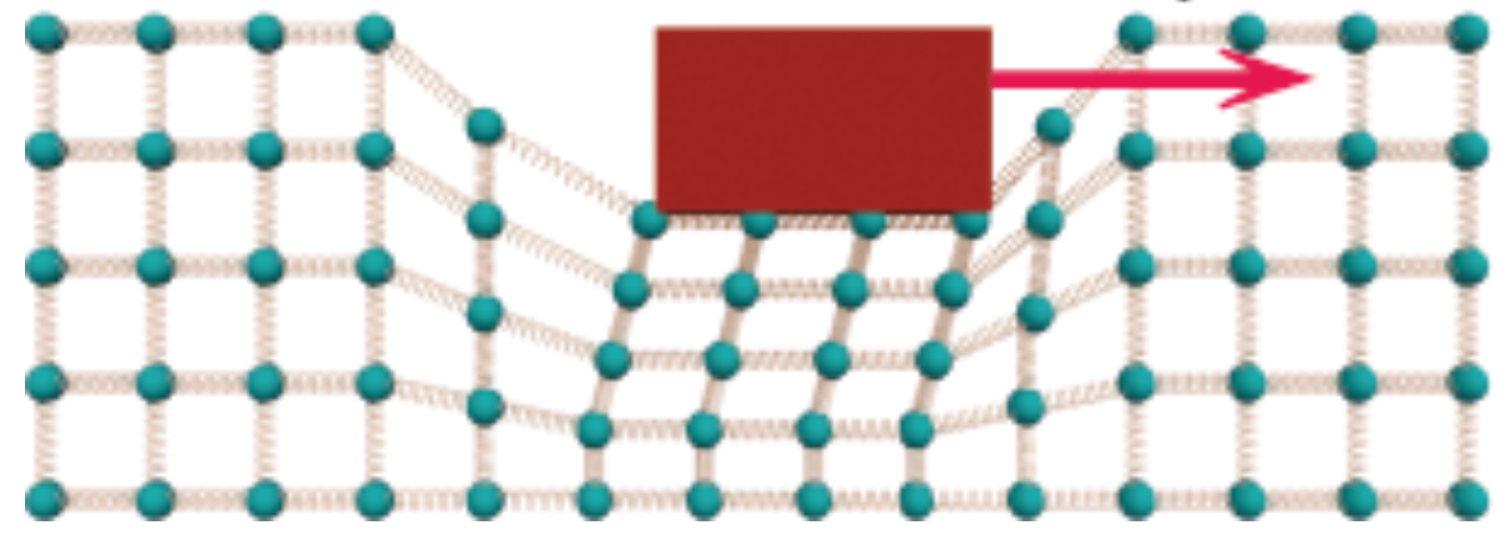
Fonte: Chabay & Sherwood

A força de atrito cinético são forças que provocam deformações permanentes.

As deformações permanentes são irreversíveis. O piso e o bloco ficarão arranhados por mais cuidadoso que seja o empurrão.

Fonte: Chabay & Sherwood

A força do atrito cinético não é uma força elástica e, portanto, causa dissipação de energia. A força do atrito estático é uma força elástica e, portanto, não causa dissipação de energia.

Trabalho e força de atrito (cinético)

O trabalho realizado sobre um sistema é convertido em energia cinética.

W^{nc} + W^{c}=\Delta K
W_t =\Delta K

O trabalho das forças conservativas depende somente dos pontos inicial e final, mas não da trajetória. Nesse caso, existe uma função desses pontos que é a energia potencial:

W^c_{a\rightarrow b} =-\Delta U

O trabalho das forças não conservativas está associado as forças dissipativas (incoerentes). A força de atrito cinético (interna ao sistema) e a força aplicada (externa ao sistema) são alguns exemplos:

W^{nc}_{ext}+ W^{nc}_{int}- \Delta U=\Delta K

o trabalho de forças dissipativas  alteram a energia do sistema.

W^{nc}_{ext}
W^{nc}_{int}
W^{nc}_{ext}+ W^{nc}_{int}= \Delta K+ \Delta U
W^{nc}_{ext}+ W^{nc}_{int}= \Delta E_{mec}
\vec F_{at,c}
\vec F_{ap}

O trabalho das forças dissipativas é negativo e leva ao aumento da energia térmica:

W^{nc}_{int} =-\Delta E_{ter}

Nossa expressão anterior fica:

um trabalho externo não conservativo varia a energia dos sistema.

W^{nc}_{ext}
W^{nc}_{int}
W^{nc}_{ext}- \Delta E_{ter}= \Delta E_{mec}
W^{nc}_{ext}= \Delta E_{mec}+\Delta E_{ter}
W^{nc}_{ext}= \Delta E_{sis}
\Delta r = d_{efetivo}
\vec F_{at,c}
\vec F_{ap}
\Delta E_{ter}=-\vec F_{at,c}\cdot \Delta \vec r_{ef}
\Delta E_{ter}=+F_{at,c} d

Trabalho e força de atrito (cinético)

Ao desenhar um diagrama de energia, não escolha um sistema para o qual ocorra atrito nos contornos do sistema, pois pode ficar difícil analisar o trabalho de uma força distribuída como atrito.

\Delta K
\Delta U
\Delta E_f
\Delta E_t
W
?
?

Sistema: Pessoa + Caixa

Fonte: www.pixbay.com

Trabalho e força de atrito (cinético)

Ao desenhar um diagrama de energia, escolha um sistema para o qual ocorra atrito no sistema.

\Delta K
\Delta U
\Delta E_f
\Delta E_t
W

Sistema: Pessoa + Caixa + Terra

F
F

Fonte: www.pixbay.com

Trabalho e força de atrito (cinético)

A força de atrito estático realiza trabalho em um sistema?

Fonte: Nikita Golubev

\vec a
\vec a

Fonte: Luiz Felipe

pessoa

pacote

\vec F^n_{sp}
\vec F^e_{sp}
\vec F^G_{Tp}
y
x

O atrito estático não envolve nenhum movimento das duas superfícies em relação uma à outra

O trabalho requer um deslocamento do ponto de aplicação da força diferente de zero

W=F_R\Delta r_F

Nos dois casos, o sistema ganha energia cinética. De onde vem essa energia e qual é o papel do atrito estático em cada caso?

Trabalho e força de atrito (estático)

\vec F^c_{sp}

A força de atrito estático realiza trabalho em um sistema?

Fonte: Nikita Golubev

\vec a
\vec a

Fonte: Luiz Felipe

pessoa

pacote

\vec F^n_{sp}
\vec F^e_{sp}
\vec F^G_{Tp}
y
x
\vec F^c_{sp}

Há somente a componente horizontal da aceleração:

F_{Rp} = m_p a_p\Rightarrow a_p = \frac{F^e_{sp}}{m_p}

O deslocamento da força de atrito estático não é nulo para o pacote: \(\Delta r_F = d\). Daí

W=F_{Rp}d

O deslocamento da força de atrito estático é nulo para a pessoa: \(\Delta r_F = 0\). Daí

W=F_{Rp}\Delta r_F\equiv 0

Trabalho e força de atrito (estático)

\Delta r_F = v\Delta t
0
\Delta \vec r_f
v=0
W=(m_pa)_pd

Exemplo 1 (A9.P12-03 )

Um bloco de madeira de 0,50 kg que viaja inicialmente a 1,0 m/s desliza 0,50 m em um piso horizontal antes de atingir o repouso. Qual é a taxa média na qual a energia térmica é gerada?

Exemplo 2 (A9.P12-04 )

Um carro requer 300 kJ de energia para superar a resistência do ar e manter uma velocidade constante de 20 m/s por uma distância de 1,0 km. Qual é a força da resistência do ar exercida no carro?

Exemplo 3 (A9.P12-05 )

Um carro de 2000 kg, movendo-se com uma rapidez inicial de 25 m/s em uma estrada horizontal, desliza até parar 60 m adiante. (a) Determine a energia dissipada pelo atrito. (b) Determine o coeficiente de atrito cinético entre os pneus e a estrada. (Nota: Ao parar sem deslizar e usando freios convencionais, 100 por cento da energia cinética é dissipada pelo atrito nos freios. Com freios regenerativos, como os utilizados em veículos híbridos, apenas 70 por cento da energia cinética é dissipada.)

Exemplo 4 (A9.P12-06 )

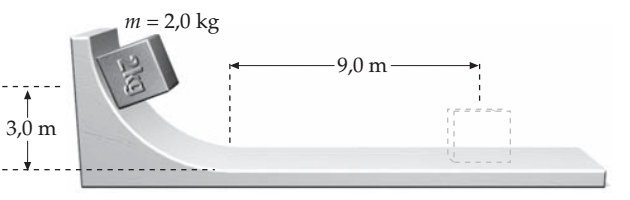
O bloco de 2,0 kg da figura desliza para baixo, ao longo de uma rampa curva sem atrito, partindo do repouso de uma altura de 3,0 m. O bloco desliza, então, por 9,0 m, ao longo de uma superfície horizontal rugosa antes de atingir o repouso. (a) Qual é a rapidez do bloco na base da rampa? (b) Qual é a energia dissipada pelo atrito? (c) Qual é o coeficiente de atrito cinético entre o bloco e a superfície horizontal?

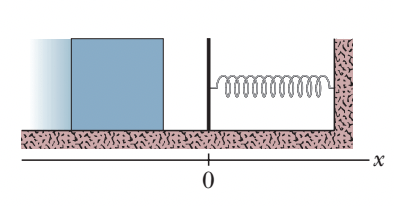
Exemplo 5 (A9.P12-07)

Na figura, um bloco de massa m = 2,5 kg desliza de encontro a uma mola de constante elástica k = 320 N/m. O bloco para após comprimir a mola 7,5 cm. O coeficiente de atrito cinético entre o bloco e o piso é 0,25. Enquanto o bloco está em contato com a mola e sendo levado ao repouso, determine (a) o trabalho realizado pela mola e (b) o aumento da energia térmica do sistema bloco–piso. (c) Qual é a velocidade do bloco imediatamente antes de se chocar com a mola?

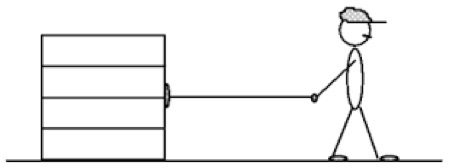
Exemplo 6 (A9.P12-10 )

Uma caixa de 7,5 kg está sendo levantada por uma corda leve que passa por uma única polia, leve e sem atrito, que está presa ao teto. (a) Se a caixa está sendo levantada com uma rapidez constante de 2,0 m/s, qual é a potência desenvolvida pela pessoa que puxa a corda? (b) Se a caixa é levantada, com uma aceleração constante, a partir do repouso no chão, até a uma altura de 1,5 m acima do chão, em 0,42 s, qual é a potência média desenvolvida pela pessoa que puxa a corda?

Exemplo 7 (A10.P2-08 )

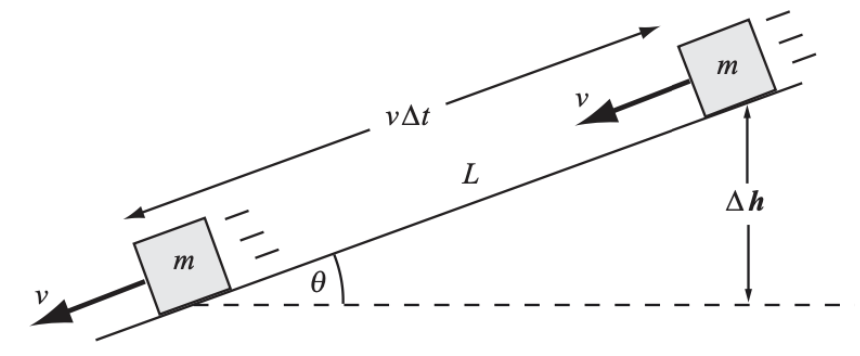
Um bloco de massa m desliza com rapidez constante v para baixo sobre um plano inclinado de um ângulo   com a horizontal. Deduza uma expressão para a energia dissipada pelo atrito durante o intervalo de tempo  .

Exemplo 8 (A10.P2-10 )

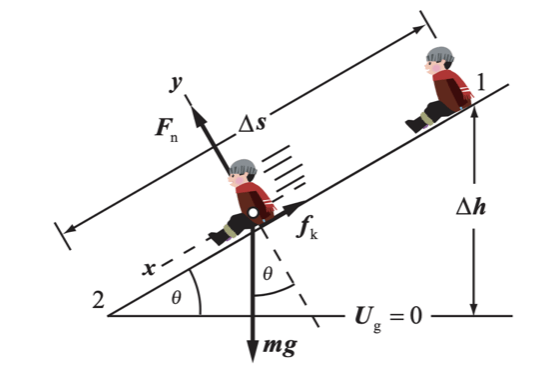
Uma menina de 20 kg desce por um escorregador cujo desnível vertical é de 3,2 m. Quando ela chega à base do escorregador, sua rapidez é 1,3 m/s. (a) Quanta energia foi dissipada pelo atrito? (b) Se a inclinação do escorregador é de 20° com a horizontal, qual é o coeficiente de atrito cinético entre a menina e o escorregador? T7.66

Exemplo 9

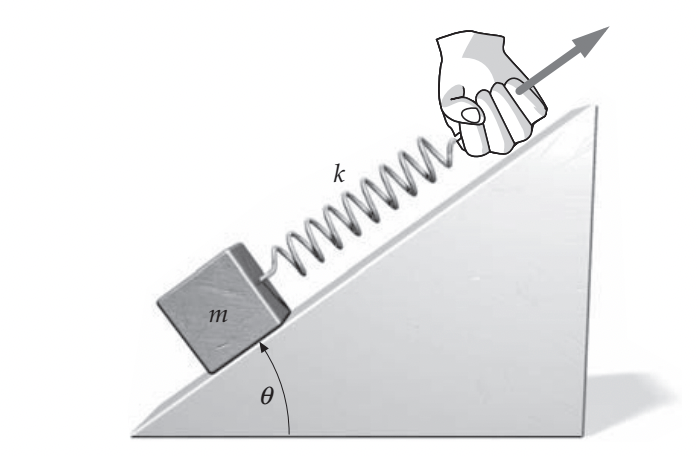
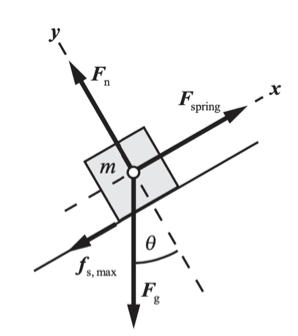
Um bloco de massa m está sobre um plano inclinado de um ângulo   com a horizontal (Figura). Uma mola, de constante de força k, está presa ao bloco. O coeficiente de atrito estático entre o bloco e o plano é \(\mu_e\). A mola é puxada para cima paralelamente ao plano, muito lentamente. (a) Qual é a distensão da mola, no momento em que o bloco começa a se mover? (b) O bloco pára de se deslocar justo quando a distensão da mola que se contrai chega a zero. Expresse  o coeficiente de atrito cinético em termos de  coeficiente de atrito estático e do ângulo de inclinação do plano. T7.70

Exemplo 10 (A9.P12-13)

Um sistema consiste em um jogador de basquete de 110 kg, o aro da cesta e a Terra. Suponha zero a energia potencial deste sistema quando o jogador está de pé no chão e o aro está na horizontal. (a) Encontre a energia potencial total deste sistema quando o jogador está pendurado na frente do aro. Suponha, também, que o centro de massa do jogador está a 0,80 m do chão quando ele está de pé no chão, e 1,30 m acima do chão quando ele está pendurado. A constante de força do aro é 7,2 kN/m e a parte da frente do aro é deslocada para baixo de uma distância de 15 cm. (b) Qual a fonte dessa energia supondo que não há dissipação da energia? (c) Qual seu impulso inicial?

Exemplo 11 (A9.P12-13)

Um sistema consiste em um jogador de basquete de 110 kg, o aro da cesta e a Terra. Suponha zero a energia potencial deste sistema quando o jogador está de pé no chão e o aro está na horizontal. (a) Encontre a energia potencial total deste sistema quando o jogador está pendurado na frente do aro. Suponha, também, que o centro de massa do jogador está a 0,80 m do chão quando ele está de pé no chão, e 1,30 m acima do chão quando ele está pendurado. A constante de força do aro é 7,2 kN/m e a parte da frente do aro é deslocada para baixo de uma distância de 15 cm. (b) Qual a fonte dessa energia supondo que não há dissipação da energia? (c) Qual seu impulso inicial?

Exemplo 12 (A9.P12-14)

Exemplo 13 (A9.P12-15)

É comum observar fenômenos como esse seja em um canteiro de obra ou mesmo pessoas socorrendo pessoas em situação de perigo que pulam dos seus apartamentos em um ato de salvar a vida.

Como analisar fenômenos como esse.

(a) Qual a velocidade do saco de cimento ao atingir o trabalhador que está no chão?

(b)Ele pode se ferir gravemente?

(c) Quanto tempo ele leva caindo?

https://youtu.be/48BVtvH-eOM?si=ZP5ZQXdqTN_Lho9p

Made with Slides.com