
Aula 13
Fundamentos de Mecânica
Prof. Ronai Lisbôa
UFRN - ECT - BCT
Objetivos
Reconhecer a energia potencial como energia interna.
Distinguir os tipos de energia potencial (gravitacional e elástica)
Aplicar o princípio da conservação da energia mecânica.
Identificar a energia interna em um sistema isolado.
Bibliografia.
Tipler - Cap. 7
Seções: 7.2 (até pag. 210)
- Refaça os exercícios resolvidos.
O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)
Para usar I.A. você deve saber ou ter ideia do que está fazendo. Se não é só informação fugaz.
Uma partícula livre e que não tem estrutura tem apenas energia cinética.
O trabalho externo
A energia cinética pode ser alterada por meio de trabalho externo (interação externa).
O trabalho interno
Para um sistema de partículas que interagem entre si (força interna), há uma energia associada as interações internas.
A energia cinética pode ser alterada por meio de trabalho interno.
O trabalho interno está relacionado a forças que dependem apenas da posição relativa entre as partículas ou em alguns casos apenas da distância que as separam.
Trabalhos interno e externos

A energia cinética pode ser alterada por meio de trabalho externo (forças externas) e interno (forças internas).
Os trabalhos externo e interno podem ser associados a uma nova categoria de energia que não está associada ao movimento, mas apenas associada à força e à posição relativa entre as partículas do sistema: a energia potencial.
Uma colisão dita elástica:
No instante do impacto, a bola tem velocidade zero e perdeu toda a energia cinética que possuía ao se mover em direção à parede. A energia cinética foi convertida em energia interna.

Fonte: www.gifer.com
A energia interna
Diagrama da energia cinética da bola em um sistema fechado.
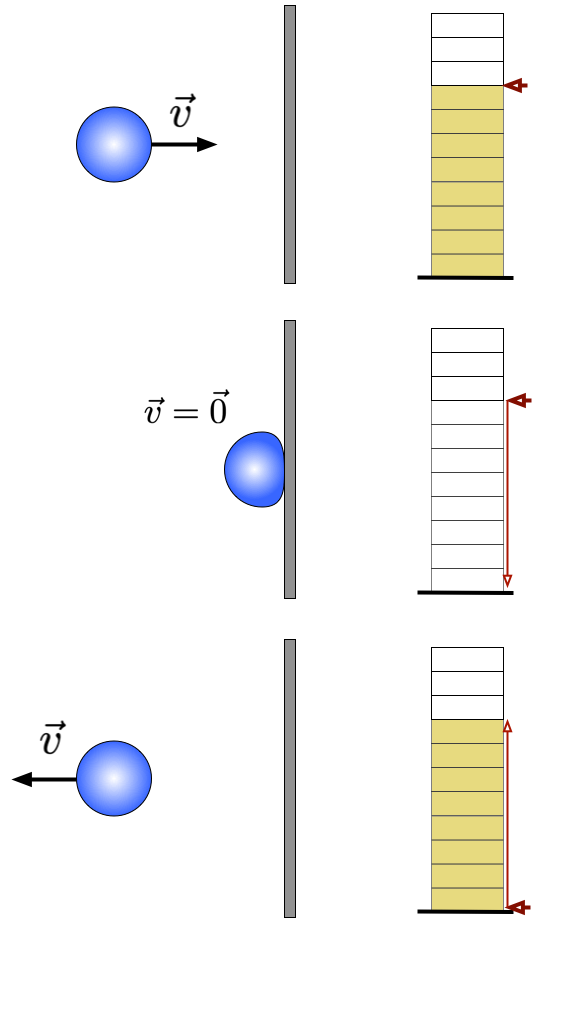


Inicial
Durante
Final
Se a energia cinética em um sistema isolado (\(W_{ext} = 0\)) não pode sumir, para onde ela foi?
A energia interna é a energia armazenada no sistema devido às posições relativas e às velocidades das partículas que o compõem, sem considerar a energia associada ao movimento do sistema como um todo no espaço (cinética).
Esse "desaparecimento" da energia cinética não compromete a conservação de energia. A energia cinética "ausente" durante a interação foi convertida temporariamente em energia interna.

Fonte: www.gifer.com
A energia interna
Após o impacto, a bola recupera sua forma original e a energia interna é convertida em energia cinética. As energias (cinética e interna) são convertidas reversivelmente.
A interação mudou a forma da bola. Essa mudança de forma pode ser associada a uma energia interna devido à reconfiguração das ligações moleculares da bola.
Uma colisão dita elástica:
Na colisão dita inelástica ou totalmente inelástica
No instante do impacto, a lâmpada tem velocidade zero e perdeu toda a energia cinética que possuía ao se mover em direção à chão.
A interação mudou a forma da lâmpada. A energia cinética é convertida em energia interna.
Após o impacto, a lâmpada não recupera sua forma original. As energias (cinética e interna) são convertidas irreversivelmente.

Fonte: www.gifer.com
A energia interna
A colisão elástica é um processo reversível.
A colisão inelástica é um processo irreversível.
A energia interna
Existem muitas formas de energia interna, todas relacionadas à maneira como os objetos em interação se organizam espacialmente.
Energia cinética Energia interna Energia cinética
100 %
=100 %
Energia cinética Energia interna Energia cinética
100 %
< 100 %

Fonte: Wikimedia CommonsEnergia interna
A energia é armazenada em alterações reversíveis no estado de configuração do sistema, isto é, no arranjo espacial dos componentes do sistema em interação.
Pressionar uma bola altera o estado de configuração dos arranjos no nível atômico.
À medida que a bola é pressionada, a forma muda, energia potencial elástica é armazenada no sistema dos arranjos atômicos-moleculares.

Fonte: https://tenor.com
FORMA
POSIÇÃO
À medida que a massa é içada para cima, a forma de energia energia potencial gravitacional é armazenada no sistema Terra-Massa.
Elevar uma massa altera o estado de configuração do sistema Terra-Massa.

No sistema isolado Terra-massa, as forças são internas e a aceleração da bola é tal que:
Multiplicando pela massa da bola, em ambos os lados, temos:
Matematicamente:
Integrando ambos os lados:
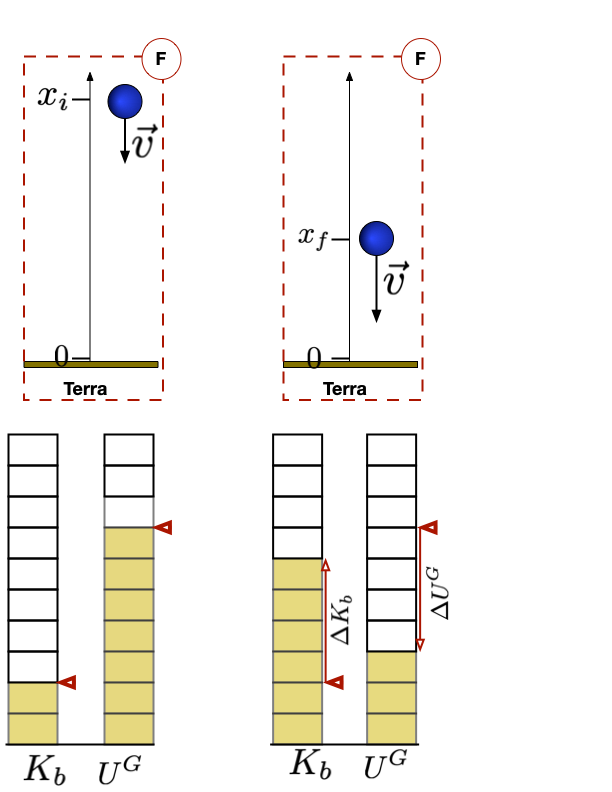
E energia potencial gravitacional
INICIAL
FINAL
Como todos os objetos que caem perto da superfície da Terra experimentam a mesma aceleração a energia potencial gravitacional do sistema Terra-massa é dada pela expressão:
E a variação dessa energia é:
A energia potencial gravitacional
Se o sistema é a massa e a Terra é a vizinhança, o trabalho da força peso é:
A variação da energia potencial gravitacional é o negativo do trabalho da força peso.
Integrando ambos os lados:
Fonte: http://www.edukapa.com.br
Matematicamente:
Multiplicando pela massa da bola, em ambos os lados, temos:
A energia potencial elástica
No sistema isolado massa-mola, as forças são internas e a aceleração da bola é tal que:
Para pequenas deformações (elásticas) em torno da origem a energia potencial elástica do sistema massa-mola é dada pela expressão:
E a variação dessa energia é:
A energia potencial elástica
Se o sistema é a massa e a vizinhança é a mola, o trabalho da força elástica é:

A variação da energia potencial elástica é o negativo do trabalho da força elástica.

Geogebra: LINKEm um sistema isolado o trabalho das forças peso e elástica é igual ao negativo da variação da energia potencial do sistema:
Isto é uma variação da energia cinética deve aparecer como uma variação da energia potencial,
A conservação da energia mecânica
A partir do Teorema trabalho-energia cinética,
Em um sistema isolado no qual ocorrem apenas interações internas não dissipativas, a energia mecânica (a soma das energias cinética e potencial) é constante ou conservada.

onde
A escolha do sistema determina as categorias de energias que precisamos considerar.

Há somente forças internas.
Há forças externas e internas.
A energia potencial está associada às forças internas conservativas.
O trabalho externo está associado às forças externas conservativas (ou não).
Somente por meio de trabalho externo é possível alterar a energia do sistema.
A conservação da energia mecânica

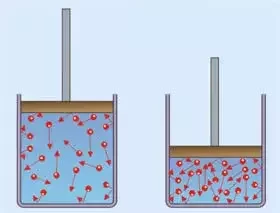
Fonte: Google
No sistema isolado bola + Terra, as forças são internas e conservativas. A energia cinética é convertida em energia potencial e vice-versa.
Para o sistema isolado: bola+Terra em que a bola cai:
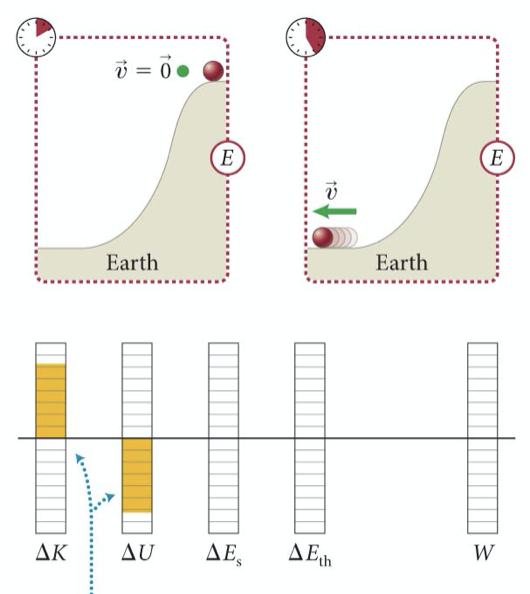
Há um aumento da energia cinética as custas da diminuição da energia potencial gravitacional.
A escolha do sistema
Temos uma energia interna devido as forças internas ao sistema.
Fonte: Mazur
Para o sistema fechado: bola em que a bola cai:
Há um aumento da energia cinética devido ao aumento do trabalho externo realizado pela força peso na queda da bola:
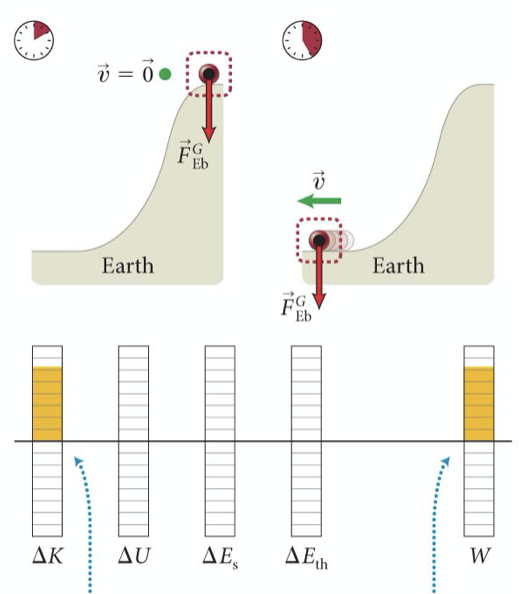
Temos trabalho externo devido as forças externas ao sistema. O trabalho externo positivo aumentou a energia (cinética) do sistema. Então, \(W^G=-\Delta U\).
Nos sistema fechado bola+Terra, há a força externa conservativa que a Terra exerce sobre a bola. A energia cinética varia as custas do trabalho externo:
A escolha do sistema
Fonte: Mazur

Quando as forças são conservativas o trabalho é igual ao negativo da variação da energia potencial.

Ao definir um sistema estamos estabelecendo as energias envolvidas e uma vez conhecidas as energias nós podemos controlá-las.
A escolha do sistema
Fonte: Mazur
Fonte: Mazur
Ao definir um sistema estamos estabelecendo as energias envolvidas e uma vez conhecidas as energias nós podemos controlá-las.
A escolha do sistema
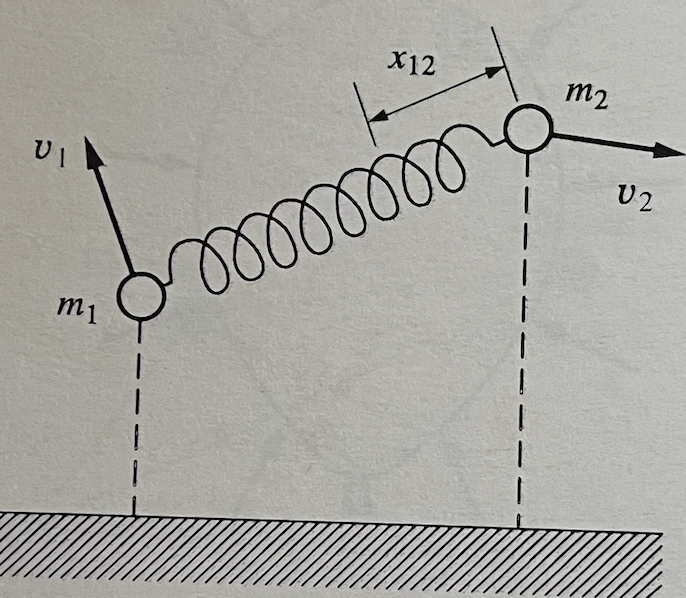
Como seria a energia total desse sistema de duas partículas cujas interações são modelas por uma mola?
Exemplo 1
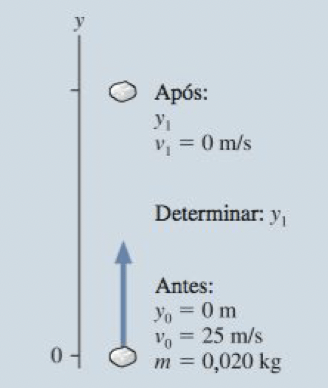
Bob usa um estilingue para atirar uma pedrinha de 20 g diretamente para cima a 25 m/s. Que altura máxima atingirá a pedrinha?
Fonte: Randall
Exemplo 2
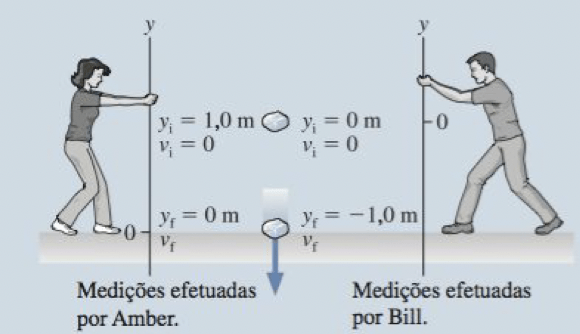
A pedra de 1,0 kg mostrada da figura é solta do repouso. Use tanto o ponto de vista de Amber quanto o de Bill para calcular os valores de velocidade da pedra calculados por eles imediatamente antes da pedra tocar no solo.
Fonte: Randall
Exemplo 3
Christine corre empurrando seu trenó a 2,0 m/s. Quando está no topo de uma rampa de 5,0 m de altura, ela pula para cima do trenó. Qual será a sua rapidez na base?
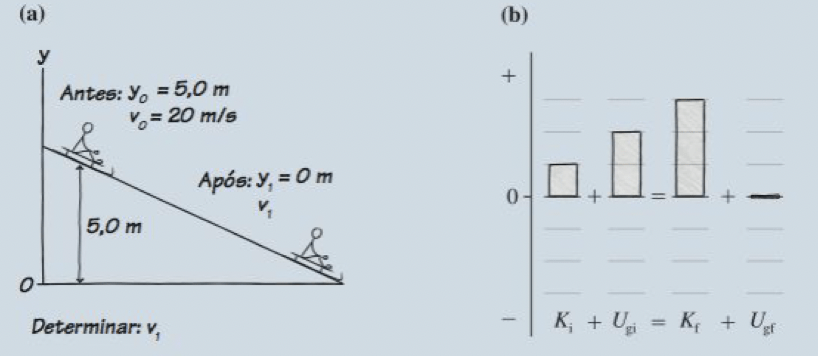
Fonte: Randall
Exemplo 4
Uma arma de brinquedo acionada por uma mola interna lança uma bola plástica de 10 g. A mola, de constante elástica de 10 N/m, é comprimida em 10 cm quando a bola é empurrada para dentro do cano da arma. Quando o gatilho é puxado, a mola é liberada e arremessa a bola para fora. Qual é a rapidez da bola ao sair do cano? Considere que o atrito seja desprezível.
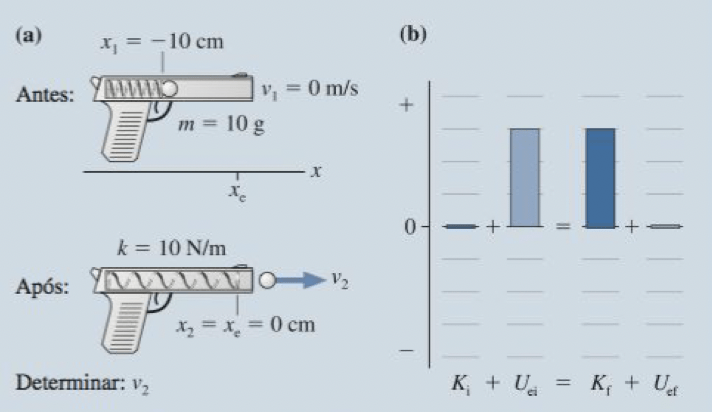
Fonte: Randall
Exemplo 5
O príncipe Harry, o Horrível, desejava ser o primeiro a lançar um satélite. Ele colocou uma carga de 2,0 kg em cima de uma mola muito dura com 2,0 m de comprimento e constante elástica de 50.000 N/m. O príncipe, então, ordenou que seu homem mais forte usasse uma manivela para comprimir a mola até que ela tivesse apenas 80 cm de comprimento. Ao ser liberada, a mola arremessou a carga diretamente para cima. Que altura esta atingiu?

Fonte: Randall
Exemplo 6
O objeto de 3,00 kg da figura é largado do repouso de uma altura de 5,00 m em uma rampa curva sem atrito. Na base da rampa está uma mola com uma constante de força de 400 N/m. O objeto desliza rampa abaixo e até a mola, comprimindo-a de uma distância x até atingir momentaneamente o repouso. (a) Encontre x. (b) Descreva o movimento do objeto (se ocorrer) após o repouso momentâneo. T7.39

Fonte: Tipler
Exemplo 7
Uma caixa de 2,0 kg desliza para baixo sobre um longo plano inclinado de 30°, sem atrito. Ela parte do repouso no tempo t = 0 no topo do plano, a uma altura de 20 m acima do solo. (a) Qual é a energia potencial da caixa em relação ao solo em t = 0? (b) Use as leis de Newton para encontrar a distância que a caixa percorre durante o intervalo 0,0 s < t < 1,0 s, e sua rapidez em t = 1,0 s. (c) Encontre a energia potencial e a energia cinética da caixa em t = 1,0 s. (d) Encontre a energia cinética e a rapidez da caixa justo quando ela alcança o solo na base do plano inclinado. T7.21
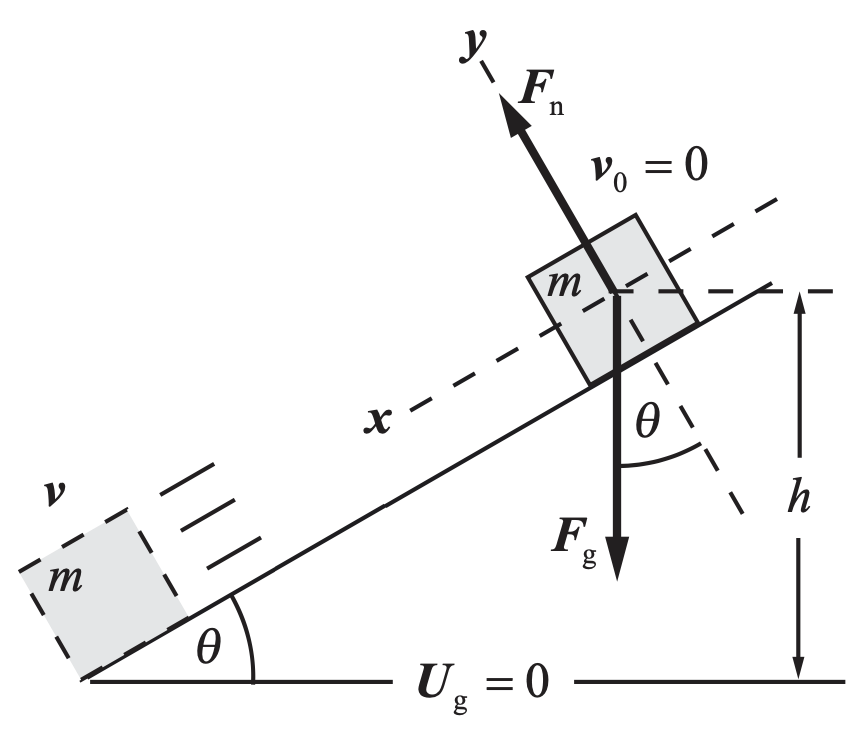
Fonte: Tipler
Exemplo 8
Uma menina de massa m está levando um lanche para o piquenique da vovó. Ela amarra uma corda de comprimento R ao galho de uma árvore, sobre um riacho, e começa a se balançar, a partir do repouso, de um ponto que é R/2 mais baixo do que o galho. Qual é a menor tensão de ruptura que a corda pode ter para não se romper atirando a menina no riacho? T7.46
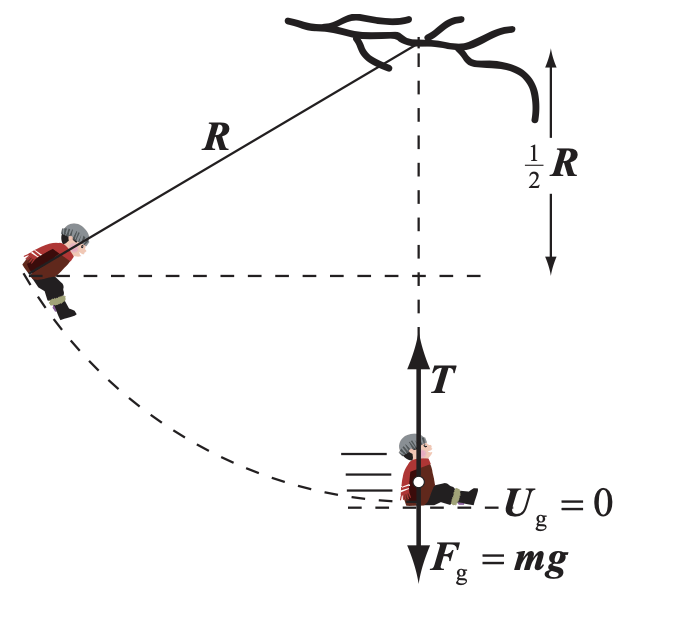
Fonte: Tipler
Exemplo 9
Um pêndulo consiste em uma bola de 2,0 kg presa a um fio leve de 3,0 m de comprimento. Quando suspensa em repouso, com o fio na vertical, a bola recebe um impulso horizontal que lhe imprime uma velocidade horizontal de 4,5 m/s. No instante em que o fio forma um ângulo de 30° com a vertical qual é (a) a rapidez da bola, (b) a energia potencial gravitacional (relativa a seu valor no ponto mais baixo) e (c) a tensão no fio? (d) Qual é o ângulo do fio com a vertical, quando a bola atinge sua altura máxima? T7.54
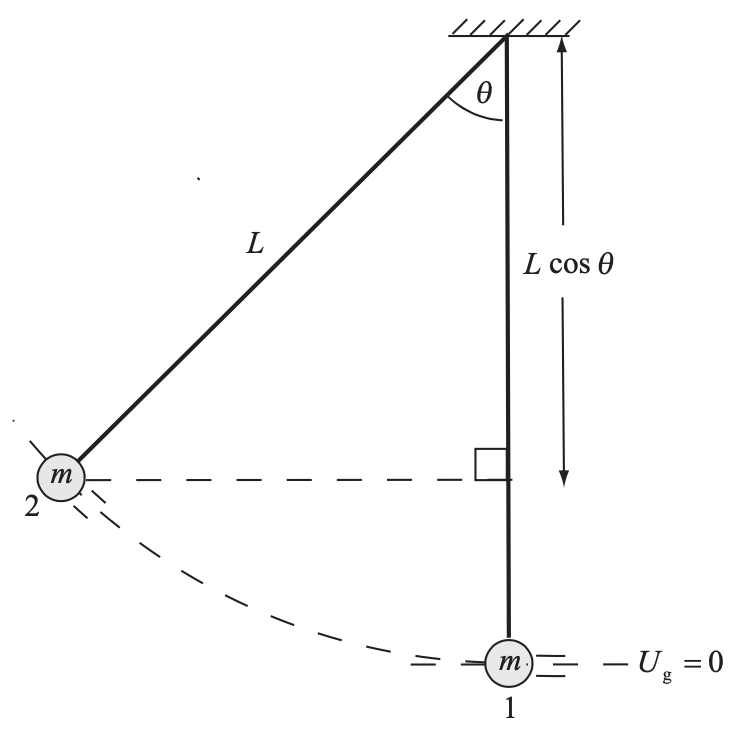
Fonte: Bauer
Exemplo 10
Uma montanha-russa consiste em um único laço. O carrinho é, inicialmente, empurrado, adquirindo a energia mecânica exatamente necessária para que os passageiros se sintam “sem peso” no ponto mais alto do arco circular. Eles se sentirão com qual peso ao passarem pela base do arco (isto é, qual é a força normal exercida para cima quando eles estão na base do laço)? Dê sua resposta como um múltiplo de mg (o peso real dos passageiros). Desconsidere atrito e resistência do ar. T7.49
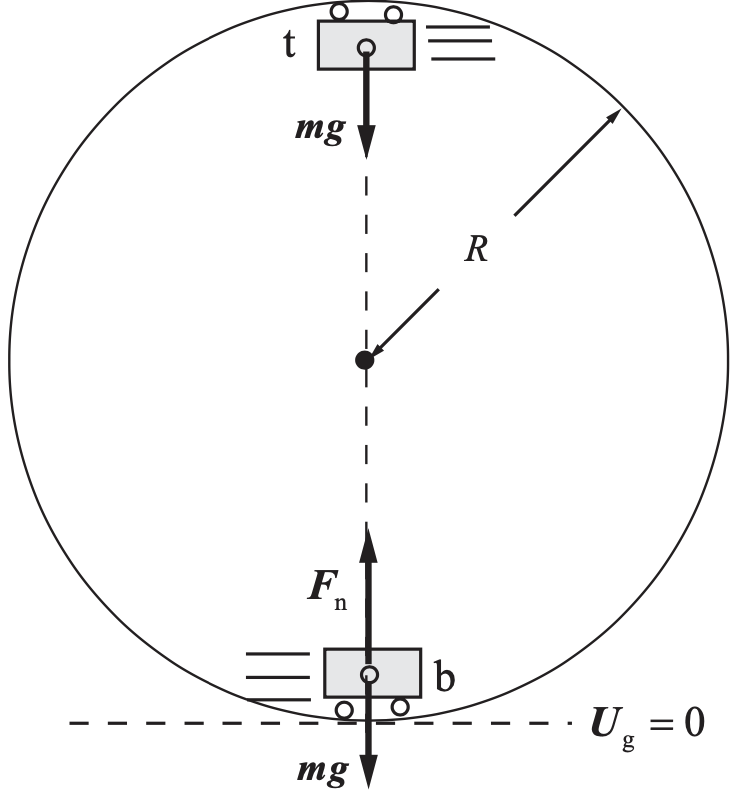
Fonte: Bauer
Exemplo 11 (A7.P2-06)
Um carrinho com massa m = 0,200 kg está em repouso sobre um trilho de ar sem atrito, ligado a uma mola cuja constante é dada por k = 5,00 N/m. Você puxa o cavaleiro fazendo a mola se alongar 0,100 m e a seguir o libera a partir do repouso. O cavaleiro começa a se mover retornando para sua posição inicial (x = 0). Qual é o componente x da sua velocidade no ponto x = 0,080 m?
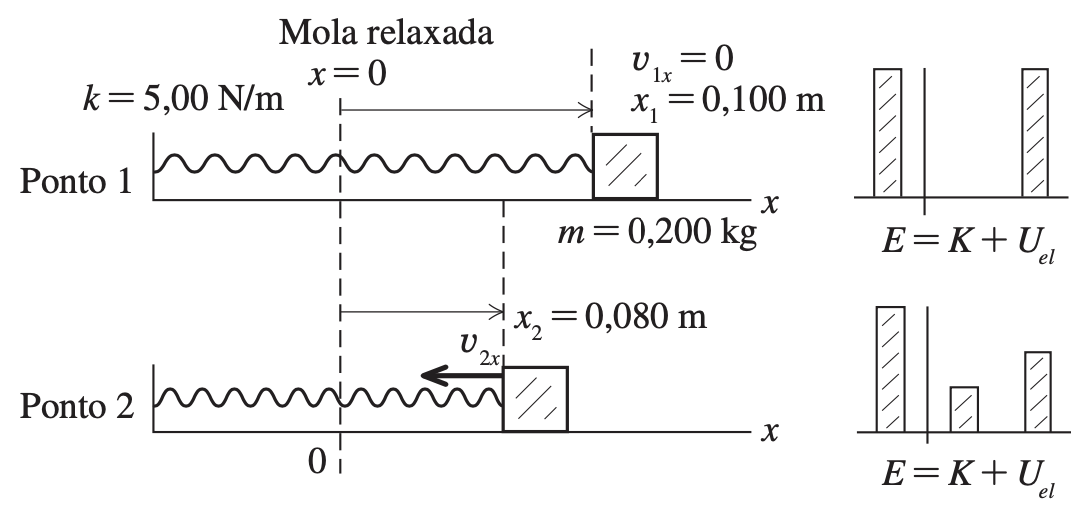
Fonte: Eric Mazur
Exemplo 12 (A7.P2-07)
Um bloco, de massa m = 2,0 kg, é deixado cair de uma altura h = 40 cm sobre uma mola de constante elástica k = 1960 N/m. Determine a variação máxima de comprimento da mola ao ser comprimida.
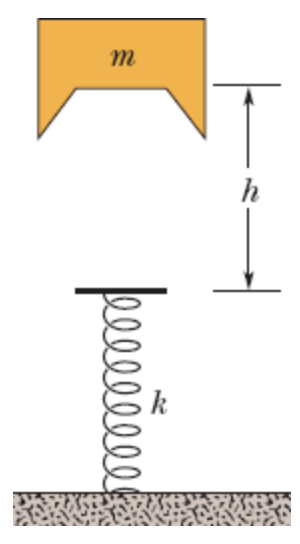
Fonte: Halliday
Exemplo 13 (A7.P2-08)
Duas massas estão conectadas por um barbante fino e inextensível que passa por uma polia leve e sem atrito, conforme mostra a figura. A massa de 10 kg é liberada e cai por uma distância vertical de 1 m antes de atingir o solo. Use a conservação de energia mecânica para determinar:
a) com que velocidade a massa de 5 kg está se movendo logo antes da massa de 10 kg atingir o solo; e
b) a altura máxima atingida pela massa de 5 kg.
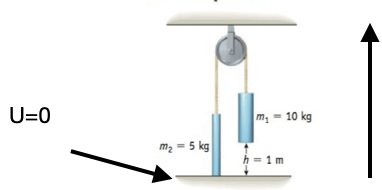
Fonte: Bauer
Exemplo 14 (A7.P2-09)
Você está em um balanço com uma corrente de 4,0 m de comprimento. Se o seu deslocamento máximo da vertical for relativo a um ângulo de 35°, com que velocidade estará se movendo na parte inferior do arco?
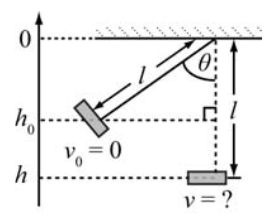
Fonte: Bauer