Aula 14

Fundamentos de Mecânica

Prof. Ronai Lisbôa

UFRN - ECT - BCT

Quantos exercícios você já resolveu sobre tópicos dessa aula?

Objetivos

Saber como obter a energia potencial a partir da força.

Saber como obter a força a partir da energia potencial.

Analisar os tipos/pontos de equilíbrio em uma curva de energia potencial.

Verificar se uma força é conservativa ou não.

Bibliografia.

Tipler - Cap. 7

Seção: 7.2 (pag. 210 a 213)

- Refaça os exercícios resolvidos.

O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)

Para usar I.A. você deve saber ou ter ideia do que está fazendo. Se não é só informação fugaz.

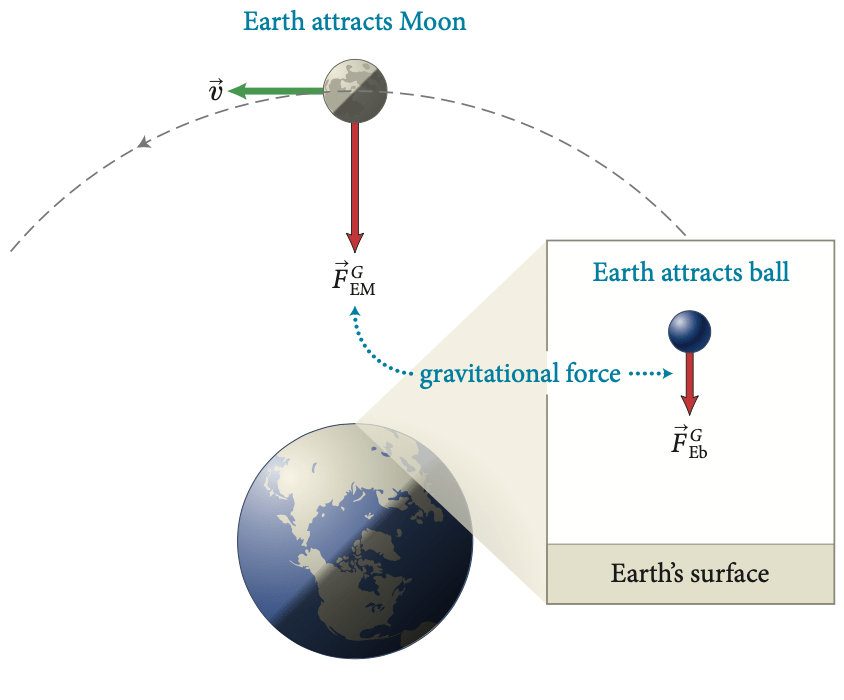
O trabalho da força peso em qualquer uma das trajetórias (1,2,3) é sempre o mesmo:

Forças conservativas

W_1=W_2=W_3 = mg(y_b-y_a)

Fonte: descomplica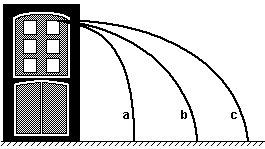

\Delta U_1=\Delta U_2=\Delta U_3 = -mg(y_b-y_a)

Para o sistema Terra+bola, a variação da energia potencial é sempre a mesma:

\Delta U=-W_P

A energia potencial associada a uma força conservativa é função da posição da partícula. Então,

Então, se \(\vec F\) é uma força conservativa (como as forças peso e elástica)

W=\int_a^b \vec F\cdot d\vec r = -(U_b-U_a)=-(mgy_b-mgy_a)

Quando conhecida a expressão da energia potencial, o trabalho de uma força conservativa pode ser calculado sem referência à trajetória seguida.

W = -(U_b-U_a)

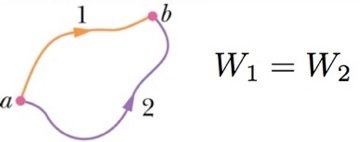
Forças conservativas

Fonte: Halliday

O trabalho de uma força conservativa independe da trajetória. E importa somente os pontos (a,b), isto é, \(U(b)\) e \(U(a)\). Então,

\Delta K=-\Delta U

\Delta U + \Delta K = 0

\Delta E = 0

W = -\Delta U

Uma força é conservativa se o trabalho em um caminho fechado é nulo!

A partir da definição do trabalho de uma força conservativa:

W_{P\rightarrow Q} = \int_P^Q \vec F_c\cdot d\vec r

Se a força é conservativa, o trabalho tem sempre o mesmo valor independente da trajetória escolhida.

W^1_{P\rightarrow Q} = W^2_{P\rightarrow Q}

Forças conservativas

No sentido contrário, ao longo do caminho 2:

W^2_{Q\rightarrow P} = -W^2_{P\rightarrow Q}

W = \oint \vec F_c\cdot d\vec r \equiv 0

W =W^2_{P\rightarrow Q}-W^2_{P \rightarrow Q}

O trabalho total no caminho fechado:

W =W^1_{P\rightarrow Q}+W^2_{Q \rightarrow P}

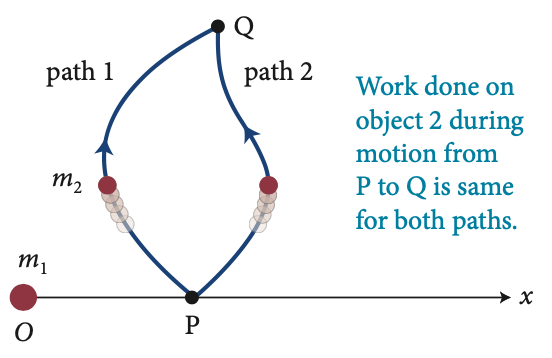
Trabalho feito sobre 2 durante o movimetno de P a Q é o mesmo para ambos os caminhos

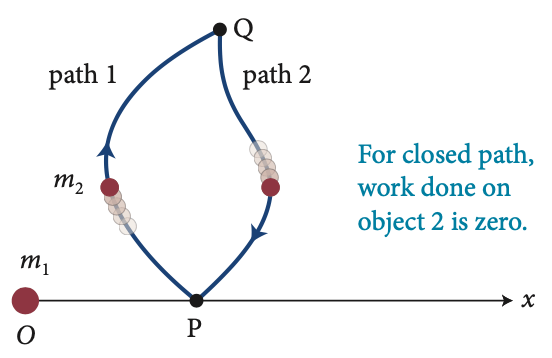
Para o caminho fechado, o trabalho feito sobre 2 é zero.

Fonte: Eric Mazur

Então, a relação entre energia potencial e trabalho para uma força conservativa é :

W = -\Delta U

A força conservativa tem a direção da diminuição da energia potencial de um sistema.

A força da gravidade (peso) sempre aponta para a menor energia potencial.

A força elástica sempre aponta para a menor energia potencial.

A partir da definição do trabalho de uma força constante em uma dimensão:

W = F_R\Delta x

Obtemos uma importante relação entre força conservativa e energia potencial:

F_R = -\frac{\Delta U}{\Delta x}

Forças conservativas

\vec P

\vec v

\vec F_e

\vec F = -\frac{dU}{dr}\hat r

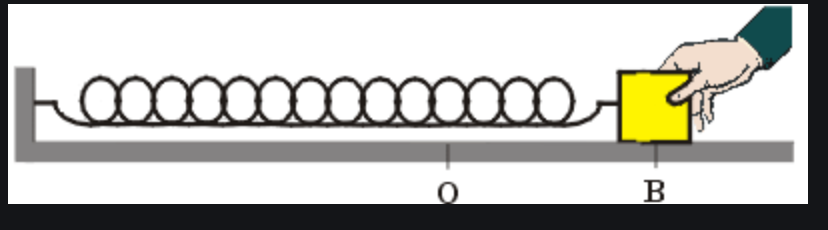
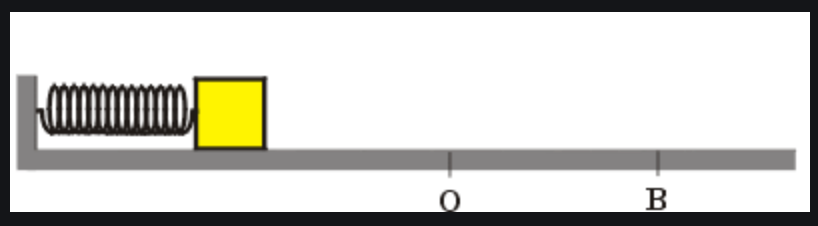
menor energia potencial

A energia potencial é uma função única da posição.

U=U(x)

No ponto de equilíbrio a energia potencial é mínima e a energia cinética é máxima.

Nos pontos de retorno a energia potencial é máxima e a energia cinética é mínima.

A Energia Mecânica é conservada no sistema massa-mola porque a força elástica é conservativa.

Fonte: https://www.compadre.org/Physlets/mechanics/illustration7_3.cfm?NOH=1

Então há forças conservativas e a soma das energias cinética e potencial deste sistema isolado é constante.

E_{mec}

Pontos de equilíbrio e retorno

A função energia potencial

A força conservativa é numericamente igual à inclinação da curva em um gráfico de U(x) verus x.

F = -\frac{dU}{dx}

Fonte: https://phet.colorado.edu/pt_BR/simulation/energy-skate-park-basics

Fonte: Randall Knight

A função energia potencial

É interessante analisar os pontos de retorno e os pontos de equilíbrio.

F = -\frac{dU}{dx}

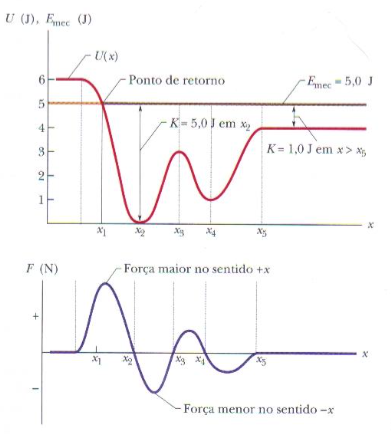
Considere uma energia total E = 5,0 J

E = U + K

Se K = E - U, temos que U ≤ E;

A partícula não será observada na região \(x<x_1\).

A força é positiva e atua no sentido do eixo x positivo;

K não pode ser negativa;

K será mínima em \(x_1\): K = 0 J.

U será máxima em \(x_1\): U = E =5,0 J.

Em \(x_2\):

K será máxima: K = E = 5,0 J.

U será mínima: U = 0 J.

Em \(x_5\):

A partícula é livre e se move com velocidade constante.

Fonte: Wolfgang & Bauer

A função energia potencial

Para E = 4 J.

Os pontos de retorno são \(x_1\) e \(x_5\).

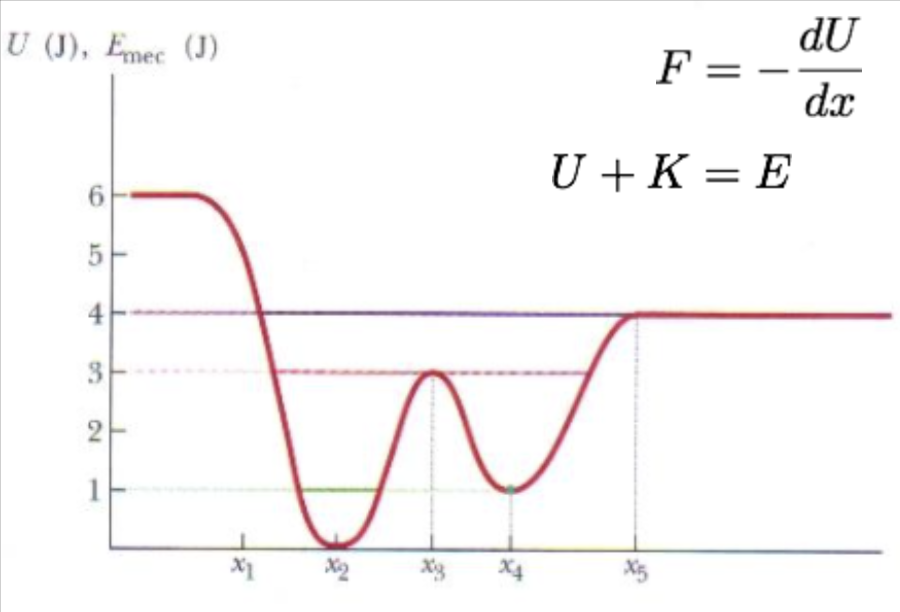
Para \(x > x_5\) o equilíbrio é dito indiferente.

Para E = 3 J.

Os pontos de retorno estão entre \(x_1,x_3\) e \(x_3,x_5\).

Para \(x = x_3\) o equilíbrio é instável.

Para E = 1 J. A partícula oscila em torno do ponto de equilíbrio estável \(x=x_2\). Há uma força restauradora.

No ponto de equilíbrio estável \(x=x_4\) a partícula não se move.

É interessante analisar os pontos de retorno e os pontos de equilíbrio.

F = -\frac{dU}{dx}

E = U + K

Fonte: Wolfgang & Bauer

As ligações moleculares obedecem a uma função energia potencial. A força pode ser repulsiva ou atrativa dependendo da região onde se definir a energia do sistema.

Potencial de Lennard-Jones:

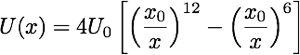
Força de Lennard-Jones:

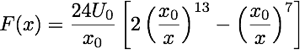
Ponto de mínimo, \(F(x_{min}) =0\) e \(U ''(x)=0\):

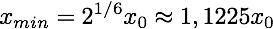
Fonte: https://phet.colorado.edu/pt_BR/simulation/atomic-interactions

Qual a energia necessária para sair do poço de potencial?

A pipoca vai saltar mais facilmente na panela mais rasa.

O poço de potencial é maior para a panela mais funda.

A pipoca vai pular da panela quando no mínimo, a sua energia cinética for igual à energia potencial.

E = K + U

E = \frac{1}{2}mv^2 + mg(y_f-y_i)

K=E-U<0

A pipoca fica ligada à panela:

pois não tem energia cinética suficiente para escapar do poço de potencial.

-h

U> E

E = 10 J

U= 20 J

Qual a energia necessária para sair do poço de potencial?

A energia cinética para lançar algo para fora do poço deve ser, no mínimo, igual à energia potencial do poço.

E = K + U

E = \frac{1}{2}mv^2 + mg(y_f-y_i)

y_f

y_i

K=E-U\geq 0

U< E

Algo não fica ligado ao poço

pois tem energia cinética suficiente para escapar do poço de potencial.

E = 21 J

U= 20 J

Qual a energia necessária para sair do poço de potencial?

A energia cinética para lançar um foguete para fora do poço de potencial da Terra deve ser, no mínimo, igual à energia potencial do poço.

E = K + U

E = \frac{1}{2}mv^2 -\frac{GMm}{R_T}

y_f

v_{escape}=\sqrt{\frac{2GM}{R_T}}

A velocidade de escape quando \(K=U\) é:

y_i

Por que próximo à superfície da Terra?

\Delta U(y)=mg\Delta y

Por que longe da superfície da Terra?

\Delta U(y)=-\frac{GMm}{r}

Exemplo 1 (A10.P2-01)

Para calcular o trabalho realizado por uma força \(\vec F\) ao longo de uma curva fechada (ou de um caminho fechado) C, calculamos \(\oint \vec F\cdot d\vec l\) , onde o círculo no sinal de integral significa que a integração é efetuada para um percurso completo ao longo de C. Para \(\vec F(x) = Ax\hat i\) , calcule \(\oint \vec F\cdot d\vec l\) para o caminho C mostrado na figura.

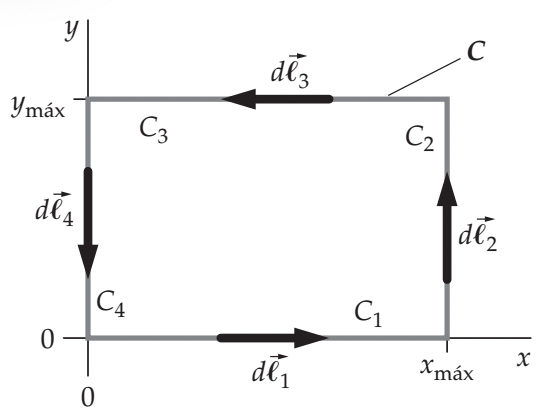
Fonte: Tipler & Mosca

Exemplo 2 (A10.P2-02)

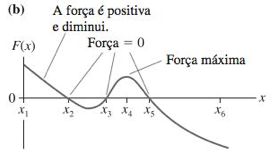
A Figura mostra o gráfico de uma função energia potencial U versus x. (a) Para cada ponto indicado, informe se a componente x da força associada a esta função é positiva, negativa ou zero. (b) Em que ponto a força tem a maior magnitude? (c) Identifique possíveis pontos de equilíbrio, indicando se o equilíbrio é estável, instável ou indiferente.

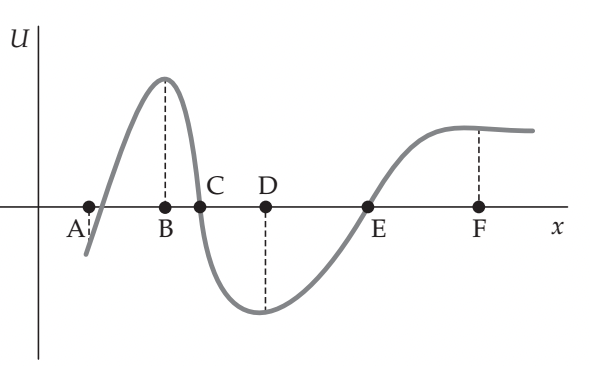
Fonte: Tipler & Mosca

Exemplo 3 (A10.P2-03)

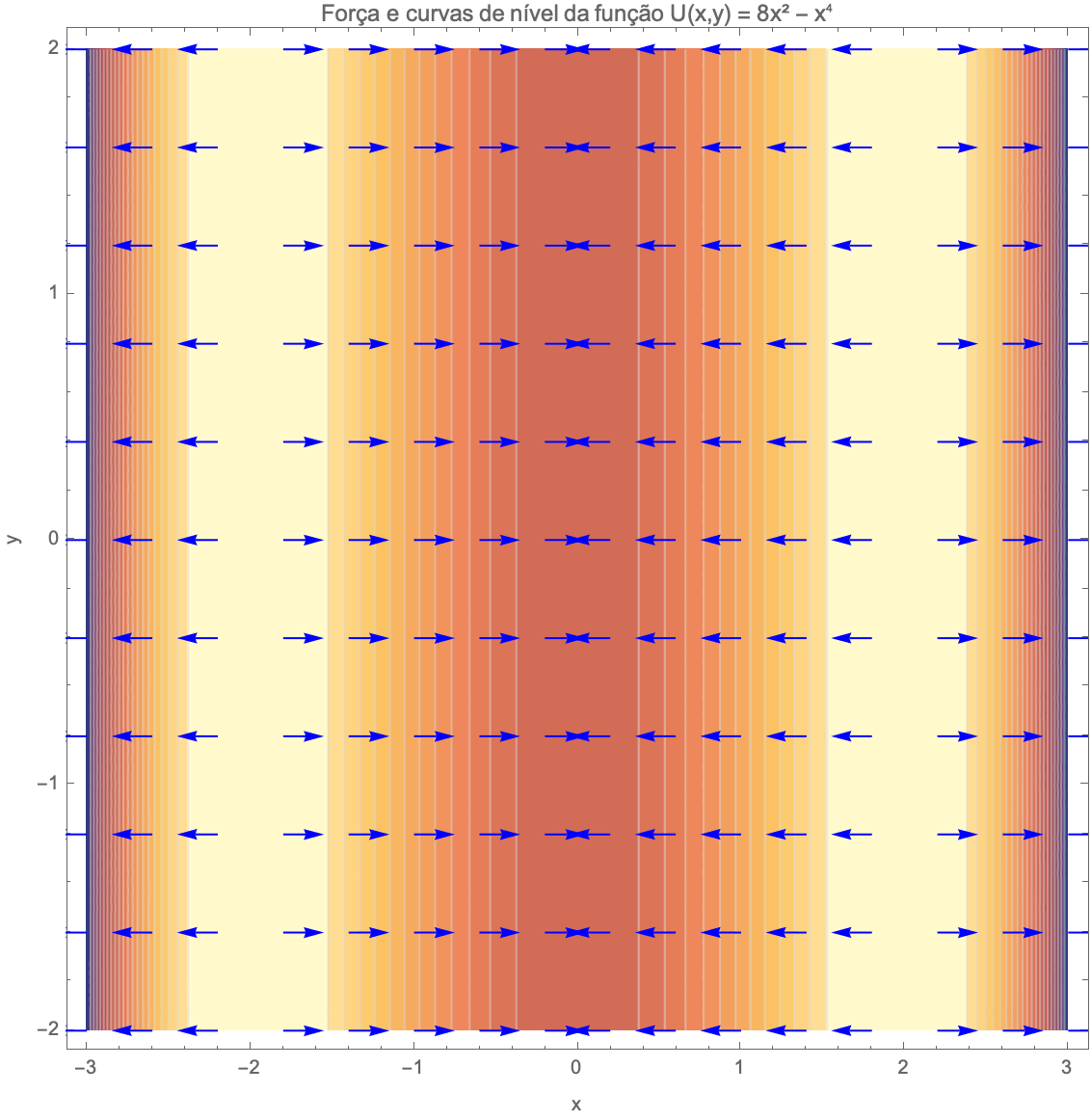
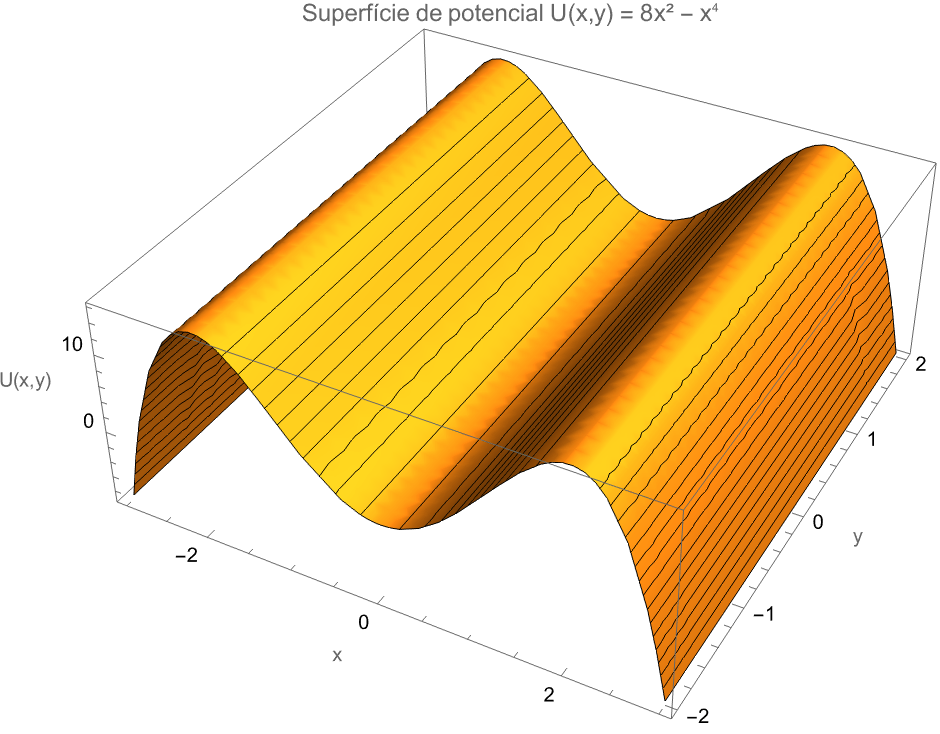
A energia potencial de um corpo restrito ao eixo \(x\) é dada \(U(x) = 8x^2-x^4\). Determine a força \(F_x\) associada a esta função energia potencial. (b) Supondo que não haja outras forças atuando sobre o corpo, em que posições o corpo está em equilíbrio? (c) Quais destas posições de equilíbrio são estáveis e quais são instáveis?

U(x)=8x^2-x^4

F(x)=4x^3-16x

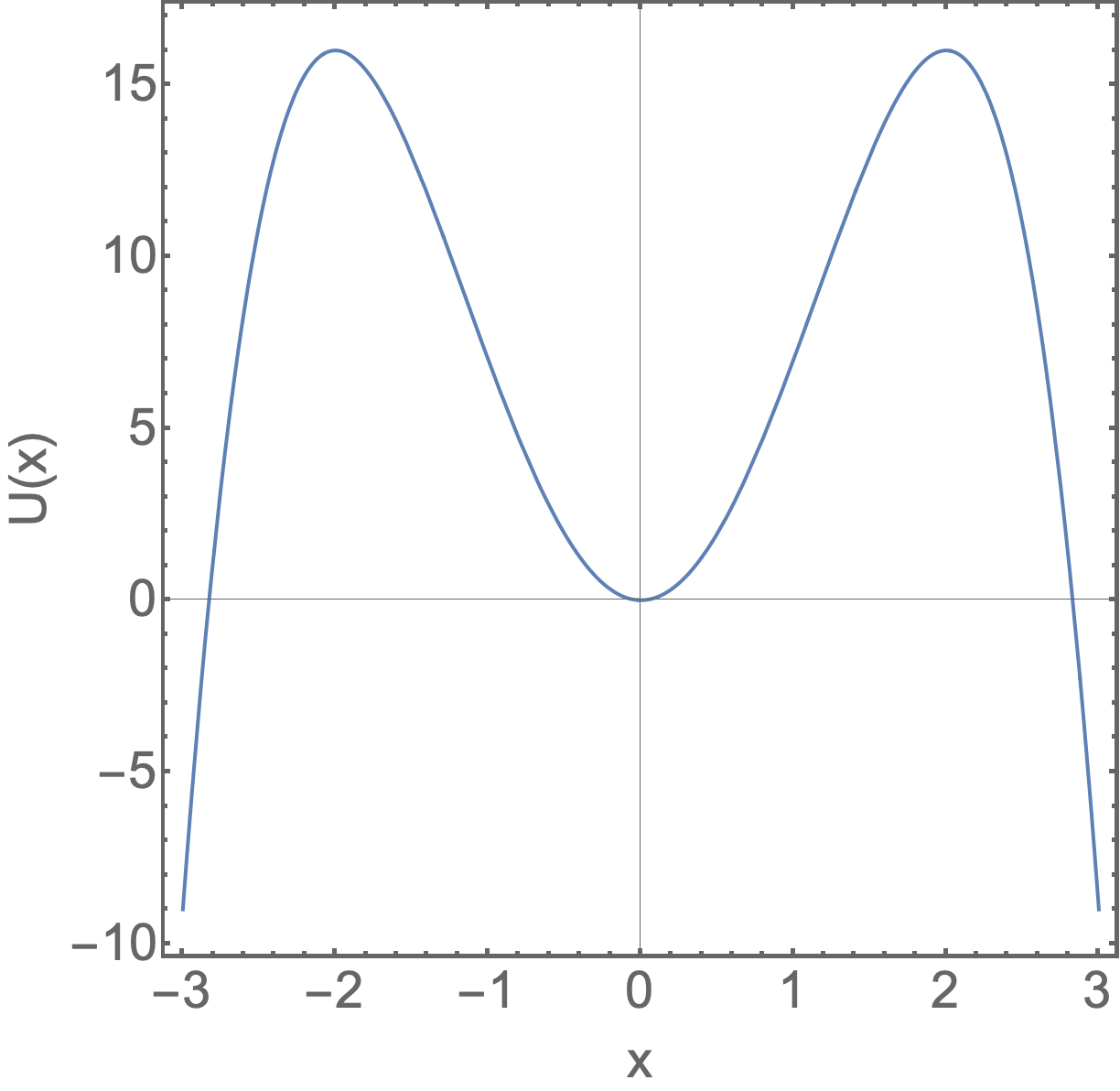
Exemplo 4 (A10.P2-04)

Uma força é dada por \(F(x) = Ax^{-3}\), onde A = 8,0 \(N.m^3\). (a) Para valores positivos de \(x\), a energia potencial associada a esta força aumenta ou diminui com o aumento de \(x\)? (Você pode encontrar a resposta para esta questão imaginando o que acontece com uma partícula que é colocada em repouso em algum ponto \(x\) e depois largada.) (b) Encontre a função energia potencial U associada a esta força, tal que \(U\) tende a zero quando x tende a infinito. (c) Esboce \(U\) versus \(x\).

Exemplo 5

A energia potencial de um corpo restrito ao eixo x é dada \(U(x) = 3x^2 - 2x^3\). Determine a força \(F_x\) associada a esta função energia potencial. (b) Supondo que não haja outras forças atuando sobre o corpo, em que posições o corpo está em equilíbrio? (c) Quais destas posições de equilíbrio são estáveis e quais são instáveis?

Exemplo 6 (A7.P2-02)

Escolha um nível de referência para a energia potencial gravitacional de uma preguiça. Este exemplo ilustra um ponto importante: A escolha da configuração de referência para a energia potencial é arbitrária, mas deve ser mantida durante toda a resolução do problema. Uma preguiça, pesando 2,0 kg, está pendurada a 5,0 m acima do solo (a) Qual é a energia potencial gravitacional U do sistema preguiça-Terra se tomarmos o ponto de referência y = 0 como estando (1) no solo, (2) no piso de uma varanda que está a 3,0 m acima do solo, (3) no galho onde está a preguiça, e (4) 1,0 m acima do galho? Considere a energia potencial como nula em y = 0. (b) A preguiça desce da árvore. Para cada escolha do ponto de referência, qual é a variação ΔU da energia potencial do sistema preguiça-Terra?

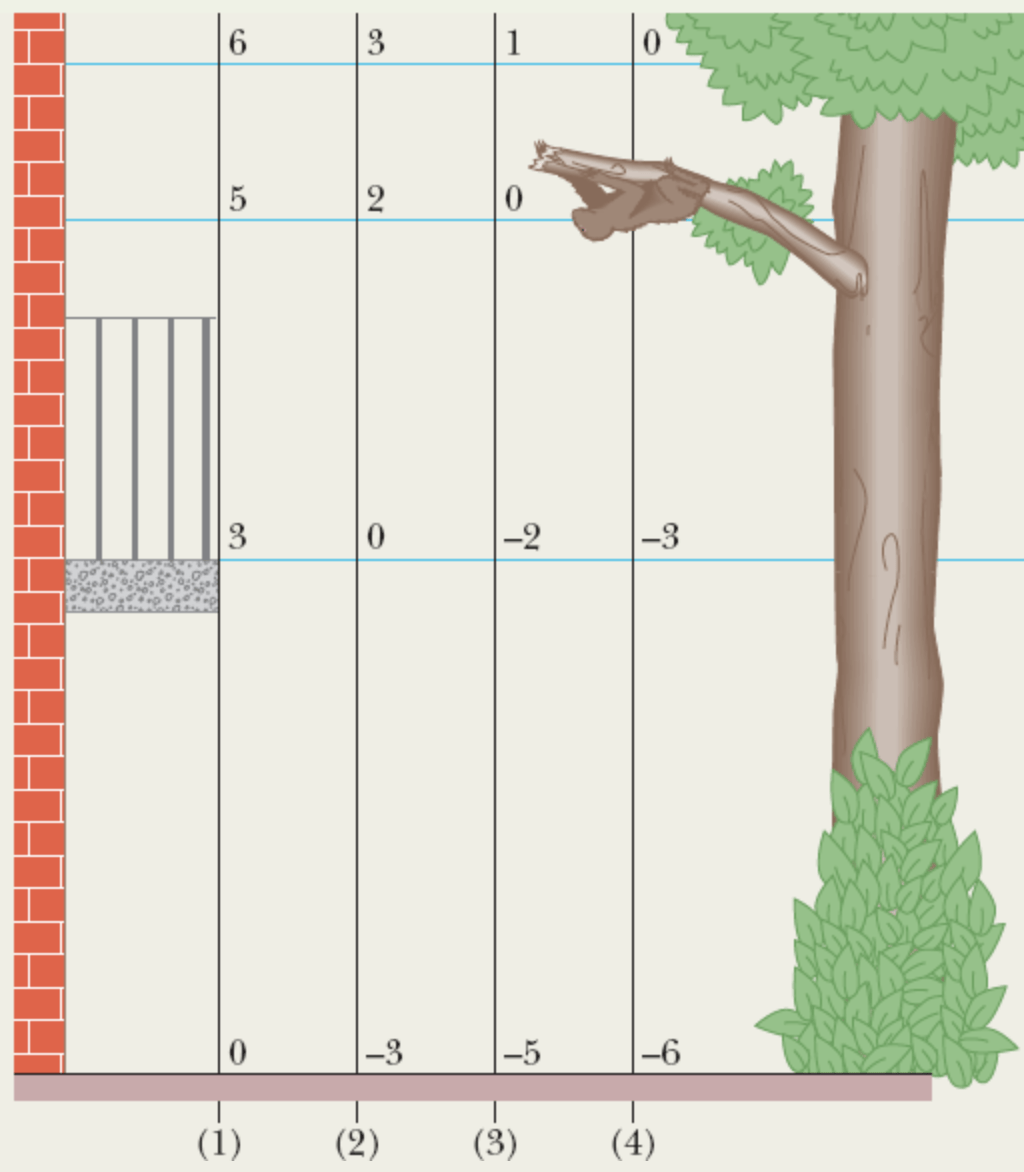
Fonte: Halliday & Resnick

Exemplo 7

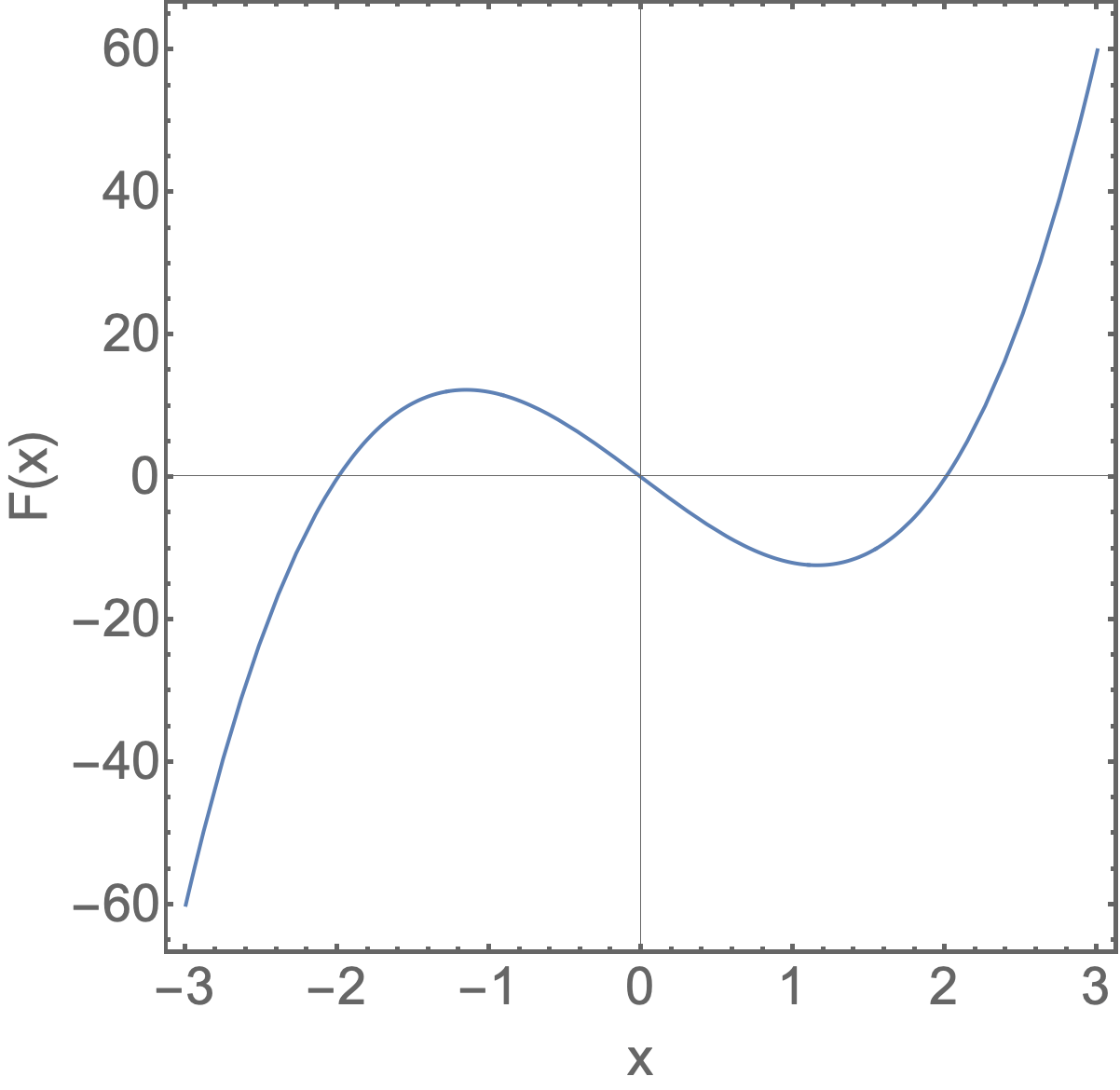
Uma partícula participa de apenas uma interação com um objeto fixo. A interação faz com que a energia potencial seja armazenada no sistema de objeto de partícula conforme a partícula se move ao longo de um eixo x. A partícula é liberada do repouso em x0 = -3,0 m, e a quantidade de energia potencial armazenada (em joules) é dada por \(U(x) = ax + bx^2+cx^3\), onde a = +12 J/m, b = +3,0 J/m^2, e c = -2,0 J/m^3. (a) Faça um gráfico da energia potencial que também exiba a energia mecânica da partícula. (b) Em qual direção a partícula se move inicialmente? (c) Descreva o movimento da partícula após a posição x0. (d) Em quais posições ao longo da curva que você desenhou na parte (a) a partícula está acelerando e em quais posições ela está desacelerando? (e) Qual é a energia cinética da partícula em x = -1,0 m, x = + 1,0 m, e x = +3,0 m.

Exemplo 8

Em 2013, um grande meteoro, com uma massa estimada em 1,2 × 10^7 kg, caiu na Terra em uma região próxima a Chelyabinsk, na Rússia. (Esse meteoro explodiu de modo espetacular a uma altura de cerca de 30 km, causando um dano considerável em objetos na superfície da Terra.) Considere um meteoro de mesma massa caindo em direção à Terra. Escolha a Terra mais o meteoro como sistema. Qual é a variação da energia cinética do meteoro, quando ele cai desde uma altura de 1 × 10^8 m do centro da Terra até uma altura de 1 × 10^7 m? Explique os sinais das variações de energia cinética e energia potencial do sistema.

Não ministrado

A energia potencial gravitacional

Se escolhermos o eixo x apontando para a direita, conforme indicado na figura, a componente x da força exercida pelo objeto 1 no objeto 2 quando o objeto 2 está em alguma posição arbitrária x é

F^G_{12}=-G\frac{m_1m_2}{x^2}=F(x)

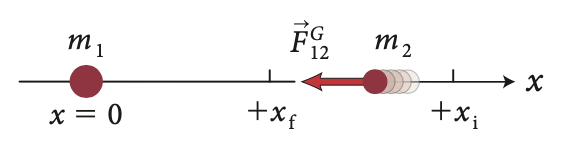
A força gravitacional varia com a distância e, portanto, para avaliar o trabalho feito pelo objeto 1 no objeto 2:

W_{12}=\int_{x_i}^{x_f} F(x)dx

W_{12}=Gm_1m_2 \left(\frac{1}{x_f}-\frac{1}{x_i} \right)

Fonte: Erick Mazur

W=Gm_1m_2 \left(\frac{1}{x_f}-\frac{1}{x_i} \right)

Como a força e o deslocamento apontam na mesma direção, sabemos que o trabalho deve ser positivo. De fato, o lado direito também é positivo porque \(x_f < x_i\).

À medida que o objeto 2 se move de \(x_i\) para \(x_f\), ele acelera e, portanto, sua energia cinética aumenta.

Como nenhuma outra energia associada a ele muda, o aumento na energia cinética deve ser igual ao trabalho feito nele pelo objeto 1:

W_{12}=\Delta K_2 > 0

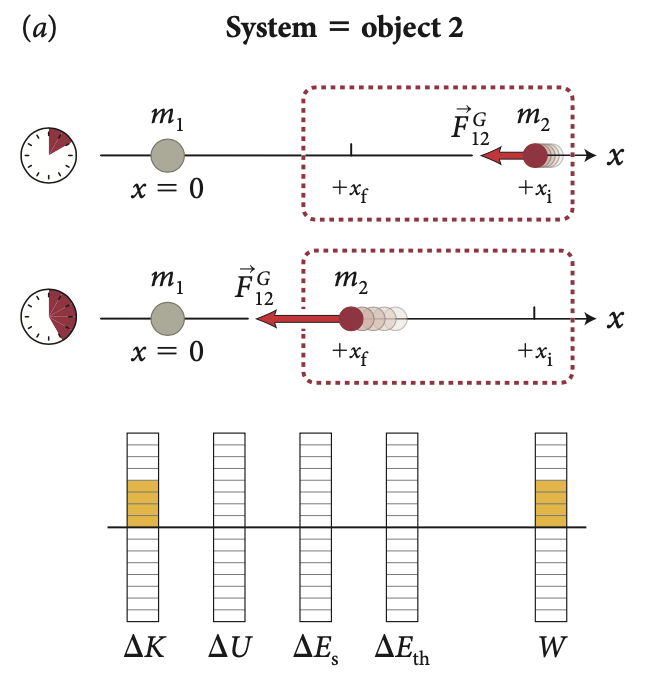
A energia potencial gravitacional

Fonte: Erick Mazur

\Delta U^G=-\Delta K_2

Agora, consideramos o sistema (fechado) dos dois objetos interativos como um todo, então o aumento na energia cinética do objeto 2 não se deve ao trabalho feito pela força gravitacional externa exercida pelo objeto 1 sobre ele, mas a uma diminuição na energia potencial gravitacional do sistema

Essa energia potencial gravitacional é uma medida da configuração do sistema. A mudança na energia potencial gravitacional do sistema é, portanto,

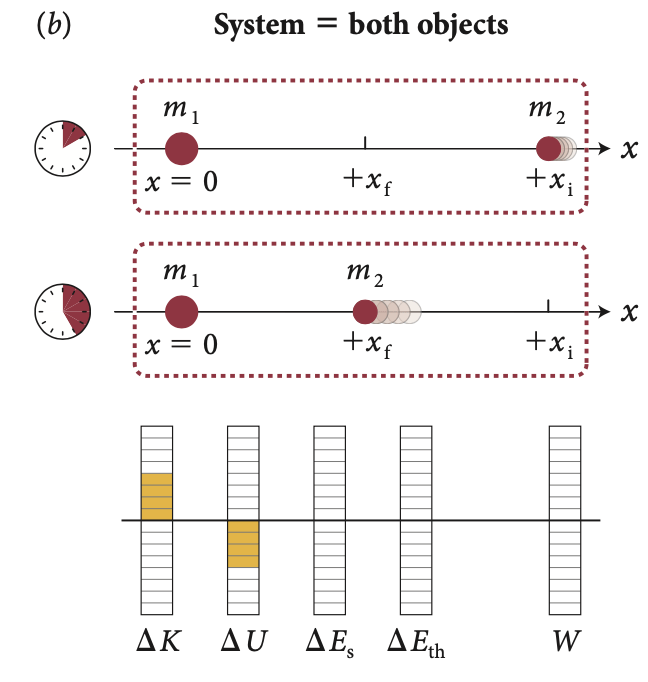
A energia potencial gravitacional

À medida que o objeto 2 se move de \(x_i\) para \(x_f\), ele acelera e, portanto, sua energia cinética aumenta.

Fonte: Erick Mazur

\Delta U^G=-\Delta K_2

Então, se deixarmos o objeto 2 se mover de x = ∞ para uma posição arbitrária x sob a influência da aceleração gravitacional devido ao objeto 1:

\Delta U^G=-Gm_1m_2 \left(\frac{1}{x_f}-\frac{1}{x_i} \right)

\Delta U^G=Gm_1m_2 \left(\frac{1}{x_i}-\frac{1}{x_f} \right)

A variação energia potencial gravitacional, em relação ao infinito:

\Delta U^G=- \left(\frac{Gm_1m_2}{x} \right)

A energia potencial gravitacional

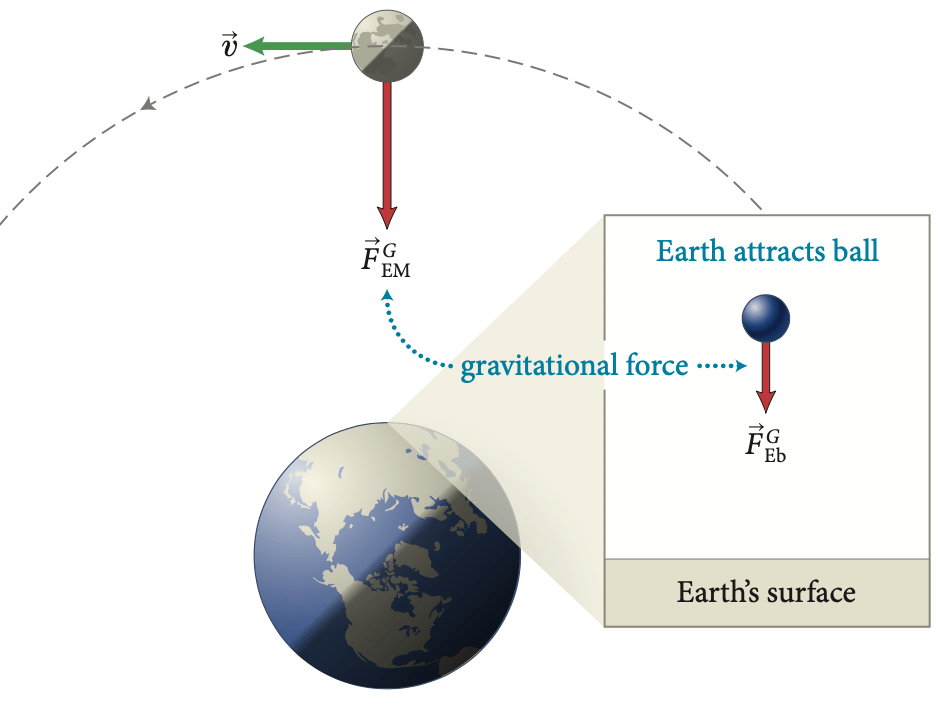
A força gravitacional que a Terra exerce sobre um satélite é conservativa.

Ao longo do segmento RQ (arco de um círculo), tal força é perpendicular ao deslocamento. O trabalho é nulo.

Ao longo do segmento PR (reta), a força tem a mesma direção e sentido contrário ao deslocamento e não é nulo.

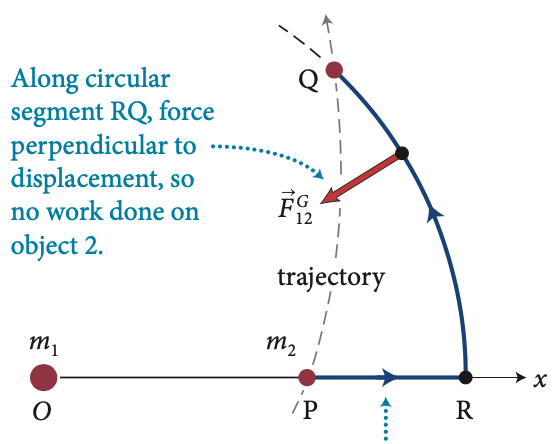
W_{R\rightarrow Q} = \int_R^Q \vec F^G_{12}\cdot d\vec r=0

Força gravitacional sobre o satélite

trajetória real

W_{P\rightarrow R} = \int_P^R \vec F^G_{12}\cdot d\vec r\neq 0

F^G_{12}(x)=-G\frac{m_1m_2}{x^2}

A energia potencial gravitacional

Fonte: Erick Mazur

O trabalho da força gravitacional nos segmentos PQ ( próximo da trajetória real) é,

Uma melhor aproximação do caminho real do objeto 2 pode ser obtida dividindo o movimento em pequenos segmentos e aproximando cada segmento pela soma dos deslocamentos radiais e circulares:

Nenhum trabalho é feito aqui

Segmentos radiais se somam até o comprimento de PR

W_{P\rightarrow Q} = \sum W_{P\rightarrow r} + \sum W_{r\rightarrow q}

W_{P\rightarrow Q} = \int_P^r \vec F^G_{12}\cdot d\vec r + \int_r^Q \vec F^G_{12}\cdot d\vec r

W_{P\rightarrow Q} = \int_P^Q \vec F^G_{12}\cdot d\vec r

W_{P\rightarrow Q}=Gm_1m_2 \left(\frac{1}{r_Q}-\frac{1}{r_P} \right)

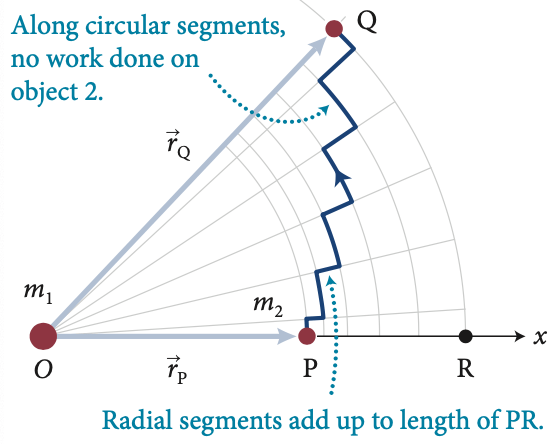
O trabalho de uma força conservativa depende apenas dos pontos inicial (\(r_Q\)) e final \(r_P\) e não depende da trajetória.

A energia potencial gravitacional

Fonte: Erick Mazur

Para um satélite em órbita, nós temos:

F_r=\frac{mv^2}{r}

A energia potencial gravitacional

\frac{GMm}{r^2}=\frac{mv^2}{r}

mv^2 =\frac{GMm}{r}

Dividindo ambos os lados por um fator 2:

\frac{1}{2}mv^2 = \frac{1}{2}\frac{GMm}{r}

A energia mecânica do sistema:

E=K+U

E = \frac{GMm}{2r}-\frac{GMm}{r}

K = \frac{1}{2}|U|

E =- \frac{GMm}{2r}

E=-K

A velocidade orbital e escape são:

v_t=\sqrt{\frac{GM}{r}}

A energia total do sistema é negativa e igual, em valor absoluto, à energia cinética nessa órbita.

v_e=\sqrt{2}v_t

Fonte: Erick Mazur

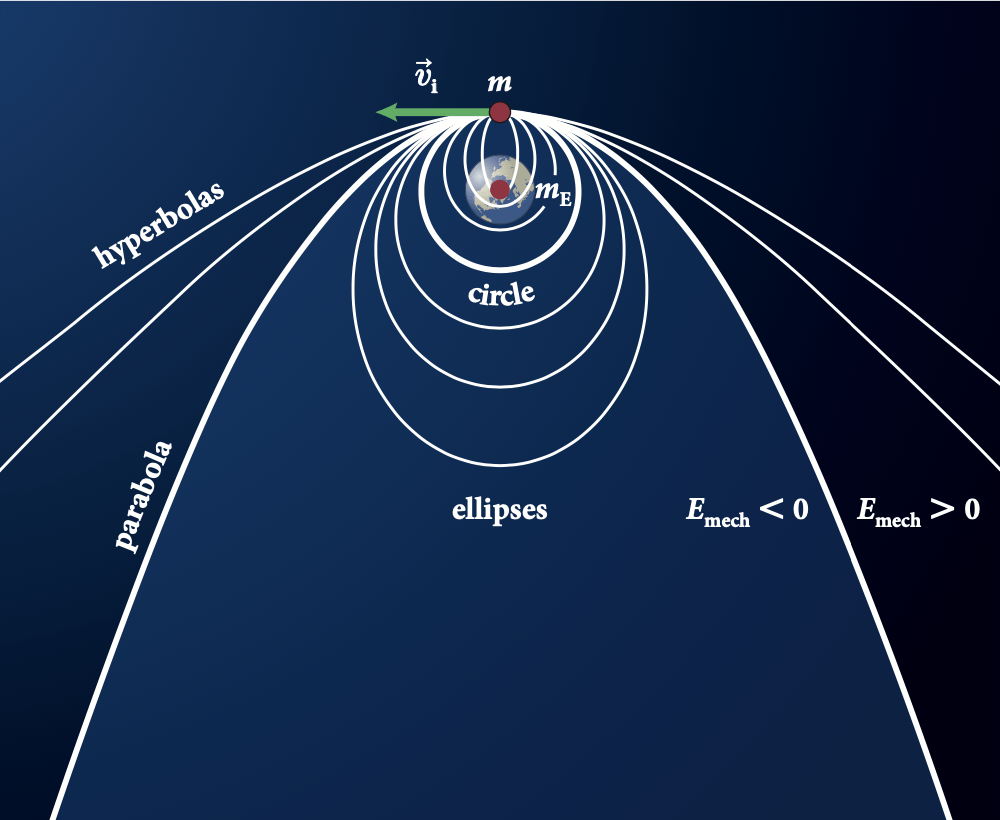
Para \(E_{mec}\) negativa, o satélite está ligado ao planeta: ele não pode escapar para o infinito porque não tem energia cinética suficiente. As órbitas são circulares ou elípticas.

Para \(E_{mec}\) positiva, o satélite não está ligado porque tem energia suficiente para “escapar” para o infinito. Nesse caso, a energia potencial gravitacional é sempre menor do que \(E_{mec}\), ainda há uma quantidade positiva de energia cinética. As órbitas são hipérboloes ou parábolas.

A energia potencial gravitacional

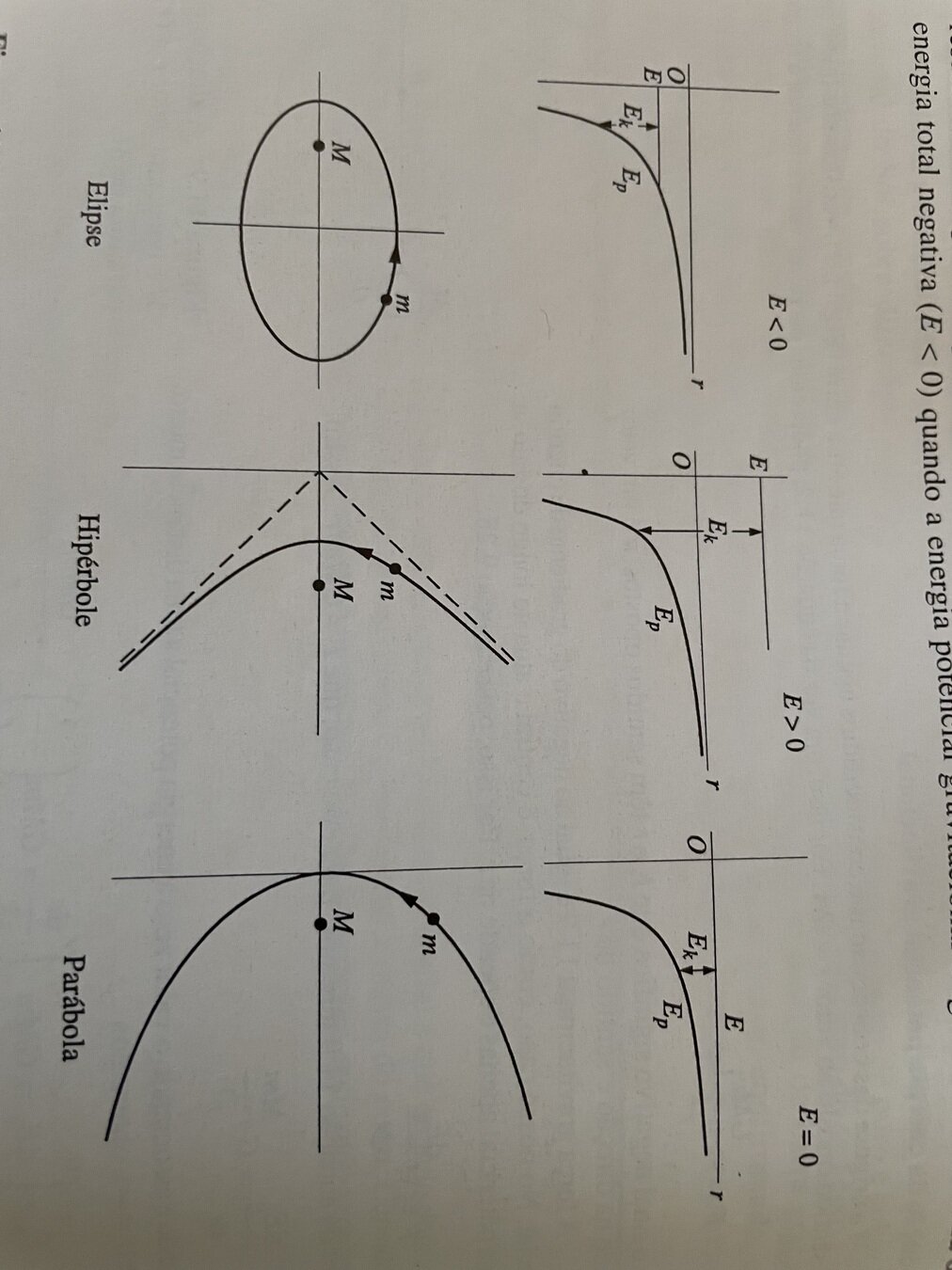
Fonte: Alonso & Finn

Fonte: Eric Mazur

E = \frac{1}{2}mv^2-\frac{GMm}{r}

Para um satélite, nós temos:

onde \(v\) é a velocidade do satélite e \(r\) é a distância entre o satélite e a planeta.

E=\frac{1}{2}mv^2-\frac{GMm}{r}

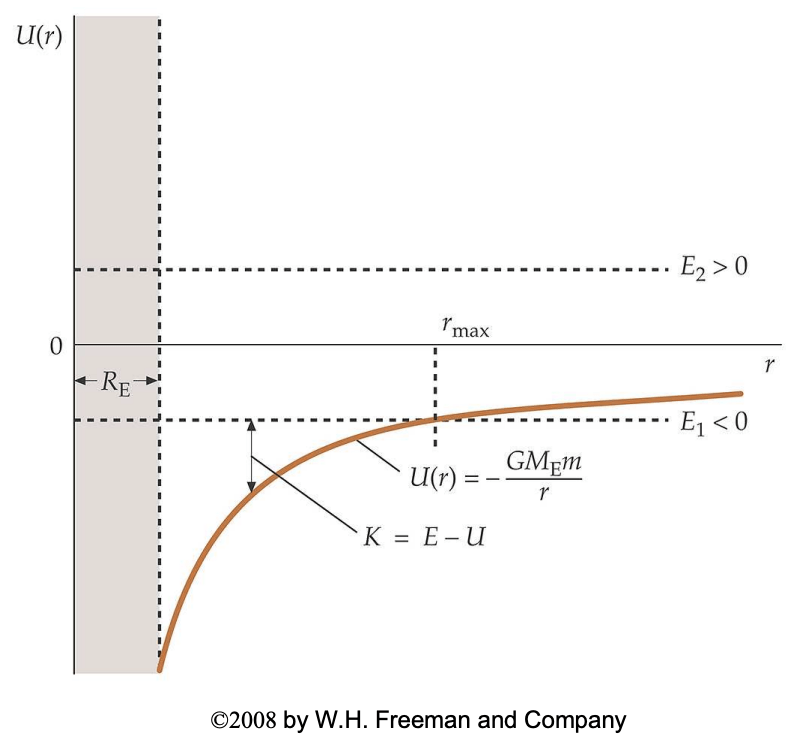
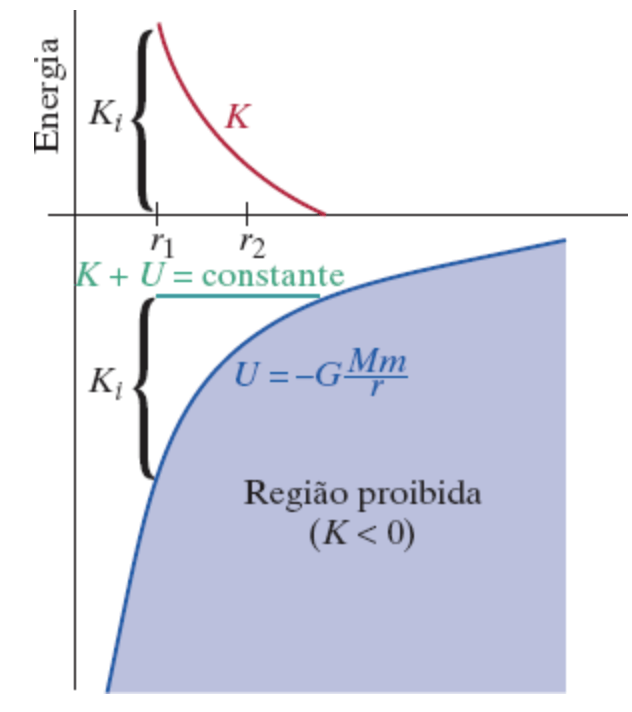
Se a energia \(E\) do sistema for negativa, então há um valor \(r = r_{max}\) para o qual \(U^G = E_{mec}\) — toda a energia mecânica está na forma de energia potencial e, portanto, a energia cinética do satélite é zero.

A energia potencial gravitacional

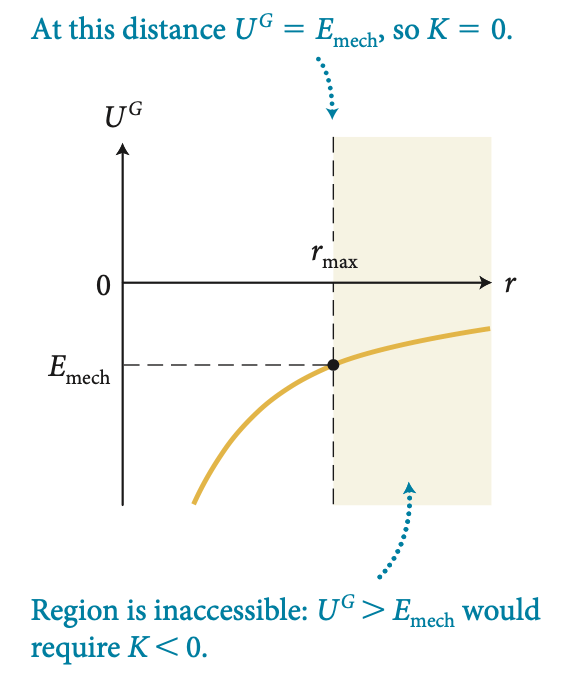
Nessa distância, \(U^G = E\) e \(K=0\).

Região proivida, \(U^G > E\) e \(K<0\).

Para \(r > r_{max}\) para o qual \(U^G > E_{mec}\) a energia cinética do satélite seria negativa e isso não pode ocorrer.

r_{max}=\frac{GMm}{-E_{mec}}

Fonte: Erick Mazur

Exemplo 9

Uma nave espacial robô aterriza em um asteroide, coleta uma amostra e parte de volta em direção à Terra; sua massa total é 1500 kg. Quando ela está a uma distância de 200 km (2 × 10^5 m) do centro do asteroide, sua velocidade escalar é 5,0 m/s e os seus foguetes são desligados. Ela segue viagem, e, quando está a 500 km (5 × 10^5 m) do centro do asteroide, sua velocidade escalar diminui para 4,1 m/s. (a) Faça um diagrama mostrando os estados inicial e final, identificando-os. (b) Faça um gráfico de energia do sistema. (c) Considere uma velocidade de lançamento inicial menor.

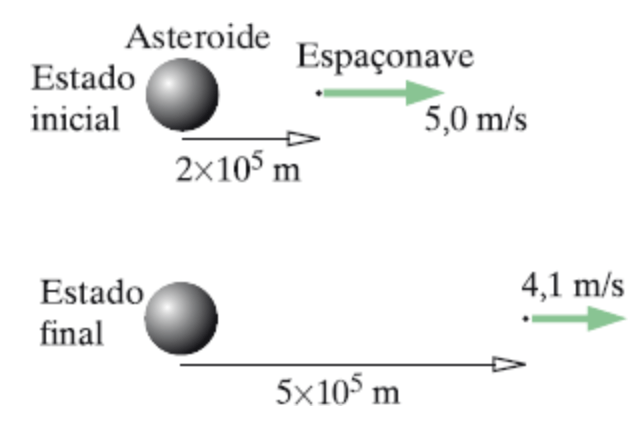
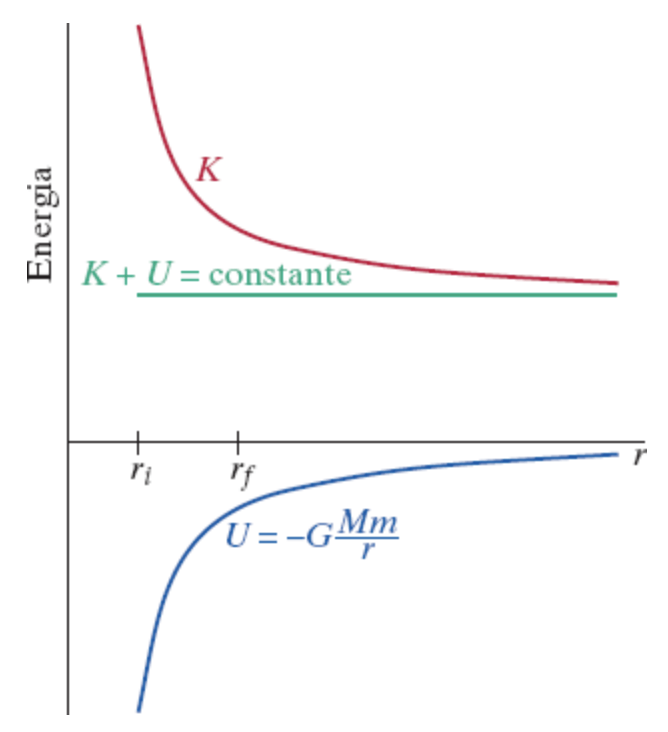
Fonte: Ruth & Sherwood