Aula 16

Fundamentos de Mecânica

Prof. Ronai Lisbôa

UFRN - ECT - BCT

Objetivos

Obter a expressão para o momento linear.

Enunciar a lei da conservação do momento linear.

Aplicar a lei da conservação do momento linear.

Bibliografia.

Tipler - Cap. 8

Seção: 8.1 (pag. 241 a 247)

- Refaça os exercícios resolvidos.

Relacionar a taxa de variação do momento linear à força.

O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)

 

Para usar I.A. você deve saber ou ter ideia do que está fazendo. Se não é só informação fugaz.

Momento linear

A grandeza física que mede o movimento de uma dada massa inercial é o momento linear.

Superpetroleiros são os maiores navios já construídos. Eles podem ter massa de até 650.000 toneladas e transportar mais de dois milhões de barris (318 milhões de litros) de petróleo. Porém, suas dimensões grandes criam problema de ordem prática. A navegação de um navio desse tamanho é extremamente difícil. Por exemplo, quando o capitão dá a ordem de reverter os motores e parar, o navio pode continuar a se mover para frente por mais de 5 km, pois o sistema é quase isolado.

Fonte: Wolfgang

\vec p = m\vec v

Momento linear

É um conceito em física e que se aplica a uma partícula ou a um sistema de partículas.

Define-se como,

\vec p = m\vec v
\frac{[M] [L]}{[T]}\equiv\frac{\text{kg.m}}{\text{s}}\equiv \text{N.s}

dimensão e unidade S.I.

onde \(m\) é a massa e \(\vec v\) é a velocidade de cada partícula do sistema em relação a algum referencial inercial.

A vantagem do momento linear está na sua versatilidade para descrever o movimento e a dinâmica de uma ou mais partículas.

\Leftrightarrow

O momento linear é conservado (constante) quando a partícula é livre.

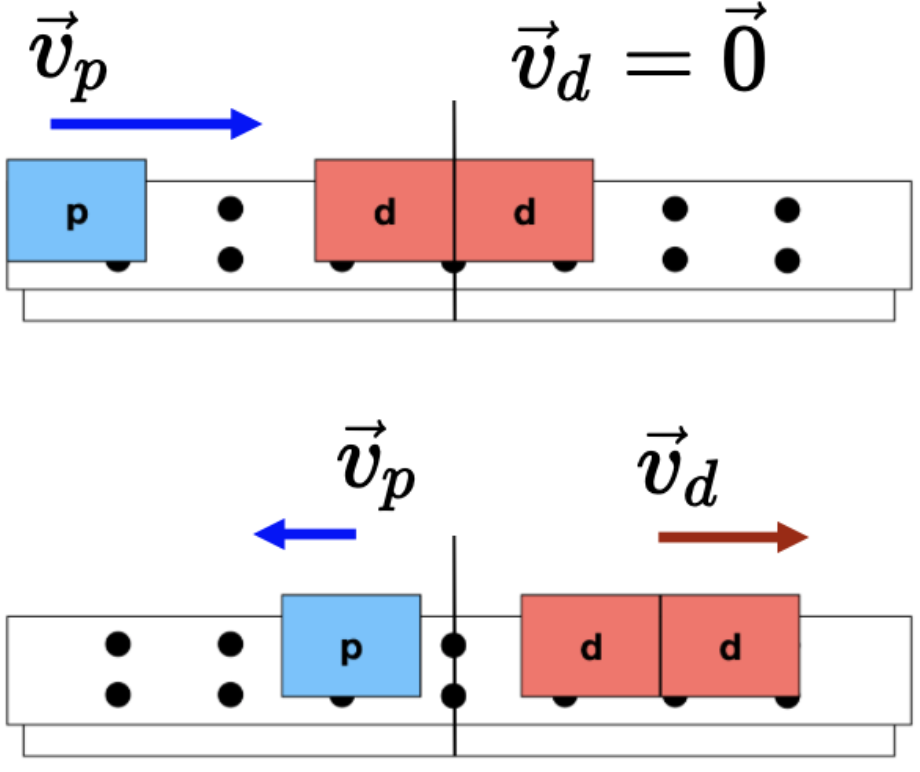
Momento linear e um sistema de duas partículas (CASO 1)

Para um sistema isolado de duas partículas, nós podemos observar alguns fenômenos.

Fonte: https://www.geogebra.org/m/qd8ZtEQp

Massa iguais: \(m_1 = m_2\):

As variações das velocidades:

A razão das variações das velocidades:

\frac{\Delta v_1}{\Delta v_2} = -1
v_{1i} = +0,60 \text{ m/s}
v_{2i} = 0 \text{ m/s}
v_{1f} =\hspace{1.0cm} \text{ m/s}
v_{2f} =\hspace{1.0cm} \text{ m/s}
\Delta v_{1} = \hspace{1.0cm} \text{ m/s}
\Delta v_{2} = \hspace{1.0cm} \text{ m/s}
+0,60
0
-0,60
+0,60

Para um sistema isolado de duas partículas, nós podemos observar alguns fenômenos.

Fonte: https://www.geogebra.org/m/qd8ZtEQp

Massa iguais: \(m_1 = m_2\):

As variações das velocidades:

Momento linear e um sistema de duas partículas (CASO 2)

v_{1f} =\hspace{1.0cm} \text{ m/s}
v_{2f} =\hspace{1.0cm} \text{ m/s}
v_{1i} = +0,60 \text{ m/s}
v_{2i} = -0,20 \text{ m/s}
\Delta v_{1} = \hspace{1.0cm} \text{ m/s}
\Delta v_{2} = \hspace{1.0cm} \text{ m/s}
-0,20
+0,60
-0,80
+0,80

A razão das variações das velocidades:

\frac{\Delta v_1}{\Delta v_2} = -1

Você pode repetir esse experimento com muitas velocidades iniciais diferentes, com os carros com massas iguais se movendo no mesmo sentido ou em sentidos opostos, e sempre observará que a colisão intercambia as velocidades dos carros.

Se a velocidade de um carro padrão diminui em uma certa quantidade como resultado da colisão, a velocidade do outro carro padrão aumenta exatamente a mesma quantidade se as massas inerciais são iguais.

A quantidade de material que compõe cada carrinho afeta o movimento?

v_{1,i}=+0,60\text{ m/s}
v_{1,f}=-0,20\text{ m/s}
\rightarrow
v_{2,i}=-0,20\text{ m/s}
v_{2,f}=+0,60\text{ m/s}
\rightarrow

ANTES

DEPOIS

VARIAÇÃO

\Delta v_1=-0,80\text{ m/s}
\Delta v_2=+0,80\text{ m/s}
\rightarrow
\rightarrow

Momento linear e um sistema de duas partículas

Para um sistema isolado de duas partículas, nós podemos observar alguns fenômenos.

Fonte: https://www.geogebra.org/m/qd8ZtEQp

Massas diferentes: \(m_2 = 2m_1\):

As variações das velocidades:

v_{1i} = +0,60 \text{ m/s}
v_{2i} = 0 \text{ m/s}
v_{1f} =\hspace{1.0cm} \text{ m/s}
v_{2f} =\hspace{1.0cm} \text{ m/s}
+0,40
-0,20
\Delta v_{1} = \hspace{1.0cm} \text{ m/s}
\Delta v_{2} = \hspace{1.0cm} \text{ m/s}

A razão das variações das velocidades:

\frac{\Delta v_1}{\Delta v_2} = -2
-0,80
+0,40

Momento linear e um sistema de duas partículas (CASO 3)

Para um sistema isolado de duas partículas, nós podemos observar alguns fenômenos.

Fonte: https://www.geogebra.org/m/qd8ZtEQp

Massa diferente: \(m_2 = m_1/2\):

As variações das velocidades:

Momento linear e um sistema de duas partículas (CASO 4)

v_{1i} = +1,60 \text{ m/s}
v_{2i} = -0,60 \text{ m/s}
v_{1f} =\hspace{1.0cm} \text{ m/s}
v_{2f} =\hspace{1.0cm} \text{ m/s}
\Delta v_{1} = \hspace{1.0cm} \text{ m/s}
\Delta v_{2} = \hspace{1.0cm} \text{ m/s}

A razão das variações das velocidades:

\frac{\Delta v_1}{\Delta v_2} = -0,50
+2,33
+0,13
+2,93
-1,47

Não importa como os carros se movam (ou não se movam) inicialmente, as variações das velocidades serão diferentes quando os carros têm massas diferentes.

\Delta \vec v_1 \neq\Delta \vec v_2

Caso 3

Caso 4

\frac{\Delta v_p}{\Delta v_d}=-2
\Delta \vec v_p
\Delta \vec v_d
\Delta \vec v_p
\Delta \vec v_m
\Delta v_p = -0,80\text{ m/s}
\Delta v_d = +0,40\text{ m/s}
\Delta v_p = -1,47\text{ m/s}
\Delta v_m = +2,93\text{ m/s}
\frac{\Delta v_p}{\Delta v_m}=0,5
\Rightarrow
\Leftarrow

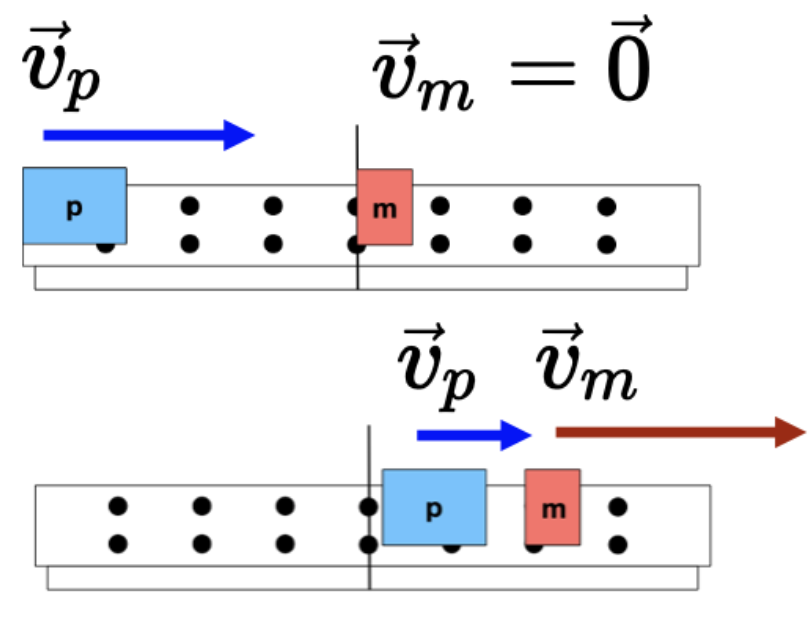
A massa inercial parece ditar como serão as variações das velocidades antes e depois da colisão.

Momento linear e um sistema de duas partículas

Experimento Carro 1 Carro 2
1 e 2 padrão padrão 1,0 1,0
3 padrão dobro 2,0 2,0
4 padrão metade 0,5 0,5

Massa inercial (\(m\))

Razão das inércias

Razão inversa da variação das velocidades

m_2/m_1
|\Delta v_1|/|\Delta v_2|

Verificamos "experimentalmente" que a massa inércia é uma medida da tendência de um objeto a resistir a qualquer variação em sua velocidade.

A razão das velocidades dos dois carros é igual à razão inversa de suas massas inerciais.

\frac{|\Delta v_1|}{|\Delta v_2|} = \frac{m_2}{m_1}
\frac{\Delta v_1}{\Delta v_2} =- \frac{m_2}{m_1}
\Rightarrow

Definição do momento linear

Definição do momento linear

A partir do conceito de massa inercial na interação de dois objetos e da variação da velocidade:

definimos o momento linear. Vamos reescrever a equação acima,

m_1\Delta v_{1}+m_2\Delta v_{2}=0
m_1(v_{1,f}-v_{2,i})+m_2(v_{2,f}-v_{2,i})=0
(m_2v_{2,f}-m_2v_{2,i})+ (m_1v_{1,f}-m_1v_{1,i})=0
\frac{m_1}{m_2}= -\frac{\Delta v_{2}}{\Delta v_{1}}

O produto da massa inercial (\(m\)) e a velocidade (\(v\)) de um objeto é chamado de momento linear (\(p\)):

\vec p \equiv m \vec v
(p_{2,f}- p_{2,i})+ (p_{1,f}- p_{1,i})=0
\Delta p_{2}+\Delta p_{1}=0
(p_{2,f}+ p_{1,f})- (p_{2,i}+ p_{1,i})=0
P_{sis,f}+P_{sis,i}=0

Definição do momento linear

O momento linear final do sistema é sempre igual ao momento linear inicial do sistema. Isto é, o  momento linear de um sistema isolado é conservado:

P_{sis}= p_1+p_2+\cdots =const.
P_{sis,f}= P_{sis,i}
\Delta P_{sis,f}=0

Note que o momento linear de cada objeto do sistema pode mudar, mas a soma das variações deve ser nula,

\Delta( p_{2}+p_{1})=0
\Delta p_{2}+\Delta p_{1}=0

Vamos calcular o momento do sistema antes e depois da colisão nos quatro casos analisados:

Definição do momento linear

Caso 1:

Fonte: https://www.geogebra.org/m/XZNtHeU4
0
0

A interação altera o momento linear de cada objeto, mas não altera o momento linear do sistema.

v_{1i} = +0,60 \text{ m/s}
v_{2i} = 0 \text{ m/s}
v_{1f} =0 \text{ m/s}
v_{2f} =+0,60 \text{ m/s}
m_1=m_2=4,0\text{ kg}
\Delta P_{1}=\hspace{1.0cm} \text{N.s}
\Delta P_{2}=\hspace{1.0cm} \text{N.m}
\Delta P_{sis}=\hspace{1.0cm} \text{N.s}
P_{sis,i}=\hspace{1.0cm} \text{N.s}
P_{sis,f}=\hspace{1.0cm} \text{N.s}
\Delta P_{sis}=\hspace{1.0cm} \text{N.s}
+2,4
-2,4
+2,4
+2,4

Vamos calcular o momento do sistema antes e depois da colisão em dois dos casos analisados:

Definição do momento linear

Caso 3:

Fonte: https://www.geogebra.org/m/XZNtHeU4
+1,6
-1,6
0
+1,2
+1,2
0
v_{1i} = +0,60 \text{ m/s}
v_{2i} = 0 \text{ m/s}
v_{1f} =-0,20 \text{ m/s}
v_{2f} =+0,40 \text{ m/s}
\Delta P_{1}=\hspace{1.0cm} \text{N.s}
\Delta P_{2}=\hspace{1.0cm} \text{N.s}
\Delta P_{sis}=\hspace{1.0cm} \text{N.s}
P_{sis,i}=\hspace{1.0cm} \text{N.s}
P_{sis,f}=\hspace{1.0cm} \text{N.s}
\Delta P_{sis}=\hspace{1.0cm} \text{N.s}
m_2=2m_1
m_1=2,0\text{ kg}

A interação altera o momento linear de cada objeto, mas não altera o momento linear do sistema.

Princípio da conservação do momento linear e as leis de Newton

Para quaisquer massas e velocidades,

\vec P_{sis,f}=\vec P_{sis,i}

quando as únicas forças que atuam no sistema são as interações entre as partículas (forças de contato = internas ).

Para um sistema isolado (resultante das forças externas nulas),

O PRINCÍPIO DE CONSERVAÇÃO DO MOMENTO LINEAR:

O MOMENTO LINEAR TOTAL DE UM SISTEMA SE CONSERVA SE AS FORÇAS EXTERNAS SE ANULAM.

O momento linear varia no tempo quando há uma interação.

Testes como este podem ser usados para melhorar o projeto de estruturas críticas, como reatores nucleares, de forma que possam aguentar o impacto de uma colisão de uma aeronave. 

\frac{d\vec p}{dt} = \frac{d(m\vec v)}{dt}

Fonte: Wolfgang

Fonte: Colisão de avião com reator nuclear

Fonte: A física de um desastre aéreo

Princípio da conservação do momento linear e as leis de Newton

Princípio da conservação do momento linear e as leis de Newton

A primeira lei de Newton

\vec P_{sis}=constante

Todo corpo continua em seu estado de repouso ou de movimento uniforme em uma linha reta, a menos que seja forçado a mudar aquele estado por forças imprimidas sobre ele.

x
y
\vec p
\Delta \vec P_{sis}=\vec 0
\vec P_{f,s} = \vec P_{i,s}

A força resultante externa é nula.

Sistema

Princípio da conservação do momento linear e as leis de Newton

A segunda lei de Newton

A mudança de movimento é proporcional à força motora imprimida, e é produzida na direção da linha reta na qual aquela força é imprimida.

\vec F_{ext} = m\vec a
\vec F_{ext} = m\frac{d\vec v}{dt}
\vec F_{ext} = \frac{d(m\vec v)}{dt}
\vec F_{ext} = \frac{d\vec p_{sis}}{dt}
\vec p_i
x
y
\vec p_f

A força resultante externa não é nula.

Sistema

Vizinhança

Princípio da conservação do momento linear e as leis de Newton

A terceira lei de Newton

A toda ação há sempre oposta uma reação igual, ou, as ações mútuas de dois corpos, um sobre o outro, são sempre iguais e dirigidas a partes opostas.

\vec F_{12} =-\vec F_{21}
\frac{d\vec p_1}{dt}+ \frac{d\vec p_2}{dt}=\vec 0
\vec F_{12} +\vec F_{21}=\vec 0
\frac{d\vec P_{sis}}{dt}=\vec 0
x
y
\vec p_{1,f}
\vec p_{1,i}
\vec p_{2,i}
x
y
\vec p_{2,f}
\Delta \vec p_{1}+\Delta\vec p_{2} = 0

As forças internas não alteram o momento linear do sistema.

Sistema

\vec F_{21}
\vec F_{12}

Resumo

O momento linear de cada partícula é dada pelo produto

\vec p_i = m\vec v_i

O momento linear total do sistema de partículas é dado pela soma

\vec P_{sis} =\sum_i \vec p_i

Se a força resultante externa sobre o sistema é nula

\vec P_{sis} =constante

Se a soma das forças externas sobre um sistema permanece zero, então o momento linear total do sistema permanece constante.

Exemplo 1 (A4.P1-02)

Informe as velocidades antes e depois da interação e as variações das velocidades para os carrinhos 1 e 2. Repare que temos um gráfico da posição versus o tempo.

\vec v_1

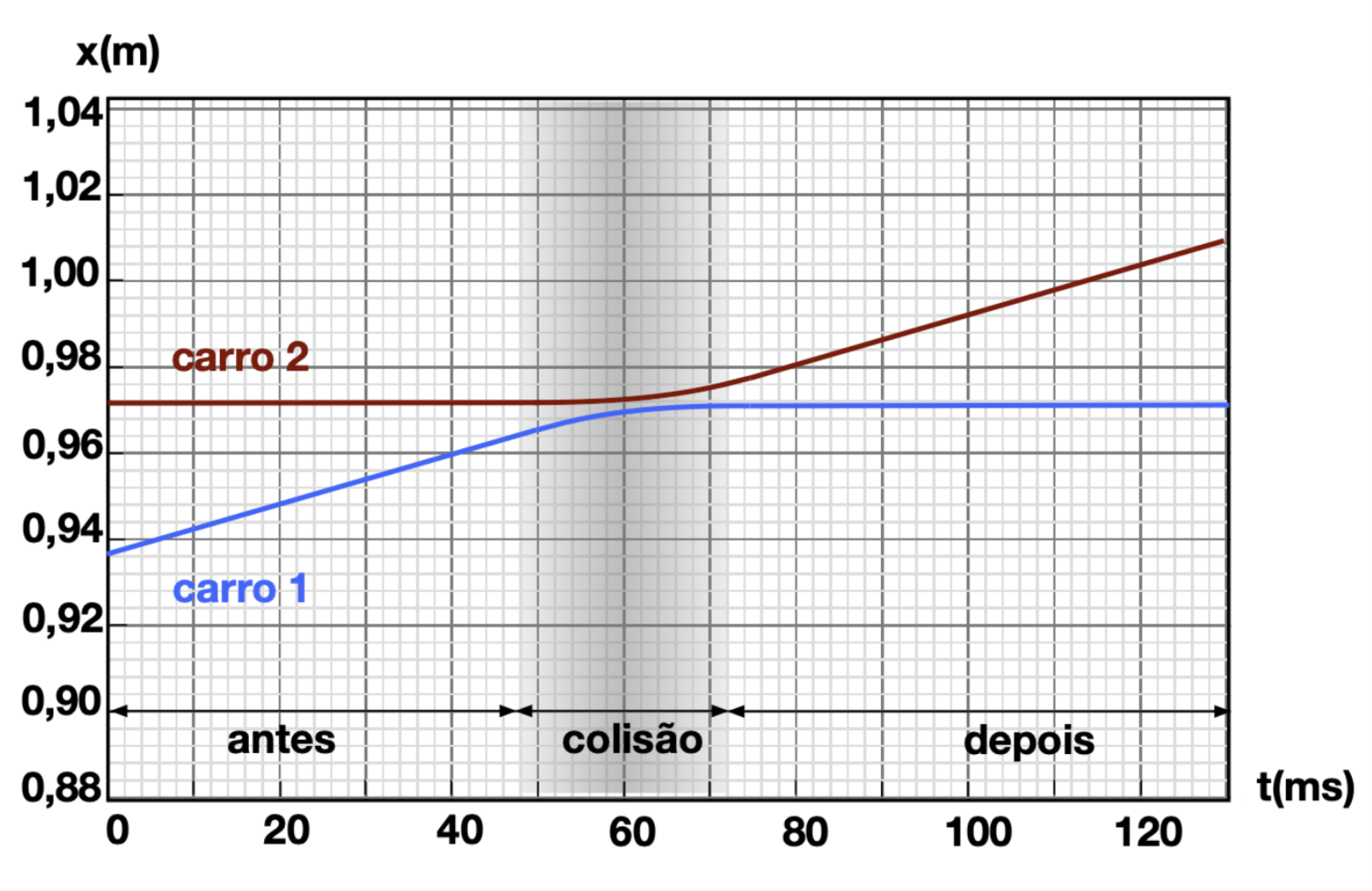
Antes

Durante

\vec v_2

Depois

Exemplo 2 (A4.P1-03)

Qual é a variação na velocidade do:

(a) carrinho 1 ?

(b) do carrinho 2 ?

(c) O que você nota sobre suas duas respostas?

Repare que temos um gráfico da velocidade versus o tempo.

\vec v_{1i}

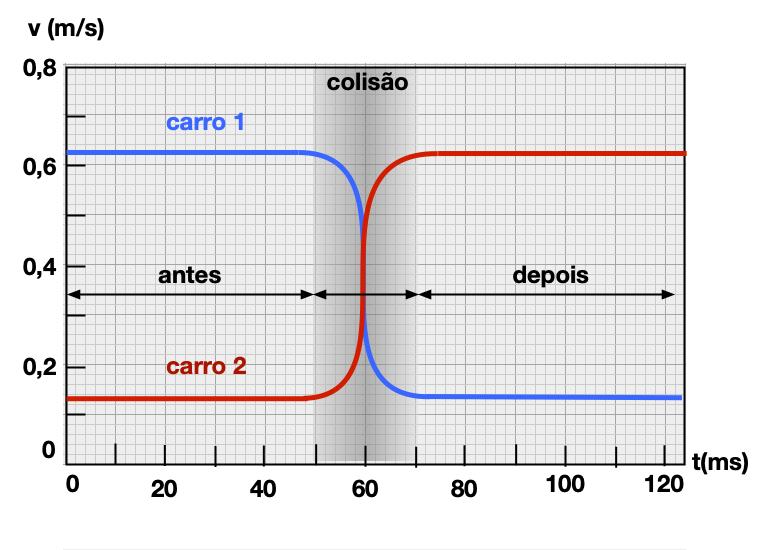
Antes

\vec v_{2i}

Durante

\vec v_{2f}

Depois

\vec v_{1i}

Exemplo 3 (A4.P1-04)

O componente x da velocidade final do carrinho padrão na figura é positivo.

Você pode torná-la negativa ajustando a velocidade inicial do carro padrão e mantendo o carrinho metade inicialmente em repouso?

\vec v_p
\vec v_m
\vec v_p
\vec v_m = \vec 0

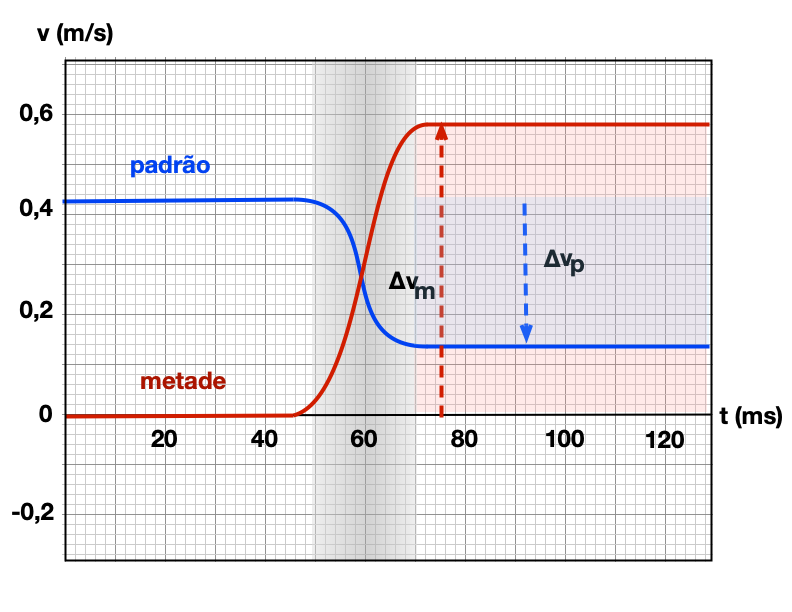
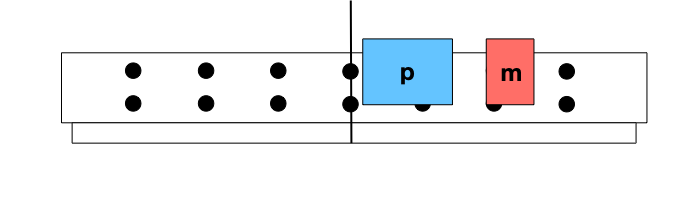
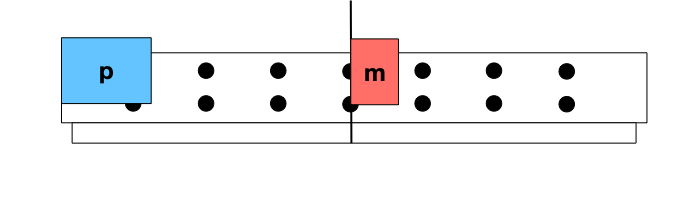
Exemplo 4 (A4.P1-05)

Uma pequena pedra é presa ao topo de um carrinho de inércia padrão de 1 kg para formar uma combinação de inércia \(m_d\) desconhecida. Um segundo carrinho padrão é então lançado com uma velocidade inicial dada por \(v_{1,i}\) = +0,46 m/s em direção à combinação que está inicialmente em repouso. Após a colisão, o componente x da velocidade do carrinho com a pedra é \(v_{2,f}\) = +0,38 m/s e o do carrinho padrão é \(v_{1,f}\) = -0,08 m/ s. Qual é a massa inercial da pedra?

\vec v_{1,i}
\vec v_{2,i}=\vec 0
\vec v_{1,f}
\vec v_{2,f}
\Delta \vec v_1
\Delta \vec v_2

Exemplo 5 (A4.P1-06)

Uma bola de tênis de massa 58 g move-se com velocidade 50 m/s em direção a uma parede. Após ricochetear na parede, observa-se que a bola de tênis se move praticamente com mesma rapidez, no sentido oposto. (a) Desenhe um diagrama mostrando os momentos inicial e final da bola de tênis. (b) Qual a variação do momento da bola de tênis? (c) Compare a variação da magnitude do momento da bola de tênis com a magnitude da variação do momento da bola de tênis.

Exemplo 6 (A4.P1-07)

Uma patinadora cuja massa é 50 kg move-se com momento constante 400 kg·m/s. Em um instante particular de seu programa de patinação ela cruza a posição 3 m. Qual era sua posição um tempo 3 s mais cedo?

Exemplo 7 (A4.P1-08)

No instante \(t_1\) = 12 s, um carro de massa 1300 kg está localizado em x = 94 m e tem momento 4500 kg·m/s. O momento do carro não está variando. No instante \(t_2\) = 17 s, qual a posição do carro?

Exemplo 8 (A4.P1-09)

Compare a magnitude do momento de uma bala de 0,010 kg disparada de uma espingarda a 1300 m/s e uma bola de boliche de 6,5 kg se arrastando pelo chão a 4,0 m/s.

 

Exemplo 9 (A4.P1-10)

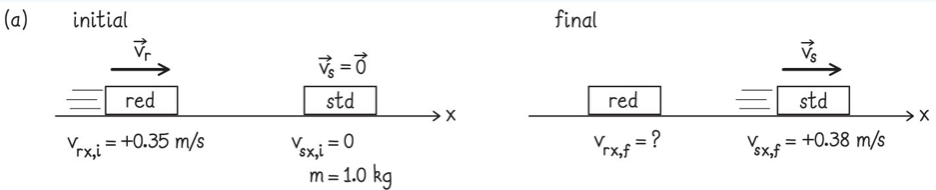
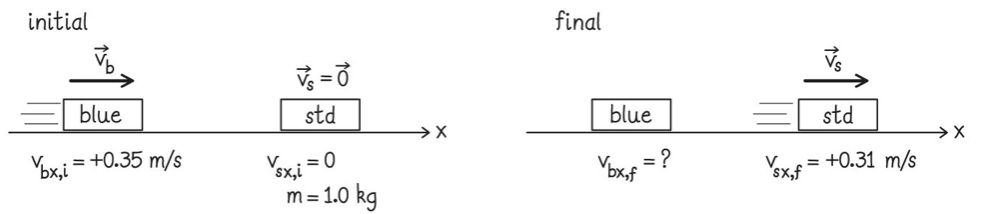
Um carrinho vermelho com uma velocidade inicial de 0,35 m/s colide com um carrinho padrão estacionário \(m_{red}=1,0\) kg. Após a colisão, o carrinho padrão se afasta a uma velocidade de 0,38 m/s.

(a) Qual é a variação do momento para cada carrinho?

(b) O experimento é repetido com um carrinho azul e agora a velocidade final do carrinho padrão é de 0,31 m/s. Qual é a variação do momento para cada carrinho nesta segunda colisão?

(c) Se nas colisões \(v_{red,f}\) = +0,032 m/s e \(v_{blue,f}\)= -0,039 m/s, quais são as inércias dos carros vermelho e azul?

Exemplo 10 (A4.P2-02)

(a) As variações de velocidade na figura são iguais em magnitude? Por que sim ou por que não? (b) Determine as variações de velocidade dos carrinhos e verifique se \(m_1/m_2 = -∆v_2/∆v_1\) nessa figura. (c) Determine o momento inicial e final dos dois carros. (d) Qual é o momento do sistema antes da colisão? (e) Após a colisão? (f) As variações de momento são iguais em magnitude e opostas em sentido? Por que sim ou por que não?

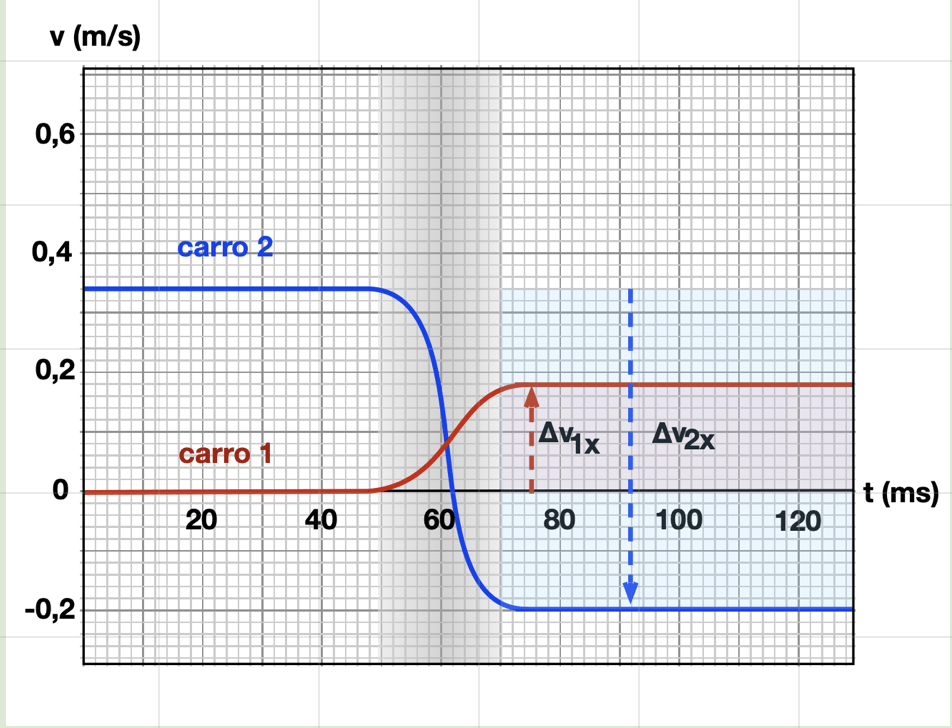
Dados:

\(m_1 = 0,36\) kg

\(m_2 = 0,12\) kg

Exemplo 11 (A4.P2-04)

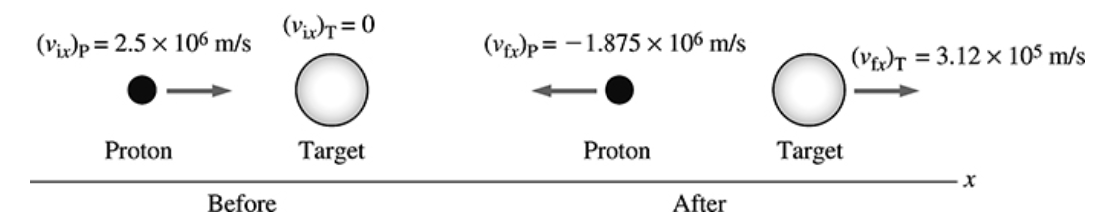
Um próton (massa de 1 u) é lançado contra um núcleo-alvo com velocidade de 2,50 x 10^6 m/s. O próton ricocheteia com sua velocidade reduzida em 25%, enquanto o núcleo-alvo adquire uma velocidade de 3,12 x 10^5 m/s. Qual é a massa, em unidades de massa atômica, do núcleo-alvo?

Questão 12

Qual a variação do momento linear da bola? Vale 0,1 pontos na média da unidade.

Aqui temos uma simulação (idealizada) do que ocorre nos laboratórios de física.

Questão 13

O momento linear é conservado? Se sim ou se não calcule o erro relativo.  Vale 0,1 pontos na média da unidade.

Aqui temos uma simulação (idealizada) do que ocorre nos laboratórios de física.

Questão 14

O momento linear é conservado? Se sim ou se não calcule o erro relativo.  Vale 0,1 pontos na média da unidade.

Aqui temos uma simulação (idealizada) do que ocorre nos laboratórios de física.

Não ministrado

Para um sistema de duas partículas,

Sistema de partículas

\vec F_{AB}
\vec F_{BA}

As forças internas satisfazem a \(3^a\) lei de Newton:

A força resultante sobre cada partícula:

\vec F_{AB}+\vec F_{BA}=\vec 0
A
B
\vec F_{AB}+\vec F_{1}=\vec F_{res,A}
\vec F_{BA}+\vec F_{2}=\vec F_{res,B}
\vec F_1
\vec F_2

As forças externas satisfazem a \(2^a\) lei de Newton:

\vec F_{1}+\vec F_{2}=\vec F_{ext}

Para um sistema de duas partículas,

Sistema de partículas

\vec F_1
\vec F_2
\vec F_{AB}
\vec F_{BA}

O momento linear do sistema:

A força resultante sobre o sistema:

\vec P_{sis} = \vec p_A + \vec p_B
\frac{d\vec P_{sis}}{dt} = \frac{d\vec p_A}{dt} + \frac{d\vec p_B}{dt}
\frac{d\vec P_{sis}}{dt} =\vec F_{res,A}+\vec F_{res,B}
\frac{d\vec P_{sis}}{dt} =\vec F_{AB}+\vec F_{1}+\vec F_{BA}+\vec F_{2}
\frac{d\vec P_{sis}}{dt} =+\vec F_{1}+\vec F_{2}
\Rightarrow \frac{d\vec P_{sis}}{dt} =\sum\vec F_{ext}
A
B

Para um sistema de duas partículas,

A conservação do momento linear

\vec F_1
\vec F_2
\vec F_{AB}
\vec F_{BA}

Não é necessário que o sistema seja isolado, isto é, que não atuem forças externas.

A condição necessária e suficiente é que a resultante das forças externas seja nula.

\frac{d\vec P_{sis}}{dt} =\sum \vec F_{ext}
\frac{d\vec P_{sis}}{dt} =\vec 0
\vec P_{sis}=constante

Nesse exemplo, \(\vec F_1 = -\vec F_2\) constituem um binário que faz o sistema girar em torno de um ponto comum.

Para um sistema de duas partículas,

A conservação do momento linear

O sistema de partículas se move como uma partícula única com momento linear do sistema,

sob ação de uma força externa,

\vec F_{res}
\frac{d\vec P_{sis}}{dt}=\vec F_{ext}
\vec P_{sis}

A equação do movimento é,

A força externa tem a direção da variação do momento linear do sistema.

\vec F_{ext}
\vec F_1
\vec F_2

Ciência & Tecnologia

Tevatron do laboratório Fermilab, próximo a Chicago, Illinois, EUA existe um detetor de partículas, o D-Zero

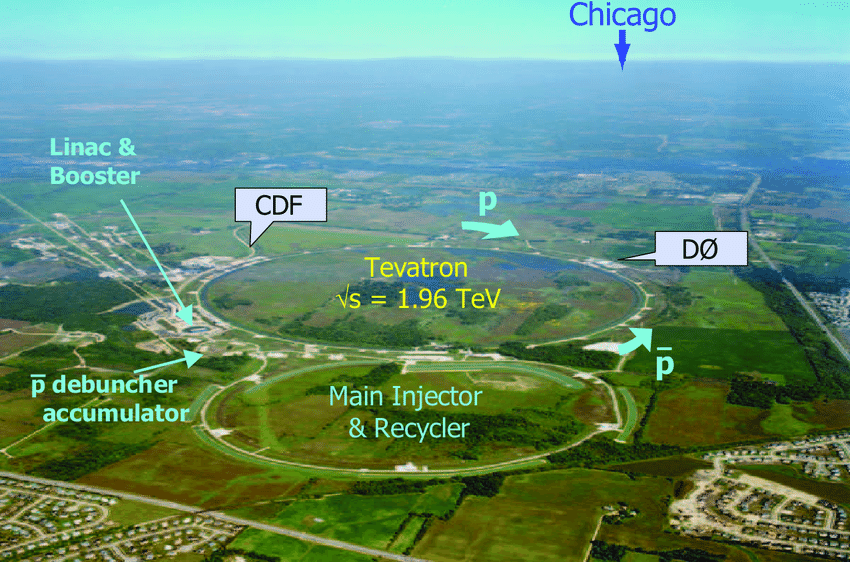
Fermilab

Tevatron

D-zero

O Tevatron está configurado de uma forma que os prótons e antiprótons se movem no anel de colisão em sentidos opostos com, para todos os fins práticos, vetores momento exatamente opostos.

Os engenheiros fizeram colidir prótons e antiprótons com energias totais de 1,96 TeV ( \(=3,1 \times 10^{-7} \) J ).

Ciência & Tecnologia

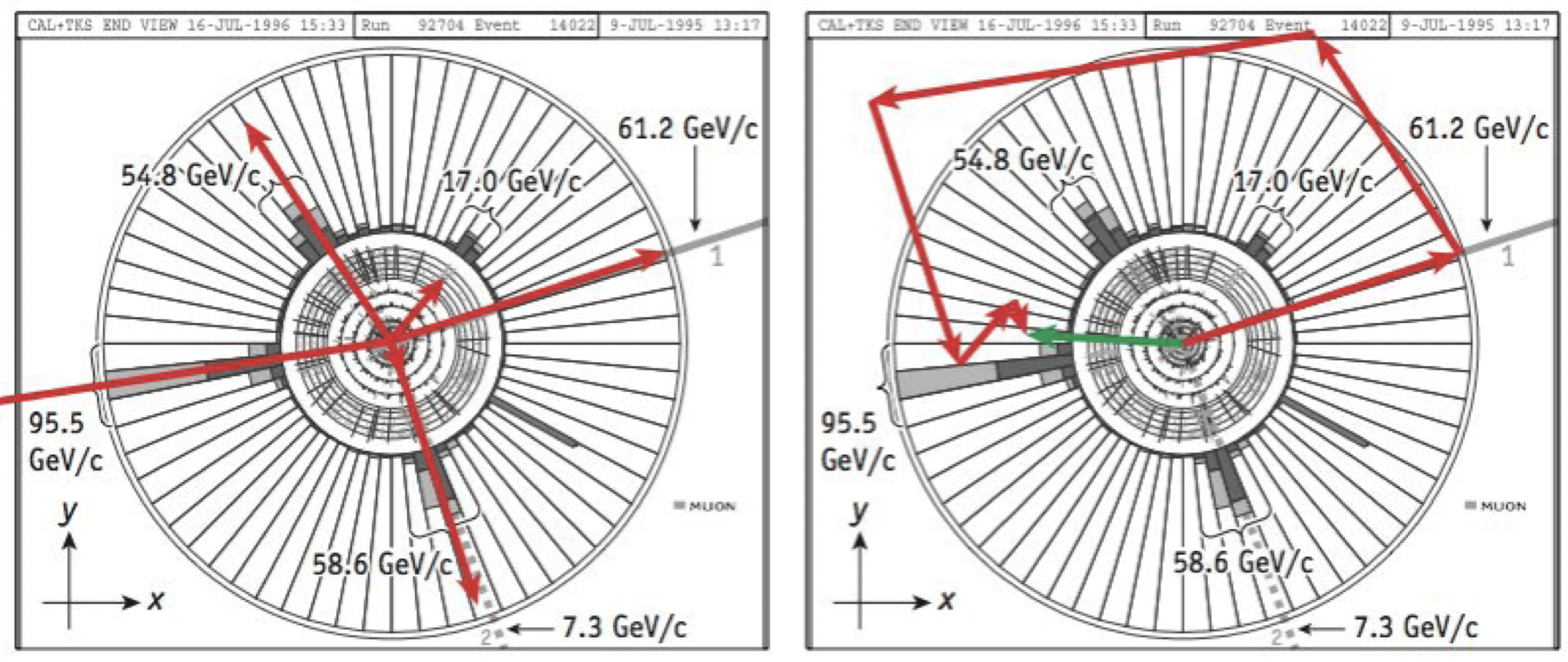
Em uma ma colisão desse tipo o rastros das partículas são geradas por computadores a partir do sinal registrado pelo detector D-Zero. 

Fermilab

O vetor momento inicial do próton aponta direto para a página, e o do antipróton aponta direto para fora da página.

Ciência & Tecnologia

Fermilab

O momento inicial total do sistema de prótons e antiprótons é zero.

Uma partícula que escapou sem ser detectada.  

O momento final total do sistema não foi nulo (seta verde).

Os físicos do Fermilab conseguiram demonstrar que o momento perdido, no evento exibido, foi de uma partícula desconhecida – conhecida como quark top.

FERMILAB

Ciência & Tecnologia

Por que desses estudos?

Ciência & Tecnologia

Supremacia energética!

Novas tecnologias!

Novos materiais!

Entre no site do SIRIUS e veja o que tem sido feito com feixes de elétrons.

Entre no site do CERNe veja o que tem sido feito com feixes de prótons.

Exemplo simples: pesquise sobre PET scan (matéria+antimatéria).

Qual a tecnologia e pessoas envolvidas no desenvolvimento;

Tudo começa com a base sólida e os fundamentos.

Made with Slides.com