Aula 17

Fundamentos de Mecânica

Prof. Ronai Lisbôa

UFRN - ECT - BCT

Objetivos

Definir a grandeza física impulso.

Enunciar o teorema do impulso-momento linear.

Aplicar o teorema do impulso-momento linear.

Bibliografia.

Tipler - Cap. 8

Seção: 8.3 (pag. 241 a 248)

- Refaça os exercícios resolvidos.

O momento linear em mais dimensões.

O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)

 

Para usar I.A. você deve saber ou ter ideia do que está fazendo. Se não é só informação fugaz.

A conservação do momento tem aplicações muito mais amplas. Governa tudo o que acontece no universo.

A conservação do momento linear é usada para resolver muitos problemas científicos e de engenharia:

  • do cálculo das forças de impacto durante colisões de veículos;
  • trajetórias dos satélites;
  • lançamento de foguetes;
  • capacidades de carga de membros artificiais.

Princípio fundamental da natureza

O momento linear é sempre conservado nos sistemas isolados em que a força resultante externa é nula.

A conservação do momento se aplica a átomos e partículas elementares na escala subatômica, as estrelas e galáxias na escala cósmica e a tudo o que está no meio.

Em muitas situações reais, o momento linear de um objeto em movimento está variando continuamente devido a sua interação com sua vizinhança, pois o sistema não é isolado ou melhor dizendo porque a resultante das forças externas não é nula.

Para predizer o movimento de um sistema nós devemos ser capazes de expressar matematicamente a relação entre interação sistema-vizinhança e a variação do momento linear.

O Princípio do Impulso faz uma conexão quantitativa entre a interação e variação do momento linear.

Para construir esse conceito vamos precisar rever o que é um contorno, vizinhança, sistema,  interação e impulso.

Princípio fundamental da natureza

Qualquer objeto ou grupo de objetos que possamos separar com um <contorno>, em nossa imaginação, do ambiente circundante ou <vizinhança> é um <sistema>.

Na colisão entre dois carros em um trilho de baixo atrito, os dois carros juntos são o sistema. O trilho é a vizinhança.

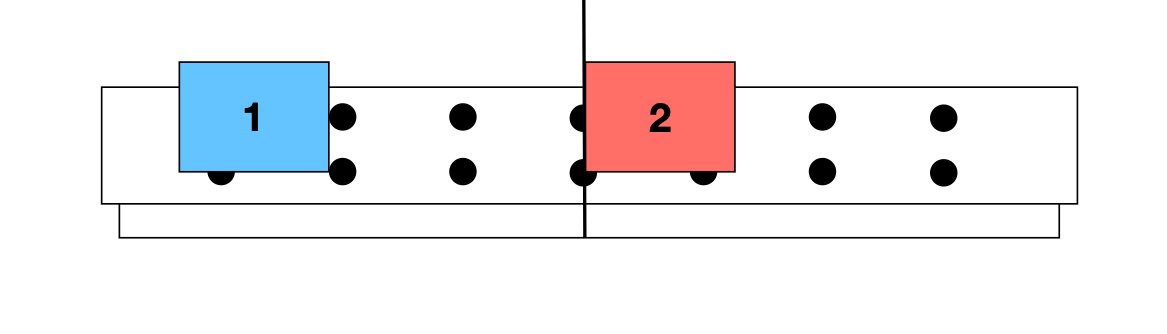
Se estamos interessados no movimento do carro 1, ele pode ser o sistema. O carro 2 e o trilho são vizinhança.

Depois de decidir incluir um determinado objeto no sistema, ele deve permanecer assim durante toda a análise.

vizinhança

sistema

contorno

sistema

contorno

vizinhança

O resultado físico independe dessa escolha, mas as escolhas adequadas podem simplificar o cálculo!

Sistema isolado x não isolado

Qual a variação do momento linear do ciclista (sistema)?

\Delta p_c = -700\text{ kg.m/s}
\Delta p_c = -875\text{ kg.m/s}

O momento linear do ciclista variou.

O que provocou a variação do momento linear do ciclista?

Pedalando a  \(v\) = 45 km/h. Então, colide no muro e tem a rapidez reduzida para \(v\)  = 0.

m=70\text{ kg}
\vec v

Pedalando a  \(v\) = 36 km/h. Então, colide no muro e tem a rapidez reduzida para \(v\)  = 0.

m=70\text{ kg}
\vec v

Fonte: https://portaldalili.com.br/beneficios-de-andar-de-bicicleta/

Fonte: https://super.abril.com.br

Sistema não isolado

\Delta p = -700\text{ kg.m/s}

A variação do momento linear do ciclista é o mesmo colidindo no colchão ou no muro.

Pedalando a  \(v\) = 36 km/h.  Então, colide no muro e tem a rapidez reduzida para \(v\)  = 0.

m=70\text{ kg}
\vec v

Qual a variação do momento linear do ciclista (sistema)?

Fonte: https://portaldalili.com.br/beneficios-de-andar-de-bicicleta/

Fonte: https://super.abril.com.br

Sistema não isolado

Por que seria preferível colidir no colchão?

\Delta p = -700\text{ kg.m/s}

colchão

Pedalando a  \(v\) = 36 km/h. Então, colide no colchão e tem a rapidez reduzida para \(v\)  = 0.

m=70\text{ kg}
\vec v

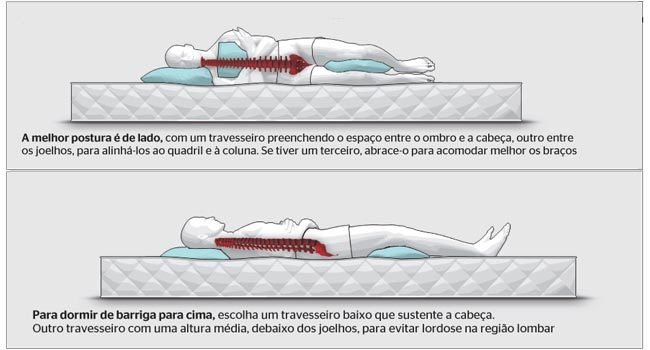
O momento linear é uma propriedade intrínseca dos objetos (do ciclista).

\Delta p = -700\text{ kg.m/s}

Ao colidir no colchão o tempo de ineração deve ser maior.

A variação do momento linear é a mesma.

m=70\text{ kg}
m=70\text{ kg}
\vec v
\vec v
v=36\text{ km/h}
v=36\text{ km/h}

A variação do momento linear ocorre a uma taxa mais lenta.

Para uma mesma variação do momento linear quanto maior o tempo da interação, menor será força do impacto.

colchão

Para uma mesma massa inercial e velocidade tanto faz colidir no muro ou no colchão.

Fonte: https://portaldalili.com.br/beneficios-de-andar-de-bicicleta/

Fonte: https://super.abril.com.br

Sistema não isolado

O que determina a magnitude da força do impacto não é o valor absoluto da variação do momento linear, mas a taxa na qual essa variação acontece.

F_{ext} = \frac{\Delta p_o}{\Delta t}
F_{ext} = \frac{\Delta p_o}{\Delta t}
= \frac{-700\text{ kg.m/s}}{5\text{ s}}
= -140 \frac{\text{ kg.m}}{{\text{s}^2}}
F_{ext} = \frac{\Delta p_o}{\Delta t}
= \frac{-700\text{ kg.m/s}}{10\text{ s}}
= -70 \frac{\text{ kg.m}}{{\text{s}^2}}

A força resultante externa exercida no ciclista é a taxa de variação no tempo do momento linear do ciclista.

Força do impacto

Variação do momento do objeto

Variação do tempo da interação = Taxa

\Delta p = -700\text{ kg.m/s}
\Delta t = 5\text{ s}
\Delta t = 10\text{ s}
\Delta p = -700\text{ kg.m/s}

colchão

\vec F_{ext}
\Delta \vec p
\vec F_{ext}
\Delta \vec p

Fonte: https://portaldalili.com.br/beneficios-de-andar-de-bicicleta/

Fonte: https://super.abril.com.br

Impulso

Considerando o ciclista como o sistema e o muro como a vizinhança percebemos que a força que o muro exerce no ciclista varia o momento linear do ciclista.

F_{ext} = \frac{\Delta p_o}{\Delta t}

Taxa de variação do momento linear e força resultante

\Delta p_o = F_{ext} \Delta t
\Rightarrow
\Delta p_o =0
p_{o,f} = p_{o,i}
\Delta p_o =F_{ext}\Delta t
p_{o,f} = p_{o,i} +F_{ext}\Delta t

Sem interação

Com interação

Fonte: https://portaldalili.com.br/beneficios-de-andar-de-bicicleta/

Fonte: https://super.abril.com.br

Impulso

Vamos definir a lei do impulso, \(\vec I\):

\Delta \vec p = \vec I
\vec p_f = \vec p_i+ \vec I

obemos a  equação do impulso:

\vec I = \vec F_R\Delta t

No Sistema internacional a unidade do impulso (ou variação do momento linear) é redefinida para:

O impulso entregue a um objeto durante um intervalo de tempo Δt - é igual ao produto da soma vetorial das forças exercidas sobre o objeto e a duração do intervalo de tempo.

\Rightarrow
1\text{N.s}\equiv 1\frac{\text{kg.m}}{\text{s}}

A partir da relação entre variação do momento linear, força externa resultante e intevalo de tempo.

\Delta \vec p =\vec F_R\Delta t
\vec p_f = \vec p_i +\vec F_R\Delta t
\Rightarrow

como a variação no momento de um sistema ou objeto como o impulso entregue a ele.

Princípio do impulso: Teorema impulso-momento linear

Para um sistema isolado em que as força resultante externa é nula, a conservação do momento linear significa:

\Delta \vec p_s = \vec 0
\Rightarrow \vec p_{s,f} = \vec p_{s,i}

O impulso pode aumentar (entrada: \(I>0\)) ou diminuir (saída: \(I<0\)) a magnitude do momento do linear sistema. Para um sistema isolado, o impulso é zero (\(I=0\)).

Como o momento linear é um vetor, o impulso também é um vetor e tem unidade de N.s

Para um sistema não isolado em que a força resultante externa não é nula, temos:

\Delta \vec p_s = \vec I

onde  \(\vec I\)  é o impulso e significa uma transferência de momento da vizinhança para o sistema.

\Rightarrow \vec p_{s,f} = \vec p_{s,i} + \vec I
\vec I = \vec F_R\Delta t

Princípio do impulso: Teorema impulso-momento linear

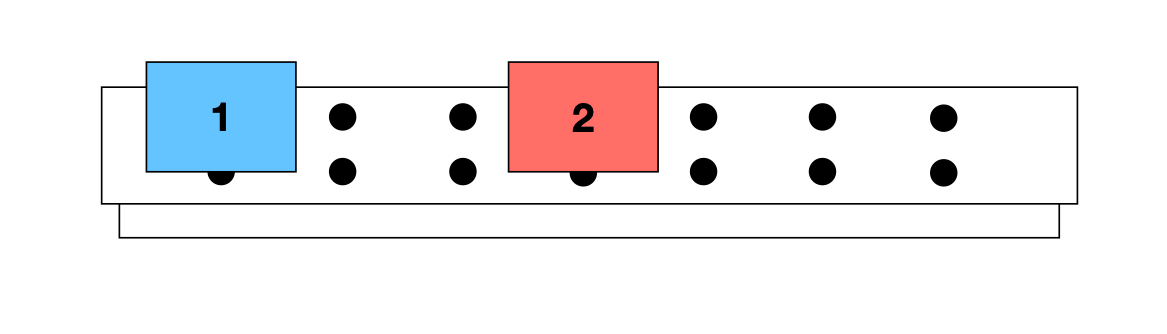
A variação de momento do carrinho 1 é compensada por uma variação no momento do carrinho 2. Vejamos a interação do sistema isolado dos carros com mola.

\Delta p_{1,c/m}=+0,096\text{ kg.m/s}
F_{\text{por 2 em 1}} = \frac{\Delta p_{1,c/m}}{\Delta t}
=\frac{+0,096\text{ kg.m/s}}{0,010\text{ s}}=+9,6\text{ N}
\Delta p_{2,c/m}=-0,096\text{ kg.m/s}
F_{\text{por 1 em 2}} = \frac{\Delta p_{2,c/m}}{\Delta t}
=\frac{-0,096\text{ kg.m/s}}{0,010\text{ s}}=-9,6\text{ N}

carro 1

carro 2

Sistema Isolado dos carros com mola

\Delta p_{1,c/m}+\Delta p_{2,c/m} = 0
(F_{21}+F_{12})\Delta t=0
F_{21}=-F_{12}
\Rightarrow
\Rightarrow
\Delta t = 10\text{ ms}
I
\vec F_{21}
\vec F_{12}

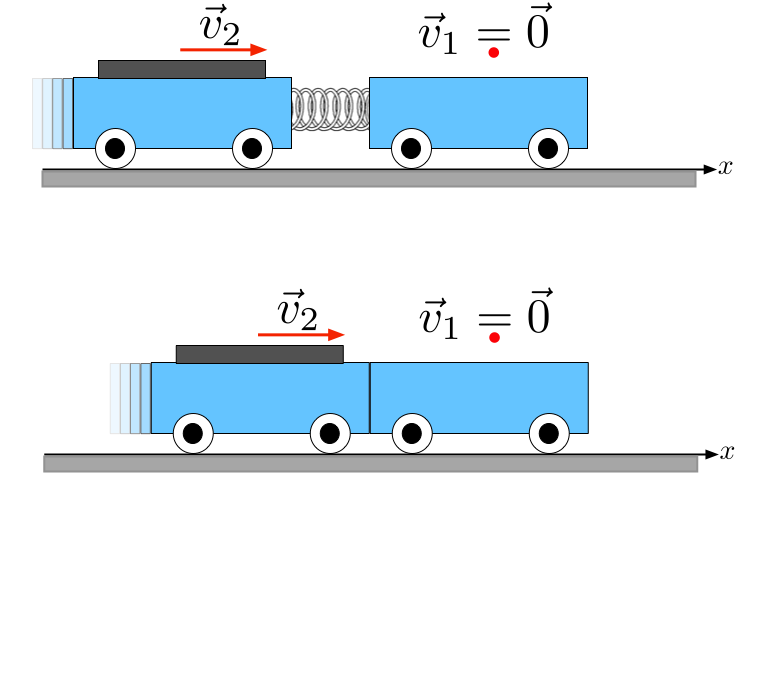
Princípio do impulso: Teorema impulso-momento linear

Em ambas as colisões a variação de momento do carrinho 1 é compensada por uma variação no momento do carrinho 2. Vejamos a interação do sistema de carros sem mola.

\Delta p_{1,s/m}=+0,096\text{ kg.m/s}
F_{\text{por 2 em 1}} = \frac{\Delta p_{1,s/m}}{\Delta t}
=\frac{+0,096\text{ kg.m/s}}{0,001\text{ s}}=+96\text{ N}
\Delta p_{2,s/m}=-0,096\text{ kg.m/s}
F_{\text{por 1 em 2}} = \frac{\Delta p_{2,s/m}}{\Delta t}
=\frac{-0,096\text{ kg.m/s}}{0,001\text{ s}}=-96\text{ N}

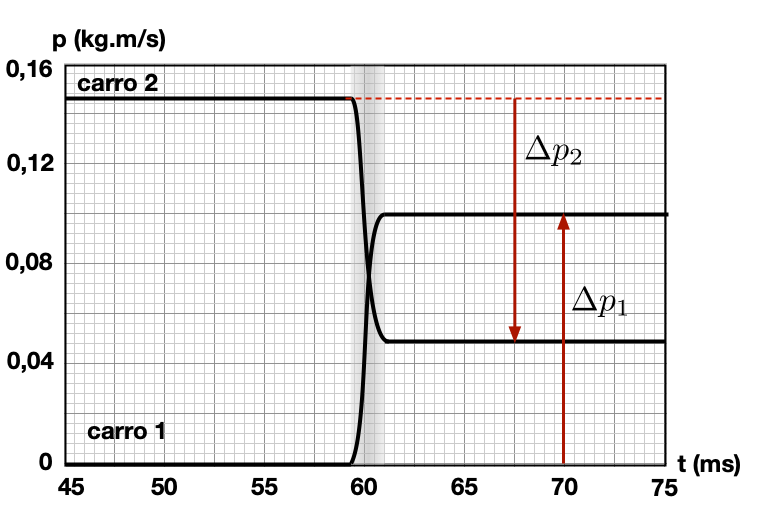
carro 1

carro 2

Sistema Isolado dos carros sem mola

\Delta t = 1\text{ ms}
\Delta p_{1,s/m}+\Delta p_{2,s/m} = 0
(F_{21}+F_{12})\Delta t=0
F_{21}=-F_{12}
\Rightarrow
\Rightarrow
I
\vec F_{21}
\vec F_{12}

Princípio do impulso: Teorema impulso-momento linear

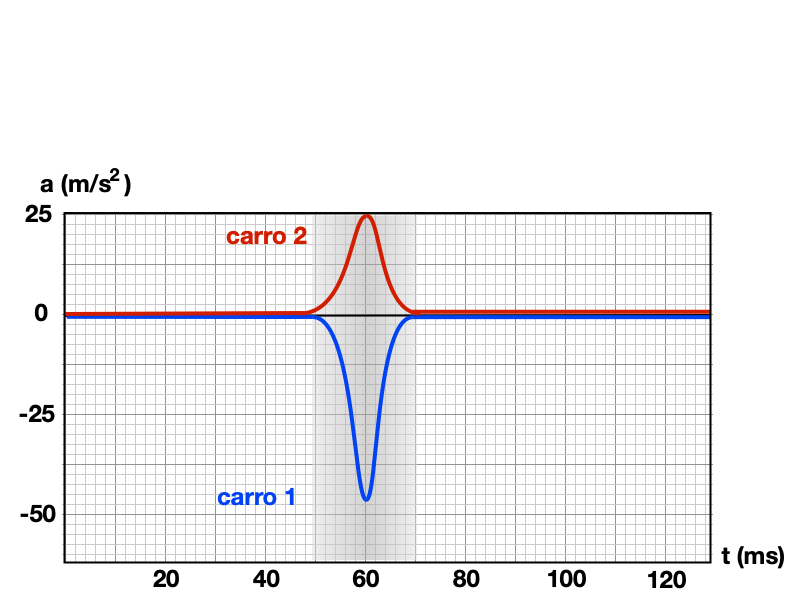
O movimento de dois carrinhos (sistema) que colidem em um trilho (vizinhança) de baixo atrito.

Princípio do impulso: Teorema impulso-momento linear

Há aceleração/desaceleração somente no momento do impacto.

Essas forças são internas e variam o momento linear de cada carrinho.

Mas as forças internas não alteram o momento linear do sistema.

A soma dos impulsos nesse caso é nula.

O movimento de dois carrinhos (sistema) que colidem em um trilho (vizinhança) de baixo atrito.

As velocidades não são constantes durante a colisão.

As acelerações não são nulas durante a colisão.

\vec v_1
\vec v_2

sistema

vizinhança

contorno

Princípio do impulso: Teorema impulso-momento linear

a=\frac{\Delta v}{\Delta t}

Forças impulsivas são forças que atuam por um dado instante de tempo:

d \vec p =\vec F_{R} d t

Fonte: Tipler & Mosca

\int_{p_1}^{p_2} d\vec p =\int_{t_1}^{t_2} \vec F_{R}(t)\,dt

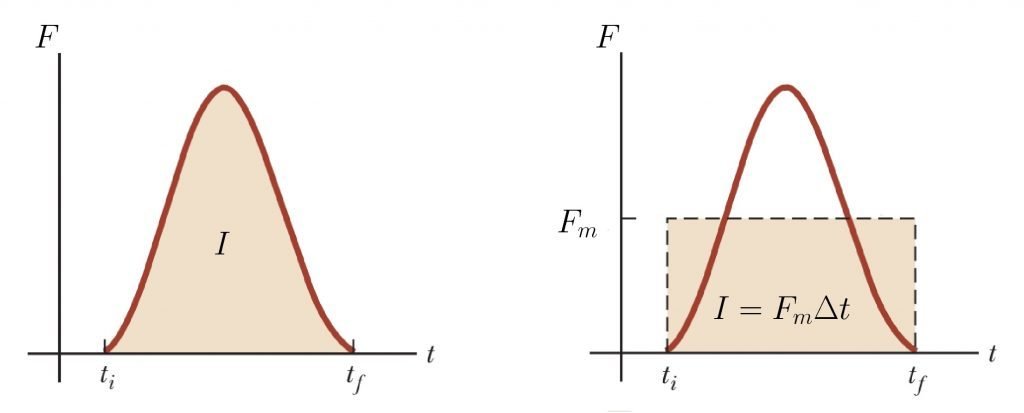
Se a força não é nula, então a variação do momento linear num intervalo de tempo \([t_1,t_2]\) é

\vec I = \Delta \vec p =\int \vec F_R(t)\,dt

Define-se como impulso da força resultante aplicada durante um intervalo de tempo,  o vetor:

A unidade do impulso é o N.s.

Devido a definição, o impulso é numericamente igual à área sob a curva no gráfico de F x t.

Princípio do impulso: Teorema impulso-momento linear

Uma força impulsiva é tal que,

\vec F \approx \vec 0 \quad \text{se}\quad t \notin[t_i,t_f]

Fonte: Tipler & Mosca

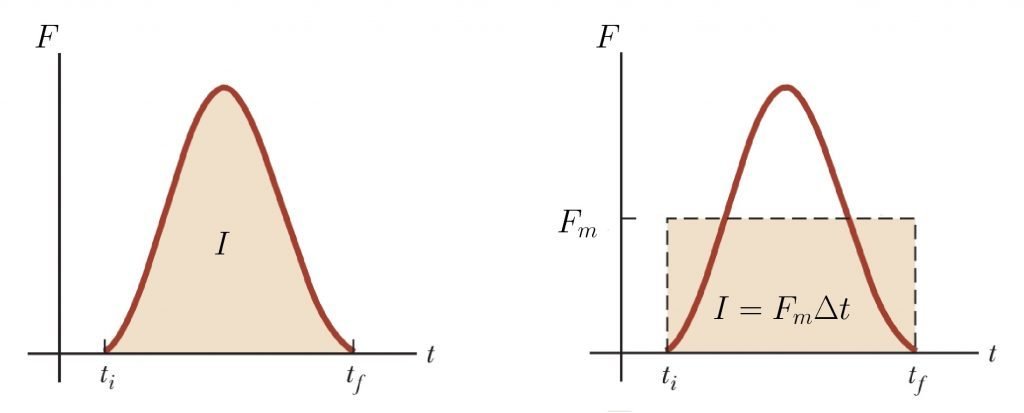
\vec F \approx \vec F_{med} \quad \text{se}\quad t \notin[t_i,t_f]

A força média impulsiva é:

\vec F_{med}=\frac{\vec I}{\Delta t}=\frac{\Delta \vec p}{\Delta t}

Devido a definição, o impulso pode ser calculado aproximadamente por:

\vec I = \vec F_{med}\Delta t

onde a força média está a meia altura da força impulsiva.

\vec I =\frac{ \vec F_{max}}{2}\Delta t
F_{max}
F_{med}

Princípio do impulso: Teorema impulso-momento linear

Dissertação de Mestrado

O papel do air-bag é vital.  Na colisão a variação do momento linear é o mesmo. Os carros partem com a mesmo momento inicial \(p_i\neq 0\) e finalizam com \(p_f = 0\).

Quanto maior a elasticidade dos materiais do carro maiores as chances da manutenção da vida.

Para uma mesma variação do momento linear, quanto maior o tempo da interação menor será a força do impacto. Isso salva vidas!

\vec F_{ext}=\frac{\Delta \vec p_o}{\Delta t}

Fonte: https://g1.globo.com/carros/noticia/2024/11/30/veja-a-lista-de-10-carros-que-reprovaram-no-teste-de-seguranca-do-latin-ncap.ghtml

\vec F_{ext}\Delta t={\Delta \vec p_o}
\vec I={\Delta \vec p_o}

Aplicando os conceitos

Os engenheiros avaliam a segurança dos carros a partir de vídeo-análise do movimento do carro e do motorista

O carro apresenta uma aceleração máxima de 200 m/s\(^2\). O impulso:

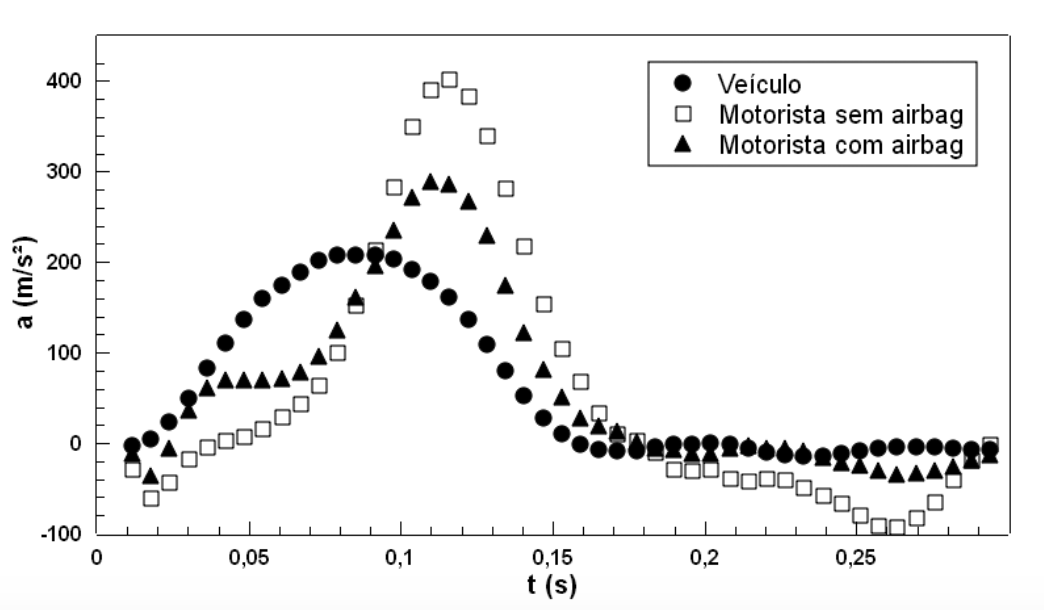
O motorista com airbag tem uma aceleração máxima de 280 m/s\(^2\). O impulso I = 1680 N.S.

O motorista sem airbag tem uma aceleração máxima de 400 m/s\(^2\). O impulso I = 1820 N.S.

FONTE: Revista Brasileira de Ensino de F ́ısica, v. 36, n. 1, 1501 (2014)

m_{carro} = 1250\text{kg}
m_{motorista} = 70\text{kg}
\Delta t = 0,16\text{ s}
\Delta t = 0,13\text{ s}
\Delta t = 0,16\text{ s}
I=F_m\Delta t
I=\frac{F_{max}}{2}\Delta t
I=\frac{(1250\text{ kg})(200\text{m/s}^2)}{2}0,16\text{s}=20000\text{ N.s}

Depois da colisão a cabeça do motorista sem airbag volta para trás (descalara) o que é um segundo risco.

Aplicando os conceitos

Profissionais que trabalham com atletas de alto desempenham trabalham com video-análise para melhorar o rendimento dos atletas.

I=F_{med}{\Delta t}
I=\frac{F_{max}}{2}{\Delta t}

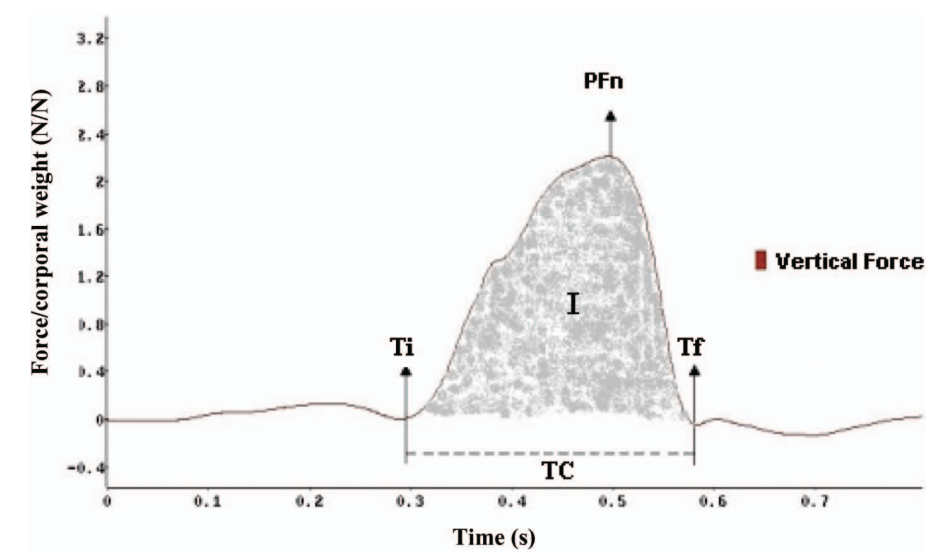
Aplicando os conceitos

Para ensinar um robô a andar é necessário entender como andamos.

I=\frac{F_{med}}{\Delta t}

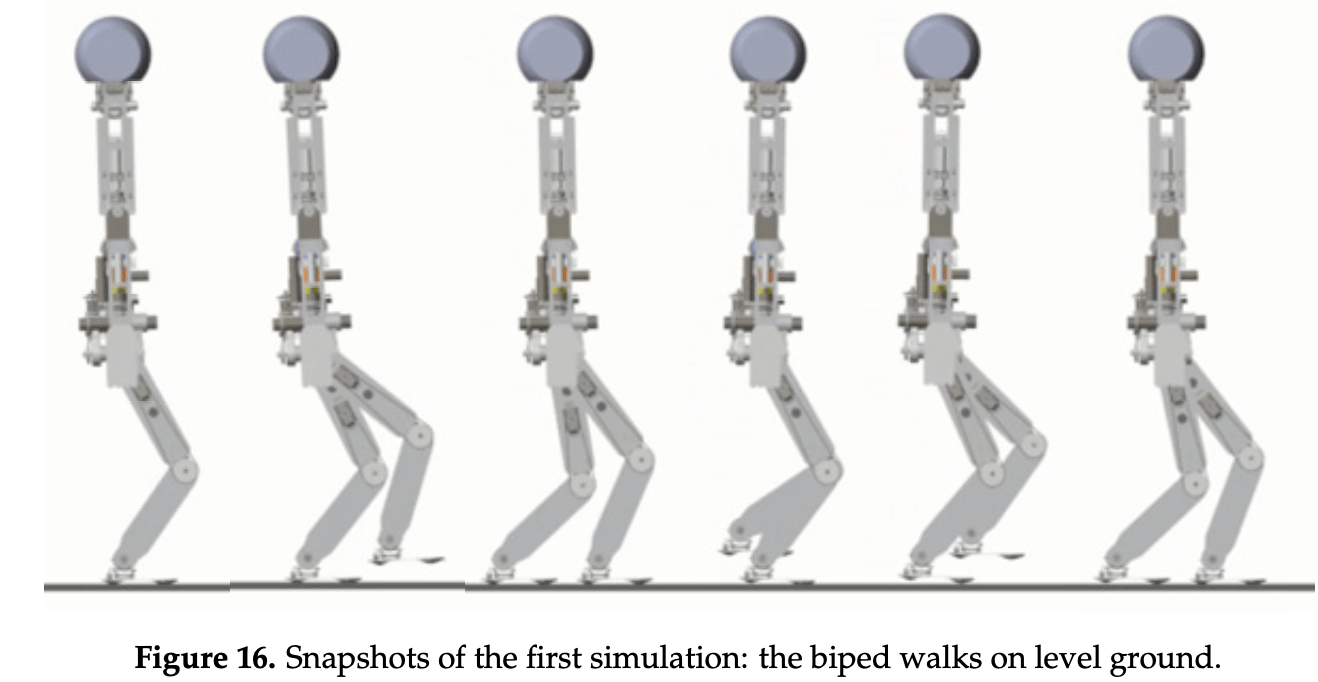
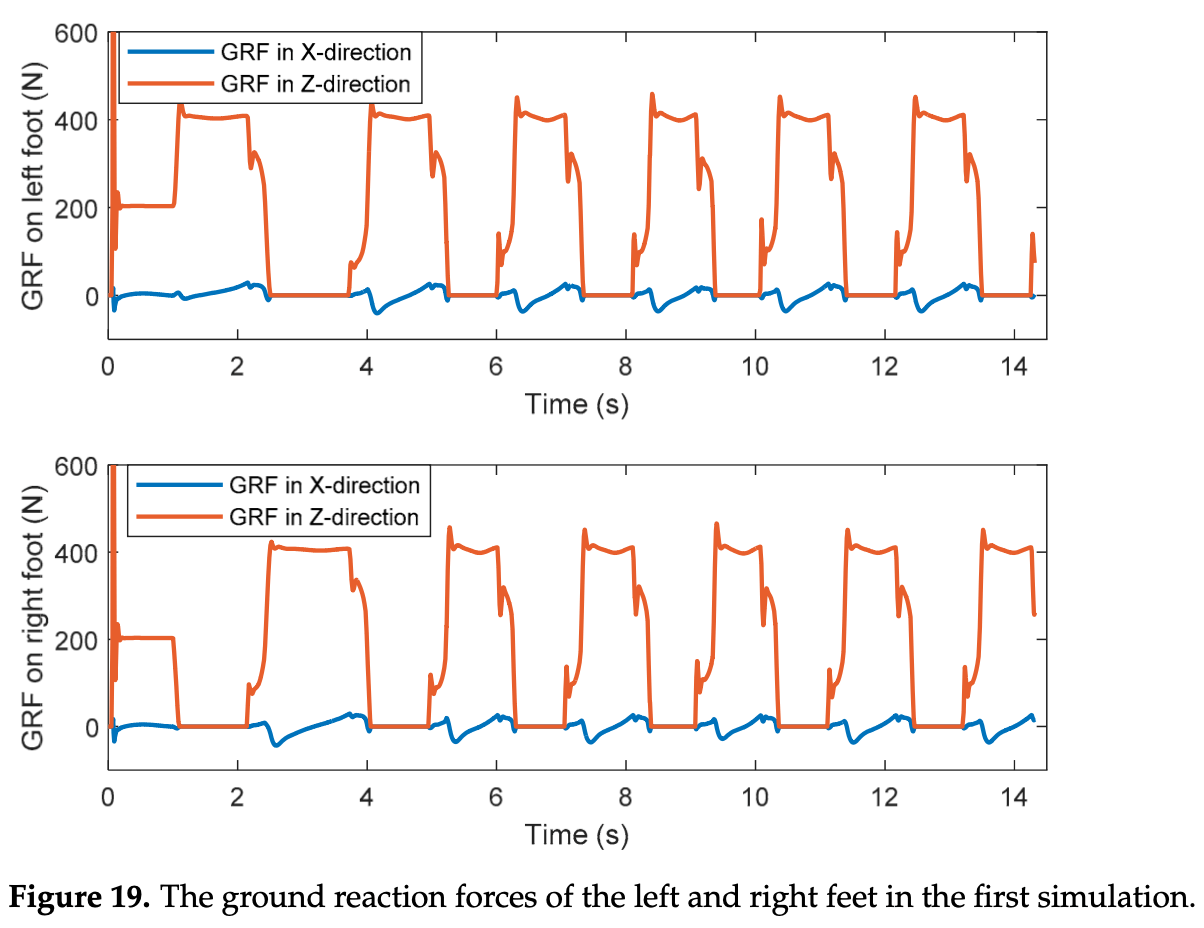
Aplicando os conceitos

Exemplo 1 (A9.P1-01)

Suponha que você tenha de escolher entre agarrar uma bola 1 de 0,50 kg que se desloca a 4,0 m/s ou uma bola 2 de 0,10 kg que se desloca a 20 m/s.

 

Qual das duas bolas seria mais fácil de agarrar?

Exemplo 2 (A9.P1-02)

Dois barcos que deslizam no gelo, apostam corrida sobre um lago horizontal sem atrito. Os barcos possuem massas m e 2m, respectivamente. A vela de um barco é idêntica à do outro, de modo que o vento exerce a mesma força constante sobre cada barco. Os dois barcos partem do repouso e a distância entre a partida e a linha de chegada é igual a d. (a) Qual dos dois barcos chegará ao final da linha com a maior energia cinética? (b) Qual deles atravessa a linha de chegada com o maior momento linear? (c) Qual deles chegará primeiramente

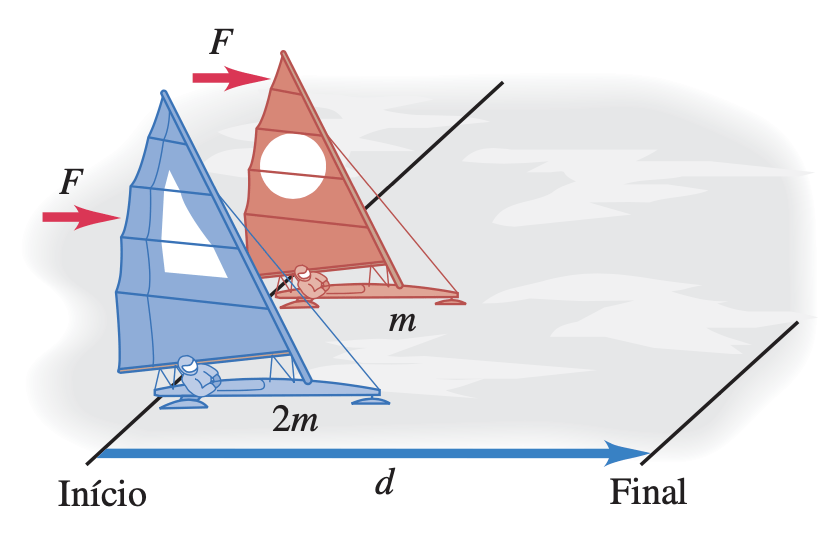
Exemplo 3 (A4.P2-02)

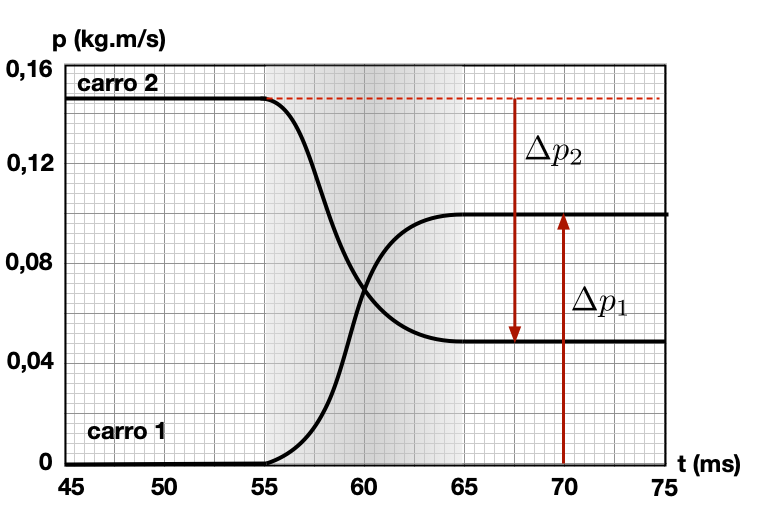
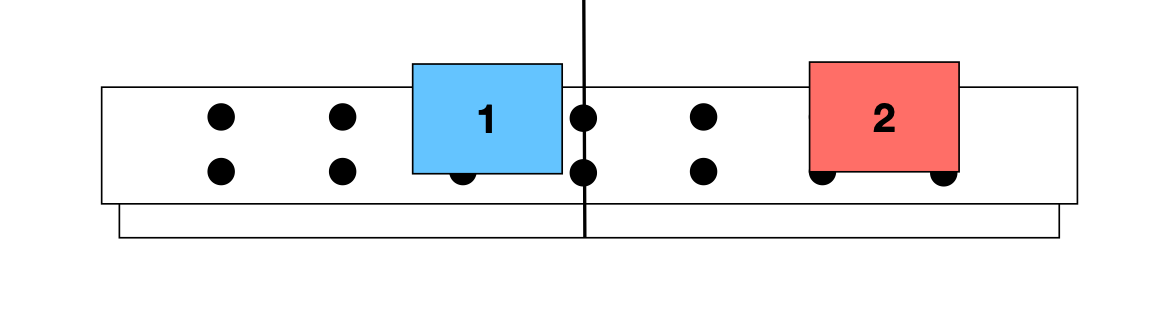
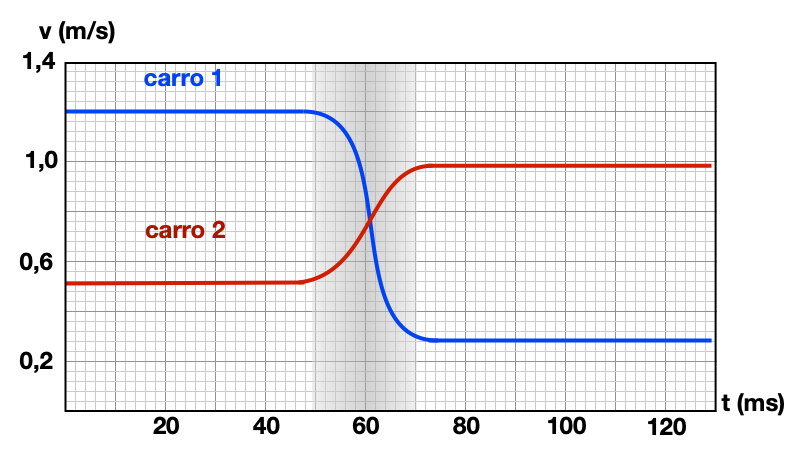
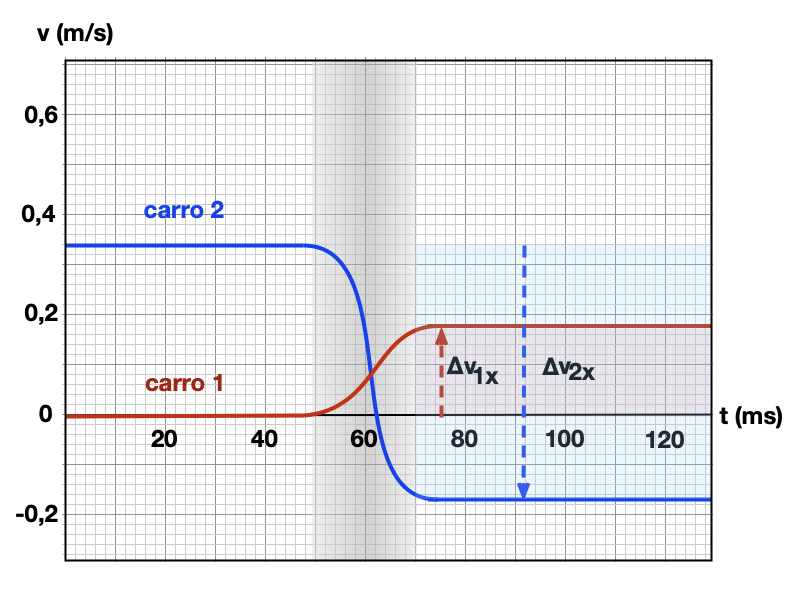
(a) As variações de velocidade na figura são iguais em magnitude? Por que sim ou por que não?

(b) Determine as variações de velocidade dos carrinhos e verifique se \(m_1/m_2 = - \Delta v_2 / \Delta v_1\) nessa figura.

(c) Determine o momento inicial e final dos dois carros.

(d) Qual é o momento do sistema antes da colisão?

(e) Após a colisão? 

(f) As variações de momento são iguais em magnitude e opostas em sentido? Por que sim ou por que não?

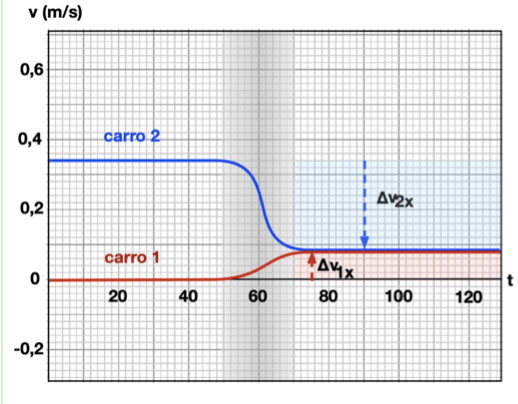
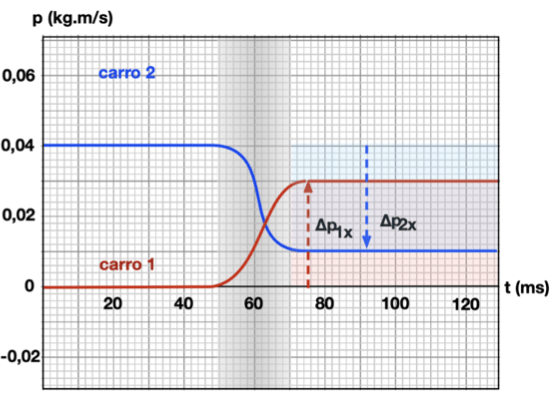
Exemplo 4 (A4.P2-03)

(a) Qual é a magnitude do impulso entregue ao carrinho 1 na figura?

(b) Escreva o impulso entregue ao carrinho 1 em forma de vetor.

(c) O fato de a variação no momento do carrinho 1 ser diferente de zero significa que o momento não é conservado?

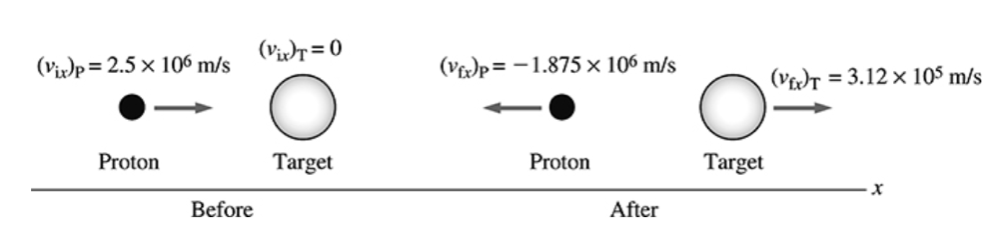
Exemplo 5 (A4.P2-04)

Um próton (massa de 1 u) é lançado contra um núcleo-alvo com velocidade de  \(2,50 \times 10^6\) m/s. O próton ricocheteia com sua velocidade reduzida em 25%, enquanto o núcleo-alvo adquire uma velocidade de \(3,12 \times 10^5\)  m/s. Qual é a massa, em unidades de massa atômica, do núcleo-alvo?

Exemplo 6 (A4.P2-05)

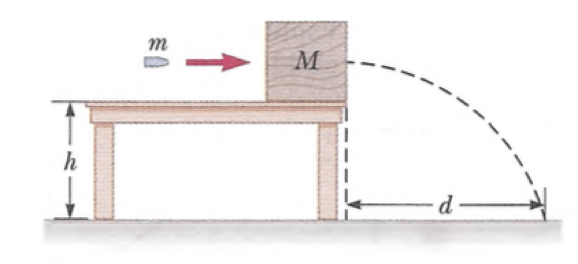
Uma bala de massa m é atirada contra um bloco de massa M inicialmente em repouso na beira de uma mesa sem atrito de altura h. A bala permanece no blo­co, e depois do impacto o bloco aterrissa a uma distância d da parte inferior da mesa. Determine a velocidade escalar inicial da bala.

Exemplo 7 (A4.P2-06)

A força \(F_x(t) = 10 \sin(2\pi t/4,0)\)é exercida durante o intervalo 0 ≤ t ≤ 2,0 s sobre uma partícula de 250 g. Se a partícula parte do repouso, quanto vale sua velocidade em t = 2,0 s?

Exemplo 8 (A4.P2-07)

Em um instante, um trenó de 17,5 kg está se movendo em uma superfície horizontal de neve a 3,50 m/s. Depois de pas­sados 8,75 s, o trenó para. Utilize uma abordagem de mo­mento para encontrar a força de atrito média sobre o trenó enquanto ele estava se movendo. 

Exemplo 9 (A4.P2-08)

Uma partícula de massa m encontra-se em repouso em t = 0.  Para t > 0, seu momento é dado por \(p(t) = 6t^2\), onde t está em s. Determine uma expressão para \(F(t)\), a força exercida sobre a partícula em função do tempo.

Exemplo 10 (A4.P2-10)

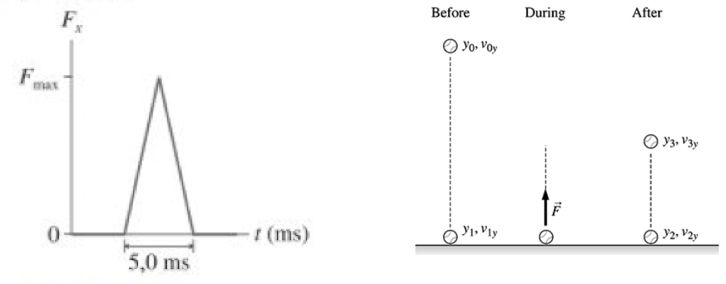
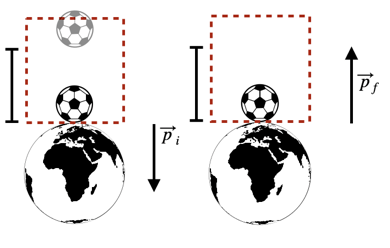
Uma bola de borracha de 0,20 kg é largada de uma altura de 2,0 m sobre um piso duro e salta para cima a uma altura de 1,50 m. A figura mostra o impulso recebido do piso. Qual é a força máxima que o piso exerce sobre a bola?

Exemplo 11 (A4.P2-11)

Testes experimentais mostraram  que o osso será fraturado se estiver sujeito a uma densidade de força de \(1,03 \times 10^8 \) N/m^2. Suponha que uma pessoa de 70 kg esteja andando de patins e sem querer uma viga de metal atinja sua testa e pare completamente seu movimento para a  frente. Se a área de contato com a testa do patinador for de  1,5 cm^2, qual é a maior velocidade com que ele pode atingir  a parede sem quebrar algum osso se sua cabeça estiver em contato com a viga por 10,0 ms?

Exemplo 12 (A4.P2-12)

Uma bola de 0,060 g é atirada diretamente contra uma parede com uma rapidez de 10 m/s. Ela rebate de volta com uma rapidez de 8,0 m/s.

(a) Qual é o impulso exercido sobre a parede?

(b) Se a bola está em contato com a parede por 3,0 ms, qual é a força média exercida sobre a parede pela bola?

(c) A bola rebatida é pegada por uma jogadora que a leva ao repouso. No processo, sua mão se move 0,50 m para trás. Qual é o impulso recebido pela jogadora?

(d) Qual é a força média exercida sobre a jogadora pela bola?

Exemplo 13

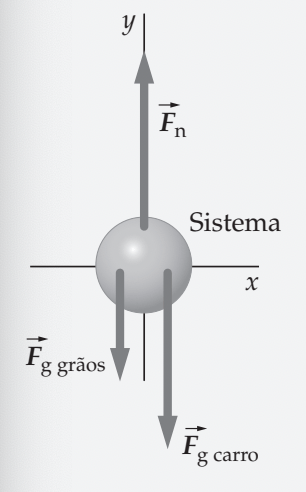
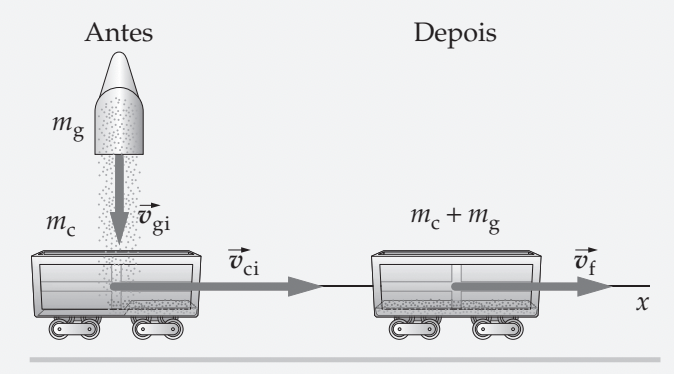
Um vagonete ferroviário de 14000 kg está se dirigindo horizontalmente, a 4,0 m/s, para um pátio de manobras. Ao passar por um silo, 2000 kg de grãos caem subitamente dentro dele. Quanto tempo leva para o carro co-brir a distância de 500 m entre o silo e o pátio de manobras? Suponha que os grãos caíram na vertical e desconsidere o atrito e o arraste do ar. (Tipler. Exemplo 8.2)

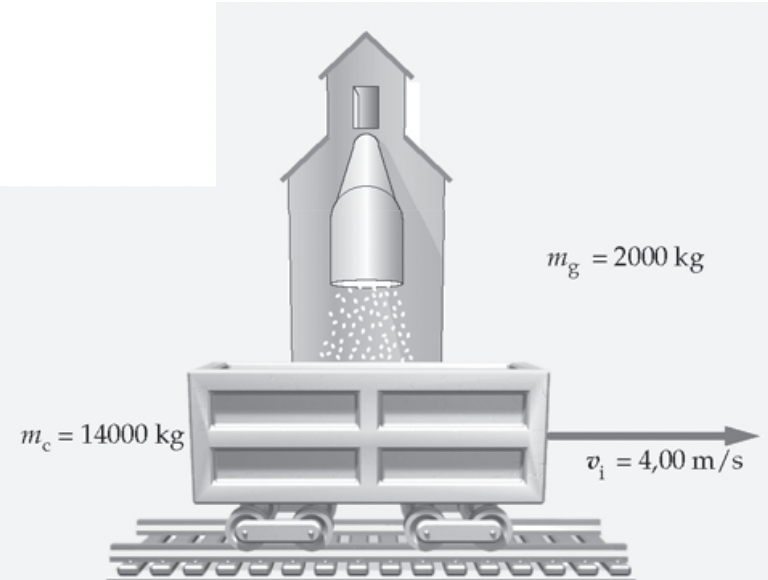
Fonte: Tipler

Não ministrado

Colisões em dimensões 2D e 3D

O espalhamento de Rutherford e o desenvolvimento do modelo do núcleo atômico.

Fonte: https://edisciplinas.usp.br

Fonte: https://phet.colorado.edu

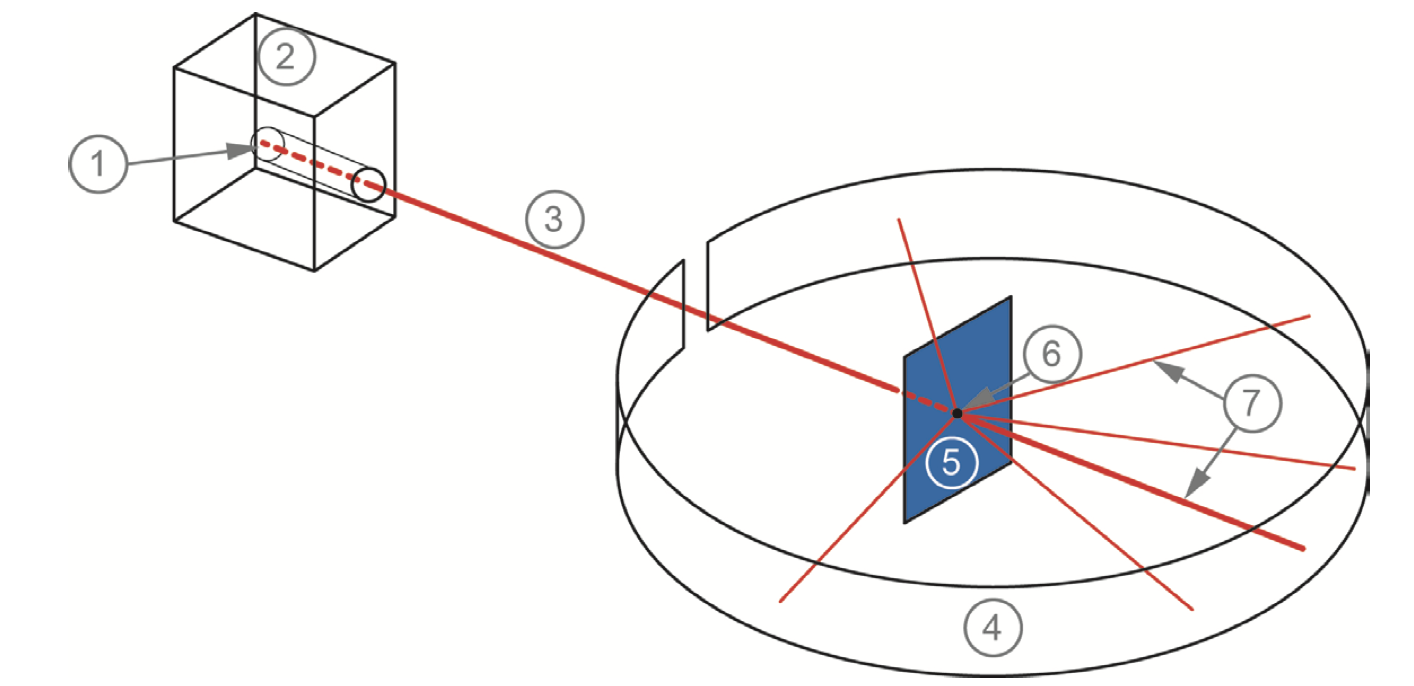
Ernest Rutherford

(1871-1937)

Tevatron do laboratório Fermilab, próximo a Chicago, Illinois, EUA existe um detetor de partículas, o D-Zero

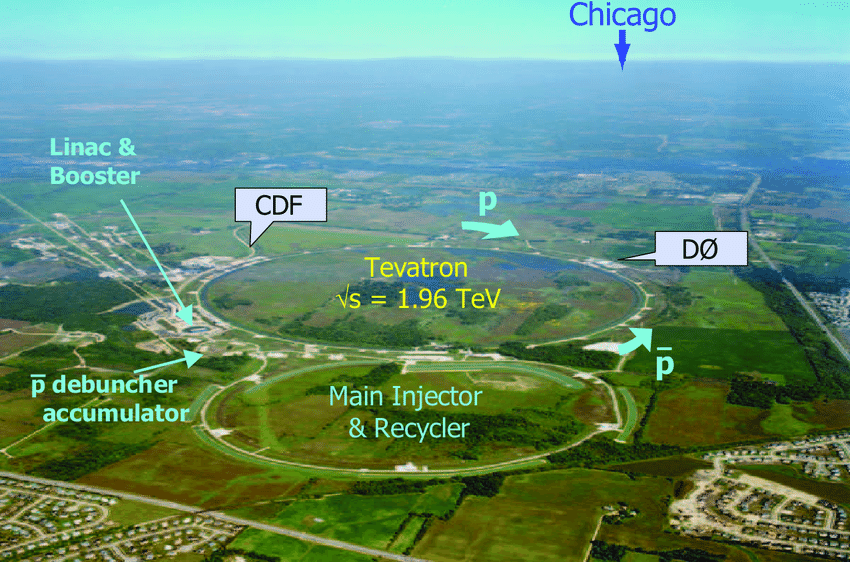
Fermilab

Tevatron

D-zero

Colisões em dimensões 2D e 3D

O Tevatron está configurado de uma forma que os prótons e antiprótons se movem no anel de colisão em sentidos opostos com, para todos os fins práticos, vetores momento exatamente opostos.

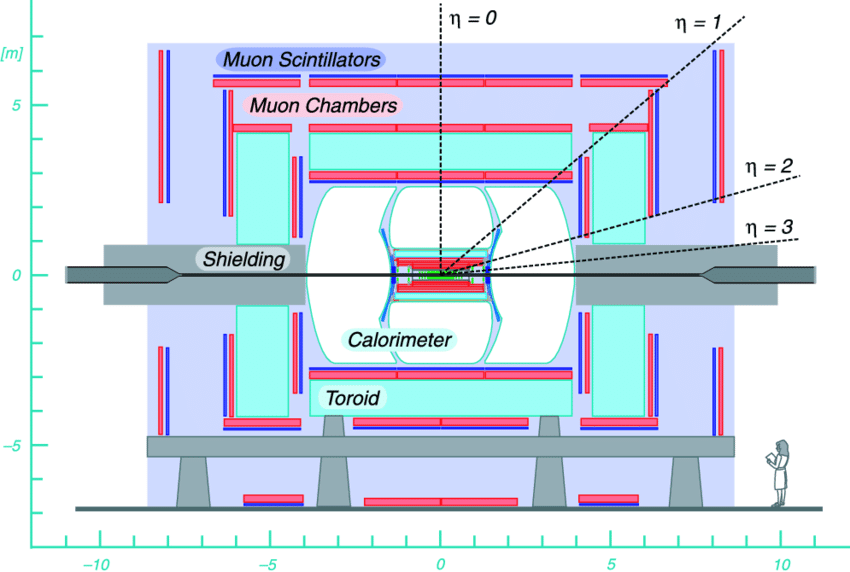
Os engenheiros fizeram colidir prótons e antiprótons com energias totais de 1,96 TeV ( \(=3,1 \times 10^{-7} \) J ).

Colisões em dimensões 2D e 3D

Em uma ma colisão desse tipo o rastros das partículas são geradas por computadores a partir do sinal registrado pelo detector D-Zero.

Fermilab

O vetor momento inicial do próton aponta direto para a página, e o do antipróton aponta direto para fora da página.

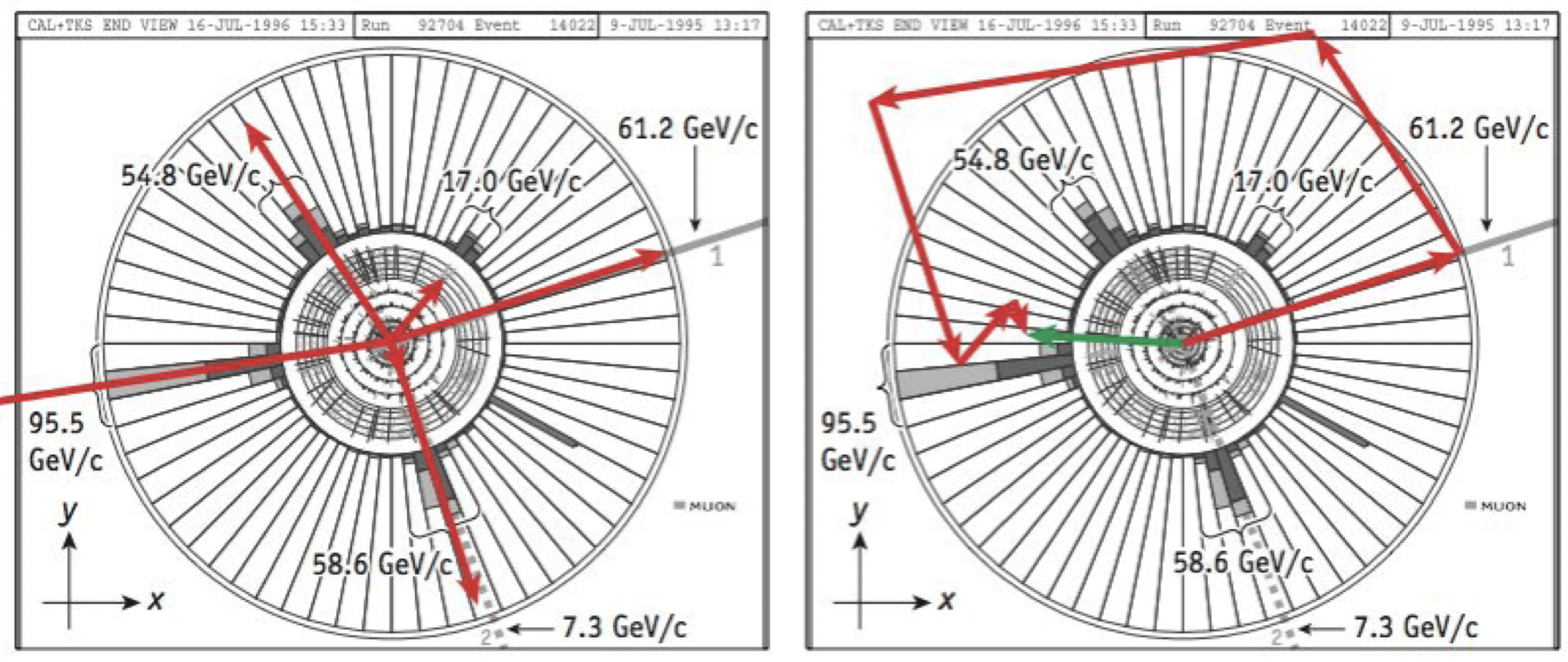
Colisões em dimensões 2D e 3D

Fermilab

O momento inicial total do sistema de prótons e antiprótons é zero.

Uma partícula que escapou sem ser detectada.  

O momento final total do sistema não foi nulo (seta verde).

Os físicos do Fermilab conseguiram demonstrar que o momento perdido, no evento exibido, foi de uma partícula desconhecida – conhecida como quark top.

FERMILAB

Colisões em dimensões 2D e 3D

O momento linear é uma grandeza vetorial.

Ao dizer que o momento linear do sistema é conservado, significa dizer que a direção, sentido e magntiude, antes, durante, após a colisão deve ser o mesmo.

Fonte: https://www.geogebra.org/m/SW4cYT5H

Devemos olhar para as componentes dos momentos lineares.

P_{sis,x,i}=(p_{1x}+p_{2x})_i
P_{sis,y,i}=(p_{1y}+p_{2y})_i
P_{sis,x,f}=(p_{1x}+p_{2x})_f
P_{sis,y,f}=(p_{1y}+p_{2y})_f

Eixo x:

Eixo y:

Colisões em duas dimensões.

Colisões em duas dimensões.

As colisões em duas dimensões ocorrem de forma independente em cada eixo coordenado do plano.

\Delta \vec p_s = 0
\vec p_{s,f} = \vec p_{s,i}
(\vec p_1 +\vec p_2)_f = (\vec p_1 +\vec p_2)_i
\theta_1
\theta_2
\theta_3
\theta_4
\Rightarrow
x
y
\vec p_{1,i}
\vec p_{2,i}
\vec p_{1,f}
\Delta \vec p_1 = -\Delta \vec p_2
\vec p_{1,i}
\vec p_{1,f}
\vec p_{2,f}
\vec p_{2,i}
\vec p_{2,f}
\Delta \vec p_2
\Delta \vec p_1

Devido a conservação do momento linear é possível dizer qual o tipo de partícula e de onde ela veio ao observar os momentos lineares após a colisão. Ou mesmo sabendo para onde ela vai!

Colisões em duas dimensões.

Para colisões no plano ainda podemos aplicar o princípio da independência dos movimentos. Mesmo para o momento linear.

\Delta \vec p = 0
\Delta p_x = \Delta p_{1x} + \Delta p_{2x}= m_1(v_{1x,f}-v_{1x,i})+m_2(v_{2x,f}-v_{2x,i})=0
\Delta p_y = \Delta p_{1y} + \Delta p_{2y}= m_1(v_{1y,f}-v_{1y,i})+m_2(v_{2y,f}-v_{2y,i})=0

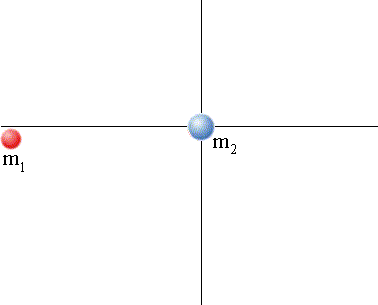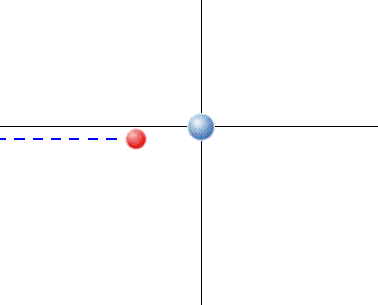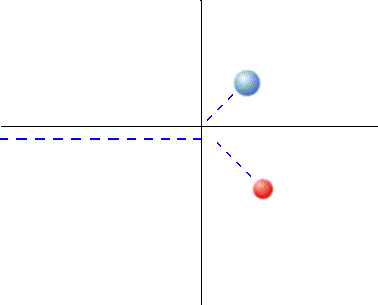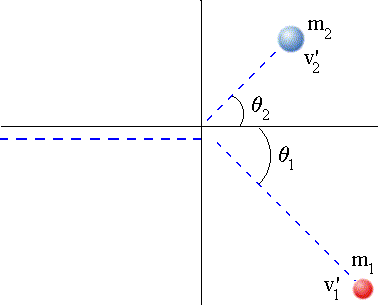
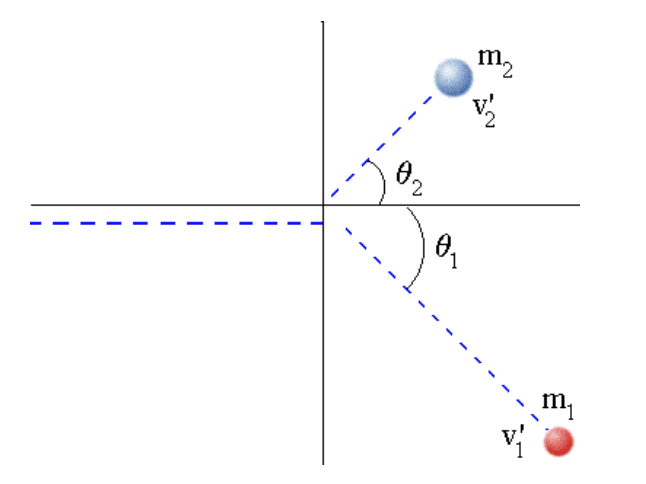
Eixo x:

Eixo y:

Na colisão mostrada:

v_{2x,i}=0
v_{2x,f}=+v_{2,f}\text{cos}\theta_2
v_{2y,f}=+v_{2,f}\text{sen}\theta_2
v_{1x,f}=+v_{1,f}\text{cos}\theta_1
v_{1y,f}=-v_{1,f}\text{sen}\theta_1

Diferentemente das colisões em uma dimensão, não podemos determinar o resultado da colisão sem algumas informações adicionais sobre as velocidades iniciais, finais e os ângulos de espalhamento.

A energia cinética também pode auxiliar

\Delta K_{sis,i}=\Delta K_{sis,f}

Colisões em duas dimensões.

Colisões em uma dimensão são inteiramente descritas por duas equações:

\Delta \vec p = 0
e = \frac{v_{12,f}}{v_{12,i}}

Conservação do momento linear do sistema em um sistema isolado

Coeficiente de restituição (próxima aula).

Em uma dimensão, as colisões são frontais. Permanecem na mesma reta.

Fonte: https://youtu.be/gVM7wGmhmV8

Em duas dimensões, as colisões que não são frontais não permanecem na mesma reta.

Exemplo 14

Os discos 1 e 2 deslizam no gelo e colidem. A inércia do disco 2 é duas vezes a do disco 1. O disco 1 se move inicialmente a 1,8 m/s; o disco 2 se move inicialmente a 0,20 m/s em uma direção que faz um ângulo de 45° com a direção do disco 1. Após a colisão, o disco 1 se move a 0,80 m/s em uma direção que faz um ângulo de 60° com sua direção original. Qual é a velocidade e a direção do disco 2 após a colisão

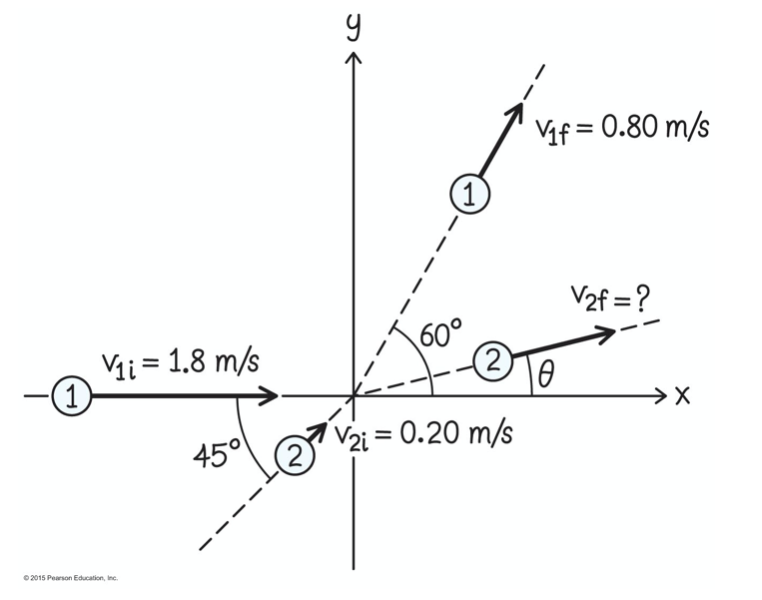
A colisão é elástica?

Fonte: Mazur

Exemplo 15

Uma mola (k = 3800 N/m) é comprimida entre dois blocos: bloco 1 de inércia 1,40 kg e bloco 2 de inércia 2,00 kg. A combinação é mantida unida por um fio (não mostrado na Figura). A combinação desliza sem girar no gelo de baixa fricção a 2,90 m/s quando de repente a corda se quebra, permitindo que a mola se expanda e os blocos se separem. Posteriormente, o bloco de 2,00 kg é observado movendo-se a um ângulo de 34,0° em relação à sua linha inicial de movimento a uma velocidade de 3,50 m/s, enquanto o bloco menor se move a uma velocidade e ângulo desconhecidos. Nenhum dos blocos gira após a separação, e você pode ignorar as inércias da mola e da corda em relação às dos blocos. (a) Determine a velocidade do bloco 1 após a separação. (b) Determine a compressão original da mola, \(x-x_0\), a partir de seu comprimento relaxado. M10.63

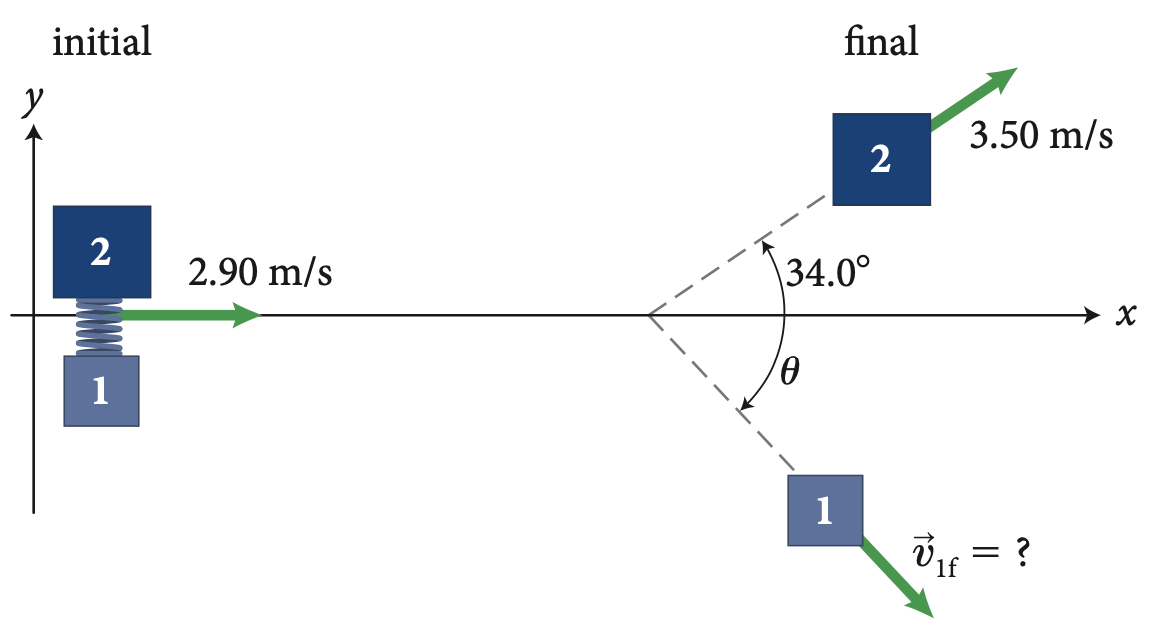
Fonte: Mazur

Exemplo 16

O disco P (inércia 0,40 kg) move-se a uma velocidade desconhecida através de uma superfície horizontal de baixa fricção e colide com o disco Q (inércia 0,70 kg), que está inicialmente em repouso. Após a colisão, os dois discos (agora ligeiramente amassados) se separam sem girar. As informações de velocidade são fornecidas nos diagramas de vista superior inicial e final (Figura 10.64). (a) Qual foi a velocidade inicial do disco P? (b) Qual fração da energia cinética inicial é convertida durante a colisão? M10.64

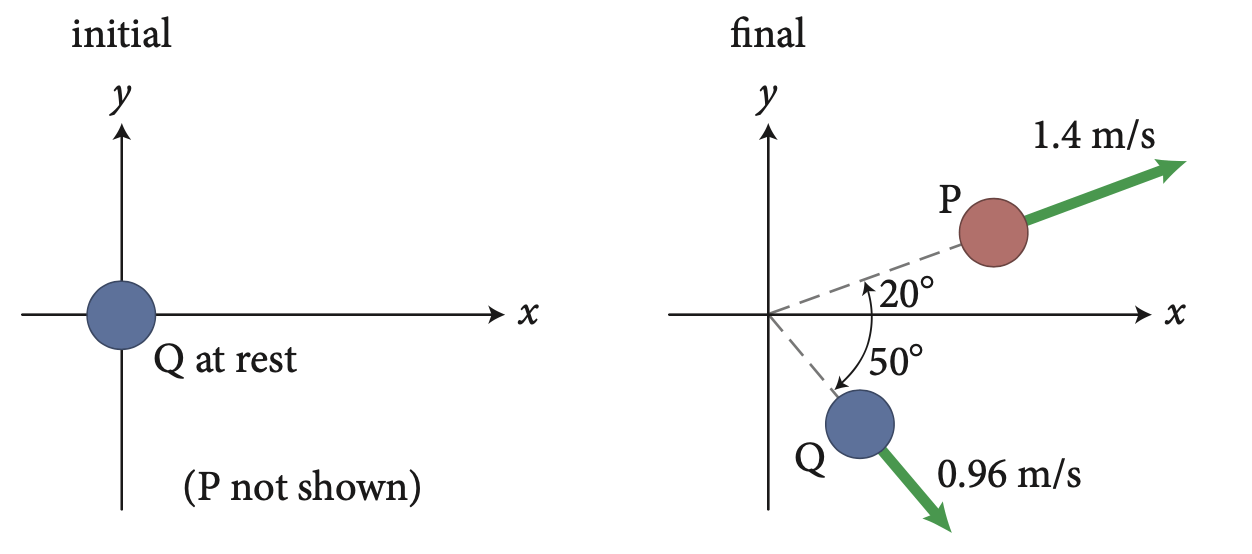
Fonte: Mazur

Made with Slides.com