Aula 21

Fundamentos de Mecânica

Prof. Ronai Lisbôa

UFRN - ECT - BCT

Objetivos

Explicar o Movimento Harmônico Simples Amortecido.

Ao final dessa aula você deve se capaz de:

Bibliografia

Tipler

Capítulo 14

Seção: 14.4

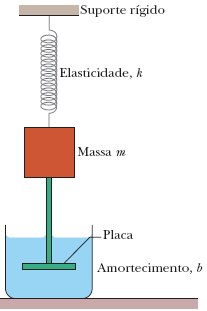
Analisar o balanço de energia no amortecimento subcrítico.

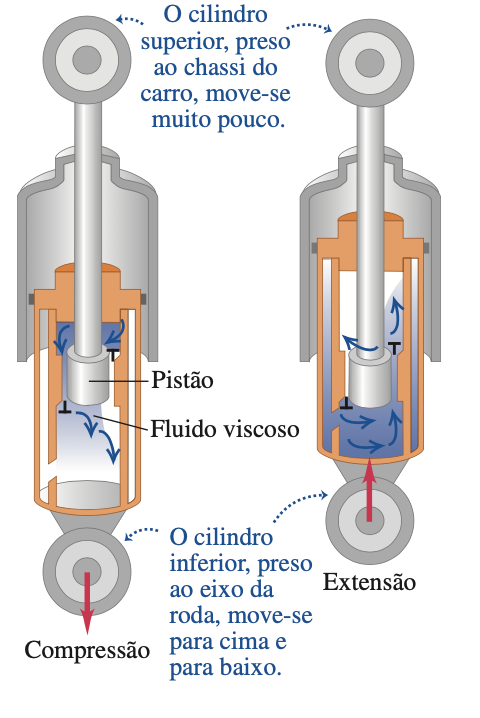
Fonte: Halliday & Resnick

Fonte: Sears & Zemansky

Identificar os três regimes de amortecimento:

Crítico

Supercrítico

Subcrítico

Analisar o fator de qualidade do amortecimento subcrítico.

Video aulas: USP, UNICAMP, UFF

(links sigaa)

Motivação

Prédios oscilam

Amplitude máxima:

Período do evento:

A = \pm 1\text{ m}

T = 5\text{ min}

Fonte: https://www.youtube.com/embed/UMLCrbGKM5M

Motivação

O Edifício Comcast na Filadélfia, Pensilvânia, que se ergue acima do horizonte, tem aproximadamente 305 metros de altura. Nessa altura, os andares superiores podem oscilar para frente e para trás devido à atividade sísmica e aos ventos flutuantes. Em Taiwan, o edifício Taipei se utiliza de uma esfera para controlar a oscilação.

Fonte: https://query.libretexts.org/

É mostrado acima um desenho esquemático de um amortecedor de massa de coluna líquida ajustado, instalado na parte superior da Comcast, consistindo em um reservatório de água de 300.000 galões para reduzir as oscilações.

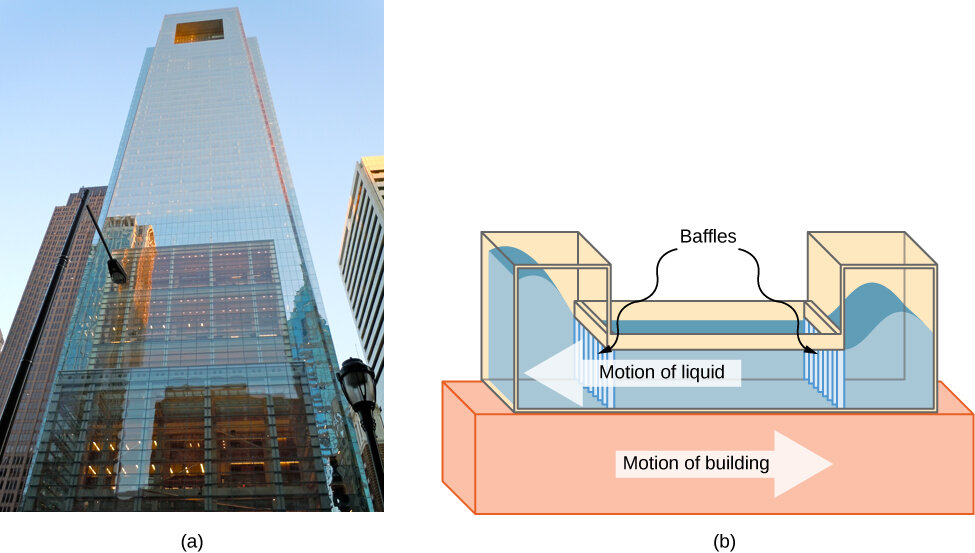
Fonte: https://youtu.be/k51nFin7Wzc?si=uBuf2WSiZybh0EaF

Motivação

Propriedades atômicas são utilizadas para medir o tempo com grande precisão.

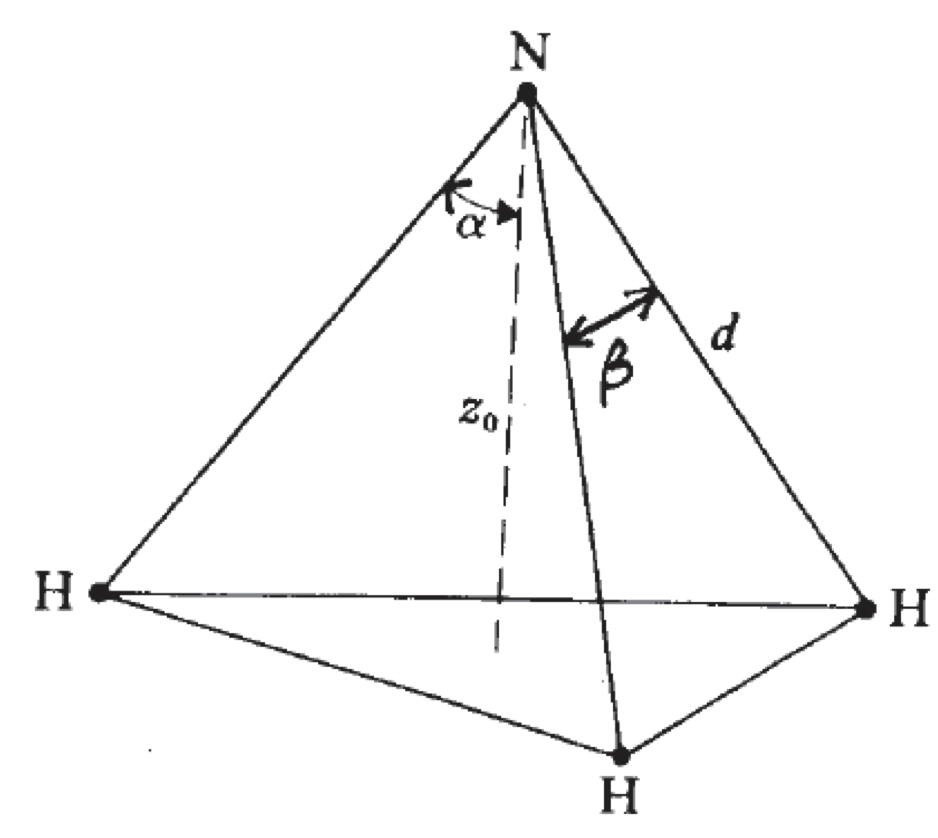
Fonte: https://repositorio.unesp.br

A molécula de amônia \(\text{NH}_3\) tem uma estrutura piramidal, com três átomos de H na base e um átomo de N no vértice.

Existe uma posição simétrica, N', do átomo de nitrogênio que se encontra à mesma distância do plano H-H-H, mas no lado oposto (não mostrado).

O átomo de N oscila entre estas duas posições de equilíbrio na razão de \(2,387 013 \times 10^{16}\) oscilações por segundo.

O primeiro relógio atômico foi baseado nesse princípio.

Em um período de 17 000 000 de anos, pode se desviar de apenas 1 segundo.

Motivação

Plataformas programáveis possuem osciladores de quartzo que definem a frequência de operação dos microcontroladores das placas e por sua vez da frequência do processamento dos dados dos programas.

Fonte: arduino.com

Nessas placas a frequência de operação está em 16 MHz.

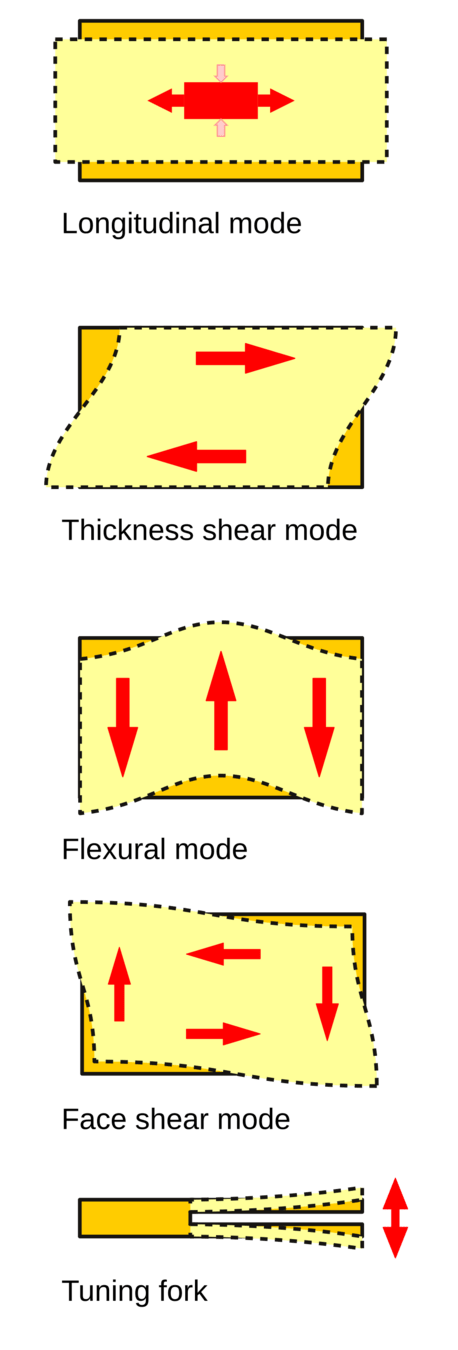
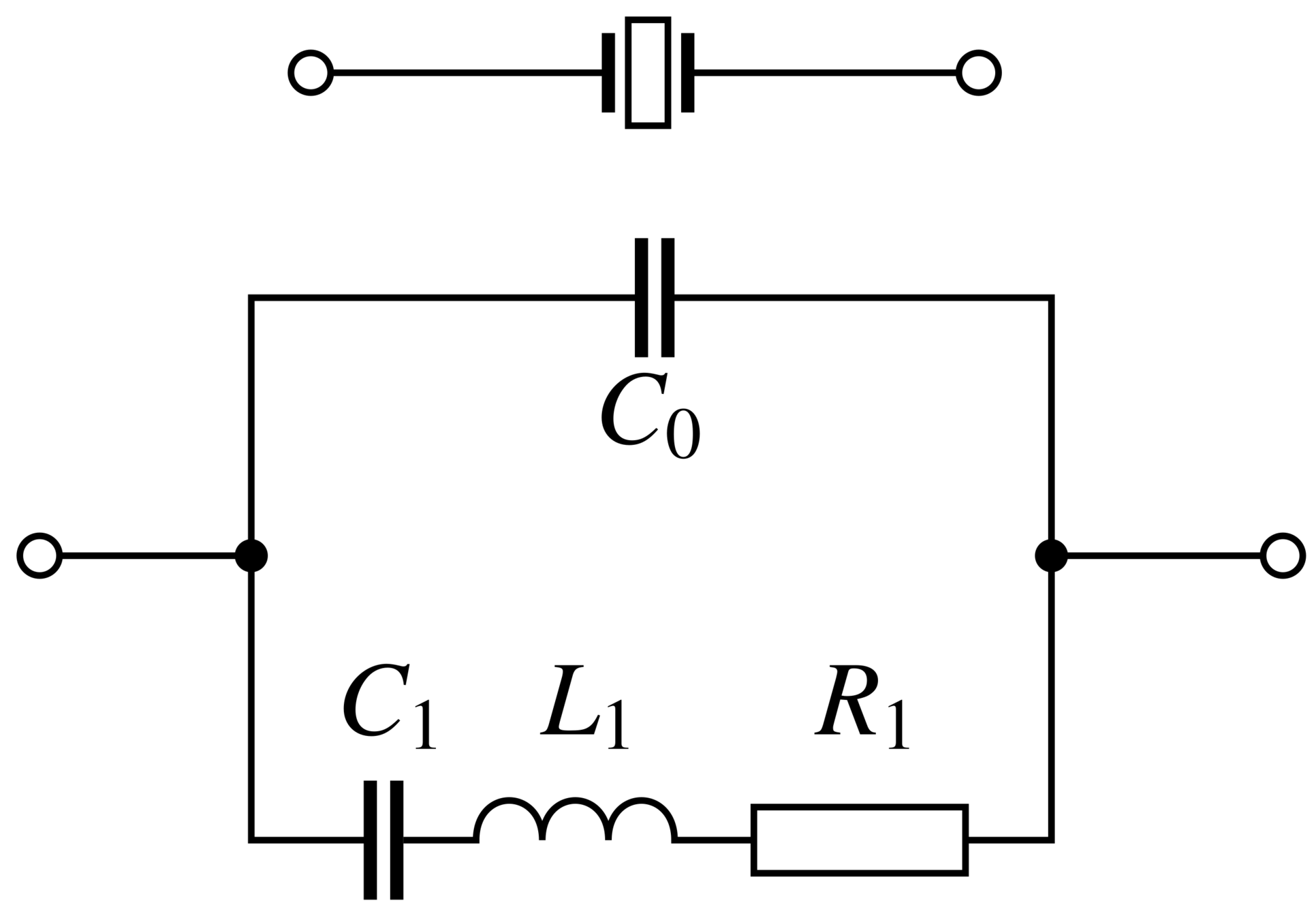
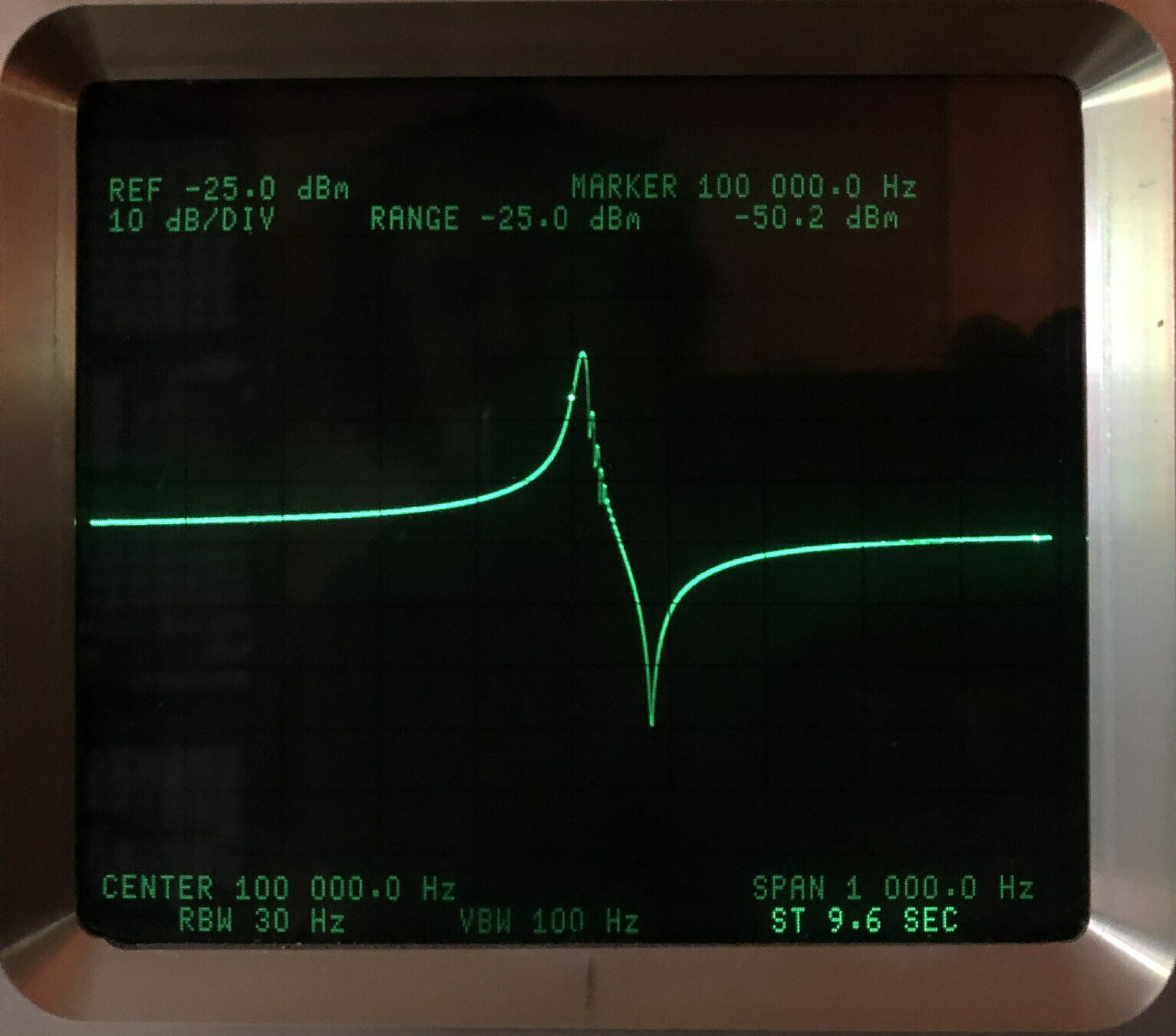
Para desenvolver tal tecnologia, começa-se a estudar as oscilações mecânicas e depois eletromagnéticas.

Oscilações Harmônicas Amortecidas

Nos osciladores harmônicos (molas e pêndulos):

A força é restauradora (e conservativa):

A energia mecânica total é conservada (Aula 20):

F=-kx

E=\frac{1}{2}kA^2=\frac{1}{2}m\omega_0^2A^2

Mas as molas e pêndulos não oscilam indefinidamente: após algum intervalo de tempo, eles atingem o repouso porque existe uma força resistiva cujo efeito é diminuir a velocidade do oscilador.

Fonte: Wikipedia.

Se a amplitude não muda, a energia mecânica não muda!

Não é rigorosamente correto descrever as oscilações livres matematicamente por uma função periódica no tempo com amplitude constante.

O oscilador harmônico livre uma vez colocado em movimento, oscilará eternamente sem nenhuma diminuição da amplitude.

A partir de agora, para melhorar a modelagem de um sistema que oscila como oscilador harmônico, vamos incorporar ao modelo:

As forças viscosas (dissipativas):

São forças de atrito exercidas por fluidos (ar, água, óleo, etc.)...

que são forças não conservativas.

Fonte: https://www.youtube.com/embed/h_JOS7ldl48

==> A energia mecânica não é conservada no tempo.

==> A amplitude da oscilação diminui com o tempo.

Existem três tipos de amortecimento.

Oscilações Harmônicas Amortecidas

Na presença de forças viscosas a energia mecânica não é conservada.

O oscilador harmônico uma vez colocado em movimento deixará de oscilar e vemos isso como uma diminuição da amplitude à medida que o tempo avança.

A diminuição da amplitude provocada por uma força dissipativa é chamada de amortecimento e o movimento correspondente denomina-se oscilação amortecida.

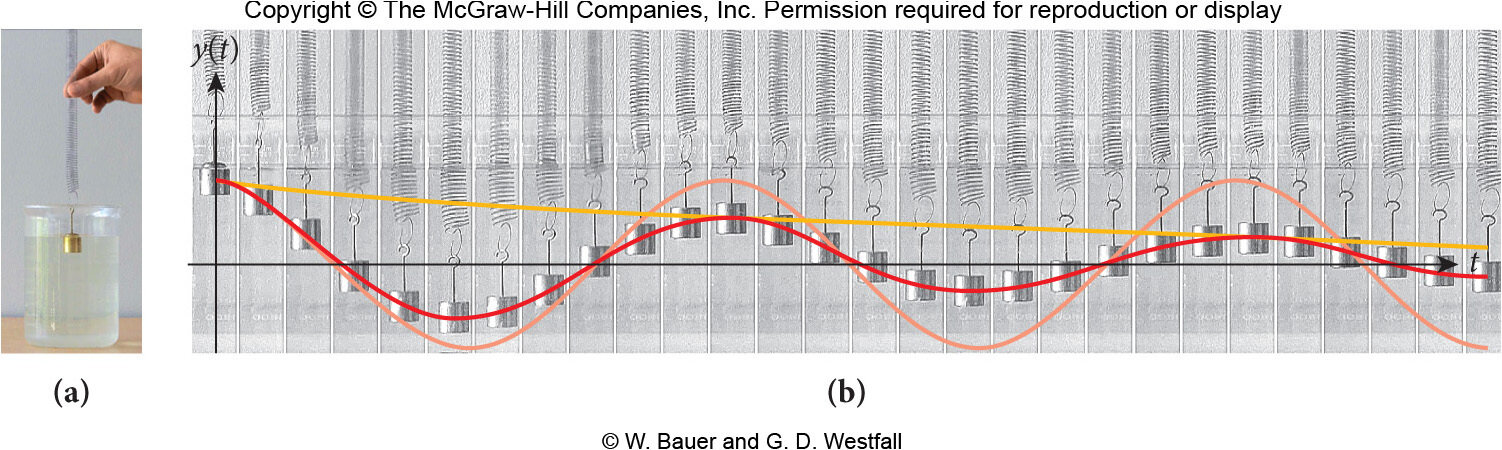
Fonte: Wolfgang & Bauer

Oscilações Harmônicas Amortecidas

Amplitude do oscilador diminui quando está dentro do fluido

Amplitude do oscilador permanece quanto está fora do fluido

As forças viscosas são opostas à velocidade do corpo que se move num fluido.

Em alguns casos, matematicamente, se escreve como:

Os parâmetros \((b,c)\) dependem da geometria e da rapidez do corpo e também da natureza do fluido.

F_a=-b\,v-cv^2

Fonte: https://youtu.be/XX0JdlXZmWs

O sinal negativo indica que a força possui sempre um sentido contrário ao da velocidade.

Para baixas velocidades do oscilador, a força de arrasto tem a forma,

F_a\approx-b\,v

A constante de amortecimento \(b\) tem dimensão de massa/tempo.

Oscilações Harmônicas Amortecidas

Você sabe mostrar isto?

\frac{\text{kg}}{\text{s}}

Para o oscilador harmônico simples do tipo massa-mola com amortecimento, a equação de movimento supondo que a massa está subindo e que a força elástica seja maior que de arrasto:

\sum \vec F = m\vec a

\vec F_a+\vec F_e = m\vec a

-bv - kx = ma

ma + bv + kx = 0

m\frac{d^2x}{dt^2} + b\frac{dx}{dt} + kx = 0

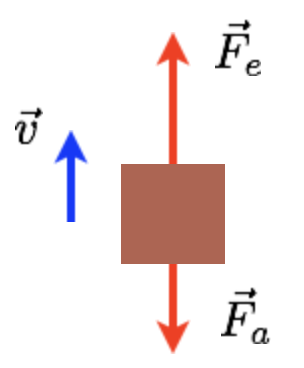
Fonte: Halliday & Resnick

Oscilações Harmônicas Amortecidas

\frac{d^2x}{dt^2} + \gamma\frac{dx}{dt} + \omega_0^2x = 0

Obtemos uma EDO de segunda ordem com um termo devido ao arraste, para a função posição:

\gamma = \frac{b}{m}

\omega_0^2 = \frac{k}{m}

frequência angular natural

fator de amortecimento

Qual é a função que satisfaz a EDO?

Dimensão

\frac{1}{tempo}

A equação de movimento de um sistema massa-mola amortecido é uma EDO,

\frac{d^2x}{dt^2} + \gamma\frac{dx}{dt} + \omega_0^2x = 0

\gamma = \frac{b}{m}=\frac{1}{tempo}

\omega_0 = \sqrt{\frac{k}{m}}=\frac{1}{tempo}

A função deve considerar que a amplitude varia exponencialmente com o tempo:

x(t)=Ae^{pt}

Oscilações Harmônicas Amortecidas

Devemos substituí-las na EDO:

(p^2Ae^{pt}+\gamma\, pAe^{pt}+\omega_0^2Ae^{pt})=0

(p^2+\gamma\, p+\omega_0^2)Ae^{pt}=0

Devemos testá-la:

1a. derivada:

\frac{dx}{dt}=pAe^{pt}

2a. derivada:

\frac{d^2x}{dt^2}=p^2Ae^{pt}

Para \(x(t)\) não nulo, a igualdade será zero se e somente se:

(p^2+\gamma\, p+\omega_0^2)=0

equação do segundo grau em \(p\).

É necessário resolver uma equação do segundo grau na variável \(p\):

As raízes da equação são (Bhaskara):

p^2+\gamma\, p+\omega_0^2=0

p_{\pm}=-\frac{\gamma}{2}\pm \sqrt{\left( \frac{\gamma}{2} \right)^2-\omega_0^2}

\Rightarrow p_{\pm}=-\frac{\gamma}{2}\pm \omega^{\prime}

\omega^{\prime} =\sqrt{\left( \frac{\gamma}{2} \right)^2-\omega_0^2}

Oscilações Harmônicas Amortecidas

Essas frequências angulares são diferentes

Supercrítico:

\omega ' > 0

Raiz positiva =>

\frac{\gamma}{2} >\omega_0

\Rightarrow b>b_c

Subcrítico:

\omega ' < 0

Raiz complexa =>

\frac{\gamma}{2} <\omega_0

\Rightarrow b< b_c

\(\omega_0\) - freq. natural

\(\omega'\) - freq. de amortecimento

\(\gamma\) - fator de amortecimento

\omega^{\prime} =\sqrt{\frac{1}{4m^2}( {b} ^2-4m{k}})

O comportamento de \(x(t)\) vai depender da frequência de amortecimento, \(\omega '\) ou da relação entre os fatores (\(\gamma,\omega_0\)).

Crítico:

\omega ' = 0

Raiz nula =>

\frac{\gamma}{2} =\omega_0

\Rightarrow b_c = \sqrt{4mk}

A frequência que interessa é:

É necessário resolver uma equação do segundo grau na variável \(p\):

As raízes da equação são (Bhaskara):

p^2+\gamma\, p+\omega_0^2=0

p_{\pm}=-\frac{\gamma}{2}\pm \sqrt{\left( \frac{\gamma}{2} \right)^2-\omega_0^2}

\Rightarrow p_{\pm}=-\frac{\gamma}{2}\pm \omega^{\prime}

\omega^{\prime} =\sqrt{\left( \frac{\gamma}{2} \right)^2-\omega_0^2}

onde

Oscilações Harmônicas Amortecidas

Essas frequências angulares são diferentes

Supercrítico:

\omega ' > 0

Raiz positiva =>

\frac{\gamma}{2} >\omega_0

\Rightarrow b>b_c

Subcrítico:

\omega ' < 0

Raiz complexa =>

\frac{\gamma}{2} <\omega_0

\Rightarrow b< b_c

\(\omega_0\) - freq. natural

\(\omega'\) - freq. de amortecimento

\(\gamma\) - fator de amortecimento

\omega^{\prime} =\sqrt{\frac{1}{4m^2}( {b} ^2-4m{k}})

x(t)= A_+e^{+pt}+ A_-e^{-pt}

As soluções serão uma combinação linear das raízes:

x(t)=e^{-\gamma/2}( A_+e^{+\omega´ t}+ A_-e^{-\omega´ t})

O comportamento de \(x(t)\) vai depender da frequência de amortecimento, \(\omega '\) ou da relação entre os fatores (\(\gamma,\omega_0\)).

Crítico:

\omega ' = 0

Raiz nula =>

\frac{\gamma}{2} =\omega_0

b= b_c = \sqrt{4mk}

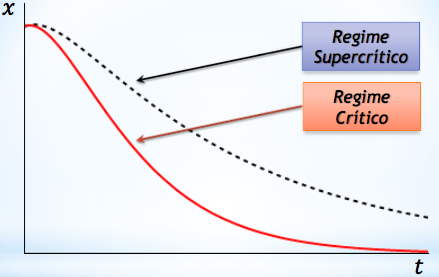
Não há oscilações nos regimes crítico e supercrítico. O sistema vai mais rapidamente para o equilíbrio no regime crítico que no supercrítico.

O oscilador tem período constante, mas a amplitude da oscilação decai exponencialmente com o tempo (modulada pela envoltória).

Fonte: Prof. Tarciro Mendes

Fonte: Prof. Tarciro Mendes

Período amortecido

Envoltória

Oscilações Harmônicas Amortecidas

\omega' > 0

\omega' = 0

\omega' < 0

+Ae^{-(\gamma/2)t}

-Ae^{-(\gamma/2)t}

\Rightarrow b>b_c

\Rightarrow b_c = \sqrt{4mk}

\omega ' < 0

\Rightarrow b< b_c

\omega^{\prime} =\sqrt{\frac{1}{4m^2}( {b} ^2-4m{k}})

\Rightarrow b\geq b_c

\Rightarrow b< b_c =\sqrt{4mk}

\omega^{\prime} =\sqrt{\frac{1}{4m^2}( {b} ^2-4m{k}})

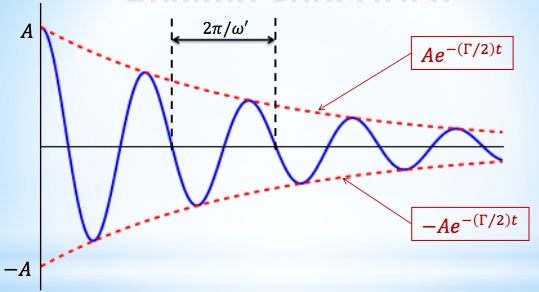
Oscilações Amortecidas. Regime subcrítico.

O fator de amortecimento é menor que a frequência natural:

\omega^{\prime} = \sqrt{\left( \frac{b}{2m}-\frac{k}{m} \right)^2} = \pm i \sqrt{\left( \frac{k}{m} \right)^2 -\frac{b}{2m}}

\Rightarrow b< b_c =\sqrt{4mk}

Fonte: https://www.geogebra.org/m/ZzKbkvnz

A amplitude decai exponencialmente no tempo, e com oscilação devido ao número complexo \(i\):

x(t) = Ae^{-\frac{\gamma}{2}t} \cos(\omega 't+\delta)

x(t) = e^{-\frac{\gamma}{2}t}[ A_+ e^{+i\,\omega ' t}+ A_- e^{-i\,\omega ' t}]

Mostre que se \(x(0)=x_0\) e \(v(0)=v_0\), temos:

A_+ =x_0

A_- = \frac{v_0 +x_0\frac{\gamma}{2}}{ \sqrt{\omega_0^2 -(\gamma/2)^2} }

Mostre isso. Apresente para mim e ganhe bônus. Desafie-se!

Condições iniciais

Simule:

\(x_0 = 10\) cm

\(v_0 = 0\) cm/s

\(m = 1,0\) kg

\(k = 4,0\) N/m

\(b = 2\) kg/s

Calcule: \(b_c; \gamma/2,\omega_0; A_+;A_-\).

ATENÇÃO: \(c\equiv b ; y(0)=x_0\)

Oscilações Amortecidas. Balanço da energia.

As energias cinética e potencial no MHS-livre variam no tempo:

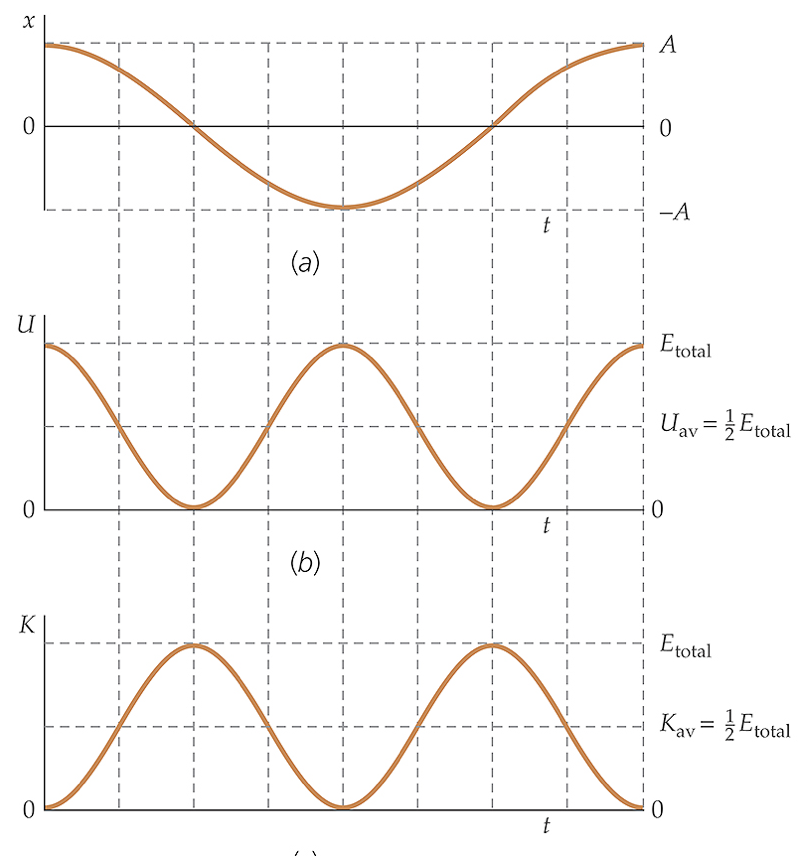
K(t)=\frac{1}{2}mv^2=\frac{1}{2}m\omega_0^2A^2\text{sen}(\omega_0 t+\delta)

U(t)=\frac{1}{2}m\omega_0^2x^2=\frac{1}{2}m\omega_0^2A^2\text{cos}(\omega_0 t+\delta)

Fonte: Halliday & Resnick

Integre essas funções no SYMPY e mostre que os resultados são os valores médios das energias apresentados. Lembre-se que \(T=2\pi/\omega_0\). Apresente seu resultado e ganhe bônus.

Simulador: https://www.geogebra.org/m/jwq5gucu

A energia mecânica no MHS é uma constante no tempo, a potência é nula:

E = \frac{1}{2}m\omega_0^2A^2

P=\frac{dE}{dt} = 0

\Rightarrow

Os valores médios dessas energias em uma oscilação, são:

\overline{K(t)} \equiv \frac{1}{T}\int_0^T K(t) dt = \frac{1}{4}m\omega_0^2A^2

\overline{U(t)} \equiv \frac{1}{T}\int_0^T U(t) dt = \frac{1}{4}m\omega_0^2A^2

\Rightarrow \overline{K(t)}=\frac{1}{2}E

\Rightarrow \overline{U(t)}=\frac{1}{2}E

Em um período \(T\) a energia é intercambiada entre cinética e potencial.

Oscilações Amortecidas. Balanço da energia.

P=\frac{dE}{dt} = \vec F_v\cdot \vec v=-b\,\vec v\cdot \vec v=-bv^2

No MHS amortecido, a energia mecânica decresce no tempo porque a força do amortecimento realiza trabalho (negativo) sobre o sistema.

v=\frac{dx}{dt}

onde

A potência dissipada é:

A potência média dissipada pelo oscilador não é nula e para cada ciclo (período):

O membro direito da equação é negativo sempre que o corpo oscilante estiver em movimento, independentemente de a velocidade \(v\) ser positiva ou negativa. Essa dissipação é máxima quando o oscilador passa pela posição de equilíbrio (\(v=v_{max}\)). Nos pontos de retorno (\(v=0)\) não há dissipação de energia.

\overline{P}=\overline{\frac{dE}{dt}} =-b\overline{v^2}=-b\frac{\overline{E}}{m}

\Rightarrow \frac{\overline{dE}}{\overline{E}}=-\frac{b}{m}dt

\overline{K(t)}=\frac{1}{2}E

\frac{1}{2}m\overline{v^2}=\frac{1}{2}E

\overline{v^2}=\frac{\overline{E}}{m}

\Rightarrow \int_{E_0}^{E}\frac{\overline{dE}}{\overline{E}}=\int_0^t-\frac{b}{m}dt

Integrando, vemos que a energia mecânica diminui exponencialmente no tempo:

onde

E_0=\frac{1}{2}m\omega_0^2A^2

E(t)=E_0 e^{-\frac{b}{m}\,t}

Oscilações Amortecidas. Balanço da energia.

Para o oscilador harmônico fracamente amortecido a energia cai exponencialmente com um tempo característico ou constante de tempo (\(\tau\)). Para fins práticos é o tempo de vida da oscilação - o quanto ela dura.

onde

E(t)=E_0 e^{-{\gamma}\,t}

\tau = \frac{1}{\gamma}=\frac{m}{b}

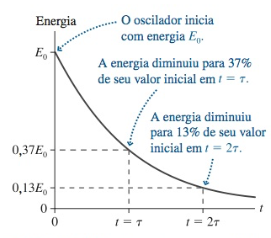
Fonte: Randall Knight

O tempo característico de decaimento da amplitude é o dobro do tempo característico de decaimento da energia.

x(t) = A(t) \cos(\omega 't-\delta)

A(t)=Ae^{-\frac{\gamma}{2}\,t}

onde

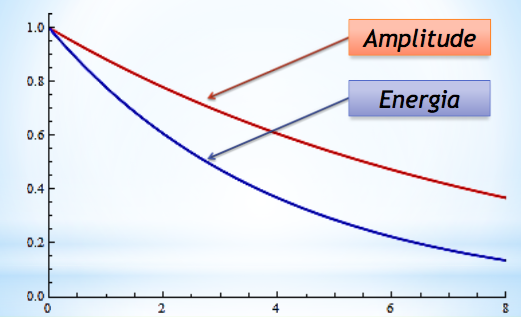
O fator \(\gamma\) é o recíproco do tempo necessário para a energia diminuir \(1/e\) do seu valor inicial.

Quanto tempo leva para a amplitude diminuir?

Para \(t=2/\gamma\) a amplitude de oscilação cai por um fator \(1/e \approx 37\%\)

Fonte: Prof. Tarciro Nortarson

Oscilações Amortecidas. Balanço da energia.

As aplicações práticas exigem a avaliação da qualidade do oscilador pelo assim chamado fator de qualidade, \(Q\) do oscilador:

E(t)=E_0 e^{-\frac{1}{\tau}\,t}

\Rightarrow \frac{dE}{dt} =-\frac{E}{\tau}

\Rightarrow \frac{dE}{E} =-\frac{dt}{\tau}

\left(\frac{|\Delta E|}{E} \right)_{ciclo}=\frac{T}{\tau}

\left(\frac{|\Delta E|}{E} \right)_{ciclo}=\frac{2\pi}{\omega_0\tau}

Q=\omega_0\tau=\frac{\omega_0}{\gamma}

\Rightarrow \frac{T}{\tau} =\frac{2\pi}{Q}

onde

O fator de qualidade (\(Q\)) é inversamente proporcional à dissipação relativa da energia por ciclo:

Q=\frac{2\pi}{|\Delta E|/E}=\omega_0\tau=\frac{\omega_0}{\gamma}

Quanto maior Q melhor é o oscilador (\(\gamma\) é grande!)

Para um período:

Sound Cars e Sound Cars

\tau = \frac{1}{\gamma}=\frac{m}{b}

Oscilações Amortecidas. Balanço da energia.

O fator de qualidade (\(Q\)) é um número que é grande comparado à unidade para sistemas oscilatórios com pequenas taxas de dissipação de energia.

\omega^{\prime} =\sqrt{\omega_0^2-\left( \frac{\gamma}{2} \right)^2} = \sqrt{\omega_0^2-\left( \frac{\omega_0}{2Q} \right)^2} =\omega_0\sqrt{1- \frac{1}{4Q^2} }

Se (\(Q\)) é grande comparado a unidade obtemos que \(\omega ' \approx \omega_0\). Para amortecimento fraco (\(\gamma \rightarrow 0\)):

x(t) = Ae^{-\frac{\gamma}{2}\,t} \cos(\omega 't-\delta) \approx Ae^{-\frac{\omega_0}{2Q}\,t} \cos(\omega_0t-\delta)

A(t) = Ae^{-\frac{\omega_0}{2Q}\,t}

O fator (\(Q\)) está relacionado ao número de ciclos da oscilação sobre a qual a amplitude da oscilação diminui por um fator \(1/e\).

Para \(n\) oscilações, \(t = nT = 2\pi n/\omega_0\) e:

A(n) = Ae^{-\frac{n\pi}{Q}}

Para \(n=Q/\pi\) a amplitude de oscilação cai por um fator \(1/e \approx 37\%\)

Quantas oscilações leva para a amplitude diminuir?

O que ocorre com a amplitude se \(Q\rightarrow \infty\)?

Q=\omega_0\tau=\frac{\omega_0}{\gamma}

Oscilações Amortecidas. Regime crítico.

O fator de amortecimento assume um valor mínimo para impedir a oscilação:

x(t) = e^{-\frac{\gamma}{2}t} \left( A_+ + A_- \,t \right)

Mostre que se \(x(0)=x_0\) e \(v(0)=v_0\), temos:

\omega^{\prime} =\sqrt{\left( \frac{\gamma}{2} \right)^2-\omega_0^2} = \sqrt{\left( \frac{b}{2m} \right)^2-\frac{k}{m}}

\Rightarrow\omega ' = 0

A_+ =x_0

A_- =v_0 +x_0\frac{\gamma}{2}

Simule:

\(x_0 = 10\) cm

\(v_0 = 0\) cm/s

\(m = 1,0\) kg

\(k = 4,0\) N/m

\(b = 4,0\) kg/s

Calcule: \(b_c; \gamma/2,\omega_0; A_+;A_-\).

A amplitude decai exponencialmente no tempo e não há oscilação. A função movimento fica:

\Rightarrow b_c = 2\sqrt{mk}

x(t) = e^{-\frac{\gamma}{2}t}(A_+ e^{+\omega ' t}+ A_- t\,e^{-\omega ' t})

Fonte: https://www.geogebra.org/m/ZzKbkvnz

ATENÇÃO: \(c\equiv b ; y(0)=x_0\)

Mostre isso. Utilize as condições inicias na função movimento.

Condições iniciais

\text{e}\,\omega ' = 0

Oscilações Amortecidas. Regime supercrítico.

O fator de amortecimento é predominante em comparação à frequência natural:

Mostre que se \(x(0)=x_0\) e \(v(0)=v_0\), temos:

\omega^{\prime} =\sqrt{\left( \frac{\gamma}{2} \right)^2-\omega_0^2} = \sqrt{\left( \frac{b}{2m} \right)^2-\frac{k}{m}}

\Rightarrow\omega ' > 0

A_+ = \frac{1}{2}x_0 - \frac{ x_0(\gamma/2)+v_0}{2 \sqrt{(\gamma/2)^2 - \omega_0^2 }}

A_- = \frac{1}{2}x_0 + \frac{ x_0(\gamma/2)+v_0}{2 \sqrt{(\gamma/2)^2 - \omega_0^2 }}

Simule:

\(x_0 = 10\) cm

\(v_0 = 0\) cm/s

\(m = 1,0\) kg

\(k = 4,0\) N/m

\(b = 5,0\) kg/s

Calcule: \(b_c; \gamma/2,\omega_0; A_+;A_-\).

A amplitude decai exponencialmente no tempo e sem oscilação:

\Rightarrow b>b_c = 2\sqrt{mk}

Fonte: https://www.geogebra.org/m/ZzKbkvnz

x(t) = e^{-\frac{\gamma}{2} t}(A_+ e^{+\omega ' t}+ A_- e^{-\omega ' t})

ATENÇÃO: \(c\equiv b ; y(0)=x_0\)

Mostre isso. Apresente para mim e ganhe bônus. Desafie-se!

Condições iniciais

Oscilações Amortecidas.

Fonte; https://www.geogebra.org/m/cvveycvd

Questão 1

No laboratório, um estudante do BCT/ECT estuda um pêndulo analisando o ângulo θ (graus) que o fio faz com a vertical em função do tempo t(s), obtendo o gráfico θ x t mostrado na figura

Fonte: Wolfgang & Bauer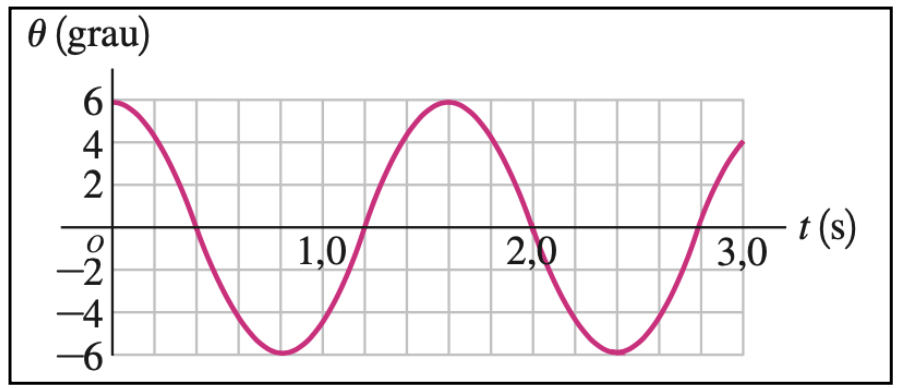

a) A partir da leitura do gráfico informe e/ou calcule as grandezas físicas: período (T), a frequência (f), a frequência angular (𝜔) e a amplitude do movimento do pêndulo (θ0).

b) O pêndulo é puxado lateralmente até um ângulo θ0 com a vertical e a seguir é liberado a partir do repouso. Em que instantes de tempo, a partir da leitura do gráfico acima, o pêndulo passará pelo ponto mais baixo tal como mostrado no desenho abaixo? Justifique.

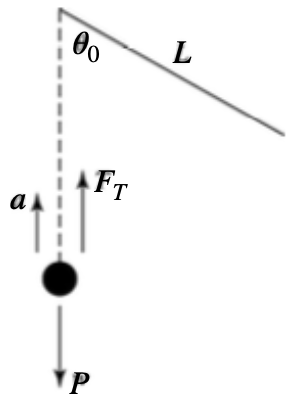
c) Nos tempos indicados na sua resposta do item (c), calcule a magnitude da velocidade da esfera neste ponto mais baixo da trajetória.

Questão 2

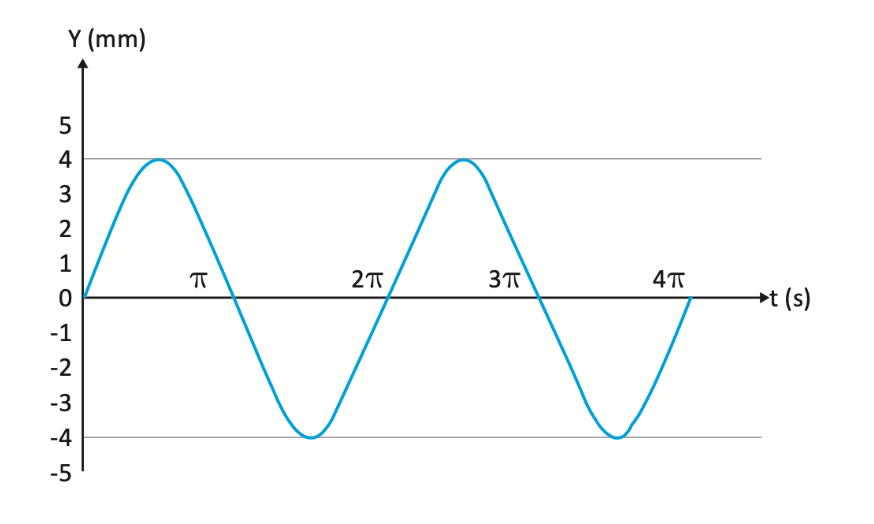
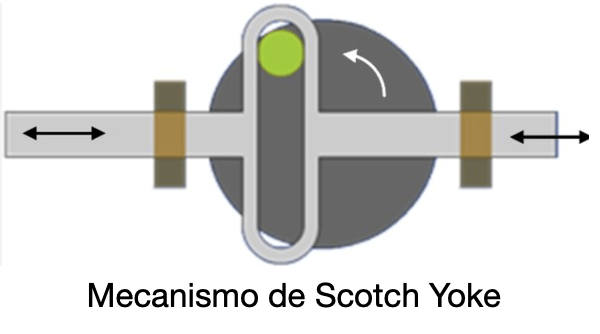
Considere que um mecanismo do tipo Scotch Yoke tenha sido utilizado em uma mesa de vibração em um processo industrial e que ensaios experimentais determinaram o gráfico do deslocamento do êmbolo do mencionado mecanismo, conforme mostra a figura a seguir.

Enade 2023 - Engenharia Mecânica Q25.

Considerando o gráfico desse mecanismo, avalie as afirmações a seguir.

O tempo para que o movimento se repita, a partir do repouso, é de 4π segundos.
O máximo valor atingido pelo êmbolo, ou seja, sua amplitude, é de 8,0 mm.
A frequência desse sistema é dada por f = 1/(2π) Hz.
A frequência angular do êmbolo é de ω = 1 rad/s.

É correto o que se afirma em:

A - I e II, apenas.
B - I e IV, apenas.

C - II e III, apenas.

D - III e IV, apenas.

E - I, II, III e IV.

Questão 3

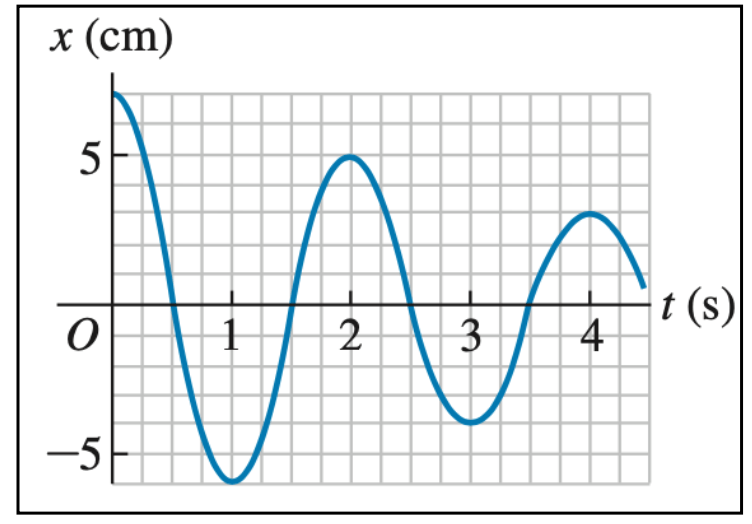
Uma massa está vibrando na extremidade de uma mola com constante de mola igual a 225 N/m. A figura mostra um gráfico de sua posição x(cm) em função do tempo t(s). Nos instantes t = 0 s, 1 s, 2 s, 3 s e 4 s, a massa está instantaneamente em repouso.

Fonte: Sears & Zemansky

a) A partir da leitura do gráfico percebemos queda da amplitude com o tempo. Calcule o fator de amortecimento, ɣ, a partir desta informação

b) A partir do gráfico é possível determinar a frequência angular amortecida, \(\omega'\) . Calcule seu valor e unidade.

c) [0,5 pt] A partir dos itens (a) e (b) é possível determinar a massa do oscilador. Calcule seu valor em quilogramas.

d) [1,0 pt] Calcule a energia que esse sistema continha originalmente no instante t = 0 s. No instante t = 4 s, a energia do sistema diminuiu para 0,101 J, aproximadamente. Calcule a energia dissipada neste intervalo de tempo e, em seguida, o fator de qualidade.

Ronai, Não se esqueça de comentar sobre o fator de qualidade Q.

Questão 4

Para um oscilador amortecido: m = 250 g, k = 85 N/m e b = 70 g/s.

(a) Qual o período do movimento?

(b) Qual é o tempo necessário para que a amplitude das oscilações amortecidas se reduza à metade do valor inicial?

(d) Qual o fator de qualidade?

Questão 5

Um corpo com massa de 20 g é suspenso por uma mola cuja constante vale 2,0 N/m. Qual deve ser o valor da constante de arraste b para que a frequência do oscilador seja metade da frequência natural?

Questão 6

Quando a tecla do dó central do piano (262 Hz) é tocada, ela perde metade de sua energia após 4,00 s. (a) Qual é o tempo de decaimento, 𝛕? (b) Qual é o fator Q para esta corda de piano? (c) Qual é a perda relativa de energia por ciclo?

Questão 7

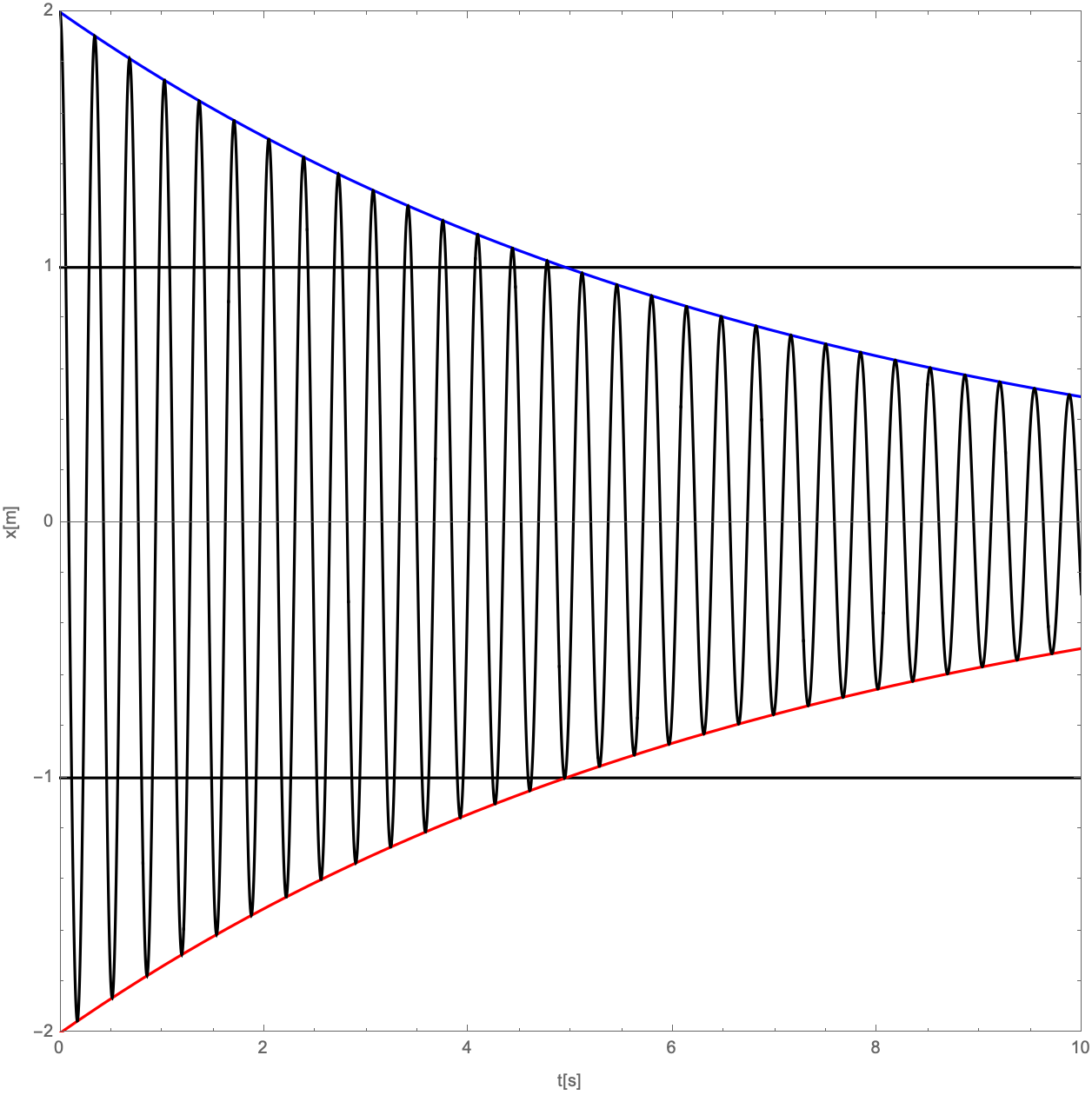
Uma mola de constante elástica k = 1,00 N/m tem um objeto de massa m = 1,00 kg preso a ela, que se move em um meio de constante de amortecimento b = 2,00 kg/s. O objeto é solto, do repouso, da posição x = +5 cm em relação à posição de equilíbrio. Onde ele estará após 1,75 s?

Questão 8

Um pequeno objeto com massa 3,0 kg caiu do telhado de um edifício alto e adquiriu uma rapidez terminal de 25 m/s. Considere que uma força de atrito exercida sobre o objeto tem a mesma forma de uma força de arrasto de um oscilador amortecido; isto é, a força é oposta ao movimento, e sua magnitude é linearmente proporcional à rapidez do objeto.

Um objeto idêntico ao que caiu é fixado a uma mola vertical (k = 230 N/m) e colocado para oscilar no ar com uma amplitude inicial de 0,20 m.

(a) Qual é o fator de qualidade para este oscilador?

(b) Quanto tempo leva para a amplitude diminuir para metade do seu valor inicial?

(d) Quanta energia foi dissipada neste intervalo de tempo?

Questão 9

Encontre as soluções para as seguintes equações diferenciais, descreva o caráter da solução (CRÍTICA, SUPERCRÍTICA, SUBCRÍTICA). Determine as constantes: \(m, \gamma, k, \omega_0, \omega', T\)

(i) y'' + 2y' + y = 0,

ii) y'' + 2y' + 10y =0,

(iii) y'' + 9y = 0

(iv) y'' - y + 6y =0,

Questão 10

Em um oscilador amortecido com m = 250 g, k = 85 N/m e b = 70 g/s, qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos? H15.58

RESUMO

FONTE: https://youtu.be/vLaFAKnaRJU

É possível habilitar as legendas em português (clique no símbolo de engrenagem no canto inferior direito do vídeo).

Oscilações Amortecidas. Balanço da energia.

No oscilador harmônico simples

Em um período \(T\) a energia é intercambiada entre cinética e potencial. O valor médio da energia é,

A potência dissipada pelo oscilador é nula,

E = \frac{1}{2}m\omega_0^2A^2

\overline{K(t)}=\frac{1}{2}E

\overline{U(t)}=\frac{1}{2}E

P=\frac{dE}{dt} = 0

Fonte: https://www.geogebra.org/m/jwq5gucu

Simule:

m = 10 \text{ kg}

k = 10 \text{ N/m}

Calcule:

\omega_0=\quad\text{rad/s}

Simule:

L = 3 \text{ m}

\gamma = 0 \text{ m}

No simulador é chamado de \(\alpha\)

Oscilações Amortecidas. Balanço da energia.

No oscilador harmônico amortecido a energia mecânica não é conservada. Afinal, a amplitude é função do tempo!

A energia cinética varia no tempo e sua amplitude diminui no tempo:

x(t) = Ae^{-\frac{\gamma}{2}t} \cos(\omega 't+\delta)

K(t)=\frac{1}{2}mv(t)^2

v(t) = \frac{1}{2} A e^{-\frac{\gamma}{2} t} [\gamma \cos( \omega ' t +\delta) + 2 \omega ' \text{sen}(\omega ' t +\delta)]

A energia potencial varia no tempo e sua amplitude diminui no tempo:

U(t)=\frac{1}{2}m\omega'^2x(t)^2

Fonte: https://www.geogebra.org/m/jwq5gucu

v(t) = A e^{-\frac{\gamma}{2} t} \sqrt{\gamma ^2+(2\omega ')^2} [\cos( \omega ' t +\delta) - \beta]

\beta = \arctan\left( \frac{2\omega'}{\gamma} \right)

Prove a última expressão. Apresente seu resultado e ganhe bônus. Dica: Utilize propriedades trigonométricas: A cos[a -b] + B sen[a-b] = ???