
Aula 02
Fundamentos da Mecânica
Prof. Ronai Lisbôa
BCT - ECT - UFRN
Objetivos
Definir o referencial inercial.
Identificar o papel da cinemática.
Estudar a posição e tempo de um objeto em movimento.
Distinguir as grandezas distância e deslocamento.
Descrever o movimento em uma dimensão.
Definir as grandezas rapidez, velocidade media e velocidade instantânea.
Bibliografia:
Tipler - Cap. 2
Seção 2.1 (pag. 27 a 34)
- Refaça os Exemplos resolvidos.
- Faça os exercícios recomendados no SIGAA.
O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA ou Google Classrooom)
O movimento é relativo.
Referencial inercial
Fonte: Juan Carlos Casado

A Terra não é um referencial inercial! Não porque se move somente. Mas porque se move num movimento curvilíneo.
Devido a sua rotação diária e a sua órbita, a Terra não é um referencial inercial.
Fonte: Juan Carlos Casado
As estrelas distantes parecem estar em repouso ou em movimento com velocidade constante umas em relação as outras e são ditas referenciais inerciais.

Este conjunto de estrelas constituem um referencial inercial com boa aproximação.

Fonte: www.nasa.gov
Entende-se sobre referencial inercial que:
As estrelas distantes são referenciais inerciais. Qualquer observador ou referencial fixo nas estrelas distantes é também um observador ou referencial inercial.
Referenciais inerciais devem estar em repouso ou em movimento à velocidade constante em relação a outros referenciais inerciais.
Se a relação abaixo é satisfeita, podemos considerar que os referenciais fixos na Terra são bons referenciais inerciais para o estudo do movimento dos corpos.
Referencial inercial

Fonte: www.pixbay.com
Fonte: www.pixbay.com
O meu referencial pode não ser igual ao seu. O que importa é que eles se movam à velocidade constante.
Referencial inercial
Depois de sair da mão do professor, a aceleração da bolinha é diferente em cada referencial?
Não. Os observadores nos referenciais inerciais medirão o mesmo valor para o observável físico.
Nos referenciais inerciais são válidas as leis de Newton!
A primeira Lei de Newton define os referenciais inerciais.
repouso
MRU
A cinemática não considera as causas e efeitos do movimento (força e aceleração); seu objetivo é simplesmente fornecer uma descrição quantitativa do movimento (direção e sentido, por exemplo).
Como descrição quantitativa do movimento, entende-se:
concreto \(\rightarrow\) abstrato
Cinemática
Diagramas do movimento
Tabelas
Gráficos

Funções
Fonte: Eric Mazur
No filme, o Shinkansen está em movimento?
Para responder a essa questão podemos medir a rapidez do trem bala em relação ao referencial da plataforma da estação.
Basta acompanhar a posição do trem em tempos diferentes em relação ao referencial.
- Se a posição variar no tempo, o objeto está em movimento.
- Se a posição não variar no tempo, diz-se que o objeto está em repouso.
Cinemática
Quão rápido o trem bala está se movendo?
Fonte: https://youtu.be/SIzOFZug8C8
eixo de referência
Origem
| Quadro | x (m) | t(s) |
|---|---|---|
O movimento é descrito ao informar as grandezas físicas de posição (x) e tempo (t).

A partir da origem, as distâncias aumentam no sentido (positivo) do eixo de referência.
Posição e tempo
Diagrama do movimento
Tabela
0,4 m
0,5 s


1,2 m
1,5 s


1,6 m
2,0 s

1,0 s

0,8 m

O vetor posição final \(\vec r_f\) pode ser determinado a partir do vetor posição inicial \(\vec r_i\) e do vetor do deslocamento \(\Delta \vec r\):
Deslocamento



Em uma dimensão podemos escrever:
onde \(\hat i\) é o vetor base unitário:
Podemos representar o movimento de um objeto que se move de uma posição para outra por um vetor posição que aponta da posição inicial para a posição final.
O componente do deslocamento é um escalar.
O componente x do deslocamento de um objeto é a variação em sua coordenada x.
Deslocamento e distância são grandezas com significados diferentes.
A distância é o módulo do deslocamento.
Distância percorrida
= |posição final - posição inicial|
= posição final - posição inicial
Componente
do deslocamento
Deslocamento e distância



\(x_i\) = 0,4 m
\(x_f\) = 1,6 m
Para frente


O componente x do deslocamento de um objeto é a variação em sua coordenada x.
A distância é o módulo do deslocamento.
Deslocamento e distância são grandezas com significados diferentes.
= posição final - posição inicial
Componente
do deslocamento
Distância percorrida
= |posição final - posição inicial|



\(x_f\) = 1,0 m
\(x_i\) = 1,6 m
Deslocamento e distância
Para trás: Moonwalk


O componente x do deslocamento de um objeto é a variação em sua coordenada x.
A distância é a soma dos módulos dos deslocamentos.
Deslocamento e distância são grandezas com significados diferentes.
= posição final - posição inicial
Componente
do deslocamento
Distância percorrida
= |posição final - posição inicial|
Deslocamento e distância
\(x_2\) = 1,6 m
\(x_1\) = 0,4 m
\(x_3\) = 1,0 m
Resultante
Moon-Walk




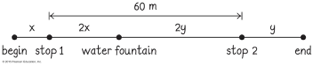
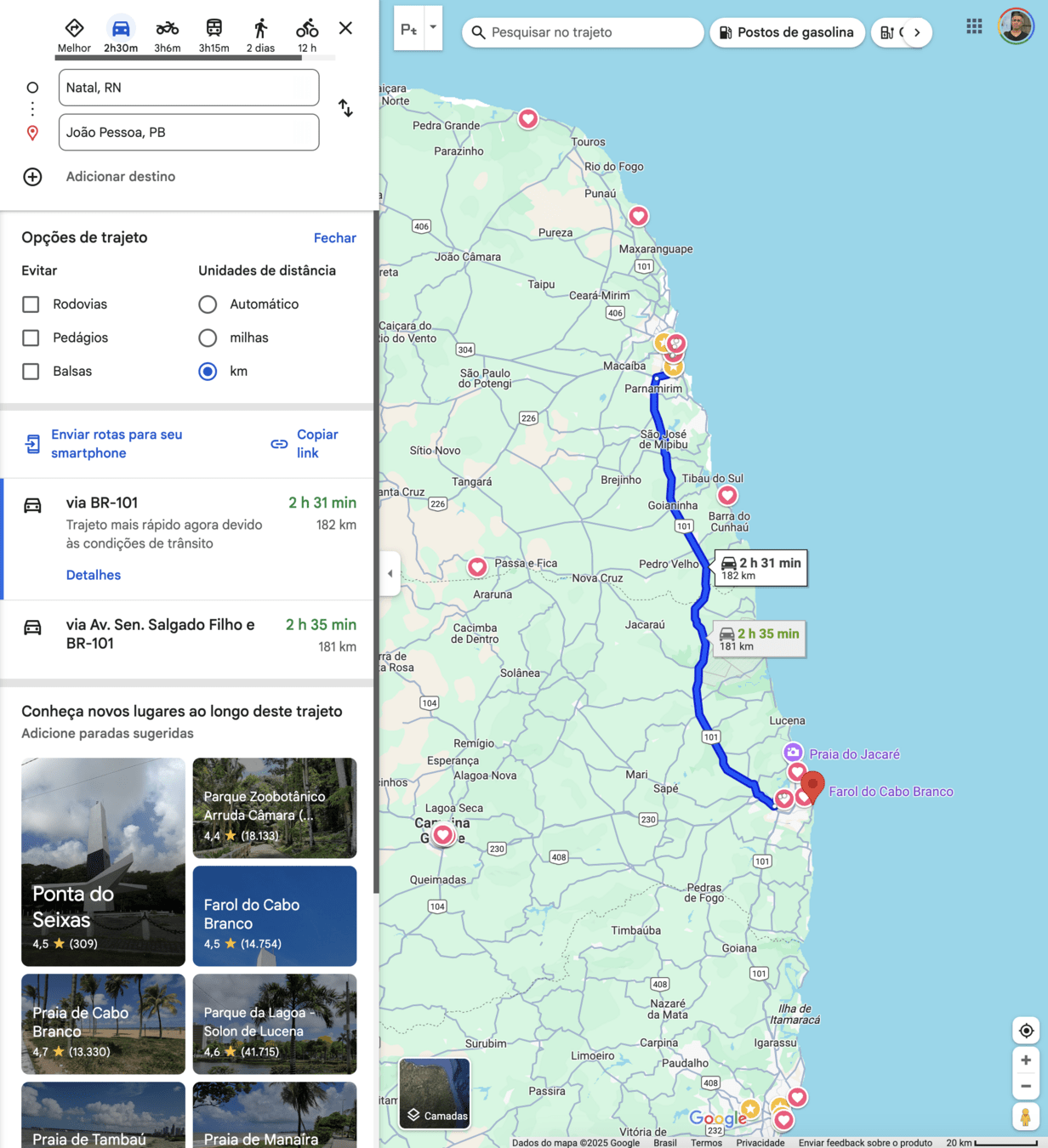
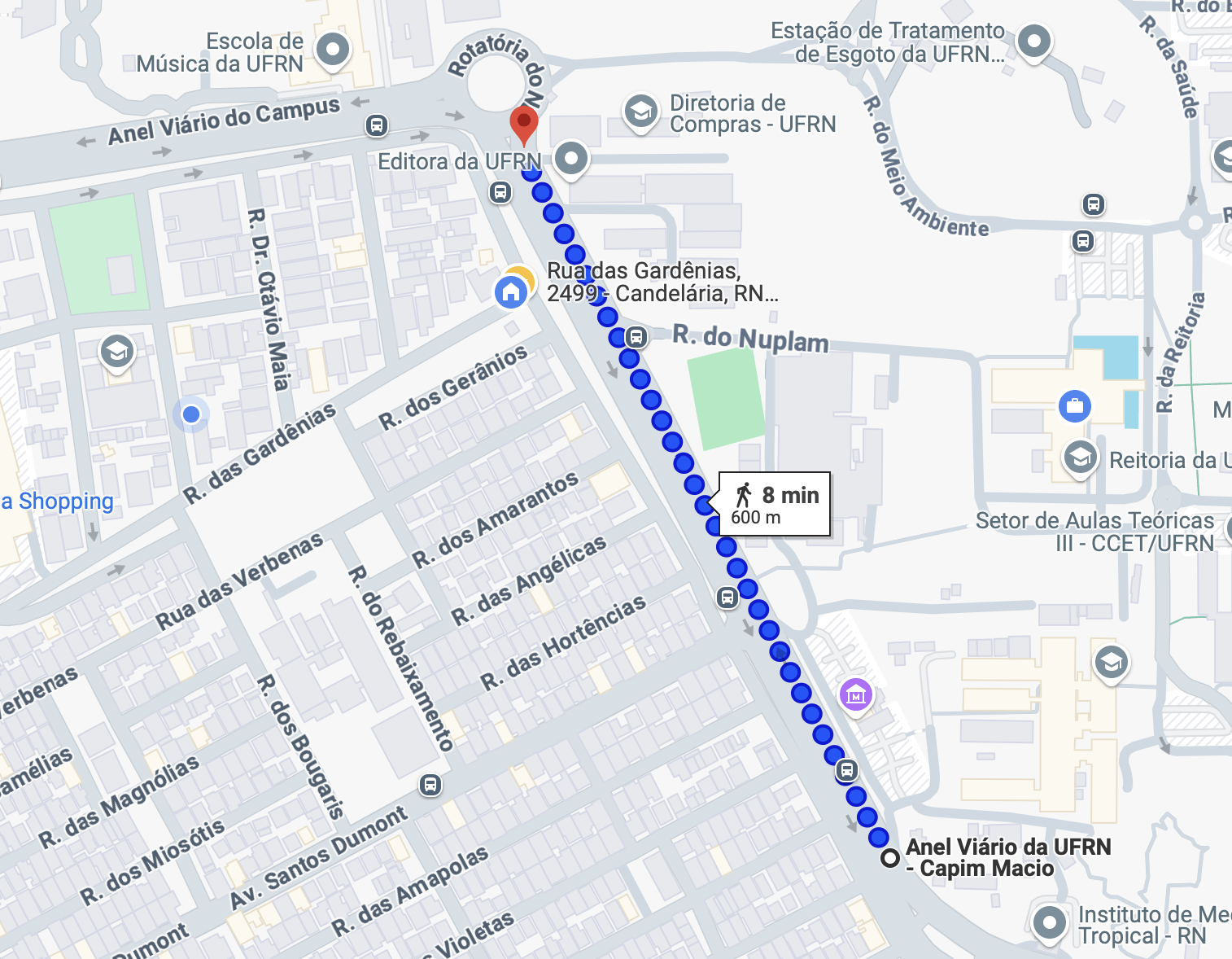
No movimento de um estudante em frente à ECT/UFRN representado pelos pontos azuis sobre o Google Maps, avalie:
- A distância percorrida, em km.
- O deslocamento percorrido, em km.
Deslocamento e distância
Fonte: https://youtu.be/M1Zu-pQD7skExemplo 1
Suponha que você ande em linha reta de um ponto P a um ponto Q, a 2 m de distância de P e depois caminhe de volta pela mesma linha até P.
(a) Qual é o componente x do seu deslocamento para a ida e volta?
(b) Que distância você viajou durante a viagem de ida e volta?
Lição 1: A distância percorrida é o trajeto realizado por um objeto em movimento ao longo do caminho de seu movimento.
Lição 2: A distância percorrida é sempre positiva.
Exemplo 2
(a) Um objeto se move de uma posição inicial em x = +3,1 m para uma posição final em x = +1,4 m. Qual é o componente do deslocamento do objeto? (b) O componente do deslocamento de um objeto é +2,3 m. Se a posição inicial do objeto é x = +1,6 m, qual é a coordenada de sua posição final? (c) Após sofrer um deslocamento de -1,3 m, um objeto está em x = -0,4 m. Qual é a coordenada da posição inicial do objeto?
Lição 1: Desenhe um diagrama do movimento.
Lição 2: A posição final é determinada quando se conhece a posição inicial e o componente do deslocamento.
(a) \(\Delta x = x_f - x_i = +1,4 - (+3,1) = -1,7 \) m
(b) \(\Delta x = x_f -x_i \Rightarrow x_f = \Delta x + x_i = +2,3 + 1,6 = +3,9\) m.
(c) \(\Delta x = x_f -x_i \Rightarrow x_i = x_f - \Delta x = -0,4 - (-1,3) = +0,9\) m.
+1,4 m
+3,1 m
eixo de referência
\(\Delta x\)
+1,6 m
eixo de referência
\(\Delta x = +2,3\) m
-0,4 m
eixo de referência
\(\Delta x = -1,3\) m
Exemplo 3
Um objeto move-se do ponto P em x = + 2,3 m para o ponto Q em x = + 4,1 m e, em seguida, para o ponto R em x = + 1,5 m. (a) Qual é o componente do deslocamento do objeto após viajar de P para R? (b) Qual é a distância entre as posições inicial e final do objeto? (c) Qual a distância percorrida pelo objeto?
Lição 1: Desenhe um diagrama do movimento.
Lição 2: Lembre-se que componente do deslocamento e distância são conceitos distintos.
(a) \(\Delta x_{r} = \Delta x_1+\Delta x_2 = (4,1 - 2,3) + (1,5 - 4,1) = -0,8\) m
(b) d = |\(\Delta x_{r}| = 0,8\) m
(c) \( d_r = |\Delta x_{1}| + |\Delta x_2| = |(4,1-2,3)|+|(1,5-4,1)| = 4,4\) m
P
+2,3 m
+4,1 m
eixo de referência
\(\Delta x_1\)
Q
R
+1,5 m
\(\Delta x_1\)
\(\Delta x_2\)
Rapidez média (ou velocidade escalar média)
Uma grandeza escalar que mede a rapidez ou a lentidão de um objeto é sua rapidez média, definida como a razão:
Fonte: Globo Esporte
Cesar Cielo, marcou o tempo de 20 segundos e 91 centésimos na prova dos 50 m livres (Recorde Mundial).
Fonte: https://youtu.be/Kszu_5wA6Co
A rapidez média foi de:
A vitória pertence ao corredor com maior rapidez média.
Observe que a unidade SI é o metro por segundo (m/s) e a resposta é dada com 2 algarismos significativos.
Calcule a rapidez média.
Rapidez e velocidade médias
O campeão mundial, Cesar Cielo, marcou o tempo de 46 segundos e 91 centésimos na prova dos 100 m livre (Roma 2009).
A velocidade média é nula porque nos 100 m livre o atleta chega ao mesmo ponto de partida. Logo, seu deslocamento (vetor) é nulo: \(\Delta x = 0\), pois \(x_f=x_i\):
É uma grandeza vetorial que fornece a direção, sentido e magnitude do deslocamento por intervalo de tempo:
A rapidez média não é nula porque mede o quão rápido ele foi na prova, a distância é \(d= 100\) m.
1D
Rapidez média
Velocidade média
É calculada pela razão:
É calculada pela razão:
É um número (escalar).
É um vetor (vetorial).
É não negativo.
Pode ser negativo, nulo ou positivo.
A magnitude é numericamente igual à inclinação da reta.
É igual à velocidade média quando o objeto tem a mesma direção e sentido do movimento.
Velocidade média
No sistema internacional
No movimento de um estudante em frente à ECT/UFRN representado pelos pontos azuis sobre o Google Maps, avalie:
- A rapidez média, em m/s.
- A velocidade média, em m/s.
Rapidez média e velocidade média
Fonte: https://youtu.be/M1Zu-pQD7skA rapidez é sempre positiva. Já a velocidade pode ser negativa, nula ou positiva.
Rapidez média e velocidade média
Para a velocidade é importante avaliar o referencial.
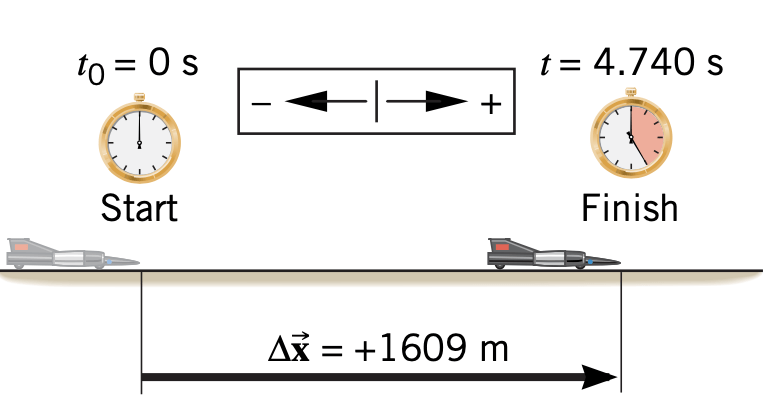
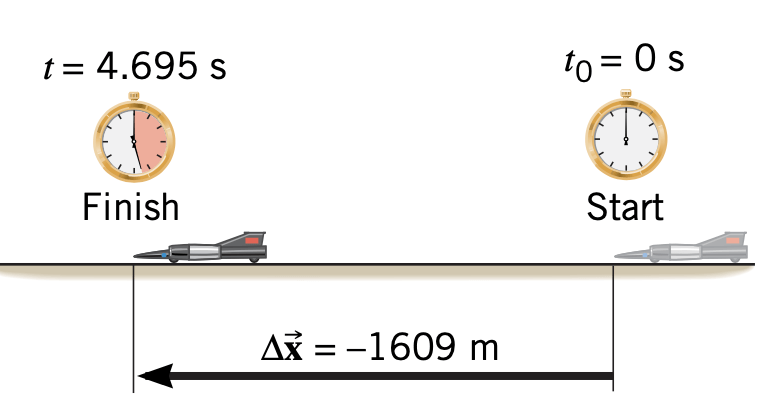
O sinal de menos indica que a velocidade média, assim como o deslocamento, apontam para a esquerda, isto é, contrários ao referencial. Qual cenário é o mais rápido?
O gráfico da posição e tempo é uma representação do movimento do objeto.
O eixo vertical representa a posição e o eixo horizontal representa o tempo.
Gráfico
Tabela
A tabela e o gráfico trazem informações que se complementam.
| Quadro | x(m) | t(s) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
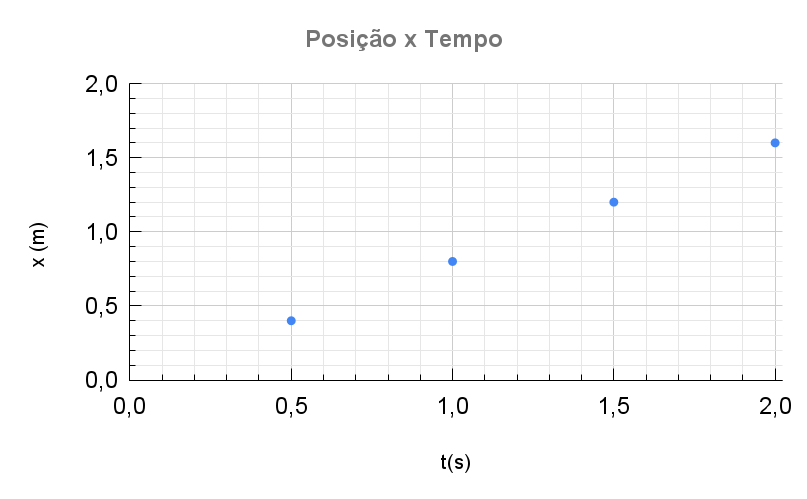








Que informações podemos obter a partir do gráfico?
Função posição (Equação horária)
Como obter um modelo (função) para o movimento a partir do gráfico?
Gráfico
Análise de dados
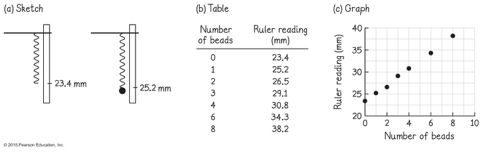
Os deslocamentos são sempre os mesmos entre os mesmos intervalos de tempo:
| Quadro | t(s) | x(m) |
|---|---|---|
| 1 | 0,5 | 0,4 |
| 2 | 1,0 | 0,8 |
| 3 | 1,5 | 1,2 |
| 4 | 2,0 | 1,6 |

Função posição (Equação horária)
O deslocamento total vale \(\Delta x = 0,8 \text{ m}\) em um intervalo de tempo total \(\Delta t = 1,5 \text{ s}\).
A inclinação da reta é numericamente igual à velocidade média.
ou reescrevendo:
Função posição (Equação horária)
inclinação \(\equiv\)
Para velocidade média constante, a reta tem inclinação constante no gráfico posição x tempo.
Quando a velocidade é constante a função posição é a equação da reta:
Gráfico
Análise de dados

Observe que o deslocamento é lido na vertical.
As provas de natação são movimentos em uma dimensão. A atleta vai em um sentido nadando 50 m e depois retorna completando a mesma distância. Ao final terá nadado 100 m.

Mundo real
Fonte: Olympics. LINK.Qual o gráfico mais adequado para representar a prova?
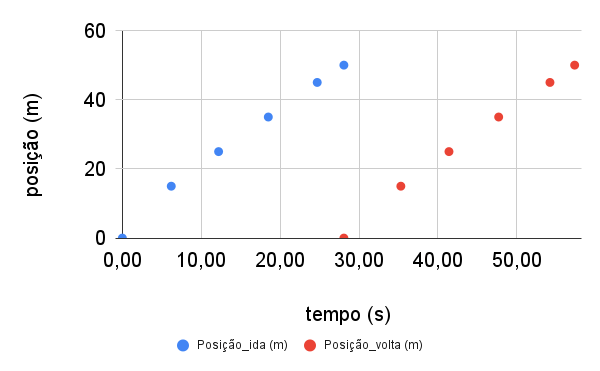
Movimento retilíneo uniforme
(a)
(b)
(c)
(d)
As provas de natação são movimentos em uma dimensão.
Modelagem

Mundo real
Fonte: Olympics. LINK.Medidas
Fonte: analysisswim.com. LINK.Kaylee MCKeown (AUS) completou a prova de 100 m com o tempo de 57,33 s.
Ela foi a mais rápida e venceu.
Ela foi mais rápida em todo percurso? O que signifca ser rápido?
Fonte: Google Planilhas. LINK.
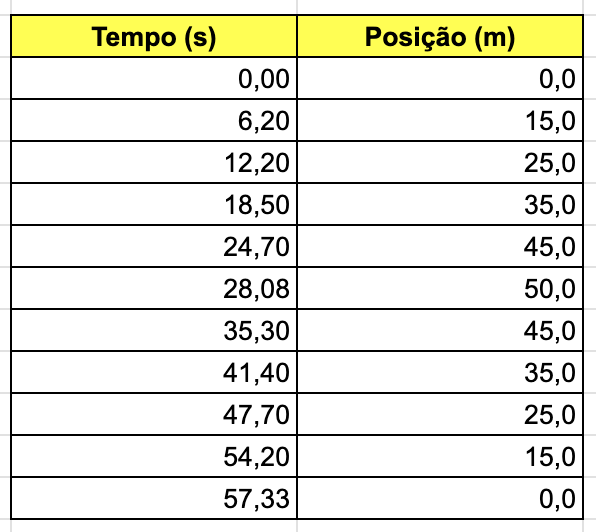
Movimento retilíneo uniforme
(d)
Calcule a velocidade média na ida e na volta.
Estudo de caso: 100 m nado costas - Paris 2024.
- Entre t = 28,08 s e 57,33 s. \(\Delta x\) = -50,0 m.
- Entre t = 0 s e 28,08 s. \(\Delta x\) = +50,0 m.
Na ida a velocidade média foi \(v_m=+1,78\) m/s e na volta \(v_m = -1,71\) m/s.
Na ida a rapidez média foi \(v_m=1,78\) m/s e na volta \(v_m = 1,71\) m/s. A atleta foi mais rápida na ida!
A velocidade média no trajeto ida-volta é \(v_m=0\). A rapidez média ida-volta é \(v_m = 1,74\) m/s.
Movimento retilíneo uniforme
Estudo de caso: 100 m nado costas - Paris 2024.
A função movimento na ida:
A função movimento na volta:
As funções de movimento ajustadas no Google Planilhas e utilizando dados reais.
Para um modelo mais simples (sem ajuste), elas seriam:
Isso ocorre porque no mundo real, a velocidade constante não é fácil de ser mantida. Imagine nadando!
Movimento retilíneo uniforme
- Entre t = 12,20 s s e 18,50 s. \(\Delta x\) = +10,0 m.
- Entre t = 18,50 s e 24,70 s. \(\Delta x\) = +10,0 m.
- Entre t = 0 s e 6,20 s. \(\Delta x\) = +15,0 m.
Em cada intervalo considerado a velocidade média não é constante. Um valor aceito é a média das velocidades médias mais ou menos sua incerteza.
Estudo de caso: 100 m nado costas - Paris 2024.
Calcule a velocidade média para cada intervalo de tempo na ida.
- Entre t = 24,70 s e 28,08 s. \(\Delta x\) = +5,0 m.
- Entre t = 6,20 s e 12,20 s. \(\Delta x\) = +10,0 m.
na ida. E na volta?
Movimento retilíneo uniforme
Um ciclista mantém uma velocidade constante na ida de uma viagem, velocidade zero enquanto parado e outra velocidade constante no caminho de volta. A Figura mostra o gráfico posição-tempo correspondente. Usando os intervalos de tempo e posição indicados no desenho, obtenha as velocidades para cada segmento da viagem.
Fonte: CutnellExemplo 5
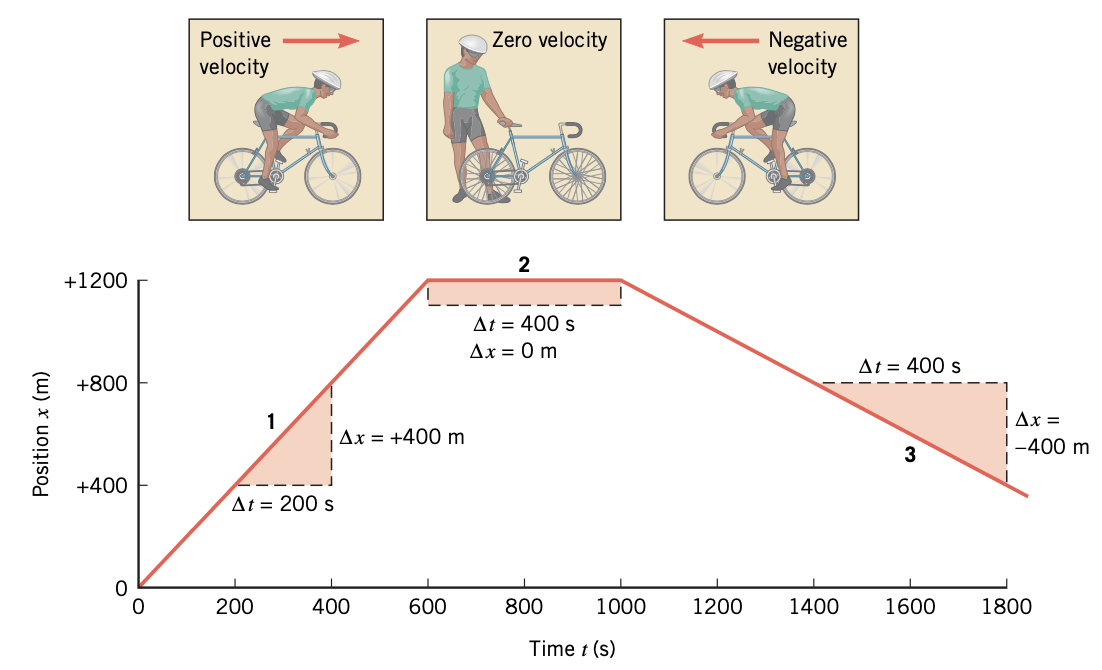
ida
Repare que o movimento se dá em uma dimensão (linha reta)
parado
volta
Como a velocidade é constante (inclinação constante) em cada trecho, basta escolher adequadamente os deslocamentos e intervalos de tempo.
Gráfico da velocidade em função do tempo
A velocidade média é aproximadamente constante na ida e na volta na prova dos 100 m.
Entre t = 0 s e t = 28,08 s, o movimento é para frente (\(\Delta x > 0\)) e a velocidade é constante e positiva: \(v=+1,78\) m/s.
Em t = 28,08 a velocidade é instantaneamente nula \(v=0\) m/s, pois temos um ponto de retorno.
Entre t = 28,08 s e t = 57,33 s o movimento é para trás (\(\Delta x < 0\)) e a velocidade é constante e negativa: \(v=-1,71\) m/s.
eixo 0
Movimento para frente
(p/ longe da origem)
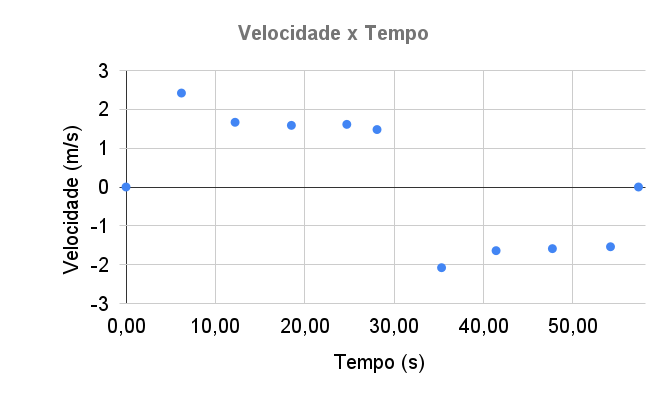
Movimento para trás
(p/ perto da origem)
Gráfico da velocidade em função do tempo
Em um gráfico da velocidade em função do tempo, o deslocamento é numericamente igual à área sob a curva da velocidade.

CUIDADO:
dimensão de área: m\(^2\).
dimensão de deslocamento: m
O deslocamento para frente é \(\Delta x = |\text{v}| \Delta t\) = (1,78 m/s) x (28,08 s) = 49,98 m ~ 50 m.
O deslocamento para trás é\(\Delta x = |\text{v}| \Delta t\) = |-1,71 m/s| x (29,25 s) = 50,01 m ~ 50 m.
Você faz uma integração a todo momento quando responde a pergunta abaixo.
Suponha que você esteja viajando a 100 km/h, em sua Lamborghini, durante 20 min. Qual o seu deslocamento?

Fonte: https://www.gta-sa.com.br
Mundo Real
Mundo Real
Você usa uma função linear toda vez que responde a questão abaixo.
Se você passou pelo marco 10 km no tempo t = 1,33 h, com uma rapidez de 100 km/h.
Onde você estará no tempo t = 2,0 h mantendo a mesma velocidade constante (olhe o velocímetro)?

Fonte: https://www.gta-sa.com.br
Exemplo 6
A figura mostra o gráfico de posição versus tempo para a parte do movimento de um objeto em movimento a velocidade constante. (a) Qual é o componente da velocidade do objeto? (b) Escreva uma expressão para x(t) , a coordenada da posição do objeto em um momento arbitrário . (c) Qual é a coordenada da posição do objeto em t = 25 s?
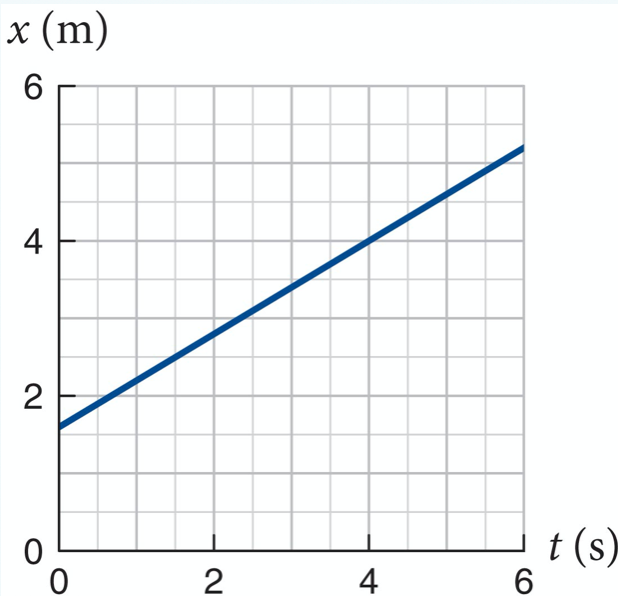
\(v_x = \frac{\Delta x}{\Delta t} = \frac{4,0-2,5}{4,0-1,5} = +0,60 \frac{\text{m}}{\text{s}}\)
(a) Pegue números de fácil leitura sobre a reta.
(b) \(x_f = x_i + v(t_f - t_i\)).
\(x_f = +1,6 + 0,60(t_f-0)\)
(c) \(x_f = +1,6 + 0,60t_f\).
\(x_f = +1,6+0,60*25 = +17\) m
A função permite prever o futuro! Daí sua importância!
Fonte: Eric Masur
Exemplo 7 (A2.P1-10)
Um corredor de 18 anos consegue completar um percurso de 10,0 km com uma velocidade escalar média de 4,39 m/s. Um corredor de 50 anos consegue cobrir a mesma distância com uma velocidade média de 4,27 m/s. Quanto tempo depois (em segundos) o corredor mais jovem deveria começar de modo a completar a corrida no mesmo instante que o corredor mais velho? C2.8
Exemplo 8 (A2.P1-11)
Uma ciclista faz um passeio composto de três partes, cada uma na mesma direção e sentido (de sul para norte) ao longo de uma estrada reta. Na primeira parte, ela pedala durante 22 minutos a uma velocidade média de 7,2 m/s. Durante a segunda parte, ela pedala durante 36 minutos a uma velocidade média de 5,1 m/s. Finalmente, durante a terceira parte, ela pedala durante 8,0 minutos a uma velocidade média de 13 m/s.
(a) Que distância a ciclista percorreu durante todo o passeio?
(b) Qual o seu vetor velocidade média durante o passeio?
Exemplo 9 (A2.P1-13)
Um turista que está sendo perseguido por um urso furioso está correndo em linha reta em direção ao seu carro a uma velocidade de 4,0 m/s. O carro está a uma distância d. O urso está a 26 m do turista e correndo a 6,0 m/s. O turista alcança o carro com segurança. Qual o valor máximo possível para d? C2.9
Exemplo 10
A função posição de um objeto que se move à velocidade constante é dada por:
onde \(x\) está em metros e \(t\) está em segundos.
(a) Qual a posição inicial?
(b) Qual o instante inicial?
(c) Qual a velocidade instantânea?
(d) Em que posições ele estará no instante \(t=0,2 s\) e \(t=2,0 s\)?
(e) Qual o deslocamento entre esses dois instantes?
(f) Como são os gráficos \(x \times t\) e \(v \times t\)?
Essa atividade não está resolvida. Caso você a entregue na próxima aula, você obtem 0,1 pontos extras na média da unidade.
Velocidade instantânea
A partir do gráfico podemos notar que se \(\Delta t \rightarrow dt \), então o \(\Delta x \rightarrow dx\).
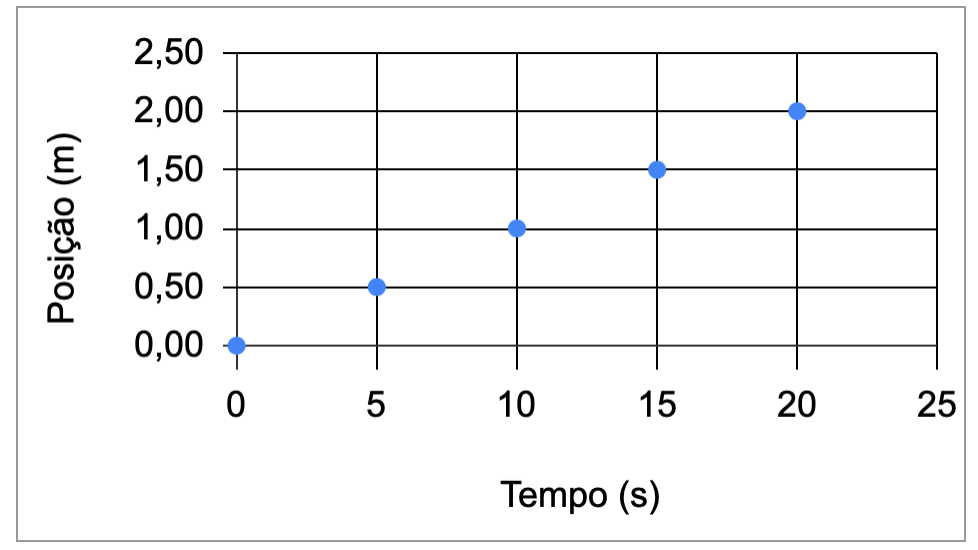
A velocidade média é numericamente igual à secante (reta passando por dois pontos).
À medida que \(\Delta t \rightarrow 0\), a reta secante tende à reta tangente.
Quando a velocidade média é constante, os subintervalos do deslocamento divididos pelos intervalos de tempo têm o mesmo valor.
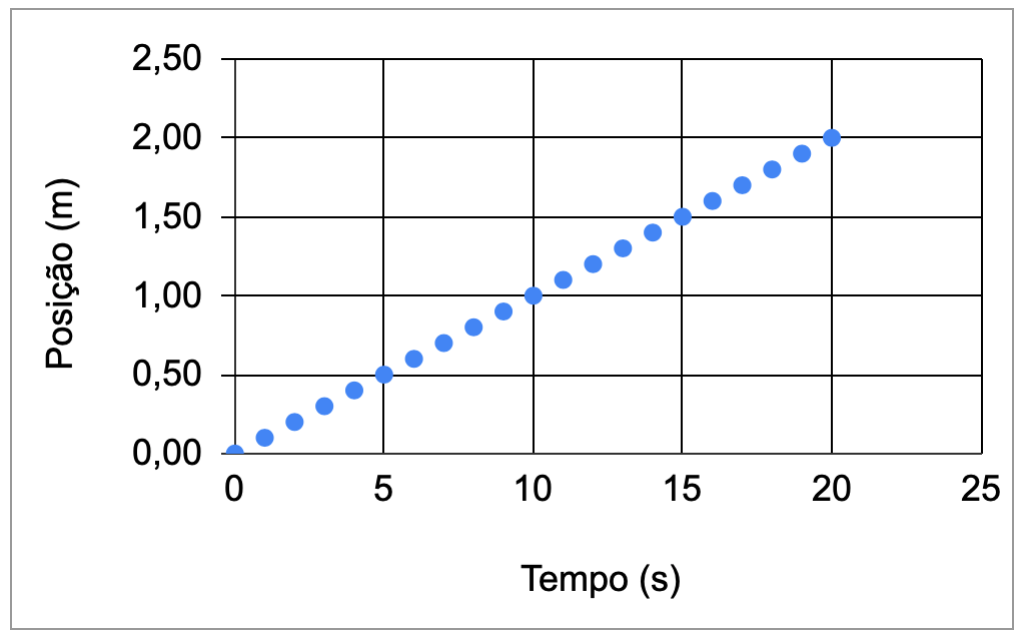
Velocidade instantânea
Quando a velocidade média é constante, os subintervalos do deslocamento divididos pelos intervalos de tempo têm o mesmo valor.
Nos subintervalos, os valores de \(\Delta x_n\) e \(\Delta t_n\) são reduzidos. Podemos definir a velocidade instantânea:
Rigorosamente, é a derivada da função posição no tempo:
derivada da função posição no tempo

Se a velocidade é conhecida, é possível obter a função posição empregando o cálculo integral. Determinamos a primitiva (antiderivada):
isto é um deslocamento infinitesimal. Integrando ambos os lados:
Para velocidades constantes:
Quando a velocidade é constante a velocidade média é igual à velocidade instantânea.
O movimento é denominado de Movimento Retilíneo Uniforme (MRU).
Velocidade instantânea
Exemplo 4
Suponha a função: \(x(t) = 5,0 + 4,0t\). A velocidade média:
A velocidade instantânea via o cálculo do limite.
A velocidade instantânea via o cálculo da derivada.
Para movimentos com velocidade constante a velocidade média é igual à velocidade instantânea.
Planilha: LINKMas se um referencial se move aceleradamente as medidas das grandezas físicas não serão as mesmas.
Referencial não inercial
O carro está acelerado. O que fez o objeto se mover para trás? Aliás, ele se moveu para trás?
Observadores em referenciais não inerciais não medirão o mesmo valor para o observável físico.
Nos referenciais inerciais não são válidas as leis de Newton!
É necessário levar em consideração as forças chamadas de inerciais ou fictícias.
É necessário levar em consideração o princípio de equivalência.
O que é o movimento? Por que estudamos esse conceito?
Unificando conceitos
Os conteúdos
Aplicações
| Relações: - Deslocamento, Distância - Velocidade, Rapidez - Vetores, escalares. |
|---|
| Entendendo os padrões e escalas do movimento |
|---|
| Sistemas e modelos - Sistema de coordenada global - Movimento é relativo ao nosso sistema de coordenadas - Sistema de posicionamento global. |
|---|
| As leis físicas são observadas ao nosso redor. |
|---|
| Medidas de latitude e longitude |
|---|
| Medidas de velocidade e rapidez |
|---|
| Algarismos significativos |
|---|
| Taxas de variação |
|---|
| Escalares e vetores |
|---|
| Gráficos e análise de dados |
|---|
| Medindo deslocamento e distância |
|---|
| Compreendendo o sistemas de coordenadas global |
|---|
| Determinação das melhores linhas de ajuste e determinação de inclinações a partir de gráficos |
|---|
| Sistemas testes |
|---|
| Cálculos com planilhas |
|---|
| Sistemas testes |
|---|
| Caminhando, correndo, dirigindo |
|---|
| Sistema solar |
|---|
| Deriva continental |
|---|
| Comunicações |
|---|
| Navegação |
|---|
| Telemetria da vida selvagem |
|---|
| Acompanhamento do movimento das pessoas |
|---|
Fonte: Lawrence Berkeley LaboratoryMovimento
Tudo no universo está em constante movimento.
Quão rápido a Terra está se movendo ao redor do Sol?
Movimento
Tudo no universo está em constante movimento.
Quão rápido o caracol está se movendo?



Movimento
Tudo no universo está em constante movimento.
Continentes “derivam” a velocidades muito lentas (2,5 cm/ano), mas podem mover-se longas distâncias ao longo de milhões de anos.
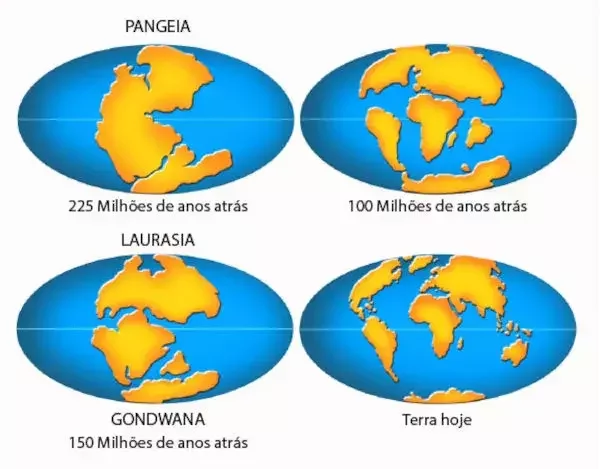
Movimento
Tudo no universo está em constante movimento.
Os sistemas de tempestades geralmente se movem lentamente, mas a velocidade do vento dentro de um furacão ou tornado pode resultar em devastação significativa.
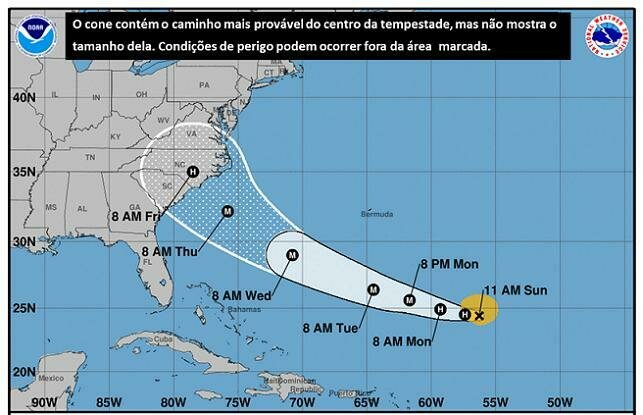
Movimento
Tudo no universo está em constante movimento.
A luz pode viajar distâncias extremamente longas em altas velocidades.
Fonte: https://exame.com
Movimento
Tudo no universo está em constante movimento.
Ondas eletromagnéticas viajam próximas à velocidade da luz em circuitos elétricos.
Fonte: https://olhardigital.com.br
Blackwell, custará entre US$ 30 mil e 40 mil por unidade

A velocidade de deriva dos elétrons em um circuito é aproximadamente a velocidade de um caracol.
Fonte: https://es.linkedin.comMovimento
Tudo no universo está em constante movimento.
A velocidade média dos átomos de hélio a 25° é 1255 m/s
Blackwell, custará entre US$ 30 mil e 40 mil por unidade

Movimento
Tudo no universo está em constante movimento.
Bactérias Salmonella se movem lentamente em curtas distâncias. Proteínas, também!
Blackwell, custará entre US$ 30 mil e 40 mil por unidade
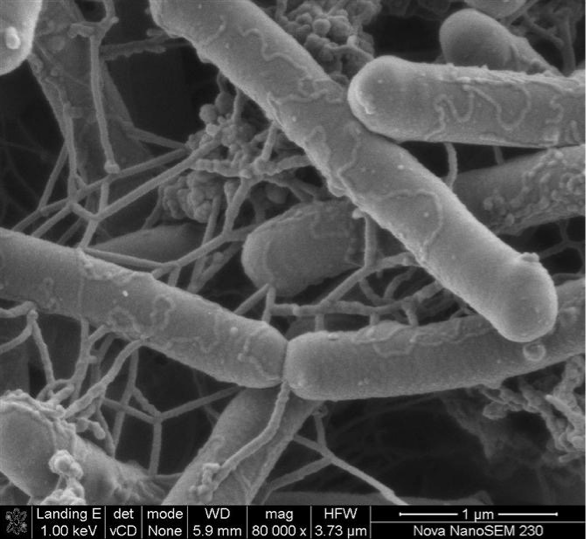
Movimento
Tudo no universo está em constante movimento.
A vida depende do movimento em uma ampla gama de escalas
Blackwell, custará entre US$ 30 mil e 40 mil por unidade
Fonte: https://coenfeba.com/
Movimento
Tudo no universo está em constante movimento.
O controle de movimento é um grande negócio.



Fonte: https://www.estadao.com.brMovimento
Tudo no universo está em constante movimento.
O movimento é um que permite as pessoas se mudarem de um lugar para outro.


Fonte: Pedro Vitorino/Cedida
Fonte: https://passeiospipa.com.brMovimento
Hoje podemos usar o Sistema de Posicionamento Global (GPS) para medir nossa localização e nos guiar para novos locais.
Fonte: Google Maps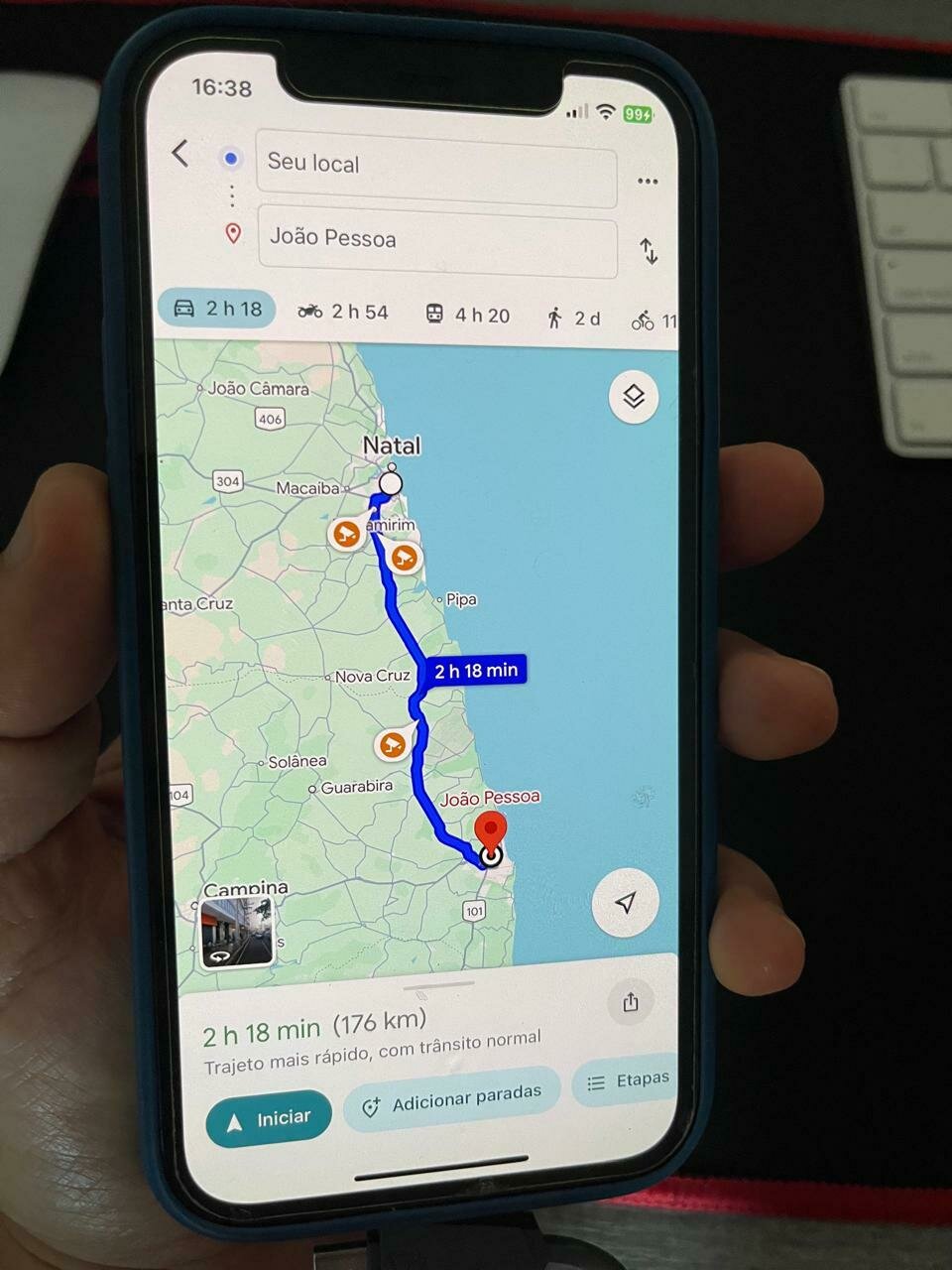
Exploraremos o movimento examinando o deslocamento e a velocidade de pessoas/objetos enquanto viajam curtas distâncias pela superfície da Terra.
Movimento
O sistema de Geoposicionamento completo inclui 24 satélites que ficam orbitando a Terra.
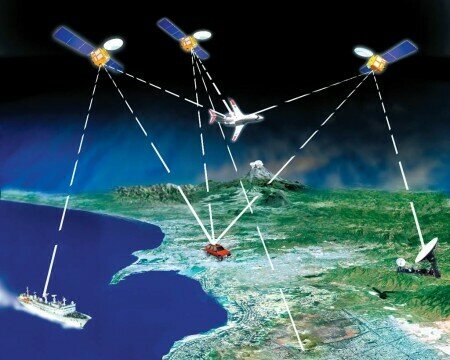
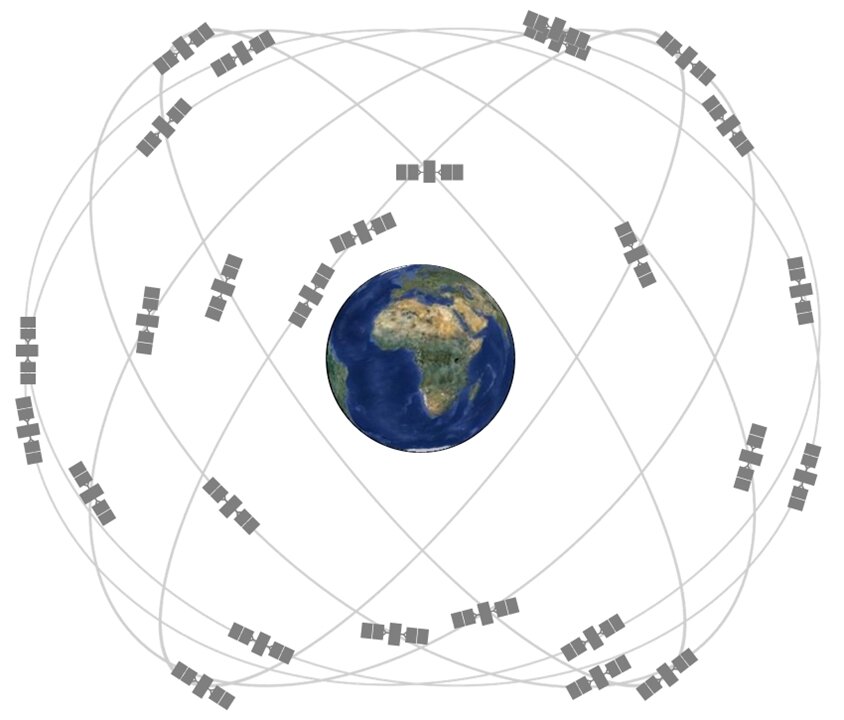
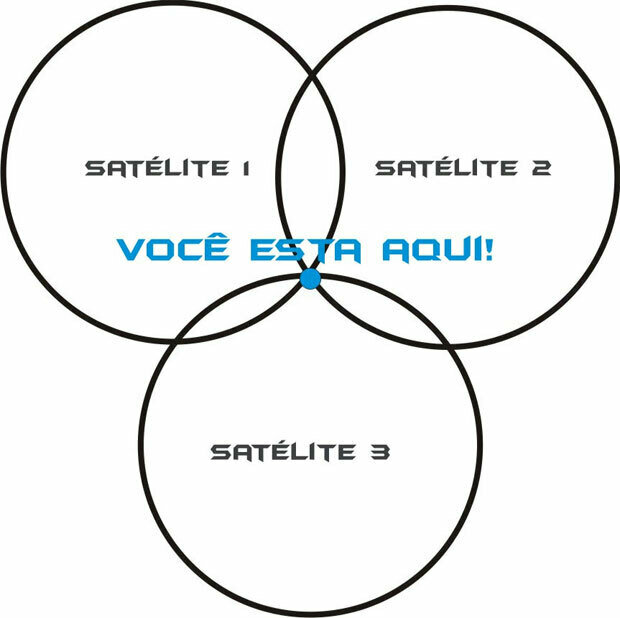
Quando você liga o seu receptor GPS e pede para ele te dizer onde você está, na verdade, você está entrando em contato com 4 desses satélites e pedindo informação.
Ao cruzar esses círculos, o ponto onde os três se cruzam é exatamente onde você está.
Movimento
Antes de passarmos a usar o GPS, vamos tirar um momento para apreciar um pouco da física envolvida na criação deste sistema.
Fonte: INPE




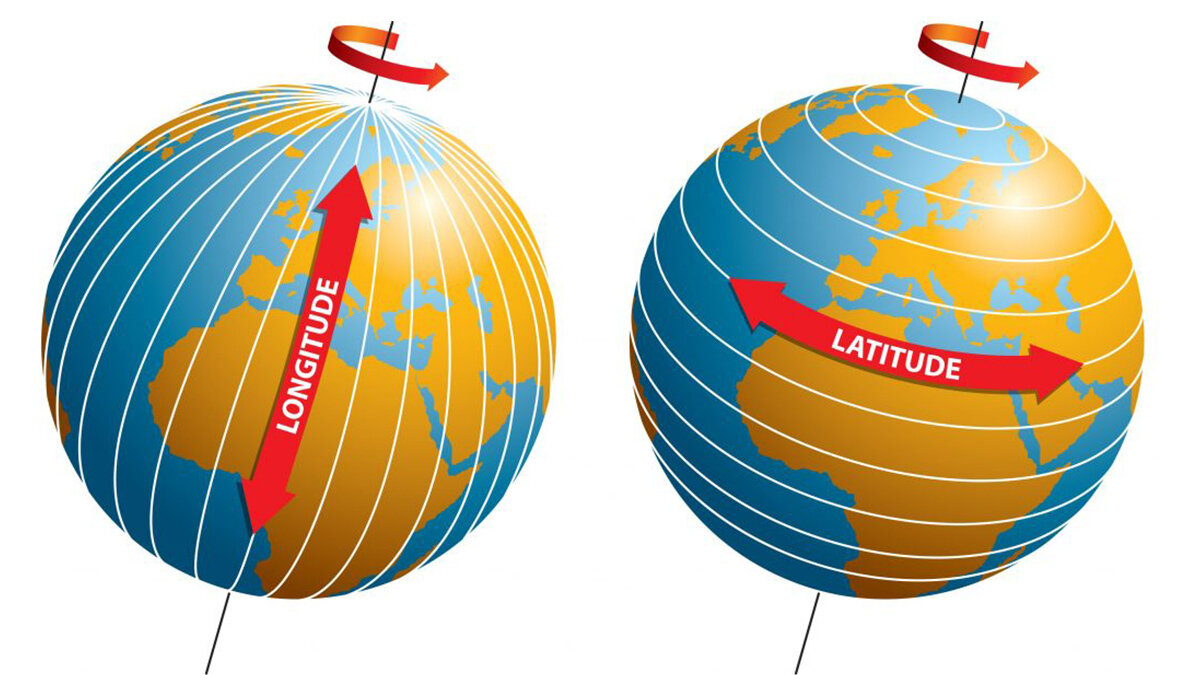
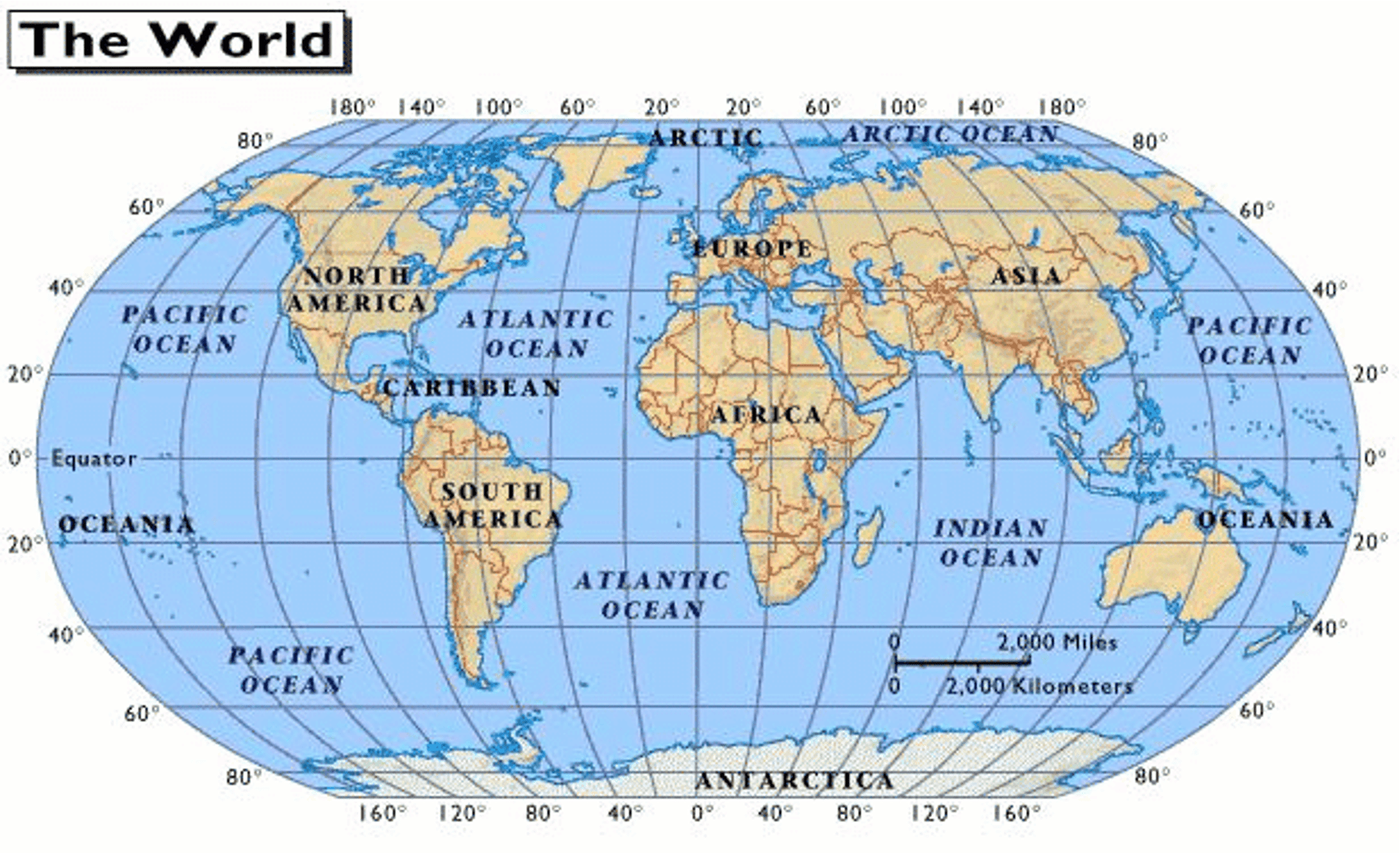
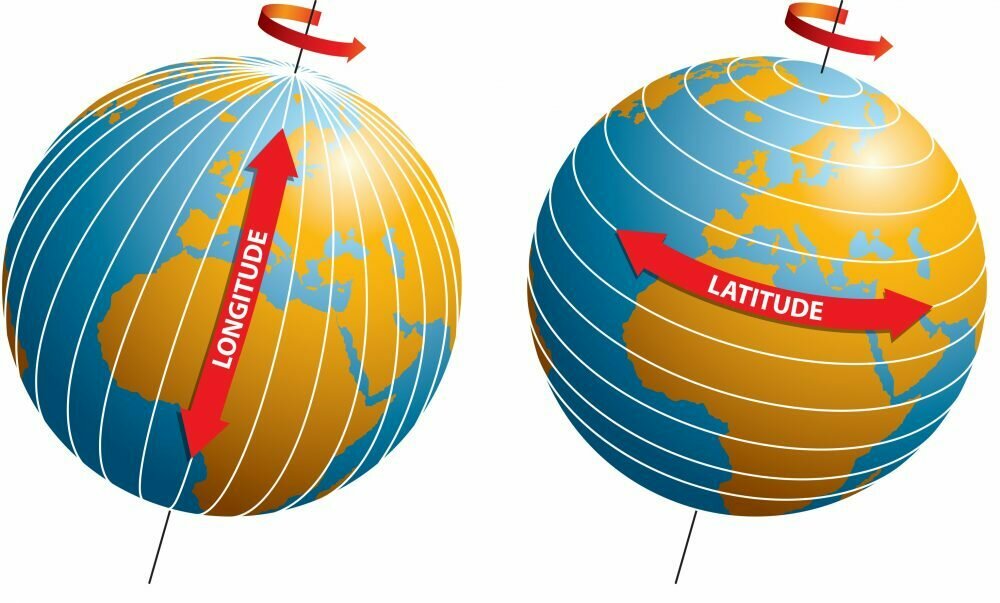
Sistema de Coordenadas Geográficas
Linhas imaginárias de latitude e longitude definem um sistema de coordenadas por meio do qual a posição ou localização de qualquer lugar na superfície da Terra pode ser determinada.
Fonte: GOOGLE
Sistema de Coordenadas Geográficas
A latitude é medida em graus (°), minutos (′) e segundos (″), variando de 0° no Equador a 90° nos polos (Norte e Sul).
Fonte: Shutterstock.com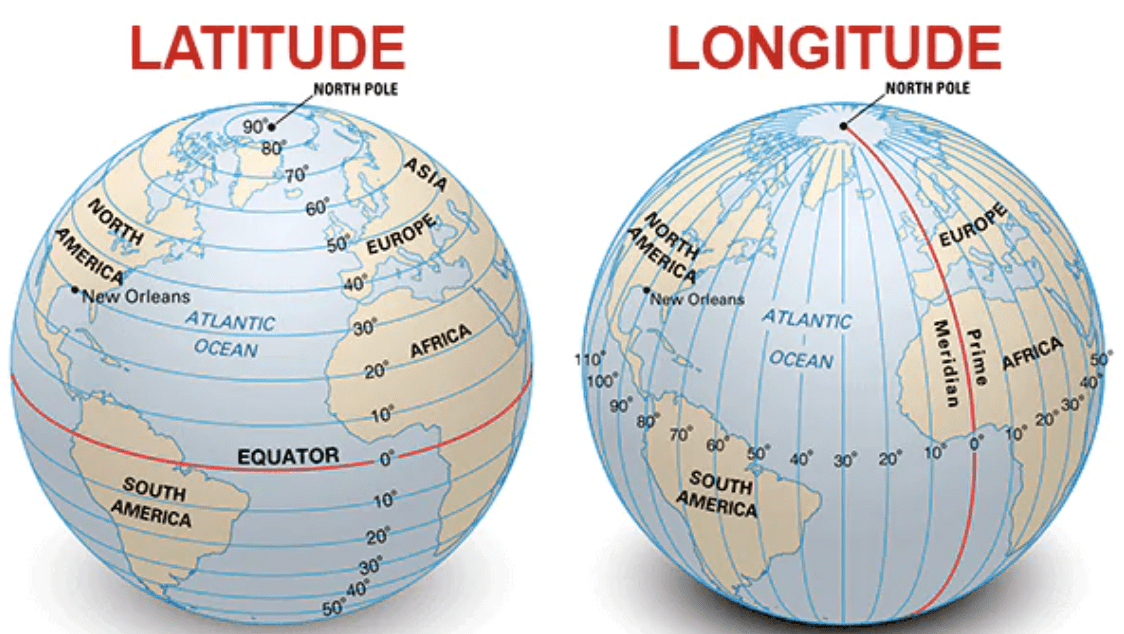
A longitude também é medida em graus, minutos e segundos, variando de 0° no Meridiano de Greenwich a 180° a leste ou oeste.
ECT - Anel Viário Contorno do Campus s/n - Capim Macio, Natal - RN, 59078-970
Latitude
Longitude
Fonte: Google MapsSistema de Coordenadas Geográficas
Identifique a latitude e longitude de algums pontos.
Estime a distância utilizando a escala da figura.
Norte
Sul
Leste
Oeste
Latitude e Longitude
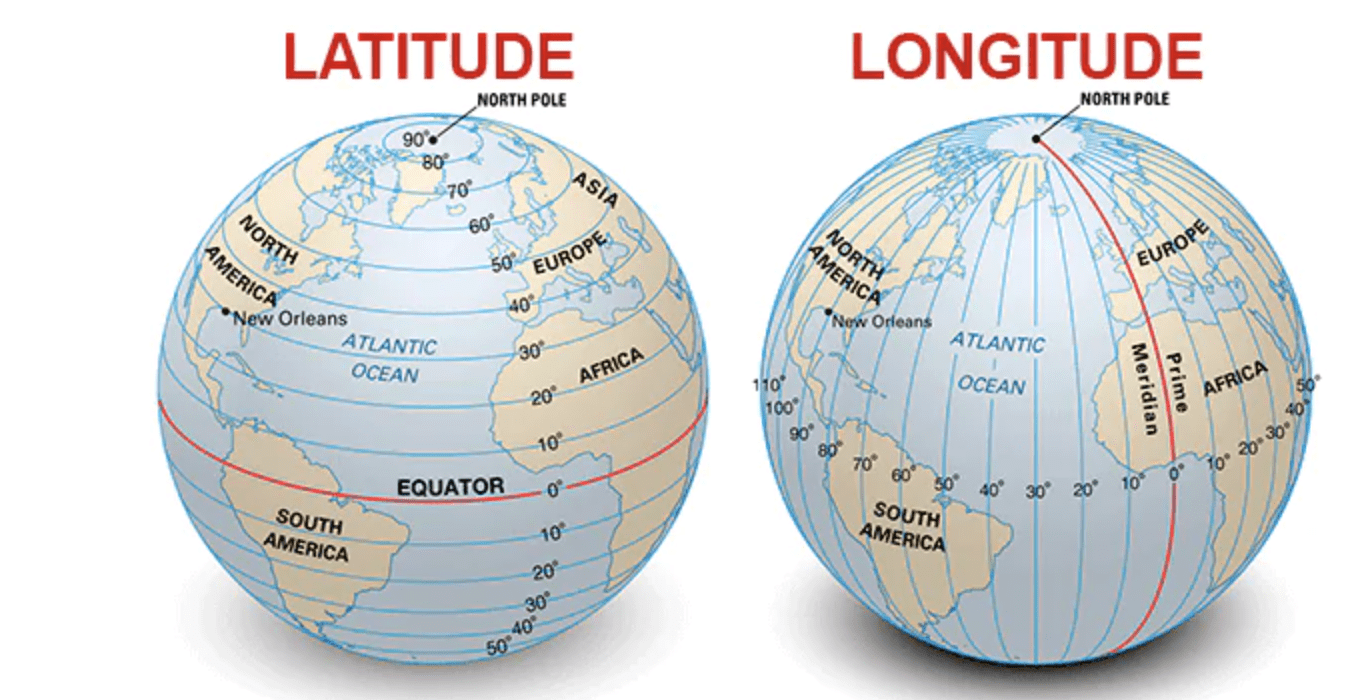
Latitude e longitude nada mais são do que nomes que as coordenadas geográficas únicas obtidas para cada ponto da superfície terrestre.
A latitude é o ângulo formado entre o ponto de interesse e o equador terrestre. A mesma é medida ao longo do meridiano que passa pelo lugar de interesse.
A longitude geográfica é o ângulo formado entre o meridiano de Greenwich e o meridiano que passa pelo ponto considerado.
Latitude e Longitude
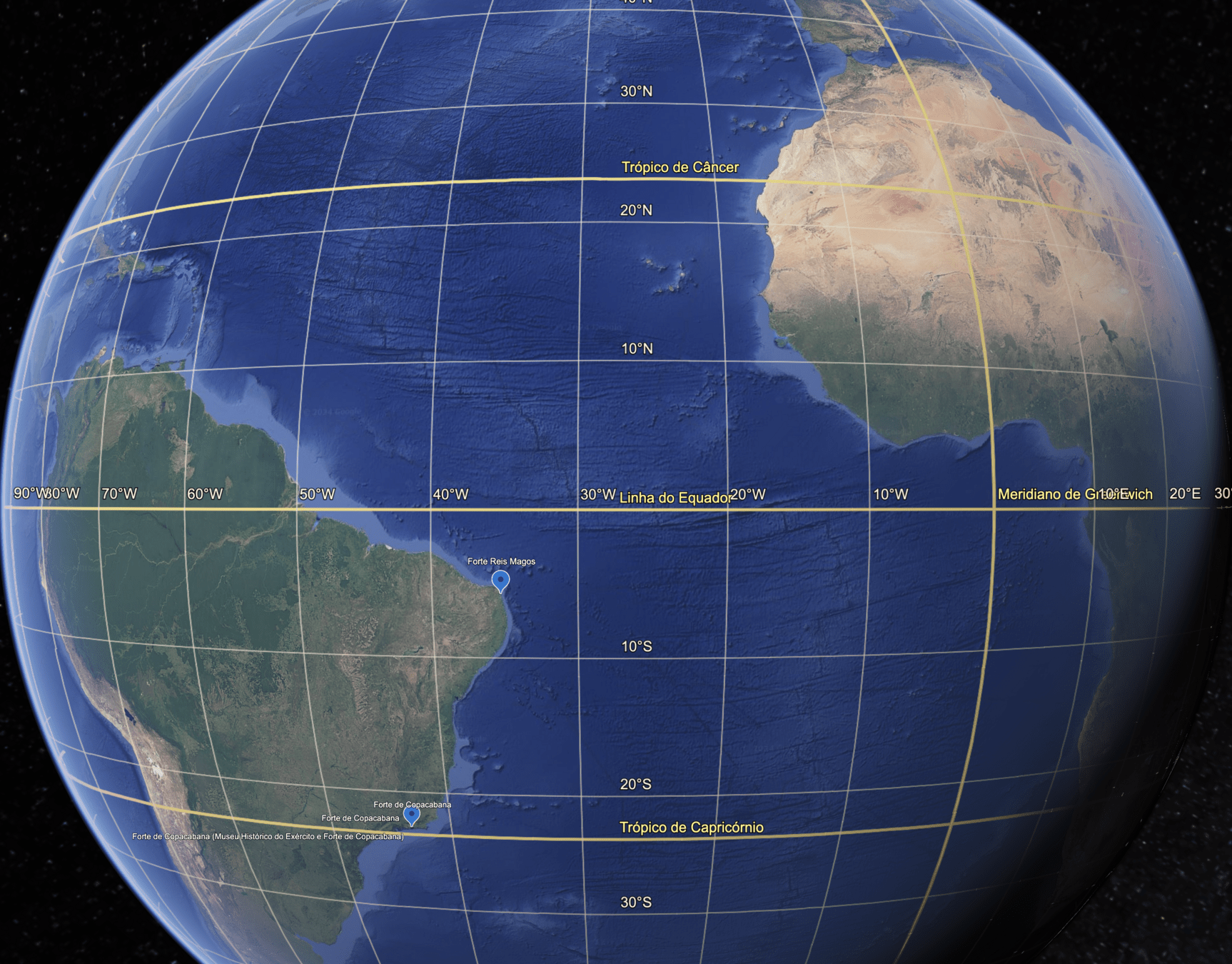
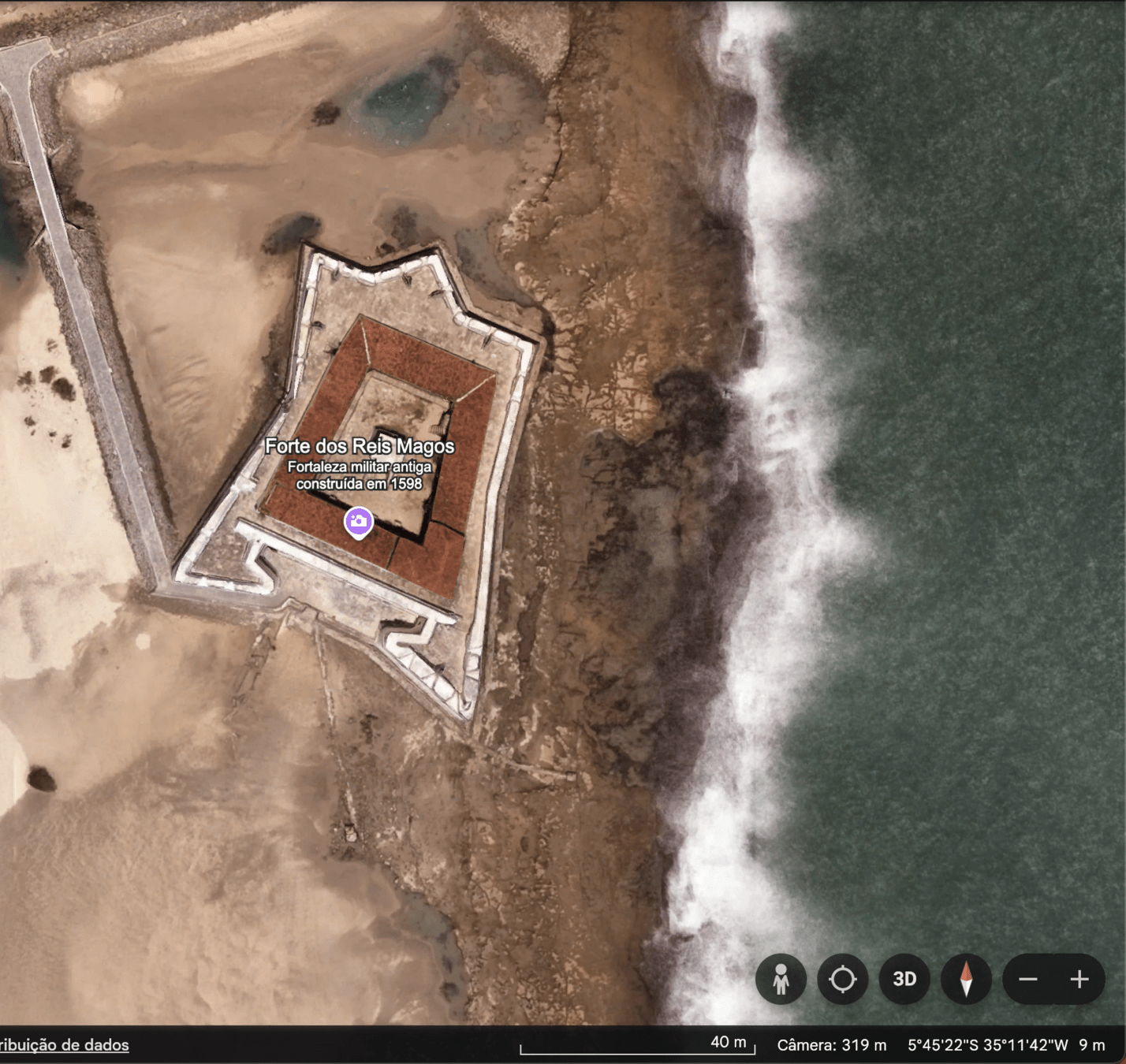

Latitude e Longitude
Início: Forte Reis Magos
Fim: Biblioteca Central UFRN
Distância:
A latitude mudou
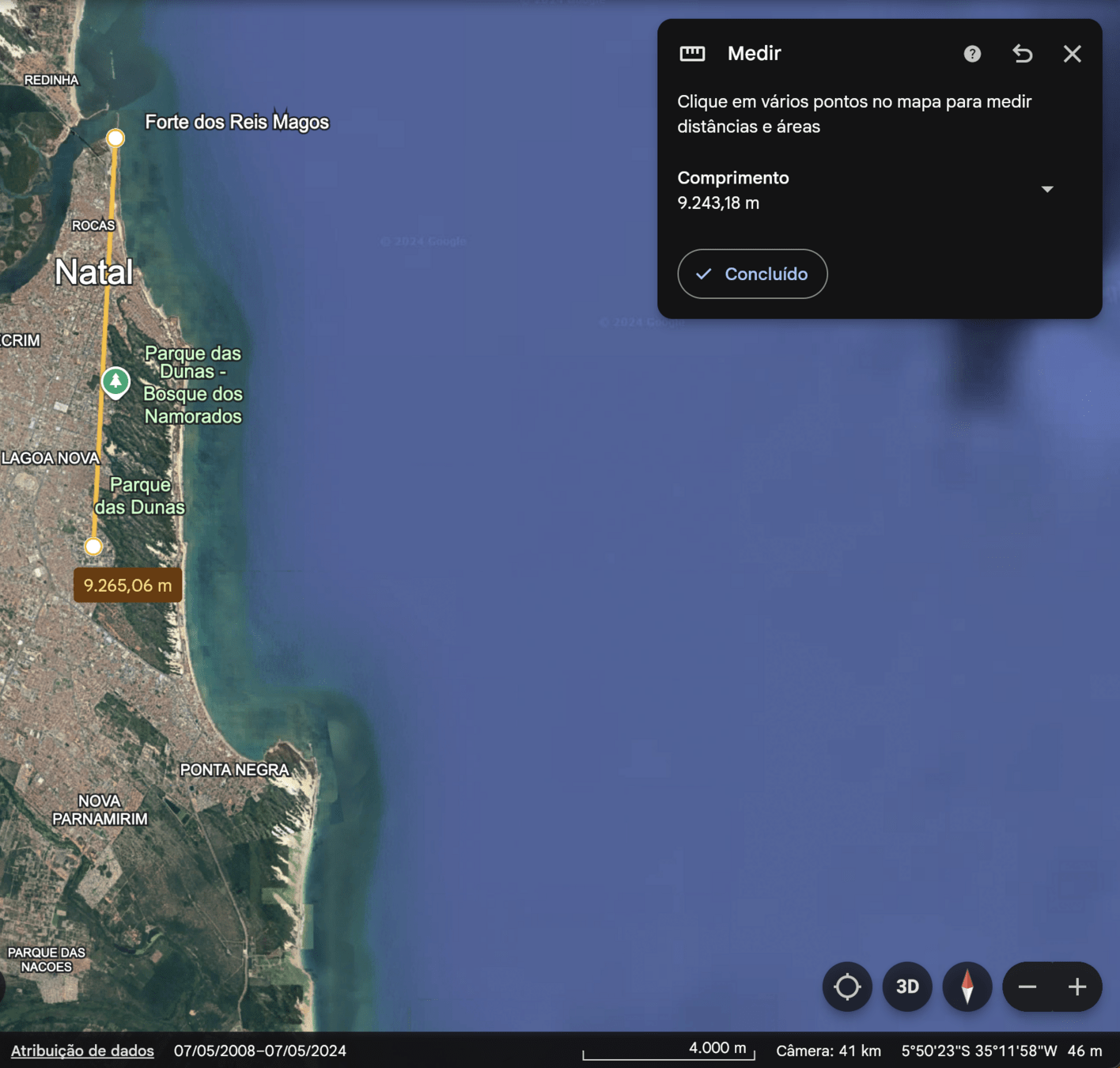
Latitude e Longitude
Início: Forte Reis Magos
Fim: Rio Santana
Distância:
A longitude mudou

Latitude e Longitude
Início: Forte Reis Magos
Fim: Rio Santana
Distância:

A longitude mudou

Sistema de Coordenadas Geográficas
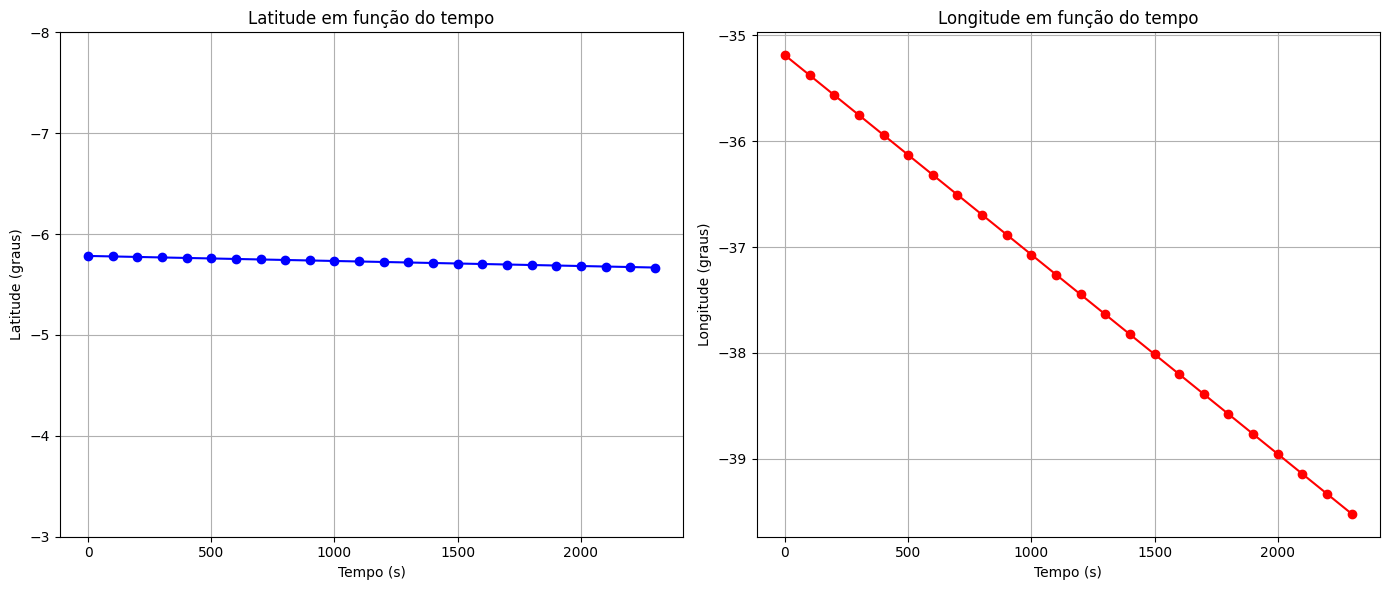
O que mudou mais no trajeto AB, em amarelo, abaixo do equador? Longitude ou Latitude?
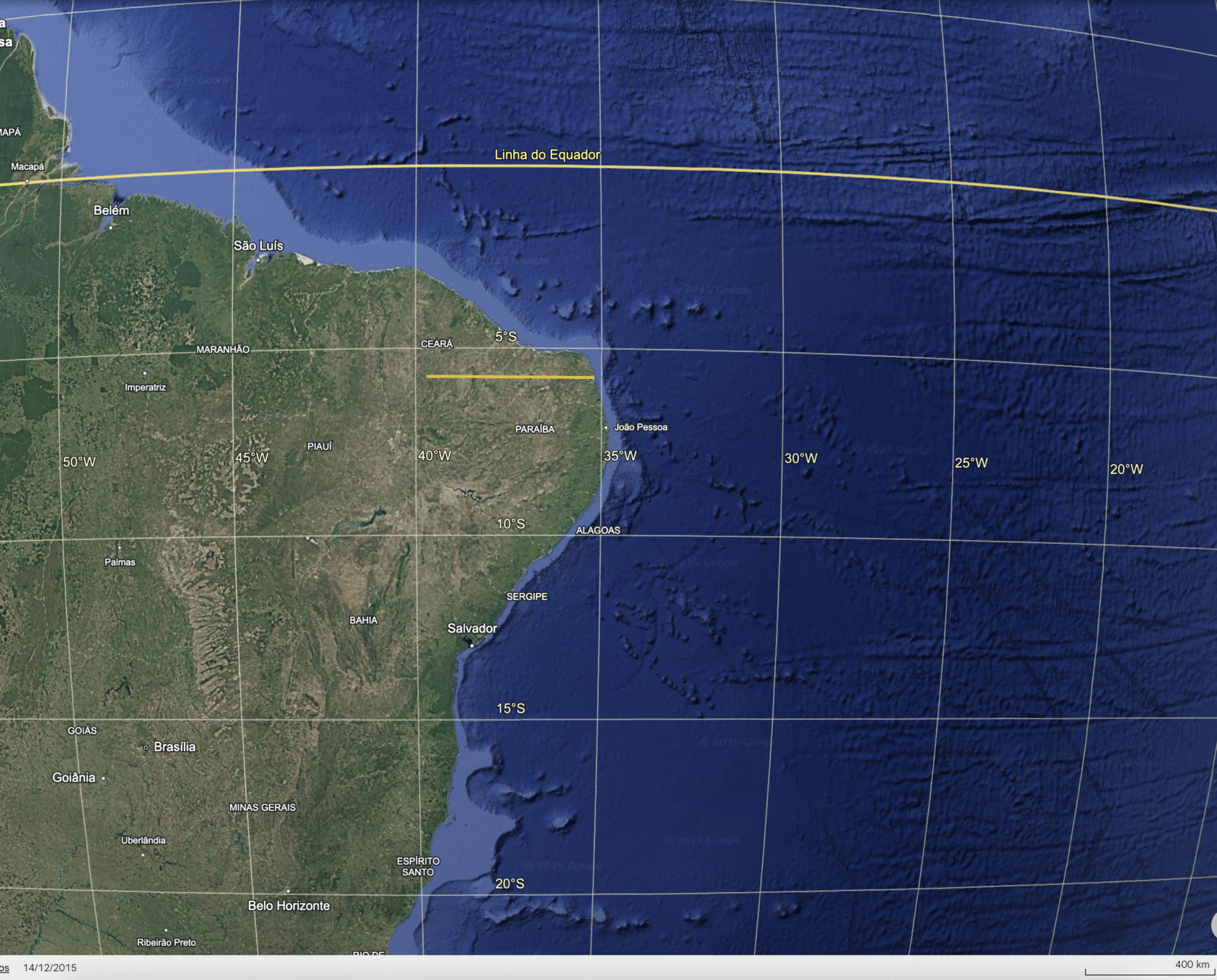


O movimento foi de:
- Leste para Oeste ?
- Oeste para Leste ?
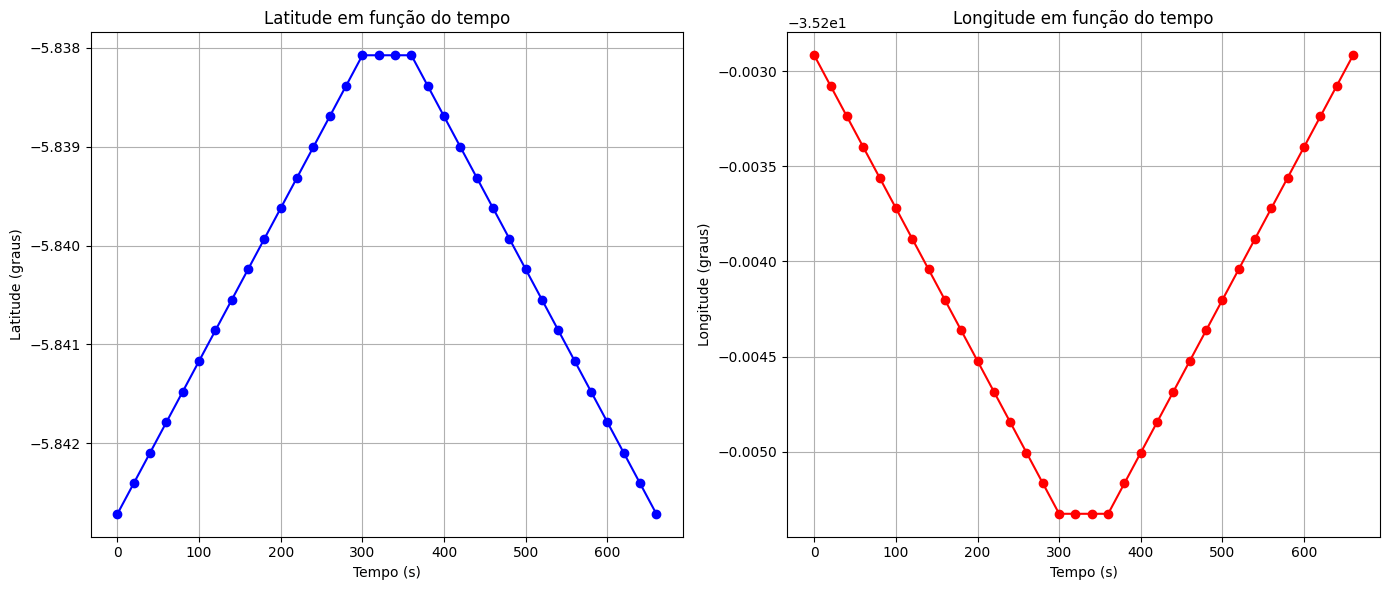
Gráficos de Latitude e Longitude em função do tempo de A para B.
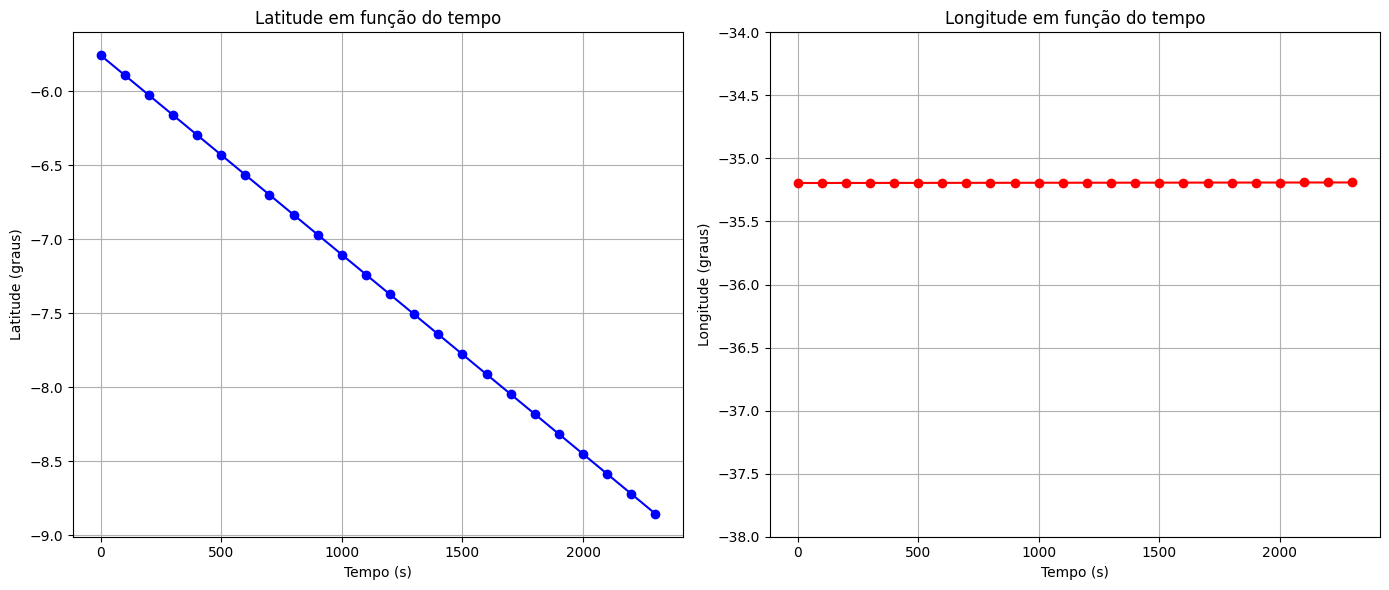
Sistema de Coordenadas Geográficas
O que mudou mais no trajeto AB, em vermelho? Longitude ou Latitude?
O movimento foi de:
- Norte para Sul ?
- Sul para Norte ?
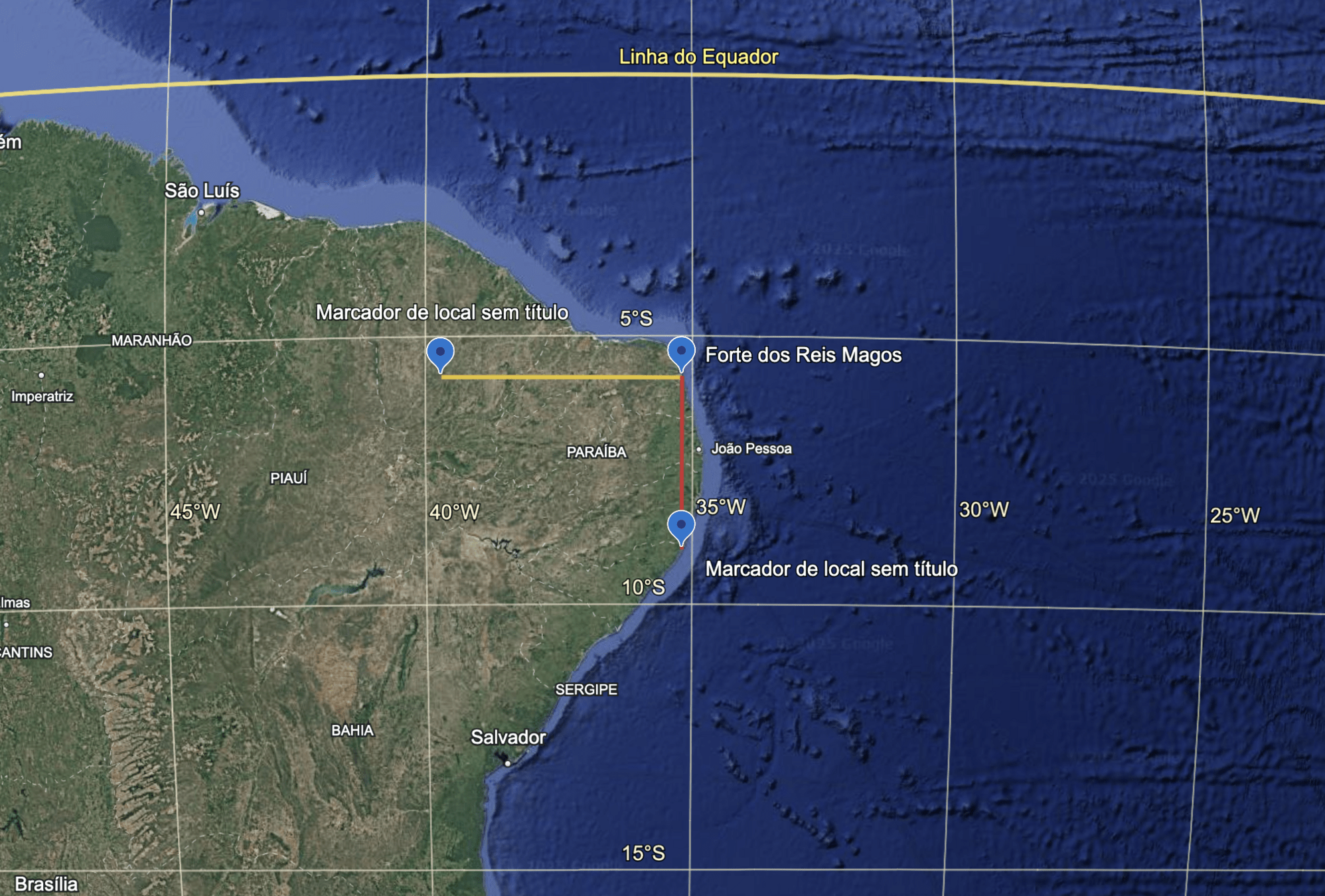


Gráficos de Latitude e Longitude em função do tempo de A para B.
Sistema de Coordenadas Geográficas
Como seriam os gráficos de Latitude e Longitude entre os dois pontos abaixo (BR101)?
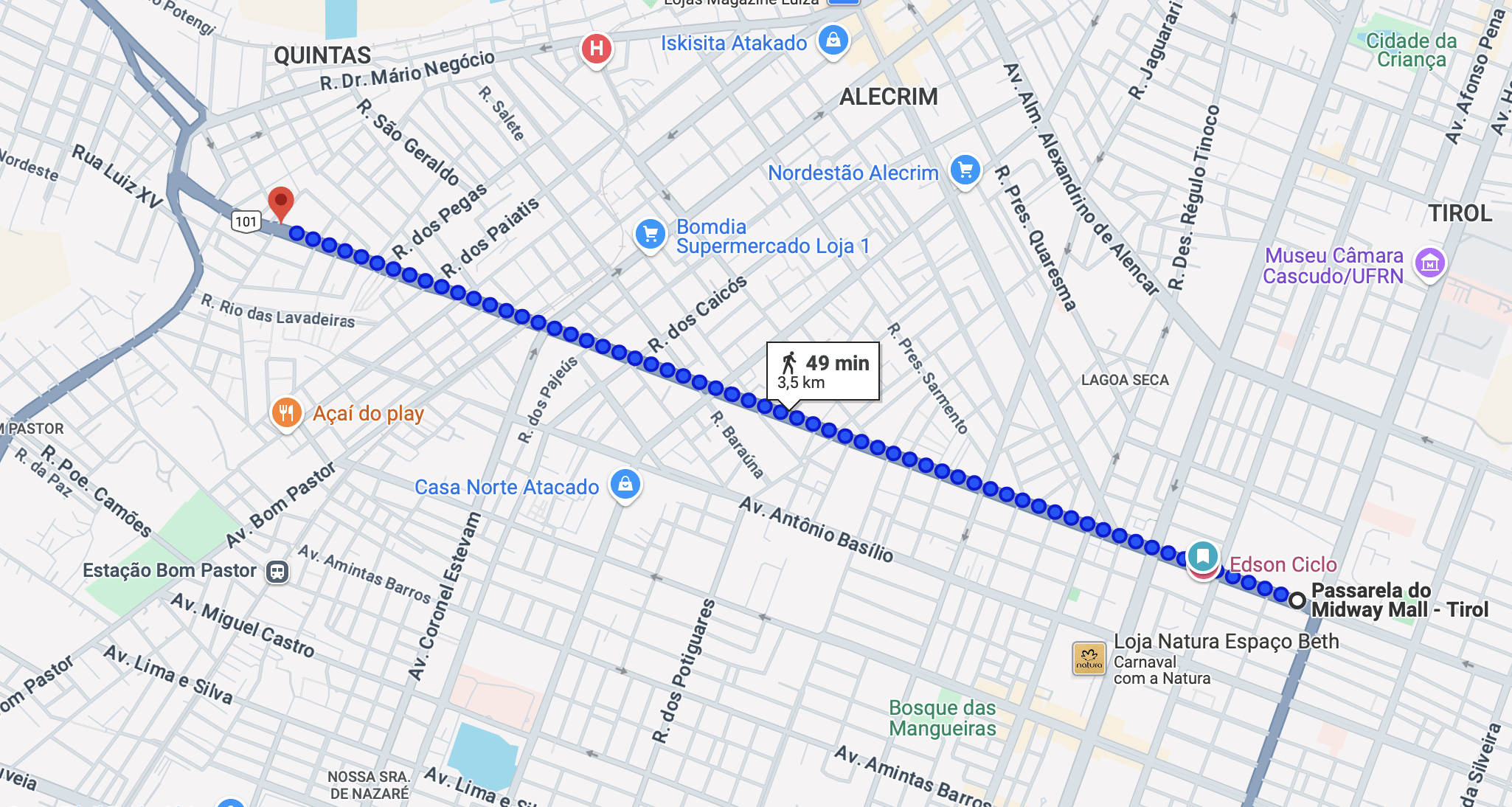
Ponto A:
Lat: -5,812595
Lon: -35,205303
Ponto B:
Lat: -5,801684
Lon: -35,235262
Fonte: https://www.google.com.br/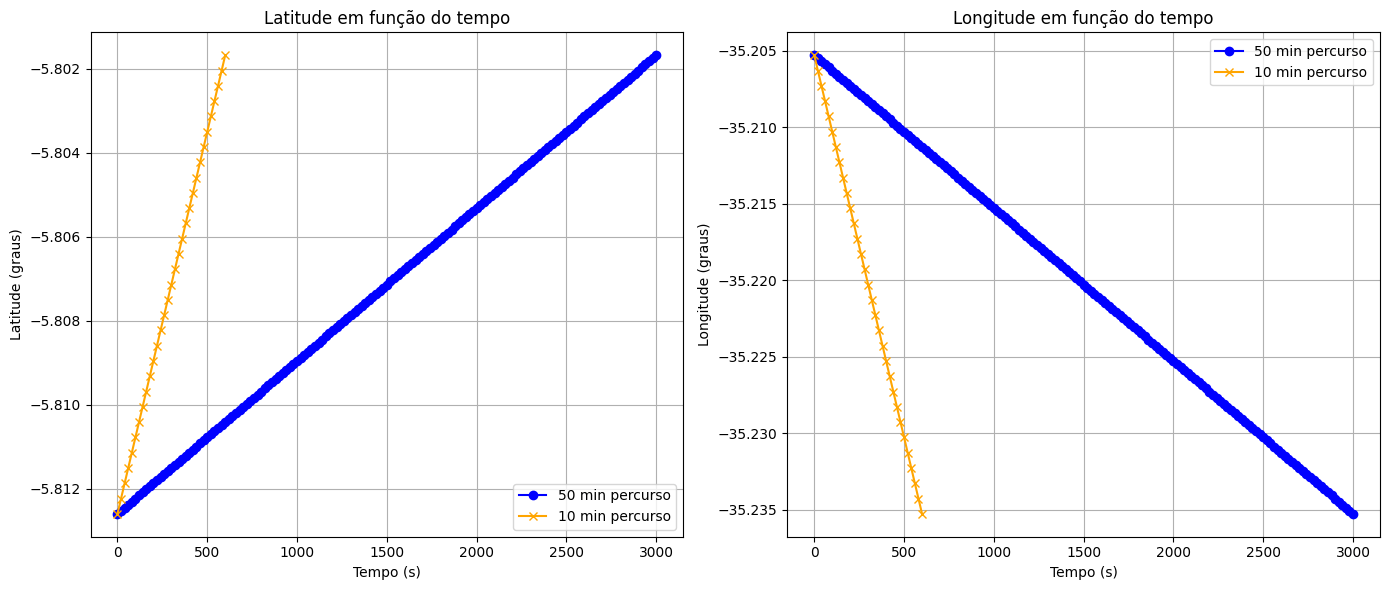
Qual o significado das linhas amarela e azul?
Estamos indo mais ao Norte ou mais ao Sul?
Estamos indo mais ao Oeste ou mais ao Leste?
Sistema de Coordenadas Geográficas
Considerando os gráficos de Longitude e Latitude. Qual seria o mapa correspondente, de ida e volta entre A e B, mas com uma paradinha em B antes
de retornar até A?
Fonte: Google Maps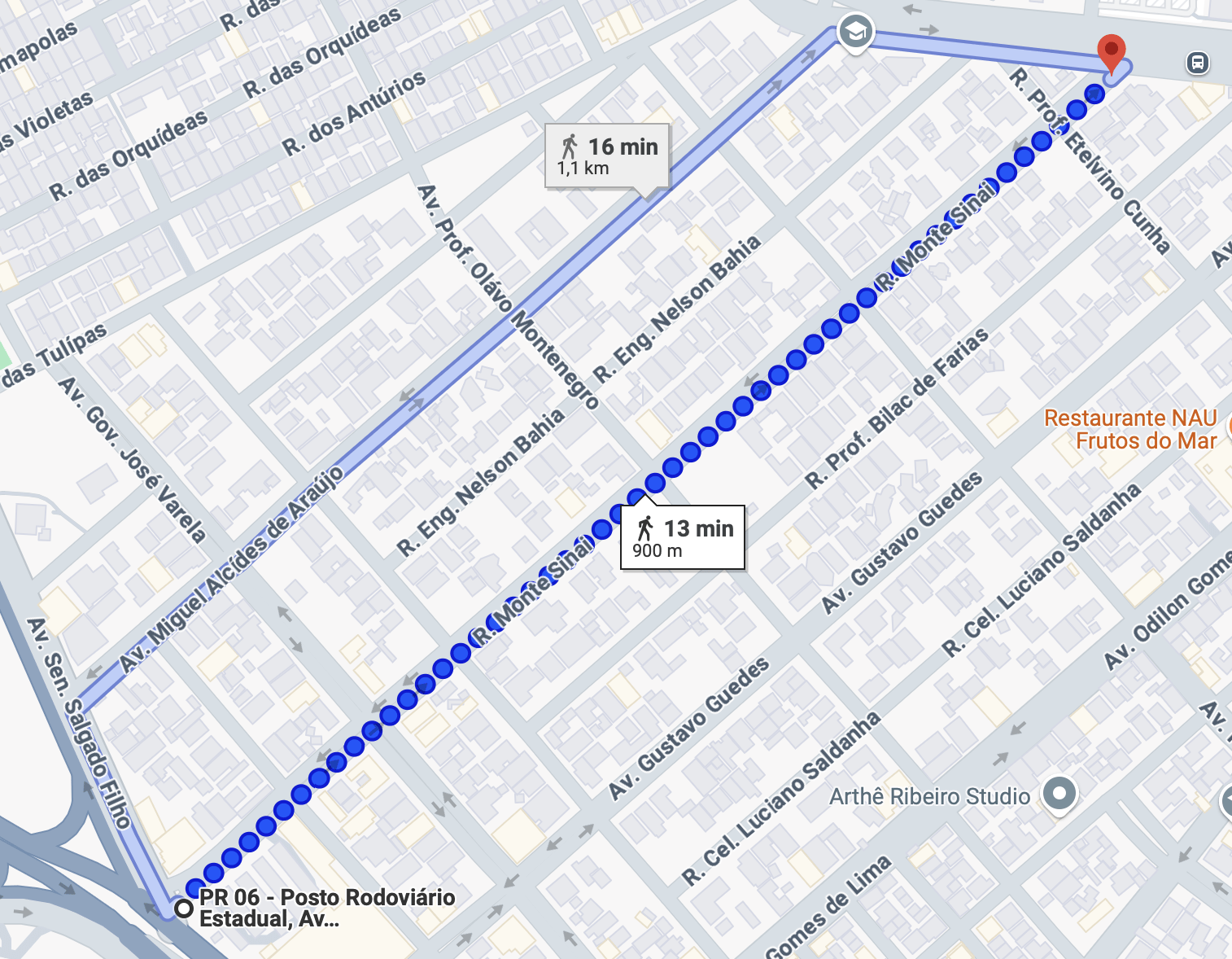
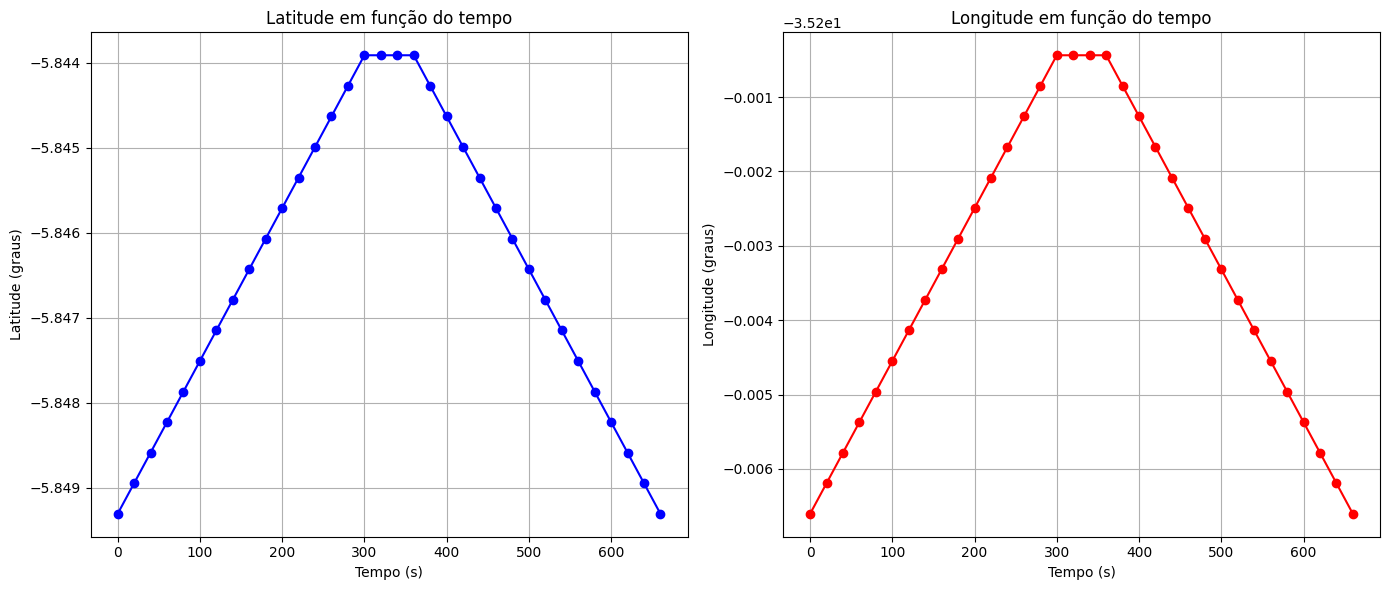
Mapa 1
Mapa 2
Fonte: Google MapsComo seria o gráfico do outro mapa?
Sistema de Coordenadas Euclidianas


Parque da cidade
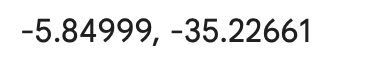
Como calcular a distância em sistema de coordenadas esféricas para pequenos deslocamentos a partir das coordenadas geográficas de longitude e latitude?
Calculamos a distância em um sistema de coordenadas esféricas para pequenos deslocamentos.
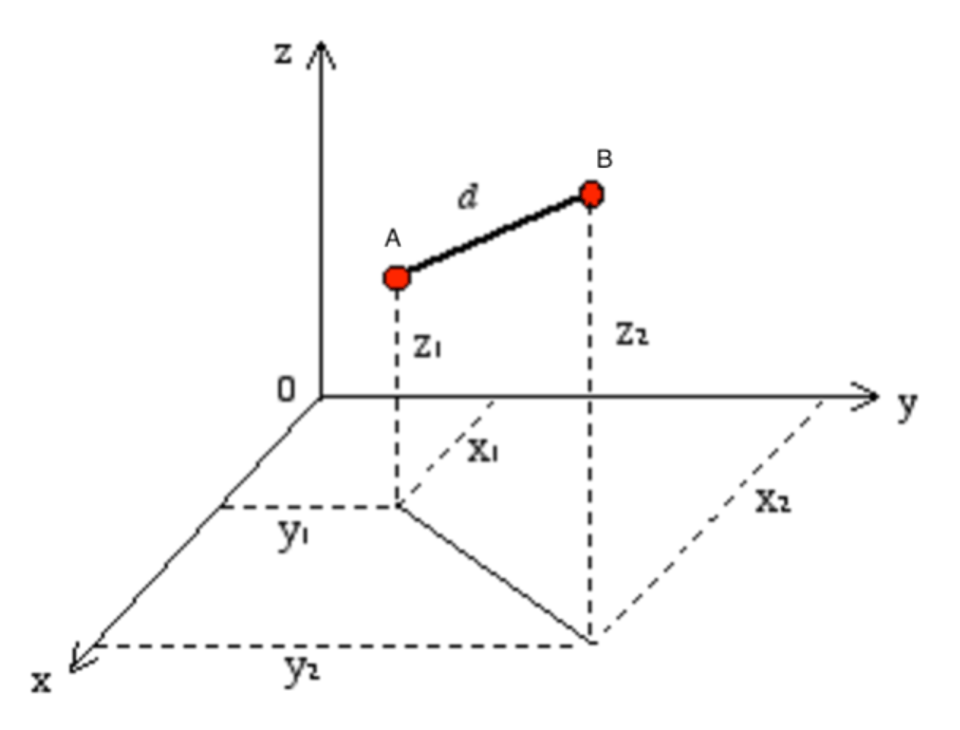
Sistema de Coordenadas Euclidianas
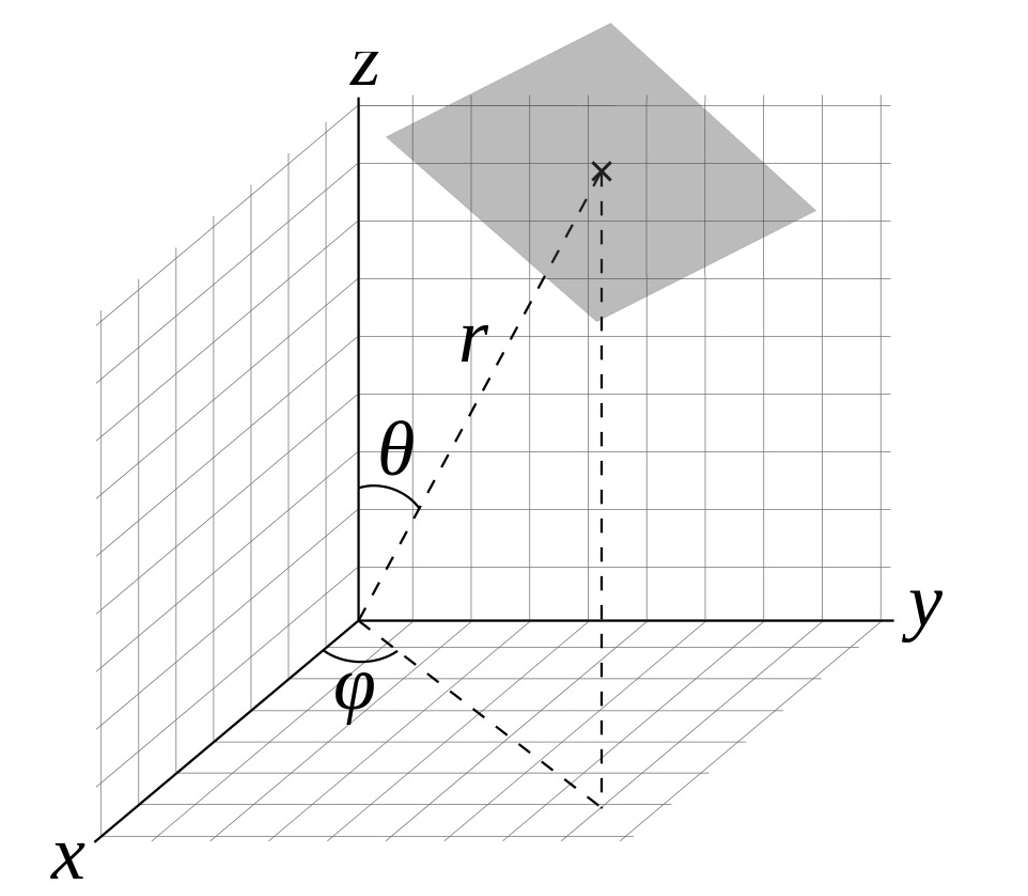
Vivemos em um planeta esférico, então precisamos usar esse sistema.
Em um sistema de coordenadas esféricas, um ponto é identificado por r, θ e φ.
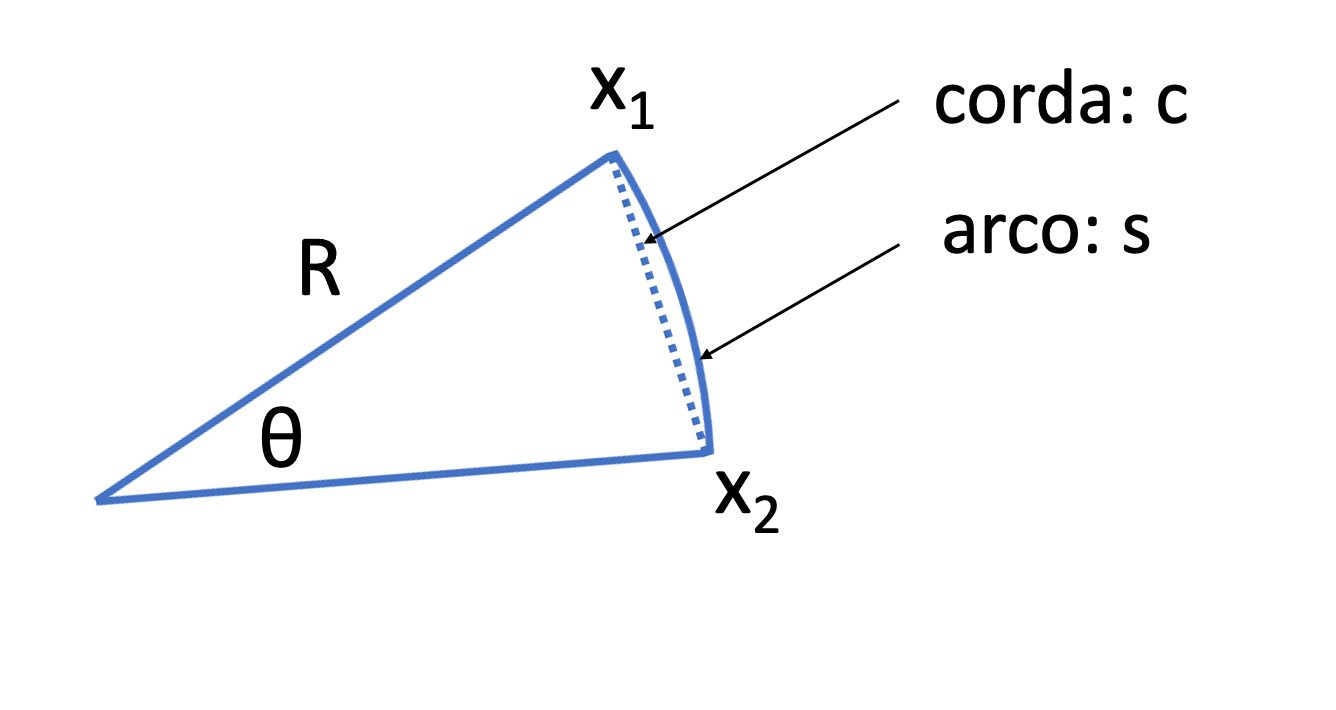
A distância entre \(x_1\) e \(x_2\) ao longo de uma linha reta é o comprimento da corda,
\(c = 2R \sin(\theta /2)\)
Sistema de Coordenadas Euclidianas
Vivemos em um planeta esférico, então precisamos usar esse sistema.

A distância entre \(x_1\) e \(x_2\) ao longo de uma linha reta é o comprimento da corda,
\(c = 2R \sin(\theta /2)\)
Distância entre \(x_1\) e \(x_2\) ao longo do arco é o comprimento do arco,
\(s = R\theta\)
Para \(R\) longo e pequeno \(\theta\), \(\sin(\theta) \approx \theta\).
Então, a corda \( c = 2R\sin(\theta/2) \approx R\theta = s\).
Sistema de Coordenadas Euclidianas
Vivemos em um planeta esférico, então precisamos usar esse sistema.

Conforme você viaja em uma linha de longitude, o raio do seu círculo é o raio da Terra, o ângulo que você cobre é \(Lat_2 – Lat_1\).
A distância percorrida ao longo da longitude
\(x \approx R(Lat_2-Lat_1)\).
Conforme você viaja em uma linha de latitude, o raio do seu círculo depende da sua longitude como \(R \cos(Lat)\). (Raio de latitude grande no equador e pequeno perto dos polos.)
O ângulo que você cobre é \(Long_2 – Long_1\). Na aproximação de ângulo pequeno:
Distância percorrida ao longo da latitude
\((y) ≈ R \cos(Lat) (Long_2 – Long_1)\)
Sistema de Coordenadas Euclidianas
Vivemos em um planeta esférico, então precisamos usar esse sistema.

Ao alterar a longitude e a latitude, combine os dois lados iguais do triângulo para obter a distância total percorrida:
Para localizações com \(Lat_1, Long_1\) e \(Lat_2, Long_2\), em graus:
onde R = 6,356 km é o raio da terra e \(\pi/180\) converte graus para radianos.