
Aula 03
Fundamentos da Mecânica
Prof. Ronai Lisbôa
BCT - ECT - UFRN
Objetivos
Descrever o movimento acelerado.
Obter a função posição do movimento acelerado.
Obter a função velocidade do movimento acelerado.
Definir a aceleração.
Estudar os gráficos:
Posição em função do tempo; Velocidade em função do tempo; Aceleração em função do tempo.
Identificar o Movimento Retilíneo Uniforme Variado (MRUV).
Bibliografia:
Tipler - Cap. 2
Seções 2.2 e 2.3 (págs. 35 a 46)
- Refaça os Exemplos resolvidos.
- Faça os exercícios recomendados no SIGAA.
O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)
Quando a velocidade é constante no tempo.
É observado que os deslocamentos são uniformes em intervalos de tempos iguais.

A função movimento é a equação de uma reta:
A velocidade é calculada a partir da derivada da função posição no tempo:
O gráfico da velocidade em função do tempo \((v\times t)\) é uma reta paralela ao eixo dos tempos.
No Movimento Retilíneo Uniforme a velocidade é constante.
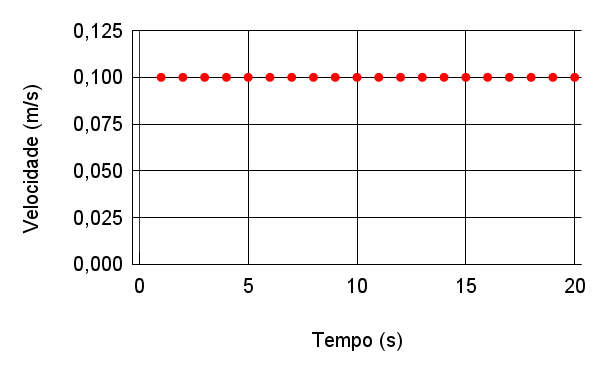
com inclinação constante no gráfico \(x\times t\).
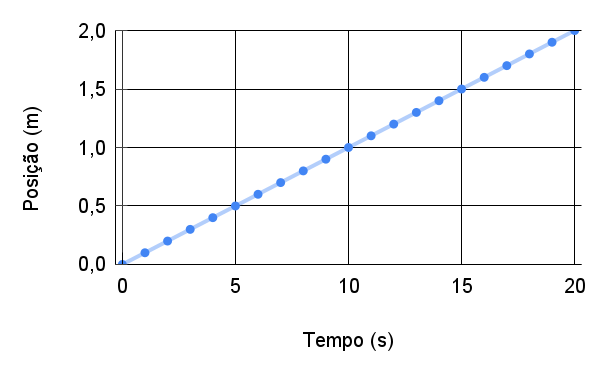
Às vezes, a velocidade de um objeto é constante.
Uma vez que a velocidade é um vetor, ela pode variar de duas maneiras:
O módulo pode mudar, indicando uma variação da rapidez.
A orientação pode mudar, indicando uma alteração da orientação do movimento do objeto.
\(\vec v_1\) é constante
\(\vec v_2\) é constante
Com mais freqüência, a velocidade de um objeto varia enquanto ele se move.
\(\vec v_3\) não é constante
\(\vec v_4\) não é constante
Quando a velocidade não é constante no tempo
Movimentos onde a velocidade varia no tempo são mais comuns.
Quando a velocidade não é constante no tempo
Movimentos onde a velocidade varia no tempo são chamados de acelerados.

Na prova dos 100 m nado costas a rapidez não é constante a cada intervalo de tempo (olhe as inclinações diferentes entre cada par de dados).
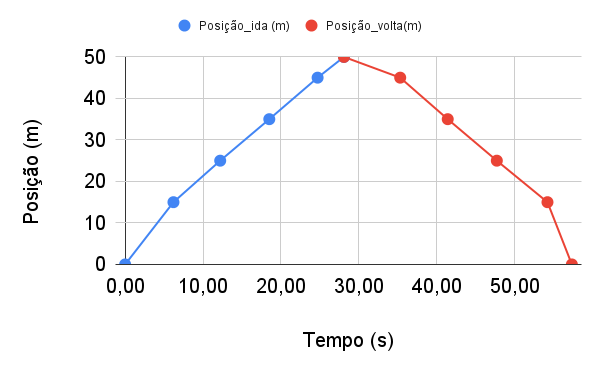
No gráfico posição x tempo, a inclinação da reta muda indicando que a velocidade não é constante.
No gráfico velocidade x tempo, a inclinação da reta não é exatamente paralela ao eixo dos tempos.
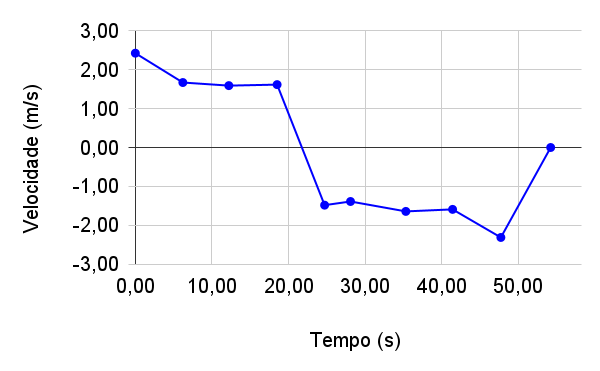
Movimentos acelerados são observados frequentemente na natureza.



Caindo ou pulando de uma pequena altura
Descendo ou subindo sobre uma rampa
Correndo ...
Movimentos acelerados (variação da velocidade no tempo)
Queda livre
Plano inclinado
Correndo aceleradamente!
Fonte: https://www.pxfuel.com
Fonte: https://en.wikipedia.org
Fonte: www.pixbay.com
Nós vamos estudar três tipos de movimentos onde a aceleração é constante.
Veículos usualmente aceleram. O que isso significa?
Movimentos acelerados (variação da velocidade no tempo)
Ferrari 488 Pista Spider
0 - 100 km/h em 2,8 s
SF90 Stradale
0 - 100 km/h em 2,5 s
Ferrari 812 Superfast
0 - 100 km/h em 2,9 s
Ferrari 812 Competizione A
0 - 100 km/h em 2,9 s
Ferrari Daytona SP3
0 - 100 km/h em 2,8 s
Ferrari Roma
0 - 100 km/h em 3,4 s
Que grandeza é esta?
O que significa?
Como avaliar?
A aceleração média de um objeto é a variação no componente da velocidade dividida pelo intervalo de tempo durante o qual essa variação ocorreu.
A palavra média reforça a ideia de que a velocidade pode variar a taxas diferentes.
No Sistema Internacional:
metros por segundo por segundo
Se \(v\) varia de 0 a +5,0 m/s em 1,0 s:
O componente da velocidade aumenta por +5,0 m/s a cada segundo.
Se \(v\) varia de +5,0 m/s a +10,0 m/s em 1,5 s:
O componente da velocidade aumenta por +3,3 m/s a cada segundo.
Definição de aceleração média
Se a velocidade de um objeto está variando no tempo, o objeto está acelerando.
A velocidade varia de 0 a 100 km/h em 2,9 s.
A velocidade varia de 0 a 200 km/h em 7,8 s.
\(v_{max}\) = 340 km/h
O componente da velocidade aumenta por +9,6 m/s a cada segundo.
O componente da velocidade aumenta por +7,1 m/s a cada segundo.
A velocidade varia de 0 a 27,8 m/s em 2,9 s.
A velocidade varia de 0 a 55,6 m/s em 7,8 s.

Ferrari F8
a aceleração é constante nesse intervalo de tempo.
a aceleração é constante nesse intervalo de tempo.
Definição de aceleração média
O vetor aceleração média define de quanto o vetor velocidade varia por unidade de tempo.
A aceleração da Ferrari 348TB é constante nos intervalos de tempo analisados.
A aceleração é constante, \(a_1=a_2\):
Aceleração vetorial média



Isso significa que a velocidade aumenta de 5,56 m/s a cada segundo. Após 5 s, a velocidade será
O aceleração vetorial média tem a direção da variação do vetor velocidade no intervalo de tempo decorrido.
Acelerado x Desacelerado
A rapidez aumenta e \(\vec a \text{ é paralelo } \vec v\).
A rapidez diminui e \(\vec a \text{ é antiparalelo } \vec v\).
Acelerando
Desacelerando






Aceleração constante e velocidade crescente
Aceleração constante e velocidade decrescente
O movimento acelerado é aquele em que a aceleração e velocidade têm os mesmos sentidos.
Exemplo 1
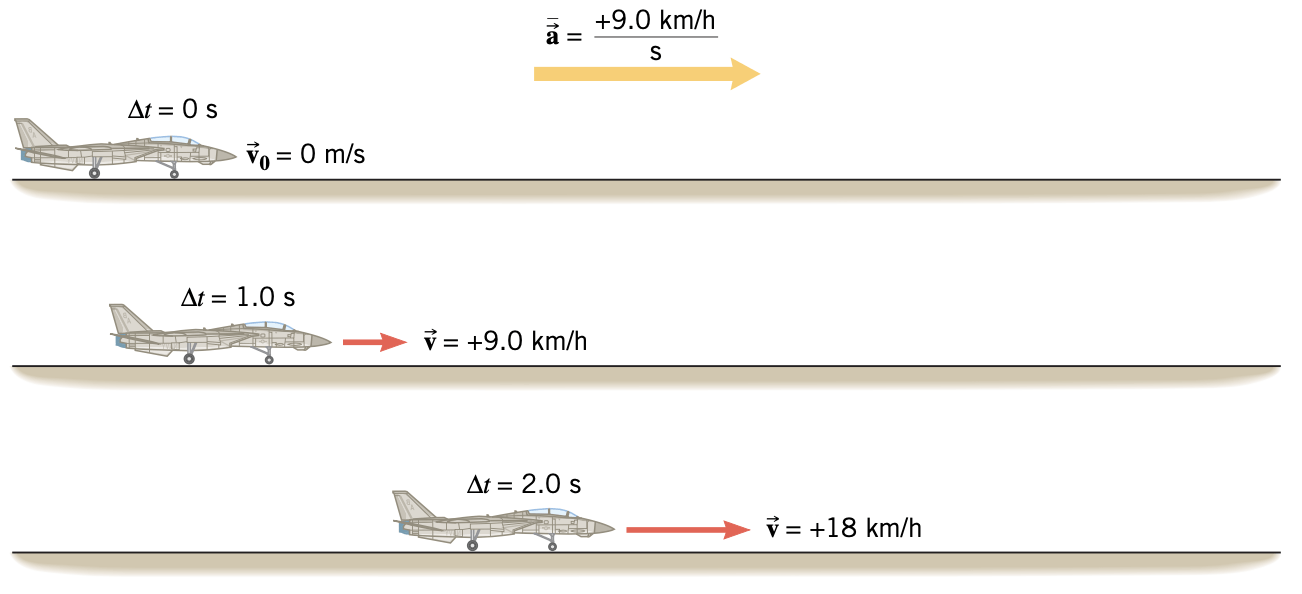
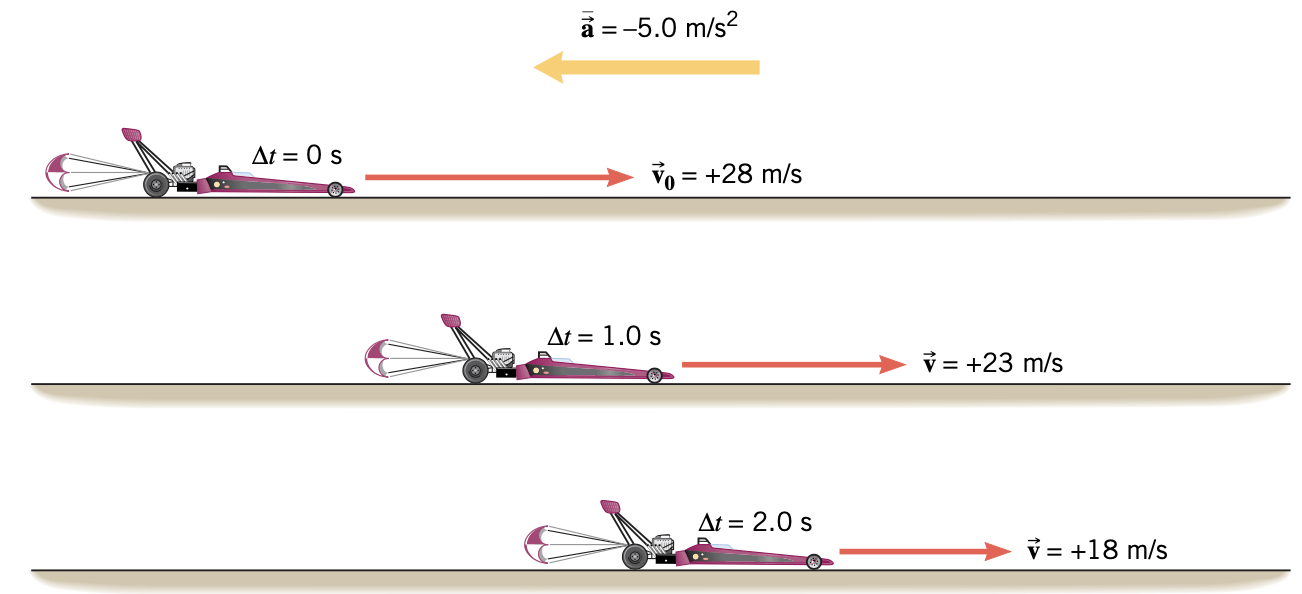
O movimento desacelerado é aquele em que a aceleração e velocidade têm sentidos opostos.
O movimento desacelerado é aquele em que a aceleração e velocidade têm sentidos opostos.
Calcule a aceleração e mostre o valor da velocidade final.
Como a aceleração é constante, a velocidade varia a uma taxa constante. Após 2,0 s,
Exemplo 2
O componente da velocidade de um carro aumenta de 0 para +5,0 m/s em 1,0 s e depois de +5,0 m/s a +10 m/s nos próximos 2,0 s.
Qual é o componente de sua aceleração média:
(a) durante o primeiro segundo,
(b) durante os últimos 2 segundos e
(c) durante todo o intervalo de 3,0 s?
a)
b)
c)
0
5 m/s
0 m/s
1 s
2 s
3 s
1 s
10 m/s
Exemplo 3
O componente x da velocidade de um carro muda de -10 m/s para -2,0 m/s em 10 s.
(a) O carro está viajando na direção x positiva ou negativa?
(b) \(\Delta \vec v\) aponta no sentido x positivo ou negativo?
(c) O componente x da aceleração do carro é positivo ou negativo?
(d) O carro está aumentando ou diminuindo a rapidez?
Ao trabalhar com objetos que viajam na direção negativa, não confunda “componente positivo da aceleração” com “rapidez aumentando”. O componente da velocidade nesse exemplo, por exemplo, está aumentando (fica menos negativo, isto é -10 m/s < - 2,0 m/s !) e, portanto, \(a_x\) é positivo, mesmo que o carro esteja ficando mais lento.
Ele está desacelerando porque as velocidades são contrárias à aceleração.
No movimento acelerado observamos deslocamentos variados em tempos iguais.
Como será a função posição?
A velocidade varia uniformemente no tempo. Qual será a função velocidade?
Sabemos que a aceleração média é constante e é dada por meio da equação:

Função velocidade e posição para o movimento com aceleração constante
Quando a aceleração média é constante é bastante fácil obter a função velocidade.
Desenvolvendo essa equação:
A função velocidade é a equação de uma reta no gráfico \(v_x \times t\).
As constantes (\(v_{0x},t_0\)) são as condições iniciais e não alteram o valor da aceleração.

\(a_{m,x} \equiv \) inclinação
A inclinação da reta é constante e numericamente igual à aceleração.
Gráfico da velocidade em função do tempo
Função velocidade para o movimento com aceleração constante
Exemplo 4
Um objeto tem uma velocidade inicial \(v_i = 8\) m/s no instante inicial \(t_i = 0\) s e sua aceleração é constante e vale \(a = 3\) m/s\(^2\).
Qual o valor da aceleração média entre os tempos t = 1 s e t = 4 s.
Agora, a velocidade inicial passa a ser \(v_i = 23\) m/s, no instante inicial \(t_i = 5\) s. A aceleração ainda é constante e vale \(a = 3\) m/s\(^2\).
Escreva a função velocidade.
Escreva a função velocidade.
Qual o valor da aceleração média entre os tempos t = 6 s e t = 8 s.
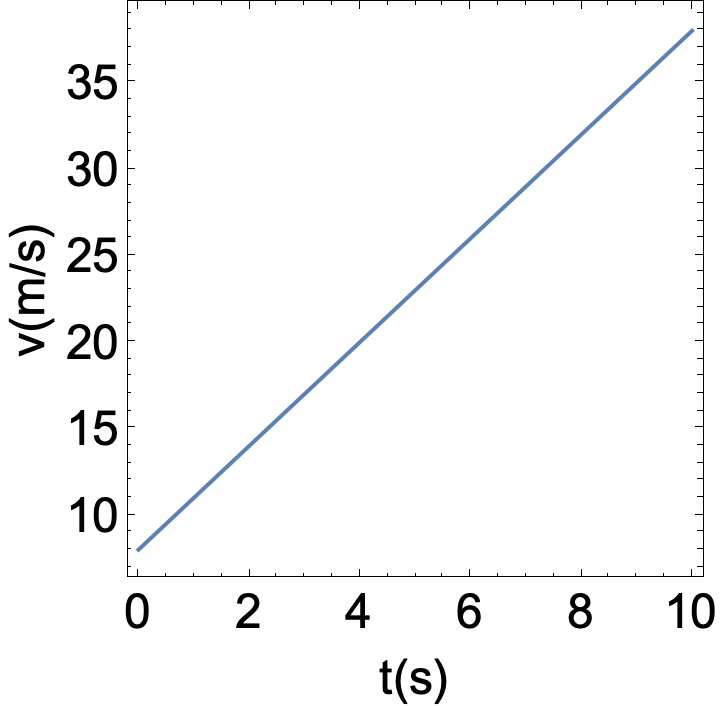
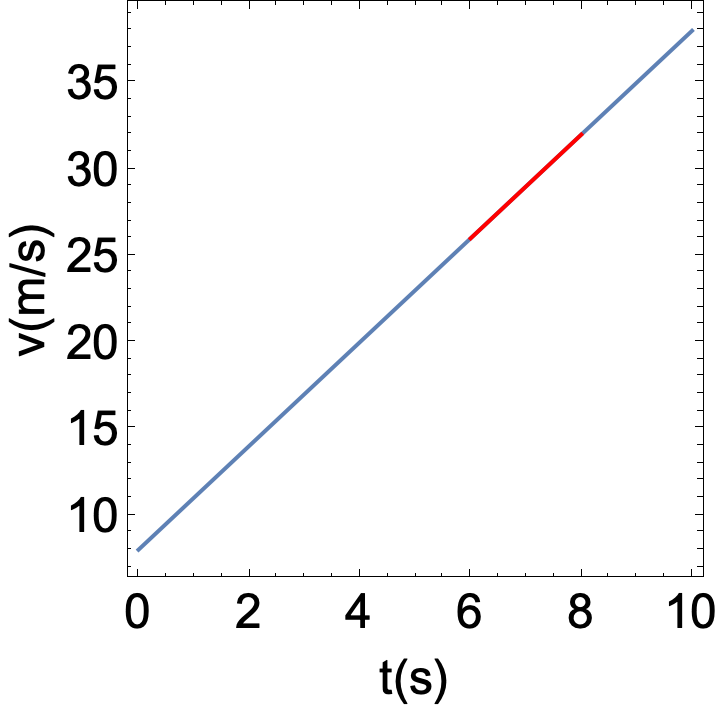
A função posição pode ser obtida facilmente a partir do gráfico da velocidade em função do tempo e da definição da aceleração média: \(a_{m,x}=\Delta v/\Delta t\).
A área sob a curva da velocidade é numericamente igual ao deslocamento do objeto!

\(a_x \equiv \) inclinação
Gráfico da velocidade em função do tempo

Note que: .
Então:
A dimensão dessa equivalência é comprimento. Assim, \(A\equiv \Delta x\) e
A função posição para o movimento com aceleração constante é:
Função posição para o movimento com aceleração constante
Função posição para o movimento com aceleração constante
O movimentos com aceleração constante é chamado de Movimento Retilíneo Uniforme Variado.
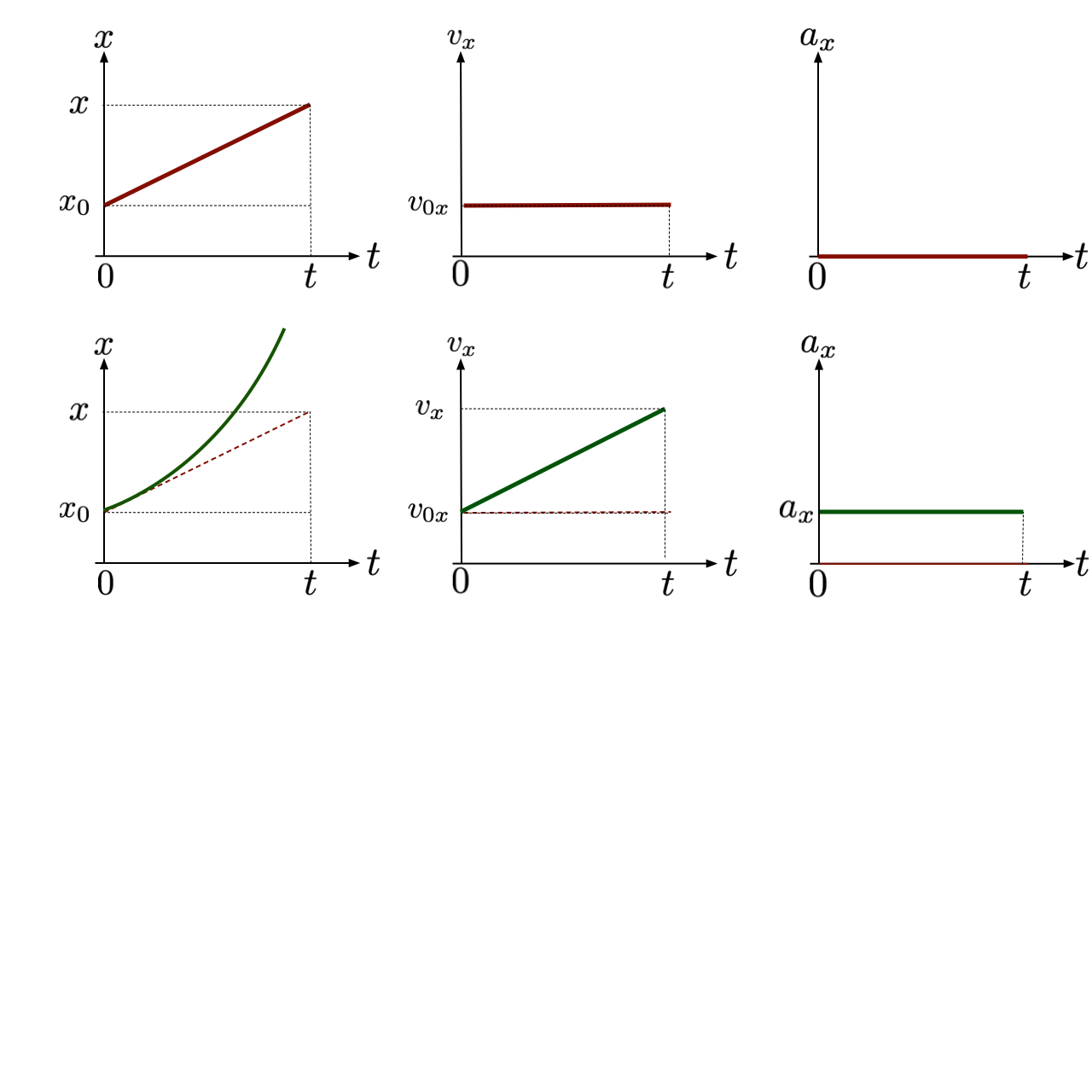
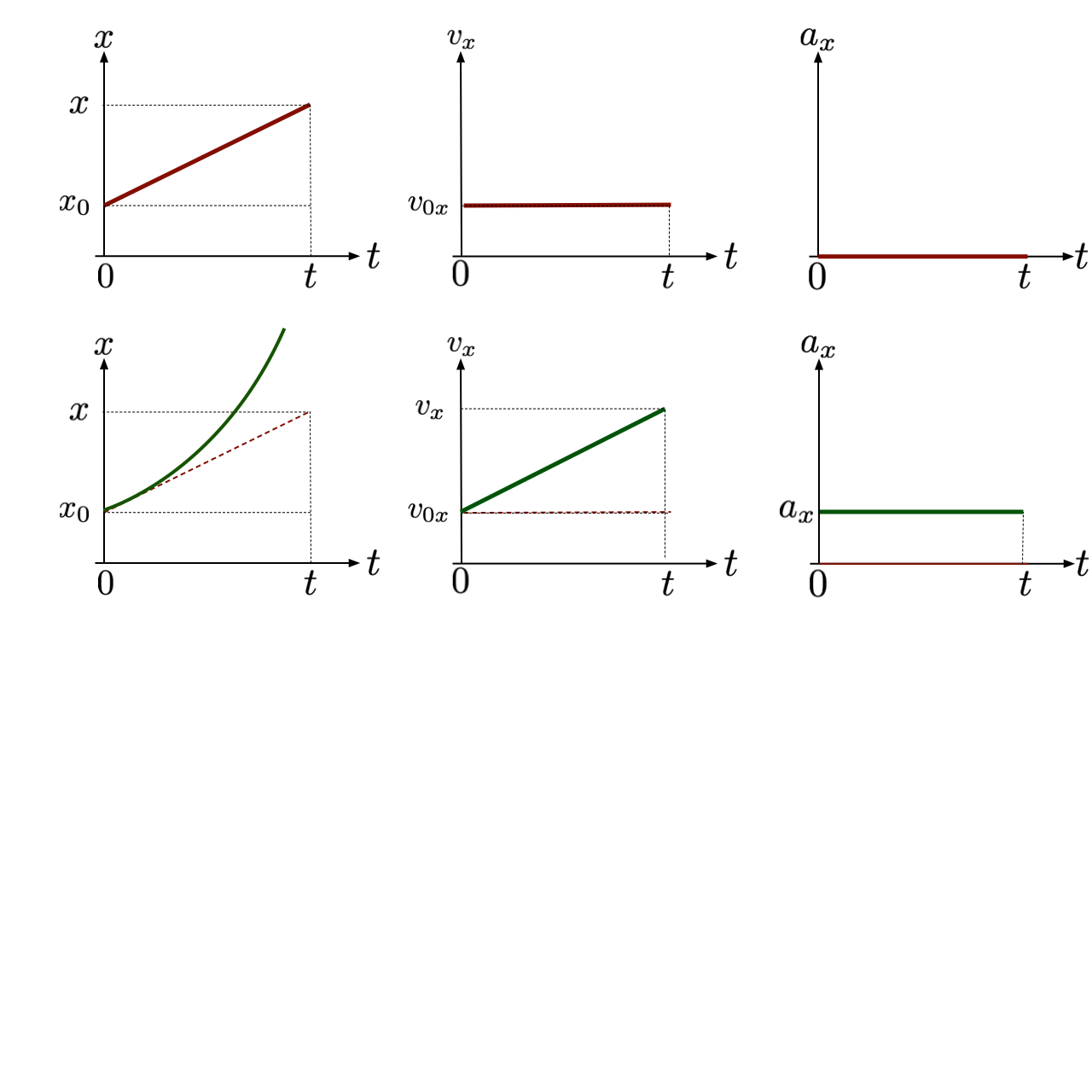
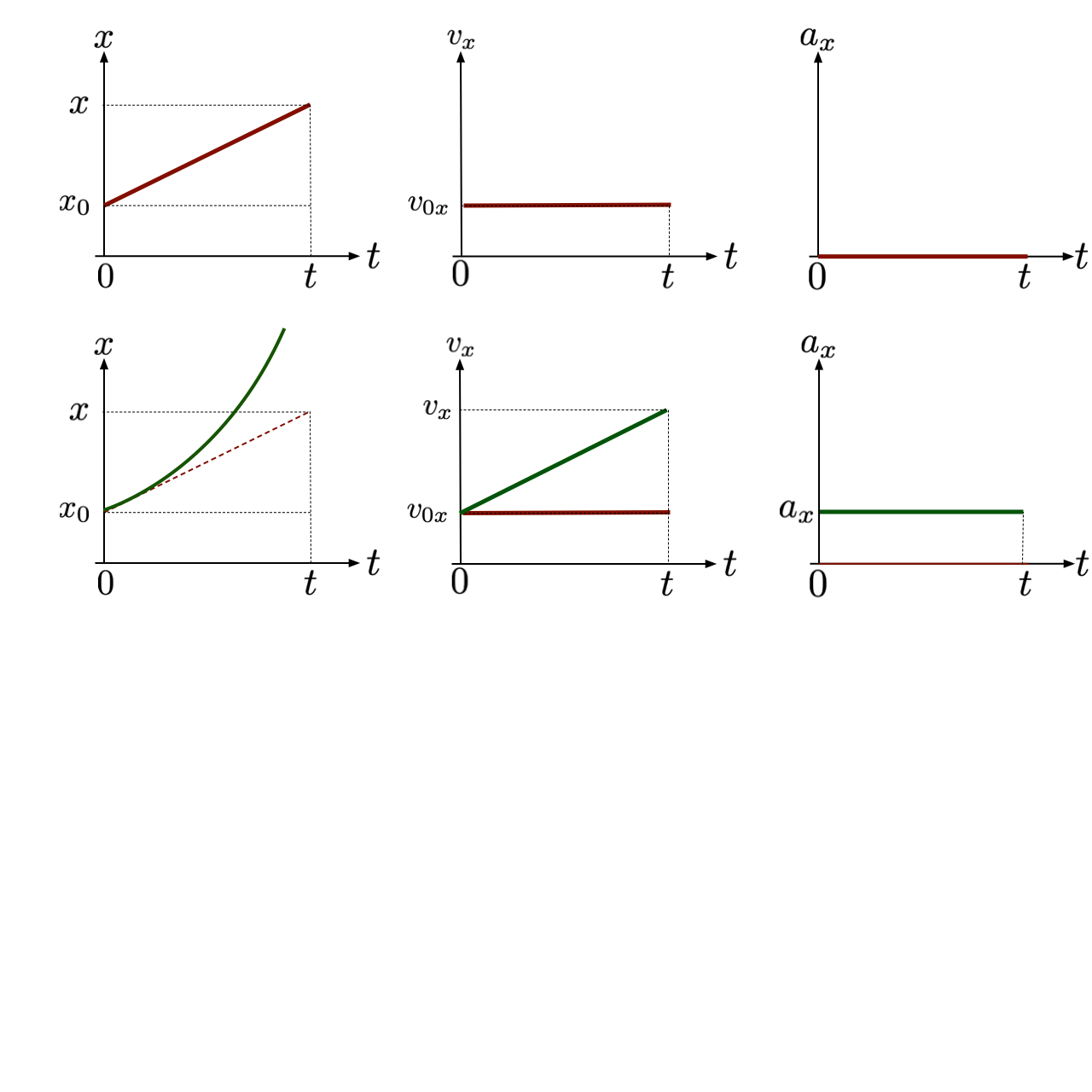
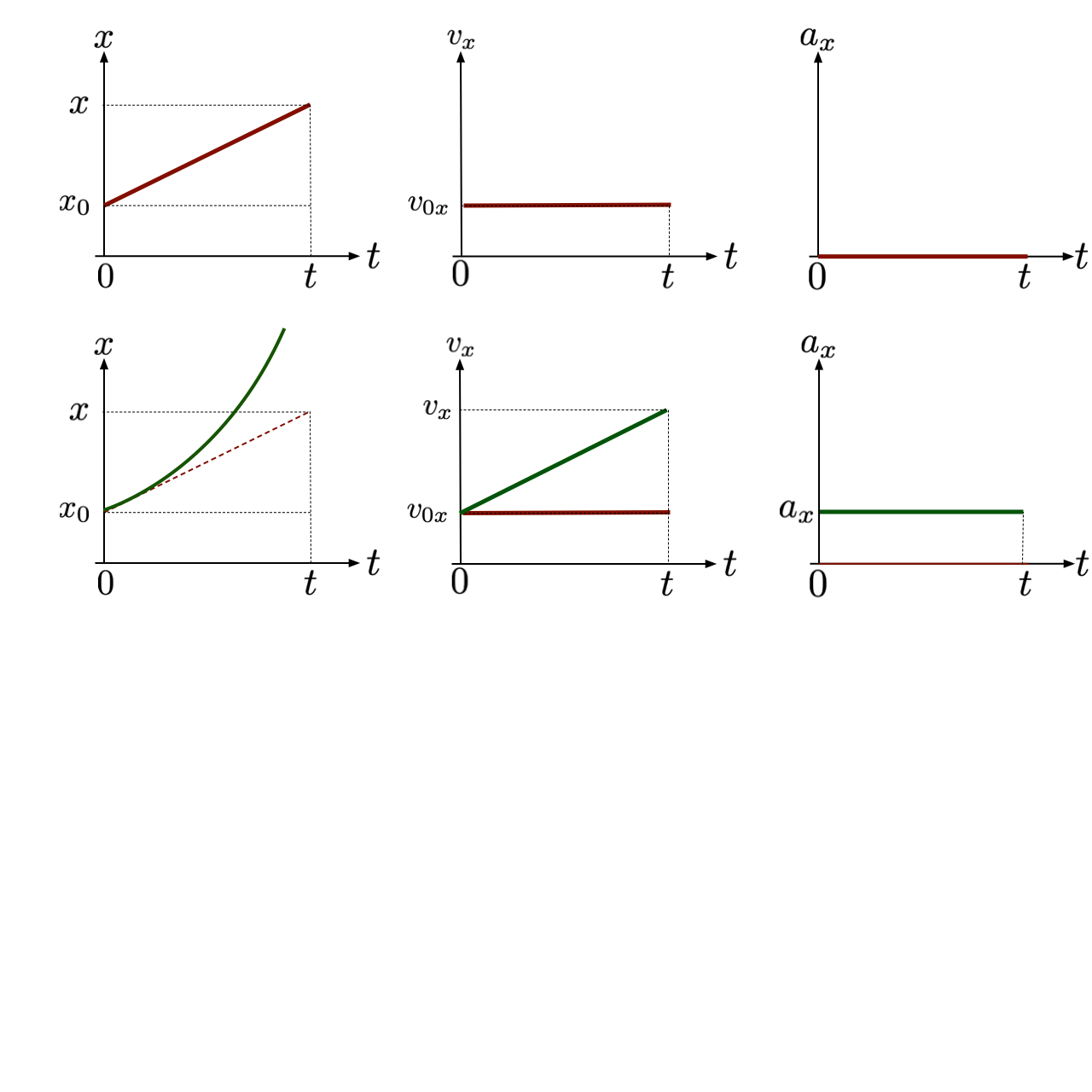
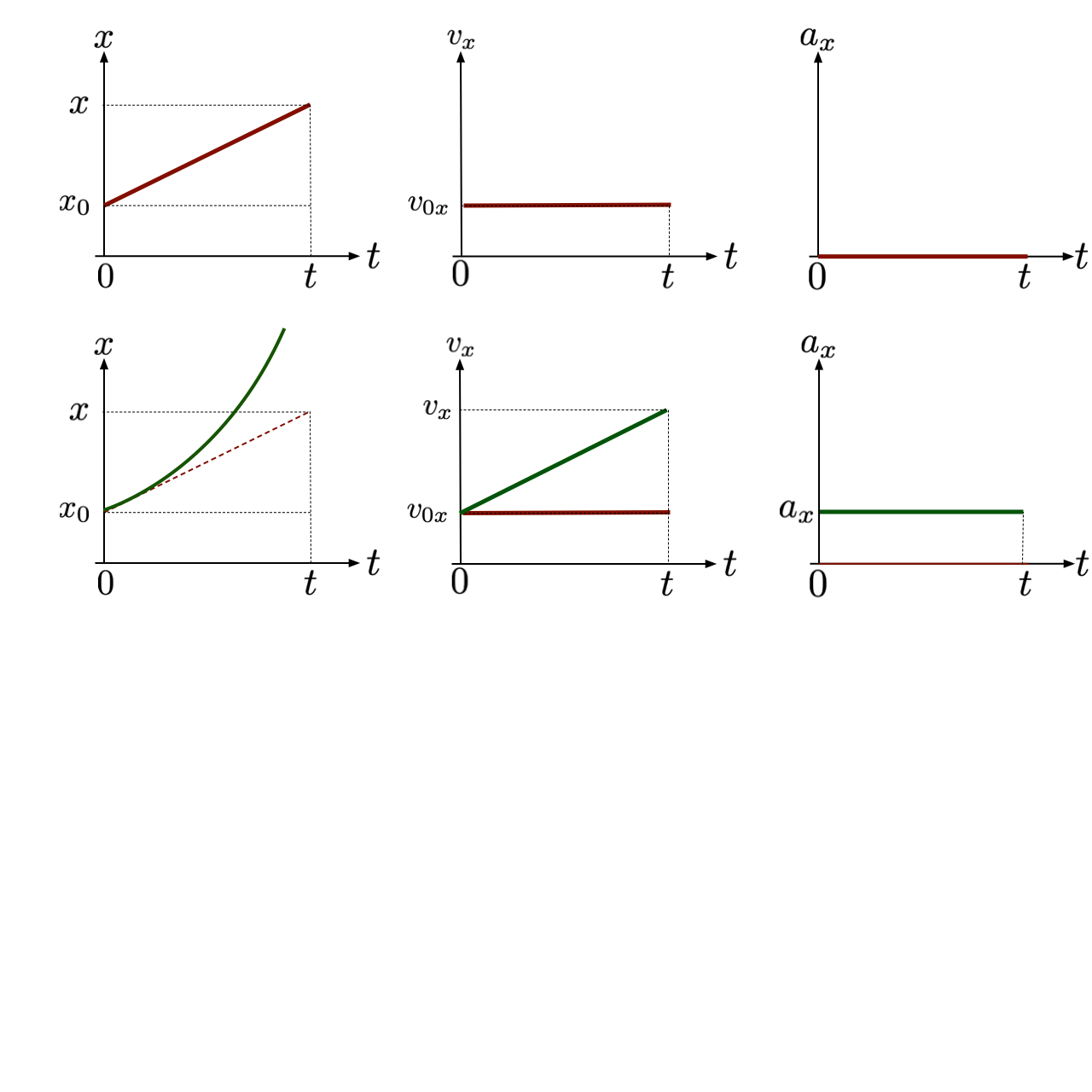
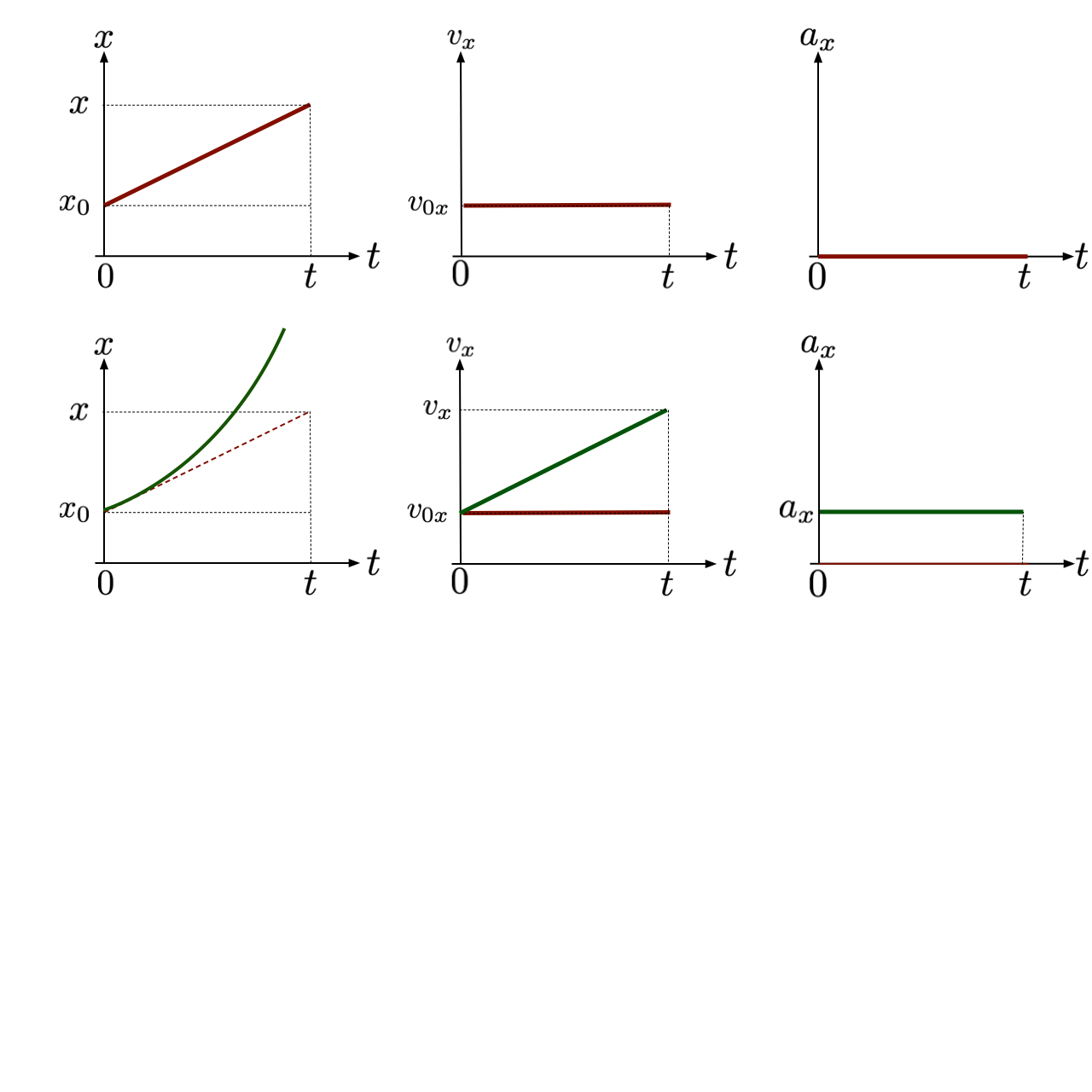
Velocidade Constante (MRU)
Aceleração Constante (MRUV)
Os gráficos para movimento
com aceleração constante
Função posição para o movimento com aceleração constante
O gráfico da aceleração em função do tempo é uma reta paralela ao eixo dos tempos.

A variação da velocidade é numericamente igual à área sob a curva
Os gráficos para movimento
com aceleração constante
O gráfico da velocidade em função do tempo é uma reta inclinada em relação ao eixo dos tempos.

O deslocamento é numericamente igual à área sob a curva
A aceleração é numericamente igual à inclinação da curva.
Os gráficos para movimento
com aceleração constante
Você está pilotando sua Lamborghini e mantém a velocidade constante (mostrada na figura) em linha reta por um intervalo de tempo de 1 min.
Qual o deslocamento?

Suponha que a velocidade mudou de 100 km/h para 180 km/h em apenas 1 min.
Qual o deslocamento, nesse caso?
O Aventador SVJ, por exemplo, leva 24 segundos para acelerar de 0 a 300 km/h. Qual seria o deslocamento?

Mundo Real


Movimento acelerado
Repare que a curva está acima da tangente
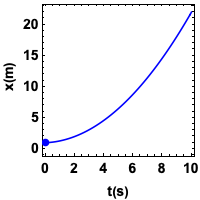
Viajando para frente: \(v > 0\).
Se \(v_x\) e \(a_x\) possuem o mesmo sinal, o movimento é acelerado.
A velocidade ficou "mais positiva". Então, aumentou.
Fonte: www.pixbay.com
Estudo 1. Aceleração constante. Correndo aceleradamente.
\(a\) e \(v\) no mesmo sentido.
Se \(v\) e \(a\) possuem o mesmo sinal, o movimento é dito acelerado.
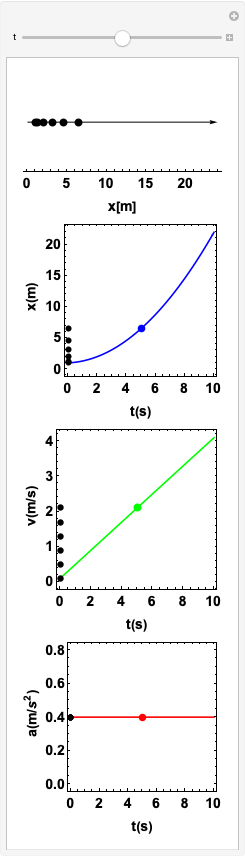
Estudo 1. Aceleração constante. Correndo aceleradamente.
A função posição
A função velocidade
A função aceleração
O objeto viaja no sentido positivo do eixo x: \(v>0\)
Por definição, a aceleração \(\vec a_{m}\) sempre aponta na mesma direção que a variação da velocidade \(\Delta \vec v\).
O componente \(x\) da velocidade do carro aumentou:
A variação do componente \(x\) da velocidade é positiva:
A componente \(x\) da aceleração é positiva e constante:


Movimento retardado
Repare que a curva está abaixo da tangente
Viajando para frente: \(v>0\)
Se \(v_x\) e \(a_x\) possuem os sinais opostos, o movimento é retardado.
A velocidade ficou "menos positiva". Então, diminuiu.
Fonte: www.pixbay.com
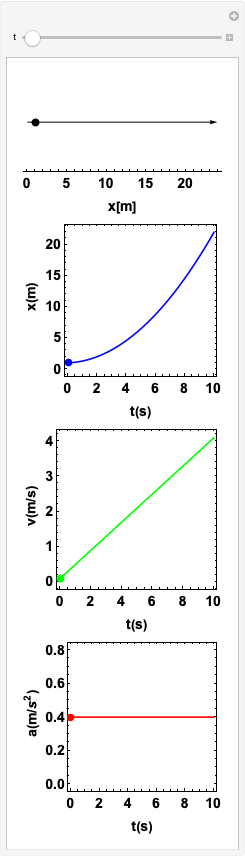
Estudo 1. Aceleração constante. Correndo aceleradamente.
\(a\) e \(v\) são opostos.
Se \(v_x\) e \(a_x\) possuem os sinais opostos, o movimento é dito retardado.
A função posição
A função velocidade
A função aceleração
O objeto viaja no sentido positivo do eixo x: \(v > 0\).
Por definição, a aceleração \(\vec a_{m}\) sempre aponta na mesma direção que a variação da velocidade \(\Delta \vec v\).
O componente \(x\) da velocidade do carro diminuiu:
A variação do componente \(x\) da velocidade é negativa:
A componente \(x\) da aceleração é negativa e constante:
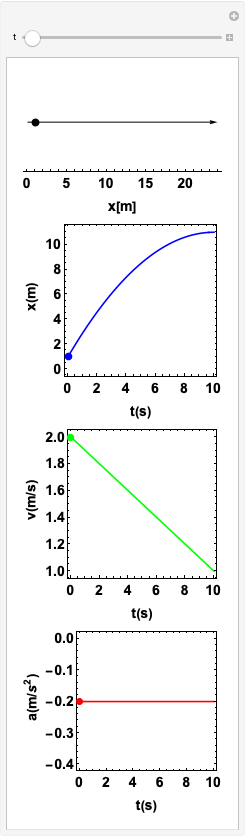
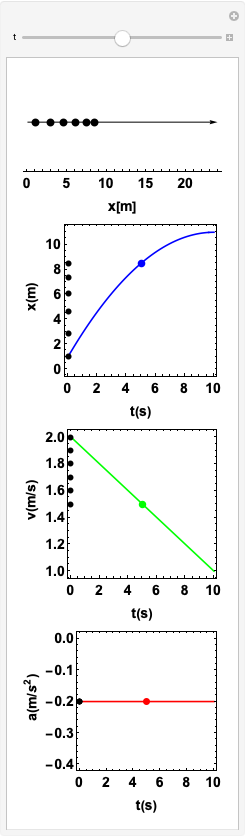
Estudo 1. Aceleração constante. Correndo aceleradamente.
Movimento acelerado
Repare que a curva está abaixo da tangente
Viajando para trás: \(v < 0\)


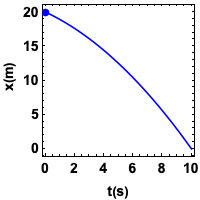
Se \(v\) e \(a\) possuem o mesmo sinal, o movimento é acelerado.
A velocidade ficou "mais negativa". Então, diminui.
Fonte: www.pixbay.com
Estudo 1. Aceleração constante. Correndo aceleradamente.
\(a\) e \(v\) no mesmo sentido.
A função posição
A função velocidade
A função aceleração
O objeto viaja no sentido negativo do eixo x: \(v < 0\)
Por definição, a aceleração \(\vec a_{m}\) sempre aponta na mesma direção que a variação da velocidade \(\Delta \vec v\).
O componente \(x\) da velocidade do carro diminuiu:
A variação do componente \(x\) da velocidade é negativa:
A componente \(x\) da aceleração é negativa e constante:
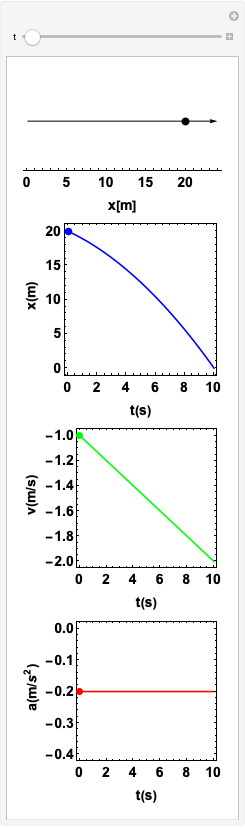
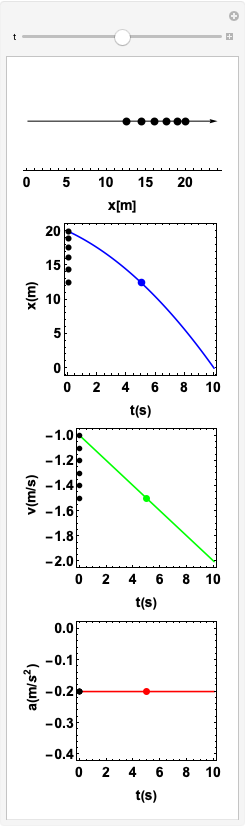
Se \(v_x\) e \(a_x\) possuem o mesmo sinal, o movimento é dito acelerado.
Estudo 1. Aceleração constante. Correndo aceleradamente.
Movimento retardado
Repare que a curva está acima da tangente
Viajando para trás: \(v < 0\)
Se \(v\) e \(a\) possuem sinais contrários, o movimento é retardado.


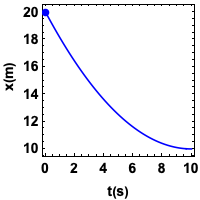
A velocidade ficou "menos negativa". Então, aumentou.
Fonte: www.pixbay.com
Estudo 1. Aceleração constante. Correndo aceleradamente.
\(a\) e \(v\) são opostos.
A função posição
A função velocidade
A função aceleração
O objeto viaja no sentido negativo do eixo x: \(v < 0\)
Por definição, a aceleração \(\vec a_{m}\) sempre aponta na mesma direção que a variação da velocidade \(\Delta \vec v\).
O componente \(x\) da velocidade do carro aumentou:
A variação do componente \(x\) da velocidade é positiva:
A componente \(x\) da aceleração é positiva e constante:
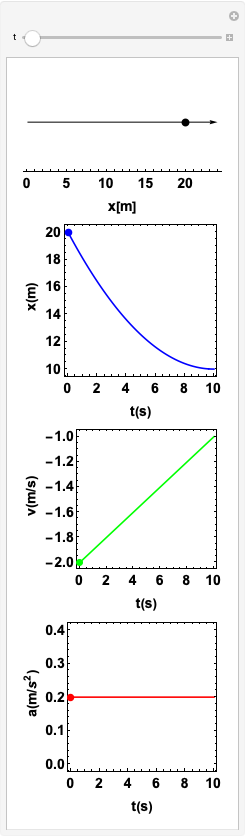
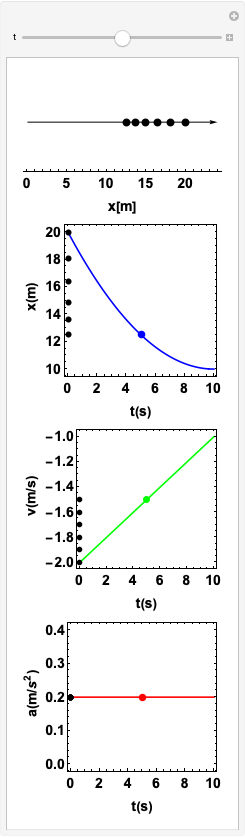
Se \(v\) e \(a\) possuem os sinais opostos, o movimento é dito retardado.
Estudo 1. Aceleração constante. Correndo aceleradamente.
Tente simular os movimentos para as quatro situações apresentadas antes de resolver os exercícios. Entenda o movimento!
Exemplo 5
Para cada um dos quatro gráficos x versus t na figura, responda às seguintes questões:
(a) A velocidade no tempo \(t_2\) é maior, menor ou igual à velocidade no tempo \(t_1\)?
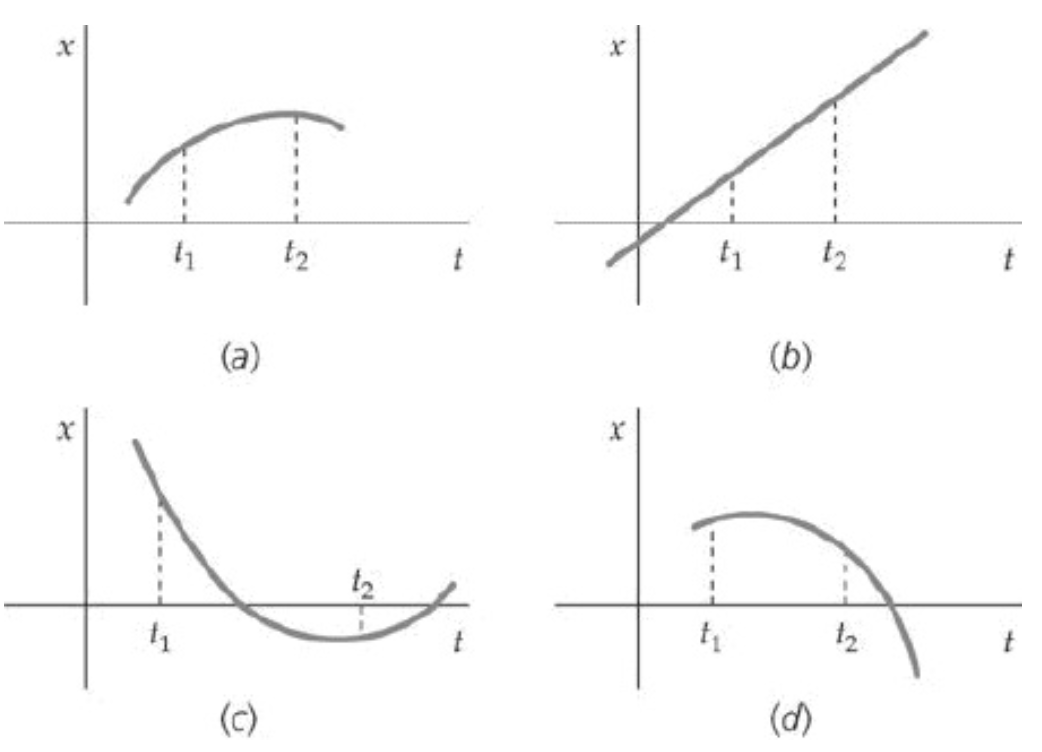
No movimento unidimensional, a velocidade é a inclinação de um gráfico de posição-tempo e pode ser positiva ou negativa. Por outro lado, a rapidez é a magnitude da velocidade e só pode ser positiva.
(b) A rapidez no tempo \(t_2\) é maior, menor ou igual à rapidez no tempo \(t_1\)?
Exemplo 6
Verdadeiro/falso:
(a) Se a aceleração de um objeto é sempre zero, então ele não pode estar se movendo.
(b) Se a aceleração de um objeto é sempre zero, então sua curva x versus t deve ser uma linha reta.
(c) Se a aceleração de um objeto é não-nula em um instante, ele pode estar momentaneamente em repouso nesse instante.
(a) F
(b) V
(c) V
Exemplo 7
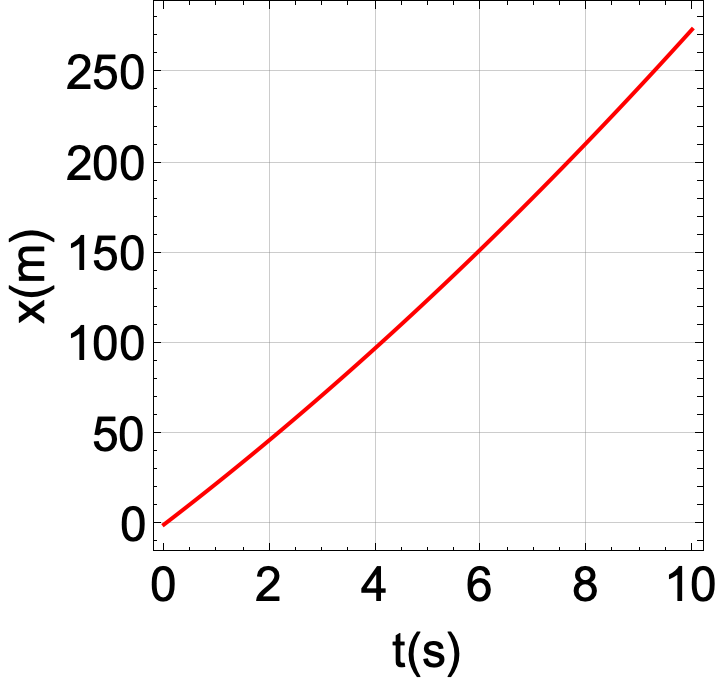
Você está dirigindo um Porsche que acelera uniformemente de 80,5 km/h em t = 0,00 s para 113 km/h em t = 9,00 s.
(a) Qual dos gráficos da figura melhor descreve a velocidade de seu carro?
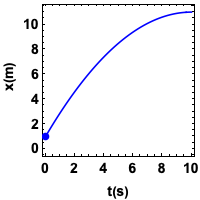
(b) Esboce um gráfico posição versus tempo mostrando a localização de seu carro durante estes nove segundos, supondo que sua posição x é zero em t = 0.
Exemplo 8
Quais das curvas posição versus tempo da figura mostram melhor o movimento de um objeto:
(1) com aceleração positiva,
(2) com velocidade constante positiva,
(3) que está sempre em repouso e
(4) com aceleração negativa?
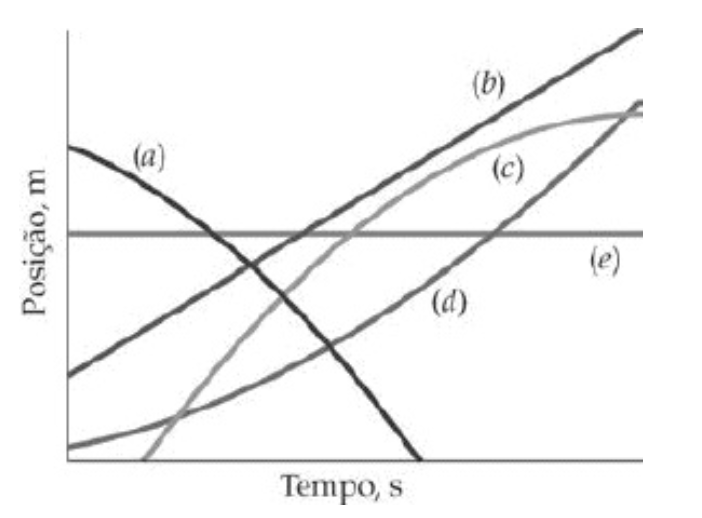
(1) d
(2) b
(3) e
(4) a, c
Atenção: Aceleração negativa não significa desaclerar!
Exemplo 9
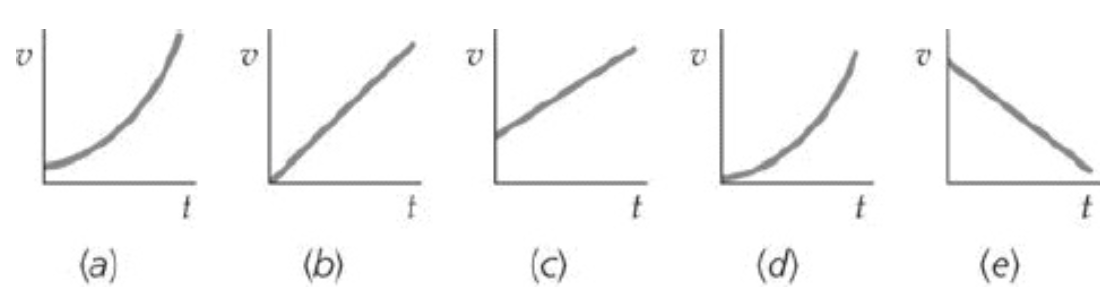
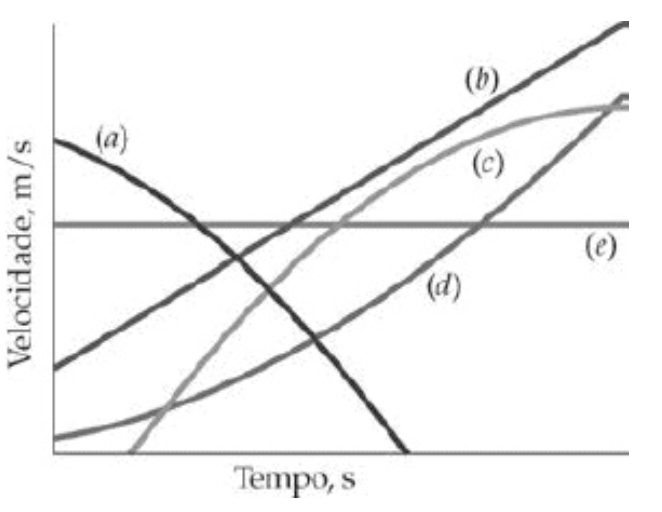
Quais das curvas velocidade versus tempo da figura melhor descrevem o movimento de um objeto:
(1) com aceleração constante positiva,
(2) com aceleração positiva que decresce com o tempo,
(3) com aceleração positiva que cresce com o tempo e
(4) sem aceleração?
(1) b
(2) c
(3) d
(4) e
Atenção: Aceleração negativa não significa desaclerar!
Exemplo 10
O vídeo foi gravado a 60 frames por segundo. Então, de um frame para o outro há \(\Delta t = (1/60) s\). Essa é a dica 1.
Considere que a nave começa a se mover no frame = +180 quando a ponta do foguete está na marca 0 da escala.
Considere o frame = +490 quando a ponta do foguete está na marca 110 m da escala.
Se você for sagaz, será capaz de obter a posição da ponta do foguete e o frame respectivo enquanto ele sobe de 0 para 110 m.
Crie uma tabela da posição pelo frame. Transforme o número do frame em tempo, em segundos (dica 1). Faça um gráfico da posição em função do tempo e obtenha a aceleração do foguete.
Você não pode usar o tempo do filme, pois não corresponde ao tempo do movimento real do foguete. Você deve usar a dica 1. Tente registrar um mesmo intervalo de tempo (mesmo número de frames, se possível). Isso vale 0,2 pontos extras na média da unidade se entregue até a próxima aula.