
Aula 05
Fundamentos da Mecânica
Prof. Ronai Lisbôa
BCT - ECT - UFRN
Objetivos
Analisar o movimento no plano.
Estudar o lançametno oblíquo.
Estudar o lançamento horizontal.
O mínimo obrigatório é estudar a referência e a lista de exercícios (veja SIGAA)
Bibliografia ( mesma da aula anterior ):
Tipler - Cap. 3
Seções 3.1 e 3.2 (págs. 63 a 65 e 67 a 78)
- Ignorar a secão Velocidade Relativa.
- Faça os exercícios resolvidos.
Obter a equação da trajetória e alcance.
Referencial do Carro x Referencial da Terra
O movimento é relativo
O movimento é relativo
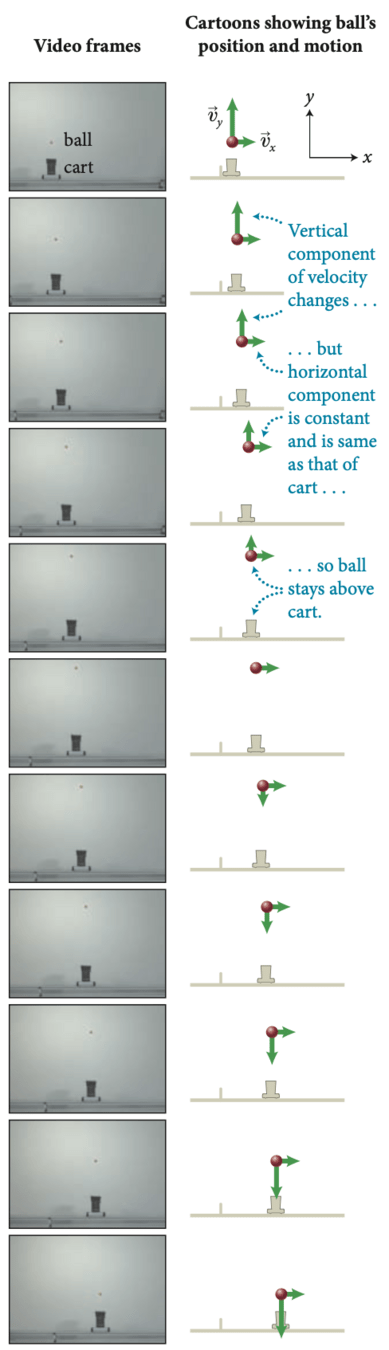
Considere o movimento de uma bola lançada do topo de um canhão anexado a um carrinho que se move a velocidade constante ao longo de uma pista horizontal:
É um movimento acelerado em linha reta, no referencial do carrinho \(\vec v_{carro} = \vec 0\).
Fonte: https://www.compadre.org
É um movimento acelerado curvilíneo, no referencial da Terra \(\vec v_{carro} = \vec c\).
Como os dois referenciais são inerciais (\(\vec v_c = constante\)) ambos observadores medem a mesma aceleração de queda livre para a bola:
O movimento depende do referencial do observador.
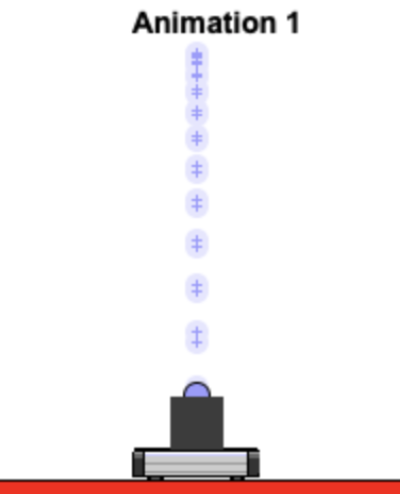
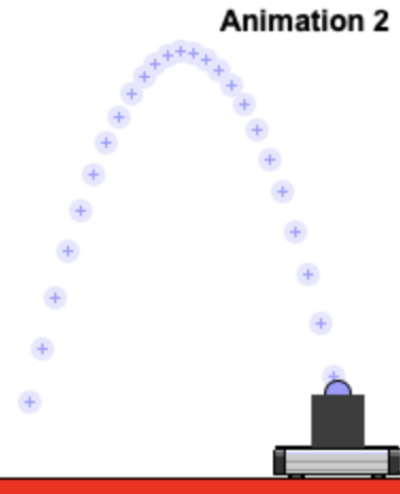
As animações 4 e 5 não são referenciais inercial!
Referencial do Carro x Referencial da Terra
O movimento é relativo
O movimento da bola no referencial da Terra pode ser dividido em duas partes:
Movimento de lançcamento vertical e queda livre na direção vertical (chamada componente vertical do movimento)
Nesse caso, há um MRUV.
Movimento à velocidade constante na direção horizontal (chamado de componente horizontal do movimento).
Nesse caso, há um MRU.
Fonte: https://www.compadre.org
Estamos estudando a independência dos movimentos de Galileu.
Referencial do Carro x Referencial da Terra
Fonte: https://www.compadre.org

Movimento no plano. Referencial da Terra
Vejamos, primeiramente as coordenadas da bolinha no referencial da Terra em dois instantes de tempo distintos.
Fonte: https://www.compadre.org
Fonte: https://www.compadre.org
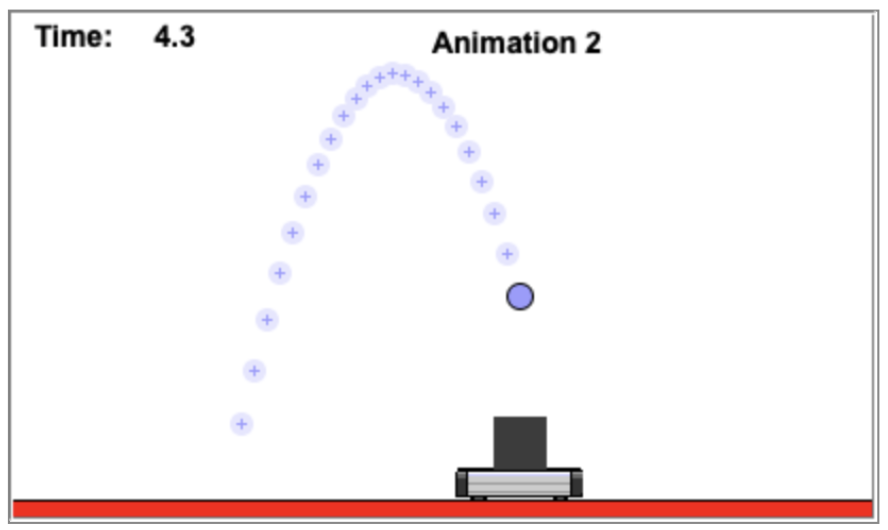
No tempo t = 4,3 s.
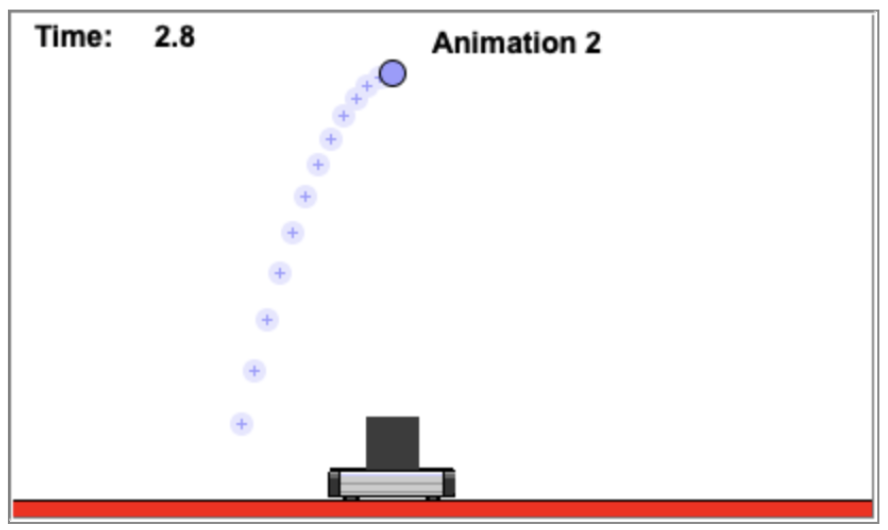
No tempo t = 2,8 s.
Para qualquer tempo t:
A partir dos vetores posições \(\vec r_1\) e \(\vec r_2\) é possível determinar o deslocamento (\(\Delta \vec r \)) da bolinha no plano.
O vetor deslocamento da bola:
Esse é o deslocamento entre os dois instantes de tempo \(t_1\) e \(t_2\).
Os vetores posições da bolinha são:
Veja, isso vale \(+1,5\hat i\)
Veja, isso vale \(-2,5\hat j\)
Movimento no plano. Referencial da Terra
A velocidade média é calculada para cada uma das componentes.
O vetor velocidade média é dado por:
Se o vetor deslocamento é dado por:
O vetor velocidade média tem a direção e sentido do vetor deslocamento.
Movimento no plano. Referencial da Terra
O vetor aceleração média é dado por:
Na horizontal (MRU):
Na vertical (MRUV):
O vetor aceleração média tem a direção da variação do vetor velocidade.
A aceleração média é calculada para cada uma das componentes. No movimento de queda livre, lançamento horizontal e vertical há somente a componente vertical da aceleração.
Aqui você precisa das funções: \(v_x,v_y\)!
Movimento no plano. Referencial da Terra
pois \(v_{x,i}=v_{x,f}\)
pois \(v_{x,i}\neq v_{x,f}\)
Os movimentos no plano são úteis para estudar os lançamentos oblíquos e os lançamentos horizontais.
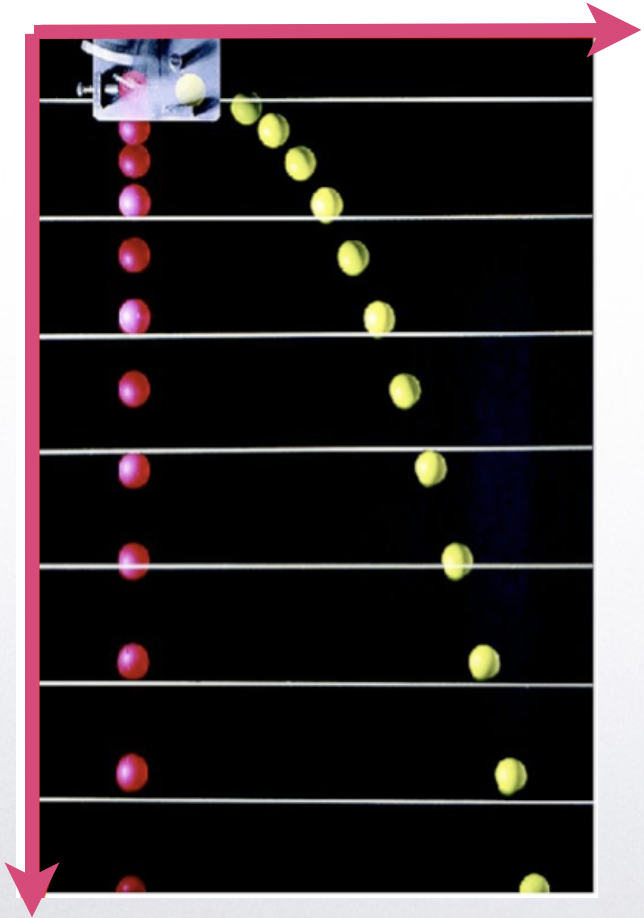
Fonte: Tipler & Mosca
Movimento no plano: Lançamento oblíquo
Na horizontal (MRU):
Na vertical (MRUV):
A velocidade é a composição dos movimentos MRU e MRUV:
O movimento na horizontal é independente do movimento na vertical. Isso é chamado de independência dos movimentos de Galileu.
A velocidade inicial de lançamento:
Movimento no plano. Referencial da Terra
Verifique na simulação a representação dos vetores.
Fonte: https://phet.colorado.edu
Movimento no plano: Lançamento oblíquo
A trajetória. Composição do movimento.
Fonte: Ralliday & Resnick
A altura:
O alcance:
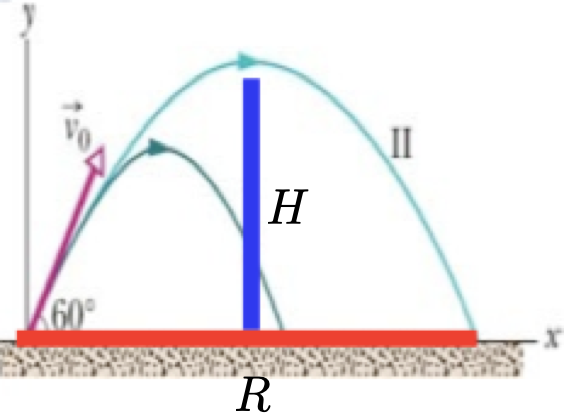
A trajetória do movimento oblíquo.
É uma função quadrática no alcance!
\(|b|> |4 a c|\)
As trajetórias mudam conforme as condições iniciais!
Condições iniciais: \(v_0, \theta, y_0, x_0\)
Movimento no plano: Lançamento oblíquo
import math
def calcular_raizes(H, V, theta):
# Constante da gravidade
g = 9.81 # m/s^2
# Cálculo dos coeficientes a, b, c
c = H
b = -math.tan(math.radians(theta))
a = g / (2 * V**2 * math.cos(math.radians(theta))**2)
# Imprimir os valores de c, b, a com quatro casas decimais
print(f"c = {c:.4f}")
print(f"b = {b:.4f}")
print(f"a = {a:.4f}")
# Passar para a forma clássica da equação quadrática aR^2 + bR + c = 0
discriminante = b**2 - 4*a*c
if discriminante < 0:
print("Erro: Não há raízes reais porque b < 4ac")
else:
R1 = (-b + math.sqrt(discriminante)) / (2*a)
R2 = (-b - math.sqrt(discriminante)) / (2*a)
# Imprimir as raízes com quatro casas decimais
print(f"As raízes são R1 = {R1:.4f} e R2 = {R2:.4f}")
# Exemplo de uso:
H = 1.0 # exemplo de altura
V = 10.0 # exemplo de velocidade inicial
theta = 45.0 # exemplo de ângulo em graus
calcular_raizes(H, V, theta)O vetor velocidade instantânea é dado por:
Na horizontal (MRU):
Na vertical (MRUV):
O vetor velocidade instantânea é tangente à trajetória e não tem a mesma direção que o vetor deslocamento \(\Delta \vec r\).
A velocidade instantânea é calculada para cada uma das componentes.
O vetor velocidade instantânea é tangente à trajetória e tem a direção do vetor deslocamento infinitesimal \(d \vec r\).
Aqui você precisa das funções: \(v_x,v_y\)!
Movimento no plano. Referencial da Terra
O vetor aceleração instantânea tem a direção do vetor velocidade infinitesimal.
Na horizontal (MRU):
Na vertical (MRUV):
A aceleração média é calculada para cada uma das componentes. No movimento de queda livre, lançamento horizontal e vertical há somente a componente vertical da aceleração.
Aqui você precisa das funções: \(v_x,v_y\)!
Movimento no plano. Referencial da Terra
Pontos particulares:
Altura vertical (\(v_y = 0\)).
Altura vertical máxima (\(\theta = 90^o)\).
Alcance horizontal (\(H = 0\)).
Alcance horizontal máximo (\(H = 0, \theta = 45^o\)).
Podemos aplicar o princípio da independência dos movimentos de Galileu no movimento parabólico.
Fonte: https://phet.colorado.edu
Movimento no plano: Lançamento oblíquo
Movimento no plano: Lançamento horizontal
No instante do lançamento, observa-se:
A velocidade inicial na vertical é nula.
A velocidade inicial na horizontal é constante:
Podemos aplicar o princípio da independência dos movimentos de Galileu no lançamento horizontal.
Fonte: https://phet.colorado.edu
A função movimento na horizontal é:
A função movimento na vertical é:
Posição
Movimento no espaço
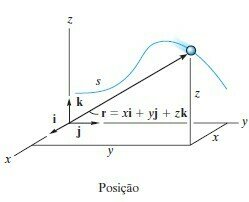
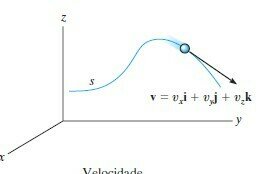
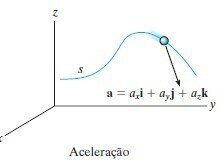
Velocidade
Aceleração
Os estudos anteriores se aplicam ao movimento no espaço (3D). Basta conhecer as funções de movimento ao longo de cada direção do espaço.
Eixo-x
Movimento no espaço
O movimento de um drone no espaço pode ser modelado por uma função movimento.
Eixo-y
Eixo-z
Move-se para a esquerda e direita.
Move-se para dentro e fora do plano da página.
Move-se de baixo para cima.
Se você observasse cada movimento independente em cada direção veria essas trajetórias.
Mas as funções do tempo não são as trajetórias. Nos dizem a posição em um dado instante.
Movimento no espaço
As funções movimentos são mostradas abaixo:
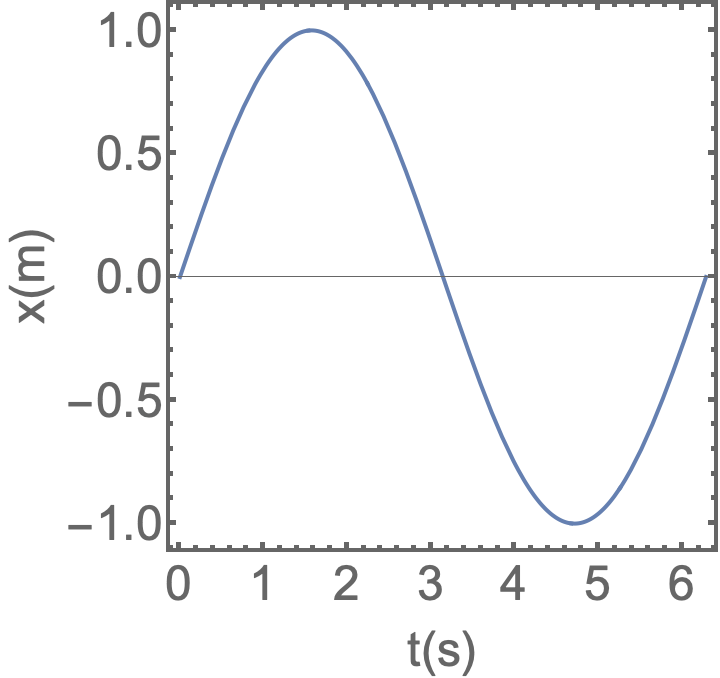
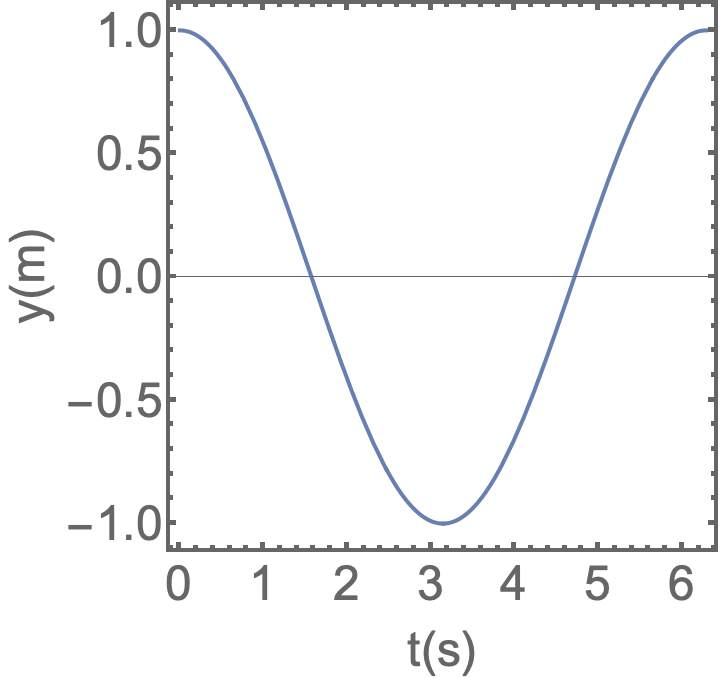
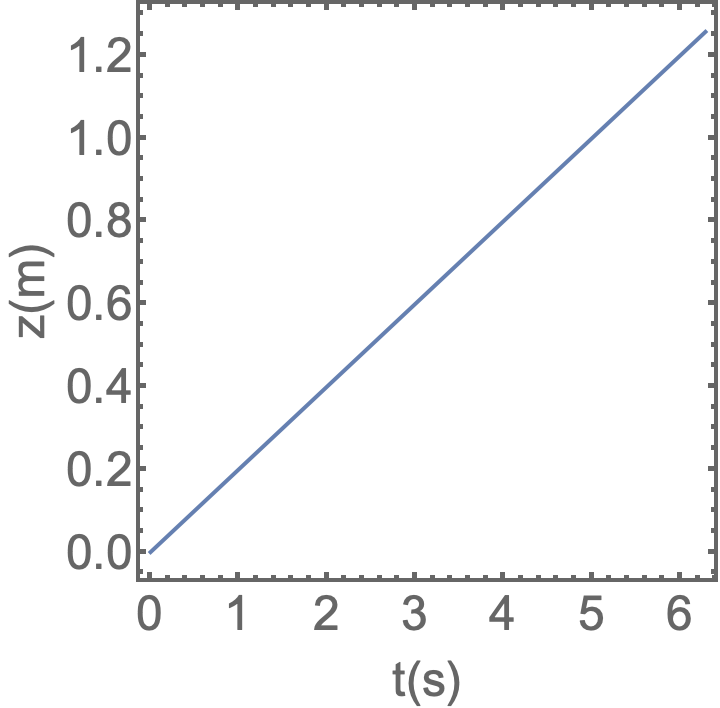
As funções movimentos não são o que observamos.
Nos eixos x e y a partícula oscila em linha reta em torno de um centro comum.
No eixo z a partícula se move em linha reta para longe do centro comum.
Movimento no espaço
A trajetória é dada pela parametrização das funções.
A trajetória é na verdade:
Um círculo no plano (\(x,y\)) olhando de cima.
Uma trajetória helicoidal no espaço (\(x,y,z\)) olhando lateralmente.
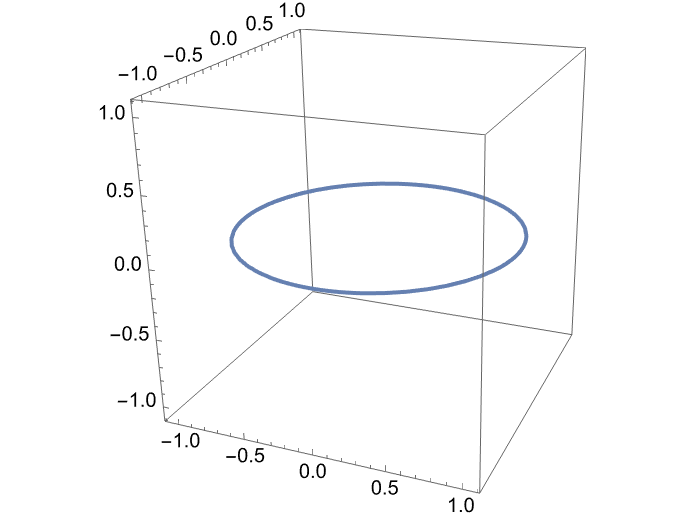
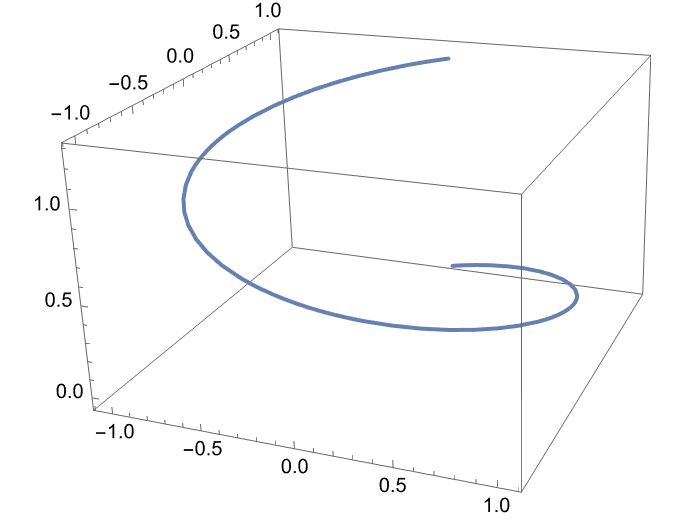
Como traçar a trajetória numericamente?
Exemplo 1 (A10.P1-01)
Dado o plano cartesiano na figura determine:
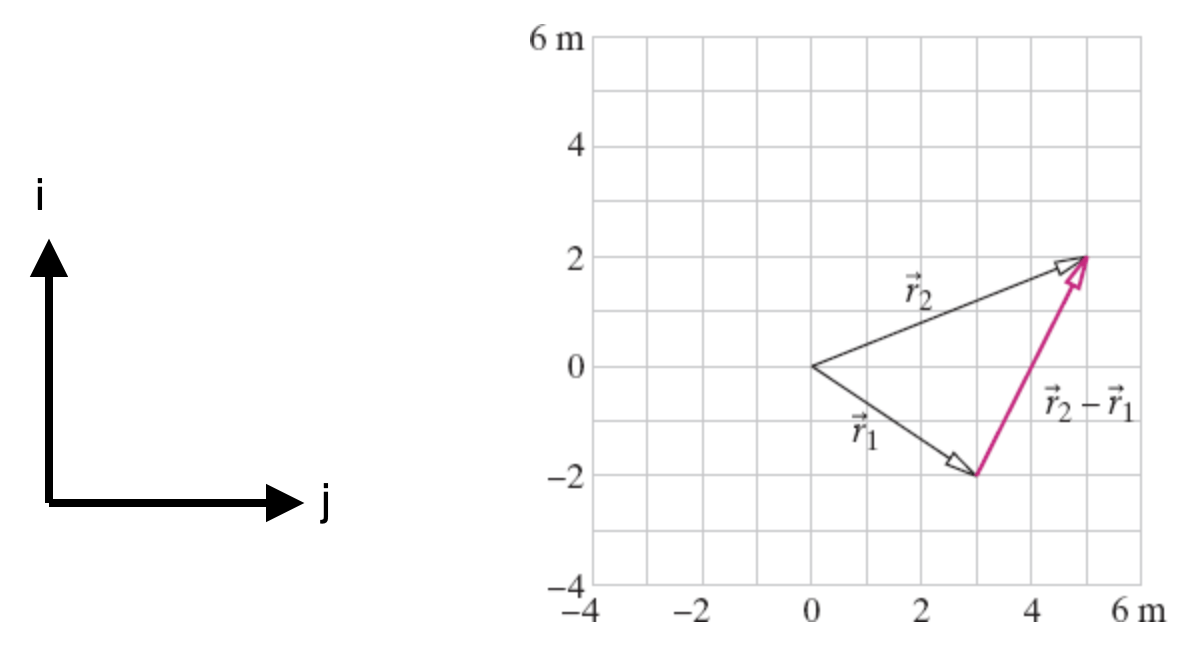
- Os vetores \(\vec r_1\) e \(\vec r_2\) e em função dos componentes vetoriais e dos vetores unitários.
- O vetor soma \(\vec s = \vec r_1 + \vec r_2\) em função dos componentes vetoriais e dos vetores unitários.
- O vetor diferença \(\Delta \vec r =\vec r_2 -\vec r_1\).
- Os ângulos \(vec r_1\) e \(\vec r_2\) que e fazem com o eixo horizontal.
Fonte: Chabay & Sherwood
Exemplo 2 (A10.P1-02)
O vetor posição de um íon é inicialmente r = (5,0 i + 6,0 j + 2,0 k) e 10 s depois passa a ser r = - 2,0 i + 8,0 j - 2,0 k, com todos os valores em metros. Na notação de vetores unitários, qual é a velocidade média \(v_{med}\) durante os 10 s?
Exemplo 3 (A10.P1-03)
A figura mostra três situações nas quais projéteis iguais são lançados do solo (a partir do mesmo nível) com a mesma velocidade escalar e o mesmo ângulo. Entretanto, os projéteis não caem no mesmo terreno. Ordene as situações de acordo com a velocidade escalar final dos projéteis imediatamente antes de aterrissarem, começando pela maior.
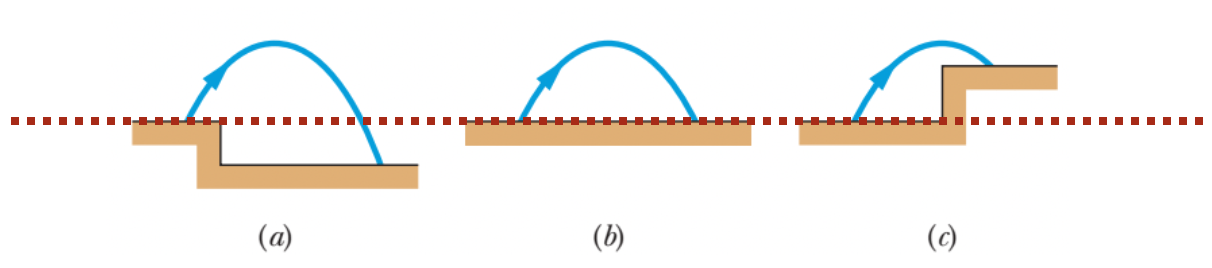
Fonte: Halliday
Exemplo 4 (A10.P1-04)
A figura mostra três trajetórias de uma bola de futebol chutada a partir do chão. Ignorando os efeitos do ar, ordene as trajetórias de acordo (a) com o tempo de percurso, (b) com a componente vertical da velocidade inicial, (c) com a componente horizontal da velocidade inicial e (d) com a velocidade escalar inicial, em ordem decrescente.
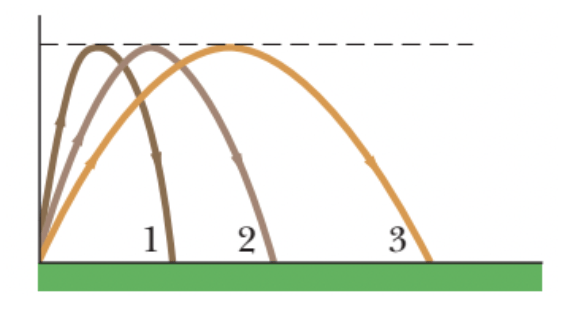
Fonte: Halliday
Exemplo 5 (A10.P1-05)
A posição r de uma partícula que se move em um plano xy e dada por
com \(\vec r\) em metros e \(t\) em segundos. Na notação de vetores unitários \(\hat i ,\hat j\), calcule:
(a) \(\vec r\)
(b) \(\vec v\)
(c) \(\vec a\)
para t = 2,00 s.
Exemplo 6 (A10.P1-06)
Uma partícula deixa a origem com uma velocidade inicial \(\vec v_0 \) = ( 3,00 i )m/s e uma aceleração constante \(\vec a\) = (-1,00 i - 0,500 j) m/s\(^2\). Quando a partícula atinge o máximo valor da coordenada x, quais são (a) a velocidade e (b) o vetor posição?
Exemplo 7 (A10.P1-07)
Um projétil é disparado horizontalmente de uma arma que está 45,0 m acima de um terreno plano, saindo da arma com uma velocidade de 250 m/s. (a) Por quanto tempo o projétil permanece no ar? (b) A que distância horizontal do ponto de disparo o projétil se choca com o solo? (c) Qual é o módulo da componente vertical da velocidade quando o projétil se choca com o solo
Exemplo 8 (A10.P1-08)
Na figura, uma pedra é lançada no alto de rochedo de altura h com uma velocidade inicial de 42,0 m/s e um ângulo \(\theta_0\) = 60,0° com a horizontal. A pedra cai em um ponto A, 5,50 s após o lançamento. Determine (a) a altura h do rochedo, (b) a velocidade da pedra imediatamente antes do impacto em A e (c) a máxima altura H alcançada acima do solo.
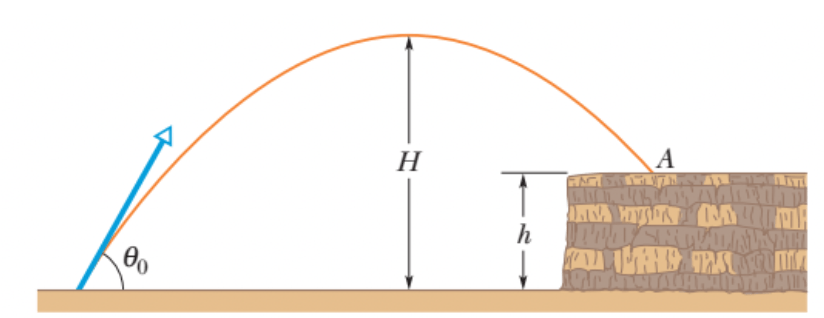
Fonte: Halliday
Exemplo 9 (A10.P1-09)
Uma bola de futebol é chutada a partir do chão com uma velocidade inicial de 19,5 m/s e um ângulo para cima de 45°. No mesmo instante, um jogador a 55 m de distância na direção do chute, começa a correr para receber a bola. Qual deve ser a velocidade média do jogador para que alcance a bola imediatamente antes de tocar o gramado?
Exemplo 10 (A10.P1-10)
Com que velocidade inicial o jogador de basquetebol da figura deve arremessar a bola, com um ângulo θ0 = 55o acima da horizontal, para converter o lance livre? As distâncias horizontais são d1 = 1,0 ft e d2 = 14 ft e as alturas são h1 = 7,0 ft e h2 = 10 ft.
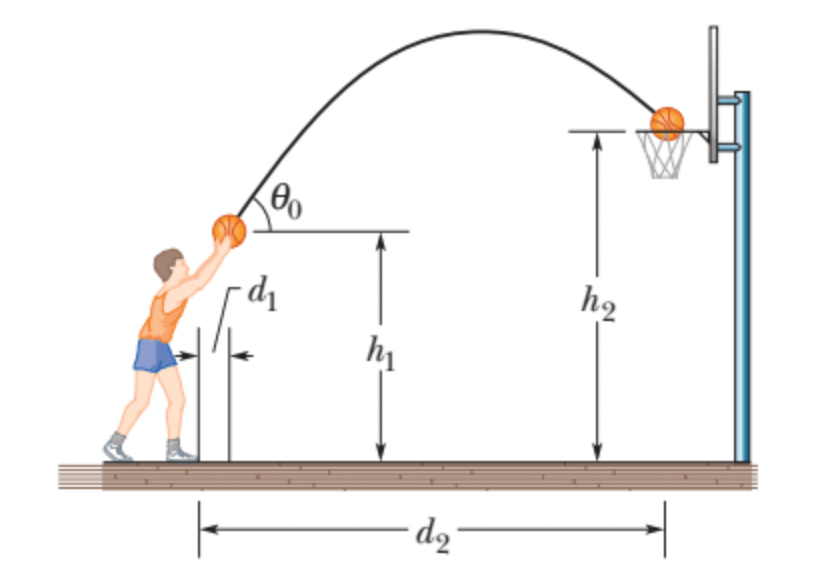
Fonte: Tipler
Exemplo 11
Um drone manobrado com aceleração constante é observado com as posições e velocidades mostradas na figura.
Qual é a aceleração \(\vec a\) do drone?
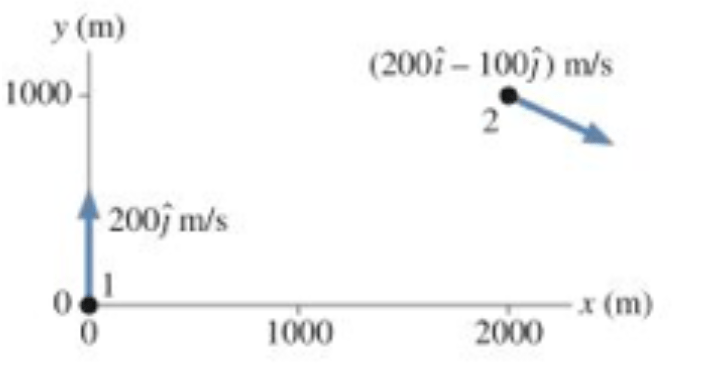
Fonte: Randall & Knight
Exemplo 12
Um robô da lego é controlado remotamente sobre um piso horizontal onde o atrito é reduzido. A figura mostra os gráficos de \(v_x\) e \(v_y\), os componentes x e y da velocidade do disco. Ele parte da origem.
(a) Qual é o módulo da aceleração do disco?
(b) A que distância da origem ele se encontra em t = 0 s e t = 10 s?
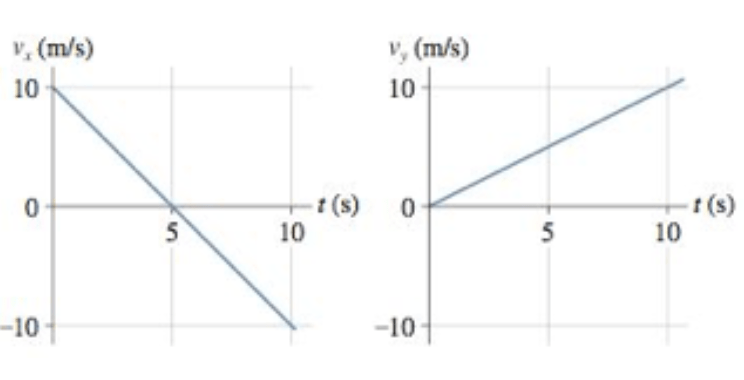
Fonte: Randall & Knight
Exemplo 13
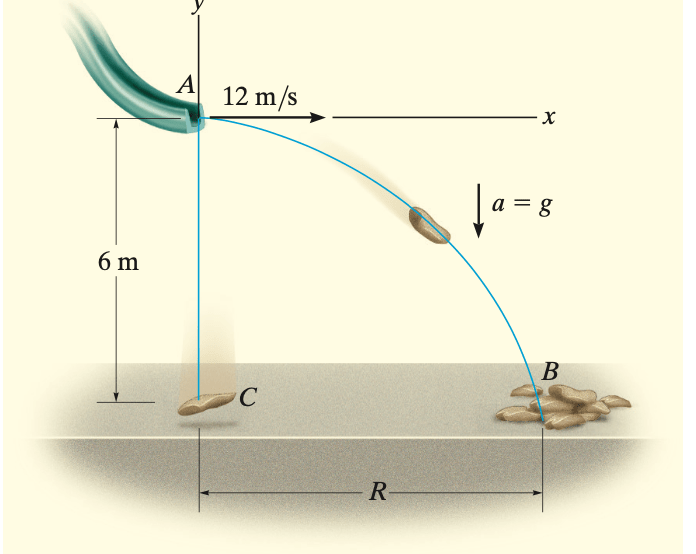
Um saco desliza da rampa, como mostrado na Figura, com uma velocidade horizontal de 12 m/s. Se a altura da rampa é de 6 m a partir do piso, determine o tempo necessário para o saco atingir o piso e a distância R até onde os sacos começam a se empilhar.
Fonte: Hibbeler
Para especificar a posição da bola, precisamos de uma coordenada x para especificar a posição ao longo do eixo x e uma coordenada y para especificar a posição ao longo do eixo y.
Referencial do Carro x Referencial da Terra
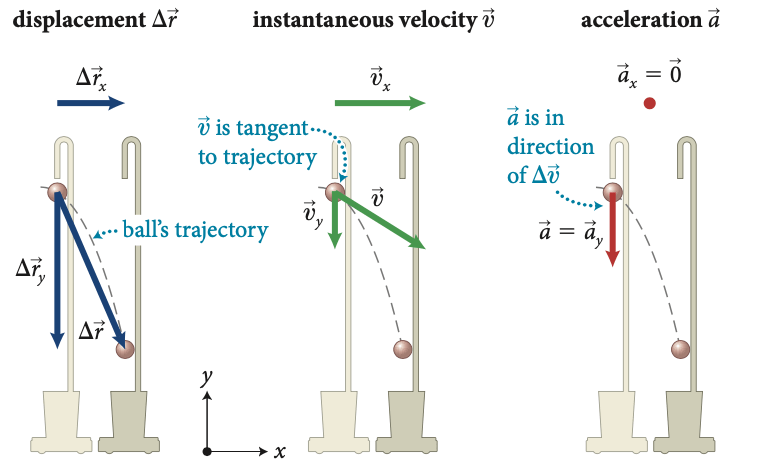
Fonte: Eric Mazur
deslocamento \(\Delta \vec r\)
vel. instantânea \(\vec v\)
aceleração \(\vec a =\vec 0\)
\(\vec v\) é tangente à trajetória
trajetória da bola
\(\vec a\) está na direção de \(\Delta \vec v\)
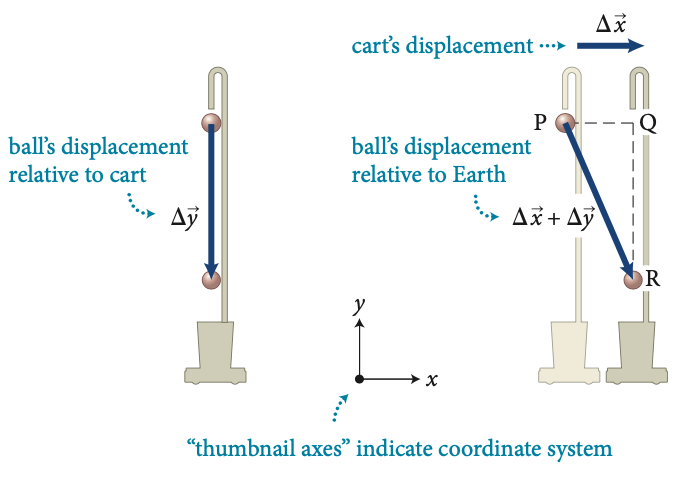
Fonte: Eric Mazur
deslocamento da bola relativamente ao carro
deslocamento do carro
deslocamento da bola relativamente à Terra
Eixo de referência indica o sistema de coordenadas
O movimento é relativo