Aula 06
Fundamentos da Mecânica
Prof. Ronai Lisbôa
BCT - ECT - UFRN
Objetivos
Reconhecer uma FORÇA como uma grandeza vetorial.
Reconhecer que uma força altera o movimento ou altera a forma de um objeto.
Classificar as forças de curto alcance e de longo alcance.
Representar as forças em um diagrama de corpo livre.
Classificar as forças atrativas e repulsivas.
Bibliografia.
Tipler - Cap. 4
Seções 4.1 a 4.8 ( todas!)
- Faça os exercícios resolvidos.
Hoje, intuitivamente sabemos que...
Força se deve a uma interação
o movimento é alterado pela ação do que costumamos chamar de forças.
Exercendo forças somos capazes de colocar objetos em movimento ou ...
alterar seu estado de movimento ou deformá-los.
Mas o que são forças?
Quais são os efeitos das forças?
Quais os tipos de forças?
Por que é importante o estudo das forças?
O que é força?
Força se deve a uma interação


Por enquanto, uma força é um empurrão ou um puxão.
Uma força representa uma ação sobre um objeto
Força é uma interação.
Força é exercida sobre um objeto.
Uma força requer um agente.
que altera o movimento e/ou altera a forma.
Força se deve a uma interação
Você pode conseguir diferentes efeitos no movimento do objeto se uma força tem intensidade, direção e sentido distintos.
Força é um vetor.

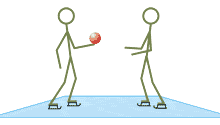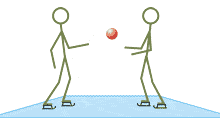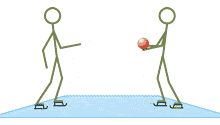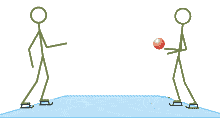
As forças existem entre o agente e o objeto sobre o qual elas são exercidas.
As forças são influências mútuas entre dois objetos que produzem: variações do movimento ou mesmo mudanças físicas.
A única forma de alterar o estado de repouso ou movimento de um objeto é fazê-lo interagir com alguma outra coisa.
O que é força?
Interação
Quais são os tipos de forças?
Força se deve a uma interação
As forças podem ser de curto alcance ou de longo alcance.
As forças podem ser atrativas e repulsivas.

As interações podem ser atrativas.
As interações podem ser repulsivas.
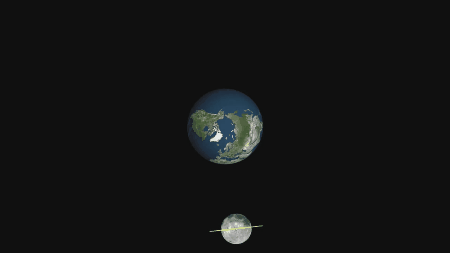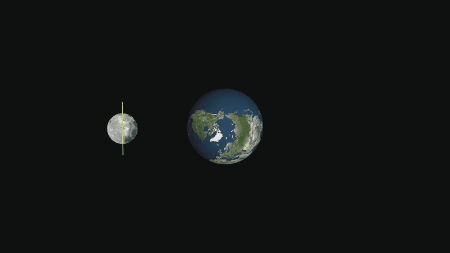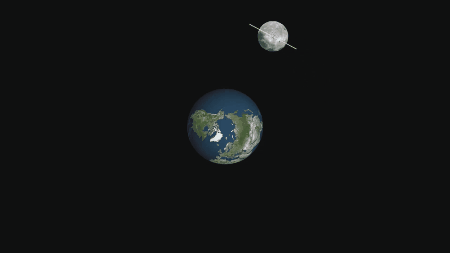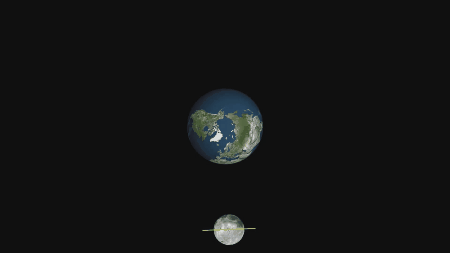
Os corpos com interação atrativa aceleram um em direção ao outro.
Os corpos com interação repulsiva aceleram para longe um do outro.
Entre as massas
Entre os pólos iguais de um ímã
Atractive gravitational force

Fonte: www.gifer.com

Fonte: https://gfycat.com
Força se deve a uma interação
Forças atrativas x repulsivas
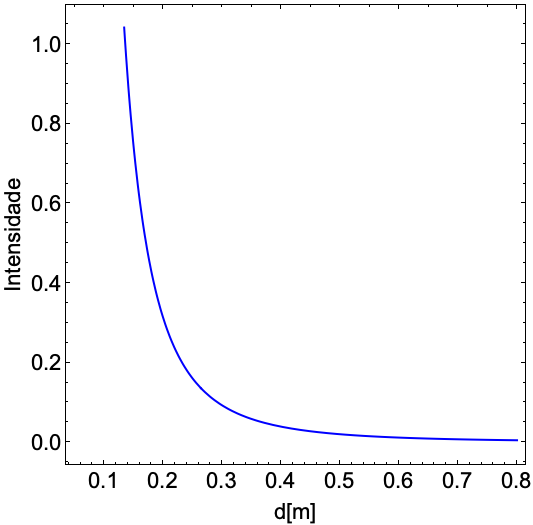
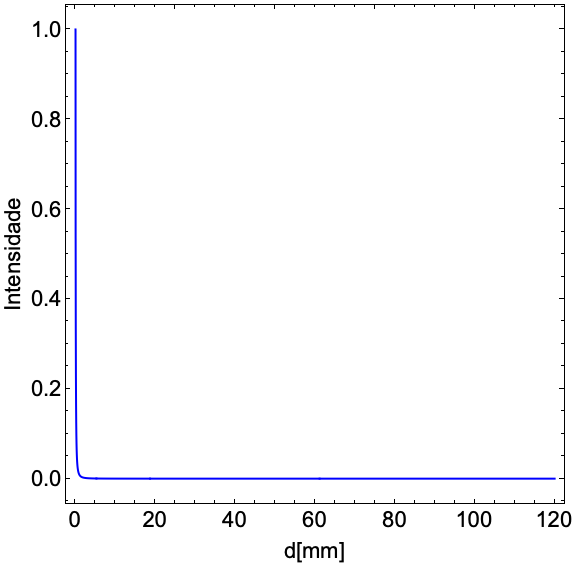
Em qualquer caso a interação é uma função da distância que separa os objetos.
Para ímãs a interação é de longo alcance.
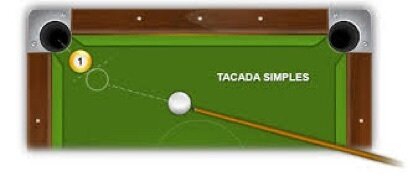
Para bolas de bilhar a interação é de curto alcance.
O contato físico entre dois objetos é, portanto, uma interação de curto alcance.




Fonte: www.pixbay.com
Fonte: www.pixbay.com
Força se deve a uma interação
Forças de longo alcance x curto alcance
Forças de campo são forças associadas ao que é chamado de “ação à distância”. Nesse caso, os objetos que exercem forças um no outro não precisam estar fisicamente se tocando. Para qualquer objeto maior que átomos, as forças gravitacional (G) e eletromagnética (E) são as únicas forças de campo.
Gravitacional
Eletromagnética
Força se deve a uma interação


Forças de longo alcance ou ação à distância
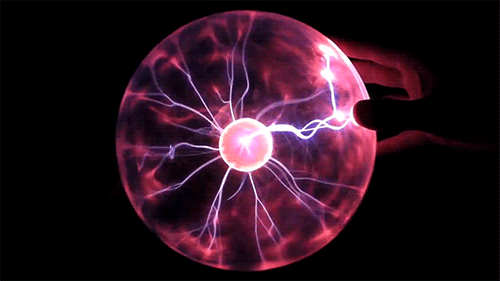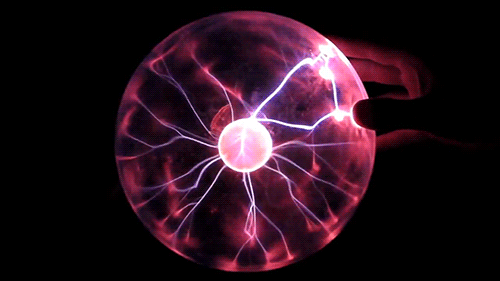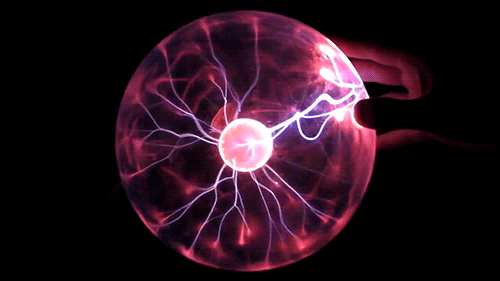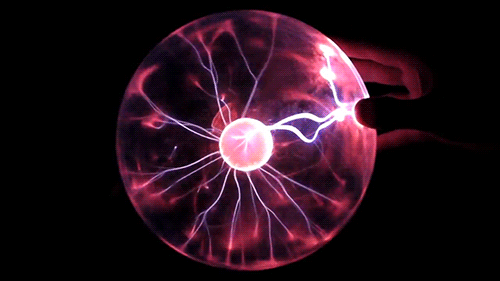
A interação de longo alcance é modelada via o conceito de campo que contém informações sobre todo o histórico do objeto.
Os objetos são cercados por um campo, cujas propriedades são determinadas pelos atributos do objeto.
Um objeto eletricamente carregado gera um campo elétrico.
Um objeto magnético gera um campo magnético.
Um objeto com massa gera um campo gravitacional.

Fonte: www.gifer.com

Fonte: https://futurism.com/
Força se deve a uma interação
Forças de longo alcance ou ação à distância
Forças de contato (c) são forças que surgem quando os objetos se tocam fisicamente. Essa categoria de forças inclui forças devido a tensões, compressões, atrito.
As interações de contato são interações de natureza elétrica!!!
Tensões e Compressões
Empurrando ou puxando um objeto extenso esse pode deforma-se temporariamente, permanentemente ou mesmo romper-se: molas, cordas, fios, barras e superfícies.
Atrito
Interação entre duas superfícies em contato: caixa e piso; blocos e planos inclinados.
Força se deve a uma interação
Forças de curta alcance ou contato
No nível macroscópico, o contato físico significa exatamente isso: duas superfícies se tocando.
No nível atômico, no entanto, dois átomos se atraem ou se repelem, mesmo quando separados por distâncias várias vezes o seu tamanho.
Não existe o "toque" no nível atômico e, portanto, não existe o contato físico.
Seus pés são sustentados por inúmeras interações entre os átomos dos pés e os que estão no chão.
No nível atômico, porque os átomos interagem sem contato físico, até os pés "tocando" o chão são realmente uma interação sem contato físico!
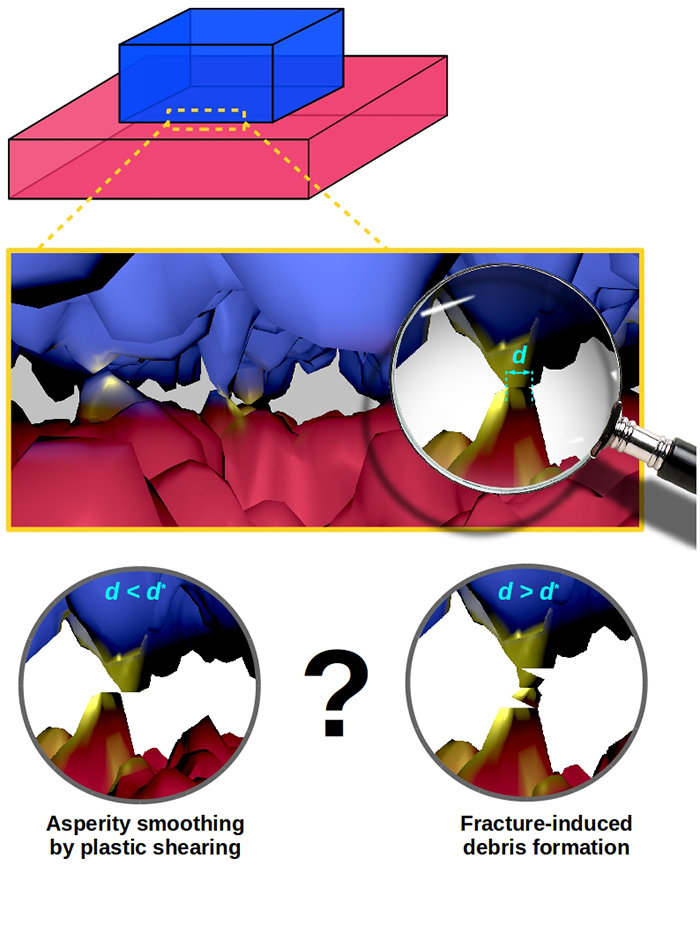
Forças de curta alcance ou contato
Força se deve a uma interação
As forças de contato se ajustam à medida que as forças são aplicadas aos objetos.
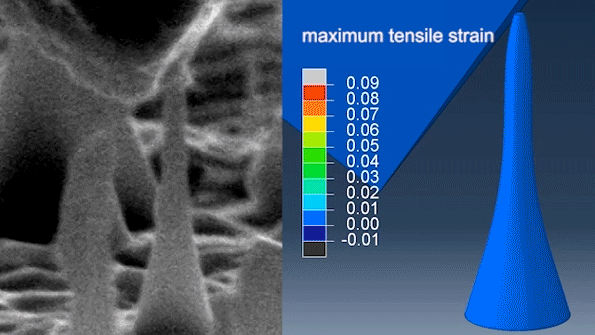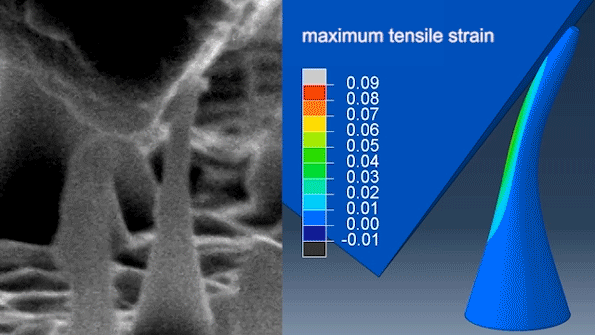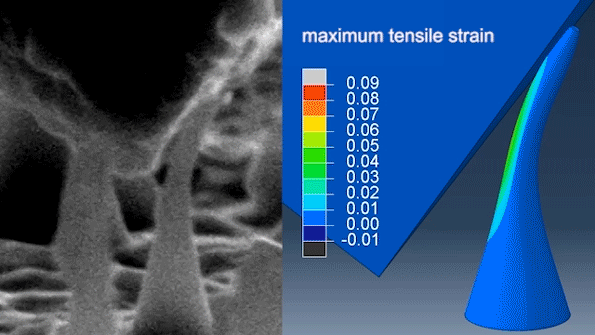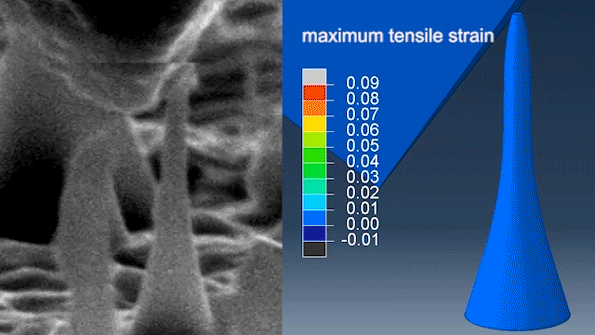
Um estudo recente determinou que os diamantes podem ser dobrados e esticados elasticamente quando transformados em agulhas ultrafinas. A equipe demonstrou que suas agulhas de diamante em nanoescala podiam flexionar e esticar até 9% sem quebrar e retornar à sua forma original.
O diamante é o material mais forte que ocorre naturalmente na Terra.
Se mesmo o diamante se dobra a uma força aplicada o que pensar de superfícies ordinárias: mesas, pisos, fios, cordas, etc.!
Força se deve a uma interação
Forças de curta alcance ou contato
As superfícies exercem sobre objetos uma força de contato que equilibra a força aplicada.
A deformação da superfície será maior ou menor dependendo da sua dureza.


Fonte: https://sleepopolis.com
Força se deve a uma interação
Forças de curta alcance ou contato
Objetos exercem força, sim! Porque são feitos de átomos!
Objetos exercem uma força sobre você quando você interage com eles.
Você cai na porta se abrindo porque a força exercida pela porta sobre você foi subitamente removida.
Seu movimento inicial se dá na direção e sentido da força que você aplicava na porta.
Imagine-se encostado a uma porta. O que acontece quando alguém de repente abre a porta?

Fonte: https://pixabay.com/
Objetos exercem força, sim! Porque são feitos de átomos!
Força se deve a uma interação
Forças de curta alcance ou contato
É uma manifestação de interações entre um sistema de objetos.
É uma grandeza vetorial.
O efeito da força depende de como ela é aplicada. Isso é uma propriedade de grandezas vetoriais.
Força se deve a uma interação
Quais são os efeitos das forças?
Gerou uma translação
Gerou uma rotaçao
Represente o objeto como uma partícula.
Força se deve a uma interação


Objeto
Agente
Localize a cauda do vetor força sobre a partícula.
Desenhe o vetor força como uma seta orientada e de comprimento proporcional à intensidade da força.
Denote o vetor apropriadamente.

O vetor representa a força que a Terra exerce sobre o objeto.
Quais são os efeitos das forças?
Represente o objeto como uma partícula.
Força se deve a uma interação
Objeto
Agente 2
Desenhe os vetores forças como uma seta orientada e de comprimentos proporcionais à intensidade de cada força
Denote os vetores apropriadamente.

Represente a soma vetorial dos vetores sobre o objeto.
Agente 1
O vetor resultante vai indicar a direção e sentido do movimento do objeto.
Podemos substituir as duas forças \(\vec F_{1o}\) e \(\vec F_{2o}\) por uma única força \(\vec F_{Ro}\).
Quais são os efeitos das forças?

Fonte: RandallO livro não se move. A soma vetorial das forças exercidas sobre ele deve ser zero: \(\vec F_{Rl} = \vec 0\)
Quais forças são exercidas no livro?
TERRA

Par de interação
Gravitacional (campo)
Par de interação
Compressão (contato)
TERRA

O livro está em repouso porque as duas forças exercidas nele cancelam uma a outra exatamente.
A força da gravidade e a força de compressão.
Atuam em objetos diferentes:

Atuam em objetos diferentes:
Atuam no mesmo objeto. Não são um par de interação.
Fonte: https://a-casa.colorir.com
Fonte: https://a-casa.colorir.com
Fonte: http://www.pixbay.com
Diagrama de corpo livre: Equilíbrio.
Força se deve a uma interação
Para identificar as forças exercidas sobre o objeto devemos usar o diagrama de corpo livre.

piso
livro
Planeta Terra
Quais as forças exercidas sobre o livro?
Fonte: http://www.pixbay.com
Regras:
Identifique o objeto que sobre a ação da força:
Represente o objeto como uma partícula.
LIVRO
Identifique os agentes que exercem as forças:
PISO
TERRA
Localize a cauda de cada vetor força sobre a partícula.
O comprimento do vetor é proporcional à intensidade da força.
Desenhe uma referência.
Diagrama de corpo livre: Equilíbrio.
Diagrama de corpo livre
Para separar as forças exercidas sobre o objeto devemos usar o diagrama de corpo livre.

piso
livro
terra
Quais as forças exercidas sobre o livro?
Essas forças não são um par de interação porque atuam no mesmo objeto e são de naturezas diferentes (campo e contato)!
A força da gravidade e a força de compressão.
Fonte: http://www.pixbay.com
Diagrama de corpo livre
Para separar as forças exercidas sobre o objeto devemos usar o diagrama de corpo livre.
Quais as forças exercidas sobre a argola?
Essas forças não são um par de interação porque atuam no mesmo objeto e são de naturezas diferentes (campo e contato)!
A força da gravidade e as tensões.
Diagrama de corpo livre
Para separar as forças exercidas sobre o objeto devemos usar o diagrama de corpo livre.
Quais as forças exercidas sobre a mulher?
Essas forças não são um par de interação porque atuam no mesmo objeto e são de naturezas diferentes (campo e contato)!
A força da gravidade e compressão.
Força de ação à distância
Para um objeto em queda livre perto da superfície da Terra, a única força exercida sobre o objeto é a força gravitacional \(\vec F^G_{To}\) exercida pela Terra sobre o objeto.
A aceleração de queda livre (g) é o campo gravitacional da Terra.
O peso (P) do objeto próximo da superfície da Terra depende da inércia do objeto (m) e do campo gravitacional da terra (g).


Fonte: https://www.pngwing.com
(Força peso)

Fonte: http://www.pixbay.com
Se suspendermos a mola em um teto e prendermos o peso na parte inferior, o peso alonga a mola que fica em uma posição abaixo do comprimento relaxado da mola.
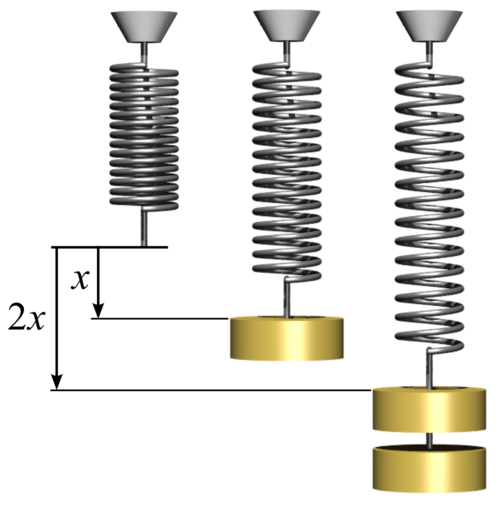
O peso está sujeito a uma força de gravidade para baixo e uma força de contato para cima - um puxão - exercido pela mola.
peso
mola
Terra
teto

As forças de contato
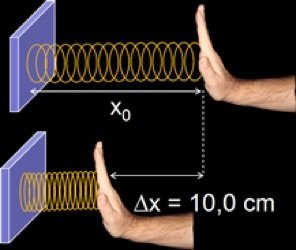
A força exercida pela mola (força elástica) é contrária a deformação da mola (\(\Delta x\)).
A força exercida pelo peso é a favor da deformação da mola.
Fonte: Tipler & Mosca
(Força elástica)
Se você posicionar uma mola na vertical e colocar um peso em cima dela, o peso comprime a mola e fica em uma posição abaixo do comprimento relaxado da mola.

peso
mola
Terra

As forças de contato
A força exercida pela mola (força elástica) é contrária ao deformação da mola (\(\Delta x\)).
A força exercida pelo peso é a favor da deformação da mola.
O peso está sujeito a uma força de gravidade para baixo e uma força de contato para cima - um empurrão - exercido pela mola.
Fonte: Tipler & Mosca
(Força elástica)
A força elástica modela as interações atômicas dos átomos que compõem a superfície.
Quando um fio ou uma superfície suportam um objeto pesado, as ligações entre os átomos, similares a molas, se alongam bastante, porque cada ligação deve aguentar o peso de tudo que está abaixo dela.
As forças de contato

Terra
bola
fio
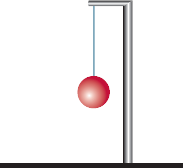
Fonte: Charbay & Sherwood
(Força tensão/tração)
Uma corda é esticada pelo peso do tijolo. As ligações interatômicas também podem ser modeladas como uma rede de um sistema de molas e massas.
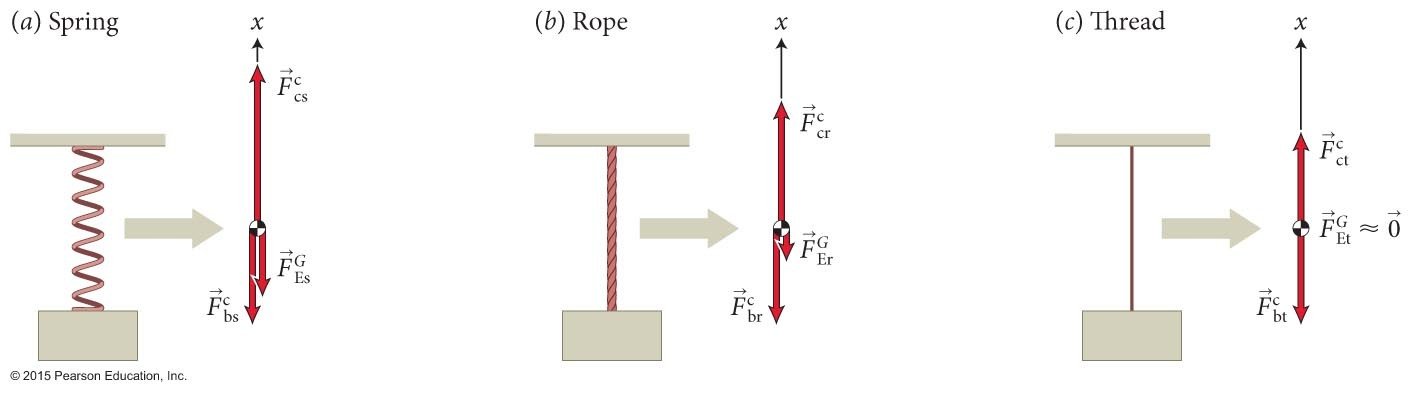


A corda sofre uma deformação — suas “molas” interatômicas são alongadas.
Denomina-se a força aplicada para baixo exercida pelo peso de “força de tensão” ou "força de tração".
A força tensão \(T\) tem natureza elétrica!
Se a corda é muito fina de modo que sua inércia é muito pequena, a força da gravidade é muito menor do que as forças de contato. Nesse caso idealizado, a corda simplesmente transmite a força de tensão entre suas pontas.
teto
peso
corda
Fonte: Eric Mazur
Força de contato
Tensão (T)
Para molas, cordas, fios e mesmo correntes cujas inércias são muito menores que as cargas que suportam, as forças de tensão são muitos maiores que a força da gravidade.
Portanto, se ignorarmos a força da gravidade há apenas uma transmissão de forças.
Se você prender uma corda a um tijolo e puxar uma extremidade da corda, ela se estica um pouco e a extremidade oposta da corda transmite sua força ao tijolo.
Força de contato
corda
tijolo

Se a força da gravidade na corda é irrelevante...
... então a força exercida pela pessoa na corda é transmitida intacta à caixa.
Não são par de interação
Não são par de interação
Fonte: Eric Mazur
Tensão (T)
A superfície (s) exerce sobre o bloco (b) uma força de contato resultante: \(\vec F^c_{sb}\).
Componente normal => Força normal (\(\vec N\)).
Componente tangencial => Força de atrito (\(\vec F_{at}\)).
E existe uma diferença entre esses componentes normal e tangencial.
Essa força de contato tem duas componentes:
As Forças de contato
(Normal e Atrito)
As Forças de contato
A força de contato da mesa sobre o tijolo é uma soma de duas componentes perpendiculares:
A força de compressão (normal) perpendicular à superfície da mesa e a força de deformação paralela à superfície de contato (atrito).

A força de atrito vai se ajustando à força aplicada até que a velocidade do bloco tenha velocidade constante (\(F_{aplicada} = F_{atrito}\)) ou acelerado (\(F_{aplicada} \neq F_{atrito}\)).
As forças normal e atrito são componentes de uma força de contato.
Fonte: Chabay & Sherwood
Fonte: Chabay & Sherwood
(Normal e Atrito)
A força de contato tem sentido contrário 'a resultante das forças aplicadas e gravitacional!
A força de contato tem duas componentes: normal à superfície (deformação) e tangente à superfície (atrito)
O atrito é um fenômeno que envolve a deformação de objetos e tem natureza interatômica.
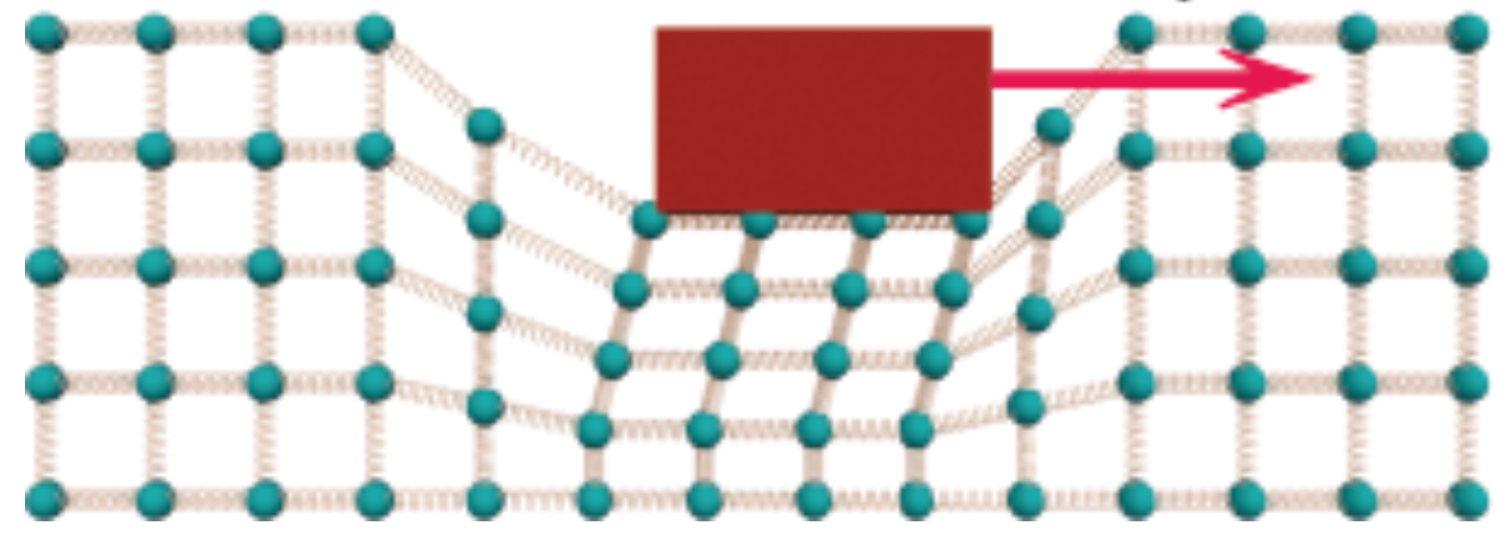
Quando você aplica uma força sobre o tijolo \(\vec F_{aplicada}\), ele pressiona os átomos da mesa, comprimindo as ligações interatômicas à sua frente e esticando as que estão atrás (a escala está exagerada).
O efeito resultante dessa deformação da mesa surge como uma força paralela e oposta à deformação chamada “força de atrito”.


A força elástica (deformação) se opõe à força aplicada.

Fonte: Chabay & Sherwood
Fonte: Chabay & Sherwood
Fonte: Chabay & Sherwood
Força de atrito
A superfície é comprimida pelo peso do bloco. As ligações interatômicas da superfície podem ser modeladas como uma rede de um sistema de molas (interação elétrica) e massas (átomos).

A superfície sofre uma deformação — suas “molas” interatômicas são comprimidas.
Denomina-se a força para cima exercida pela superfície de “força de compressão”, mas a denominação usual para uma força desse tipo é “força normal”, pois ela é perpendicular à superfície.
A força normal se ajusta à força peso.
Fonte: Chabay & Sherwood
Força normal
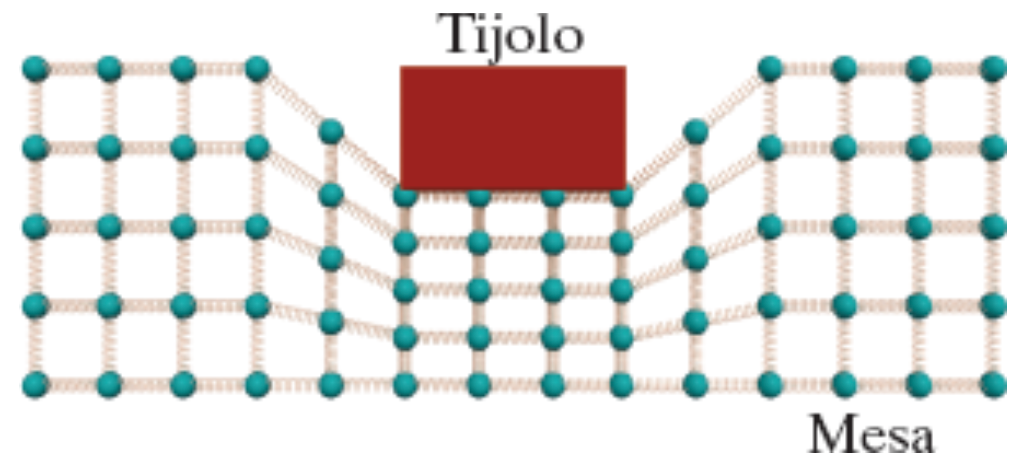
Fonte: Chabay & Sherwood
bloco
A força normal se ajusta para equilibrar a força peso.
Força normal
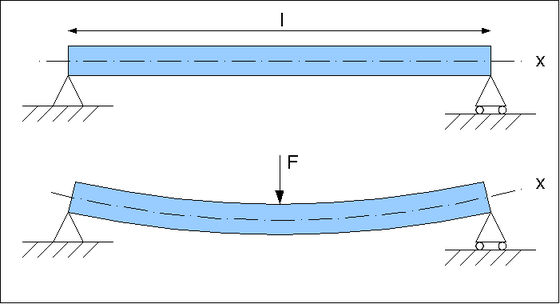
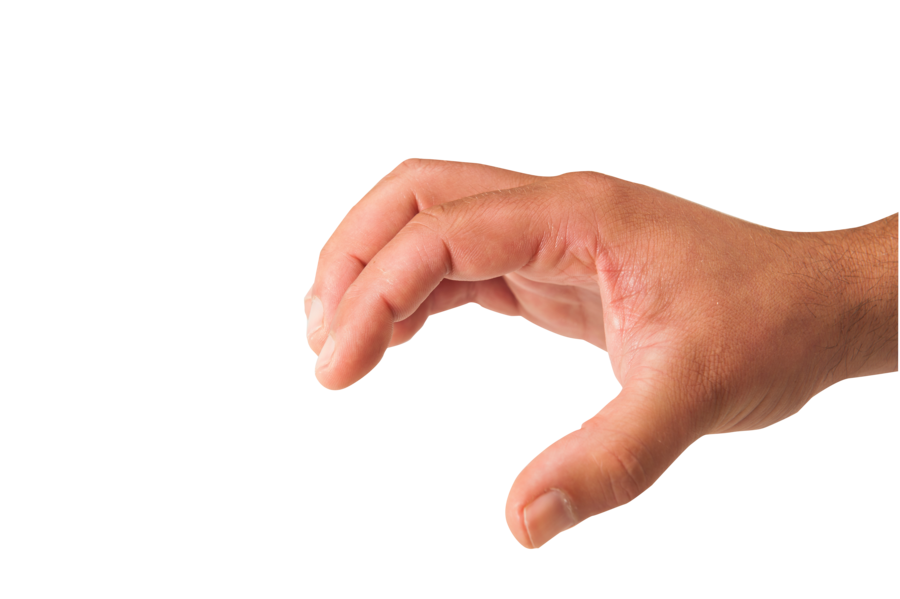
Fonte: https://www.gratispng.com


Se a força aplicada pela mão superar as interações interatômicas da superfície ela se quebra. Nesse momento:
Exemplo 1
Identifique todas as forças exercidas no objeto em itálico em cada situação:
(a) Um livro está deitado em cima de uma revista sobre uma mesa.
(b) Uma bola se move ao longo de uma trajetória pelo ar.
(c) Uma pessoa está sentada em uma cadeira no chão de uma sala.
(d) Um ímã que flutua acima de outro ímã que está sobre uma mesa.



Fonte: https://images.app.goo.glFonte: https://images.app.goo.glFonte: Ronai LisboaSe o livro um estivesse em queda livre ao invés de apoiado no chão, como seria o diagrama de corpo livre?
Exemplo 2

Fonte: https://images.app.goo.gl/Desenhe um diagrama de corpo livre para a pessoa.
Exemplo 3
Você joga uma bola para cima. Desenhe um diagrama de corpo livre para a bola
(a) enquanto ela ainda toca sua mão e está acelerando para cima;
(b) no ponto mais alto; e
(c) no caminho de volta para baixo.
Exemplo 4

Fonte: https://images.app.goo.gl
Fonte: https://images.app.goo.gl
Exemplo 5
(a) Na figura a força de contato exercida pela mesa no livro e a força gravitacional exercida pela Terra no livro são um par de interação?
(b) O que impede que o livro caia em queda livre?
TERRA


TERRA

Fonte: https://a-casa.colorir.com
Fonte: http://www.pixbay.com
Se duas pessoas, A e B, puxam as extremidades opostas de uma corda que está em repouso, cada uma exercendo uma força elástica horizontal de magnitude F, a tensão na corda é T = F. Suponha, em vez disso, que uma extremidade da corda esteja amarrada a uma árvore e A puxe a outra extremidade por ela mesmo com a mesma força de magnitude F. A tensão na corda é maior que, igual ou menor que a tensão quando A e B puxar extremidades opostas?
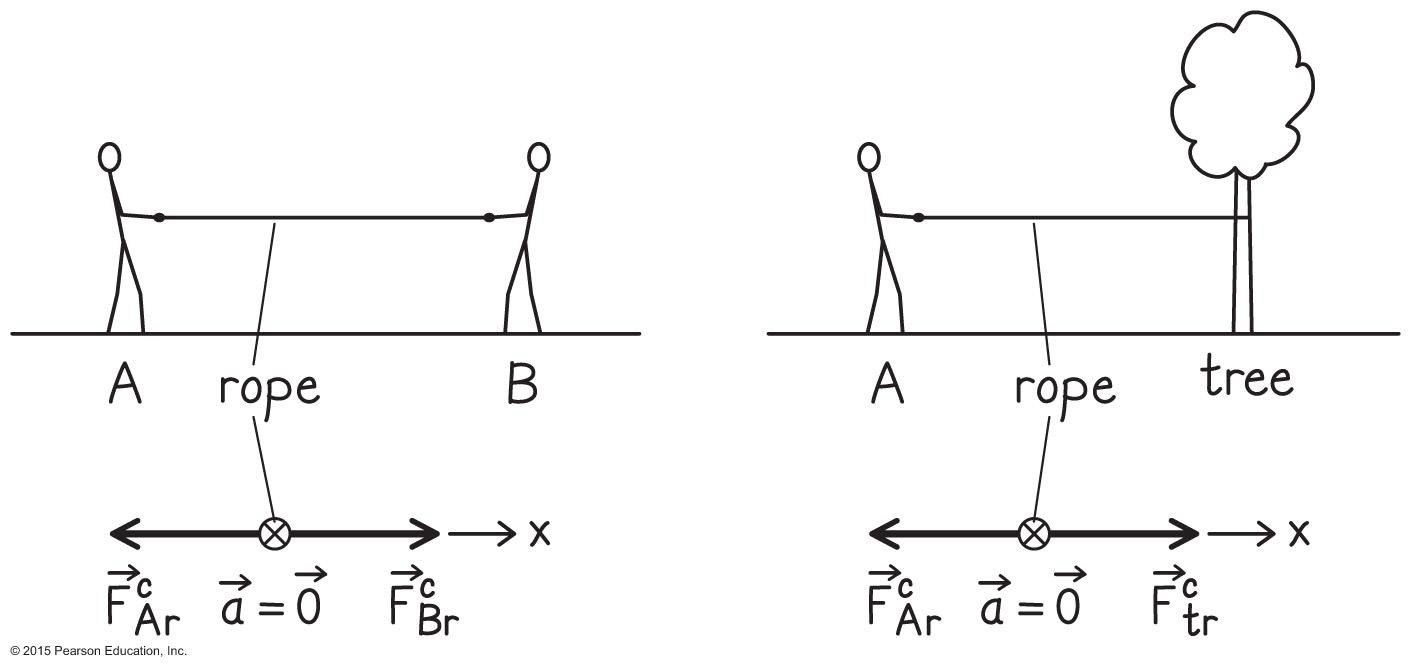
Como A puxa a corda com uma força de magnitude F, a árvore deve puxar com uma força de magnitude F na direção oposta e, portanto, a tensão na corda é T = F, que é a mesma de quando A e B puxam as extremidades opostas.
Exemplo 6
No Exemplo 6, suponha que as duas pessoas puxem a mesma extremidade da corda, cada uma exercendo uma força F, enquanto a outra extremidade ainda está presa à árvore. A tensão na corda é maior que, igual a ou menor que a tensão quando as duas pessoas puxam em extremidades opostas?
Exemplo 7
Interação gravitacional
Essa interação de longo alcance se manifesta como uma atração entre todos os objetos que têm massa e é mediada por uma partícula de calibre ainda não detectada, chamada graviton.

É a interação fundamental mais fraca, manifestada pela observação de que você não pode senti-la agindo entre seu corpo e qualquer objeto próximo, embora ambos possuam massa.
A interação gravitacional entre a Terra e seu corpo, por exemplo, é perceptível.
Fonte: http://www.nasa.gov
Interações fundamentais
Interação eletromagnética
Essa interação de longo alcance é responsável pela maior parte do que acontece à nossa volta: estrutura de átomos e moléculas, por todos os processos químicos e biológicos, pela coesão da matéria em líquidos e sólidos, pela interação repulsiva entre objetos como um taco e bola, bem como pela luz. e outras radiações eletromagnéticas.
O atributo da matéria responsável por essa interação é chamado de carga elétrica, que vem em duas variedades: positiva e negativa (em repouso), cada uma aparecendo em números iguais no universo. Quando em movimento origina magnetismo (pólos sul e norte). A partícula mediadora associada à interação eletromagnética é o fóton.
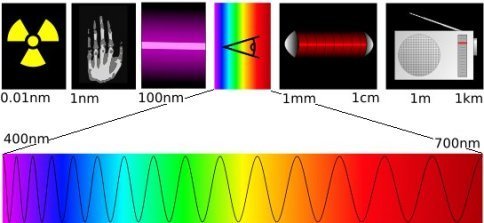

Fonte: https://gfycat.com
Fonte: www.gifher.com
Interações fundamentais
Interação nuclear fraca (eletrofraca)
Essa interação repulsiva é responsável por alguns processos de decaimento radioativo e pela conversão de hidrogênio em hélio nas estrelas.
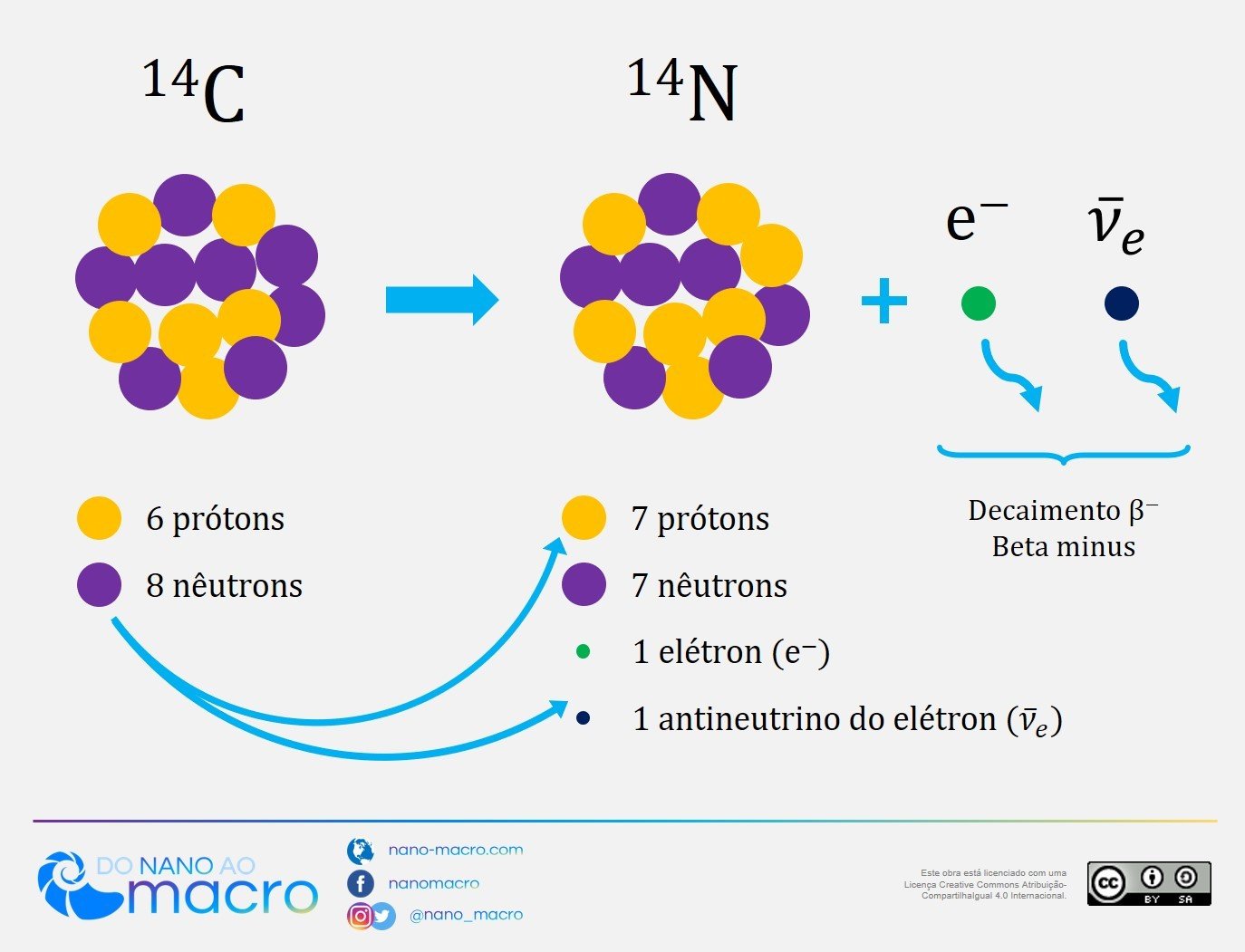
Quando a interação fraca faz com que uma partícula subatômica decaia, a energia interna da partícula original é convertida em energia cinética dos produtos da decomposição. Tal como nos átomos a energia química é convertida em energia cinética dos produtos da reação. As interações elétrica/fraca foram unificadas na interação eletrofraca.

Fonte: www.nano-macro.com
Fonte: www.nist.gov
Interações fundamentais
Interação nuclear forte
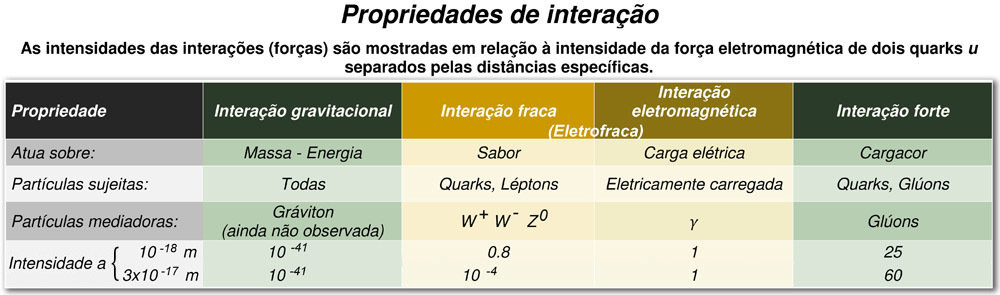
A interação forte atua entre os quarks, que são os blocos de construção de prótons, nêutrons e outras partículas. Essa interação, que pode ser atrativa ou repulsiva, é tão forte que supera completamente todas as outras interações entre partículas. O atributo necessário para essa interação é a carga de cor e as partículas do medidor são chamadas de glúons.
Os quarks sempre se organizam de tal maneira que os efeitos da interação forte sejam cancelados. Somente a uma distância muito curta é que parte da interação forte permanece. Essa interação forte residual é responsável por manter o núcleo de um átomo unido.
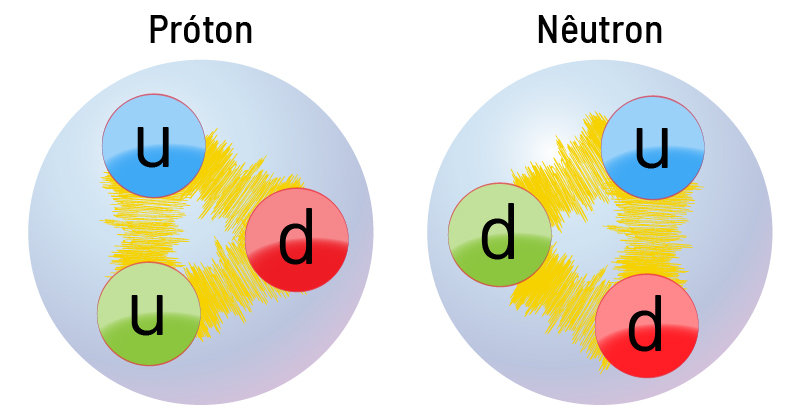

Fonte: https://www.sciencenews.org
Interações fundamentais
Um modelo alternativo explica interações em termos de uma troca de partículas fundamentais denominadas partículas de calibre (partículas de gauge).
Os físicos mostraram experimentalmente que toda interação é causada pela troca correspondente de partículas mediadoras.
Interações fundamentais
Uma interação é fundamental se não puder ser explicada em termos de outras interações.

Fonte: https://pixabay.com
Fonte: https://pixabay.com/
Fonte: www.cbs.com
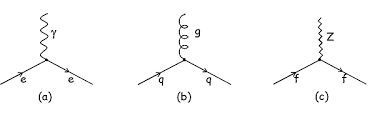
carga elétrica
(fóton)
carga cor
(glúon)
carga fraca
(bósons)
Interações fundamentais
Uma interação é fundamental se não puder ser explicada em termos de outras interações.
Todas as interações conhecidas podem ser atribuídas a apenas quatro interações fundamentais, duas delas familiares da vida cotidiana e duas não.