Tópico 6
Fundamentos da Mecânica
Prof. Ronai Lisbôa
BCT - ECT - UFRN
Objetivos
Trabalho no centro de massa
Estudar um sistema de partículas
Colisões no referencial do centro de massa
Movimento do centro de massa (c.m.)

O centro de massa se move como se toda a massa do bastão estivesse nele concentrada e como se todas as forças externas estivessem aplicadas sobre o centro de massa.
O movimento das partes do bastão não afetam o movimento do centro de massa.
Fonte: MIT - https://youtu.be/DY3LYQv22qY?si=yu4KV3WKZ5juS_Yv
Fonte: Tipler
Cinemática do movimento do centro de massa (c.m.)
A localização do centro de massa no referencial do laboratório.
No referencial do laboratório em 2D:
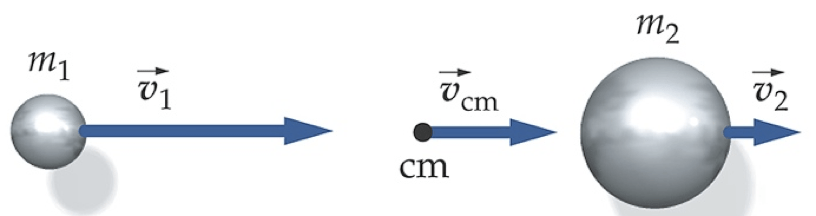
1D
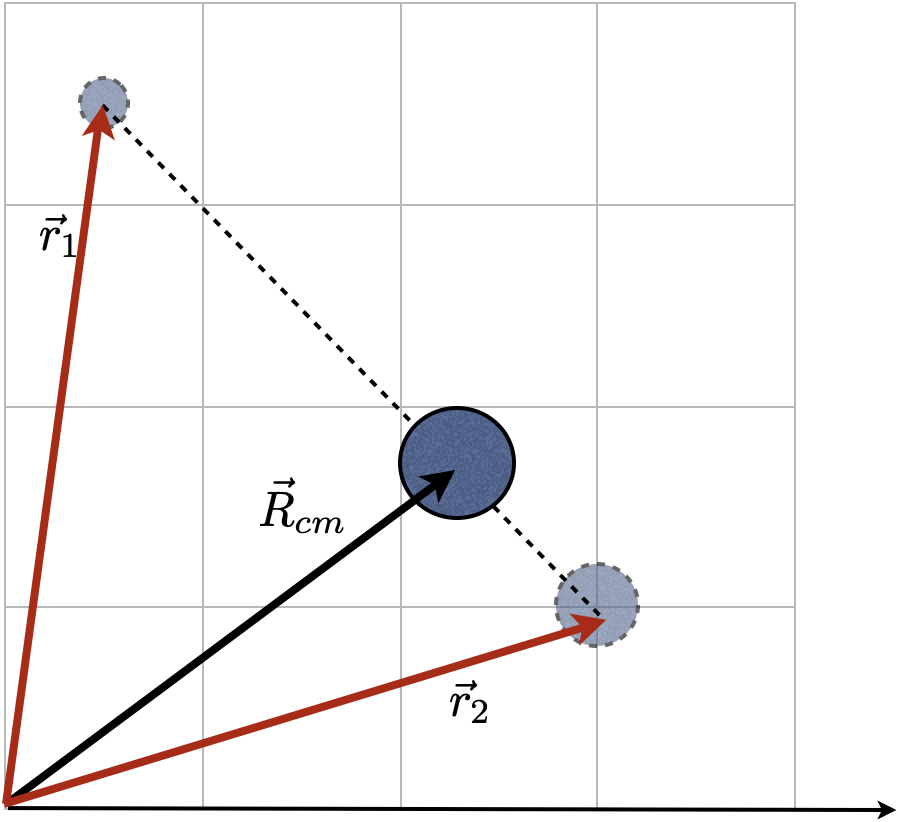
2D

A velocidade do centro de massa no referencial do laboratório.
A aceleração do centro de massa no referencial do laboratório.

Então,
Cinemática do movimento do centro de massa (c.m.)
O centro de massa de um sistema de dois objetos é definido pela coordenada:
Se \(m_1=m_2=m\):
Se \(m_2=2m_1\):
Cinemática do movimento do centro de massa (c.m.)
A velocidade do centro de massa é a taxa de variação da coordenada do centro de massa:
Se \(m_1=m_2=m\) e \(v_1=v_2=v\):
Se \(m_2=2m_1\) e \(v_1 = 2v_2\):
Cinemática do movimento do centro de massa (c.m.)
A aceleração do centro de massa é a taxa de variação da coordenada da velocidade do centro de massa:
Se \(m_1=m_2=m\) e \(a_1=a_2\):
Se \(m_2=2m_1\) e \(a_1 = 2a_2\):
Cinemática do movimento do centro de massa (c.m.)
O movimento do centro de massa é mais mais fácil de ser estudado.
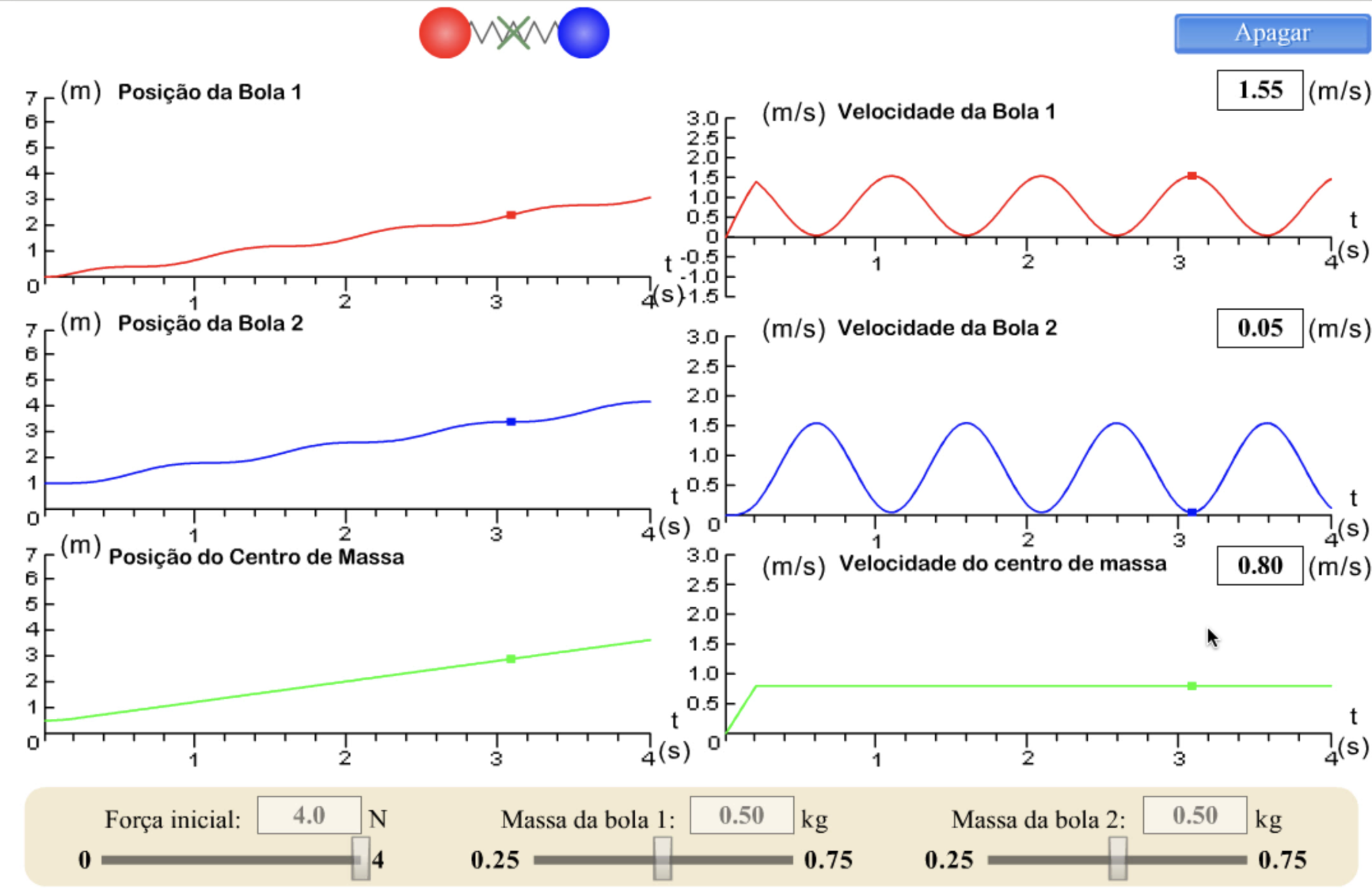
As posições oscilam no tempo
A posição do c.m. varia uniformemente no tempo.
As velocidades oscilam no tempo
A velocidade do c.m. é constantes no tempo
Cinemática do movimento do centro de massa (c.m.)
Analise o simulador abaixo.
Cinemática do movimento do centro de massa (c.m.)
O movimento do rapaz é bastante complexo como um todo, mas o movimento de centro de massa é semelhante ao movimento de um único objeto com uma massa total localizada no centro de massa.
É possível substituir o movimento de todas as partes do sistema pelo movimento do centro de massa.
Fonte: Filipe Varela

Dinâmica do movimento do centro de massa (c.m.)
O c.m. se move como se toda a massa do sistema estivesse nele concentrada e como se todas as forças externas estivessem aplicadas sobre ele.
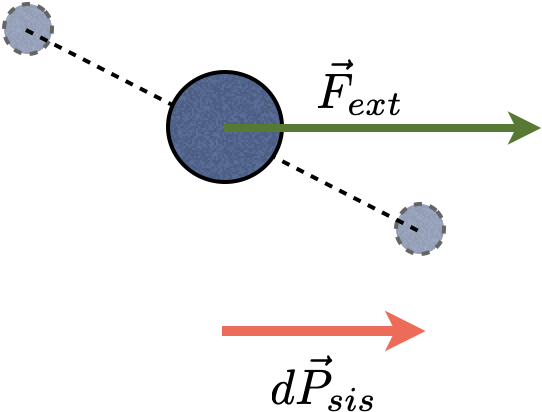

Dinâmica do movimento do centro de massa (c.m.)
Para sistemas com dois objetos, é útil fazer uma distinção entre forças exercidas de dentro do sistema (forças internas: \(\vec F^{in}_{12}\) e \(\vec F^{in}_{21}\)) e forças exercidas de fora do sistema (forças externas: \(\vec F_{ext\,1}\)).
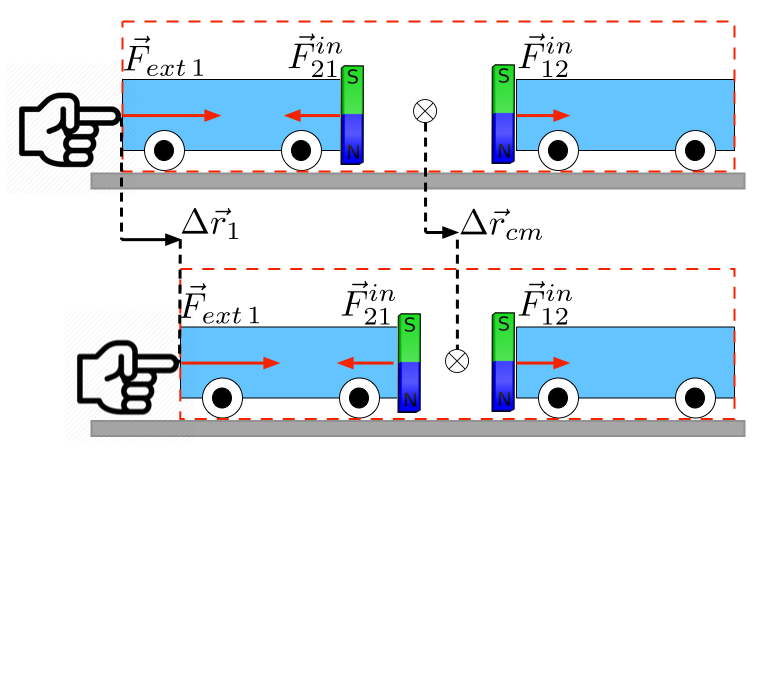
A taxa de variação do momento linear é:
A força resultante sobre o carrinho 1:
A força resultante sobre o carrinho 2:
Para um par de interação.
Então:
Dinâmica do movimento do centro de massa (c.m.)
Quando um força externa atua sobre um sistema isolado a taxa de variação do momento linear do sistema não é nula:

interação de par
Uma vez que as forças internas formam um par de interação: (\(\vec F^{in}_{12}\) = - \(\vec F^{in}_{21}\)), então:
O momento linear do sistema isolado varia somente se houver uma força externa resultante atuando sobre ele:
Existe uma sutileza nessa equação! Os momentos lineares são aqueles dos dois carrinhos! É o momento linear do sistema como um todo!
Dinâmica do movimento do centro de massa (c.m.)
Apenas a força externa exercida no sistema variam o momento linear do sistema:
O momento linear do centro de massa do sistema de dois carrinhos é definido como:
Como a inércia \(m=m_1+m_2\) do sistema permanece constante na interação, temos
Então:
As forças internas não têm nenhum efeito no momento linear do sistema.

Dinâmica do movimento do centro de massa (c.m.)
A equação de movimento para o centro de massa do sistema
O centro de massa de um sistema de dois objetos acelera como se toda a massa estivesse localizado no centro de massa e a força externa fosse exercida nesse ponto. Os dois objetos se comportam como um único objeto.

Dinâmica do movimento do centro de massa (c.m.)
A equação de movimento para o centro de massa do sistema
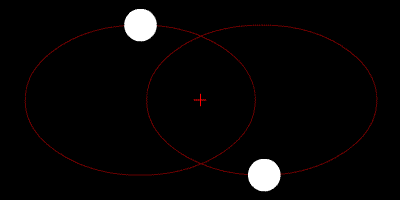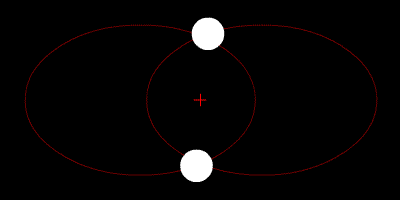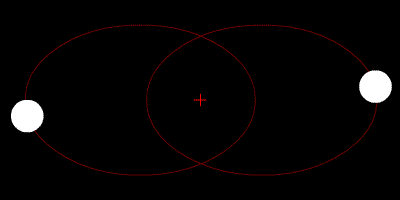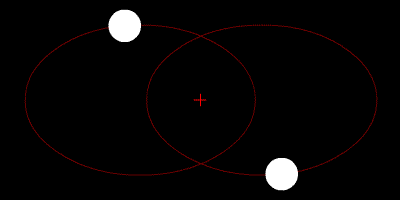
Nesse sistema isolado de duas partículas a força externa resultante é nula e a aceleração do centro de massa não varia. Isto é, o momento linear inicial é igual ao final, pois há somente forças internas.
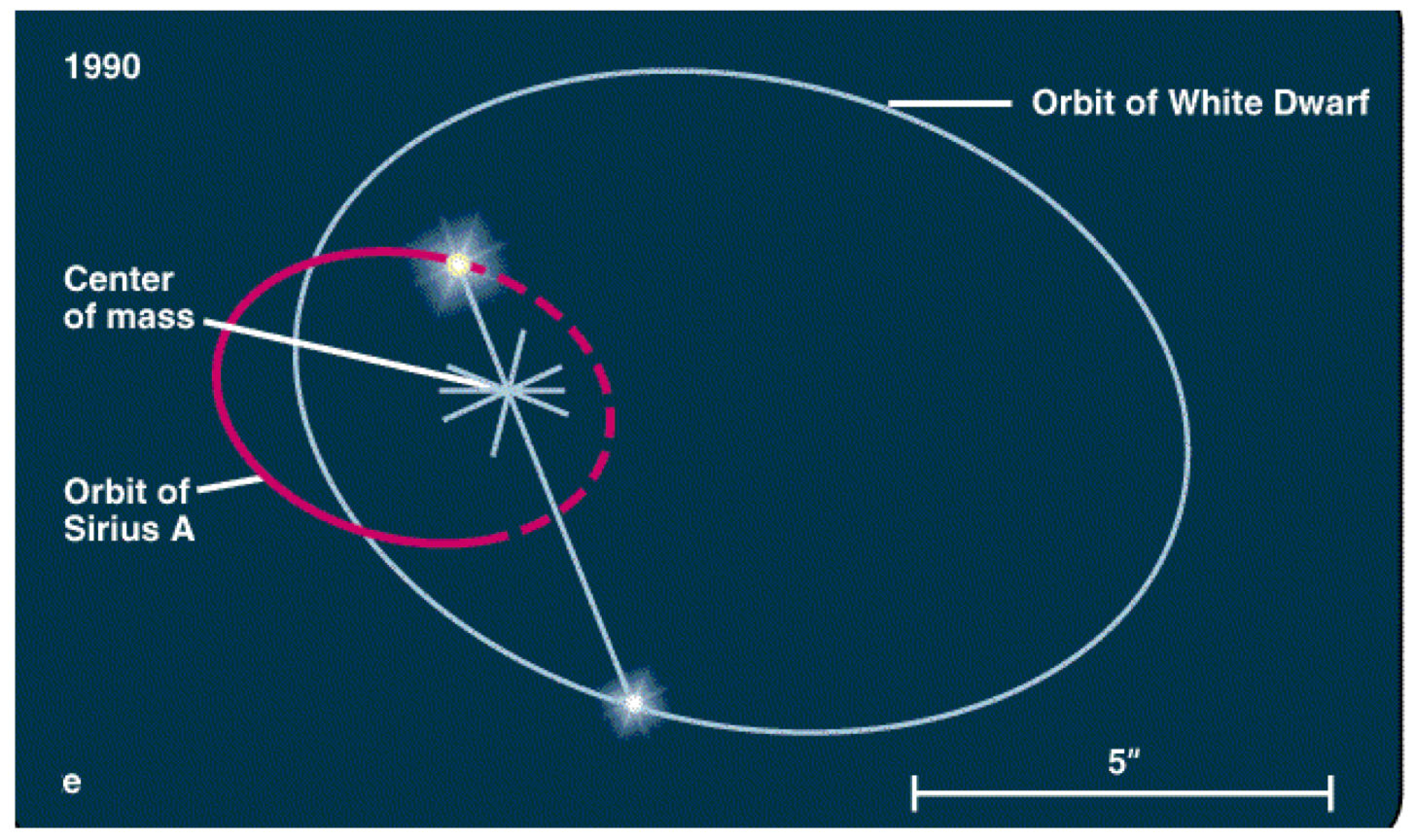
As estrelas Sirius A e B têm cada uma sua órbita. Mas as forças gravitacionais entre elas (forças internas) não alteram o movimento do centro de massa.
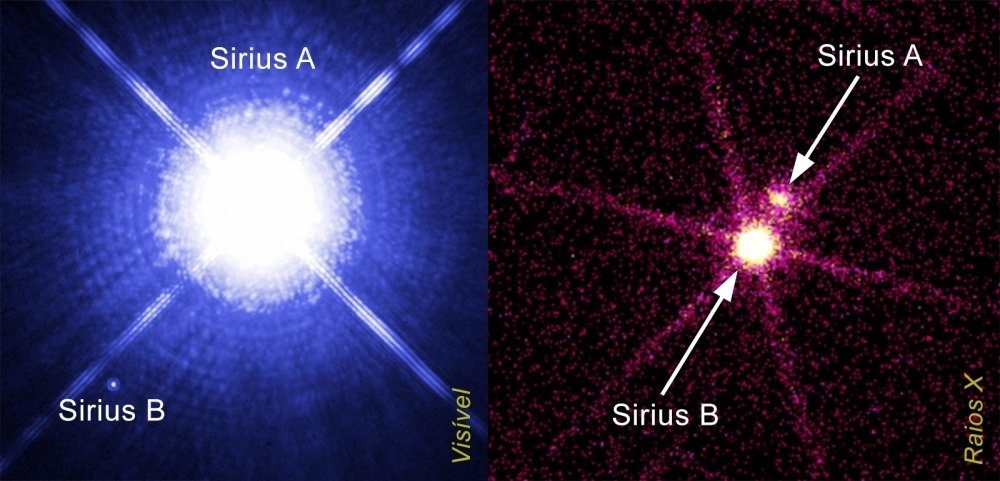
Fonte: http://www.nasa.gov
Dinâmica do movimento do centro de massa (c.m.)
A equação de movimento para o centro de massa do sistema
O centro de massa de um sistema acelera como se toda a massa estivesse localizada no centro de massa e a força externa fosse exercida nesse ponto.
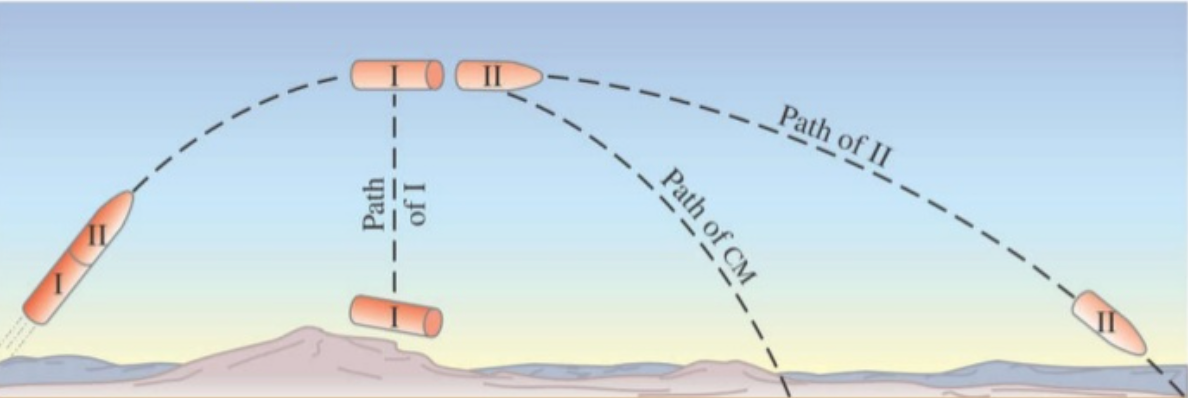
discreto
contínuo
A força da gravidade atua sobre o centro de massa. A trajetória é similar aquela de uma partícula.
Fonte: https://www.youtube.com
Fonte: http://phy-lab.blogspot.com
Dinâmica do movimento do centro de massa (c.m.)
Vamos analisar o caso de um sistema em que existem mais de dois objetos interagindo.
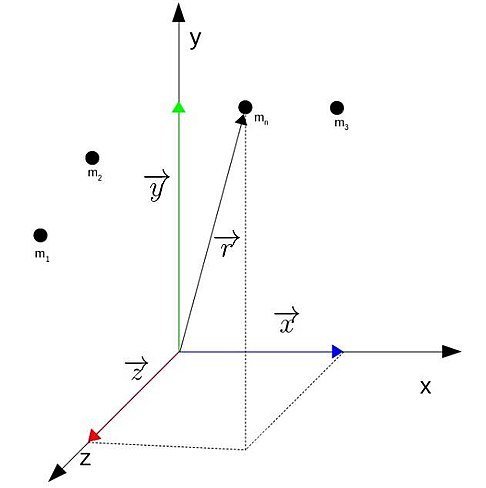
A taxa de variação do momento linear é:
onde
Dinâmica do movimento do centro de massa (c.m.)
Energia do Movimento do centro de massa (c.m.)
A cinemática de um sistema de partículas.
O movimento de um sistema de partículas é a soma da velocidade das partículas em relação ao centro de massa mais a velocidade do próprio centro de massa.
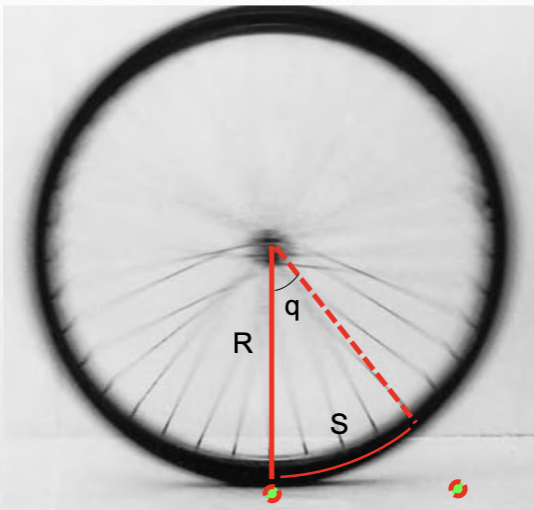
Uma vez que, a energia cinética total é:
e
onde, os termos são:
e
A cinemática de um sistema de partículas.
O movimento de um sistema de partículas é a soma da velocidade das partículas em relação ao centro de massa mais a velocidade do próprio centro de massa.
Uma vez que, a energia cinética total é:
e
onde, os termos são:
e

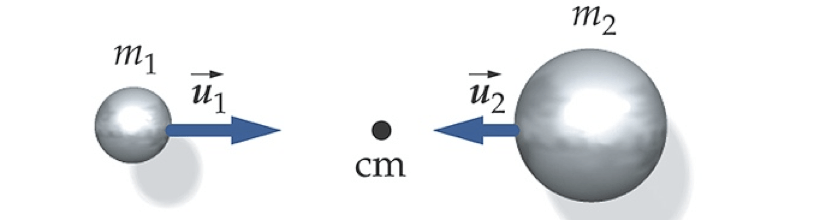
Energia do Movimento do centro de massa (c.m.)
Analise o simulador abaixo:
O disco A, deslizando sobre um trilho de ar horizontal sem atrito, se move a 1,0 m/s no sentido +x. Um disco idêntico, B, está em repouso sobre o trilho, à frente de A. A massa de cada disco é 1,0 kg e o sistema consiste nos dois discos. (a) Qual é a velocidade do centro de massa e qual é a velocidade de cada disco em relação ao centro de massa? (b) Qual é a energia cinética de cada disco em relação ao centro de massa? (c) Qual é a energia cinética total em relação ao centro de massa? (d) Os discos colidem e permanecem grudados um ao outro. Quanto passa a ser, então, a energia cinética total em relação ao centro de massa?
(a)
(b)
(c)
(d)
Energia do Movimento do centro de massa (c.m.)
Sistema de massa variável
Como pode?
Sistema de massa variável
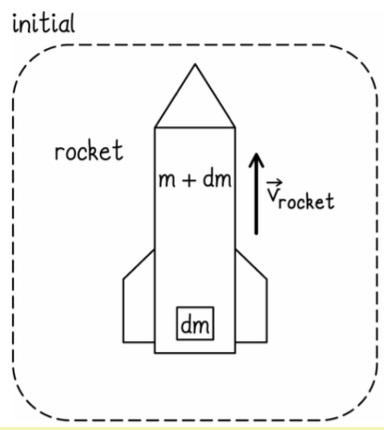
O foguete tem inércia M = (m + dm), onde dm representa uma pequena quantidade de combustível ainda a bordo, mas prestes a ser expelida. Este é o instante inicial t.
A velocidade do foguete de inércia M é \(v_{rocket}\) no tempo t.
Em seguida, uma pequena quantidade de combustível (dm) é ejetada do foguete (dentro do sistema) em um instante t + dt, pouco tempo depois.
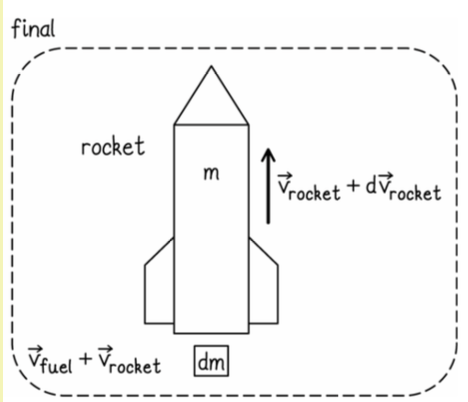
O foguete se move a uma velocidade ligeiramente maior nesse tempo futuro:
Sistema de massa variável
A velocidade do elemento de massa ejetado é
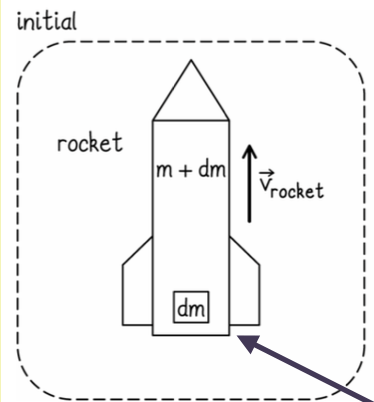
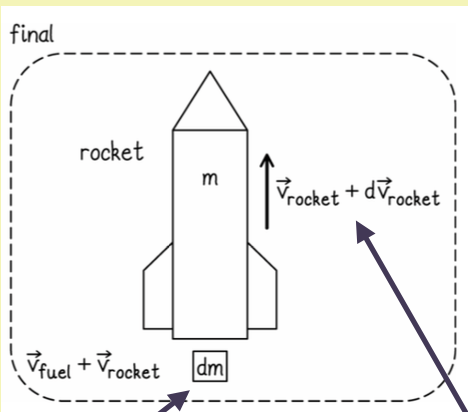
O sistema está sujeito à uma força externa resultante (peso).
inicial
final
Sistema de massa variável
Essa equação descreve uma equação diferencial da variação da velocidade do foguete que ocorre um curto intervalo de tempo:
A segunda lei de Newton para esse sistema de massa variável (referencial positivo para cima)
Para um caso particular onde a massa é queimada a uma taxa constante, \(R\), a massa do foguete varia linearmente no tempo,
A segunda lei de Newton se reduz para:
Sistema de massa variável
A força de empuxo que empurra o foguete para cima é,
A aceleração do foguete é calculada a partir da expressão,
A velocidade do foguete é calculada ao integrar a equação acima no tempo,
Sistema de massa variável
Exemplo para g = 0.
Sistema de massa variável
Exemplo para g = 9,81 m/s\(^2\).
(a)
(b)
(c)
(d)
(e)
(f)
Sistema de massa variável
Exemplo:
A partir do vídeo (LINK):
Qual é a aceleração nesses 60 m de subida inicial?
A velocidade final nesse intervalo:
LINK
Em preparação
- Exemplo 4: T8-55 - Um corpo de 5,0 kg com uma rapidez de 4,0 m/s, colide frontalmente com ouro corpo, de 10,0 kg, que se move de encontro a ele com 3,0 m/s. O corpo de 10,0 kg fica parado após a colisão.
(a) Qual é a rapidez do corpo de 5,0 kg após a colisão?
(b) A colisão é elástica?
- Exemplo 5: T8-59 - Um bloco de massa m1 = 2,0 kg desliza sobre uma mesa sem atrito com uma rapidez de 10 m/s. Diretamente à frente dele e se deslocando no mesmo sentido com uma rapidez de 3,0 m/s, está um bloco de massa m2 = 5,0 kg. Uma mola ideal, de constante elástica k = 1120 N/m, está presa ao segundo bloco.
(a) Qual é a velocidade do centro de massa do sistema?
(b) Durante a colisão, a mola sofre uma compressão máxima D. Qual é o valor de D?
(c) Os blocos acabarão por se separar novamente. Quais são as velocidades dos dois blocos, após a separação, medidas no referencial do centro de massa?
- Exemplo 6: T8-79 - Uma bola repica até 80 por cento de sua altura original.
(a) Qual fração de sua energia mecânica é perdida a cada repicada?
(b) Qual é o coeficiente de restituição do sistema bola-chão?
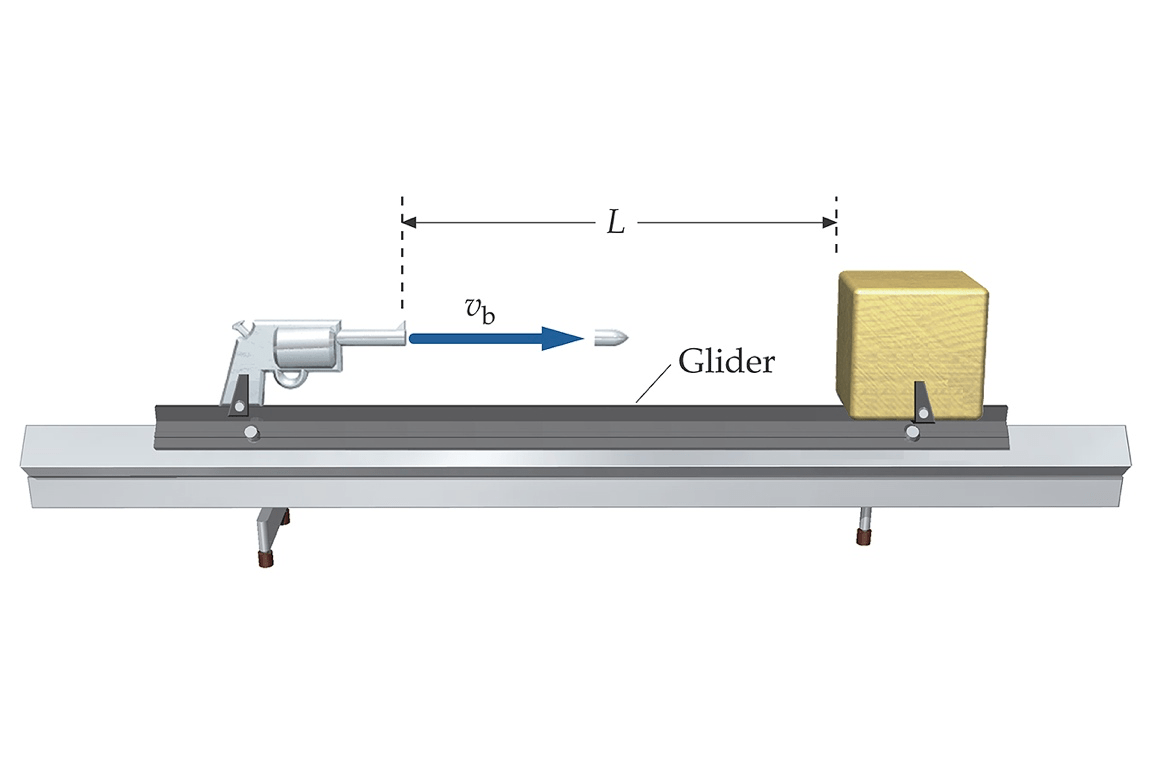
- Exemplo 1: T8-32) Um bloco de madeira e um revólver estão firmemente fixos nas extremidades opostas de uma longa plataforma montada sobre um trilho de ar sem atrito. O bloco e o revólver estão separados de uma distância L. O sistema está inicialmente em repouso. O revólver dispara uma bala que o abandona com uma velocidade vb, atingindo o bloco e nele se encravando. A massa da bala é mb e a massa do sistema revólver-plataforma-bloco é mp.
- (a) Qual é a velocidade da plataforma imediatamente após a bala deixar a arma?
- Qual é velocidade da plataforma imediatamente após a bala atingir o repouso dentro do bloco?
- (b) Qual é a distância percorrida pela plataforma, enquanto a bala está em trânsito entre o revólver e o bloco?
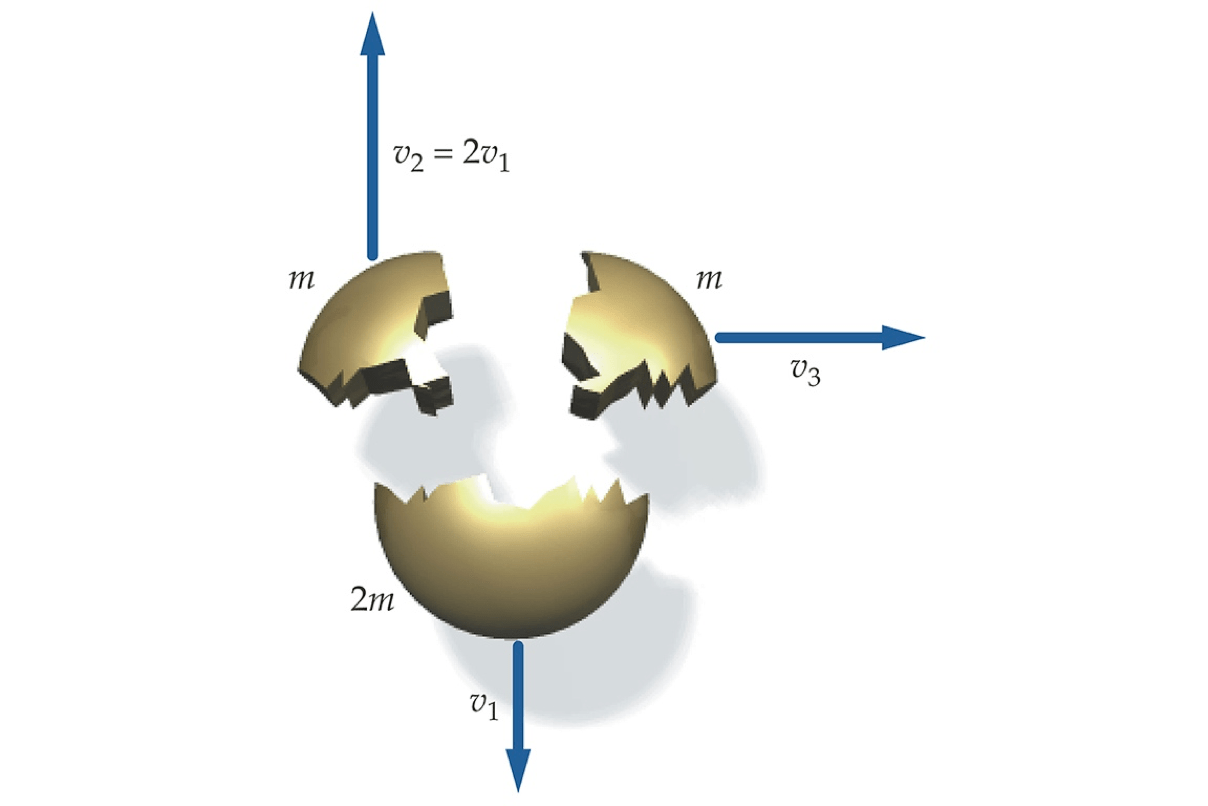
- Exemplo 2: T8-36) A figura mostra o comportamento de um projétil justo após ele ter se partido em três pedaços. Qual era a rapidez do projétil justo antes de se partir?
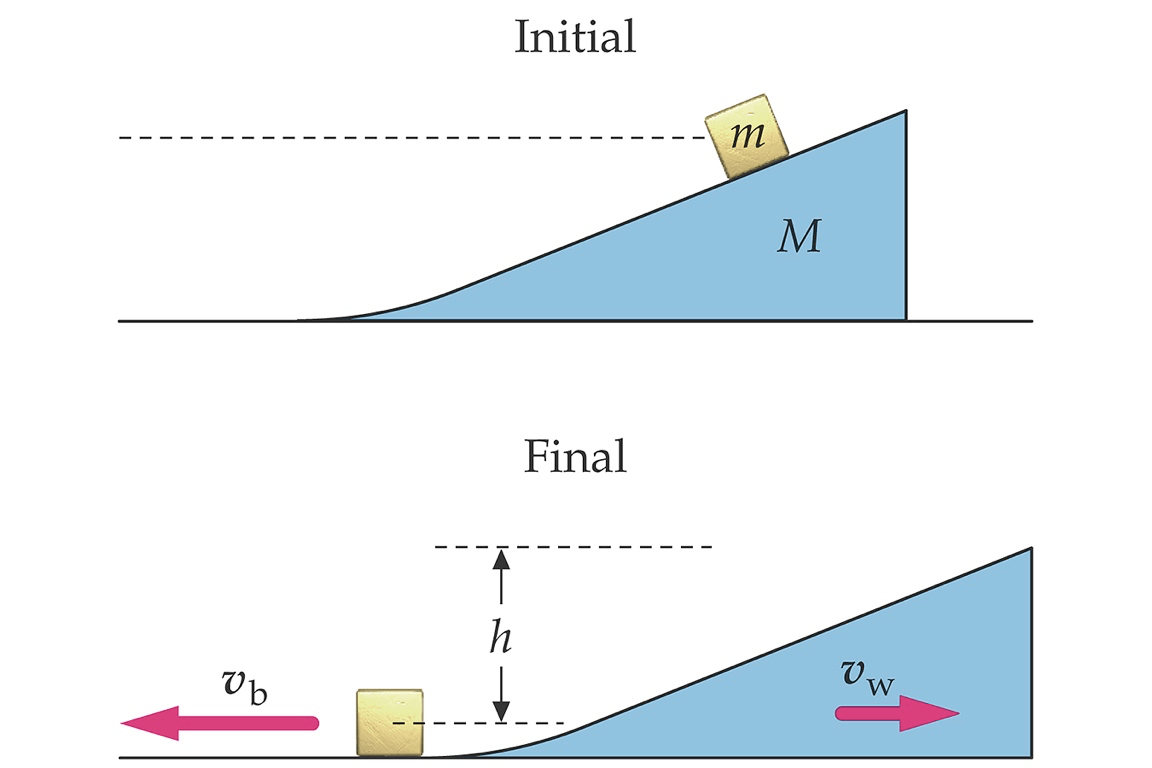
- Exemplo 4: T40) Uma cunha de massa M é colocada sobre uma superfície horizontal e sem atrito, e um bloco de massa m é colocado sobre a cunha, que também tem uma superfície sem atrito. O centro de massa do bloco desce de uma altura h, enquanto o bloco desliza de sua posição inicial até o piso horizontal.
- (a) Quais são os valores de rapidez do bloco e da cunha, no instante em que se separam, seguindo seus próprios caminhos?
- (b) Teste a plausibilidade de seus cálculos para o caso limite M >> m.
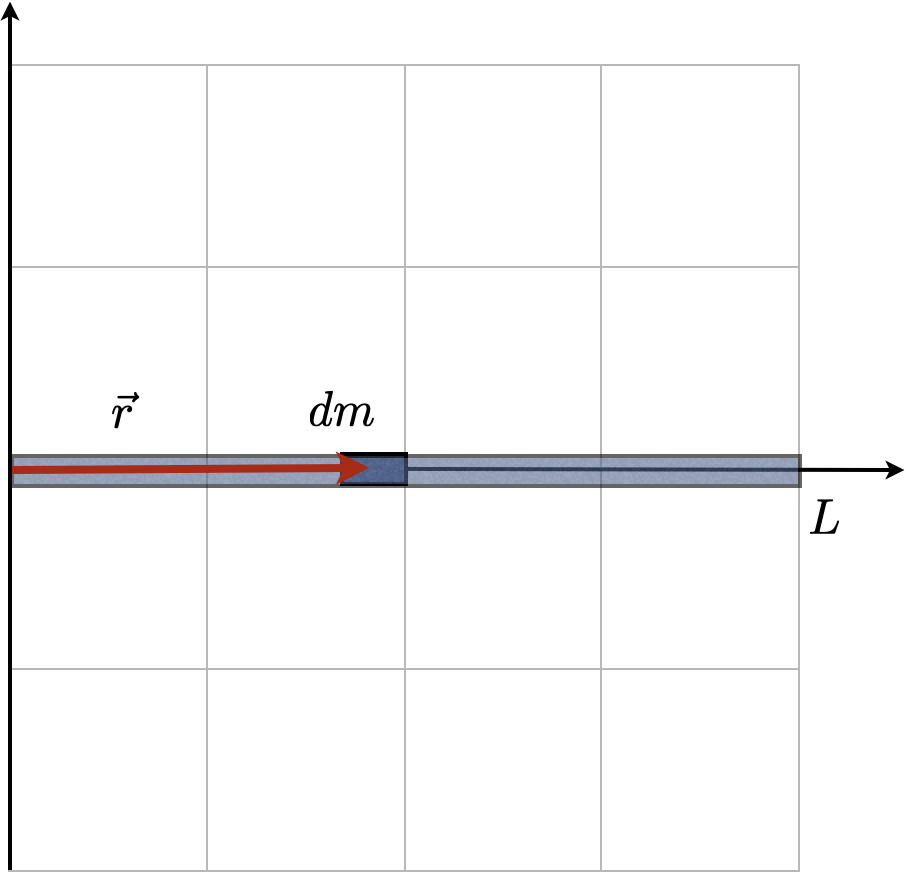
Movimento do centro de massa (c.m.)
A localização do centro de massa. Sistema contínuo.
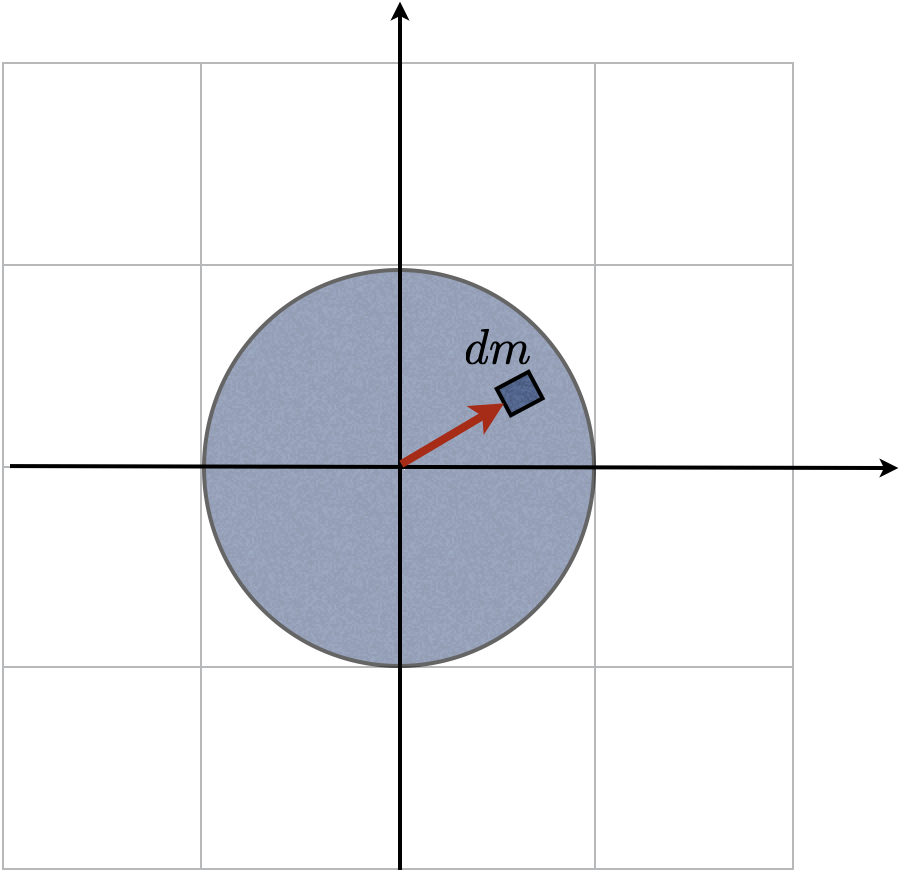
Movimento do centro de massa (c.m.)
A localização do centro de massa. Sistema contínuo.
Movimento do centro de massa (c.m.)
A localização em relação ao referencial do centro de massa.
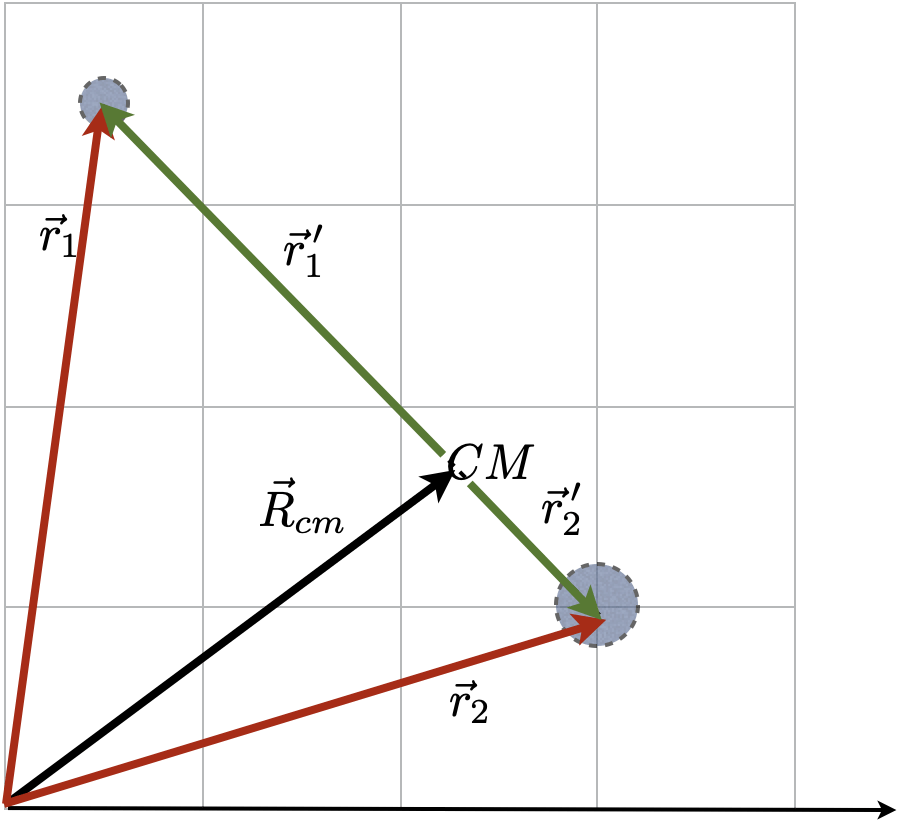
Derivando em relação ao tempo,
Dividindo membro a membro:
Movimento do centro de massa (c.m.)
No referencial do laboratório

No referencial do centro de massa
Movimento do centro de massa (c.m.)
A energia
A partir do teorema trabalho-energia cinética para um sistema de partículas
podemos estudar os processos de colisão de partículas. Se recordarmos que
Daí,
em que:
Temos o princípio da energia:
Movimento do centro de massa (c.m.)
A energia
Em uma colisão as forças externas se cancelam ou são nulas,
A velocidade do centro de massa não varia (\(F_{ext} = M A_{cm} = 0)\)
O tempo de contato é muito pequeno as variações nas posições da partículas do sistema são desprezíveis e a energia potencial interna conservativa não varia.
Daí,
Movimento do centro de massa (c.m.)
A energia
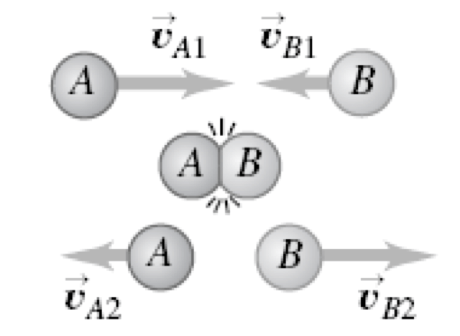
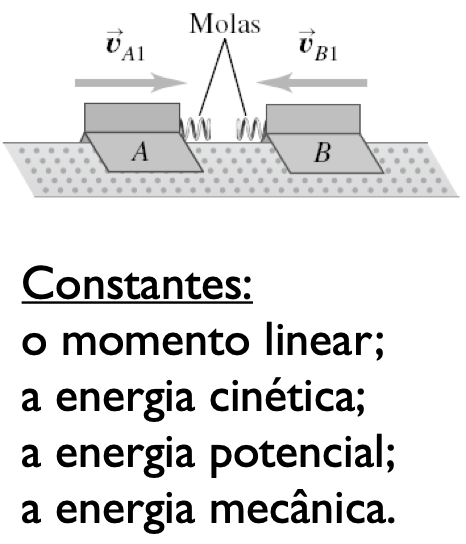
Nas colisões elásticas, o trabalho das forças internas não conservativas é nulo. A energia cinética total do sistema permanece constante.
As forças externas são nulas.
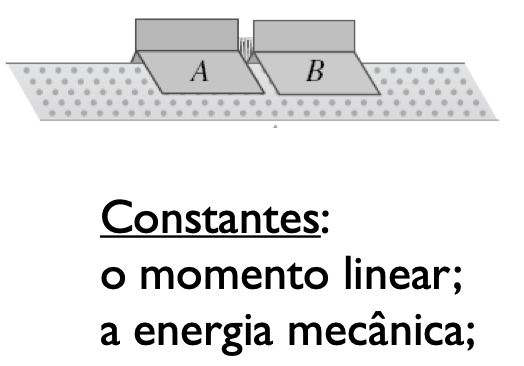
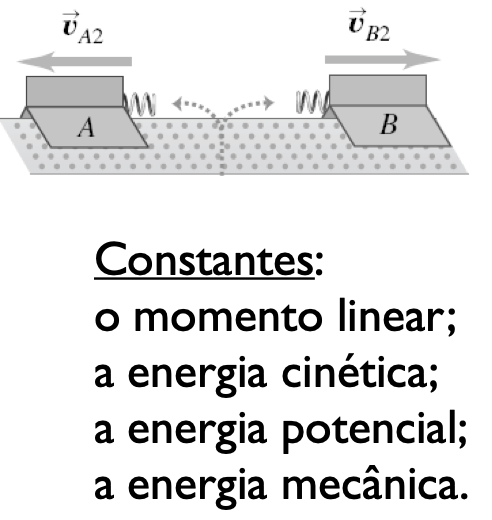
Movimento do centro de massa (c.m.)
A energia
Nas colisões inelásticas, o trabalho das forças internas não conservativas durante a colisão é diferente de zero.
As forças externas são nulas quando comparada as forças internas durante a colisão.

No dia-a-dia, parte da energia é sempre transferida da energia cinética para outras formas de energia, como a energia térmica e sonora.
A energia cinética não é conservada.
Movimento do centro de massa (c.m.)
A energia
Nas colisões perfeitamente inelásticas a distância relativa entre quaisquer partículas do sistema é constante, após a colisão.
Isso significa que derivando em relação ao tempo, após a colisão
onde \(\vec r_1^{\,\prime}\) permanece constante.
Depois da colisão, a energia cinética interna final do sistema é zero.
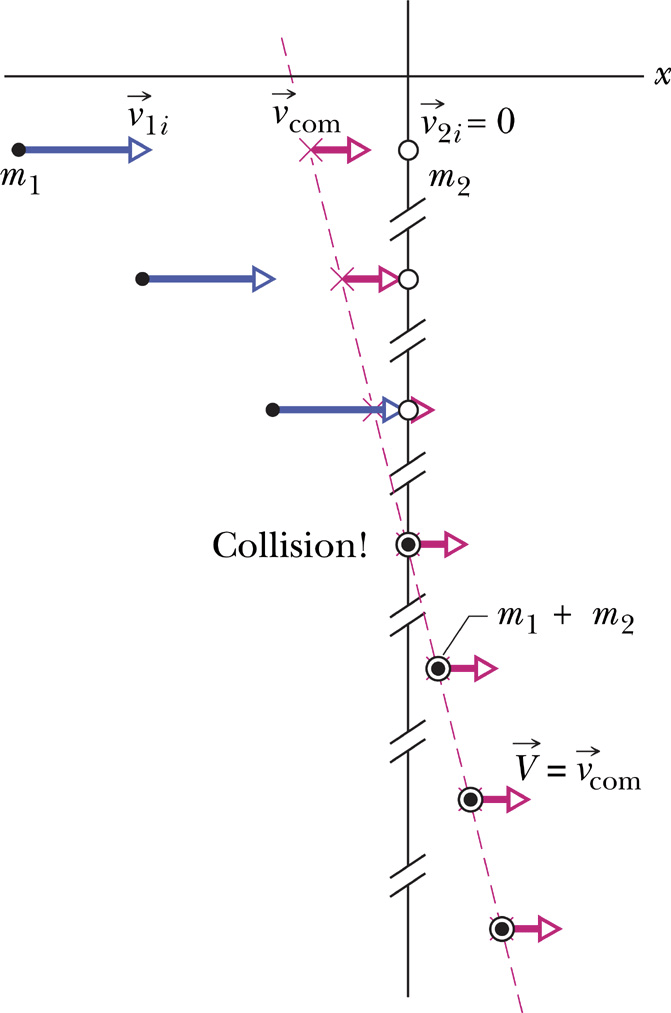
Princípio da conservação da energia
As interações entre dois sistemas pode ser interpretada como uma troca de momento, mas pode ser expressa como uma troca de energia.
A análise de sistemas de partículas em termos de energia é importante não só para a física, como também para a química, a biologia e a engenharia.

Como tratar a energia de um sistema de partículas?
Podem atuar sobre as partículas tanto forças externas como internas.
O trabalho total pode ser separado como o trabalho das forças internas e das forças externas.
Princípio da conservação da energia
A variação da energia cinética de um sistema de partículas é igual ao trabalho realizado sobre o sistema pelas forças externas e internas.
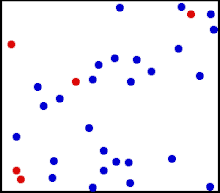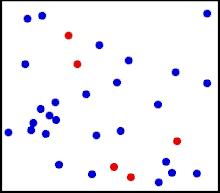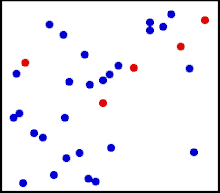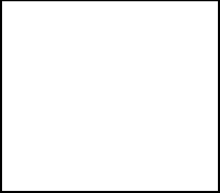
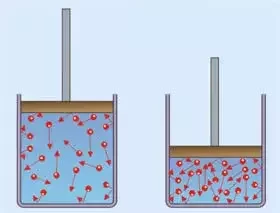
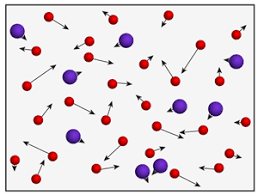
A força externa do pistão executa um trabalho externo.
As forças intermoleculares executa um trabalho interno.
O trabalho total leva a uma variação da energia cinética do sistema.
Princípio da conservação da energia
Quando as forças internas em um sistema de partículas são conservativas, existe uma energia potencial interna que depende da natureza das forças internas.
No sistema planetário e atômico as forças dependem atuam al ao longo da linha que une as duas partículas, a energia potencial interna depende apenas da distância ao centro de forças.
Nesse caso,


Princípio da conservação da energia
Em um sistema de partículas, define-se a energia própria como a grandeza:
em que


Portanto,
a variação da energia própria de um sistema de partículas é igual ao trabalho realizado sobre o sistema por forças externas.
Princípio da conservação da energia
Pode ocorrer do trabalho das forças externas ser nulo. Assim,


A soma da energia cinética com a energia potencial interna, ou energia própria, \(E\), de um sistema de partículas isolado permanece constante em relação a um observador inercial.
Em um sistema isolado existe uma conversão contínua de energia cinética em potencial interna e vice-versa.
Princípio da conservação da energia
Pode ocorrer do trabalho das forças externas ser devido à forças conservativas,
Nesse caso, temos a energia total do sistema sujeito à ação de forças externas conservativas:
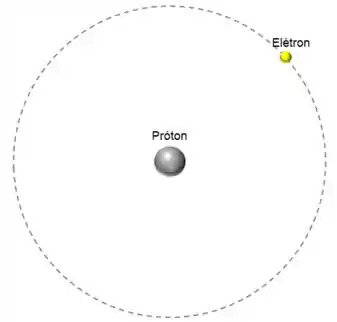
Para o átomo de hidrogênio em um campo elétrico externo:
Princípio da conservação da energia
A energia total de uma molécula diatômica sujeita ao campo gravitacional e que interage como se fosse um sistema massa mola (modelando a interação eletrostática)
A energia própria:
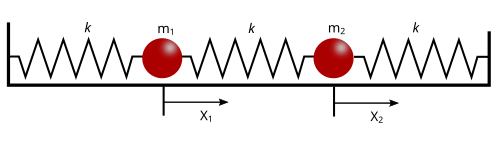
A energia total:
O trabalho realizado sobre uma partícula não é necessariamente igual ao trabalho realizado por um sistema de partículas. Tudo depende de como o centro de massa do sistema se move.
Trabalho realizado em um sistema de muitas partículas
Partícula
O movimento do centro de massa é único
Há um movimento do centro de massa e também relativo ao centro de massa
Sistema sólido indeformável
Sistema sólido deformável
Trabalho realizado em um sistema de partículas
Para um sistema de uma partícula ou um objeto rígido (indeformável):
Para um sistema de muitas partículas:
pois
A expressão \(F_{ext}\Delta x_{cm}\) não é o mesmo que \(W= F_{ext}\Delta x_F\), pois para sistemas de muitas partículas:
Trabalho realizado em um sistema de partículas
Equação de movimento
Lei da energia
Equação do trabalho
Lei da energia
Variação da energia cinética
Única partícula ou corpo rígido
Sistema de partículas ou objeto deformável
Trabalho realizado em um sistema de partículas
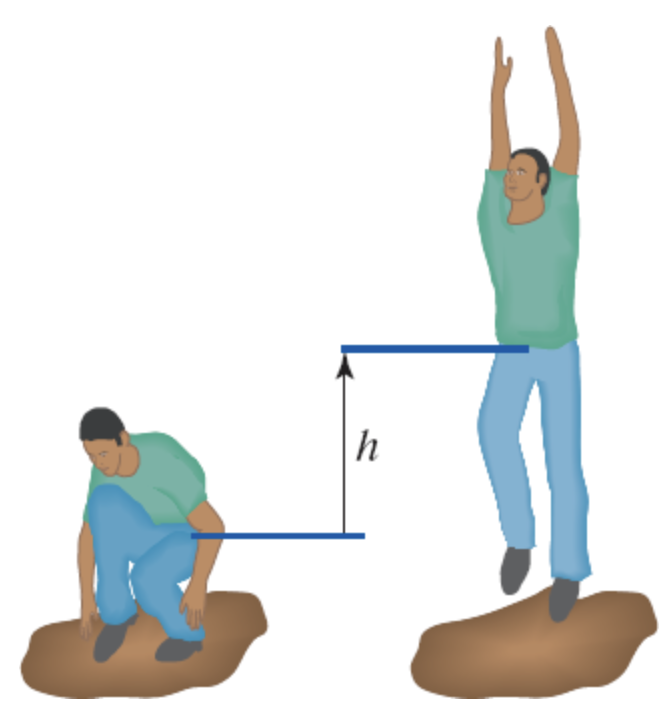
Ao pular, o saltador eleva seu centro de massa de uma altura h. O sistema sofre mudança de forma.
Modelando o saltador como um objeto extenso.
A energia do sistema inclui energia cinética do centro de massa, energia cinética relativo ao centro de massa e energia interna:
Fonte: Chabay & Sherwood
Trabalho realizado em um sistema de partículas
Ao pular, o saltador eleva seu centro de massa de uma altura h. O sistema não muda de forma.
Modelando o saltador como uma partícula.
A energia do sistema é puramente cinética. Então, desconsidera-se qualquer mudança de forma (ou energia interna):
Fonte: Chabay & Sherwood

Trabalho realizado em um sistema de partículas
Repare que as equações para os modelos são diferentes:
Podemos combinar os dois modelos. Pois o segundo nos mostrou como varia a energia cinética do centro de massa.
Fonte: Chabay & Sherwood

Modelo de partícula
Modelo de corpo extenso
Substituindo o modelo de partícula no modelo de corpo extenso:
O saltador usa a energia cinética dos seus braços e pernas, em relação ao centro de massa e alguma energia interna (energia química) para saltar. A energia sai do sistema devido ao trabalho negativo!
O trabalho realizado sobre uma partícula não é necessariamente igual ao trabalho realizado por um sistema de partículas. Tudo depende de como o centro de massa do sistema se move.
Trabalho realizado em um sistema de muitas partículas
Partícula
O movimento do centro de massa é único
Há um movimento do centro de massa e também relativo ao centro de massa
Sistema sólido indeformável
Sistema sólido deformável
Trabalho realizado em um sistema de partículas
Para um sistema de uma partícula ou um objeto rígido (indeformável):
Para um sistema de muitas partículas:
pois
A expressão \(F_{ext}\Delta x_{cm}\) não é o mesmo que \(W= F_{ext}\Delta x_F\), pois para sistemas de muitas partículas:
Trabalho realizado em um sistema de partículas
Equação de movimento
Lei da energia
Equação do trabalho
Lei da energia
Variação da energia cinética
Única partícula ou corpo rígido
Sistema de partículas ou objeto deformável
Exemplo 10.7
Os discos 1 e 2 deslizam no gelo e colidem. A inércia do disco 2 é duas vezes a do disco 1. O disco 1 se move inicialmente a 1,8 m/s; o disco 2 se move inicialmente a 0,20 m/s em uma direção que faz um ângulo de 45° com a direção do disco 1. Após a colisão, o disco 1 se move a 0,80 m/s em uma direção que faz um ângulo de 60° com sua direção original. Qual é a velocidade e a direção do disco 2 após a colisão
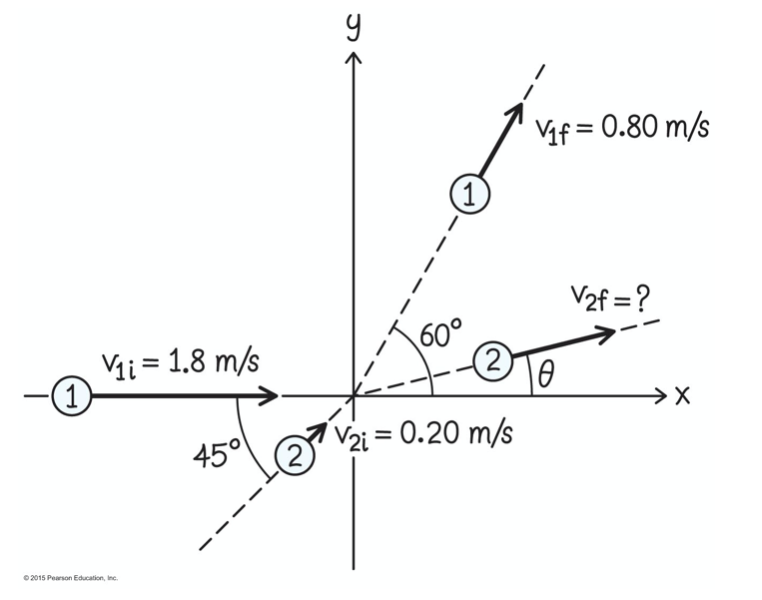
A colisão é elástica?
Exemplo 13 (A4.P2-13)
Um pequeno foguete de coleta de dados meteorológicos é lançado verticalmente para cima. Após vários segundos de vôo, sua velocidade é de 120 m/s e sua aceleração é de 18 m/s^2. Neste instante, a massa do foguete vale 48 kg, e ele perde massa a uma taxa de 0,50 kg/s enquanto queima combustível. Qual é a força resultante sobre o foguete?
Exemplo 14 (A4.P2-14)
O primeiro estágio de um veículo espacial Saturno V consumiu combustível e oxidante a uma taxa de 1,50 x 10^4 kg/s com uma velocidade escalar de exaustão de 2,60 x 10^3 m/s. (a) Calcule o impulso produzido por este motor, (b) Encontre a aceleração que o veículo teve quando acabou de deixar a plataforma de lançamento na Terra, considerando a massa inicial do veículo como 3,00 x 10^6 kg.
Exemplo 15 (A4.P1-12)
Uma corrente de comprimento L e massa total M é liberada do repouso com sua extremidade inferior apenas tocando o topo de uma mesa, como mostrado na figura a. Encontre a força exercida pela mesa sobre a corrente depois que a corrente caiu por uma distância x, como mos trado na b. (Considere que cada elo entra em repouso no instante em que toca a mesa.)