
Aulas 0 e 1
Introdução à Física Clássica II
Prof. Ronai Lisbôa
Não compreendeu algo? Algo está esquisito? Comente!

Movimento Harmônico:
Os fundamentos para entender as ondas.
Fonte: https://www.magnusmundi.comMotivação. O movimento harmônico está ao nosso redor.
O balanço no fim do mundo...
Motivação. O movimento harmônico está ao nosso redor.
O que nos permite ouvir?

Curva de Fletcher-Munson: LINK.
Fonte: G1Motivação. O movimento harmônico está ao nosso redor.
O que nos permite enxergar?
Hue-Teste: LINK

Fonte: https://coralplaza.com.br/Motivação. O movimento harmônico está ao nosso redor.
Como nos comunicamos, compartilhamos informações e percebemos a nós e o mundo?





Ondas eletromagnéticas: Imagem, Comunicações, Transporte de energia.
Ondas mecânicas: Som e imagem
Ligações moleculares
Luz visível
GPS
WiFi - Bluetooth
Transporte de enegia
Música - Voz
Imagem por ultrassom
Propriedades dos materiais
A energia radiativa é transmitida do sol para a Terra como ondas eletromagnéticas. O sol fornece a maior parte da energia do mundo.
Motivação. O movimento harmônico está ao nosso redor.
O espectro eletromagnético
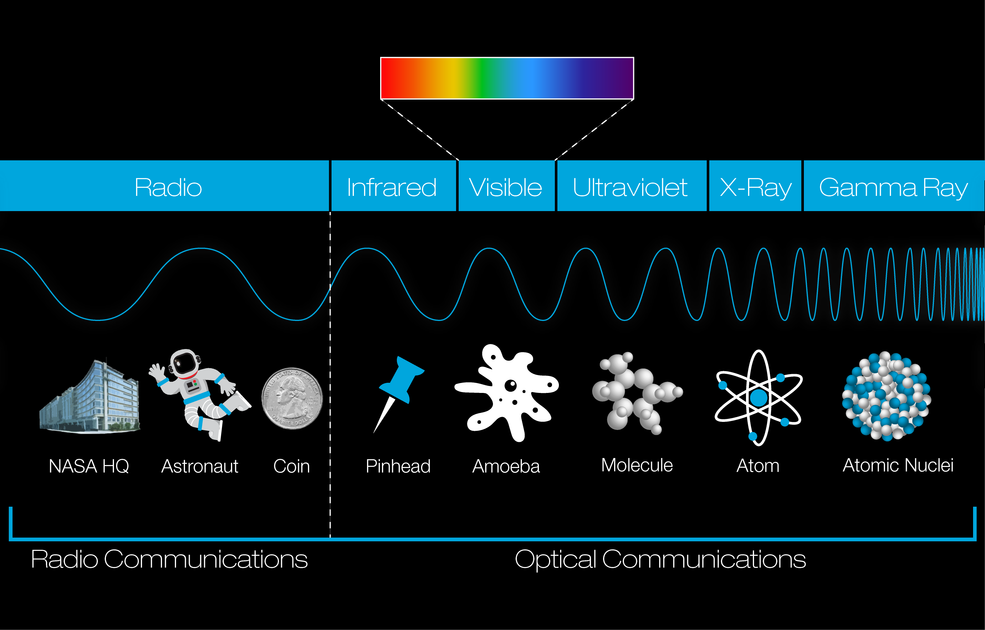
O espectro eletromagnético é composto por todas as frequências de radiação eletromagnética que propagam energia e viajam pelo espaço na forma de ondas.
Fonte: Nasa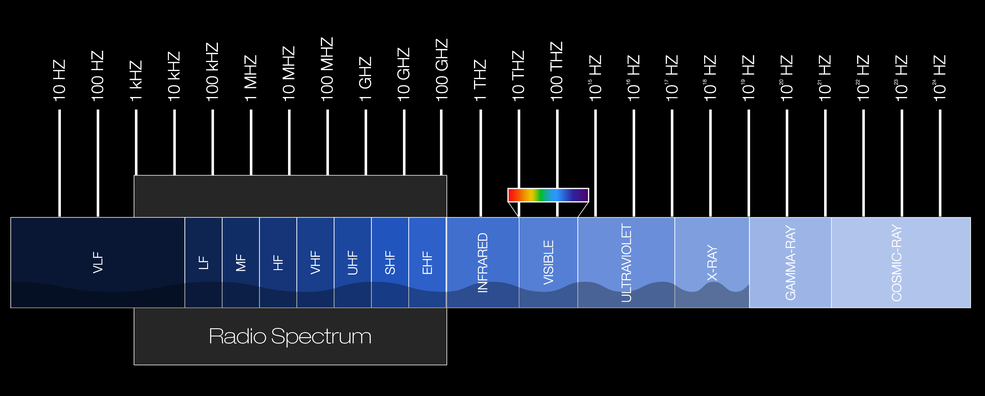
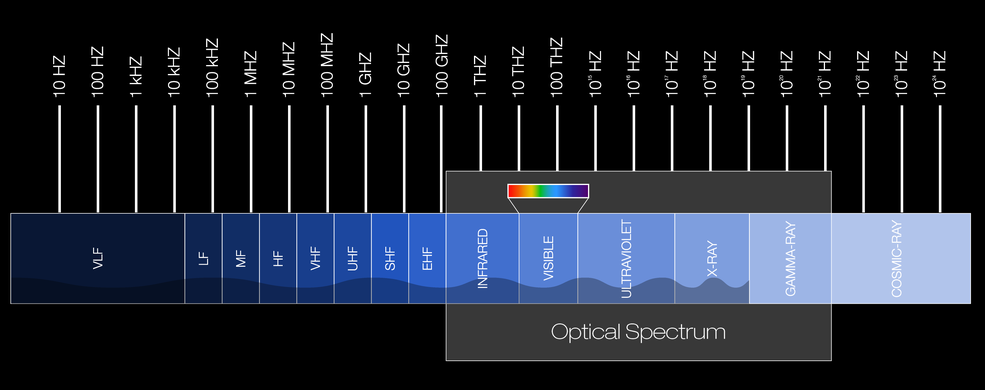
Motivação. O movimento harmônico está ao nosso redor.
O espectro é usado para todas as formas de comunicação sem fio, incluindo: telefone celular, transmissão de rádio e televisão, localização de posição GPS, navegação de rádio aeronáutica e marítima e comando e controle de satélite. O aumento da demanda exige que o espectro de rádio seja usado de forma eficiente e isso significa que processos eficazes de gerenciamento de espectro devem ser implementados. O gerenciamento de espectro é a supervisão do uso do espectro de radiofrequência.
Fonte: Nasa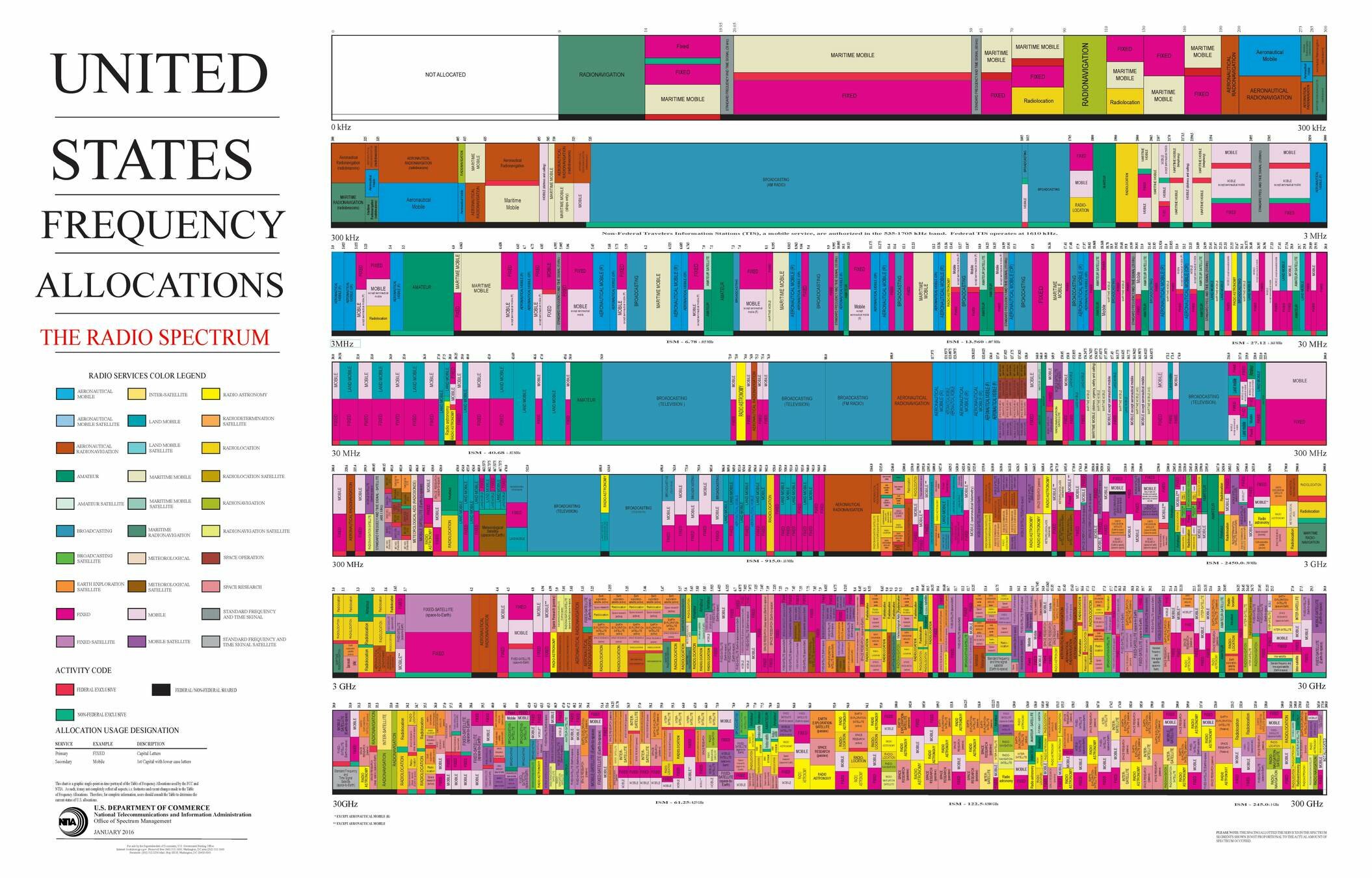
O espectro eletromagnético
Motivação. O movimento harmônico está ao nosso redor.
A compreensão das vibrações e ondas é essencial para a compreensão do nosso mundo físico.
Muito do que vemos e ouvimos só é possível por causa de vibrações e ondas.
Cientistas e engenheiros aprenderam a usar ondas para entender melhor nosso ambiente e compartilhar informações ao redor do mundo.
Motivação. O movimento harmônico está ao nosso redor.
Osciladores harmônicos fornecem a base física para entender vibrações e ondas.
Massa-mola
Pêndulo
Cordas
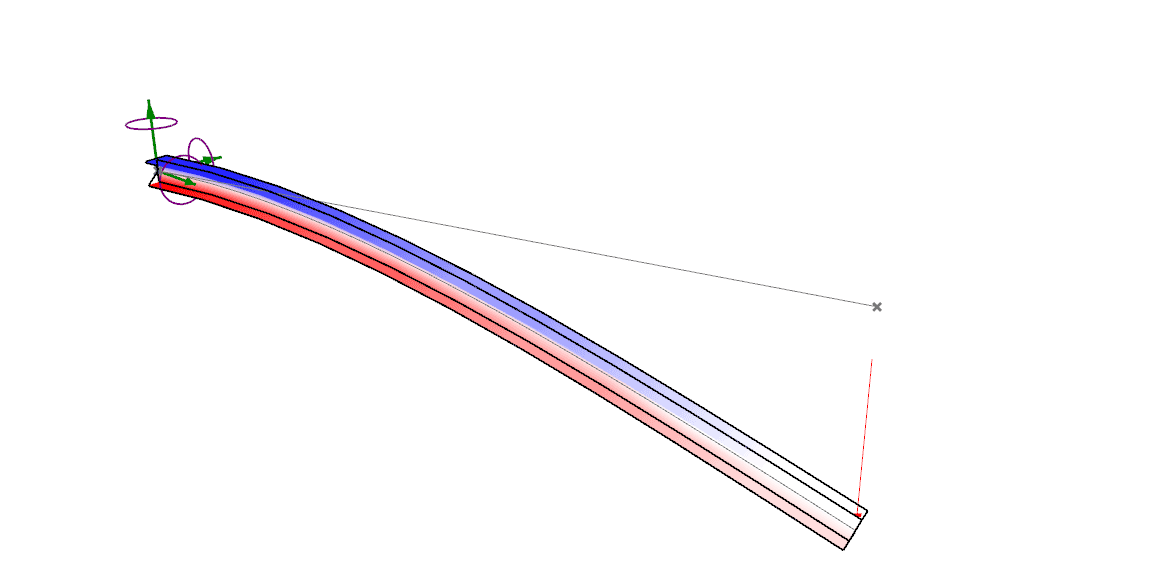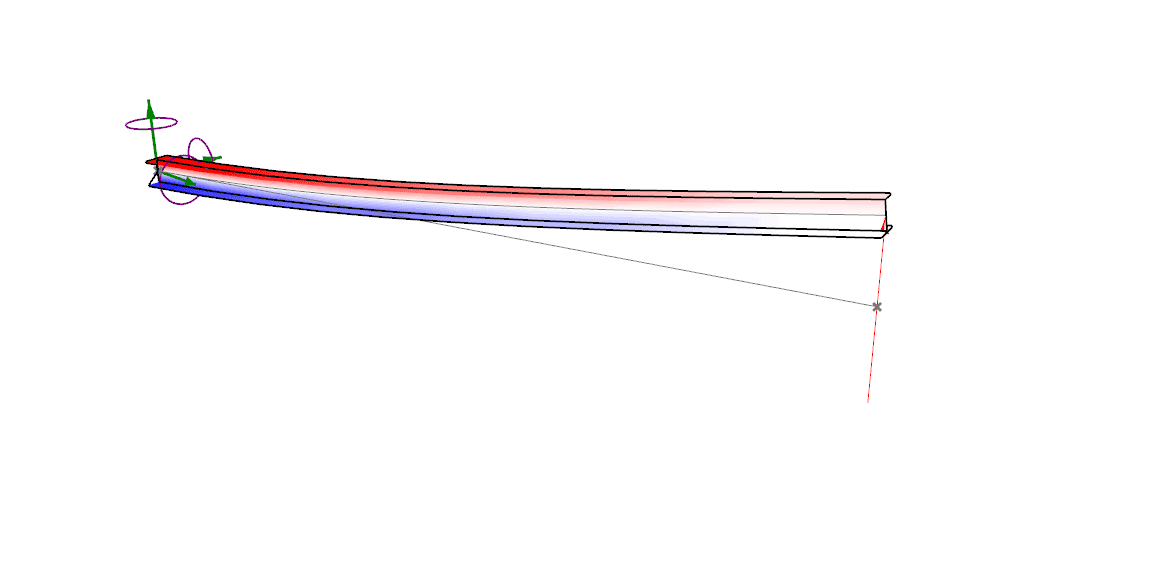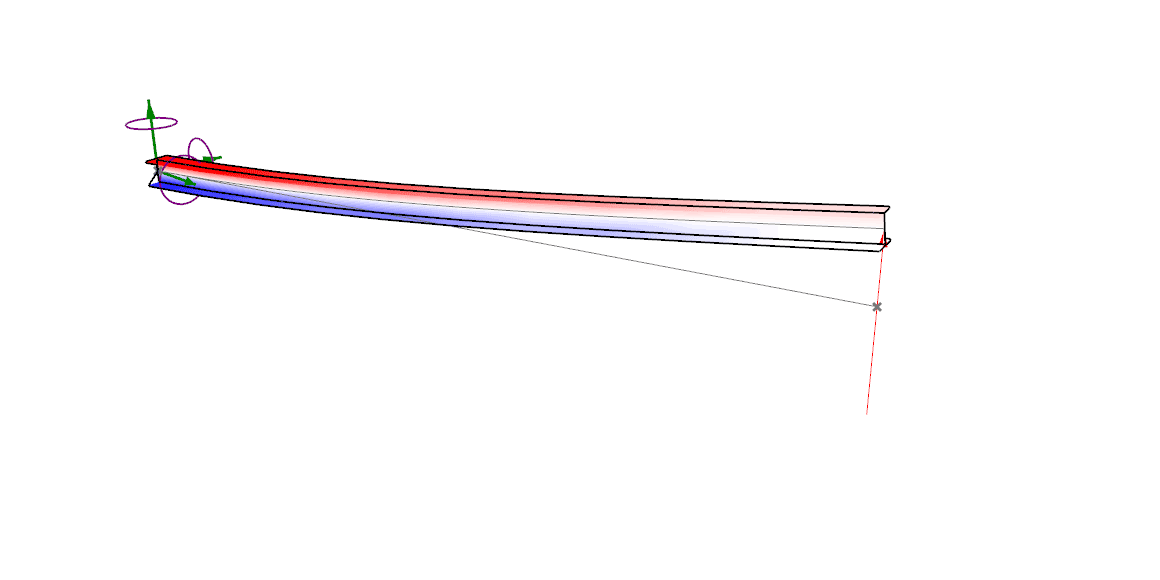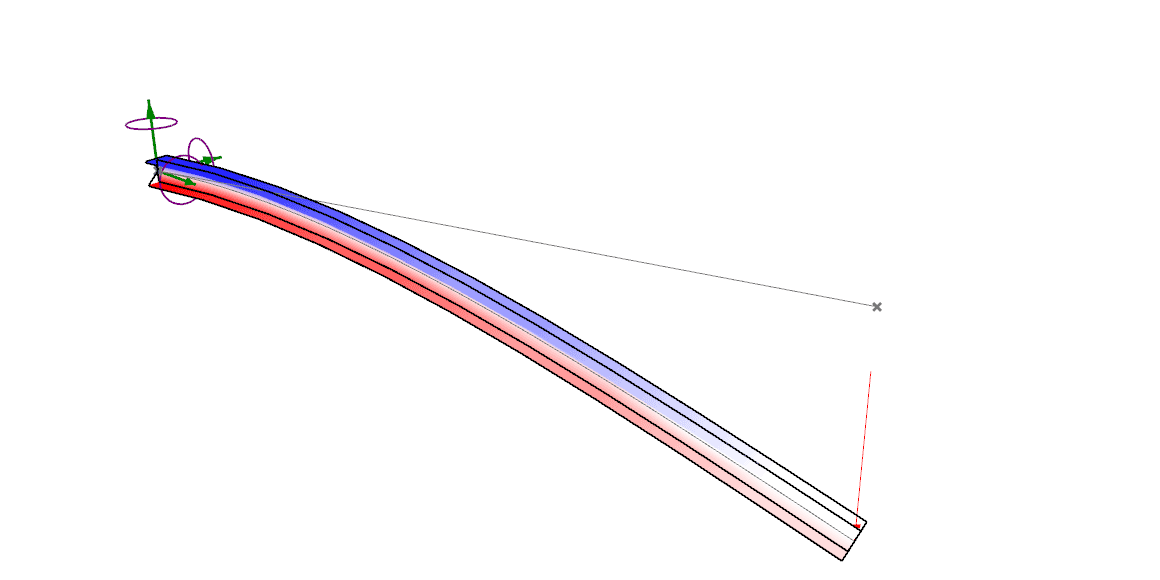
Vigas
Fonte: https://karamba3d.com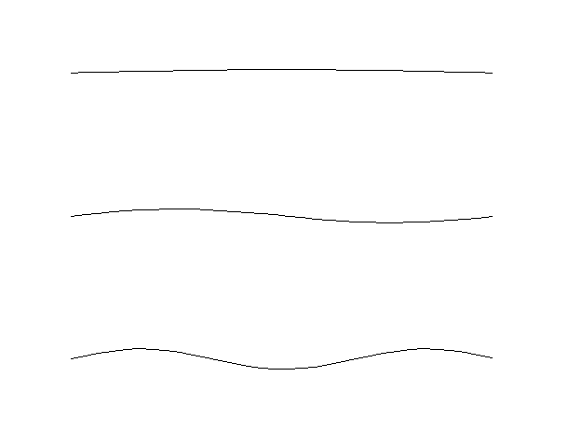
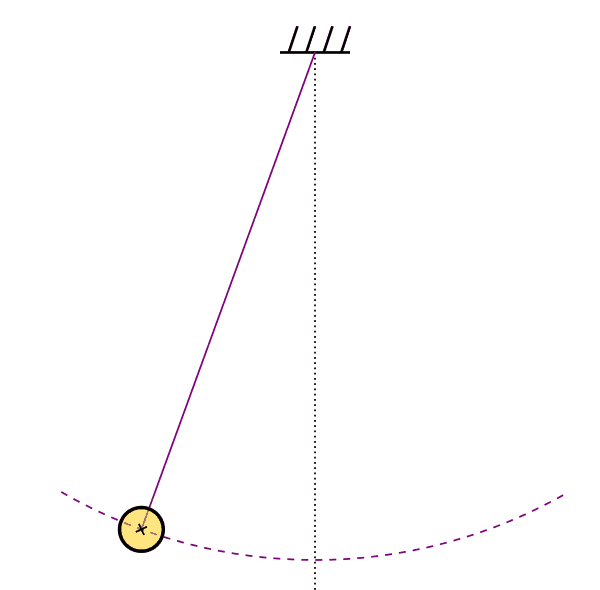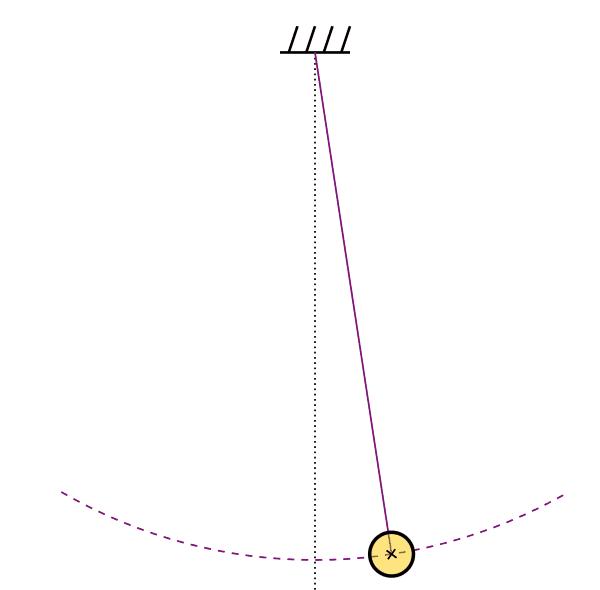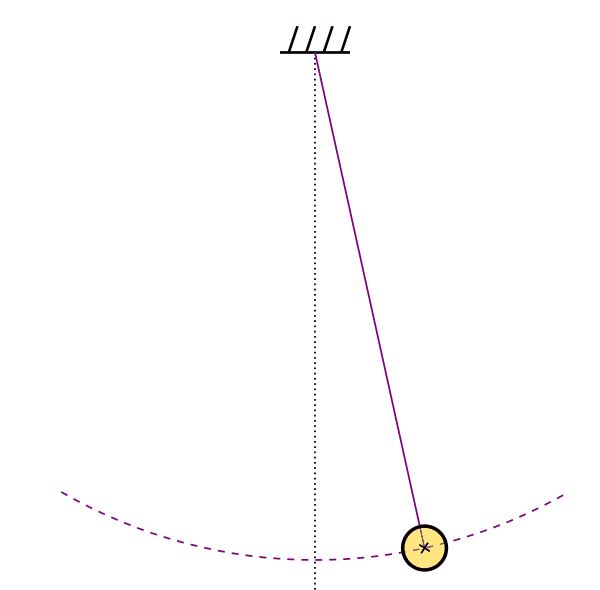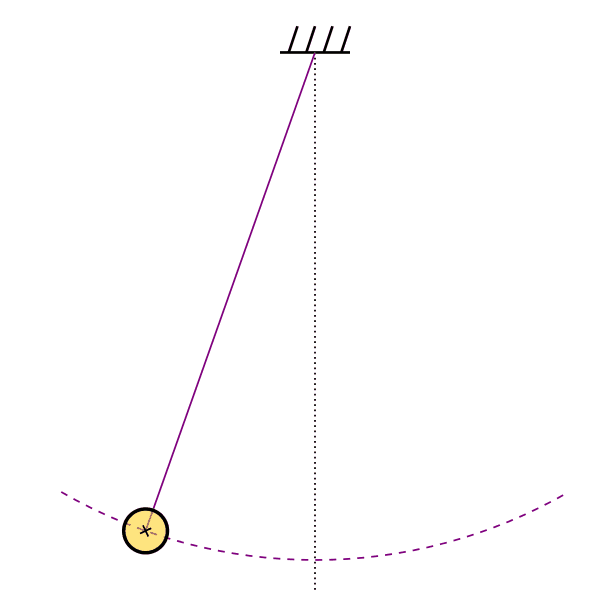
Movimento oscilatório e ondas
Conceitos Unificadores
Sistemas Físicos
Aplicações Reais
Forças restauradoras em torno de uma posição de equilíbrio produzem movimento oscilatório
Conservação e transferência de energia e momento:
Energia Cinética, energia potencial elásticas e gravitacional.
Relações dinâmicas:
Deslocamento, velocidade e aceleração.
Características das ondas:
Frequência, período, amplitude, amortecimento.
Massa em uma mola
Pêndulos
Lei de Hooke: constante elástica.
Medida do período do movimento
Calculando deslocamento e velocidade
Período x Massa
Conservação da energia
Período x Comprimento
Movimento harmônico amortecido
Força atômica microscópica
Espectroscopia molecular
Osciladores de Cristal e Eletrônica
Caracterização de vigas
Pesquisa opcional
Objetivos
Explicar o Movimento Harmônico Simples (MHS).
Ao final dessa aula você deve se capaz de:

Reconhecer o MHS em diversos fenômenos naturais e experimentos.
Analisar o movimento do sistema massa-mola:
- Equação do movimento.
- Função do movimento.
- Gráficos do movimento.
Bibliografia
Sears & Zemansky - Vol. 2 - 14a. edição.
Capítulo 13 - Movimento Periódico.
Seções: 13.1, 13.2.
Seção: 13.4 (apenas MHS na vertical)
Fonte: TiplerMODELAGEM FÍSICA E MATEMÁTICA
Os sistemas oscilatórios podem ser modelados como uma mola ou um pêndulo com a finalidade de analisar o movimento.
Procuramos uma lei física para prever o movimento periódico.
A hipótese é que o deslocamento a partir do equilíbrio varie pouco para uma dada força aplicada.
O movimento harmônico simples é um tipo especial de movimento repetitivo, exibido por um pêndulo ou um objeto sobre uma mola.
A Lei de Hooke. Movimento próximo do equilíbrio.
Fonte: PHET
No equilíbrio a força que a mola exerce sobre o pivô é nula.
A força que a mola exerce sobre o pivô sempre atua no sentido de restaurar o equilíbrio.
O sentido da força que a mola exerce sobre o pivô é sempre contrário ao do deslocamento a partir do ponto de equilíbrio.
Esse tipo de força de natureza elástica é dita uma força restauradora.
A Lei de Hooke. Movimento próximo do equilíbrio.
Fonte: PHET
Para essa força elástica restauradora. Observa-se experimentalmente, que:
1) a força é proporcional ao deslocamento a partir do equiíbrio.
2) o sentido da força é oposto ao deslocamento.
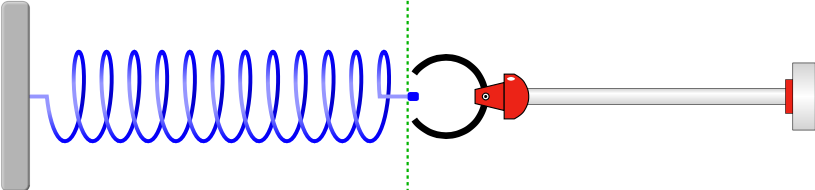
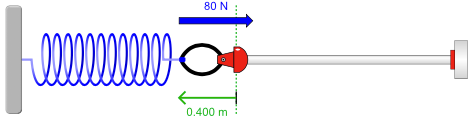
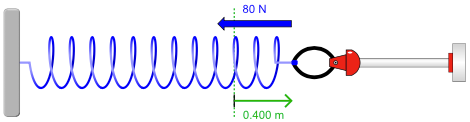
Qual a expressão matemática para a força elástica?
Equilíbrio (x = 0): \(F = 0\)
Comprimir (x = -0,400 m): \(F = +80 \) N
Estender (x = +0,400 m): \(F = -80 \) N
A Lei de Hooke. Movimento próximo do equilíbrio.
Fonte: PHET
A lei de Hooke (pequenas deformações) é escrita como:
A constante elástica (\(k\)) é a dureza da mola (dimensão força/comprimento : N/m).
A posição (\(x_0\)) é o comprimento de equilíbrio da mola (dimensão de comprimento: m).
A posição (\(x)\) é o comprimento de deformação da mola (dimensão de comprimento: m).
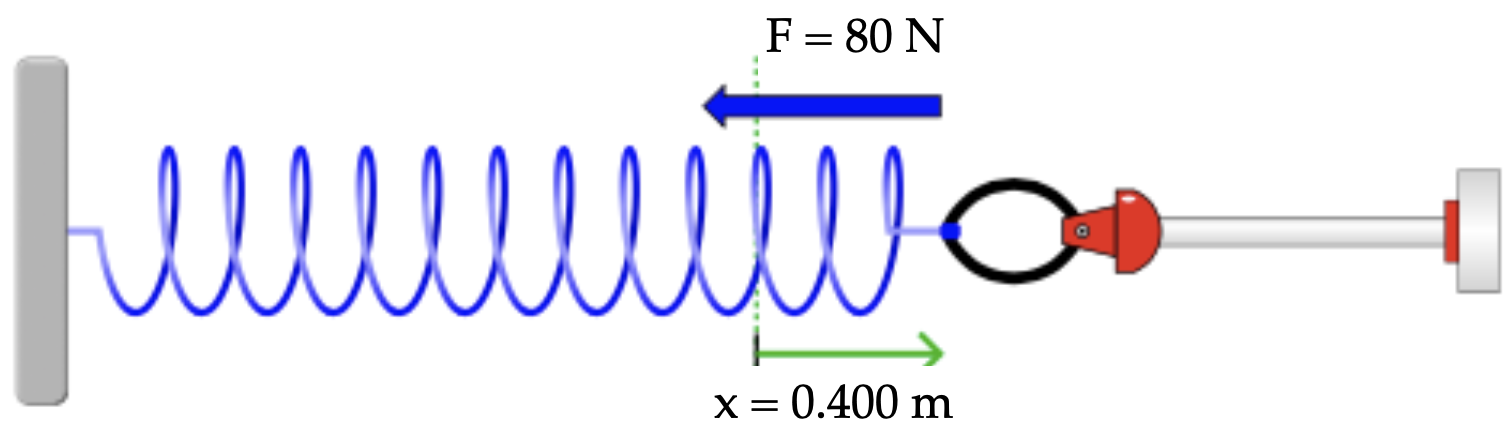
ou
Qual é o valor de \(k\)?
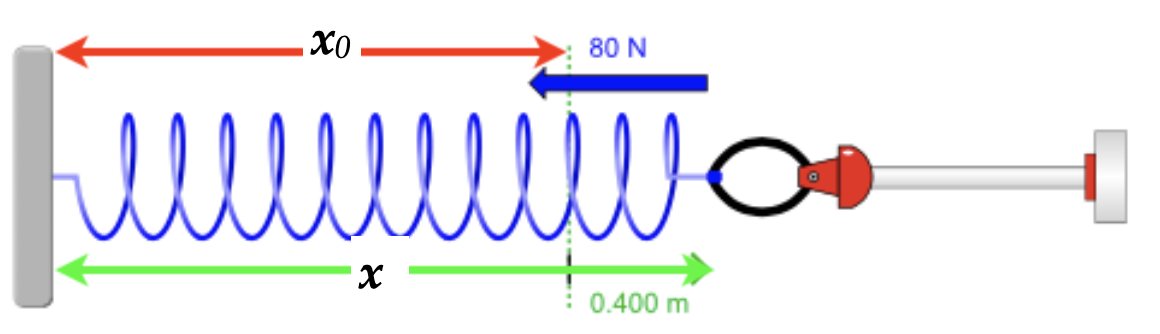
\(x_0 = \)1,000 m
\(x = \)1,400 m
O movimento harmônico simples. A equação do MHS:
A lei de Hooke define completamente o movimento do objeto para pequenos deslocamentos próximo do equilíbrio:
Sendo a força resultante atuando sobre o objeto, então, pela 2a. lei de Newton:
Aplicando o cálculo:
Qual a dimensão e a unidade de \(\omega_0\)? Qual o significado físico dessa grandeza?

onde
Algo notável sobre a Lei de Hooke é que a força não é constante. Ela muda de magnitude e sentido!
Fonte: TiplerO movimento harmônico simples. A equação do MHS:
O movimento desse sistema massa-mola é modelado por meio de uma Equação Diferencial de Segunda Ordem (EDO):
A solução da equação é a função de movimento que fornece a posição do objeto (\(x\)) para qualquer tempo (\(t\)). A solução da equação é uma função \(x(t)\).
Qual é a função que satisfaz a EDO?
Deve ser uma função que derivada duas vezes no tempo seja a própria função!
O movimento harmônico simples. A função do MHS:
A solução da EDO deve ser uma função periódica no tempo. Uma possibilidade é:
Como verificar que essa função é uma solução da EDO?
Posição
TESTE:
1) Derive uma vez no tempo:
Velocidade
2) Derive duas vezez no tempo:
Aceleração
3) Substitua na EDO:
O movimento harmônico simples. Parâmetros do MHS.
O movimento harmônico simples é modelado pela equação
A solução é uma função periódica no tempo. Exemplo:
Quais os significados dos parâmetros: \({A,\omega_0,\delta}\)?
Equação
Função
São esses os objetivos da aula.
fase
Constante de fase
Frequência angular
Amplitude
O movimento harmônico simples. Parâmetros do MHS.
O período do MHS: \(T\)
O objeto retornou a sua posição inicial e o tempo avançou do período \(T\).
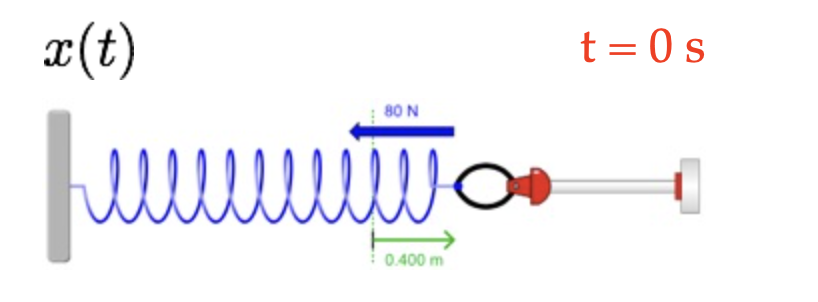
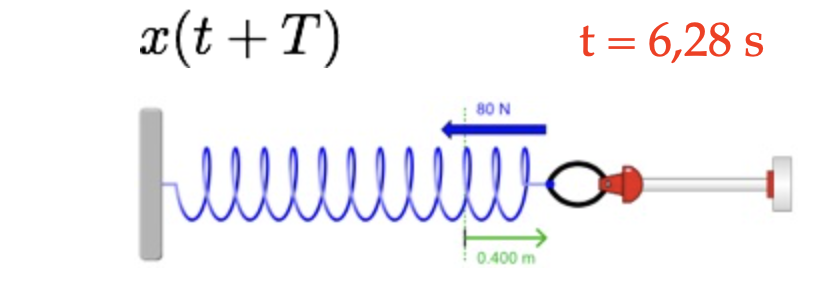
Uma vez que \(\cos(\theta +2\pi n)=\cos(\theta)\), a igualdade anterior é satisfeita quando:
O período \(T\) é o menor tempo para o ciclo se repetir (\(n=1\)):
O movimento harmônico simples. Parâmetros do MHS.
Amplitude do MHS: \(A\) ou \(x_{max}\) ou \(x_0\).
Representa a deformação máxima (\(|x_{max}|\)) a partir da posição de equilíbrio (\(x_0 = 0\)).
A amplitude não é função do tempo.
A amplitude tem dimensão de comprimento.
Não confunda a amplitude do movimento (\(x_0\) constante) com a deformação (\(x(t)\) posição variável).
Fonte: GeogebraNo simulador a amplitude é alterada no valor de \(\Delta x\).
O movimento harmônico simples. Parâmetros do MHS.
O período do MHS: \(T\)
Está relacionado ao tempo de ida e volta do objeto ao completar uma oscilação.
O tempo para uma oscilação completa tem o nome de Período, \(T\).
A dimensão do período é o tempo e a unidade é o segundo.
Varie a amplitude e verifique o tempo para completar uma oscilação.
Fonte: GeogebraNo simulador o período é alterado ao variar a massa e a constante da mola.
O movimento harmônico simples. Parâmetros do MHS.
Frequência angular do MHS: \(\omega_0\)
Está relacionada à rapidez em uma oscilação completa.
A frequência angular \(\omega_0\) é proporcional ao recíproco do período \(T\).
A frequência angular e o período não dependem da amplitude do MHS.
Tem unidade de radianos/segundo (rad/s).
Fonte: GeogebraO movimento harmônico simples. Parâmetros do MHS.
Frequência do MHS: \(f_0\)
A frequência angular, \(\omega_0\) pode ser relacionada à frequência de oscilação, \(f_0\):
A frequência é numericamente igual ao número de oscilações completadas em 1 s.
Tem dimensão de 1/s, ou hertz (Hz)
Para o sistema massa-mola:
Não importa como colocamos o bloco preso a mola para oscilar! O tempo para completar um ciclo (ir e voltar) será sempre o mesmo para o sistema massa-mola porque depende apenas das características do sistema: {m, k}.
Você compreende esta afirmação?
Deveria!
O movimento harmônico simples. Parâmetros do MHS.
A constante de fase MHS: \(\delta\) ou \(\varphi_0\)
É uma condição inicial do sistema massa-mola.
Está relacionada ao estágio onde o objeto é encontrado num tempo t tomado como inicial. Usualmente, t = 0.
A constante de fase é dada em radianos.
Todos os valores da constante de fase entre 0 e π rad correspondem a uma partícula na metade superior do círculo que se desloca para a esquerda (a partir de t = 0).
Todos os valores da constante de fase entre π e 2π rad correspondem a uma partícula na metade inferior do círculo que se desloca para a direita (a partir de t = 0).
Fonte: GeogebraQuestão 1
A bola azul na simulação é conectada à extremidade direita de uma mola que tem sua extremidade esquerda conectada a uma parede fixa.
A bola descreve um MHS que resulta de uma força resultante sobre a bola que é proporcional e oposta ao sentido do movimento a partir da posição de equilíbrio.
a. Sobre que alcance a compressão e alongamento a lei de Hooke é válida?
b. Encontre o limite elástico da mola.
c. Determine a constante elástica da mola.
d. Determine a massa da bola.
e. Sobre que alcance a compressão e alongamento da mola é o movimento de um MHS?
Questão 2
Dada a função que representa um sistema massa-mola:
a) Qual a frequência angular?
b) Qual a frequência?
c) Qual o período?
Considere a posição em metros e o tempo em segundos.
(a) No tempo indicado, em que posição está o objeto?
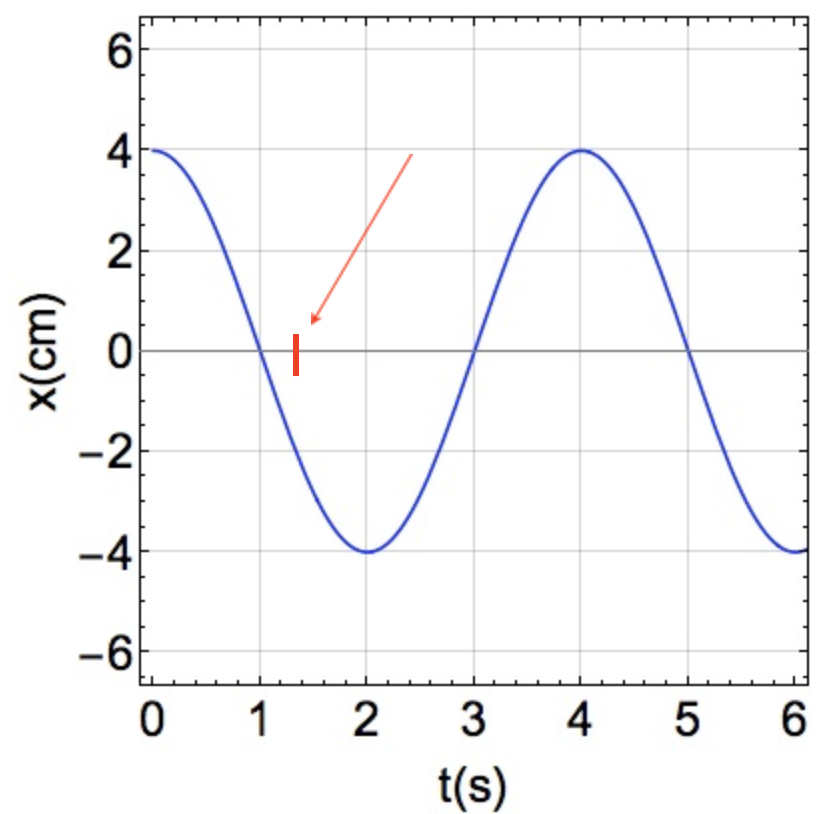
(e) Em que tempo o objeto passará novamente por essa posição?
(b) Qual é a amplitude?
(c) Qual é o período?
(d) Qual é a constante de fase?
Questão 3
O movimento harmônico simples. Cinemática.
A posição, velocidade e aceleração são lidos no eixo vertical para cada instante de tempo que é lido no eixo horizontal.
As funções \(x(t), v(t), a(t)\) são os modelos matemáticos para um objeto oscilando no tempo.
Fonte: GeogebraAs funções permitem descrever o movimento sem a necessidade de desenhar.
No MHS você sempre vai obter a relação de recorrência:
O movimento harmônico simples. Cinemática.
Cada imagem registra uma posição e um instante de tempo. Deslocando as imagens vemos que o movimento é periódico no tempo.
Conhecida a função movimento, nós obtemos toda a informação do movimento.
No equilíbrio (\(\vec F_R = \vec 0\)):
Nos pontos de retorno:
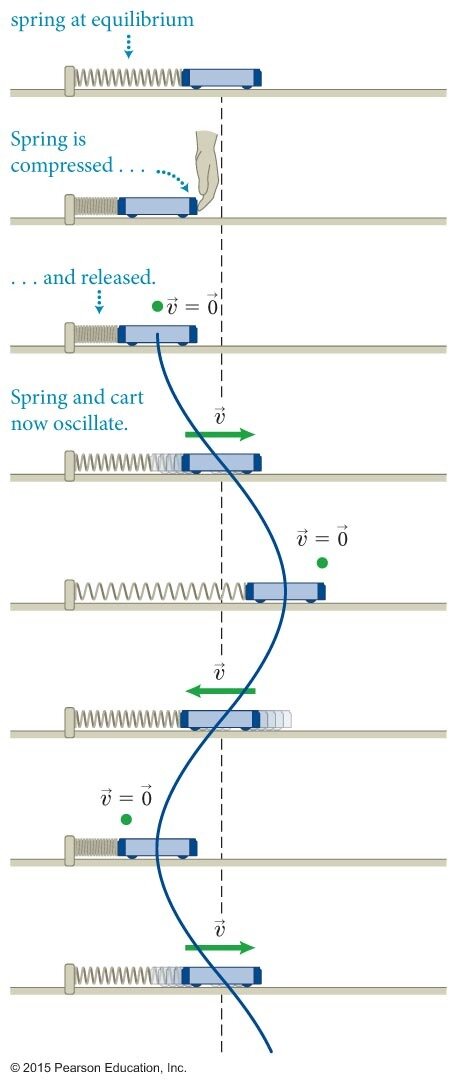
Fonte: Eric MazurVocê será avaliado se sabe dizer estas direções em um tempo t qualquer do movimento do objeto.
O movimento harmônico simples. Cinemática.
Os gráficos da cinemática fornecem diversas informações sobre o movimento.
Em quais intervalos a velocidade é negativa e positiva em um gráfico \(x(t)\)?
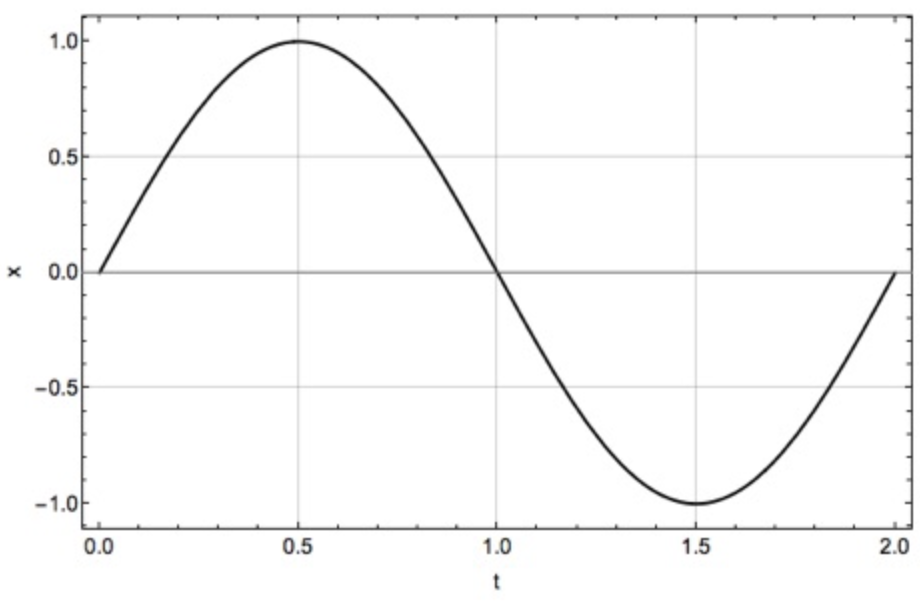
A inclinação da reta tangente (ou secante) determina o sinal da velocidade?
negativa
nula
positiva
Em quais instantes a velocidade é nula em um gráfico \(x(t)\)?
negativa
nula
positiva
Para quais intervalos a aceleração é positiva, nula e negativa?
O movimento harmônico simples. Cinemática.
Existe uma correspondência entre o MHS e o MCU.
Fonte: GeogebraO movimento circular uniforme (plano) de uma partícula de massa \(m\) em um círculo de raio \(R\) com velocidade angular \(\omega_0\) e sua projeção num movimento periódico (reta).
O movimento harmônico simples. Cinemática.
Existe uma correspondência entre o MHS e o MCU.
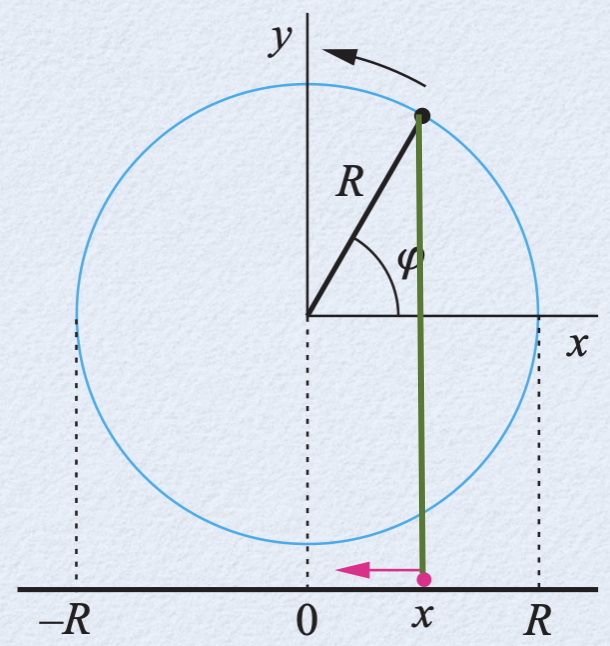
No círculo, a posição é dado pelo ângulo de fase:
Na reta é dada pela projeção do fasor na reta:
onde \(R=A\), a amplitude do deslocamento.
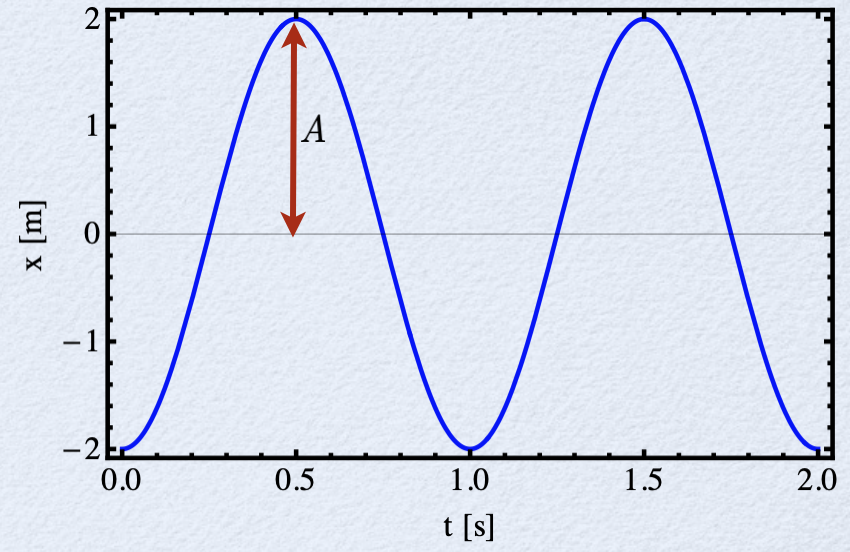
Fonte: GeogebraA posição da partícula de massa \(m\).
O movimento harmônico simples. Cinemática.
A velocidade da partícula de massa \(m\).
No círculo é dado pelo vetor tangente:
Na reta é dada pela projeção do fasor na reta:
onde \(v_0=\omega R\) é a amplitude do velocidade.
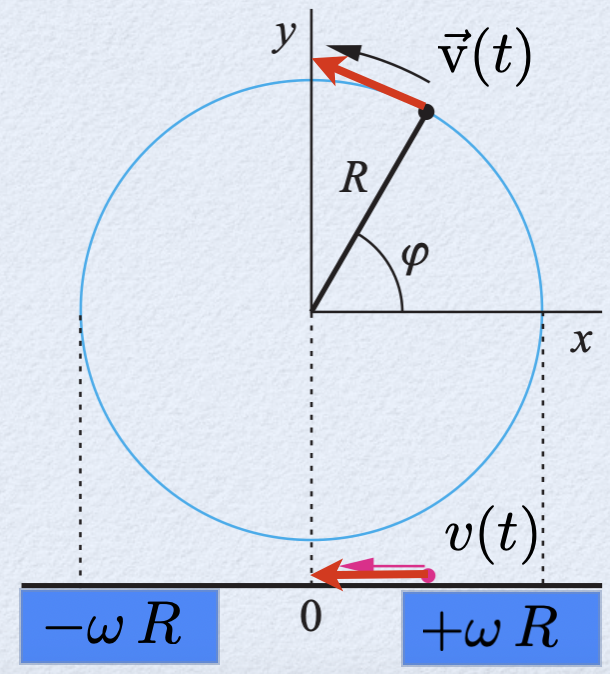
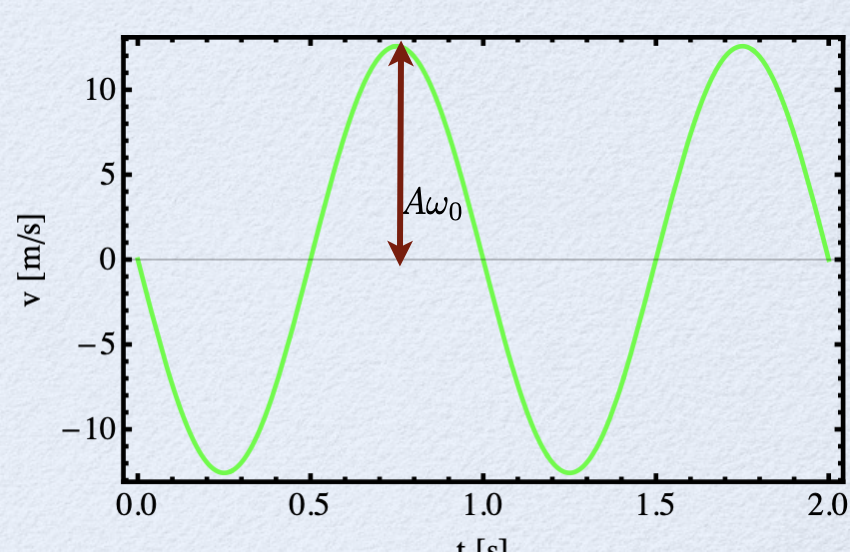
Existe uma correspondência entre o MHS e o MCU.
Fonte: GeogebraO movimento harmônico simples. Cinemática.
A aceleração da partícula de massa \(m\).
No círculo é dado pelo vetor radial:
Na reta é dada pela projeção do fasor na reta:
onde \(a_0=\omega_0^2 R\) é a amplitude da aceleração.
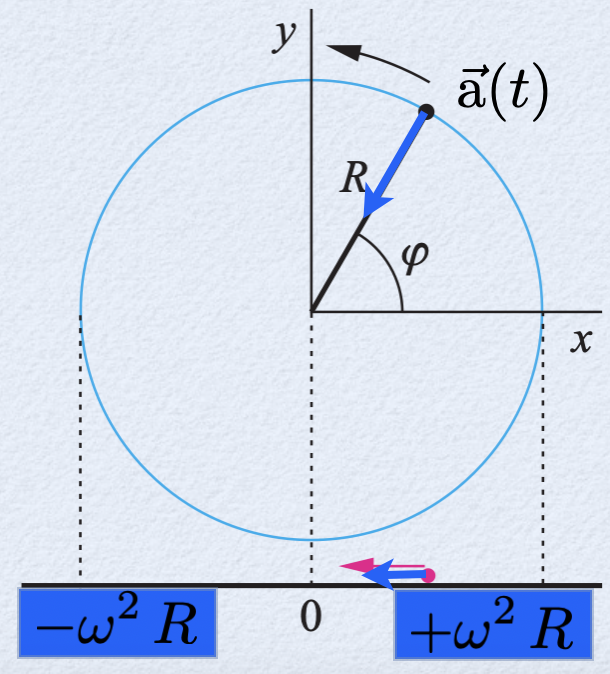
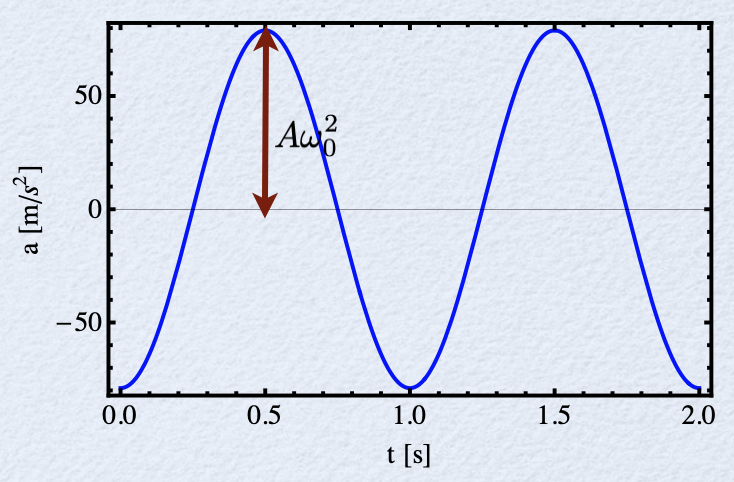
Existe uma correspondência entre o MHS e o MCU.
Fonte: GeogebraDada a função que representa um sistema massa-mola:
a) Qual a constante de fase?
b) O objeto está se deslocando no sentido positivo ou negativo do eixo x?
Considere a posição em metros e o tempo em segundos.
c) Qual a posição e a velocidade no instante t = 2,0 s?
d) Qual a posição e a velocidade no instante t = 0 s?
Questão 4
Questão 5
Dada a função que representa um sistema massa-mola:
a) Qual a posição da massa no tempo t = 2,0 s?
b) Qual a velocidade da massa no tempo t = 2,0 s?
c) Qual a aceleração da massa no tempo t = 2,0 s?
Considere a posição em metros e o tempo em segundos.
d) Se a massa tem valor \(m=2,0\) kg, qual a constante da mola?
A inclinação da reta tangente determina o sinal e a magnitude da velocidade em um instante de tempo.

A partícula está desacelerando, pois \(v > 0\) e \(a < 0\).
A partícula está acelerando, pois \(v < 0\) e \(a < 0\).
(a) Qual é a função movimento do sistema massa-mola mostrado no gráfico abaixo?
Questão 6
(b) Qual é a função velocidade do sistema massa-mola mostrado no gráfico abaixo?
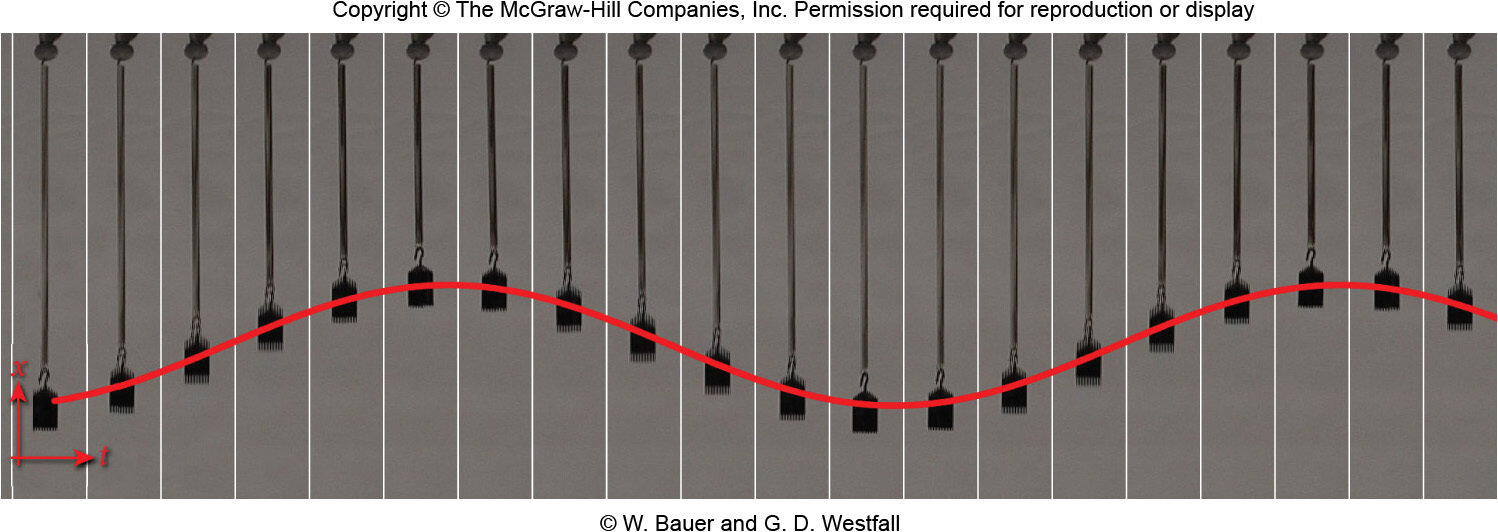
A mola oscila na vertical.
Cada imagem registra uma posição e um um instante de tempo. Deslocando as imagens vemos que o movimento é periódico no tempo. A cinemática conta a história do movimento
Para contar estudar o movimento oscilatório nós podemos empregar a dinâmica.
FONTE: GeogebraO movimento harmônico simples na vertical
O movimento harmônico simples na vertical
Fonte: PHET
Determine a constante elástica das molas.
Utilize o conceito de período.
Determine os valores das massas desconhecidas.
Verifique que para uma mesma massa, o período independe da amplitude.
Verifique o que ocorre com o período quando a massa varia. e depois quando a mola é trocada.
Planilha: LINK.
Fonte: PHET
A força peso tem sempre a orientação vertical para baixo e mesma magnitude.
A força elástica varia em magnitude e sentido.
A aceleração indica o sentido da força resultante.
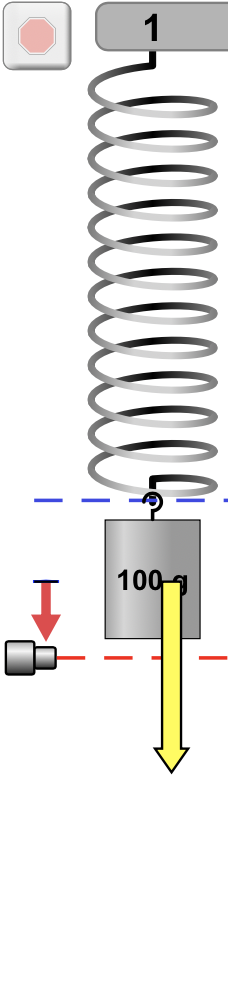
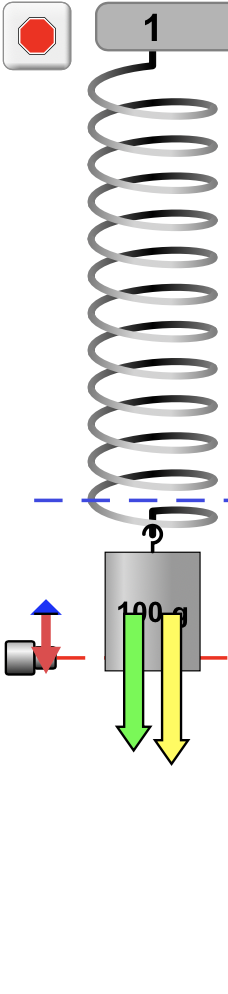
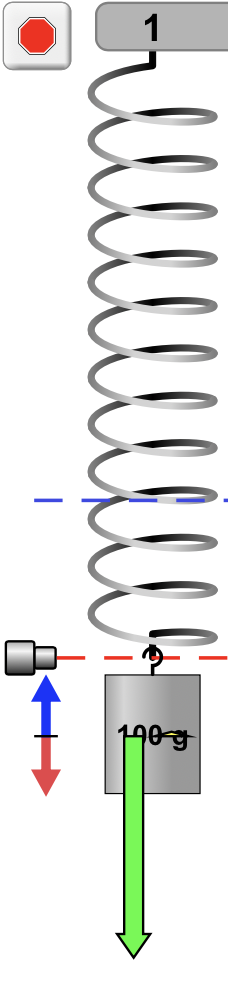
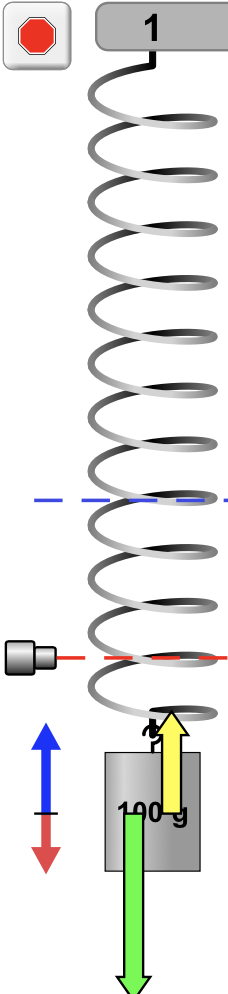
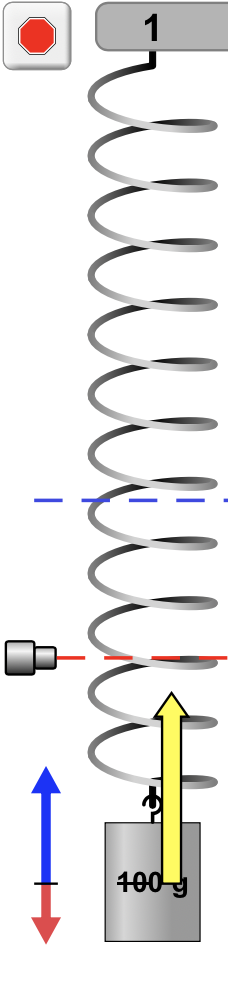
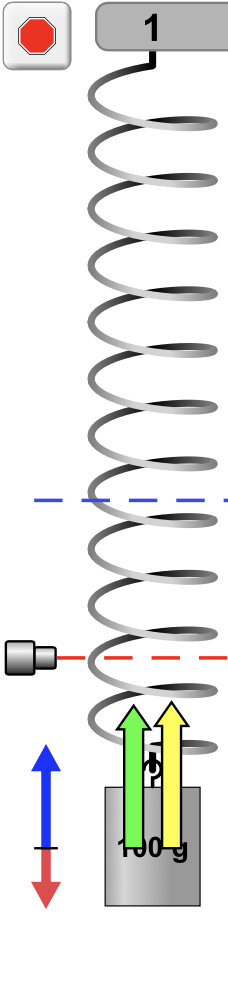
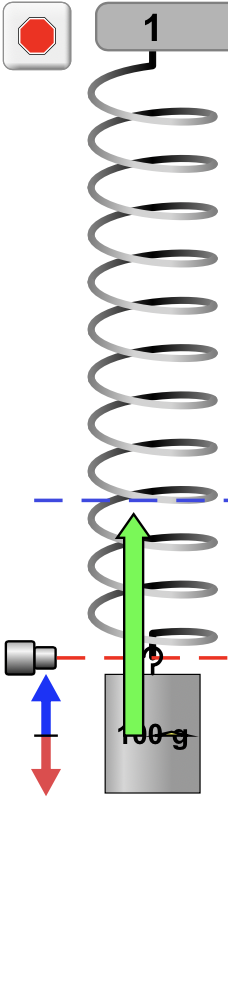
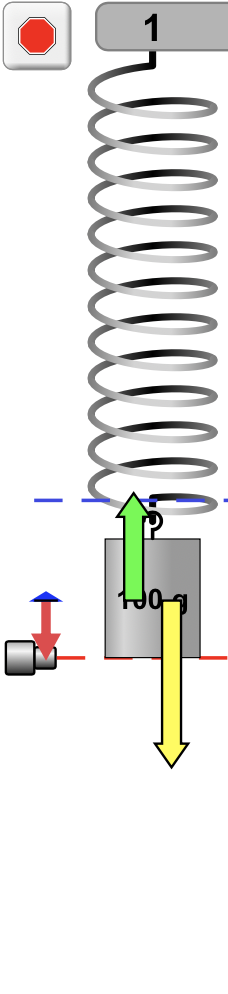
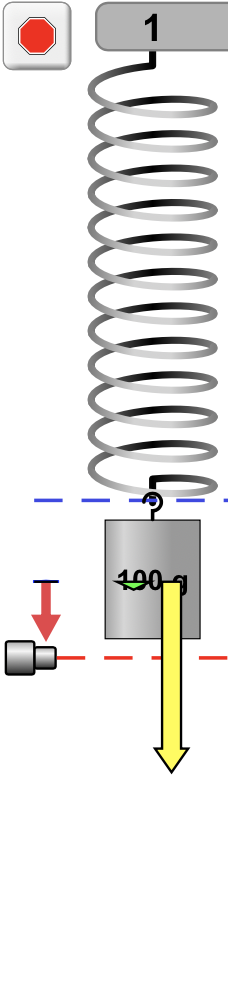
É necessário desenhar para saber onde a massa vai ser encontrada?
A velocidade indica o sentido do movimento.
A força resultante varia em magnitude e sentido.
O movimento harmônico simples na vertical
O movimento harmônico simples na vertical
Fonte: PHET
Somente no equilíbrio \(P=F_e\).
A posição de equilíbrio é \(y_0\). A massa vai oscilar em relação a esse ponto.
O efeito da força peso é meramente o de deslocar a posição de equilíbrio para \(y_0\).
E fora do equilíbrio qual é a força resultante sobre a massa?
Sem a massa, a mola ideal na vertical não fica sujeita a forças.
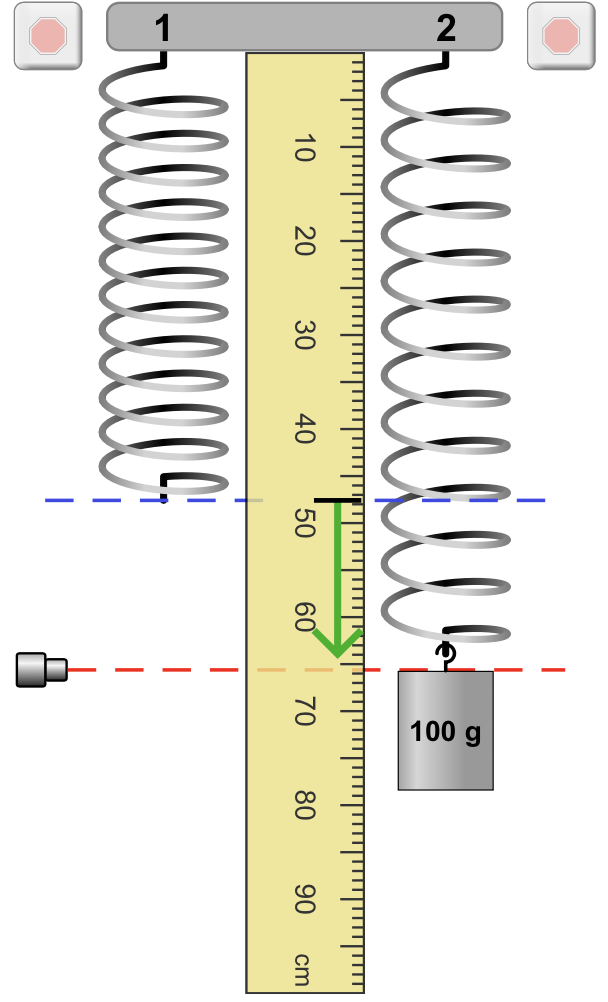
Com a massa e na posição de equilíbrio a deformação da mola é \(y_0\) e o somatório das forças sobre a massa é nula.
O movimento harmônico simples na vertical
Fonte: PHET
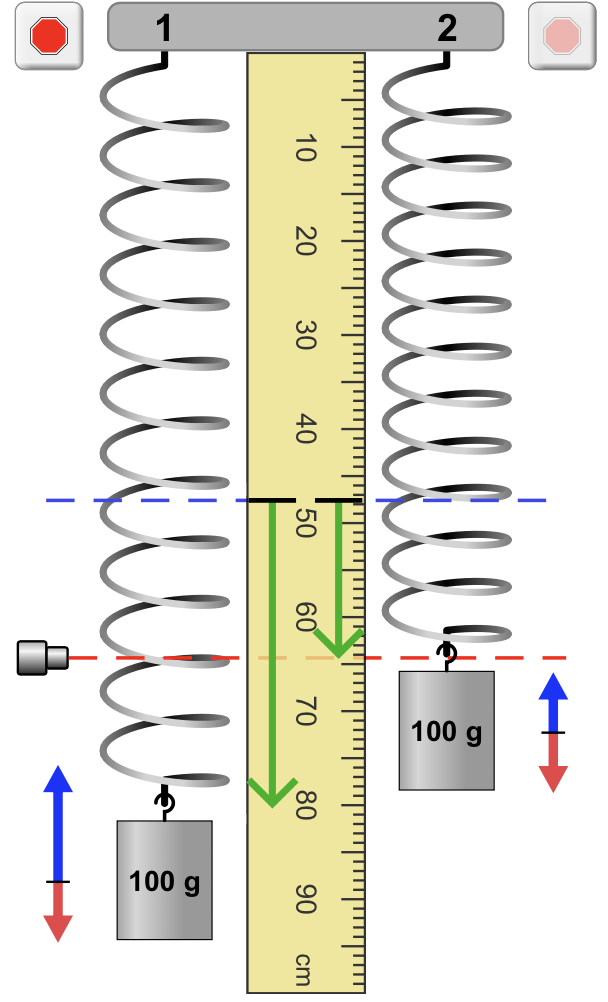
De forma geral a deformação da mola será \(y'\) em torno de \(y_0\):
Cuja solução é a função do MHS:
Fora do equilíbrio a força resultante sobre a massa não é nula:
Quando vale a amplitude?
Questão 7
Que animação mostra corretamente a posição como função do tempo?
Caso não tenha ficado claro a explicação tente estudar o simulador aqui embaixo.
Marque a caixa MHS horizontal => Oscilador massa mola na horizontal. A amplitude não muda (distância do ponto A ao P), mas a posição muda (projeção do segmento AP no eixo horizontal). Onde a projeção AP é nula no eixo horizontal? Isso significa que a massa passa pelo ponto de equilíbrio. Onde a projeção é máxima? Isso significa que a massa está nos pontos de máxima compressão.
Marque a caixa MHS vertical => Oscilador massa mola na vertical. A amplitude não muda (distância do ponto A ao P), mas a posição muda (projeção do segmento AP no eixo vertical). Onde a projeção AP é nula no eixo vertical? Isso significa que a massa passa pelo ponto de equilíbrio. Onde a projeção é máxima? Isso significa que a massa está nos pontos de máxima compressão.
O movimento harmônico simples na vertical
Questão 8
Um estudante de 83 kg está pendurado por uma corda de bungee jump com constante elástica de 270 N/m. Ele é puxado para baixo, até um ponto em que a corda está 5,0 m mais comprida do que seu comprimento não-esticado, e depois é liberado. Onde estará o aluno 2,0 s mais tarde?
Fonte: Randall Knight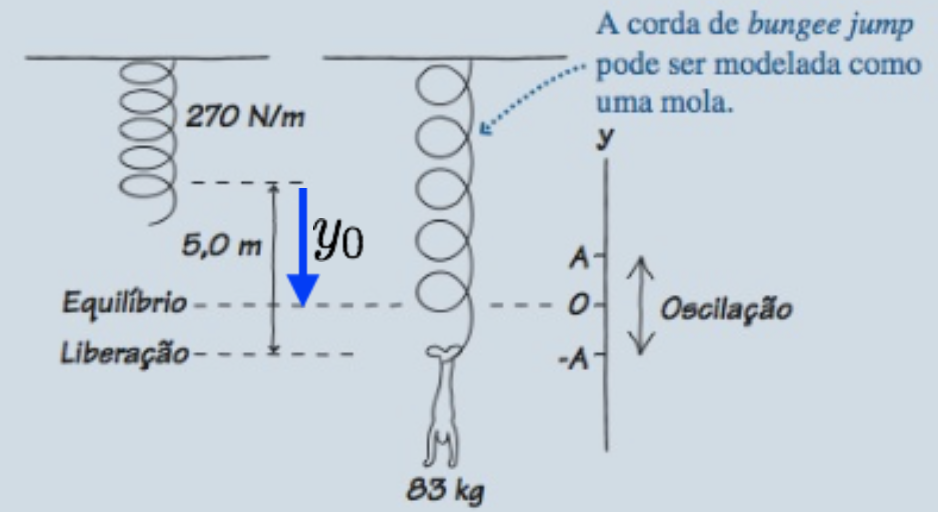
ATENÇÃO:
\(y_0\) é a posição de equilíbrio onde \(F_r = 0\).
A partir desta posição ele é puxado para baixo até a mola ter 5,0 m.
Questão 9
(c) Escreva a equação para \(x(t)\).
(a) Determine que gráfico mostra apropriadamente a posição da bola como uma função do tempo.
(b) Determine a frequência e o período do movimento.
(d) Se a massa da bola é 2 kg, qual é a constante elástica?
Questão 10
(b) Escreva a equação para \(v_x(t)\).
(a) Determine que gráfico mostra apropriadamente a velocidade da bola como uma função do tempo.
(c) Qual é a energia mecânica total do sistema (próxima aula).
Questão 11
Uma mola de constante elástica k = 56,0 N/m tem um peso de chumbo, com massa de 1,00 kg, preso na extremidade. O peso é puxado em +5,5 cm a partir do ponto de equilíbrio e depois é solto de modo a adquirir uma velocidade inicial de -0,32 m/s. Qual é a equação de movimento da oscilação resultante?

Antes de resolver:
No instante acima, qual o sentido da força elástica sobre o bloco?
No instante acima, qual o sentido da aceleração sobre o bloco?
No instante acima, a velocidade aumenta ou diminui em magnitude?
Em que região, a aceleração e velocidade têm sentidos contrários ao soltar a massa? A velocidade vai aumentar ou diminuir?
Questão 12
Suponha que pudéssemos escavar um túnel retilíneo passando pelo centro da lua, de um lado ao outro. Se, a partir de uma das extremidades deste túnel, soltássemos uma esfera de aço com 5,0 kg de massa a partir do repouso, qual seria seu movimetno subsequente?


O fato de que a lua não possui atmosfera e de que ela é de rocha sólida torna o cenário um pouco menos fantástico de que cavar um túnel através do centro da Terra.
Estação russa levou 41 anos para perfurar 12 mil metros do planeta Terra
Demonstração de elevador que atravessaria o núcleo da Terra (Fonte da imagem: Wikimedia Commons)
Questão 13
Um bloco de 1,55 kg desliza sobre um plano horizontal ligado a uma mola horizontal de constante elástica k = 2,55 N/m. O bloco é puxado para a direita por uma distância d = 5,75 cm e liberado a partir do repouso. Qual será a velocidade do bloco 1,50 s após ser liberado?
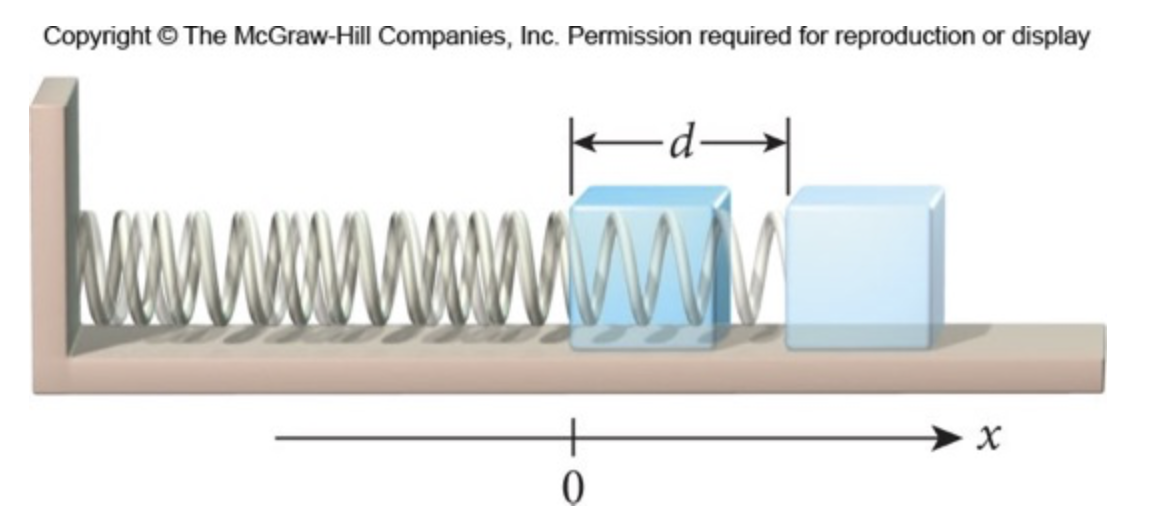
Fonte: Wolfgang & BauerQuestão 14
Astronautas no espaço não conseguem se pesar ficando em pé sobre uma balança comum de banheiro. Em vez disso, eles determinam sua massa oscilando presos a uma grande mola. Suponha que uma astronauta prenda a extremidade de uma grande mola a seu cinto e a outra extremidade a um gancho fixado no interior da nave espacial. Outro astronauta a puxa na direção oposta ao gancho e a solta. O comprimento da mola em função do tempo é mostrado na figura.
a. Qual é a massa da astronauta se a constante elástica for de 240 N/m?
b. Qual é sua velocidade quando o comprimento da mola for de 1,2 m?
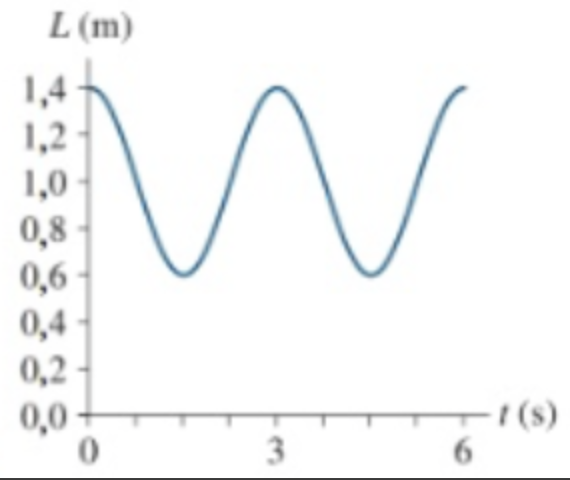
Fonte: Randall KnightRESUMO
Inicie o tutorial ao lado.
Visualize as simulações e a correspondência entre o movimento, gráficos e equações.
Aplicação
Pontes oscilam
Amplitude máxima:
Período do evento:
Fonte: https://youtu.be/mOsazjJkqCc
Aqui uma pesquisa que você pode realizar e apresentar ao professor.
Em uma pesquisa deve existir: objetivos, introdução, resultados, análises e conclusões, referências.
Motivação
Sistemas mecânicos oscilam
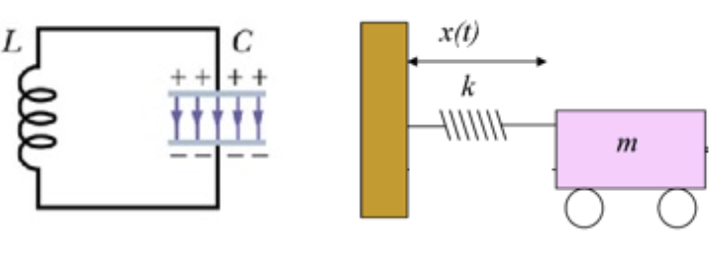
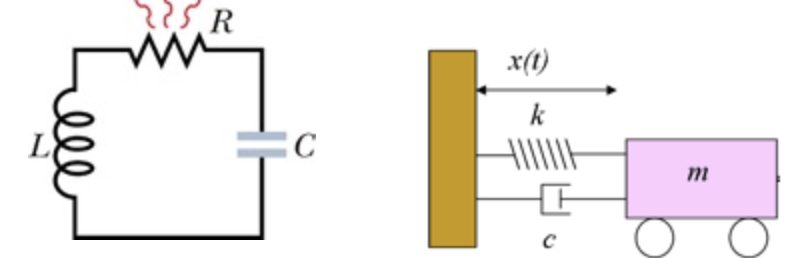
Sem amortecimento a oscilação é mantida no tempo.
Com amortecimento a oscilação diminui no tempo.
Fonte: Adaptado de PHETFonte: Adaptado de PHETMotivação
Os circuitos elétricos oscilam




Indutores
Capacitores
Resistores
Os indutores, capacitores e resistores controlam a distribuição de energia nos circuitos elétricos.
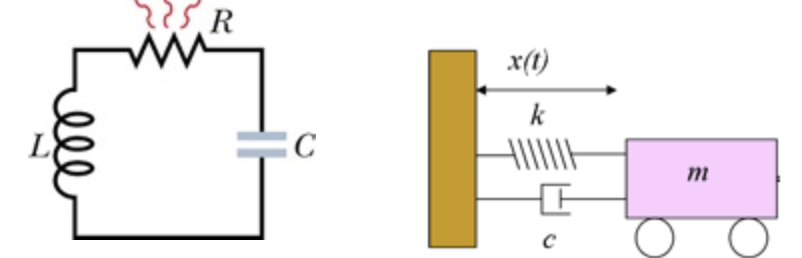
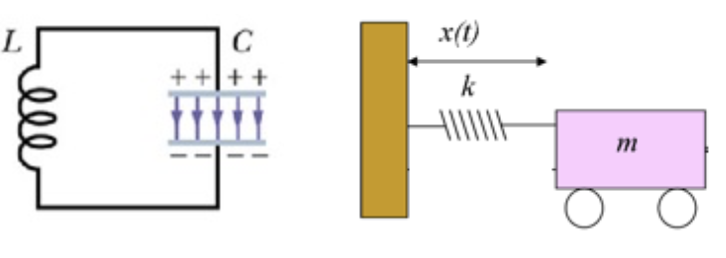
Quais os análogos eletro-mecânicos?
Motivação
O clima oscila
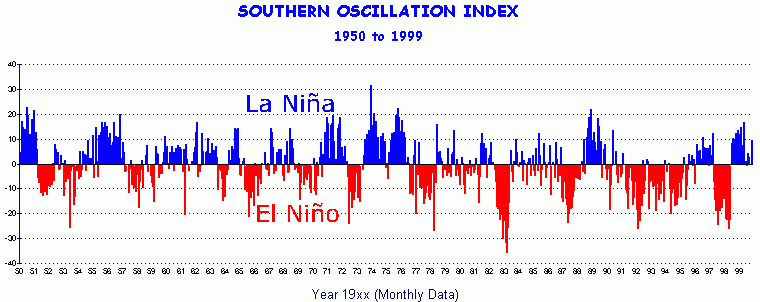
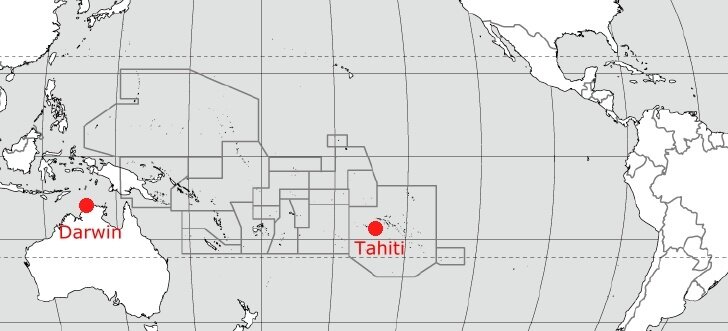
A Oscilação do Sul é a diferença na pressão do ar medida entre as regiões orientais (Tahiti) e ocidentais (Darwin, Austrália) do Oceano Pacifico. Quando a pressão é elevada em Darwin é baixa no Tahiti e vice-versa.
Valores negativos elevados em vermelho representam episódios de El Niño enquanto que valores positivos elevados a azul se referem a condições de La Niña.
FONTE: http://enos.cptec.inpe.br