Aula 02

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Explicar o Movimento Harmônico Simples (MHS).

Ao final dessa aula você deve se capaz de:

Analisar o balanço de energia no MHS.

Analisar o movimento dos sistemas:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 13 - Movimento Periódico.

Seção: 13.3.

Seção: 13.4 (MHS angular).

Seções: 13.5 e 13.6.

Fonte: Giphy. Prof. Walter Lewin - MIT

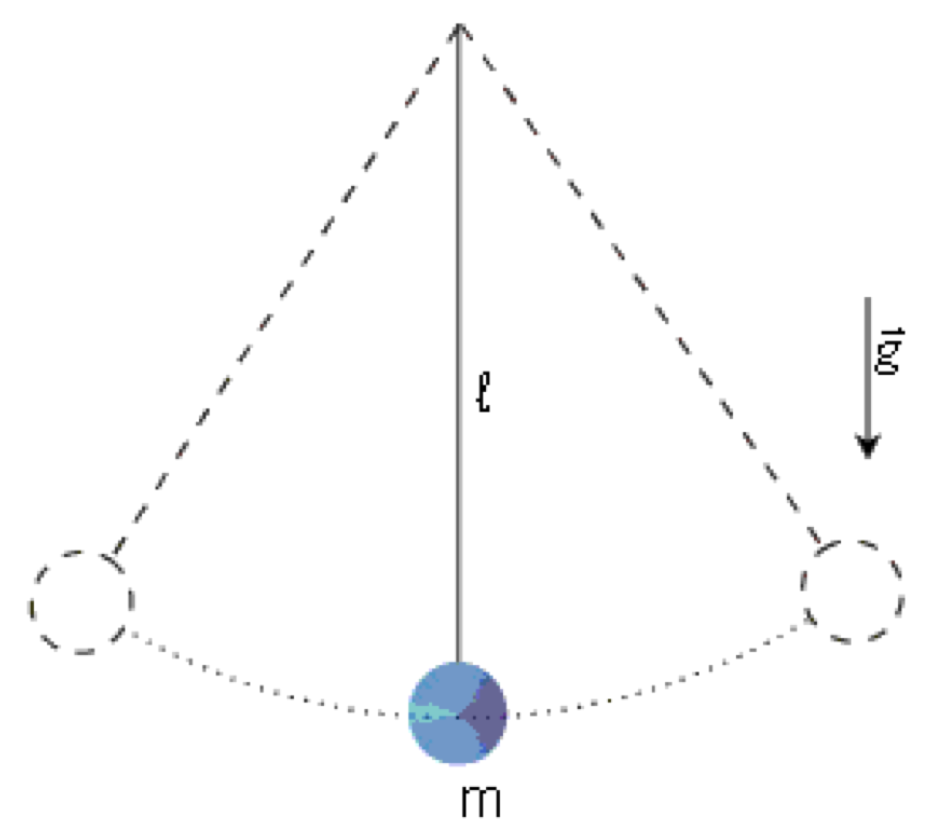
- Pêndulo simples;

- Pêndulo físico;

- Pêndulo de torção.

História e Ciência

Galileu Galilei nasceu a 15 de Fevereiro de 1564, em Pisa, Itália.

Galileu

1564 - 1642

Galileu, desenvolveu um método de pesquisa e estudo… ele queria descrever os movimentos na Terra e não somente do Cosmos.

Para Galileu a experimentação é essencial, não somente a lógica. Não é possível argumentar a natureza. É necessário ter uma hipótese e testá-la várias vezes e comprovar que sua hipótese é válida.

Uma vez descoberta ou formulada uma Lei da Natureza é necessário descrevê-la matematicamente.

História e Ciência

Galileu, durante uma missa na Catedral de Pisa (Torre de Pisa….

começou a contar quanto tempo leva para o candelabro completar uma oscilação.

descobriu o período de oscilação do pêndulo não muda por um tempo razoavelmente longo.

Fonte: https://www.youtube.com/watch?v=1CYagyW5_J8

Fonte: Wikipedia

Fonte: Wikipedia

História e Ciência

A partir da observação do candelabro da catedral de Pisa ele formula:

A lei do pêndulo.

O período do pêndulo não depende da massa e nem da amplitude, mas somente do comprimento do fio que sustenta a massa (para pequenas amplitudes em torno do ponto de equilíbrio).

Hoje, a expressão em uma linguagem matemática moderna (não geométrica) para a Lei do Pêndulo é:

T=2\pi\sqrt{\frac{L}{g}}

Na Terra, quanto maior o comprimento do fio maior será o tempo para completar um ciclo (ir e voltar) ou mais lento será o movimento.

História e Ciência

Por quê o período do pêndulo depende somente do comprimento do fio e não depende da massa (peso, para Galileu) ?

A ideia da época era que quanto maior o Peso dos objetos menor é o tempo de queda.

Um objeto mais “pesado" cai mais rapidamente (tempo menor) do que um objeto menos “pesado” (Aristóteles).

Mas o “peso” no pêndulo está caindo também. E esse tempo de queda não depende do “peso" no pêndulo (Galileu).

O que a natureza está escondendo?

História e Ciência

Por meio da experimentação Galileu e mais provavelmente o seu assistente Vicenzo Viviane (discípulo e 1o. biógrafo de Galileu) fazem o experimento da queda livre dos corpos do alto da Torre de Pisa.

Pensa-se que Viviane foi ao topo da Torre de Pisa e em uma demonstração pública mostrou que largando ao mesmo tempo duas esferas de massas diferentes o tempo de queda é praticamente o mesmo.

A diferença no tempo de queda ao tocar o piso era ínfima e então, a ideia antiga (Aristóteles) deveria ser refutada pela experimentação.

O que a natureza está escondendo?

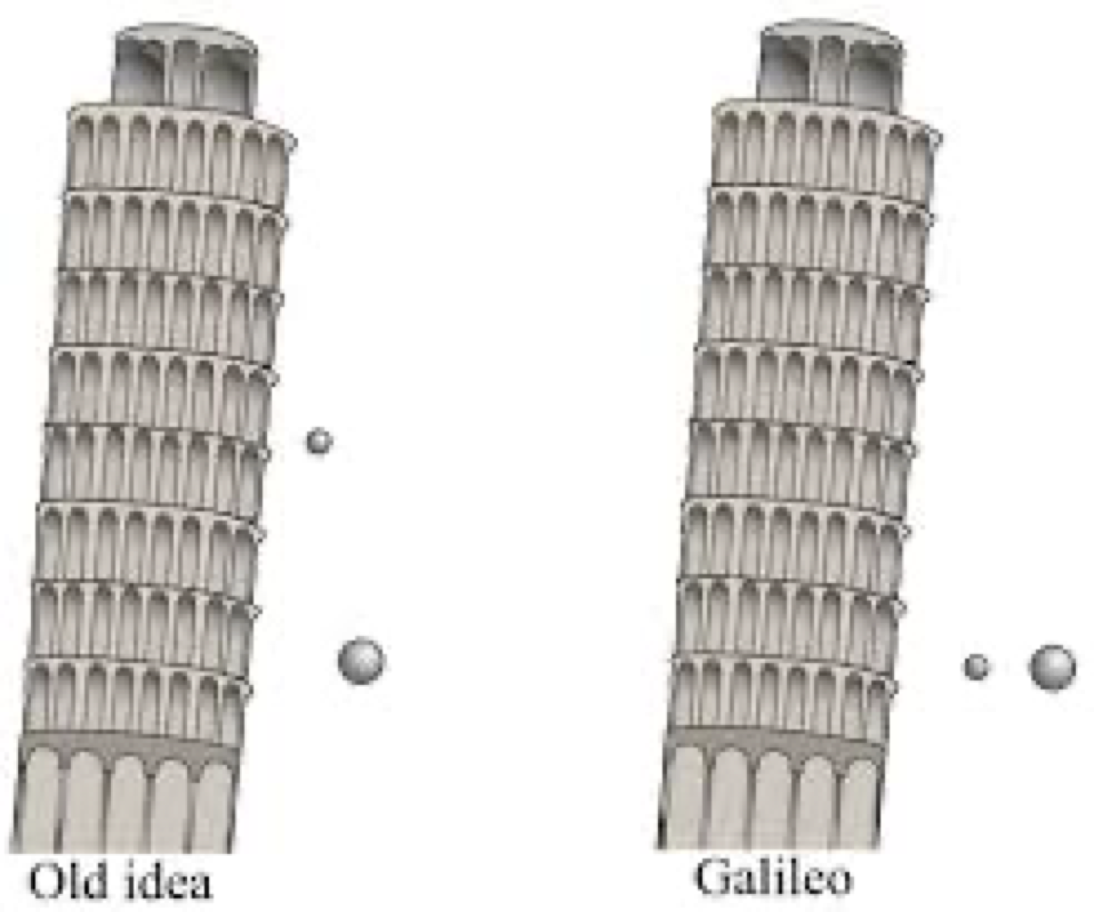
Qual é a lei de queda dos corpos? Qual o modelo? Quais as suposições a partir das observações experimentais da queda?

Hipótese: A resistência do ar deve atuar sobre os objetos mais leves e por isso levam mais tempo para tocar o chão.

Fonte: Wikipedia/Theresa Knott

História e Ciência

Galileu se depara com um problema técnico. Não havia naquela época como medir os tempos com a precisão que ele precisava para mostrar que os corpos em queda livre caem ao mesmo tempo se se desconsiderar o atrito.

Problema:

Não há relógios precisos para curtos intervalos de tempo.

Solução:

Desenvolver um relógio que permita medir a passagem do tempo entre duas posições consecutivas.

Reduzir o tempo de queda dos objetos e também reduzir o atrito.

Como:

Desenvolver e aperfeiçoar o plano inclinado.

CLEPSIDRA - Relógio d’água.

Permite adicionar intervalos de tempo

PLANO INCLINADO

Permite reduzir o tempo de queda

História e Ciência

Os experimentos pensados de Galileu com o plano inclinado mostraram que:

Uma partícula que desce de uma altura h ao longo de um plano inclinado de inclinação \(\theta_1\) adquire uma velocidade exatamente suficiente para elevá-la de uma altura h ao longo de outro plano inclinado de inclinação \(\theta_2\) , quaisquer que sejam os ângulos \(\theta_1\) e \(\theta_2\) .

Uma curva pode ser pensada como uma sucessão de planos inclinados infinitésimos, de inclinações variáveis continuamente.

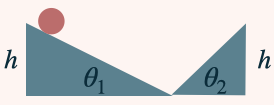
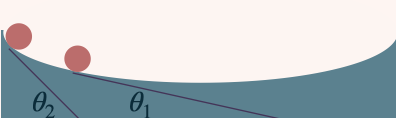
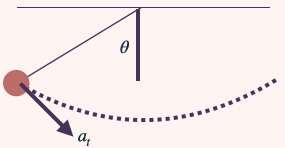
Ele aplicou esses conhecimentos do plano inclinado ao estudo do pêndulo simples.

s=\frac{1}{2}at^2

a=g\text{ sen}\theta

Motivação

Os pêndulos permitem controlar o tempo.

Fonte: https://www.youtube.com/embed/JWtsOiVxIIE em t = 2:32 min e pular para t = 5:00 min.

Fonte: https://www.youtube.com/embed/Jdcd1lSxc0w

MHS. Pêndulo Simples.

O pêndulo simples é um dispositivo mecânico que consiste de um fio inextensível e massa desprezível onde uma extremidade é fixa e na outra existe uma massa que pode oscilar segundo um MHS.

FONTE: PHET

T ={2\pi}\sqrt{\frac{L}{g}}

\approx \theta < 15^o\approx 0,25 \text{rad}

Para um dado planeta, um pêndulo comprido possui um período maior que um pêndulo curto.

Quando \(g\) aumenta o período diminui e a frequência aumenta, pois \(\omega_0 T = 2\pi\) (constante).

O período não depende da massa do pêndulo simples.

MHS. Pêndulo Simples.

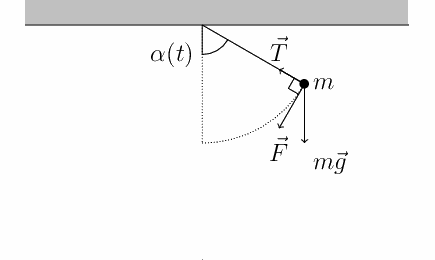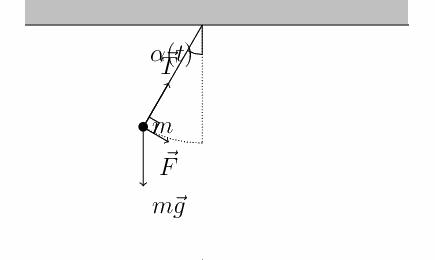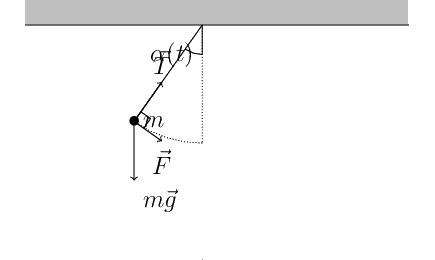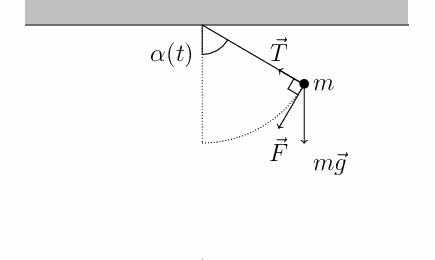
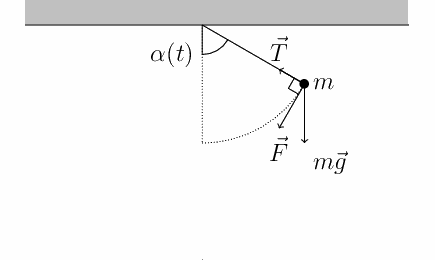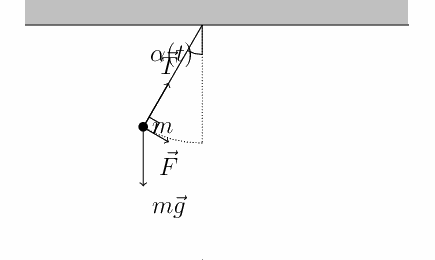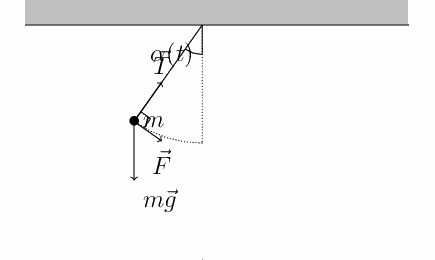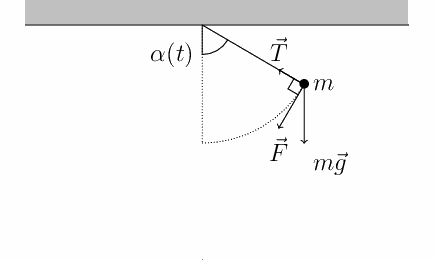
Sobre a massa há apenas duas forças:

\vec F_r = \vec T + \vec P

Tração \(\vec T\) de direção e magnitudes que variam.

Peso \(\vec P\) de direção e magnitudes que não variam.

A força resultante não é constante.

No referencial adotado as forças peso e tração têm as seguintes componentes:

P_{tan} = P \text{sen}\alpha

P_{rad} = P \text{cos}\alpha

Fonte: https://www.geogebra.org/m/sqjwr576

No ponto mais baixo da trajetória qual o valor de \(P_{tan}\)?

No ponto mais baixo qual a força resultante?

T_{tan} = 0

T_{rad} = T

A força restauradora é \(P_{\tan}\).

-mg\text{sen}(\alpha)=ma_t

A força que muda a direção é \(T-P_{rad}\).

T-mg\cos(\alpha)=m\frac{v_t^2}{r}

Fonte: https://commons.wikimedia.org/

\(W\) é a força peso (weight)

MHS. Pêndulo Simples.

A força restauradora sobre o pêndulo simples é a força tangencial (\(P_{tan}\)). Essa força varia com o ângulo \(\theta\). Há um MHS se esse ângulo é pequeno!

FONTE: Sears & Zemansky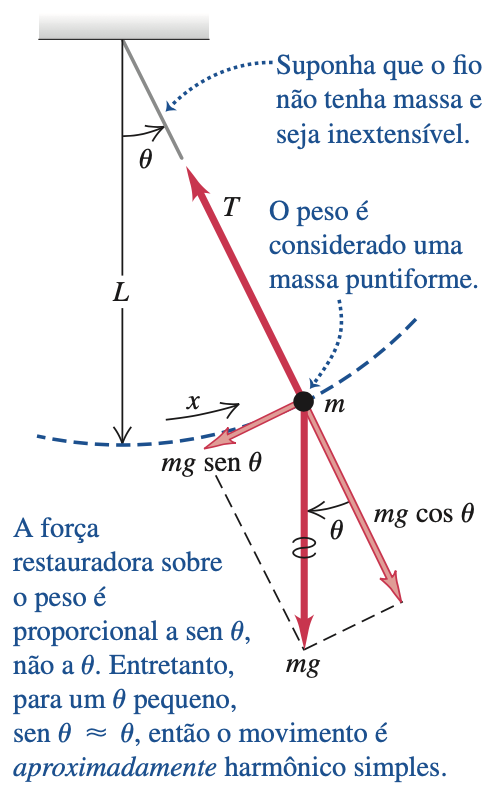

O movimento é acelerado e ao longo da força tangencial, a partir da segunda lei de Newton:

F_r = m a_t

-m g \text{ sen }\theta = m a_t

\Rightarrow \quad a_t = - g \text{ sen }\theta

\Rightarrow \quad a_t \approx - g\,\theta

\Rightarrow \quad F_r \approx -\frac{mg}{L}x

Similar à Lei de Hooke!

\text{sen }\theta\approx \theta.

Para pequenos ângulos, temos

E \(x = L\theta \). Daí,

a_t=-g\frac{x}{L}

\frac{d^2x}{dt^2}=-g\frac{x}{L}

\Rightarrow \quad\frac{d^2x}{dt^2}=-\omega_0^2 x

É a EDO que rege o movimento do pêndulo simples.

MHS. Pêndulo Simples.

Tal como o sistema massa-mola, o pêndulo simples é regido por uma EDO, tal que:

FONTE: Wolfgang & Bauer

\frac{d^2x}{dt^2}=-\omega_0^2 x

e a solução é uma função periódica no tempo:

x(t) = A\cos(\omega_0 t + \delta)

onde a frequência angular é:

\omega_0 =\sqrt{ \frac{g}{L}} = \frac{inercial}{inelástica}

A frequência e o período:

f =\frac{1}{2\pi}\sqrt{\frac{g}{L}}

T ={2\pi}\sqrt{\frac{L}{g}}

\theta(t) = \theta_0\cos(\omega_0 t + \delta)

\equiv\frac{elástica}{inercial}

\text{sen}\theta\approx \theta

\theta \approx 0,26\text{ rad}=15^o

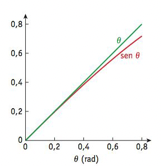
Aproximações válidas para ângulos pequenos.

Para ângulos maiores veja a seção 13.5 do Sears ou a video-aula recomendada.

x=L\theta

MHS. Pêndulo Simples.

As funções de movimento do pêndulos simples são:

\theta(t) = \theta_0\cos(\omega_0 t + \delta)

constante de fase

amplitude

frequência angular

\omega_0=\sqrt{\frac{g}{L}}

Função posição angular

Função velocidade angular

Função aceleração angular

\omega(t) = \frac{d\theta}{dt}=-\omega_0\theta_0\text{sen}(\omega_0t+\delta)

\alpha(t) = \frac{d\omega}{dt}=-\omega_0^2\theta_0\text{cos}(\omega_0t+\delta)

Função velocidade

v(t) = L\omega(t)

Função aceleração

a(t) = L\alpha(t)

Questão 1

Você dispõe de um pêndulo que oscila com período T na Terra. Você o leva para a Lua. Qual será o período do pêndulo na Lua em função do seu período na Terra?

Fonte: https://youtu.be/duyzRDq9CG4

Questão 2

Um pêndulo de comprimento igual a 45,3 cm está pendurado em um teto. Seu movimento está restrito por um pino fixado em uma parede 26,6 cm diretamente abaixo do pivô. Qual é o período de oscilação?

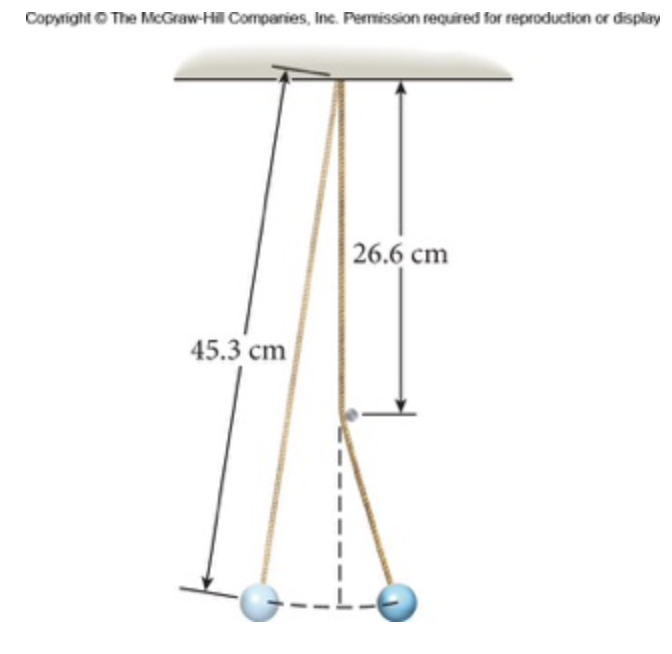
Fonte: Wolfgang & Bauer

Fonte: https://www.hq.nasa.gov/alsj/a14/Apollo14SEQ_BayPendulum.mpg

Fonte: https://www.hq.nasa.gov/alsj/a14/a14pendulum.html

Fonte: https://eaulas.usp.br/portal/video.action?idItem=19667

Balanço da Energia Mecânica no MHS.

Seja no sistema massa-mola ou nos diversos pêndulos, a força restauradora é responsável pelo MHS. Ela é do tipo: \(F = - c \,x\).

A energia total do sistema (mecânica) é conservada no tempo.

Mas as energias cinética e potencial variam no tempo!

Fonte: https://www.geogebra.org/m/wywqrzbw

Balanço da Energia Mecânica no MHS.

A força elástica é um força conservativa (depende da posição e é central):

F(x) = -kx

O trabalho realizado pela força elástica:

W = \int_{x_i}^{x_f} F(x)dx

\Rightarrow W = \frac{1}{2}kx_i^2- \frac{1}{2}k^2x_f^2

A variação da energia cinética:

\Delta K=K_f-K_i

\Rightarrow \Delta K = \frac{1}{2}mv_f^2- \frac{1}{2}mv_i^2

A variação da energia potencial elástica para uma força conservativa:

\Delta U = -W

\Rightarrow \Delta U = \frac{1}{2}kx_f^2- \frac{1}{2}kx_i^2

funções quadráticas

Note que \(x\) e \(v\) são funções do tempo!

\omega_0^2=\frac{k}{m}

Balanço da Energia Mecânica no MHS.

Somando as variações da energia cinética e potencial elástica, obtemos a variação da energia mecânica do sistema:

\Delta E = \Delta K +\Delta U

onde definimos \(E =K+U\) como a energia mecânica do sistema. Então:

E = \frac{1}{2}mv^2+\frac{1}{2}kx^2

\Delta E =\left( \frac{1}{2}mv_f^2- \frac{1}{2}mv_i^2\right)+\left( \frac{1}{2}kx_f^2- \frac{1}{2}kx_i^2\right)

\Delta E =\left( \frac{1}{2}mv_f^2+\frac{1}{2}kx_f^2 \right)-\left( \frac{1}{2}mv_i^2+ \frac{1}{2}kx_i^2\right)

\Delta E =E_f-E_i

Note que as grandezas \(v\) e \(x\) são funções do tempo! Mas a energia mecânica não é!

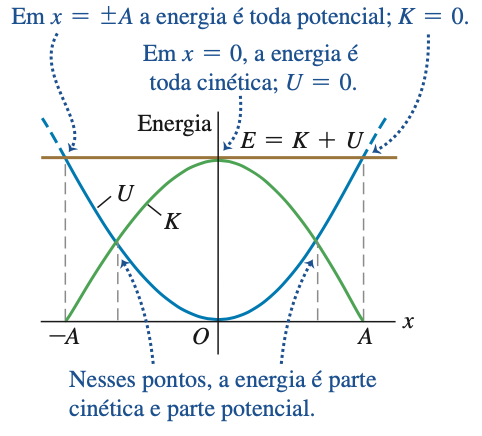
Fonte: Eric Mazur. Veja código aqui.

import numpy as np 
import math 
import matplotlib.pyplot as plt

ke=2.0
mp=2.0
En=10.0
def ve(x): 
  return  (2.0*(En-0.5*ke*x**2)/mp)**0.5
def Up(x): 
  return  0.5*ke*x**2
def Kc(x): 
  return  0.5*mp*ve(x)**2


xp = np.linspace(-3,3) 

v = ve(xp)
U = Up(xp)
K = Kc(xp)

plt.plot(xp, U,  label='Energia potencial')
plt.plot(xp, K,  label='Energia cinetica' ) 
plt.xlim([-5,5])
plt.ylim([-1,12])
plt.legend(loc=2)
plt.title('Conservação da Energia no Pêndulo Simples')
plt.xlabel('Posição [m]') 
plt.ylabel('Energia [J]')


plt.grid()

Verifique: COLAB Notebooks

Balanço da Energia Mecânica no MHS.

As funções de movimento e velocidade são funções oscilatórias no tempo:

E =K+U=\frac{1}{2}m\omega_0^2A^2

x(t) = A\cos(\omega_0 t + \delta)

v(t) = -\omega_0A\text{sen}(\omega_0 t + \delta)

U = \frac{1}{2}kx^2\,\,=\frac{1}{2}kA^2\cos^2(\omega_0t+\delta)

As funções energia potencial elástica e cinética são funções oscilatórias no tempo:

K = \frac{1}{2}mv^2=\frac{1}{2}m\omega_0^2A^2\text{sen}^2(\omega_0t+\delta)

A energia mecânica é constante no tempo.

E =K+U=\frac{1}{2}kA^2

\omega_0^2=\frac{k}{m}

Fonte: Geogebra

Fonte: https://www.compadre.org/Physlets/waves/illustration16_3.cfm?NOH=1

Balanço da Energia Mecânica no MHS.

A energia mecânica do pêndulo simples para qualquer ângulo \(\theta\):

E = K + U

E = \frac{1}{2}mv^2 + mgL[1-\cos(\theta)]

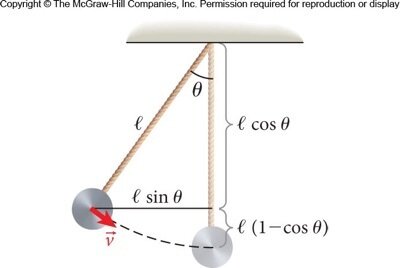
Nos pontos de retorno (\(v = 0\)):

K = 0

U=mgL[1-\cos(\theta_0)]

\Rightarrow E =mgL[1-\cos(\theta_0)]

Fonte: Wolfgang & Bauer

A energia mecânica é conservada:

E_i = E_f

\Rightarrow \quad mgL[1-\cos(\theta_0)] = \frac{1}{2}mv^2 + mgL[1-\cos(\theta)]

\Rightarrow v=\pm \sqrt{ 2gL [ \cos(\theta)-\cos(\theta_0}) ]

A velocidade do pêndulo:

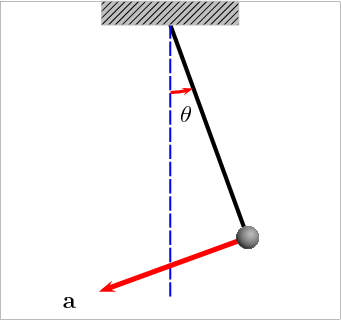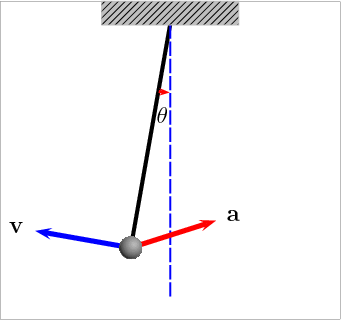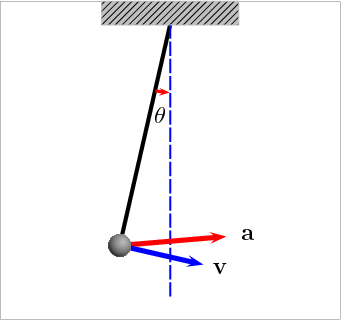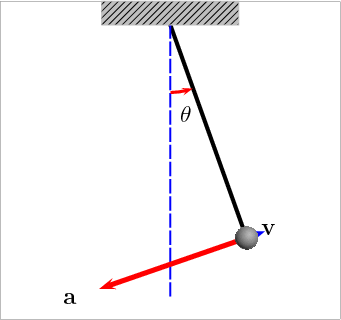
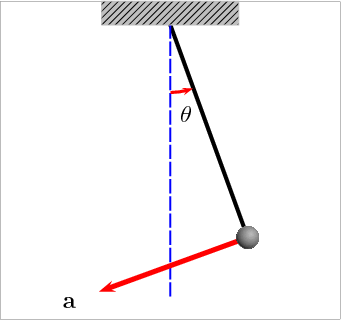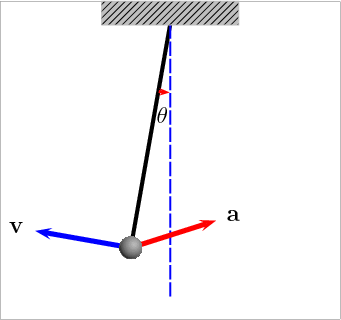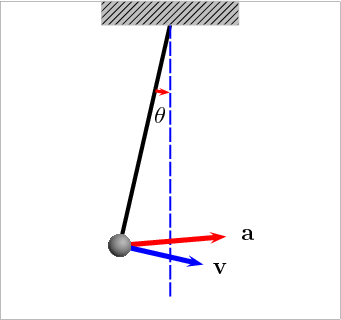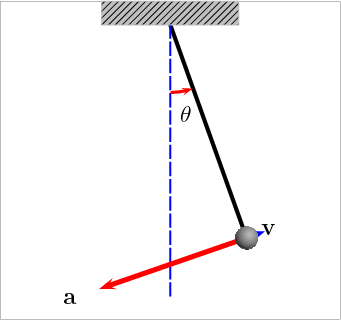
Fonte: https://pin.it/2SEybXW

Qual o tempo para ir de \(v = 0\) a \(v = v_{max}\)?

Por que o vetor aceleração muda de direção?

Questão 3

Um corpo de 3,0 kg, preso a uma mola, oscila com uma amplitude de 4,0 cm e um período de 2,0 s. (a) Qual é a energia total? (b) Qual é a rapidez máxima do corpo? (c) Em qual posição a rapidez do corpo é a metade de seu valor máximo?

Questão 4

Uma trapezista de circo inicia seu movimento partindo do repouso com a corda formando um ângulo de 45 graus com a vertical. A corda em 5,00 m de comprimento. Qual será a velocidade da trapezista no ponto mais baixo da trajetória?

Questão 5

Um bloco de 500 g, preso a uma mola, é puxado por uma distância de 20 cm e liberado. As oscilações subseqüentes são medidas, e delas se obtém um período de 0,80 s. Em que posição ou posições a velocidade do bloco vale 1,0 m/s?

MHS. Pêndulo Físico (ou composto).

O pêndulo físico é um dispositivo mecânico que consiste de um corpo com volume finito onde uma extremidade é suspensa por um pivô. Na posição de equilíbrio, o centro de gravidade está diretamente abaixo do pivô.

FONTE: https://www.laboratoriovirtual.fisica.ufc.br/pendulo-fisico

O pivô pode ser alterado e isso afeta o período de oscilação.

O movimento do centro de gravidade é um arco de circunferência: \(x= L\theta\).

Ao deslocar o centro de gravidade a força peso que atua sobre esse ponto vai exercer um torque em relação ao pivô.

Qual o valor da inércia rotacional de cada barra em relação a um pivô?

FONTE: Halliday & Resnick

A força de contato (\(\vec N = normal\)) não realiza torque, pois a linha de ação dessa força passa pelo eixo de rotação.

\vec N

\vec F_p

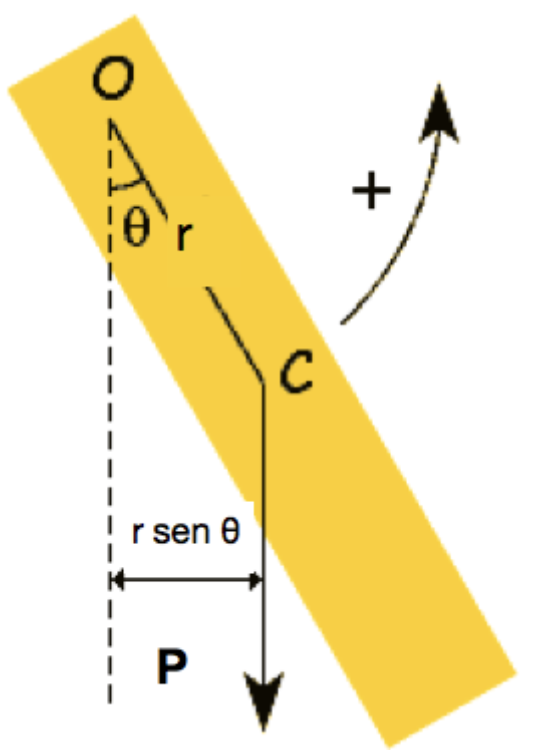
A força de ação à distância (\(\vec F_p =peso\)) realiza torque, pois a linha de ação dessa força passa pelo centro de gravidade quando a barra está deslocada:

\tau_0 = - (r\text{ sen }\theta) F_p

r_{\bot}

Aplicando a segunda lei de Newton para rotações:

\tau_0 = I_0\alpha

\Rightarrow \quad I_0\alpha = -mgr\text{ sen }\theta

\Rightarrow \quad\frac{d^2\theta}{dt^2} =- \frac{mg\,r}{I_0}\text{ sen }\theta

Para pequenos ângulos (\(\text{sen}\theta\approx \theta\)) observa-se um MHS:

\frac{d^2\theta}{dt^2} =-\omega_0^2\theta

\omega_0^2= \frac{mg\,r}{I_0}

onde

\theta(t) = \theta_0 \cos(\omega_0 t + \delta)

MHS. Pêndulo Físico (ou composto).

\tau_0 = -r_{\bot} F_p

A frequência angular e o período de um pêndulo físico são:

\omega_0^2= \frac{mg\,r}{I_0}

O pêndulo físico possui momento de inércia \(I_0\) e cujo centro de massa está a uma distância \(r\) do pivô. Se o pivô atravessa o centro de massa:

T={2\pi}\sqrt{\frac{I_0}{mg\,r}}

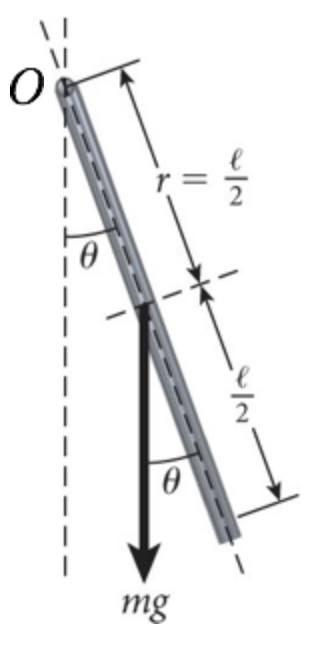
Fonte: Bauer & Wolfgang

r=\frac{l}{2}

I_{cm}=\frac{1}{12}ml^2

O período fica:

\equiv\frac{elástica}{inercial}

I_{0}=I_{cm}+mr^2

Em relação ao pivô aplicamos o Teorema dos eixos paralelos:

\Rightarrow \quad I_{0}=\frac{1}{3}ml^2

\Rightarrow \quad T = 2\pi\sqrt{ \frac{2l}{3g} }

T = 2\pi\sqrt{ \frac{r}{g}+\frac{I_{cm}}{m g r } }

MHS. Pêndulo Físico (ou composto).

Questão 6

Uma haste fina oscila sem atrito em relação a uma de suas extremidades. A haste possui massa de 2,50 kg e comprimento de 1,25 m. Através de sua extremidade inferior, a haste é deslocada para a direita de um ângulo de 20,0 graus em relação à vertical. A haste é então liberada a partir do repouso oscilando em um movimento harmônico simples. Qual é o período do movimento? Se toda a massa da haste fosse concentrada em uma esfera a uma distância L do pivô, qual seria o período do movimento?

Questão 7

Na Terra, os garimpeiros procuram um depósito de minério de ferro sob o solo. Eles decidem usar a aceleração da gravidade para descobrir onde o ferro está localizado porque a massa adicional de ferro deve mudar a aceleração da gravidade. Eles usam um pêndulo cuidadosamente feito com um comprimento de 2,00000 metros e medem o período do balanço enquanto caminham pela área onde acham que o depósito está localizado. Para o milionésimo de segundo mais próximo, quanto o período mudará se a aceleração da gravidade entre dois pontos mudar de 9,80000 m/s^2 para 9,80010 m/s^2?

MHS. Pêndulo de Torção.

Um pêndulo de torção consiste em um objeto suspenso por um fio. Quando o fio é torcido e depois liberado, o objeto descreve um movimento harmônico angular simples.

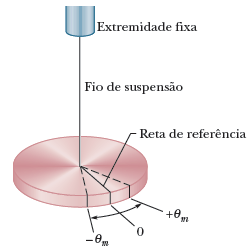
Fonte: Halliday & Resnick

A rotação do disco de um ângulo \(\theta\) em qualquer sentido produz um torque restaurador dado por:

\tau = - \kappa \theta

Aplicando a segunda lei de Newton para rotações:

I_0\alpha = -\kappa \theta

\frac{d^2\theta}{dt^2} = -\frac{\kappa}{I_0} \theta

\frac{d^2\theta}{dt^2} = -\omega_0^2 \theta

\omega_0^2=\frac{\kappa}{I_0}

onde

onde \(\kappa\) é a constante de torção que depende do comprimento do fio e do material de que é feito.

MHS. Pêndulo de Torção.

Fonte: https://www.geogebra.org/m/jhc4xvpe

Para pequenos ângulos de torção, o pêndulo de torção executa um MHS com período:

T=2\pi \sqrt{\frac{I_0}{\kappa}}

Medindo-se o período e conhecendo-se a inércia rotacional é possível determinar as propriedades do fio, isto é, do que ele é feito!

Questão 8

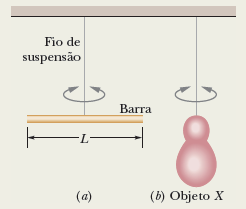
A figura (a) mostra uma barra fina cujo comprimento \(L\) é 12,4 cm e cuja massa m é 135 g, suspensa em fio longo pelo ponto médio. O valor do período do oscilador harmônico angular formado pela barra e o fio é \(T_a\) = 2,53 s. Quando um objeto de forma irregular, que vamos chamar de objeto X, é pendurado no mesmo fio, como na figura (b), e o valor do período aumenta para \(T_b\) = 4,76 s. Qual é o momento de inércia do objeto X em relação ao eixo de suspensão?

Fonte: Halliday & Resnick

Questão 9

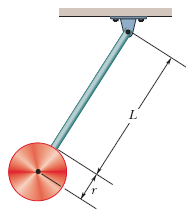
Na figura, o pêndulo é formado por um disco uniforme de raio r = 10,0 cm e 500 g de massa preso a uma barra homogênea de comprimento L = 500 mm e 270 g de massa. (a) Calcule o momento de inércia em relação ao ponto de suspensão. (b) Qual é a distância entre o ponto de suspensão e o centro de massa do pêndulo? (c) Calcule o período das oscilações.

Fonte: Halliday & Resnick

Questão 10

Uma roda de bicicleta pode girar livremente em torno do eixo, que é mantido fixo. Uma mola está presa a um dos raios a uma distância r do eixo, como mostra a figura. (a) Usando como modelo para a roda um anel delgado, de massa m e raio R, qual é a frequência angular ω para pequenas oscilações do sistema em termos de m, R, r e da constante elástica k? Qual é o valor de ω para (b) r = R e (c) r = 0?

Fonte: Halliday & Resnick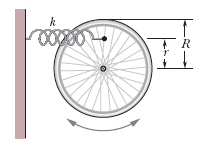

Questão 11

Um objeto de 5,00 kg que repousa em uma superfície horizontal sem atrito está preso a uma mola com k = 1000 N/m. O objeto é deslocado horizontalmente 50,0 cm a partir da posição de equilíbrio e recebe uma velocidade inicial de 10,0 m/s na direção da posição de equilíbrio. Determine (a) a frequência do movimento, (b) a energia potencial inicial do sistema massa-mola, (c) a energia cinética inicial e (d) a amplitude do movimento.

Aplicação

Pesquisadores de biomecânica usam o modelo de pêndulo para calcular o momento de inércia dos membros inferiores de animais. Essa informação é importante para analisar como um animal caminha.

Ao caminhar avançamos de um comprimento 2L, onde L é o comprimento das nossas pernas.

O período do pêndulo simples é:

T = 2\pi\sqrt{\frac{L}{g}}

A rapidez ao andar é

v=\frac{2L}{T}

\Rightarrow \quad v=\frac{1}{\pi}\sqrt{Lg}

Para \(L=1\,m\), a rapidez da caminhada é:

v\approx 1,0\text{ m/s}

Fonte: http://axpfep1.if.usp.br/~otaviano/Andar.html

Aplicação

Ao caminhar avançamos de um comprimento 2L, onde L é o comprimento das nossas pernas.

O período físico é:

T = 2\pi\sqrt{\frac{2L}{3g}}

A rapidez ao andar é

v=\frac{2L}{T}

\Rightarrow \quad v=\frac{1}{\pi}\sqrt{\frac{3}{2}}\sqrt{Lg}

Para \(L=1\,m\), a rapidez da caminhada é:

v\approx 1,2\text{ m/s}

Fonte: http://axpfep1.if.usp.br/~otaviano/Andar.html

Aplicação

Em um modelo ainda mais elaborado as pernas oscilam como pêndulos físicos invertidos.

Fonte: https://physika.info/site/documents/Prado2011.pdf

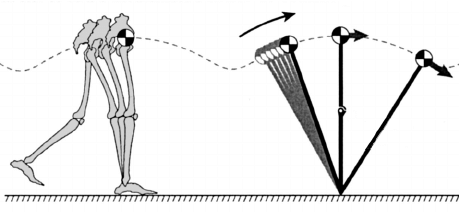
Fonte: Balbinot

Movimentos como esses são utilizados em algoritmos simplificados para controle, estimação e aprendizado de uma máquina.

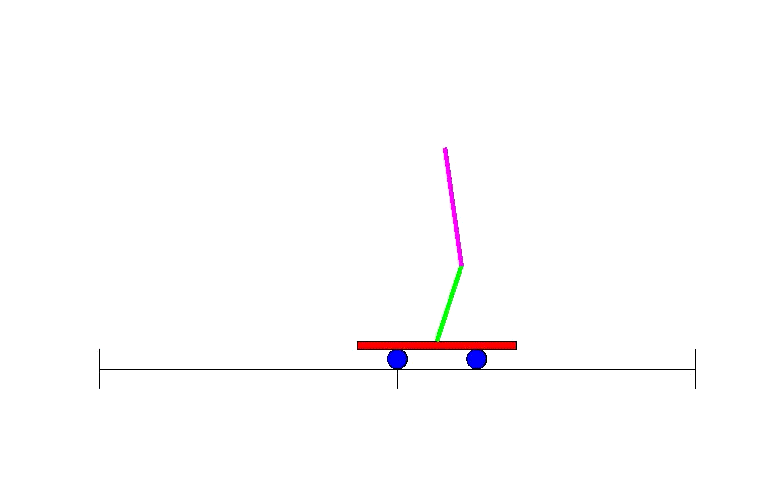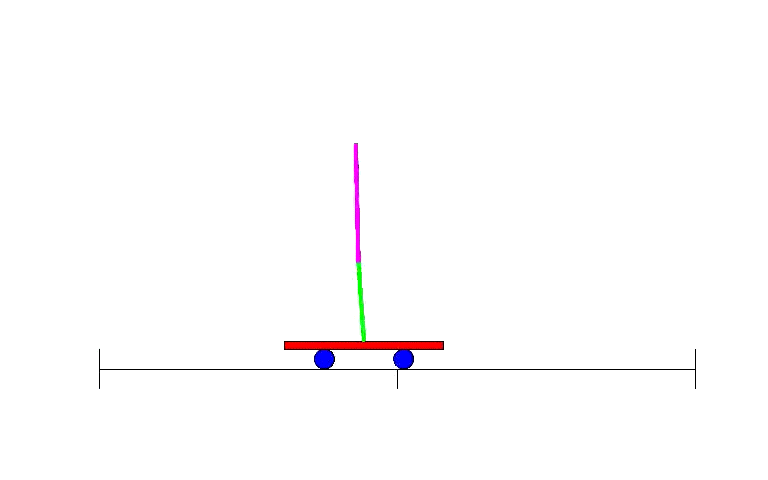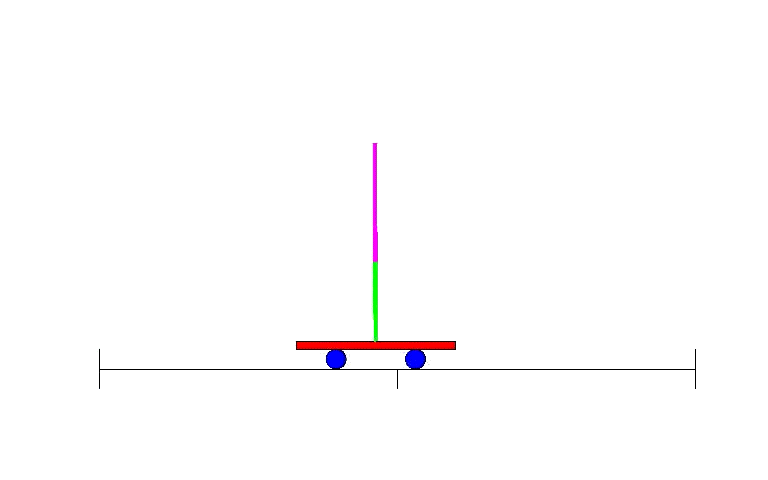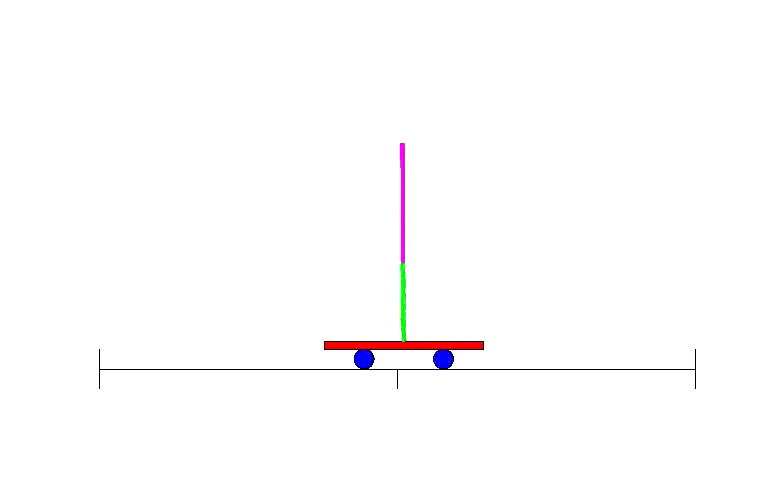
As equações estão longe do nível desse curso. Em equações diferenciais e modelagem integrada começarão a aperfeiçoar o modelo.

Aplicação

Manter o equilíbrio em robôs requer modelagem numérica.

Pêndulo invertido e automação.

Fonte: https://youtu.be/nOSTzpA0nGk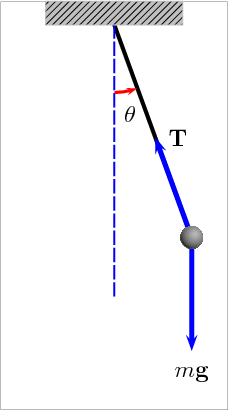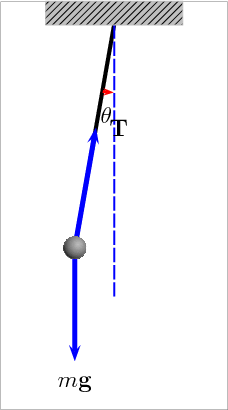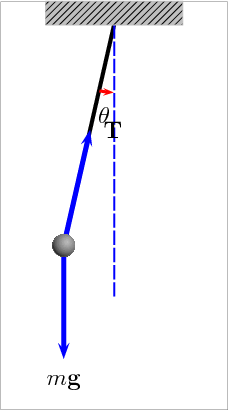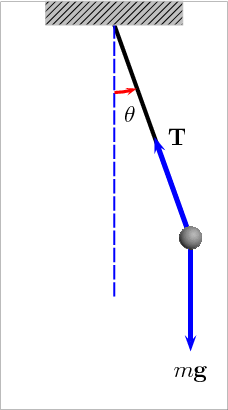

https://commons.wikimedia.org/wiki/File:PenduloTmg.gif

https://pin.it/2SEybXW