Aula 04

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Reconhecer a necessidade das oscilações forçadas para manter a oscilação natural.

Explicar o fenômeno de ressonância.

Estudar os modelos físico-matemáticos das oscilações forçadas e ressonância.

Como uma força propulsora aplicada a um oscilador na frequência certa pode provocar uma resposta muito intensa, ou ressonância?

Bibliografia:

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 13 - Movimento Periódico.

Seção: 13.8.

Motivação

O fenômeno de ressonância.

Fonte: https://www.youtube.com/embed/ynzk04wVn6k?enablejsapi=1

Oscilação forçada. A ideia.

No oscilador harmônico, a oscilação é permanente e a energia mecânica é conservada.

No oscilador harmônico amortecido, a amplitude da oscilação e a energia mecânica diminuem no exponencialmente com o tempo porque existe algum arrasto:

Como manter a amplitude da oscilação e contornar os efeitos dissipativos?

Seria possível garantir um movimento perpétuo, mas no mundo real não é esse o caso, pois existem forças de arrasto (aula 3).

E_0=\frac{1}{2}m\omega_0^2A^2

Não ocorre em sistemas físicos reais para sempre.

E= E_0e^{-\gamma\, t}

Ocorre em sistemas físicos reais nos amortecimentos fracos.

A=A_0e^{-\frac{\gamma}{2}\, t}

A=A_0

Oscilação forçada. A ideia.

Você tem algum ideia para manter o balanço oscilando?

Faça atuar sobre o oscilador uma força propulsora externa.

Transfira energia ao oscilador via trabalho motor.

Você vai produzir um movimento harmônico forçado.

Fonte: https://media3.giphy.com

Quando você empurra alguém sentado em um balanço, dá à pessoa empurrões periódicos com o propósito geral de fazê-la balançar cada vez mais alto – ou seja, aumentar a amplitude das oscilações.

Você só consegue aumentar a amplitude do movimento de balanço da pessoa se empurrá-la aproximadamente com a mesma frequência com a qual o balanço já oscila.

Oscilação livre e amortecida. Revisão.

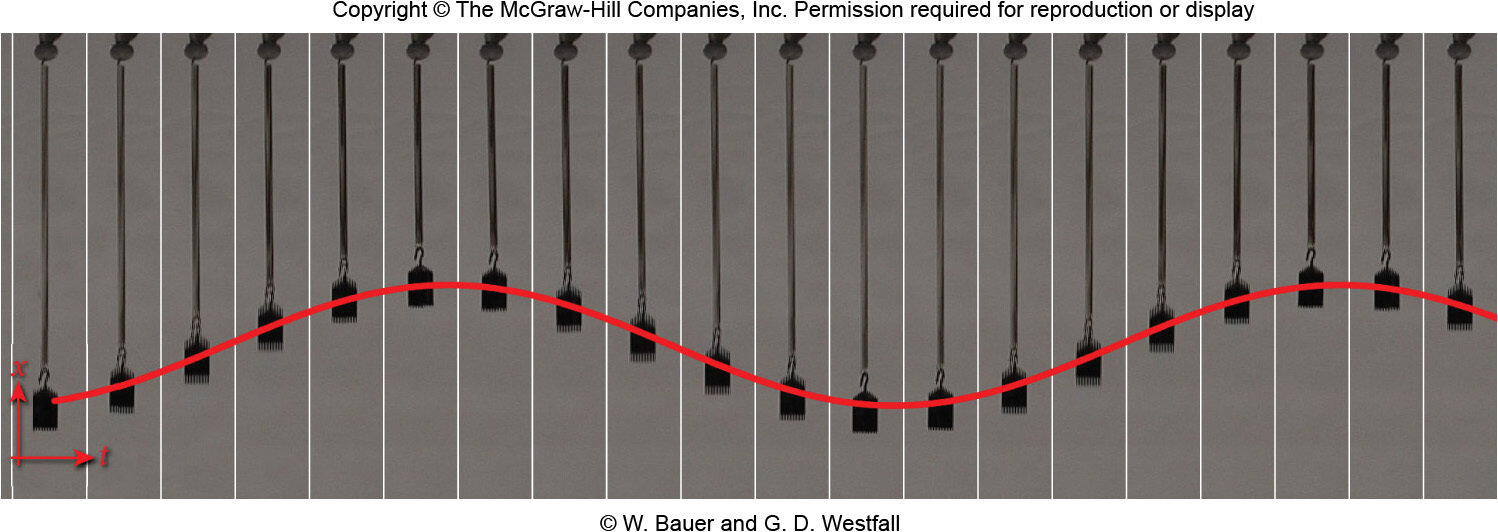
No oscilador harmônico livre:

m\ddot{x}+k x = 0

\omega_0 = \sqrt{\frac{k}{m}}

A EDO:

tem como função movimento:

x(t) = A \cos(\omega_0t +\delta)

com a frequência angular natural do oscilador:

No oscilador harmônico amortecido:

m\ddot{x}+b\dot{x}+k x = 0

\omega ' = \sqrt{ \left(\frac{k}{m}\right) - \left(\frac{b}{2m}\right)^2 }

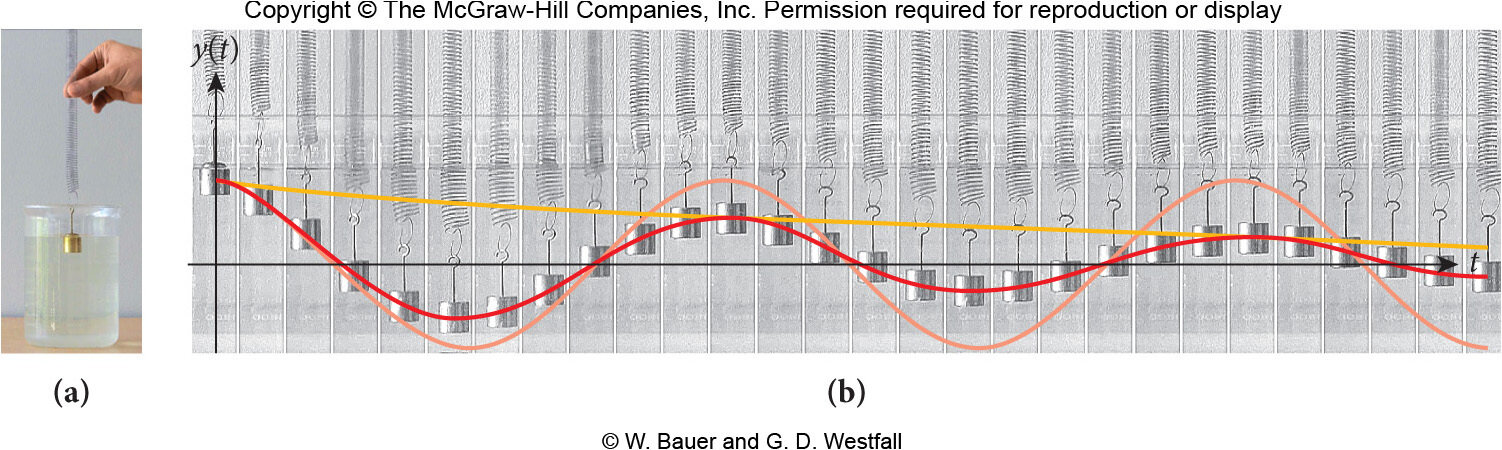
A EDO:

tem como função movimento:

x(t) = Ae^{-\frac{\gamma}{2}t} \cos(\omega 't +\delta)

com a frequência angular amortecida:

Como serão as equações do oscilador harmônico forçado?

Oscilação forçada. A EDO.

A EDO do oscilador harmônico amortecido forçado é:

m\ddot{x}+b\dot{x}+k x = F_m\cos(\omega_mt+\varphi)

Há duas frequências angulares relevantes:

A frequência natural:

A frequência motriz:

\omega_0=\sqrt{\frac{k}{m}}

\omega_m

Frequência angular motriz

Força motriz (dependente do tempo)

Para manter um sistema vibrando na presença de atrito (\(b\)), temos que continuar empurrando-o com uma força motriz periódica externa. A frequência dessa força (\(\omega_m=2\pi f_m\)) é chamada de frequência motriz, \(f_m\), que é totalmente independente da frequência natural do sistema (\(\omega_0=2\pi f_0\)).

Sistema

Externa

\vec F_m

Fonte: Tipler

força motriz

Oscilação forçada. A EDO.

A solução é a soma da parte transiente (quando a força externa é nula) com a parte estacionária (quando a força externa não é nula):

x = x_{estacionaria}+x_{transiente}

m\ddot{x}+b\dot{x}+k x = F_e\cos(\omega_et+\delta)

Dada a EDO do oscilador harmônico forçado:

A função movimento da parte transiente já conhecemos (oscilação amortecida). Precisamos descobrir a função movimento da parte estacionária.

Você tem idéia sobre como deve ser essa função estacionária?

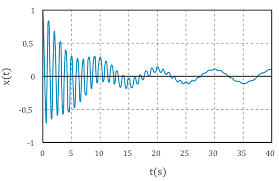
transiente

estacionária

Oscilação forçada. A EDO.

Movimento transiente. Sem a força propulsora temos um oscilador harmônico amortecido de modo que a amplitude diminui exponencialmente no tempo.

Movimento estacionário. Com a força externa a amplitude das oscilações é fica constante ao aplicar uma força que varia periodicamente com o tempo.

Fonte: https://www.geogebra.org/m/j9YbuF7E

O papel da força propulsora é manter a amplitude da oscilação.

Simule:

\(m=1,0\) kg

\(k=2,0\) N/m

\(F_0=1,0\) N

\(y_0=5,0\) N

\(b=0,2\) Kg/s

Varie a frequência da força externa:

\(1.1 \leq\omega\leq 1.8\) rad/s

Para que valor de \(\omega\) a amplitude \(x_m\) é máxima?

x_{estacionaria} = x_m\cos(\omega_mt+\varphi)

Oscilação forçada. A ressonância s/ amortecimento.

Se a constante de amortecimento é nula (\(b\rightarrow 0\)) ou o amortecimento é muito fraco:

A condição, \(\omega_0=\omega_m\) levaria a uma amplitude infinita, (\(x_m\rightarrow \infty\)).

Fonte: https://youtu.be/rvwwQAfdBWs

A condição, \(\omega_m << \omega_0\) levaria a uma amplitude finita, (\(x_m \rightarrow F_m/k\)). A força motora está em fase com o deslocamento.

A condição, \(\omega_m >> \omega_0\) levaria a uma amplitude nula, (\(x_m \rightarrow 0\)). A força motora está em oposição de fase com o deslocamento.

m\ddot{x}+k x = F_m\cos(\omega_mt+\delta)

Oscilação forçada. A ressonância s/ amortecimento.

Para o amortecimento nulo, as segunda lei de Newton permite escrever a EDO do sistema:

\vec F_e + \vec F_m=m\vec a

-kx+F_0\cos(\omega t+\delta)=ma

\Rightarrow ma+kx=F_m\cos(\omega_m t+\delta)

m\ddot x+kx=F_m\cos(\omega_m t+\delta)

\Rightarrow -m\ddot\omega^2A\cos(\omega_m t+\delta)+kA\cos(\omega_m t+\delta)=F_m\cos(\omega_m t+\delta)

x(t)

F_m

\vec F_e

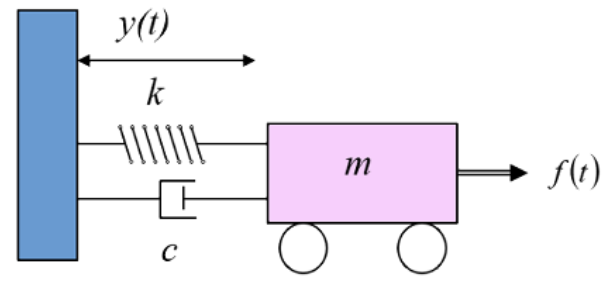
A solução da solução estacionária deve ter o mesmo comportamento da força motora:

x(t)=A\cos(\omega_mt+\delta)

\ddot x(t)=-\omega^2A\cos(\omega_m t+\delta)

A = \frac{F_m}{m (\omega_0^2-\omega_m^2) }

A amplitude da solução estacionária é:

Oscilação forçada. A ressonância s/ amortecimento.

A = \frac{F_m}{m (\omega_0^2-\omega_m^2) }

A condição, \(\omega_0=\omega_e\) levaria a uma amplitude infinita, (\(x_m\rightarrow \infty\)).

A condição, \(\omega_e << \omega_0\) levaria a uma amplitude finita, (\(A \rightarrow F_m/k\)). A força motora está em fase com o deslocamento, \(\delta = 0\).

A condição, \(\omega_e >> \omega_0\) levaria a uma amplitude nula, (\(A \rightarrow F_m/(m\omega_m^2)\)). A força motora está em fase oposta ao deslocamento, \(\delta = \pi\).

Fonte: https://farside.ph.utexas.edu/

Amplitude

Fase

0, \quad \omega_m<\omega_0

\pi, \quad \omega_m>\omega_0

\delta =

\left\{\right.

\delta\ /\pi

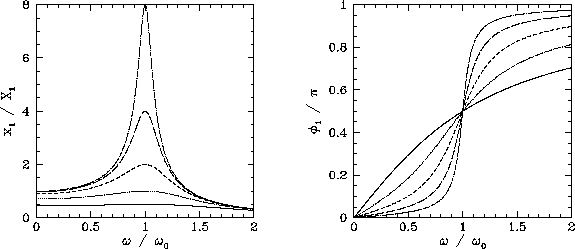
Dada a amplitude da solução estacionária:

A fase depende da relação entre as frequências:

Uma frequência externa igual à frequência natural, quando (\(b\rightarrow 0\)), é algo que deve ser evitado porque pode ser catastrófico.

Há um colapso, pois a amplitude de oscilação ou a potência média do sistema serão máximas.

Fonte: https://youtu.be/jh_9KzCBcP0

Fonte: https://youtu.be/Az1_Zv1gjVU

Oscilação forçada. A ressonância s/ amortecimento.

Em sistemas reais esse crescimento ilimitado não ocorre de fato. Sempre há algum amortecimento no sistema porque \(b\neq 0\).

A = \frac{F_m}{m (\omega_0^2-\omega_e^2) }

Para sistemas com amortecimento, a EDO fica:

x_{estacionaria}(t) = x_m\cos(\omega_mt)

A amplitude (\(x_m\)) depende das frequências natural (\(\omega_0\)), externa (\(\omega_m\)), mas também da coeficiente de amortecimento (\(b\)).

Para que parâmetros do simulador a amplitude de oscilação será máxima?

A constante de fase é,

\tan \delta = \frac{\omega_m\gamma}{(\omega_0^2-\omega_m^2)},

x_{m} = \frac{F_m}{m\sqrt{ (\omega_0^2-\omega_m^2)^2 +\gamma^2\omega_m^2 }}

Oscilação forçada. A ressonância c/ amortecimento.

m\ddot{x}+b\dot{x}+k x = F_m\cos(\omega_mt+\delta)

A partir da solução estacionária:

x(t)

f(t)

Permite que \(\omega_0 = \omega\)!

\gamma = \frac{b}{m}

0 \leq \delta\leq \pi

\omega_0^2 = \frac{k}{m}

x_{m} = \frac{F_m}{m\sqrt{ (\omega_0^2-\omega_m^2)^2 +\gamma^2\omega_m^2 }}=\frac{F_m}{b\omega_m} =\frac{F_m}{b\omega_0}

A ressonância ocorre em um sistema oscilante quando a frequência motriz se iguala à frequência natural:

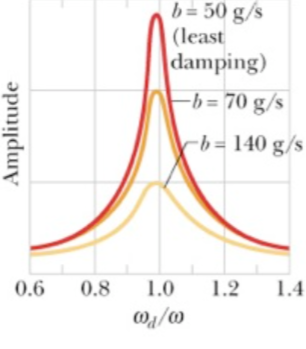
Fonte: https://www.geogebra.org/m/xgxvskbh

Para este caso especial, a amplitude do movimento torna-se máxima.

\omega_0 = \omega_m

Fonte: Halliday & Resnick

Para uma mesma força motora aplicada, a amplitude aumenta à medida que \(b\) diminui. A largura da amplitude aumenta com o aumento de \(b\).

Oscilação forçada. A ressonância c/ amortecimento.

O sistema de molas de mesma constante elástica e diferentes massas oscilarão conforme a frequência da força motora (driver).

Fonte: https://www.compadre.org/osp/EJSS/4466/252.htm

Para que parâmetros do simulador a amplitude de oscilação será máxima para cada massa?

Oscilação forçada. A ressonância c/ amortecimento.

A potência transferida ao sistema massa-mola vai depender dos coeficientes de amortecimento, da frequência natural e também da fase.

Quais as massas e frequências de ressonância de cada um dos osciladores massa-mola?

A solução completa da EDO não homogênea

Dada a equação da oscilação amortecida e forçada:

A solução completa é a soma da parte transiente e estacionária:

x(t)=Ae^{\frac{\gamma}{2}t}\cos(\omega't+\delta)+\frac{F_m}{\sqrt{m^2(\omega_0^2-\omega_m^2)+b^2\omega_m^2}}\cos(\omega_mt+\delta)

m\ddot{x}+b\dot{x}+kx=F_m\cos(\omega_mt+\varphi)

onde para um sistema massa-mola:

\omega_0=\sqrt{\frac{k}{m}}

\gamma = \frac{b}{m}

\omega' = \sqrt{\omega_0^2-\left(\frac{\gamma}{2}\right)^2}

\tan \delta = \frac{\omega_m\gamma}{(\omega_0^2-\omega_m^2)},

0 \leq \delta\leq \pi

Solução da EDO quando \(F_0 =0\).

Solução transiente.

Solução da EDO quando \(F_0 \neq 0\).

Solução estacionária.

Oscilação forçada. A potência.

No regime estacionário a potência instantânea da força viscosa(*)

p(t)=-{\vec F_v\cdot \vec v(t)}

Integrando no tempo (em um período), obtemos a potência média:

p(t)=-(-b{\vec v).\vec v}=b{v(t)^2}

{p} (t)=b(x_m^2\omega_m^2)\,{\text{sen}^2(\omega_mt+\delta)}

\overline{P} =\frac{1}{2}b(x_m^2\omega_m^2)

x_{m} = \frac{F_m}{m\sqrt{ (\omega_0^2-\omega_m^2)^2 +\gamma^2\omega_m^2 }}

\overline{P} =\frac{F_m^2}{2}b\frac{\omega_m^2}{m^2[(\omega_0^2-\omega_m^2)+\gamma^2\omega_m^2]}=\frac{F_m^2}{2b}\text{sen} \,\delta

Sabendo que \( x(t) = x_m \cos(\omega_m t + \delta) \) e \(v=dx/dt = -\omega_m x_m \text{sen}(\omega_m t + \delta) \) :

A potência média é máxima quando \(\delta = \pi/2\).

(*) o correto seria calcular a potência da força motora externa. LINK.

Contudo, a potência da força motora deve ser igual à potência da força de arrasto que está dissipando uma dada quantidade de energia no tempo.

\Rightarrow

Você saberia mostrar porque sen(\(\delta\)) surgiu na última passagem? Isto vale bônus.

Oscilação forçada. A potência.

A condição de ressonância, \(\omega_0=\omega_e\) ocorre quando \(\delta = \pi/2\) e a potência média é máxima:

\overline{P} _{max}=\frac{F_m^2}{2b}

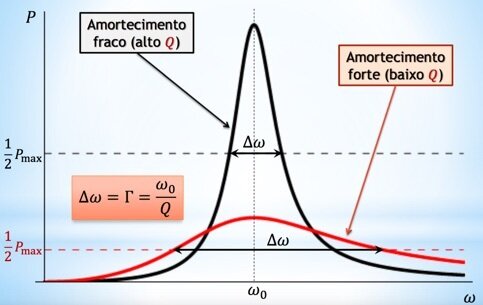
Fonte: Prof. Tarciro Mendes

No amortecimento fraco (\(b\rightarrow 0\)), o fator de qualidade (\(Q\)) é grande e a largura do pico (\(\Delta\omega\)) é pequeno.

No amortecimento forte (\(b\rightarrow \infty\)), o fator de qualidade (\(Q\)) é pequeno e (\(\Delta\omega\)) é grande.

{\Delta\omega}=\frac{{\omega_0}}{Q}

{\Delta\omega}=\frac{{b}}{m}

É possível mostrar que a largura de banda \(\Delta \omega\) (calculada à meia altura da potência média máxima) é inversamente proporcional ao fator de qualidade:

\Rightarrow

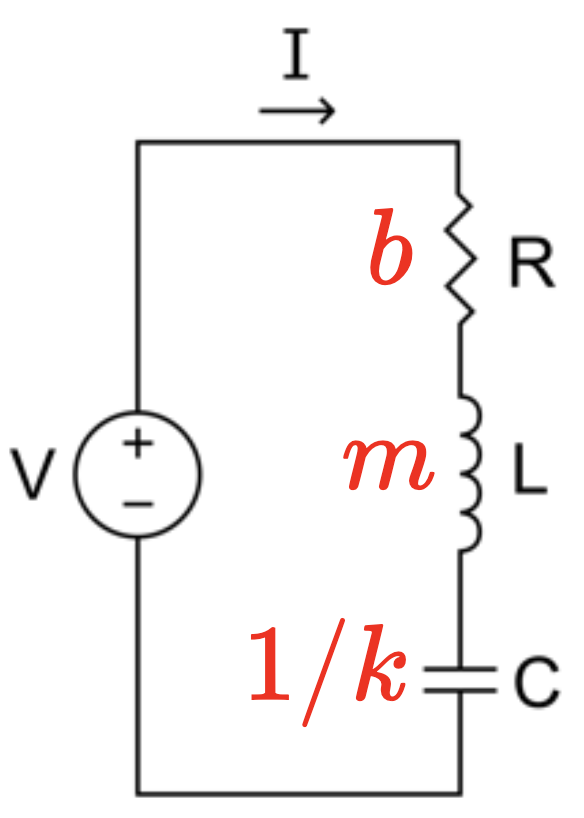
Oscilação forçada. Eletromagnetismo.

A ressonância ocorre em muitos tipos de sistemas. Num sistema RLC (radio AM):

Fonte: https://youtu.be/pQhMSOj5a98

i(t) = i_e\cos(\omega_e t +\varphi)

i_e = \frac{\mathcal{E}}{\sqrt{(\omega_eL-\frac{1}{\omega_eC})^2+R^2}}

\omega_eL=\frac{1}{\omega_eC}\Rightarrow \omega_e = \frac{1}{\sqrt{LC}}=\omega_0

A corrente elétrica no circuito:

A amplitude da corrente no circuito:

A ressonância no circuito:

Fonte: https://www.geogebra.org/m/me8qspy9

Questão 1

Um corpo de 1,5 kg de massa, preso a uma mola de constante elástica igual a 600 N/m, perde 3,0 por cento de sua energia em cada ciclo. O mesmo sistema é excitado por uma força senoidal com o valor máximo F0 = 0,50 N. (a) Quanto vale Q para este sistema? (b) Qual é a frequência angular de ressonância? (c) Se a frequência de excitação varia lentamente através da ressonância, qual é a largura de ressonância ∆ω? (d) Qual é a amplitude, na ressonância? (e) Qual é a amplitude, se a frequência de excitação é ω = 19 rad/s?

Questão 2

Um oscilador amortecido perde 3,50 por cento de sua energia a cada ciclo. (a) Quantos ciclos decorrem, até que metade de sua energia seja dissipada? (b) Qual é o seu fator Q? (c) Se a frequência natural é 100 Hz, qual é a largura da curva de ressonância quando o oscilador é excitado por uma força senoidal?

Questão 3

Um sistema massa-mola linearmente amortecido oscila a 200 Hz. A constante de tempo do sistema é 2,0 s. Em t = 0, a amplitude de oscilaçÃo é 6,0 cm e a energia do sistema oscilante é 60 J. (a) Quais são as amplitudes de oscilação em t = 2,0 s e em t = 4,0 s? (b) Quanta energia é dissipada no primeiro intervalo de 2 segundos e no segundo intervalo de 2 segundos?

Questão 4

Sismólogos e geólogos constataram que a Terra vibra com um período de ressonância de 54 min e um fator Q de cerca de 400. Após um grande terremoto, a Terra continua vibrando por até 2 meses. (a) Determine a porcentagem de energia de vibração dissipada em cada ciclo, devido às forças de amortecimento. (b) Mostre que, após n períodos, a energia de vibração é dada por \(E = E_0(0,984)^n\), onde \(E_0\) é a energia original. (c) Se a energia de vibração original de um terremoto é \(E_0\), quanto vale a energia após 2,0 dias?

Questão 5

Suponha que m = 1, k = 9, \(F_0\) = 80 e \(\omega_e\) = 5, de modo que a equação diferencial do MHS forçado não amortecido seja:

m\ddot x +kx=F_0\cos(\omega_e t)

\ddot x +9x=80\cos(5 t)

Encontre a solução geral \(x(t)\) se \(x(0)=0\) e \(\dot x(0) = 0\). Encontrar a solução e determinar os valores de A, B e C.

Sabe-se que:

x(t)=x_t(t) + x_e(t)

x_t(t) = A \cos(\omega_0 t)+ B \text{sen}(\omega_0 t)

x_e(t) = C \cos(\omega_e t)

onde:

Não está resolvida no SIGAA e vale 1,0 ponto se entregue resolvida e explicada presencialmente ao professor em dada e horário a ser combinados.

Se possível construir o gráfico x por t.

Solução da EDO quando \(F_0 =0\). Solução transiente.

Solução da EDO quando \(F_0 \neq 0\). Solução estacionária.

Questão 6

Suponha que m = 1, b= 2, k = 2, \(F_0\) = 20 e \(\omega_e\) = 2, de modo que a equação diferencial do MHS forçado amortecido seja:

m\ddot x +b\dot x+kx=F_0\cos(\omega_e t)

\ddot x +2\dot x +2x=20\cos(2 t)

Encontre a solução geral \(x(t)\) se \(x(0)=0\) e \(\dot x(0) = 0\). Encontrar a solução e determinar os valores de A, B, C e D.

Sabe-se que:

x(t)=x_t(t) + x_e(t)

x_t(t) = e^{-\frac{\gamma}{2} t}(A \cos(\omega' t)+ B \text{sen}(\omega' t))

x_e(t) = C \cos(\omega_e t)+ D \cos(\omega_e t)

onde:

\omega' =\sqrt{\omega_0^2+\frac{\gamma^2}{4}}

Não está resolvida no SIGAA e vale 1,0 ponto se entregue resolvida e explicada presencialmente ao professor em dada e horário a ser combinados.

Se possível construir o gráfico x por t.

Solução da EDO quando \(F_0 =0\). Solução transiente.

Solução da EDO quando \(F_0 \neq 0\). Solução estacionária.

Aplicação

É possível construir esta estrutura e medir as frequências de ressonância utilizando um smartphone?

Fonte: https://youtu.be/hSwjkG3nv1c?si=ifWxNlr6lIspKtUc

Fonte: https://youtu.be/q7Jh0zu8xUY