Aula 06

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 15 - Ondas Mecânicas.

Seções: 15.4, 15.5

Calcular a energia e potência em uma onda.

Enunciar o princípio de superposição.

Calcular a reflexão e transmissão de ondas em um ponto de junção.

Calcular a rapidez de propagação de uma onda em uma corda.

Qualquer onda se propagando é descrita pela equação de onda, quer ela seja periódica, quer não. A solução da equação da onda deve ter a forma:

Ondas. A equação da onda.

F_t\frac{\partial^2 y(x,t)}{\partial x^2} = \mu\frac{\partial^2 y(x,t)}{\partial t^2}

Alternativamente,

Fonte: Tipler

\frac{\partial^2 y(x,t)}{\partial x^2} = \frac{1}{v^2}\frac{\partial^2 y(x,t)}{\partial t^2}

onde a rapidez de propagação da onda é:

v=\sqrt{\frac{F_t}{\mu}}

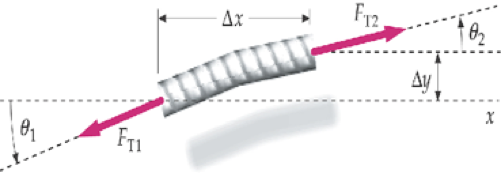
Para produzir o movimento de qualquer em um meio elástico é necessário fornecer energia mediante um trabalho mecânico realizado sobre esse meio.

As forças que as partes esquerda e direita da corda exercem sobre o sistema em estudo

a porção da corda é o sistema (meio elástico)

A equação da onda é um E.D.O. de 2a. ordem:

y(x,t)=f(x\pm vt)

A equação de movimento de onda (ou pulso) é uma EDO de segunda ordem:

Ondas. A equação da onda.

\frac{\partial^2 y(x,t)}{\partial x^2} = \frac{1}{v^2}\frac{\partial^2 y(x,t)}{\partial t^2}

A curvatura e aceleração são proporcionais a menos de um fator multiplicativo e constante \(v^2\).

A rapidez de propagação da onda é \(v\) e tem as seguintes propriedades:

\(v\) depende da tensão aplicada.

\(v\) depende do meio de propagação.

v=\sqrt{ \frac{ \text{propriedade elástica} }{ \text{propriedade inercial} } }

Curvatura

Aceleração

Força, compressibilidade, tensão, tração, etc.

Massa e densidade.

A rapidez de propagação do pulso depende apenas da força aplicada ao meio e da densidade do meio.

A velocidade transversal (\(v_y\)) de um ponto material do meio não afeta a rapidez de propagação (\(v\)).

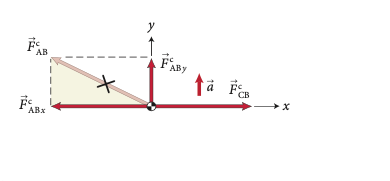
Para o segmento de corda (B), via semelhança de triângulos:

\frac{F_y}{F_x}=\frac{v_t\Delta t}{v\Delta t}

\Rightarrow {F_y}=F_x\frac{v_t}{v}

A taxa de transferência de momento da componente da força \(F_y\):

m\Delta v_t=F_y\Delta t

(\mu\Delta x)v_t=F_y\Delta t

\Rightarrow(\mu v\Delta t)v_t=F_y\Delta t

\Rightarrow v=\sqrt{\frac{F_x}{\mu}}

Fonte: Eric Mazur

Fonte: Eric Mazur

Fonte: Eric Mazur

Ondas. A equação da onda.

v\Delta t

v_t

v_tt

densidade linear de massa: \(\mu= m/\Delta x\)

\vec F^c_{AB}

\frac{\partial^2 E(x,t)}{\partial x^2} = \epsilon_0\mu_0\frac{\partial^2 E(x,t)}{\partial t^2}

onde as constantes de permissividade e permeabilidade são

Fonte: Giphy

onde,

v=\sqrt{\frac{1}{\epsilon_0\mu_0}}

A rapidez de propagação da onda eletromagnética no vácuo é constante.

\epsilon_0 = 8,854\times 10^{-12} \text{C}^2\text{/N.m}^2

\mu_0 = 4\pi\times 10^{-7} \text{N/A}^2

v=2,99796\times 10^{8}\text{m/s}=c

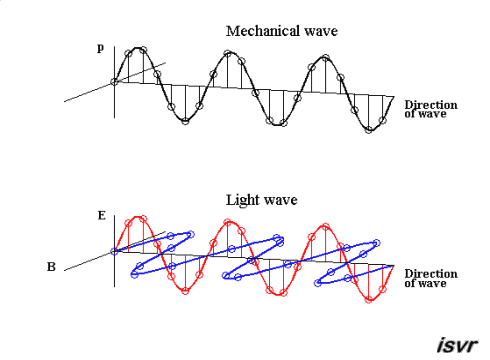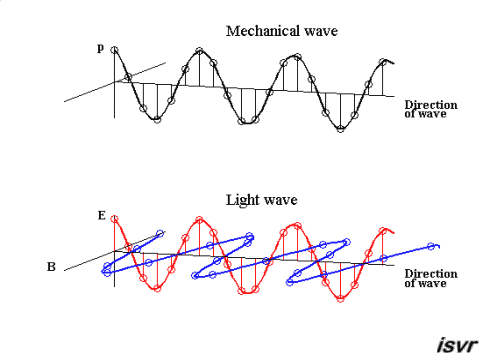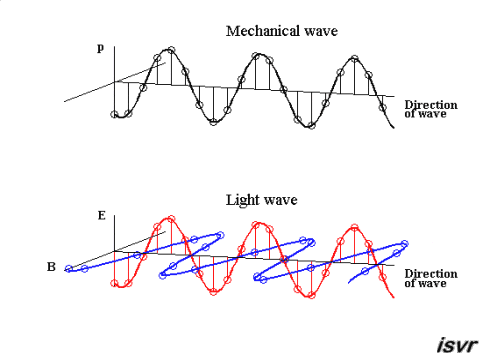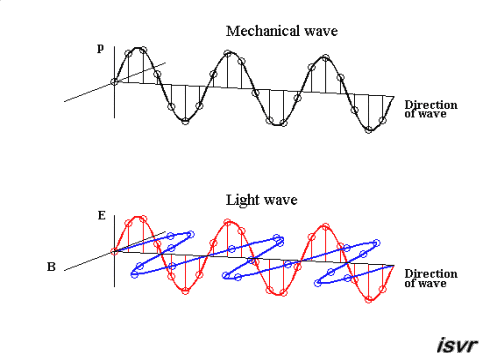
Ondas. A equação da onda.

A rapidez de propagação da luz no vácuo. Para o campo elétrico:

\Rightarrow \frac{\partial^2 E(x,t)}{\partial x^2} = \frac{1}{v^2}\frac{\partial^2 E(x,t)}{\partial t^2}

Temos uma onda eletromagnética e transversal que não precisa de um meio para se propagar.

Energia e Potência no movimento ondulatório

Onda é uma perturbação ou variação que transfere energia e momento progressivamente de um ponto ao outro em um meio que pode ter a forma de uma deformação elástica, ou de uma variação de pressão, ou de uma indensidade eletromagnética, ou temperatura.

Na Aula 5, vimos três características comuns as ondas. Entre elas, a energia.

Para produzir qualquer onda, devemos aplicar força a uma parte do meio onde a onda se propaga; o ponto sobre o qual a força é exercida se move, portanto, realizamos trabalho sobre o sistema.

À medida que a onda se propaga, cada porção do meio exerce uma força e realiza um trabalho sobre a porção adjacente.

Energia e Potência no movimento ondulatório

A força tangencial \(\vec F_T\) é a força que a corda do lado esquerdo (não mostrada) exerce sobre o lado direito da corda (cor laranja).

Essa força transfere energia e potência para a corda.

Se a velocidade transversal é máxima, a deformação também é máxima.

Se a aceleração é nula, a curvatura também é nula.

Quando as energias cinéticas e potencial elástica assumem seus valores máximos a energia mecânica tem a forma:

\overline{\frac{dE}{dx}}= \overline{\frac{dK}{dx}} + \overline{\frac{dU}{dx}}

Quais as expressões para estas densidades energias?

Fonte: Tipler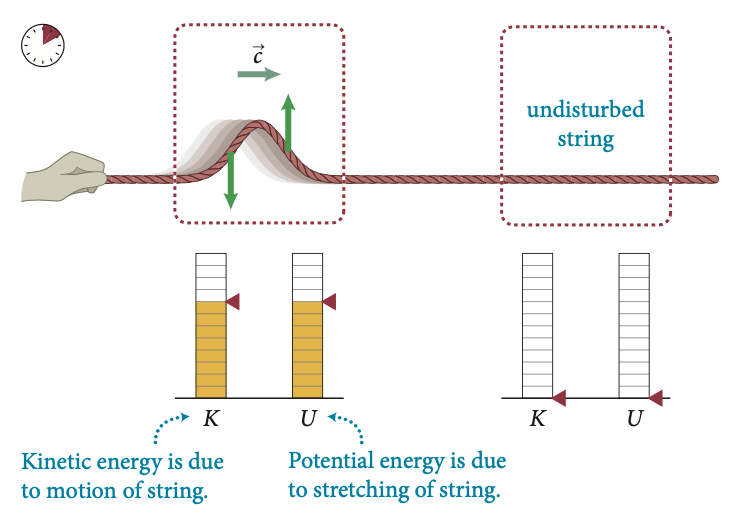

\frac{dy}{dx}

\vec v_t

Fonte: Eric Mazur

Energia cinética é devido ao movimento da corda

Energia potencial é devido à deformação da corda

Energia potencial no movimento ondulatório

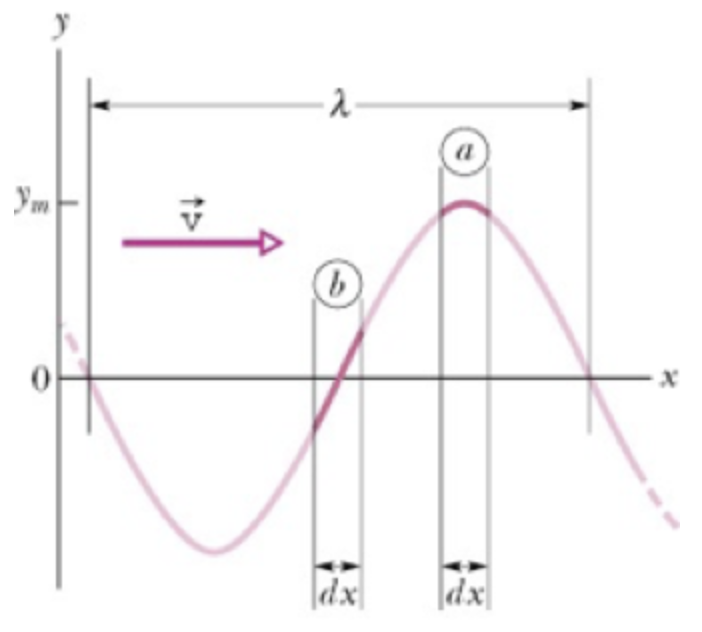
Fonte: Halliday & Resnick

\Delta x

\Delta r

\theta

\Delta y

\Delta L = \Delta r - \Delta x

\Delta L = \sqrt{\Delta x^2+\Delta y^2} - \Delta x

\Delta L = \Delta x\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2} - \Delta x

dL \approx \frac{1}{2}d x\left( \frac{\partial y}{\partial x}\right)^2

A energia potencial depende da deformação do meio, \(\Delta L\). Para uma corda:

dU=FdL

\Rightarrow dU=F \frac{1}{2}d x\left( \frac{\partial y}{\partial x}\right)^2

A energia potencial por unidade de comprimento do meio de propagação da onda:

\Rightarrow \frac{dU}{dx}=\frac{1}{2}F \left( \frac{\partial y}{\partial x}\right)^2

Se\, \theta \approx 0

Inclinação da corda

Há energia potencial quando existe uma força de tensão e alguma inclinação na corda.

Energia potencial no movimento ondulatório

Para uma onda periódica:

\overline{{\frac{dU}{dx}}}=\frac{1}{4}\mu\omega^2A^2=\frac{1}{2}\mu\, v_{0,y}^2

\Rightarrow\frac{dU}{dx}=\frac{1}{2}F k^2A^2\text{sen}^2(kx-\omega t)

y(x,t)=A\cos(kx-\omega t)

A densidade de energia potencial é uma função da posição e do tempo.

A densidade de energia potencial é máxima se \(\text{sen}^2(kx-\omega t) =1\) e mínima se \(\text{sen}^2(kx-\omega t) =0\)

\frac{dU}{dx}|_{max}=\frac{1}{2}\mu\omega^2A^2

A densidade de energia potencial média, em um período, é:

\frac{dU}{dx}=\frac{1}{2}F \left( \frac{\partial y}{\partial x}\right)^2

\frac{dU}{dx}|_{mín}=0

\frac{\partial y}{\partial x} = -kA\text{sen}(kx-\omega t)

\omega=vk

F = v^2\mu

ATENÇÃO

v_{0,y}=\omega_0A

Energia cinética no movimento ondulatório

A densidade de energia cinética é uma função da posição e do tempo:

dK=\frac{1}{2}(dm)v_y^2

A densidade de energia cinética é máxima se \(\text{sen}^2(kx-\omega_0 t) =1\) e mínima se \(\text{sen}^2(kx-\omega t) =0\)

\frac{dK}{dx}=\frac{1}{2}\mu\left( \frac{\partial y}{\partial t} \right)^2

A densidade de energia, em um período, para uma onda periódica:

\overline{\frac{dK}{dx}}=\frac{1}{4}\mu\omega^2A^2 = \frac{1}{2}\mu\, v_{0,y}^2

Para uma onda periódica:

y(x,t)=A\cos(kx-\omega t)

\frac{\partial y}{\partial t} = -\omega A\text{sen}(kx-\omega t)

\Rightarrow\frac{dK}{dx}=\frac{1}{2}\mu\, \omega_0^2 A^2\text{sen}^2(kx-\omega t)

dm = \mu dx

\frac{dK}{dx}|_{max}=\frac{1}{2}\mu\, \omega^2A^2 = \frac{1}{2}\mu v_{0,y}^2

\frac{dK}{dx}|_{min}=0

\omega=vk

F = v^2\mu

ATENÇÃO

v_{0,y}=\omega_0 A

Energia e Potência no movimento ondulatório

A densidade de energia total máxima de uma onda se propagando em um meio homogêneo é a soma das densidades de energia cinética e potencial:

{\frac{dE}{dx}}= {\frac{dK}{dx}}+ {\frac{dU}{dx}}

\Rightarrow {\frac{dE}{dx}}= \mu\omega^2A^2

A energia mecânica total média:

\overline{{dE}}= \frac{1}{2}\mu\omega^2A^2{dx}=\frac{1}{2}\mu\,v_{0,y}^2dx

A potência total média,

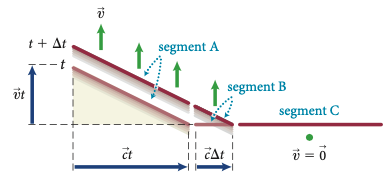
\overline{{P}}= \overline{\frac{dE}{dt}}= \frac{1}{2}\mu\omega^2A^2\frac{dx}{dt} = \frac{1}{2}\mu\,v_{0,y}^2v

As figuras mostram como se dá o processo de transferência de energia à medida que o tempo avança.

Observe que \(d\overline{K}/dx = d\overline{U}/dx\). Um pulso contém iguais quantidades de energia cinética e potencial elástica.

\Rightarrow {\frac{dE}{dx}}= \mu\,v_{0,y}^2

Nestas expressões não confunda \(v_{0,y}\) com \(v\), a rapidez de propagação da onda.

Fonte: Eric Mazur

Energia cinética é devido ao movimento da corda

Energia potencial é devido à deformação da corda

v_{0,y}

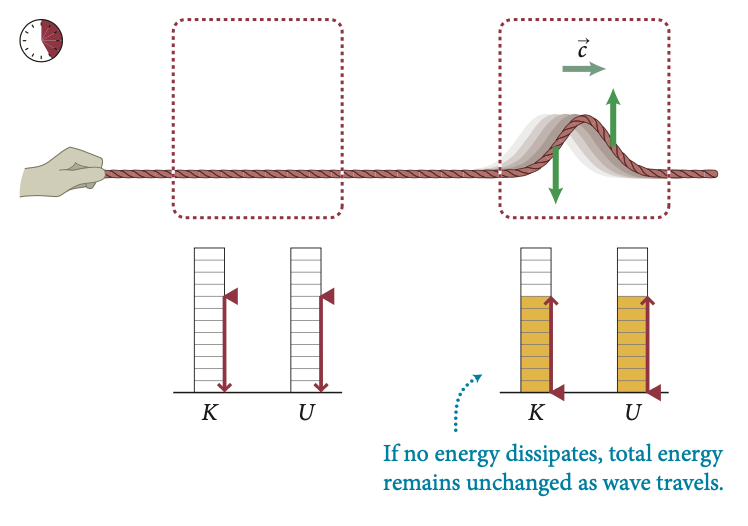
Fonte: Eric Mazur

Se nenhuma energia é dissipada, a energia total é inalterada quando a onda viaja.

v_{0,y}

Potência no movimento ondulatório

A força tangencial \(\vec F_T\) é a força que a corda do lado esquerdo (não mostrada) exerce sobre o lado direito da corda (cor laranja).

No referencial mostrado:

\vec F_T = \vec F_x\hat i + \vec F_y j

E a potência instantânea é:

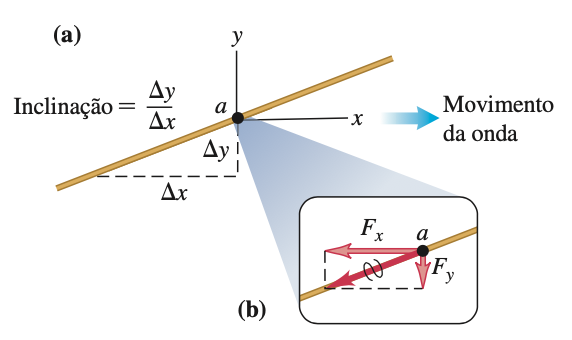
F_y = -F_T \text{sen}\theta\approx -F_T\tan\theta

Fonte: Tipler

Fonte: Sears & Zemansky

A potência somente é transferida quando existe uma inclinação e uma velocidade de perturbação da corda. A força transversal (\(F_y\)) realiza trabalho na direção da velocidade transversal (\(v_y\)).

P=\vec F_y\cdot \vec v_y

\Rightarrow P=-F_T \text{sen}\theta\,v_y

\Rightarrow P\approx-F_T \,\text{tan}\theta\, v_y

\text{Se } \theta << 1

P(x,t) = -F_T \frac{\partial y(x,t)}{\partial x} \frac{\partial y(x,t)}{\partial t}

Força que tira a corda do equilíbrio

Velocidade trasnversal

Potência no movimento ondulatório

A potência instantânea é válida para qualquer onda se propagando em uma corda seja a onda periódica ou não.

Para ondas periódicas:

A potência instantânea é:

P(x,t) = F_T\,k\,\omega\,A^2\text{sen}^2(kx-\omega t)

Fonte: Sears & Zemansky

A potência instantânea é máxima quando \(\text{sen}^2(kx-\omega t)=1\) e mínima se \(\text{sen}^2(kx-\omega t)=0\).

y(x,t) = A \cos(kx-\omega_0 t)

P_{max} =\mu \,v\,\omega^2\,A^2

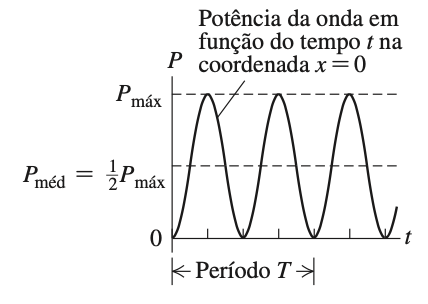
A potência média (em um período) é:

P_{med} =\frac{1}{2} \mu\,v\,\omega^2\,A^2

\omega=vk

F_T = v^2\mu

ATENÇÃO

A potência média não depende do tempo. É conservada!!!

P_{min} =0

Potência no movimento ondulatório

Em geral, para ondas mecânicas de todos os tipos, a equação é sempre válida:

Para ondas sísmicas, a potência quadruplica se a frequência for dobrada (para a mesma amplitude) ou se a amplitude for dobrada (para a mesma frequência).

Fonte: Sears & Zemansky

P_{med} =\frac{1}{2} \mu\,v\,\omega^2\,A^2

P_{med} =\frac{1}{2} \sqrt{\mu F_T}\,\omega^2\,A^2

P_{med} =\frac{1}{2} \mu\,v\,v_{0,y}^2

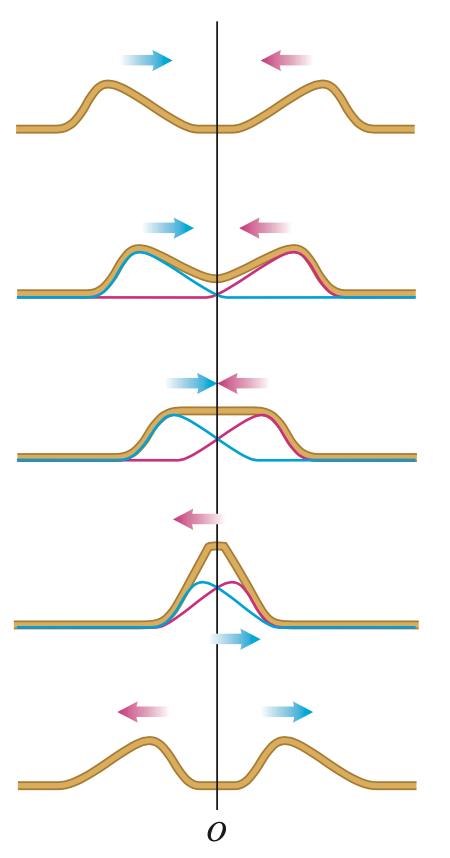
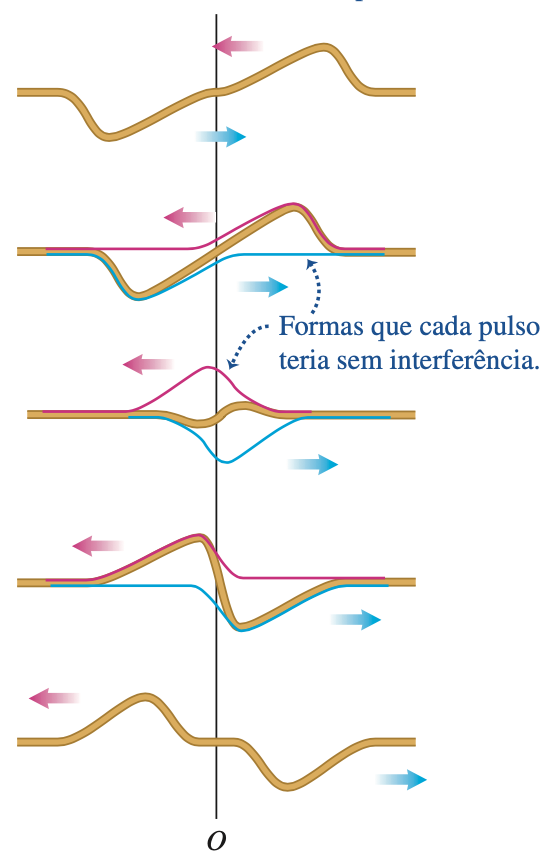
A superposição de ondas

A interferência é um fenômeno que se refere ao que acontece quando duas ou mais ondas passam pela mesma região ao mesmo tempo.

Duas ondas (ou mais) podem ocupar a mesma região do espaço no mesmo instante!

Interferência construtiva

Interferência destrutiva

Fonte: https://www.youtube.com/embed/7bkZbqcXRIA?enablejsapi=1

Fonte: https://www.youtube.com/embed/-UEj0wcgeUk?enablejsapi=1

Se duas ondas interferem em um meio que obedece à Lei de Hooke, então a função de onda resultante a qualquer instante é a soma algébrica das funções de onda individuais.

\frac{\partial^2 \Psi_1(x,t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 \Psi_1(x,t)}{\partial t^2}

\frac{\partial^2 \Psi_2(x,t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 \Psi_2(x,t)}{\partial t^2}

\frac{\partial^2 \Psi(x,t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 \Psi(x,t)}{\partial t^2}

\Psi_1(x,t)=c_1y_1(x,t)

\Psi_2(x,t)=c_2y_2(x,t)

\Psi(x,t)=c_1y_1(x,t)+c_2y_2(x,t)

Fonte: https://www.geogebra.org/m/dJrTcxYd

Onda 1

Onda 2

Interferência

Se \(y_1(x,t)\) é solução da equação da onda 1 e \(y_2(x,t)\) é solução da equação da onda 2, então a combinação linear também é solução da onda total.

Duas ondas podem passar uma através da outra sem mudança da forma da outra.

A superposição de ondas

Uma onda passa pela outra como se nada tivesse ocorrido.

Fonte: https://www.geogebra.org/m/dJrTcxYd

É possível ouvir música e ouvir alguém falando porque o som total é a soma algébrica do som produzido pela voz de quem fala e da onda produzida pelo alto-falante do aparelho de som.

Supondo que os perfis têm a mesma forma, \(|y_1(x-vt)| = |y_2(x+vt)|\), a interferência pode ser:

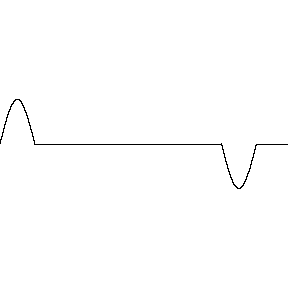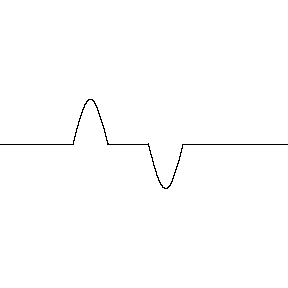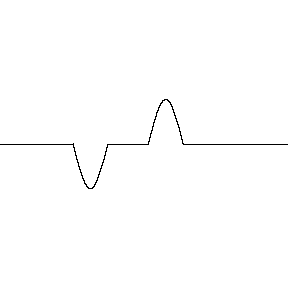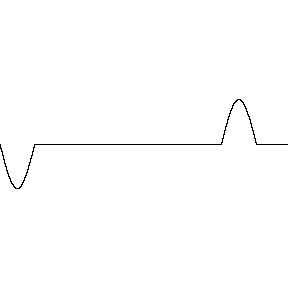
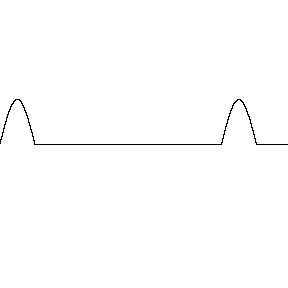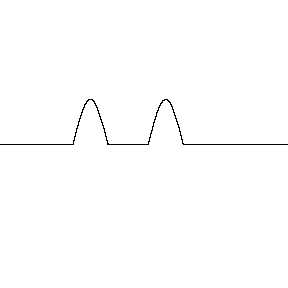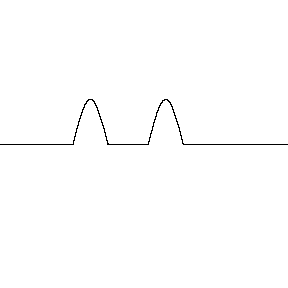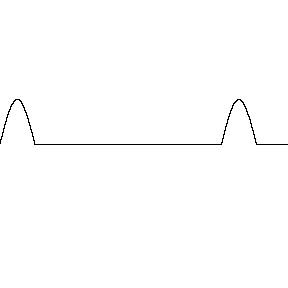
Construtiva: \(c_1 = c_2\)

Destrutiva: \(c_1 = - c_2\)

Destrutiva/Construtiva parcial: \(c_1 = -0,5 c_2 \text{ ou } c_1 = +0,5 c_2\)

Fonte: https://www.acs.psu.edu/drussell/demos.html

A superposição de ondas

Para ondas idênticas, as energias devem ser as mesmas para cada onda porque cada onda contém quantidades iguais de energia cinética e energia potencial. A energia total é conservada.

Fonte: Eric Mazur

Atenção: Na interferência destrutiva a energia potencial elástica é nula, mas não a cinética!

E_1 = K_1+U_1

E_2 = K_2+U_2

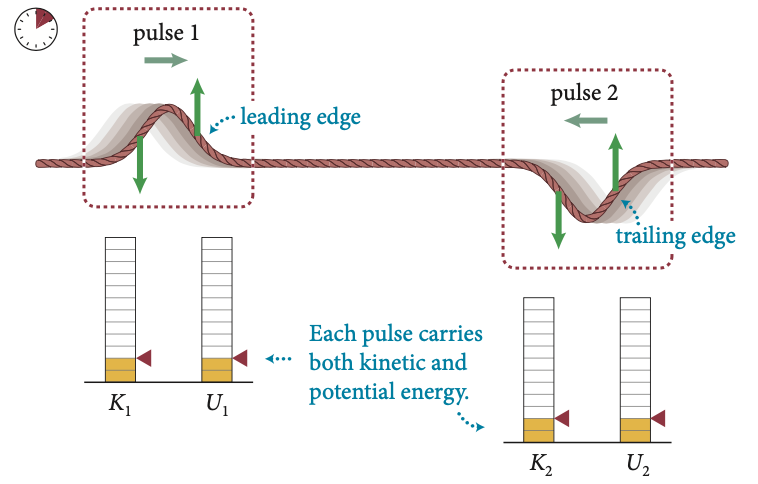
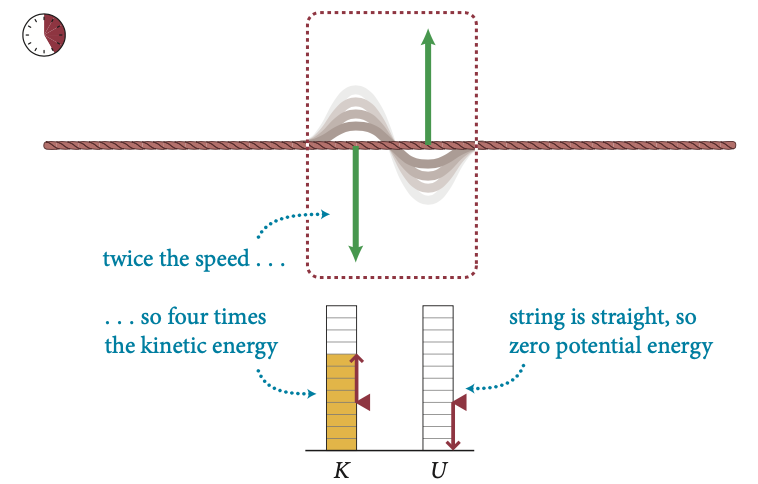
Fonte: Eric Mazur

E_{t,i} = 2K_1+2U_1

E_{t,f} = 4K_1

\Rightarrow K_1 = U_1

A velocidade trasnversal é \(v_y\).

A velocidade transversal é \(2v_y\).

A superposição de ondas

Aplicação. Transmissão e Reflexão de ondas.

Quando uma onda atinge as fronteiras de um meio, ocorre reflexão da onda inteira ou de uma parte dela. Caso seja parcial, uma parte da onda é transmitida.

Fonte: https://youtu.be/eEbM8G6YmJc

Fonte: https://youtu.be/O7aydScRbxc

Quando há uma descontinuidade do meio de propagação há uma alteração da rapidez,

Assim, pode existir ou não uma reflexão e/ou transmissão da onda incidente.

v=\sqrt{\frac{F_T}{\mu}}

Aplicação. Transmissão e Reflexão de ondas.

Ocorre superposição entre a onda incidente e a refletida na mesma região do meio quando há uma reflexão (invertida ou direita) que depende das propriedades do meio e das condições de contorno.

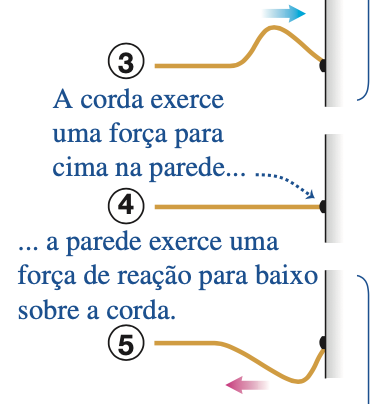
Corda com extremidade fixa em uma parede.

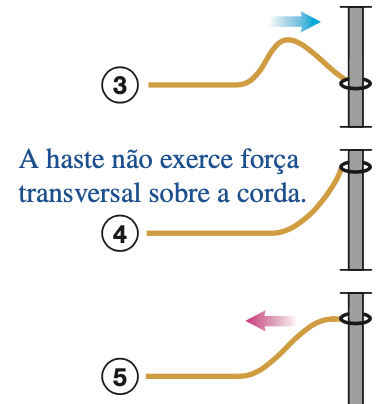
Corda com extremidade livre em uma parede.

Assemelha-se a uma interferência destrutiva.

Assemelha-se a uma interferência construtiva.

pulso refletido é invertido

pulso refletido é direito

Repare que a onda que é transmitida nunca é invertida (veja seta azul).

Fonte: Sears & Zemanxky

Fonte: Sears & Zemanxky

Fonte: Sears & Zemanxky

Fonte: Sears & Zemanxky

F_y(x,t)=-F\frac{\partial y(x,t)}{\partial y}

Fonte: https://www.acs.psu.edu/drussell/Demos/reflect/reflect.html

O pulso será parcialmente refletido (\(r\)) e parcialmente transmitido (\(t\)). Os valores de (\(r\)) e (\(t\)) dependerão da rapidez de propagação (\(v\)).

f_r=r f_i

f_t=t f_i

A reflexão e transmissão dependerão das propriedades do material em ambos os lados da junção.

Aplicação. Transmissão e Reflexão de ondas.

x=0

Animation courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State

r=\frac{v_2-v_1}{v_2+v_1}

t=\frac{2v_2}{v_1+v_2}

onde \(r,t\) são os coeficientes de reflexão e transmissão:

Caso 1: Densidades iguais.

Fonte: Halliday & Resnick

Caso 2: Densidade diminui.

Caso 3: Densidade aumenta.

v_1=v_2

(\mu_1=\mu_2)

v_1< v_2

(\mu_1>\mu_2)

v_1> v_2

(\mu_1<\mu_2)

r=0

t>0

r>0

t>0

r<0

t>0

notamos que pulso transmitido nunca é invertido. O pulso refletido é invertido se \(v_1 > v_2\).

Aplicação. Transmissão e Reflexão de ondas.

r=\frac{v_2-v_1}{v_2+v_1}

t=\frac{2v_2}{v_1+v_2}

A partir dos coeficientes de reflexão e transmissão:

A onda incidente é \(f\), a onda refletida é \(f_r\) e a transmitida é \(f_t\). Portanto,

f_r(x,t)=rf(x,t)

f_t(x,t)=tf(x,t)

r=\frac{v_2-v_1}{v_2+v_1}

t=\frac{2v_2}{v_2+v_1}

onde

Chamam-se de refletividade \(\rho\) e transmissividade \(\tau\) as alturas dos pulsos refletido e transmitido,

\rho=\frac{\overline{P_r}}{\overline{P_i}}

\tau=\frac{\overline{P_t}}{\overline{P_i}}

De modo que:

\rho+\tau = 1

\overline{P_r} + \overline{P_t} = \overline{P_i}

Aplicação. Transmissão e Reflexão de ondas.

A potência é conservada.

Você pode mostrar que a potência é conservada utilizando a expressão abaixo na refletividade e transmissividade, acima.

\overline{P} = \frac{1}{2}\mu v\omega^2 A^2

Uma onda em uma corda é dada pela função y(x,t) = 0,075 cos[1,05 x - 12,6 t].

(a) Mostre que essa função satisfaz a equação de onda.

(b) Suponha que a densidade linear da corda seja μ = 0,250 kg/m e que a tensão aplicada a corda seja F = 36,0 N, qual é a potência instantanea máxima?

Questão 1

Seja a função de onda y(x,t) = 1,0 cos[x+2t]. (a) Faça um gráfico y versus x dessa função para t = 0. (b) Sobre os mesmo eixos, faça um desenho da potência instantânea P(x,t). Considere uma tensão aplicada de 0,5 N. (c) Explique a relação entre o valor de P(x,t) e a inclinação da curva y(x,t) em função de x. Em particular, explique o que ocorre no ponto P = 0, no qual não existe nenhuma transferência de energia instantânea. (d) A grandeza P(x,t) possui sempre valor negativo. O que isso implica sobre o sentido da transferência de energia?

Questão 2

Uma das extremidades de uma corda de náilon está presa a um suporte fixo no topo de um poço vertical de uma mina com profundidade igual a 80,0 m. A corda fica esticada pela ação do peso de uma caixa de minérios com massa igual a 20,0 kg presa na extremidade inferior da corda. A massa da corda é igula a 2,0 kg. Um geólogo no fundo da mina, balançando a corda lateralmente, envia um sinal para seu colega que está no topo da mina.

(a) Qual é a velocidade da onda transversal que se propaga na corda?

(b) Considerando a massa da corda na extremidade inferior, no meio e na extremidade superior da corda.

Questão 3

Suponha que a declividade de uma praia abaixo da água seja de 12 cm de variação vertical por cada 1,0 m de distância horizontal. Uma onda se move em direção à terra e desacelera ao entrar em águas mais rasas. Qual será sua aceleração quando ela estiver a 10 m da linha da praia?

Questão 4

Questão 5

Você segura uma ponta de um barbante que está preso à parede pela outra ponta. A corda tem uma densidade de massa linear de 0,067 kg/m. Você eleva sua extremidade rapidamente a 12 m/s por 0,016 s, criando uma onda transversal que se move a 31 m/s. (a) Quanto trabalho você realizou na corda? Quais são (b) a energia, (c) a energia potencial e (d) a energia cinética da onda?

Questão 6

Dois fios de diferentes densidades lineares estão soldados um ao outro, pelas pontas, e depois submetidos a uma tração F (a mesma para os dois fios). A rapidez de onda no primeiro fio é o dobro daquela no segundo fio. Uma onda senoidal, viajando no primeiro fio, inicide sobre a emenda dos dois fios.

(a) Se a amplitude da onda incidente é A, quais são as amplitudes das ondas refletidas e transimitida?

(b) Qual é a razão entre as densidades de massa?

Uma corda com densidade de massa linear de 0,360 kg/m está presa a um oscilador harmônico que tem uma potência máxima de 200 W. (a) Com o oscilador operando nesta potência máxima e a tensão na corda fixada em 30,0 N, uma onda de amplitude de 8,00 × 10^(-3) m é criada. Qual é o comprimento de onda mínimo possível para uma onda desta amplitude? (b) Qual é a potência de saída do oscilador se a onda gerada tiver a mesma amplitude, mas o dobro do comprimento de onda calculado na parte a, e a tensão for 15,0 N?

Questão 7

Mostre que f(x, t) = e^b(x−vt), onde b e v são constantes, é uma solução para a equação da onda.

Questão 8

Motivação

Um pulso pode revelar o tipo de matéria a altas profundidades.

Basta estudar as transmissões e reflexões dos pulsos sonoros no meio.

Ondas. A equação da onda.

A rapidez de propagação na superfície de um líquido:

v=\sqrt{\frac{g\lambda}{2\pi}+\frac{2\pi \gamma}{\rho\lambda}}

h<<\lambda/2\pi

v=\sqrt{\frac{g\lambda}{2\pi}}

v\approx\sqrt{gh}

Fonte: Giphy

Ondas capilares (Galinhos)

Ondas de gravidade (Tsunamis)

h>>\lambda/2\pi

v=\sqrt{\frac{2\pi \gamma}{\rho\lambda}}

v\approx\sqrt{\frac{\gamma}{\rho\,h}}

Em mar aberto, onde a profundidade é de h ~ 5 km, o comprimento de onda é da ordem de \(\lambda\) ~ 100 km:

\frac{h}{\lambda}=\frac{5}{100}\Rightarrow v = \sqrt{gh} = 221\text{m/s}

Em baías, onde a profundidade é de h ~ 10 m, o comprimento de onda é da ordem de \(\lambda\) ~ 2 cm:

\frac{h}{\lambda}=50\Rightarrow v = \sqrt{\frac{2\pi\gamma}{\rho\lambda}}= 0,15\text{ m/s}

\(\gamma\) é a tensão superficial do fluido (newton/metro): LINK

As condições iniciais e as condições de contorno

O problema típico da teoria ondulatória é encontrar a solução geral

\Psi(x,0)=f_0(x)

# O deslocamento inicial (perfil):

As condições de contorno:

# A velocidade inicial (repouso):

\frac{\Psi(x,0)}{\partial t}=0

# Extremidades fixas (deslocamento nulo):

\Psi(0,t)= \Psi(L,t)=0

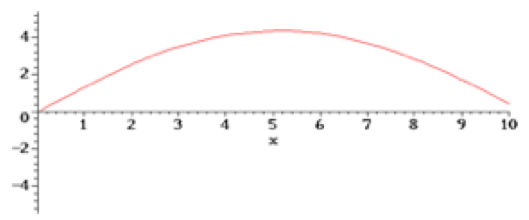
As condições iniciais.

que deve satisfazer a equação da onda. Isto é, a razão entre a curvatura e aceleração deve ser um número independente de x e t, a rapidez da onda.

É necessário especificar algumas condições físicas para se conhecer as amplitudes: \(c_1,c_2\)

\Psi(x,t)=c_1y_1(x,t)+c_2y_2(x,t)

\Psi(0,t)=0

\Psi(10,t)=0

\Psi(x,t)=f_0(x)

Geralmente, em \(t = 0\).

Geralmente, nos extremos.

A solução geral de d'Alembert

Dada a equação de onda,

qualquer solução é uma superposição de uma onda progressiva que se propaga para a direita com uma onda progressiva que se propaga para a esquerda.

\frac{\partial^2 \Psi(x,t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 \Psi(x,t)}{\partial t^2}

\Psi(x,t)=f(x-vt)+g(x+vt)

# uma onda progressiva que se propaga para a direita (\(f(x-vt)\)).

# uma onda progressiva que se propaga para a esquerda (\(g(x+vt)\)).

Essa solução geral é a solução de d'Alembert.

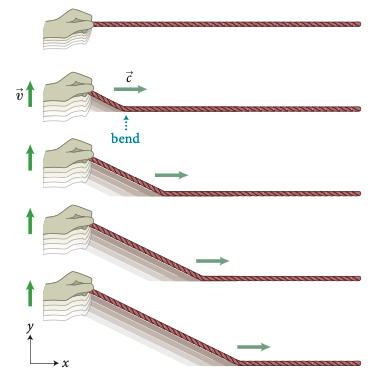
Fonte: https://youtu.be/9O3VEXzuOKI

A solução geral de d'Alembert

Suponhamos que a corda tenha um perfil inicial triangular. Como será o momento futuro?

\Psi(x,0)=f_0(x)

é solto a partir do repouso (velocidade inicial):

\frac{\Psi(x,0)}{\partial t}=0

A solução geral tem a forma:

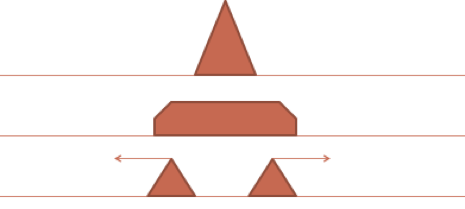
Fonte: https://www.geogebra.org/m/jfhMWxak

\Psi(x,t)=\frac{1}{2}f_0(x-vt)+\frac{1}{2}f_0(x+vt)

Simule

A condição inicial (perfil):

f_0(x)

\frac{1}{2}f_0(x-vt)

\frac{1}{2}f_0(x+vt)

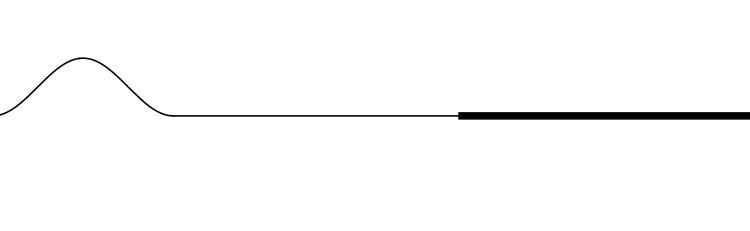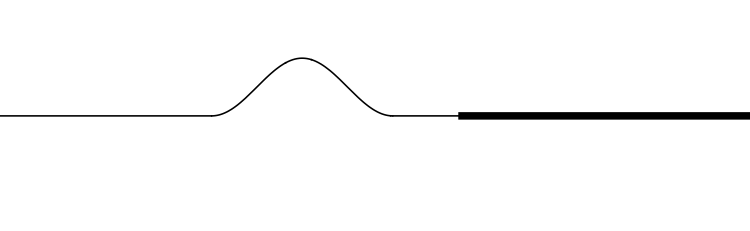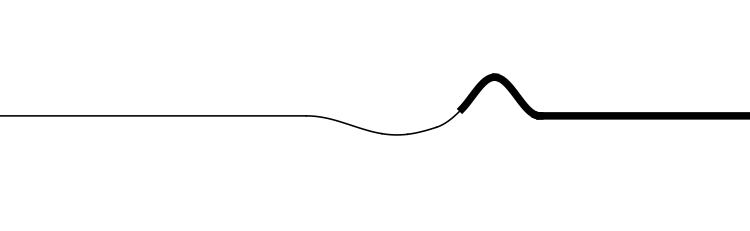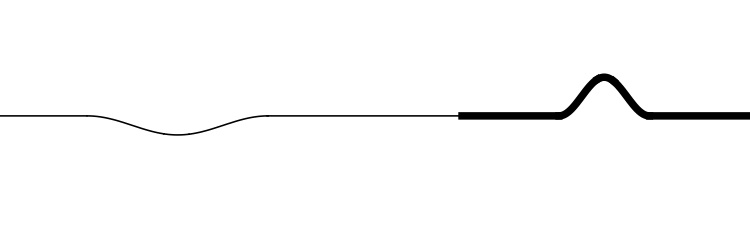
Um pulso atinge a extremidade fixa de uma corda muito longa com extremidade fixa na parede.

A solução de D'Alembert:

A condição de contorno (na parede), \(\forall \,t\):

\Psi(x,t)=g(x+vt)+f(x-vt)

\Psi(0,t)=0

A condição inicial, \(t=0\):

f(x-vt)\neq 0

g(x+vt)= 0

A solução do problema:

\Psi(x,t)=g(x+vt)-g(-x+vt)

Fonte: https://www.geogebra.org/m/t3neXVU8

x=0

O pulso reflete invertido. Na reflexão, em uma extremidade fixa há uma inversão do pulso.

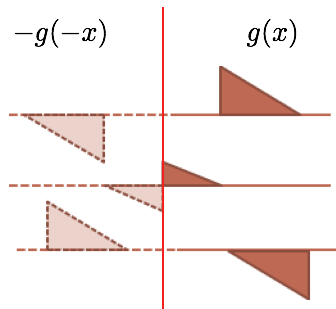
Aplicação. Transmissão e Reflexão de ondas.

x<0

x>0

Aplicação. Transmissão e Reflexão de ondas.

A solução de D'Alembert:

A condição de contorno, \(\forall \,t\):

\Psi(x,t)=g(x+vt)+f(x-vt)

\frac{\partial \Psi(0,t)}{\partial x}=0

A condição de contorno, \(x=0\):

A solução do problema:

\Psi(x,t)=g(-x+vt)+g(x+vt)

Fonte: https://www.geogebra.org/m/t3neXVU8

x=0

O pulso reflete sem inversão. Na reflexão, em uma extremidade livre não há uma inversão do pulso.

\Rightarrow f'(-vt)+g'(+vt)=0

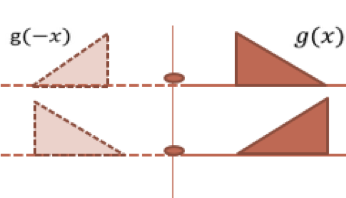
Um pulso atinge a extremidade fixa de uma corda muito longa com extremidade livre na parede.

Questão 7

Dada a EDO y’’ + 2 y = 0,

a) Mostre que y(x) = c1 cos (√2 x) + c2 sen (√2 x) satisfaz a EDO.

b) Aplique as condições de contorno y(0) = 1 e y(π) =0 à função e determine os coeficientes c1 e c2.

Atenção: A EDO não tem a forma da equação de onda. Esse exercício tem o objeto do aprendizado na aplicação de condições de contorno.