Aula 10

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 16 - Som e Audição

Seções: 16.6, 16.7.

Explicar a superposição de ondas sonoras de fontes diferentes (interferência).

Calcular a frequência e período de batimento.

Interpretar o significado de diferença de fase.

Interpretar o significado de diferença de caminho.

Motivação

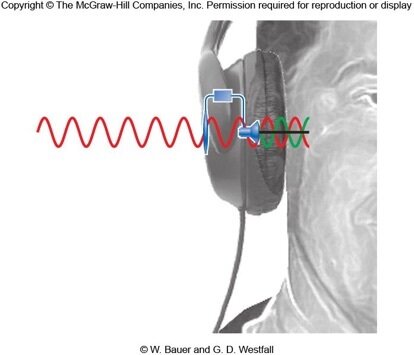
Uma onda senoidal chega ao fone de ouvido e é registrada por um microfone. Um processador inverte a fase dessa onda sonora e emite para fora a onda sonora de mesma frequência e amplitude, mas de fase oposta.

As duas ondas senoidais interferem destrutivamente.

Ao mesmo tempo, o autofalante no interior dos fones de ouvido emite a música que você quer ouvir, e o resultado é uma experiência de audição livre do ruído de fundo quando as frequências não são muito elevadas.

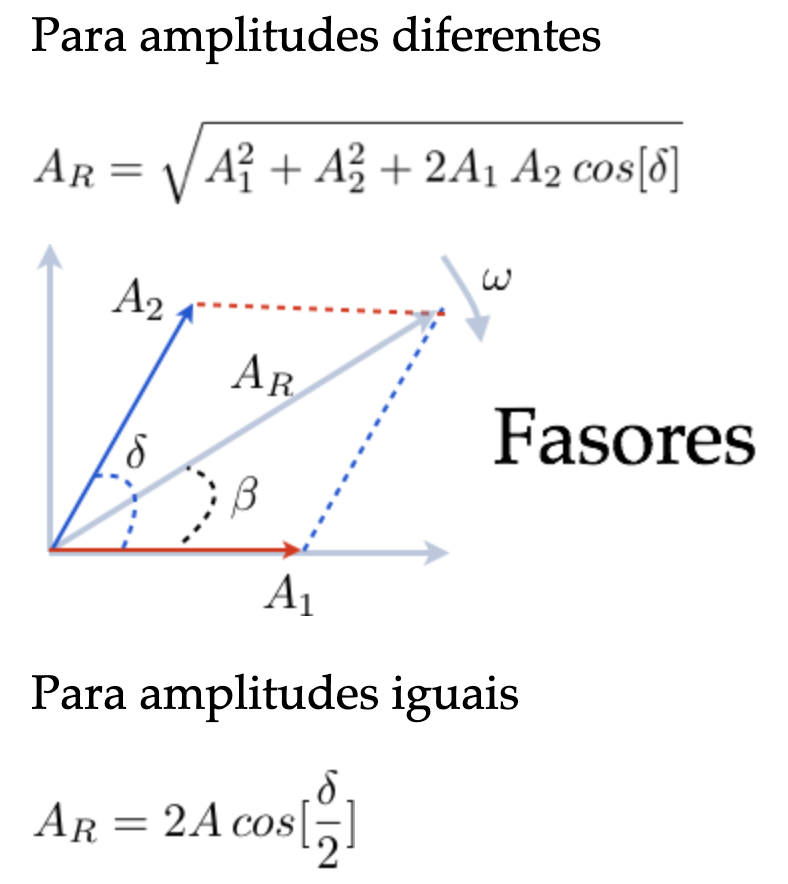
Propriedades Trigonométricas

Vamos precisar de algumas propriedades trigonométricas:

D\text{ sen}[A+B]+ D\text{ sen}[A-B]= 2D\text{ sen}[A]\cos[B]

D\text{ cos}[A+B]+ D\text{ sen}[A-B]= 2D\text{ cos}[A]\cos[B]

\text{ cos}[A-B]+ \text{ cos}[C-D]= 2 \text{ cos} \left [ \frac{A+C}{2}- \frac{B+D}{2} \right] \text{ cos} \left [ \frac{A-C}{2}- \frac{B-D}{2} \right]

\text{ sen}[A-B]+ \text{ sen}[C-D]= 2 \text{ sen} \left [ \frac{A+C}{2}- \frac{B+D}{2} \right] \text{ cos} \left [ \frac{A-C}{2}- \frac{B-D}{2} \right]

Vamos aplicar os conhecimentos prévios nos estudos das ondas harmônicas.

Interferência de ondas harmônicas

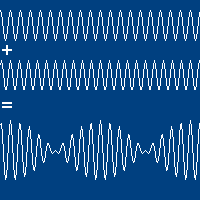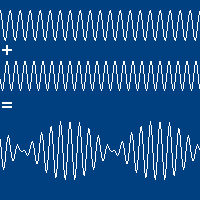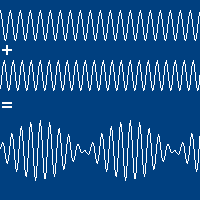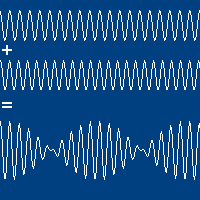
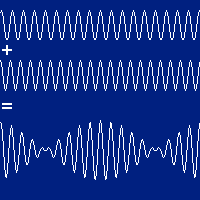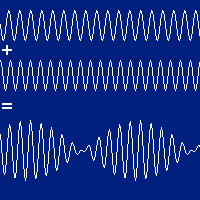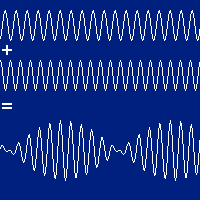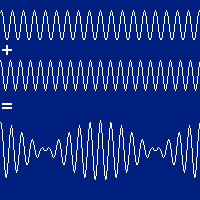
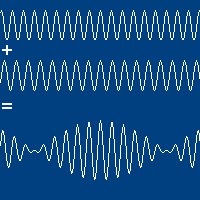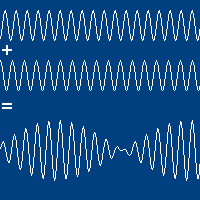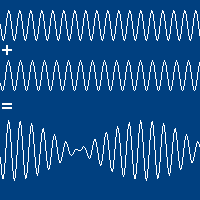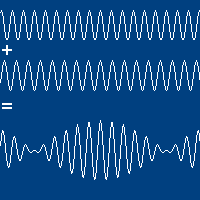
Fenômeno de batimento

Fonte: https://youtu.be/Y5gkI6joisI

O batimento é percebido auditivamente (som) quando as ondas progressivas têm:

# mesma amplitude,

# mesmo sentido de propagação,

# mas frequências ligeiramente diferentes.

A onda resultante é envelopada e possui um velocidade de propagação diferente (velocidade de grupo) da velocidade de propagação das ondas originais (velocidade de fase).

v_{grupo}

v_{fase}

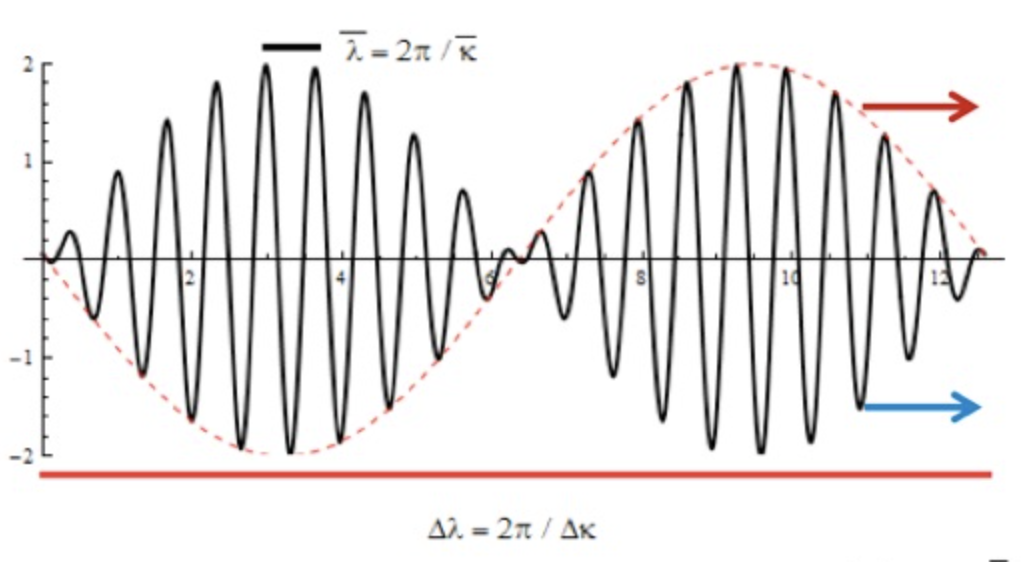
Interferência de ondas harmônicas

São geradas e percebidas quando as ondas progressivas têm mesma amplitude, mesmo sentido de propagação, mas frequências ligeiramente diferentes. O número de onda vai afetar a envoltória.

Fenômeno de batimento

y_1(x,t)=A_1\cos(k_1x-\omega_1 t)

y_2(x,t)=A_2\cos(k_2x-\omega_2 t)

Atribuindo:

A_1 = A_2

\omega_1 > \omega_2

k_1 > k_2

A onda resultante é a soma algébrica (superposição):

y_r(x,t)=2A\cos\left[ \frac{1}{2}\left( k_1-k_2 \right)x - \frac{1}{2}\left( \omega_1-\omega_2 \right)t \right] \cos\left[ \frac{1}{2}\left( k_1+k_2 \right)x - \frac{1}{2}\left( \omega_1+\omega_2 \right)t \right]

com:

\Delta \omega =\omega_1-\omega_2 << \overline{\omega} = \frac{\omega_1+\omega_2}{2}

\Delta k = k_1-k_2 << \overline{k}=\frac{k_1+k_2}{2}

Fonte: https://www.compadre.org/

Simule:

k_1=2,2\text{ rad/m}

\omega_1=1,2\text{ rad/s}

k_2=2,0\text{ rad/m}

\omega_2=1,0\text{ rad/s}

A_1=A_2=1,0\text{ m}

Propriedade 3

Interferência de ondas harmônicas

A amplitude da onda resultante é modulada pela envoltória.

Fenômeno de batimento

Define-se a frequência e o período de batimento, a diferença entre as frequências de cada onda,

y_r(x,t)=2A\cos\left[ \frac{\Delta k}{2}x - \frac{\Delta \omega}{2}t \right] \cos\left[ \overline{k}x - \overline{\omega} t \right]

com:

\Delta \omega << \overline{\omega}

Fonte: https://www.compadre.org

y_r(x,t)=a(x,t) \cos\left[ \overline{k}x - \overline{\omega} t \right]

T_{bat} = \frac{1}{f_2-f_1}

f_{bat} = \frac{\Delta \omega}{2\pi}=f_2-f_1

f_1 = 438 \text{Hz}

f_2 = 440 \text{Hz}

f_1 = 300 \text{Hz}

f_2 = 305 \text{Hz}

Simule:

f_1 = 400 \text{Hz}

f_2 = 440 \text{Hz}

Frequência ouvida

Frequência de batimento

Intervalo entre os máximos que são ouvidos

ou entre dois mínimos consecutivos

Interferência de ondas harmônicas

Há outros dois conceitos importantes no batimento:

Fenômeno de batimento

A velocidade de fase:

Fonte:

b(x,t)=\overline{k}x-\overline{\omega t}

v_f=\frac{\overline{\omega}}{\overline{k}}

A velocidade de grupo:

a(x,t)=\frac{\Delta k}{2}x-\frac{\Delta\omega}{2}t

v_g=\frac{d\omega}{dk}

\Delta \omega << \overline{\omega}

\Delta k<< \overline{k}

\Delta \lambda>> \overline{\lambda}

v_g>v_f

v_g< v_f

v_g=- v_f

Fonte: http://omnis.if.ufrj.br/~pef

Artigos interessantes sobre a luz em metamateriais:

LINK. LINK.

v_f

v_g

Interferência de ondas harmônicas

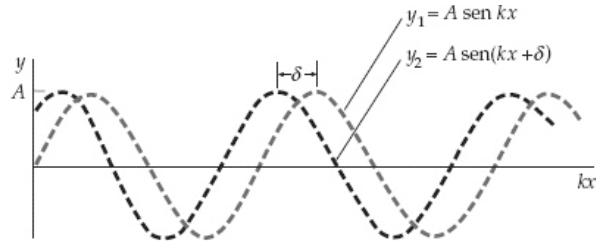
Diferença de fase: Interferências construtiva e destrutiva.

A onda resultante é progressiva com mesma rapidez e sentido de propagação das ondas originais.

\Delta \delta = \delta_1-\delta_2

A amplitude não oscilatória é dada por:

A_r = 2A\cos\left( \frac{\Delta \delta}{2} \right)

Para que valores de \(\Delta \delta\) a amplitude resultante será nula e não nula?

As ondas progressivas têm o mesmo sentido de propagação e constante de fase diferentes.

y_1(x,t) = A\cos[kx-\omega t+\delta_1]

y_2(x,t) = A\cos[kx-\omega t+\delta_2]

\delta_1 \neq \delta_2

Chamando, os parâmetros comuns por:

a=kx-\omega t

y_1(x,t) = A\cos[a+\delta_1]

y_2(x,t) = A\cos[a+\delta_2]

A onda resultante é a superposição das ondas originais:

y_r(x,t) = 2A\cos\left( \frac{\Delta \delta}{2} \right)\cos[kx-\omega t+\overline{\delta}]

y_1

y_2

Propriedade 3

Interferência de ondas harmônicas

A interferência pode ser construtiva:

Diferença de fase: Interferências construtiva e destrutiva.

As ondas estão em fase.

\cos\left( \frac{\Delta \delta}{2} \right)=1

\rightarrow \left( \frac{\Delta \delta}{2} \right)=n\pi\,,

A onda resultante fica:

y_r(x,t) = 2A.1.\cos[kx-\omega t+\overline{\delta}]

A amplitude resultante é o dobro das amplitudes das ondas originais:

Fonte: https://www.compadre.org/

y_r(x,t) = 2A\cos[kx-\omega t+\overline{\delta}]

Simule:

k_1=k_2=2,0\text{ rad/m}

\omega_1=\omega_2=1,2\text{ rad/s}

\delta_1=0\text{ rad}

\delta_2=2\pi\text{ rad}

A_1=A_2=1,0\text{ m}

A_r = 2A\cos\left( \frac{\Delta \delta}{2} \right)=2A

\Delta \delta = 2\pi\text{ rad}

\rightarrow \Delta \delta = 2n\pi

para \(n=0\,\pm 1,\pm 2,\cdots\)

Interferência de ondas harmônicas

A interferência pode ser destrutiva:

Diferença de fase: Interferências construtiva e destrutiva.

As ondas estão em oposição de fase.

\cos\left( \frac{\Delta \delta}{2} \right)=0

\rightarrow \left( \frac{\Delta \delta}{2} \right)=\left(n+\frac{1}{2}\right)\pi\,,

A onda resultante fica:

y_r(x,t) = 2A.0.\cos[kx-\omega t+\overline{\delta}]

A amplitude resultante é nula (\(A_r=0\) ).

Fonte: https://www.compadre.org/

y_r(x,t) = 0

Simule:

k_1=k_2=2,0\text{ rad/m}

\omega_1=\omega_2=1,2\text{ rad/s}

\delta_1=0\text{ rad}

\delta_2=\pi\text{ rad}

A_1=A_2=1,0\text{ m}

A_r = 2A\cos\left( \frac{\Delta \delta}{2} \right)=0

\Delta \delta = \pi\text{ rad}

\rightarrow \Delta \delta = \left(2n+1\right)\pi

para \(n=0\,\pm 1,\pm 2,\cdots\).

Interferência de ondas harmônicas

Fonte: https://youtu.be/Fgnq5ZVZCbM

Para duas fontes sonoras (alto-falantes) podemos ouvir (ver) ou não ouvir (não ver) a pertrubação dependendo da posição onde nos encontramos em relação as fontes.

Uma causa comum de defasagem entre duas ondas é a diferença de comprimentos dos caminhos entre as fontes das ondas e o ponto onde ocorre interferência.

Fonte: https://youtu.be/1aph8nCEv7s

A propagação de ondas esféricas e planas

Interferência de ondas harmônicas

A diferença de fase resulta de uma diferença de caminho e de uma diferença da constante de fase.

As duas fontes (1) e (2) oscilam como ondas harmônicas de mesmo número de onda (\(k_1=k_2=k\)) e frequência (\(\omega_1=\omega_2=\omega\)), pois têm uma fonte em comum.

\Delta \Phi =

k\Delta x

+\frac{(\delta_2-\delta_1)}{2}

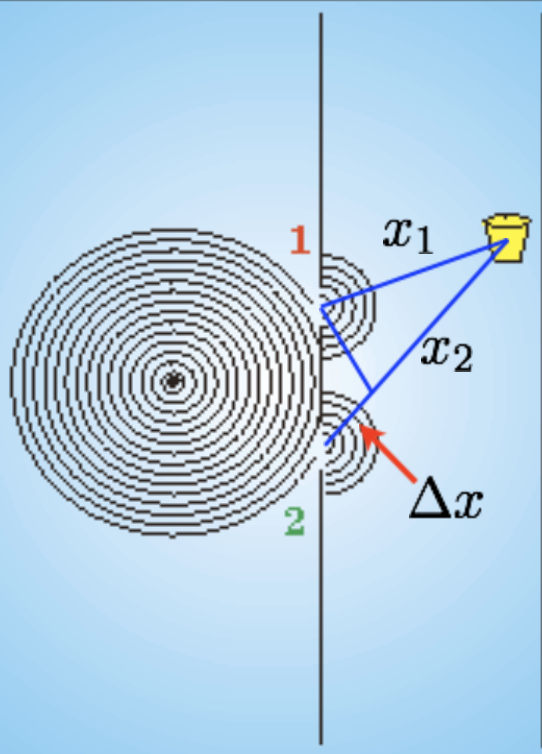
Fonte: Wolfgang & Bauer

fase 1: \(\delta_1\)

fase 2: \(\delta_2\)

fonte original: \(\omega\)

y_1(x_1,t) = A\cos[kx_1-\omega t+\delta_1]

y_2(x_2,t) = A\cos[kx_2-\omega t+\delta_2]

O caminho percorrido pelas ondas até o balde! é diferente para cada fonte.

x_1\neq x_2

As ondas são coerentes quando:

Para cada fonte note que \(x_1\neq x_2\):

\Delta \Phi =

\frac{2\pi}{\lambda}\Delta x

+\frac{(\delta_2-\delta_1)}{2}

Mostre que a diferença de fase é o argumento da amplitude da onda resultante

\delta_2 - \delta_1 = 0

\delta_2 - \delta_1=\text{constante}

Interferência de ondas harmônicas

A diferença de fase resulta de uma diferença de caminho e de uma diferença da constante de fase.

As interferências construtiva ou destrutiva pode ocorrer devido a uma diferença de caminho ou a uma diferença de fase:

\Delta \Phi =

\Delta \delta/2

\frac{2\pi}{\lambda}\Delta x

\Delta \Phi =

\frac{2\pi}{\lambda}(x_2-x_1)

+\,\frac{(\delta_2-\delta_1)}{2}

Diferença de caminho

Fonte: https://youtu.be/RR4oXgQKGQ0

Diferença de constante de fase

Fonte: https://youtu.be/ISRUTFrrXfA

\delta_2 - \delta_1 = 0

x_2 - x_1 = 0

Interferência de ondas harmônicas

Para fontes coerentes:

2n\pi=

\frac{2\pi}{\lambda}\Delta x

\Delta \Phi =

A interferência é construtiva, se:

é um múltiplo inteiro do comprimento de onda.

A intensidade da onda é máxima: \(I=4A^2\).

\Delta \Phi = 2n\pi

A diferença de caminho:

\delta_1

\delta_2

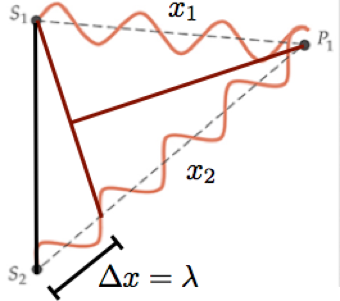
A interferência é construtiva em P1.

\Delta x = n\lambda\,,

n=0\,\pm 1,\pm 2,\cdots

Fonte: Tipler

Fonte: Sears

Amplitudes em fase (p/ cima ou p/baixo)

Interferência de ondas harmônicas

Para fontes coerentes:

\left(2n+1\right)\pi=

\frac{2\pi}{\lambda}\Delta x

\Delta \Phi =

A interferência é destrutiva, se:

é um múltiplo semi-inteiro do comprimento de onda.

A intensidade da onda é nula: \(I=0\).

\Delta \Phi = \left(2n+1\right)\pi

A diferença de caminho:

\delta_1

\delta_2

A interferência é destrutiva em P2.

\Delta x =\left( n+\frac{1}{2}\right)\lambda\,,

n=0\,\pm 1,\pm 2,\cdots

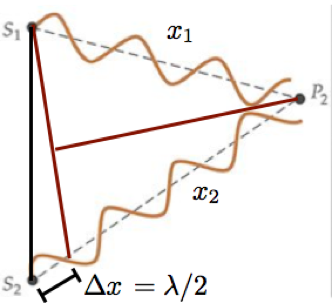
Fonte: Tipler

Fonte: Sears

Amplitudes em oposição de fase (p/ cima e p/baixo)

Interferência de ondas harmônicas

A interferência de duas fontes coerentes

Padrões de interferências em ondas esféricas cujas fontes estão separadas por uma certa distância.

\Delta x = n\lambda

\Delta x = \left(n+\frac{1}{2}\right)\lambda

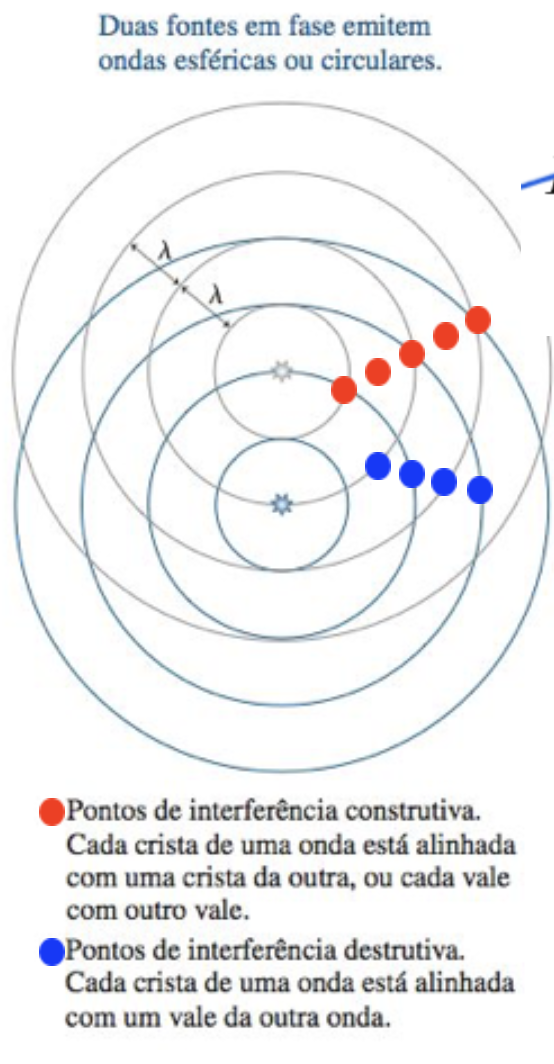
Onde as cristas e cristas (ou vales e vales) se sobrepõem, as ondas interferem construtivamente:

\Delta \Phi = 2n\pi

Onde as cristas e os vales se sobrepõem, as ondas interferem destrutivamente:

\Delta \Phi = \left(n+\frac{1}{2}\right)\,2\pi

Fonte: Bauer

Interferência de ondas harmônicas

Interferência construtiva:

\Delta x = n\lambda

\Delta x = \left(n+\frac{1}{2}\right)\lambda

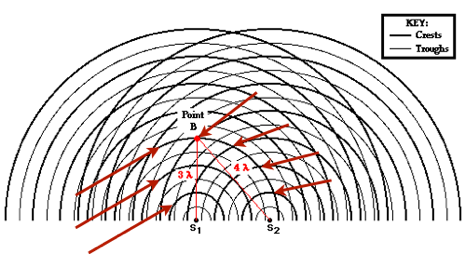
Fonte: Bauer

Interferência destrutiva:

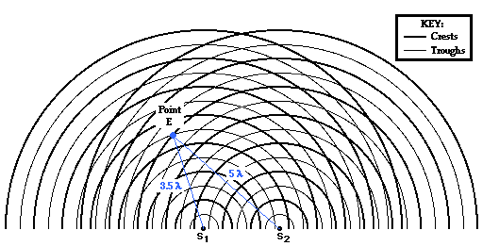
A interferência de duas fontes coerentes

Interferência de ondas harmônicas

Calculando o padrão de interferência do experimento de Young: Dupla Fenda.

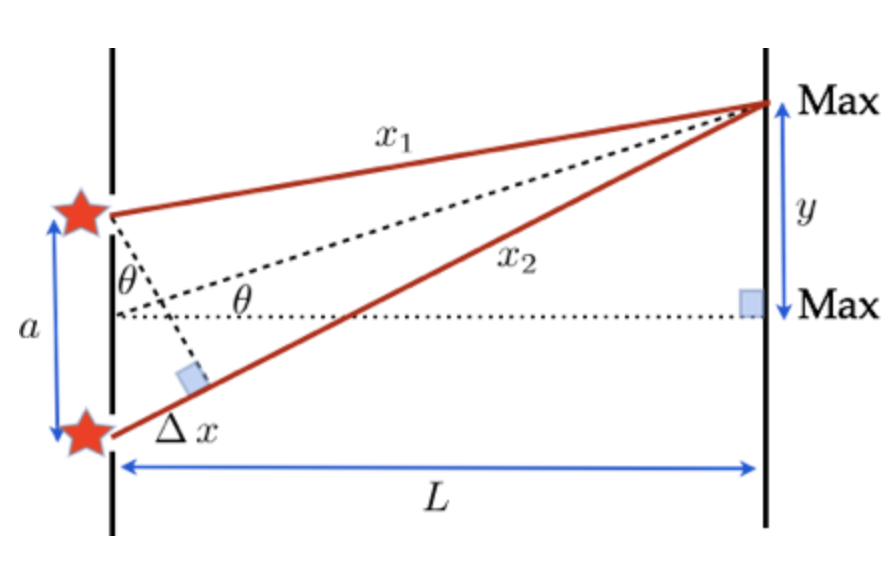
A diferença de caminho é \(\Delta x\).

\text{sen}\theta = \frac{\Delta x}{a}

\Delta x = a\text{ sen }\theta

Se a separação entre as fontes é menor do que a distância até o anteparo:

a << L

\text{sen }\theta \approx \tan \theta

\Delta x = a\text{ tan }\theta

\Delta x = a\frac{y}{L}

BRILHO:

\Delta x = n\lambda

y = \frac{nL\lambda}{2}

SOMBRA:

\Delta x = \left(n+\frac{1}{2}\right)\lambda

y =\frac{(2n+1)}{2}\frac{L\lambda}{a}

\Delta y = \frac{L\lambda}{a}

A distância entre Brilho e Sombra:

Interferência de ondas harmônicas

Calculando o padrão de interferência do experimento de Young: Dupla Fenda.

BRILHO:

\Delta x = n\lambda

y = \frac{nL\lambda}{2}

SOMBRA:

\Delta x = \left(n+\frac{1}{2}\right)\lambda

y =\frac{(2n+1)}{2}\frac{L\lambda}{a}

\Delta y = \frac{L\lambda}{a}

A distância entre Brilho e Sombra:

Fonte: https://www.geogebra.org/m/G7Yrkr8Z

Interferência de ondas harmônicas

Ondas na água, som no ar ou a luz no ar produzidos por dois único geradores separados e em fase.

FONTE: PHET

Construtiva

\Delta x = n\lambda

Destrutiva

\Delta x = \left(n+\frac{1}{2}\right)\lambda

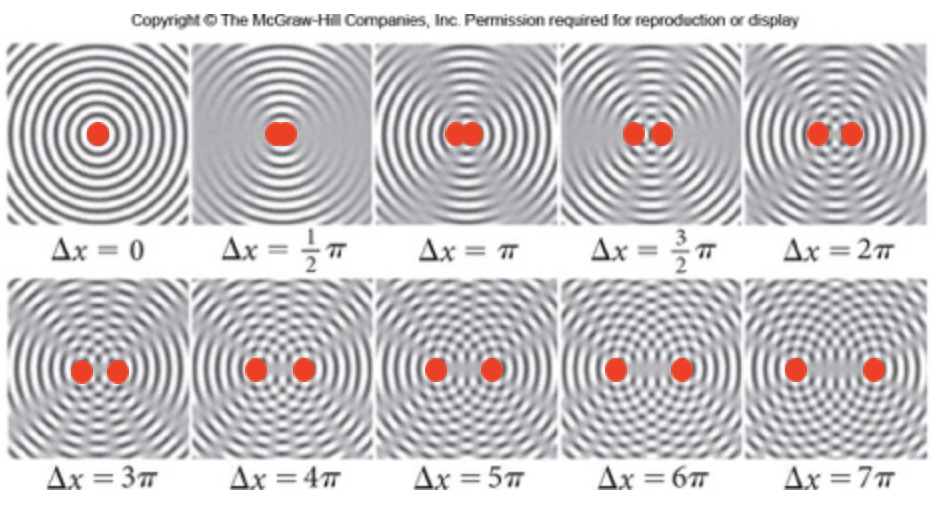
Fonte: Bauer

Calculando o padrão de interferência do experimento de Young: Dupla Fenda.

Questão 1

Um flautista toca a nota de 510 Hz enquanto um segundo flautista toca a nota de 512 Hz. Que freqüência você escuta? Qual é a freqüência de batimento?

Questão 2

Você escuta três batimentos por segundo quando dois tons musicais são tocados simultaneamente. A freqüência de um tom é 610 Hz. Qual é a freqüência do outro ?

Questão 3

Dois alto-falantes emitem ondas sonoras de 500 Hz com amplitude de 0,10 mm. O alto-falante 2 encontra-se 1,00 m atrás do alto-falante 1, e a diferença de fase entre eles é de 90 graus. Qual é a amplitude da onda sonora escutada em um ponto 2,00 m à frente do alto-falante 1.

R-ex21-9

Questão 4

Dois alto-falantes posicionados em um plano estão separados por 2,0 m e em fase um com o outro. Ambos emitem ondas sonoras de 700 Hz em um ambiente onde a velocidade do som é 341 m/s. Um ouvinte encontra-se parado a 5,0 m à frente dos alto-falantes e a 2,0 m da reta perpendicular ao plano onde estão os alto-falantes e que passa pelo ponto médio entre os mesmos.

(a) Neste ponto, a interferência é totalmente construtiva, totalmente destrutiva ou intermediária?

(b) Como mudará a situação se os alto-falantes estiverem fora de fase?

R-ex21-11

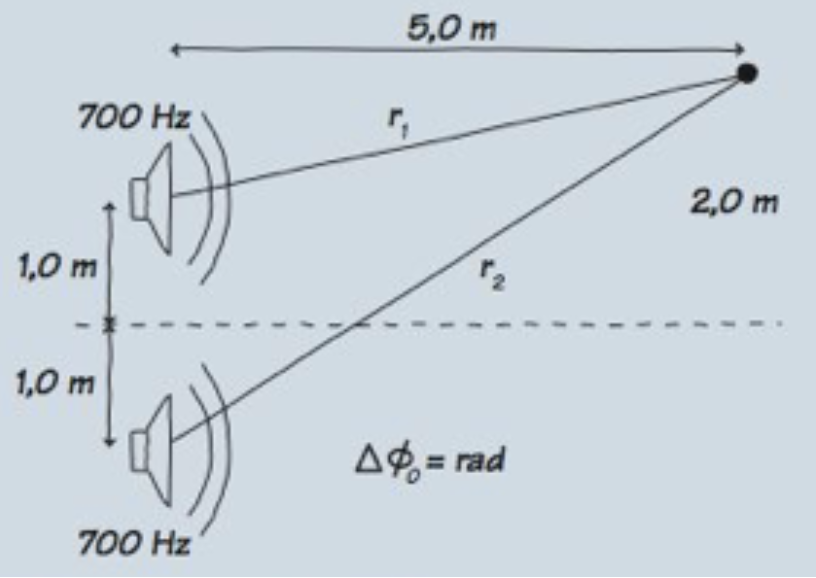
Questão 5

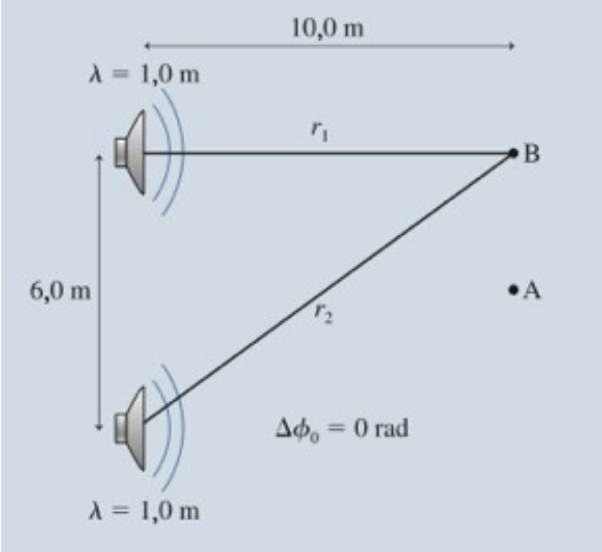
Dois alto-falantes posicionados em um plano estão separados por 6,0 m de distância e em fase. Ambos emitem ondas sonoras de mesma amplitude e comprimento de onda de 1,0 m. Cada alto-falante emite um som de intensidade I0. Um observador parado no ponto A encontra-se 10 m à frente do plano que contém os dois alto-falantes, centralizado em relação aos mesmos. Um segundo observador, parado no ponto B, encontra-se 10 m diretamente à frente de um dos alto-falantes. Em função de I0, quais são a intensidade IA no ponto A e a intensidade IB no ponto B? R-ex21-12

Questão 6

Duas ondas senoidais y1(x,t) e y2(x,t) têm o mesmo comprimento de onda e se propagam no mesmo sentido em uma corda. As amplitudes são A1(x,t) = 4,0 mm e A2(x,t) = 3,0 mm, e as constantes de fase são 0 e π/3 rad, respectivamente. Quais são a amplitude e a constante de fase delta da onda resultante? Escreva a onda resultante.

Interferência de ondas harmônicas

A propagação de ondas esféricas e planas

Fonte: https://youtu.be/wg04p9QI8f8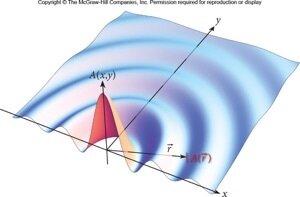

y(r,t)=\frac{A}{r}\text{sen}(kr-\omega t+\delta)

As frentes de onda correspondem às cristas, separadas pelos comprimentos de onda \(\lambda\).

Os vales situam-se a meio caminho entre as frentes de onda vizinhas.

Para mais de uma fonte podemos observar os fenômenos de interferência.

Esféricas

Fonte: Wolfgang & Bauer

y(r,t)=A\text{sen}(kr-\omega t+\delta)

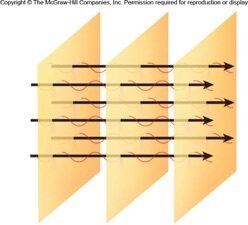
Planas

Fonte: Wolfgang & Bauer