Aula 11

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 16 - Som e Audição

Seções:

Explicar o efeito Doppler.

Explicar o cone de Mach.

Motivação

Fonte: https://youtu.be/Djz_rtnXSfY

As variações de frequências relacionadas ao movimento relativo são exemplos do efeito Doppler e ao cone de Mach para velocidades supersônicas.

Fonte: https://youtu.be/gWGLAAYdbbc

O efeito Doppler sonoro

A aproximação entre (D) e (F) leva ao aumento da frequência: \(f_D > f_F\).

f_D = f_F

\frac{v_s\pm v_D}{v_s\pm v_F}

velocidade do detector em relação ao ar

velocidade do som no ar

frequência do detector

frequência da fonte

velocidade da fonte em relação ao ar

Para o movimento do detector (D) e da fonte (F) a relação entre as frequências é:

O afastamento entre (D) e (F) leva a diminuição da frequência: \(f_D < f_F\).

f_D = f_F

\frac{v_s+ v_D}{v_s- v_F}

f_D = f_F

\frac{v_s- v_D}{v_s+v_F}

Som fica agudo

Som fica grave

O efeito Doppler sonoro

f_D = f_F

\frac{v_s\pm v_D}{v_s\pm v_F}

Para o movimento do detector (D) e da fonte (F) a relação entre as frequências é:

Fonte: https://www.compadre.org/osp/EJSS/3858/38.htm?F=1

O efeito Doppler sonoro

A velocidade da onda sonora depende somente do meio de propagação, \(v_s\).

A fonte (F) e o detector (D) parados em relação ao ar.

A distância entre duas cristas é o comprimento de onda, \(\lambda_0\).

f_D = f_F

\frac{v_s\pm v_D}{v_s\pm v_F}

\Rightarrow f_D = f_F

O tempo de propagação entre duas cristas é o período, \(T_0\).

O número de cristas emitidas por unidade de tempo é a frequência, \(f_0\).

Em qualquer local

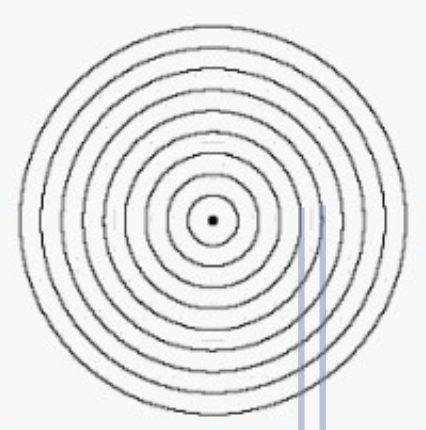
Fonte: https://www.geogebra.org/m/ffscYCRM

Fonte: Animation courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State

O efeito Doppler sonoro

A fonte (F) e o detector (D) parados em relação ao ar.

f_D = f_F

\frac{v_s\pm v_D}{v_s\pm v_F}

\Rightarrow f_D = f_F

Fonte: http://www.compadre.org/osp/items/detail.cfm?ID=7902

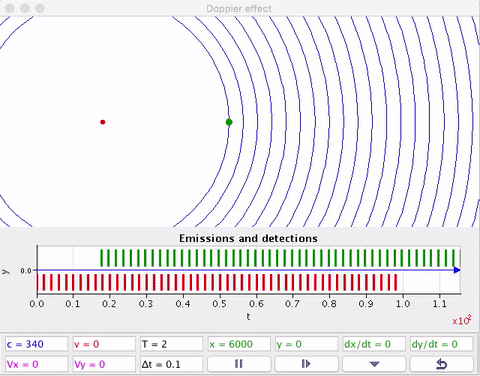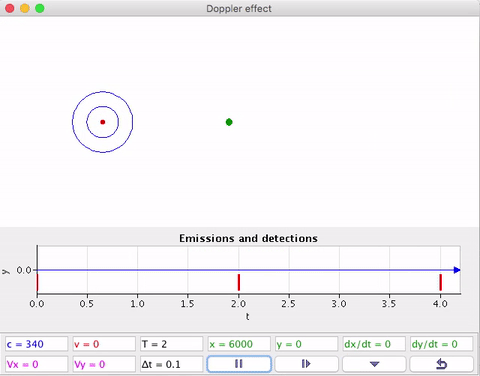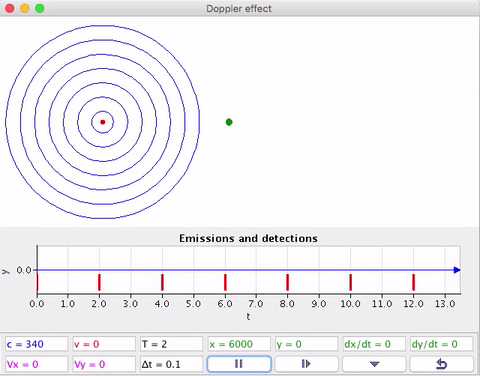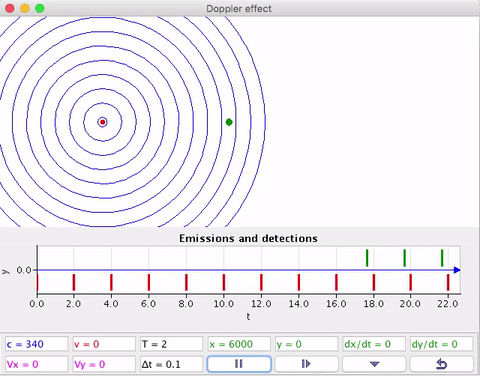
O efeito Doppler sonoro

O Detector em movimento intercepta frentes de onda quando se aproxima ou se afasta da Fonte em repouso.

A fonte (F) estacionária e o detector (D) em movimento em relação ao ar.

f_D = f_F

\frac{v_s\pm v_D}{v_s\pm v_F}

\Rightarrow f_D = f_F

Portanto, a frequência da onda sonora detectada é alterada.

A frequência aumenta ( + ) ou diminui ( - ) se o Detector se aproxima ou se afasta, respectivamente da Fonte que está parada.

\frac{v_s\pm v_D}{v_s}

Fonte: https://www.geogebra.org/m/ffscYCRM

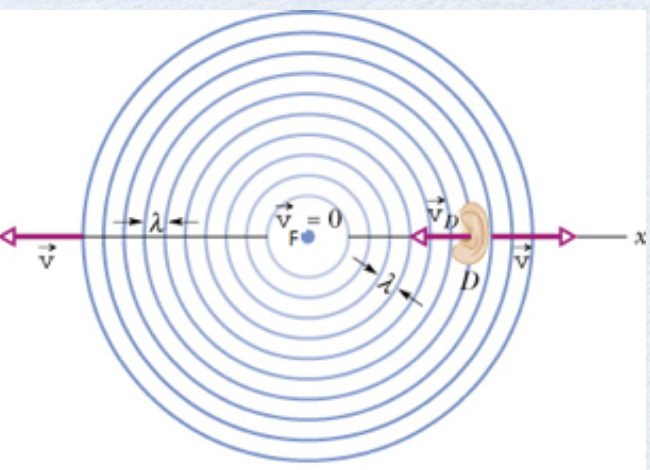
Fonte: Halliday & Resnick

O efeito Doppler sonoro

A fonte (F) estacionária e o detector (D) em movimento em relação ao ar.

\Rightarrow f_D = f_F

\frac{v_s - v_D}{v_s}

\Rightarrow f_D = f_F

\frac{v_s + v_D}{v_s}

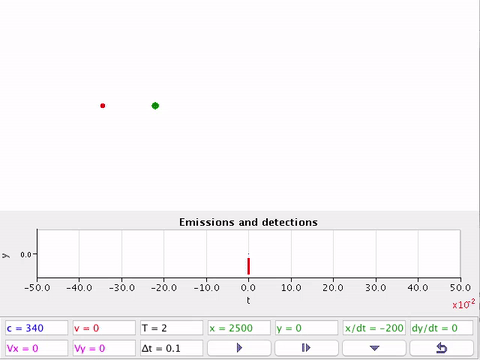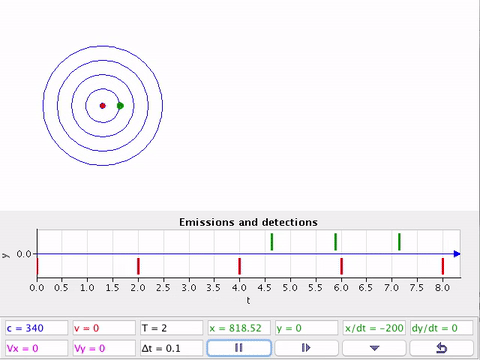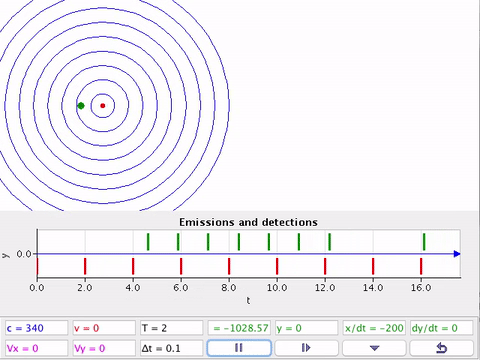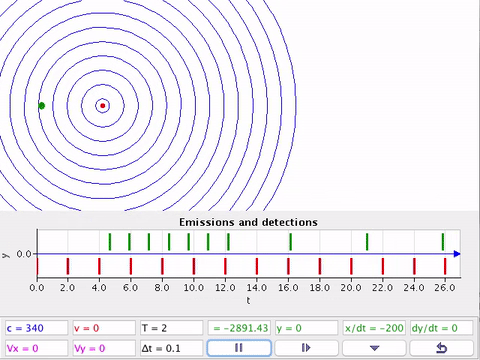
No afastamento intercepta menos frentes de onda. A frequência detectada parece diminuir. (Sinal - )

Na aproximação intercepta mais frentes de onda. A frequência detectada parece aumentar. (Sinal + )

Fonte: http://www.compadre.org/osp/items/detail.cfm?ID=7902

O efeito Doppler sonoro

O movimento da fonte altera o comprimento de onda da onda sonora. Portanto, altera a frequência detectada.

A fonte (F) em movimento e o detector (D) estacionário em relação ao ar.

f_D = f_F

\frac{v_s\pm v_D}{v_s\pm v_F}

\Rightarrow f_D = f_F

A frequência aumenta ( - ) ou diminui ( + ) se a Fonte se aproxima ou se afasta, respectivamente do Decetor que está parado.

\frac{v_s}{v_s\pm v_F}

Fonte: https://www.geogebra.org/m/ffscYCRM

Fonte: Halliday & Resnick

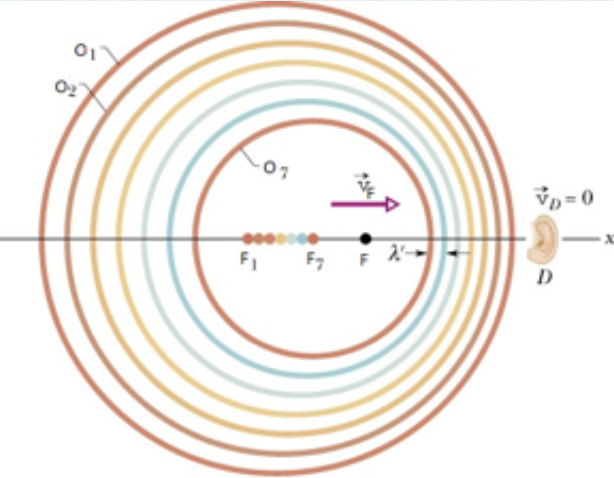
O efeito Doppler sonoro

A fonte (F) em movimento e o detector (D) estacionário em relação ao ar.

\Rightarrow f_D = f_F

\frac{v_s}{v_s+ v_F}

Fonte: http://www.compadre.org/osp/items/detail.cfm?ID=7902

\Rightarrow f_D = f_F

\frac{v_s}{v_s- v_F}

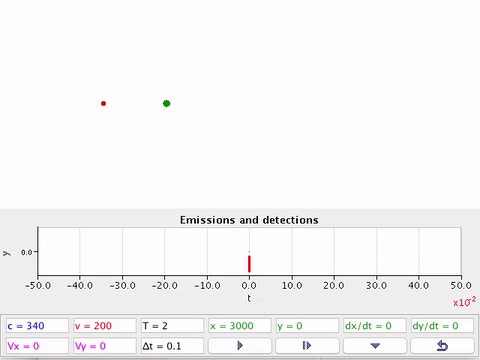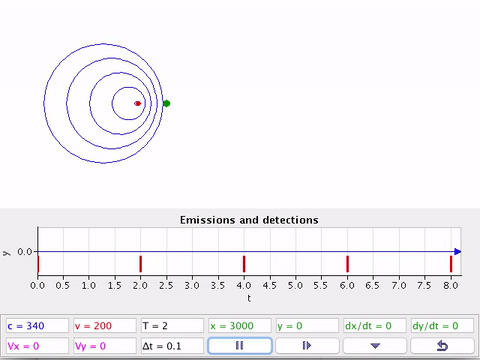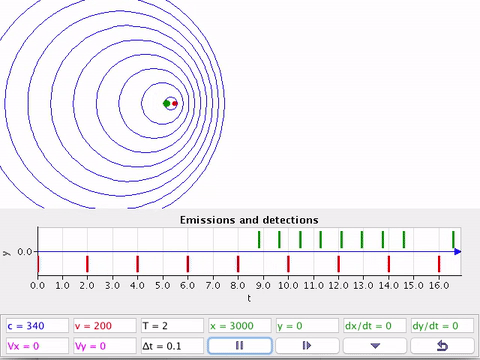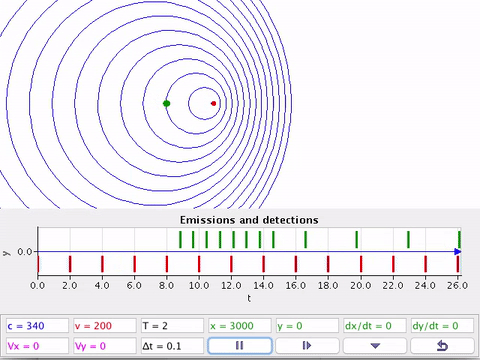
À medida que a fonte se afasta do detector em repouso comprimento de onda fica maior em relação à posição estática.

À medida que a fonte se aproxima do detector em repouso, o comprimento de onda fica menor em relação à posição estática.

\lambda > \lambda_0

\lambda < \lambda_0

\lambda_F=\frac{v_s-v_F}{f_F}

O efeito Doppler sonoro em duas dimensões.

Usualmente, o detector (D) não está na mesma linha da fonte (F) em movimento.

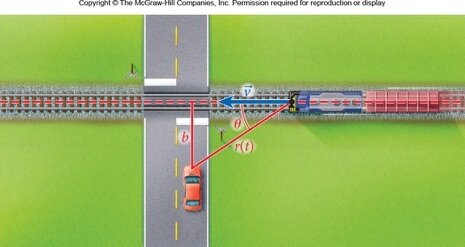
Fonte: Bauer

\cos(\theta(t))=\frac{v_st}{r(t)}

\cos(\theta(t))=\frac{v_st}{\sqrt{b^2+v^2t^2}}

v_F=v_s\cos[\theta(t)]

v_F=\frac{v_s^2t}{\sqrt{b^2+v^2t^2}}

A fonte (F) em movimento e o detector (D) parado em relação ao ar, sabemos que:

\Rightarrow f_D = f_F

\frac{v_s}{v_s\pm \frac{v_s^2t}{\sqrt{b^2+v^2t^2}}}

\Rightarrow f_D = f_F

\frac{v_s}{v_s\pm v_F}

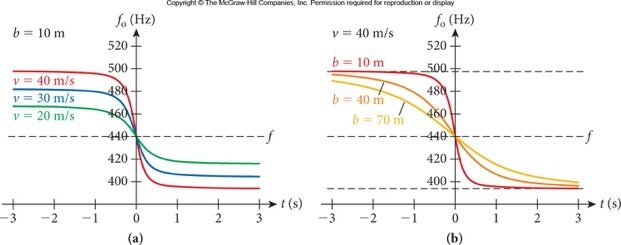
Fonte: Bauer

O efeito Doppler sonoro em duas dimensões.

Usualmente, o detector (D) não está na mesma linha da fonte (F) em movimento.

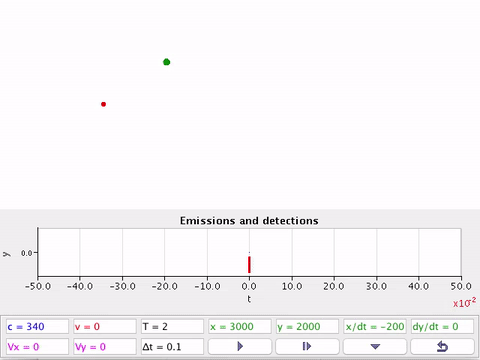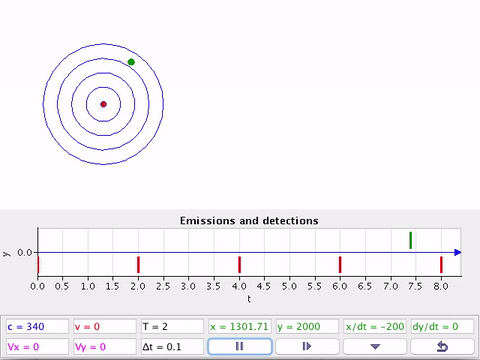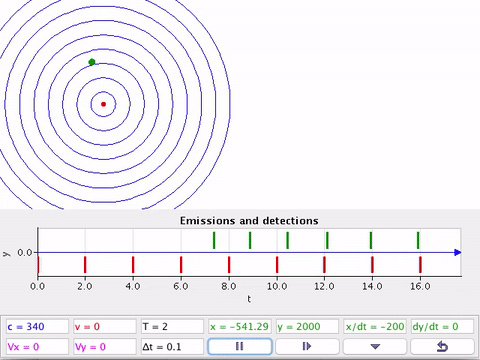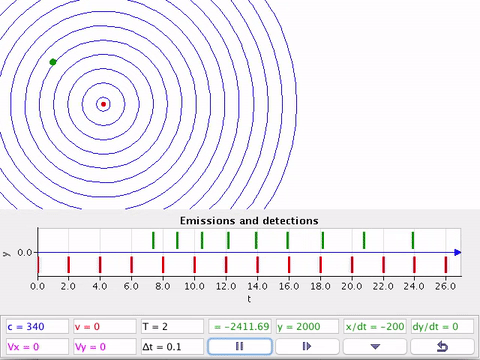
Fonte: http://www.compadre.org/osp/items/detail.cfm?ID=7902

O efeito Doppler sonoro em duas dimensões.

Usualmente, o detector (D) não está na mesma linha da fonte (F) em movimento.

\Rightarrow f_D = f_F

\frac{v_s}{v_s\pm \frac{v_s^2t}{\sqrt{b^2+v^2t^2}}}

Na aproximação, temos do referencial que t < 0. Usamos o sinal (-).

No afastamento, temos do referencial que t > 0. Usamos o sinal (+).

Fonte: https://www.geogebra.org/m/YoJb1LmP

O instante t = 0 é aquele onde a fonte, em movimento, passa o mais próximo possível do detector.

Há uma percepção gradual da variação da frequência!

O efeito Doppler sonoro. Mach = 1.

As equações do efeito Doppler não se aplicam quando as velocidades são supersônicas.

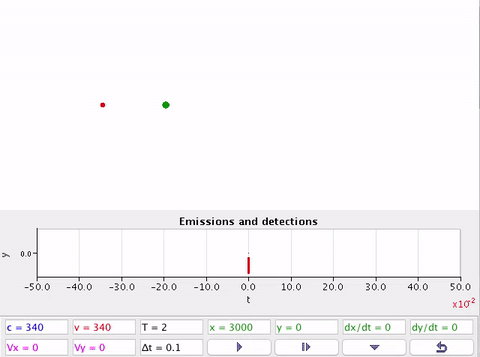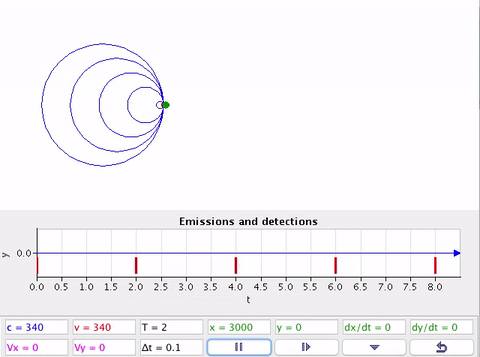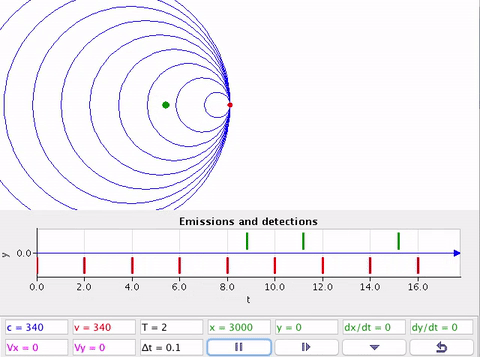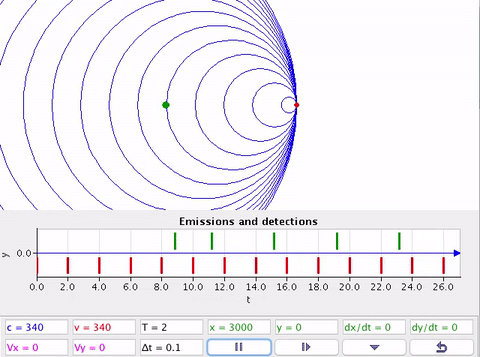
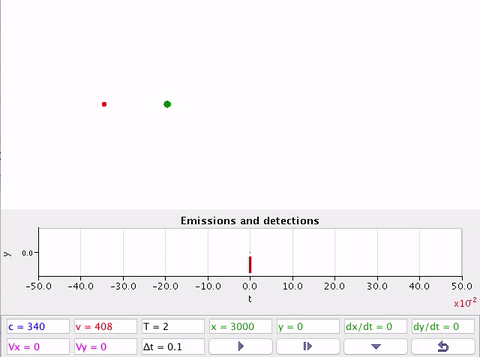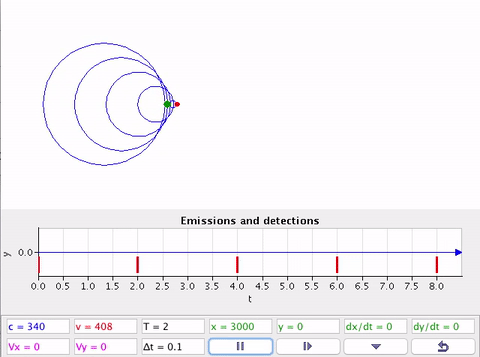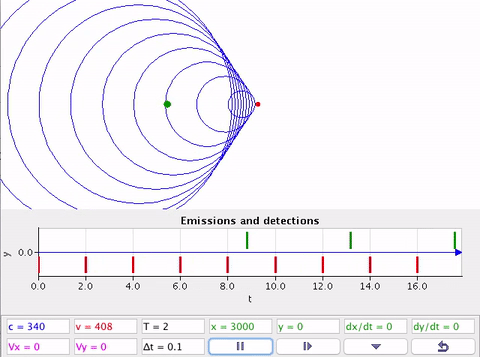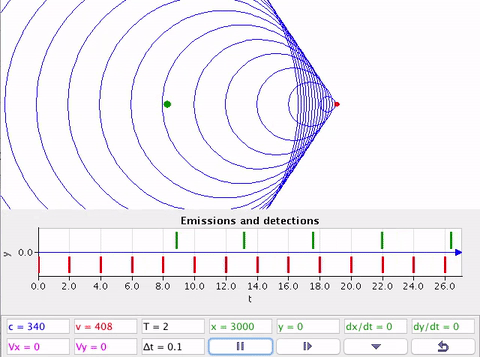
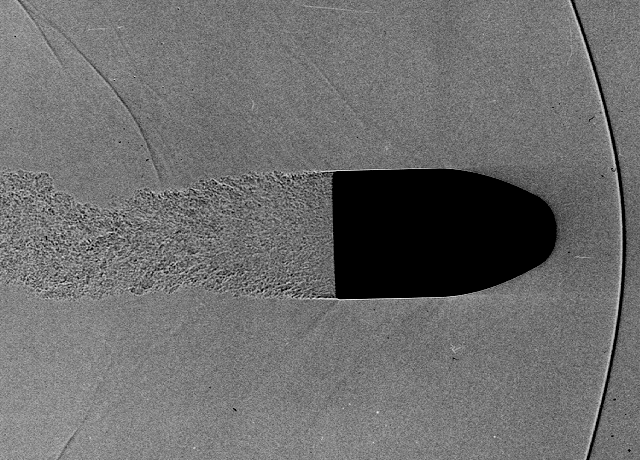
Fonte: http://www.compadre.org/osp/EJSS/3858/38.htm

Velocidade da fonte ou detector são supersônicas \(v > v_s\).

O efeito Doppler sonoro. Cone de Mach.

Na equação matemática que descreve o efeito doppler para uma fonte que se aproxima do detector parado

f_D = f_F

\frac{v_s}{v_s- v_F}

Fonte: https://www.geogebra.org/m/upwsupcf

Quando \(𝑣_𝑓 = 𝑣 \Rightarrow 𝑓_D \rightarrow \infty\). A fonte acompanha suas frentes de onda. A equação do efeito Doppler perde validade.

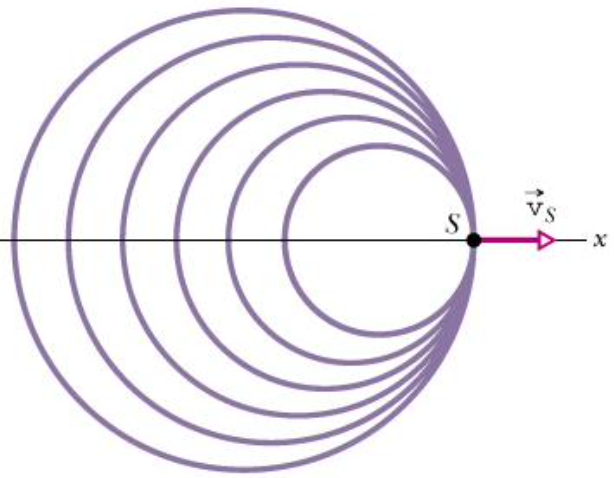
Fonte: Halliday & Resnick

O efeito Doppler sonoro. Cone de Mach.

Nesse caso, a condição para o deslocamento supersônico é dado pelo número de Mach.

Fonte: Halliday & Resnick

\text{sen}\theta = \frac{v}{v_F}>1

v_F=\frac{v}{\text{sen}\theta}>1

\frac{1}{M}=\frac{v}{v_F}

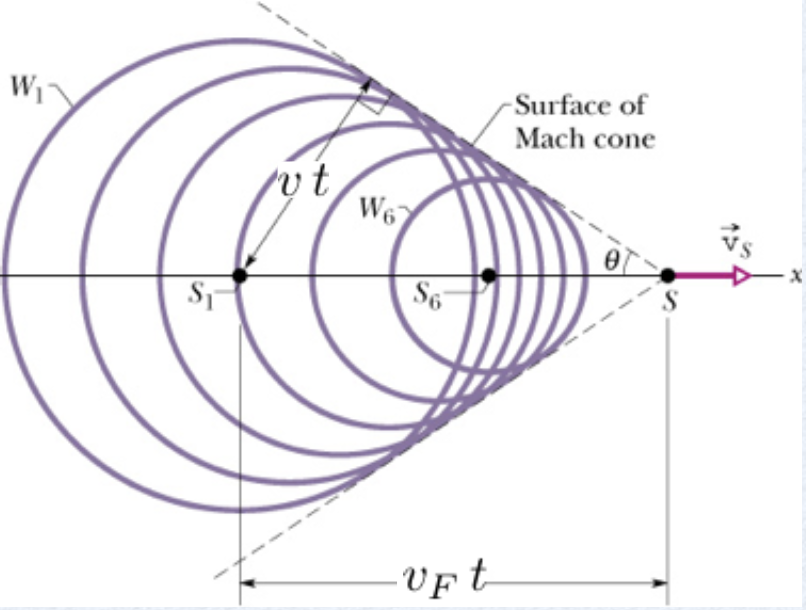
Mach 1

v_F=v

Mach 2

v_F=2v

v_F>v_{som}

v_F< v_{som}

O efeito Doppler sonoro. Cone de Mach.

A onda de choque produz um estrondo sônico:

A pressão do ar aumenta bruscamente e depois diminui para valores menores que o normal.

Fonte: https://youtu.be/Ta14puDV0VI

O efeito Doppler sonoro. Cone de Mach.

Fonte: https://www.compadre.org/Physlets/waves/illustration18_5.cfm?NOH=1

Se um avião estiver voando mais rápido que a velocidade do som, ele produzirá uma onda de choque chamada explosão sônica. Na animação, considere um avião voando do ponto A para o ponto B. Um ouvinte, o ouvido, está localizado no ponto C. Consideramos como a velocidade do avião e a posição do ouvinte afetam quando o som dos motores do avião é ouvido pelo ouvinte.

A física também é cultura. Permite compreender o mundo nerd.

Fonte: https://youtu.be/5F0YWabT7Q4

Questão 1

Uma pessoa dentro de um carro estacionado faz soar a buzina (fonte). A frequência do som emitido é de 290,0 Hz. Um motorista de um carro que se aproxima (detector) mede a frequência do som proveniente do carro estacionado como sendo de 316,0 Hz. Qual é o valor da velocidade de aproximação do carro em movimento? W16-PR4.2

Questão 2

Uma ambulância foi socorrer um escalador machucado e está se afastando perpendicularmente da parede do cânion (onde o escalador se acidentou) com uma velocidade de 31,3 m/s. A sirene da ambulância emite som de frequência de 400,0 Hz. Após a sirene ter sido desligada, o escalador acidentado consegue ouvir o som refletido pela parede do cânion por alguns segundos. A velocidade do som no ar é vs = 343 m/s. Qual é a frequência do som refletido da sirene da ambulância escutado pelo escalador dentro da ambulância? W16-PR4.4

Questão 3

Um policial com ouvido muito bom (ouvido absoluto) e uma boa compreensão do efeito Doppler encontra-se em pé na beira de uma autoestrada, assistindo a um grupo de operários trabalhando em um trecho da rodovia de velocidade limitada de 17,9 m/s. Ele nota que um carro se aproxima buzinando. Quando ele chega mais perto, o policial estuda o som da buzina como uma nota distinta B4 (494 Hz). No instante exato em que o carro passa por ele, escuta o som como uma nota distinta A4 (440 Hz). Imediatamente, ele desce da motocicleta, detém o carro e multa o motorista. Explique o raciocínio do policial? W16-38

Questão 4

Um morcego voa em direção a uma parede com uma velocidade de 7,0 m/s e emite uma onda ultrassônica com frequência de 30,0 kHz. Que frequência a onda refletida terá quando alcançar o morcedo voando? W16-42

Questão 5

Durante um filme de suspense, dois submarinos, X e Y, se aproximam um do outro a 10 m/s e 15 m/s, respectivamente. O submarino X emite um “silvo” em direção ao submarino Y, enviando uma onda de sonar com frequência 2 000 Hz. Considere que o som se propague na água a 1 500 m/s.

a)Determine a frequência da onda de sonar detectada pelo submarino Y.
b)Qual é a frequência detectada pelo submarino X da onda de sonar refletida pelo outro submarino?
c)Suponha que os submarinos passem raspando um pelo outro, então, sigam se afastando. Que frequência o submarino Y detectará para o silvo emitido pelo submarino X? Qual será seu deslocamento Doppler? W16-66.

Questão 6

Um carro trafegando a 25 m/s soa sua buzina quando se aproxima diretamente da lateral de um edifício alto. A buzina produz um som de frequência f0 = 230 Hz. O som é refletido pelo edifício de volta para o motorista do carro. A onda sonora da nota original e a refletida se combinam para gerar uma frequência de batimento. Qual é o valor da frequência de batimento e a frequência que o motorista efetivamente ouve? W16-63

Questão 7

Um carro está parado no cruzamento com uma ferrovia. Um trem passa e o motorista do carro grava a dependência temporal da frequência do som emitido pelo trem, como mostrado na figura.

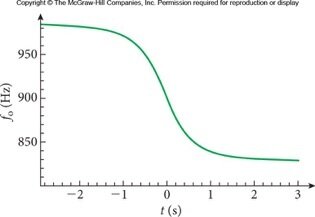
a)Que frequência é ouvida pelo motorista do trem?
b)Com que velocidade o trem se move?
c)A que distância dos trilhos se encontra o carro do motorista? W16-45

Questão 8

Um avião voa a Mach 1,3, e a onda de choque que gera atinge um homem no solo 50 s após a passagem do avião diretamente sobre sua cabeça.

a)Qual é o ângulo de Mach?
b)Qual é a altitude do avião? W16-43

Questão 9

A velocidade de uma aeronave supersônica é fornecida com frequência como um número de Mach, M. Uma velocidade de Mach 1 (M=1) significa que a aeronave desloca-se com a velocidade do som. O avião a jato comercial Concorde voava em cruzeiro a cerca de 20 000 m de altitude, onde a velocidade do som é de 295 m/s. A velocidade máxima de cruzeiro do Concorde era de Mach 2,04, M = 2,04.

A esta velocidade, qual era o ângulo do cone de Mach produzido pelo Concorde? W16-E16.4