Aula 14

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Seções: 14.4, 14.5.

Distinguir um fluido laminar de um fluido turbulento, e como a velocidade do escoamento em um tubo depende do tamanho desse tubo.

Aplicar a equação de Bernoulli em certos tipos de escoamento para relacionar a pressão à velocidade do escoamento em diferentes pontos.

Perceber como o fluido viscoso e o turbulento diferem do ideal.

Fonte: Bauer

Simulação computacional da NASA, mostrando o fluxo aerodinâmico do ar do sistema de propulsão do jato Harrier em voo. As cores das linhas de fluxo aerodinâmico indicam o tempo decorrido desde que a exaustão iniciou.

Capítulo 14 - Mecânica dos Fluidos

Motivação

Estudos aerodinâmicos permitem entender como o design dos objetos interfere no fluxo de ar ao redor deles, o que é fundamental, no futebol, para determinar a velocidade e a trajetória que podem tomar.

Fonte: http://cienciahoje.uol.com.br/blogues/bussola/2014/07/bola-das-bolas

Hidrodinâmica: fluidos em movimento.

O movimento dos fluidos é visível por meio de marcadores.

Num gas: utiliza-se fumaça.

Num líquido: utiliza-se corante.

As linhas de fluxo definem um campo de velocidades e um campo de densidades a cada posição e tempo.

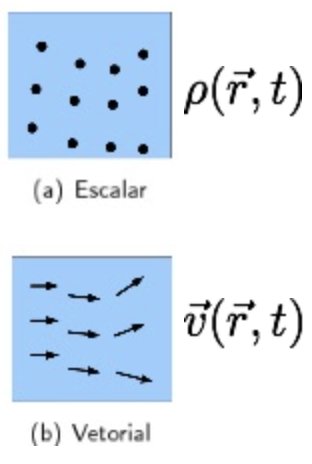
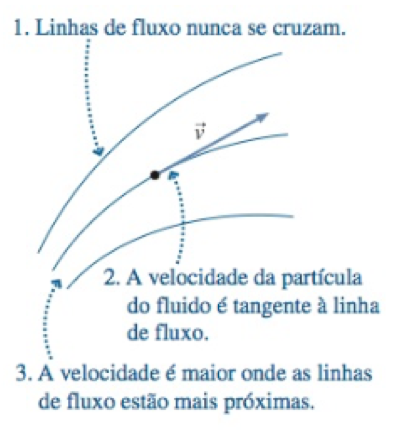
IMPORTANTE!

Fonte: Randall

Fonte: Randall

Fonte: https://www.youtube.com/embed/xW63SZ1LAqo?enablejsapi=1

Fonte: https://www.youtube.com/embed/7OVUwtRwJw8?enablejsapi=1

Hidrodinâmica: fluidos em movimento.

Na abordagem de campos de velocidades, a velocidade em um região do fluido muda de um ponto para outro (espaço) e de um instante para outro (tempo).

\vec v (\vec r, t)=\text{constante}

\vec v (\vec r, t)\neq\text{constante}

Método de Euler x Lagrange

Dá-se atenção aos valores da velocidade e densidade das diversas “células do fluido” que passam num dado ponto fixo r do espaço à medida que o tempo t avança.

O fluido é subdividido em elementos de volume suficientemente pequenos para tratar cada um deles como uma partícula e depois descrever o movimento de cada partícula do fluido.

Fonte: Bauer.

(Regime Laminar - Estacionário)

(Regime Turbulento - Não estacionário)

Hidrodinâmica: fluidos em movimento.

Fluido ideal

É um fluido com escoamento ideal ou escoamento com viscosidade nula, é aquele no qual não existem tensões de cisalhamento atuando no movimento do fluido.

Regime laminar.

A velocidade do fluido, em cada ponto do mesmo, é constante; ele não se altera com decorrer do tempo.

Trajetórias paralelas.

Regime turbulento.

A velocidade do fluido, em cada ponto do mesmo, não é constante.; ele se altera com decorrer do tempo.

Trajetórias irregulares.

Fonte: Randall

Com boa aproximação o regime laminar pode ser considerado como um fluido ideal.

Hidrodinâmica: fluidos em movimento.

Regime laminar

A velocidade e pressão em cada ponto do fluido não mudam com o tempo.

As linhas de corrente e os tubos de corrente não mudam com o tempo.

Se incompressível, a densidade não varia no tempo.

Fonte: https://youtu.be/vzFVsDE97b0

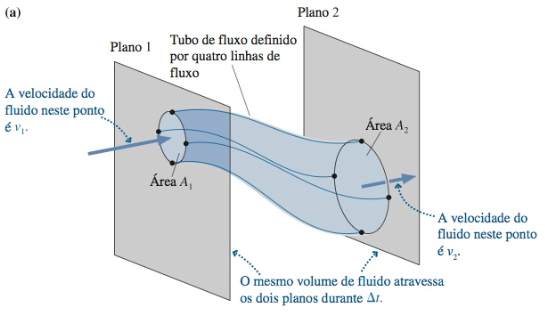
Fonte: Randall

\frac{\partial v(r,t)}{\partial t} =0

\frac{\partial p(r,t)}{\partial t} =0

\frac{\partial \rho(r,t)}{\partial t} =0

v(r,t)=\text{constante}

p(r,t)=\text{constante}

\rho(r,t)=\text{constante}

Hidrodinâmica: fluidos em movimento.

A vazão mássica através de uma superfície. A conservação de massa.

Fonte: Halliday

Superfície de entrada do tubo

Superfície de saída do tubo

Tubo de corrente

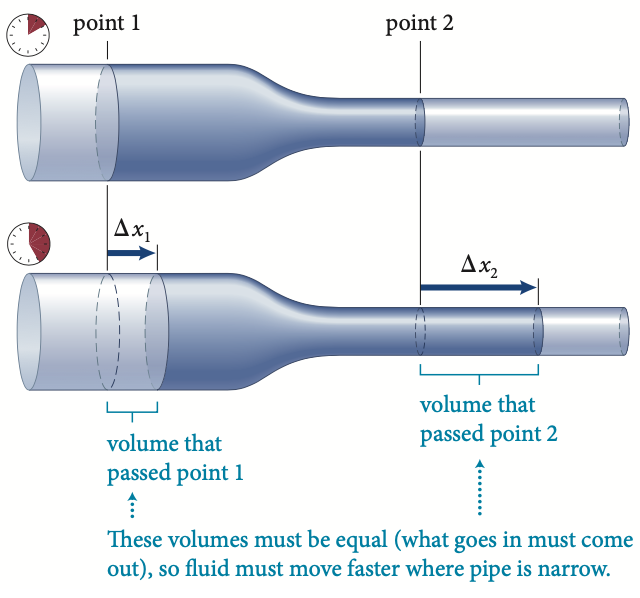
ponto 1

ponto 2

Para um fluido incompressível, se o escoamento é laminar (baixas velocidades), estacionário (velocidade constante), ideal (sem viscosidade) e sem fontes ou sumidouros de fluido:

Fonte: Eric Mazur

dm_1 = dm_2

A massa que entrou em 1 é igual à massa que saiu em 2.

dm_1

dm_2

Hidrodinâmica: fluidos em movimento.

A vazão mássica através de uma superfície. A equação da continuidade.

Vazão mássica é a taxa (em kg/s) com que o fluido atravessa uma superfície por unidade de tempo:

I_m = \frac{dm}{dt} = \rho A v

dm = \rho A\,dx

dm=\rho A\,v\,dt

dm=\rho dV

Para um elemento de massa:

Fonte: Eric Mazur

ponto 1

ponto 2

\frac{\text{kg}}{\text{s}}

dm_1 = dm_2

A massa que entrou em 1 é igual à massa que saiu em 2:

A vazão de entrada é igual à vazão de saída. Então, a equação da continuidade:

I_{m,1} = I_{m,2}

\rho_1 A_1 v_1 = \rho_2 A_2 v_2

massa por tempo

Hidrodinâmica: fluidos em movimento.

A vazão volumétrica através de uma superfície. A equação da continuidade.

Vazão volumétrica é a taxa (em m\(^3\)/s) com que o fluido atravessa uma superfície por unidade de tempo:

A vazão volumétrica deve ser uma constante em qualquer seção do tubo. Então, a equação da continuidade:

I_V = A v

Para um fluido incompressível, a densidade não varia:

\rho_1=\rho_2=\rho

A_1v_1 = A_2v_2

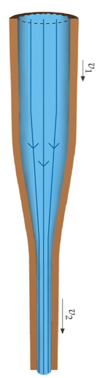
A velocidade é maior na parte mais baixa do tubo de fluxo. Assim, O diâmetro do tubo de fluxo muda à medida que a velocidade aumenta.

\Rightarrow A_2 =\frac{v_1}{v_2}A_1

A_1

A_2

\vec v_1

\vec v_2

v_2 > v_1

\frac{\text{m}^3}{\text{s}}

Fonte: Halliday & Resnick

Fonte: Halliday & Resnick

volume por tempo

\rightarrow A_2 < A_1

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli.

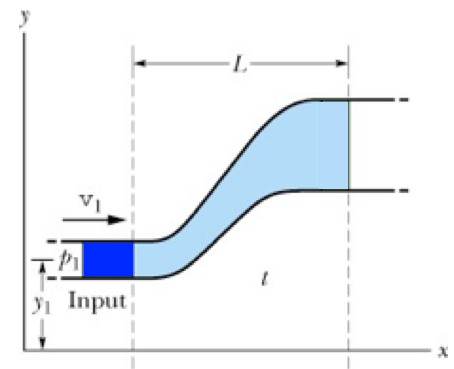
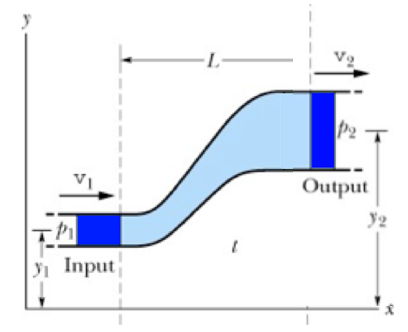
Seja um fluido sem viscosidade (ideal), incompressível (densidade constante), em regime laminar (baixas velocidades) e estacionário (velocidade independe do tempo).

No tempo \(t_1\) o fluido está na altura \(y_1\) com velocidade \(v_1\).

A pressão que o fluido exerce no tubo de corrente a sua frente é \(p_1\).

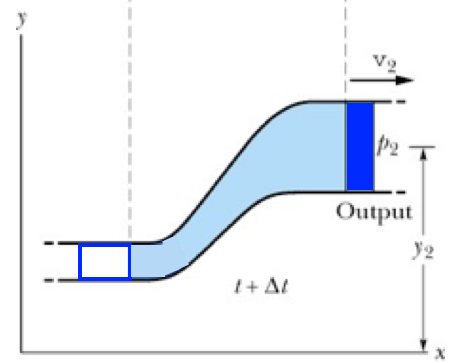
No tempo \(t_2\) o fluido está na altura \(y_2\) com velocidade \(v_2\).

A pressão que o fluido exerce no tubo de corrente a sua frente é \(p_2\).

O fluido de massa \(\Delta m\) passou de um ponto de pressão \(p_1\) e altura \(y_1\) para outro de pressão \(p_2\) e altura \(y_2\).

Fonte: Adaptado Randall

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli.

Para um fluido ideal, incompressível, laminar e estacionário a energia é conservada.

W=\Delta K

A partir do teorema trabalho-energia cinética:

onde

\Delta K = \frac{1}{2}(\Delta m)v_2^2-\frac{1}{2}(\Delta m)v_1^2

\Rightarrow W_{v}+W_{c}=\Delta K

W_v=-(\Delta m)g(y_2-y_1)

W_c=(p_1A_1)\Delta x_1-(p_2A_2)\Delta x_2

Sendo que:

V=A\Delta x

\Delta m = \rho V

Obtemos a equação de Bernoulli:

p_1+\frac{1}{2}\rho v_1^2+\rho g h_1= p_2+\frac{1}{2}\rho v_2^2+\rho g h_2

\Delta x = v\Delta t

Fonte: Adaptado Randall

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli.

A soma da pressão com densidade de energia cinética com a densidade de energia potencial é uniforme ao longo de uma linha de corrente:

p_1+\frac{1}{2}\rho v_1^2+\rho g h_1= p_2+\frac{1}{2}\rho v_2^2+\rho g h_2

A soma da altura piezométrica com a altura cinética com com a altura geométrica é uniforme ao longo de uma linha de corrente.

\frac{p_1}{\rho g}+ \frac{1}{2}\frac{v_1^2}{g}+h_1 = \frac{p_2}{\rho g}+ \frac{1}{2}\frac{v_2^2}{g}+h_2

Física

Engenharia

Todas as parcelas têm dimensão de pressão!!!!

Fonte: https://www.geogebra.org/m/ZUtgMEZt

Hidrodinâmica: fluidos em movimento.

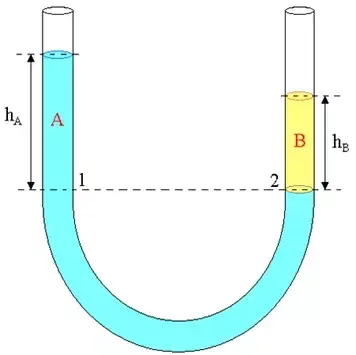
A equação de Bernoulli. Aplicações. Manômetro.

Fluido em equilíbrio estático (\(v_1=v_2=0\))

p_1+\frac{1}{2}\rho v_1^2+\rho g h_1= p_2+\frac{1}{2}\rho v_2^2+\rho g h_2

p_1+\rho g h_1= p_2+\rho g h_2

p_2= p_1+\rho g( h_1 -h_2)

Recuperamos a equação de Stevin da hidrostática!

Use Bernoulli quando há movimento do fluido.

Use Stevin quando não há movimento do fluido.

Fonte: https://mundoeducacao.uol.com.br

p_2= p_1+\rho gH

\rightarrow p_B= p_A

h_1

h_2

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Aplicações. Reservatórios.

Tubos abertos para a atmosfera (\(p_1=p_2=p_{atm}\))

p_1+\frac{1}{2}\rho v_1^2+\rho g h_1= p_2+\frac{1}{2}\rho v_2^2+\rho g h_2

\frac{1}{2}\rho v_1^2+\rho g h_1= \frac{1}{2}\rho v_2^2+\rho g h_2

\rho g (h_1 - h_2)= \frac{1}{2}\rho (v_2^2-v_1^2)

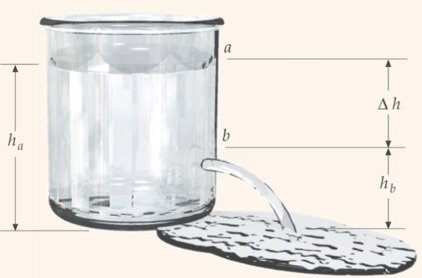
A velocidade no ponto 1 é muito menor que a velocidade em 2, \(v_1 << v_2\):

h_1

h_2

\Delta h

v_2 = \sqrt{2g\Delta h}{}

Fonte: Tipler

v_2^2=v_1^2 + 2g\Delta h

É a equação de Torricelli!

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Aplicações. Medidor Pitô.

p_A+\frac{1}{2}\rho_{ar} v_A^2= p_B+\frac{1}{2}\rho_{ar} v_B^2

Utilizado para medir a velocidade do ar nos aviões e carros de F1.

Eq. de Bernoulli sem elevação:

Calcula-se a velocidade de escoamento de um fluido se \(v_A\approx 0\):

v_B=\sqrt{2gh\frac{\rho_f}{\rho_{ar}}}

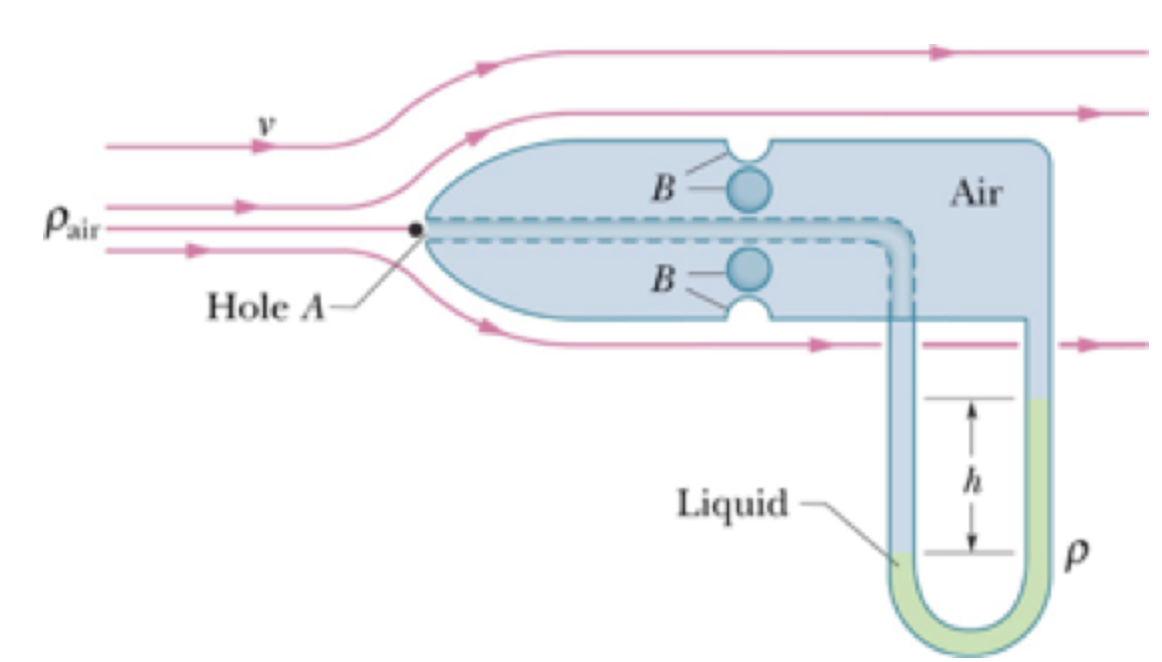
Fonte: https://youtu.be/udQI1E5vTPI

Fonte: Halliday & Resnick

v_A \approx 0

\rho_f

\rho_{ar}

p_A-p_B=\rho_f gh

Eq. de Bernoulli no equilíbrio:

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Aplicações. Efeito Venturi.

p_1+\frac{1}{2}\rho v_1^2+\rho g h_1= p_2+\frac{1}{2}\rho v_2^2+\rho g h_2

p_1+\frac{1}{2}\rho v_1^2= p_2+\frac{1}{2}\rho v_2^2

p+\frac{1}{2}\rho v^2=\text{constante}

p_1>p_2 \Rightarrow v_1 < v_2

Ao longo de uma linha de fluxo, se o fluido passa por um estrangulamento, a velocidade do fluido aumenta e a pressão do fluido diminui, e vice-versa.

A coluna do líquido vermelho sobe porque a pressão no estrangulamento é menor do que a pressão nas outra regiões do tubo.

Estrangulamento. Escoamento sem elevação (\(h_1=h_2=h\)).

Fonte: Wolfgang & Bauer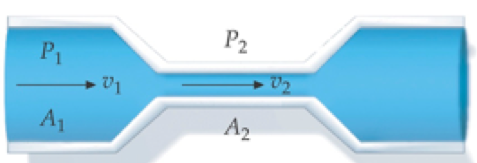

A_1v_1=A_2v_2

p_2

A_2

v_2

v_1

p_1

A_1

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Efeito Venturi.

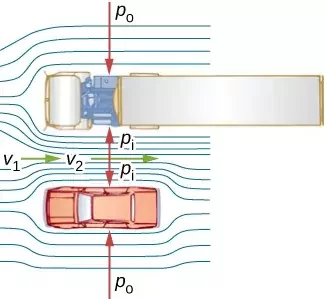
Fonte: https://openstax.org

Mantenha uma distância de 1,50 metros de um ciclista ao passar lateralmente por ele.

Fonte: https://youtu.be/MZQby7_SpFw

Fonte: https://www.youtube.com/embed/1JuoSJz3SRU?enablejsapi=1

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Aplicações. Efeito Venturi.

Medidor Venturi. Escoamento sem elevação (\(h_1=h_2=h\))

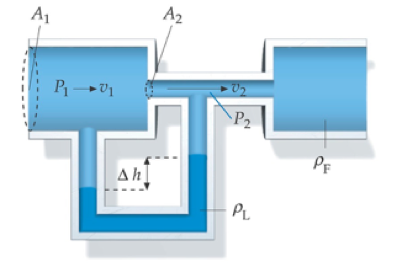
p_1+\frac{1}{2}\rho v_1^2+\rho g h_1= p_2+\frac{1}{2}\rho v_2^2+\rho g h_2

p_1+\frac{1}{2}\rho_1 v_1^2= p_2+\frac{1}{2}\rho_2 v_2^2

Desnível no líquido devido à diferença de pressão no fluido.

Eq. de Bernoulli sem elevação:

Eq. da vazão volumétrica:

v_1A_1=v_2A_2

Calcula-se a velocidade de escoamento de um fluido com auxílio das Eqs. de Stevin:

v_2=\sqrt{\frac{2(\rho_L-\rho_f)gA_1^2\Delta h}{\rho_f(A_1^2-A_2^2)}}

\rho_f\equiv \rho_{ar}

\rho_L

p_3

p_4

p_5

p_2

p_1

\odot

Fonte: Wolfgang & Bauer

Fonte: Wolfgang & Bauer

Hidrodinâmica: fluidos em movimento.

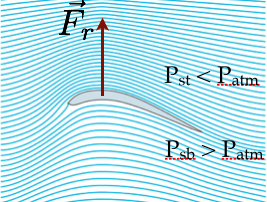
A equação de Bernoulli. Como o avião voa?

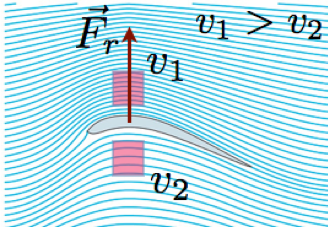
As linhas de escoamento seguem a aerodinâmica da asa.

A asa é um aerofólio assimétrico.

Para uma porção do fluido ao longo da linha de escoamento, a eq. de movimento:

\vec f +\vec\nabla p=\vec 0

\vec\nabla p=-\rho\vec a

A densidade das linhas de fluxo é maior acima da asa. Logo, a velocidade \(v_1 > v_2\).

Se \(v_1 > v_2\), então a pressão é tal que \(p_1 < p_2\).

Logo, a força resultante é orientada para cima.

A força tem a orientação da diminuição da pressão.

p_1 < p_2

Fonte: Alaor Chaves

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Empuxo Aerodinâmico.

Para quaisquer porções de ar acima ou abaixo da asa há uma força centrípeta que orienta para o centro de curvatura das linhas de fluxo.

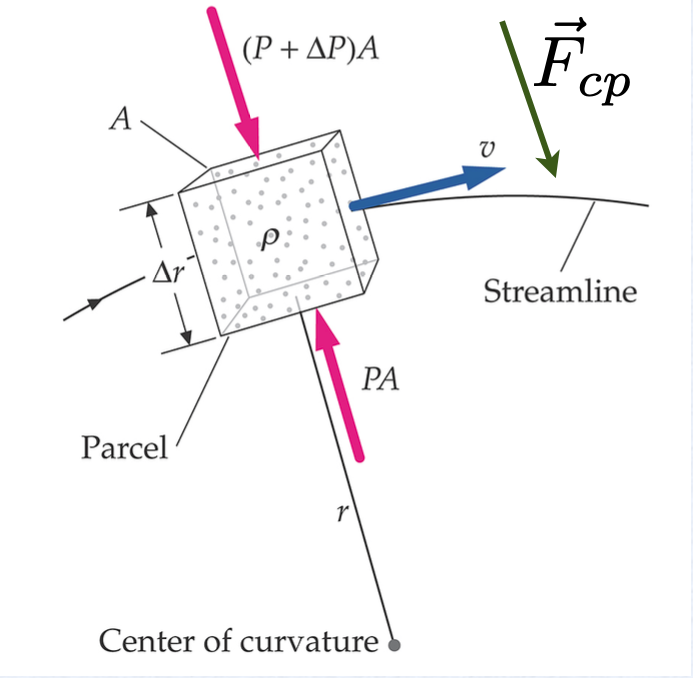
Linha de fluxo

Volume

Centro de curvatura

Acima da asa

p_{T} > p_{ST}

p_{atm} > p_{ST}

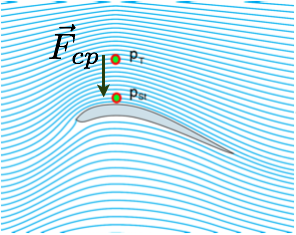
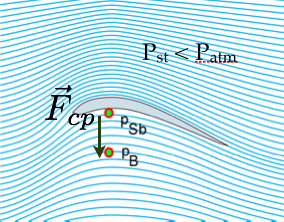
Abaixo da asa:

p_{B} < p_{SB}

p_{atm} < p_{SB}

Fonte: Alaor Chaves

Fonte: Alaor Chaves

Fonte: Tipler

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Empuxo Aerodinâmico.

A diferença de pressão entre as superfícies superior e inferior da asa é responsável pela sustentação do avião:

p_{SB} > p_{ST}

Através da asa o gradiente da pressão cresce de baixo para cima.

Fonte: Alaor Chaves

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Como o avião voa?

Na figura, \(p_1\) bem adiante da asa é maior do que \(p_2\):

p_{1} > p_{2}

Porções de ar ganham rapidez quando entram em regiões de baixa pressão.

p_{1} = p_{atm}

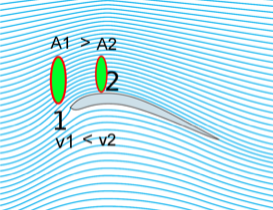
A porção de ar ao passar de 1 para 2 ganha rapidez:

v_{1} < v_{2}

A equação de Bernoulli, com boa aproximação de 1 para 2:

p_1+\frac{1}{2}\rho v_1^2= p_2+\frac{1}{2}\rho v_2^2

Fonte: Alaor Chaves

Fonte: https://youtu.be/b8lQfIr-XCg

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Como o avião voa?

A variação de pressão é, portanto:

p_2-p_1=-\frac{1}{2}\rho (v_2^2-v_1^2)

Definindo:

\overline v =\frac{v_2+v_1}{2}

\Delta v={v_2-v_1}

Reescrevemos:

p_2-p_1=-\rho \overline{v}\Delta v

O empuxo sobre a asa do avião:

E=F_1-F_2=(p_1-p_2)A

Combinando (1), (2) e (3):

E=\rho\overline v\Delta v A = \frac{1}{2}\rho(v_2^2-v_1^2)A

(1)

(2)

(3)

Fonte: Alaor Chaves

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Como o avião voa?

O empuxo

E= \frac{1}{2}\rho v_1^2\left(\frac{v_2^2}{v_1^2}-1\right)A

A vazão volumétrica para um fluido incompressível:

A_1 v_1 = A_2 v_2

O empuxo

E= \frac{1}{2}\rho v_1^2\left(\frac{A_1^2}{A_2^2}-1\right)A

E= \frac{1}{2}\rho v^2RA

onde \(R\) é o coeficiente de sustentação (aerodinâmica ao ângulo de ataque):

R=\left(\frac{A_1^2}{A_2^2}-1\right)

Fonte: Alaor Chaves

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Como o avião voa?

Para que exista sustentação:

E\geq P

A velocidade do avião:

Dados: \(M = 3,5 \times 10^5\) kg; \(g = 9,8 \text{m/s}^2 \); \(R=0,5\); \(\rho = 1,3 \text{kg/m}^3\):

\frac{1}{2}\rho v^2RA \geq Mg

Para um avião de massa \(M\):

v^2 \geq \frac{2Mg}{R\rho A}

v = 540\text{ km/h}

Para manter um Boing 747 no ar. Se ρ é menor do que \(1,3 \text{kg/m}^3\) o tamanho da pista deve ser maior para garantir a velocidade mínima de sustentação.

Fonte: Alaor Chaves

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Efeito Magnus.

Uma bola lançada com efeito mostra um desvio lateral em sua trajetória.

O plano da curvatura é determinado pela direção do eixo de giro da bola

O ar adjacente à bola tende a acompanhar o movimento da bola.

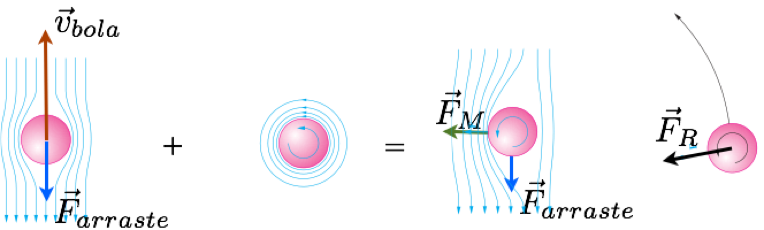
Translada

Rotaciona

Composto

v_E>v_D

p_E< p_D

A força \(\vec F_M\) tem a orientação da diminuição da pressão.

Fonte: Alaor Chaves

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Efeito Magnus.

Aplicando um pouco de álgebra vetorial é possível calcular a força do efeito Magnus:

p_1+\frac{1}{2}\rho v_1^2= p_2+\frac{1}{2}\rho v_2^2

v_1 > v_2 \Rightarrow p_1 < p_2

\vec\nabla p=-\vec f_M

\vec f_M = c(\vec\omega \times \vec v)

\vec f_M = -c\omega v\hat i

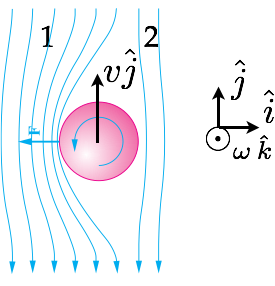
Fonte: Alaor Chaves

Fonte: https://www.youtube.com/embed/vnB_4Jtfy6A?enablejsapi=1

Questão 1

O sangue flui a 25 cm/s em uma aorta de 9,0 mm de raio. Calcule a vazão volumétrica em litros por minuto.

Questão 2

O sangue flui de uma artéria de 0,30 cm de raio, onde sua rapidez é 10 cm/s, para uma região onde o raio foi reduzido para 0,20 cm em virtude do espessamento das paredes arteriais (arteriosclerose). Qual é a rapidez do sangue na região mais estreita?

Questão 3

Água escoa a 2,0m/s em um cano horizontal, sob a pressão manométrica de 200 kPa. O cano se estreita à metade de seu diâmetro original. Qual é a pressão manométrica na secção estreita?

Questão 4

A água flui pelos canos mostrados na figura. A velocidade da água pelo cano mais baixo é de 5,0 m/s, e um manômetro marca 75 kPa. Qual é a leitura do manômetro no cano superior?

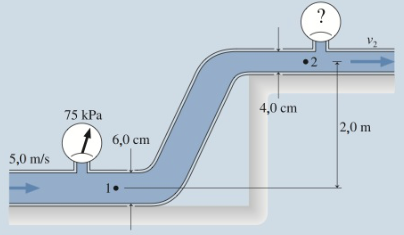
Questão 5

Pequenas usinas hidroelétricas em montanhas às vezes trazem água de um reservatório para a usina de energia através de tubos embutidos. Em uma dessas usinas, o tubo de captação de 100 cm de diâmetro, na base da represa, localiza-se 50 m abaixo da superfície do reservatório. A água desce 200 m através do tubo antes de entrar na turbina por um bocal de 50 cm de diâmetro.

a.Qual é a velocidade da água na turbina?
b.Em quanto a pressão de entrada difere da presão hidrostática àquela profundidade?

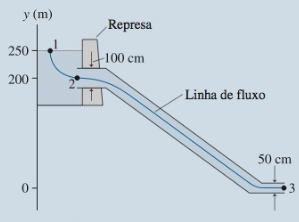
Questão 6

A água entra em uma casa através de um tubo com diâmetro interno de 2,0 cm, com uma pressão absoluta igual a 4,0 x 10^5 Pa. Um tubo com diâmetro interno de 1, 0 cm conduz ao banheiro do segundo andar a 5,0 m de altura. Sabendo que no tubo de entrada a velocidade é igual a 1, 5 m/s, ache a pressão na tubulação do banheiro.

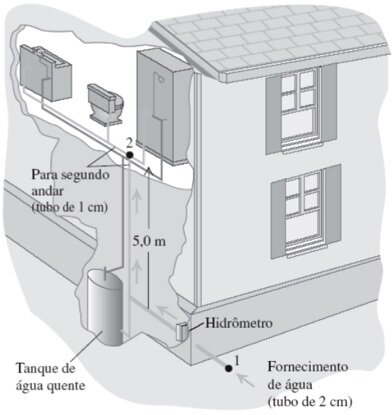
Questão 7

Considere a situação em que você toma água através de um canudo, onde sua boca é colocada na extremidade superior do canudo. A velocidade que a água deve ter ao entrar em sua boca é v_boca = 0,7 m/s. A altura de elevação da água até sua boca é h = 22 cm, como indicado na figura. A densidade da água é 1000 kg/m^3, o diâmetro do copo é muito maior que o diâmetro do canudo e a aceleração da gravidade é g = 9,8 m/s^2. Qual é a pressão manométrica necessária dentro de sua boca para esta situação ocorrer? p_atm = 1 x 10^5 Pa.

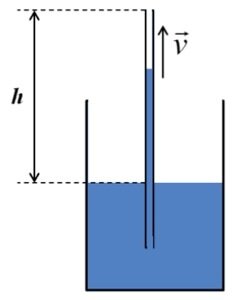
Questão 8

Um grande tanque aberto de raio R está parcialmente cheio com água. É feito no tanque um pequeno furo de área Af, situado a uma profundidade h com relação à superfície livre da água. Quanto tempo leva para escoar toda a água?

Questão 9

São dadas duas placas planas paralelas à distância de 2 mm. A placa superior move-se com velocidade de 4 m/s, enquanto a inferior é fixa. Se o espaço entre as duas placas for preenchido com óleo ( η= 0,0083 Pa.s), qual será a tensão de cisalhamento que agirá no óleo?

Hidrodinâmica: fluidos em movimento.

Para um mesmo tempo, o campo de velocidades muda de uma região para outra.

\vec v (r=1, t)\neq \vec v (r=2, t)

Para um mesma região, o campo de velocidades muda de um tempo para outro.

\vec v (r, t=0)\neq \vec v (r, t=1)

Fonte: Cortesia Prof. André Bessa

Fonte: Cortesia Prof. André Bessa

Hidrodinâmica: fluidos em movimento.

Fluido real

A viscosidade do fluido real, que determina o grau de atrito entre as camadas de fluido e entre o fluido e a parede sólida, é responsável pela variação de velocidade (gradiente de velocidade) entre as camadas.

Viscoso x Não viscoso

Newtonianos => a viscosidade dinâmica é constante para uma dada pressão e temperatura.

Não Newtonianos => a viscosidade dinâmica não é constante para uma dada pressão e temperatura.

Fonte: Eric Mazur

(a) baixa velocidade sem viscosidade.

(b) baixa velocidade com viscosidade.

(a)

(b)

(c)

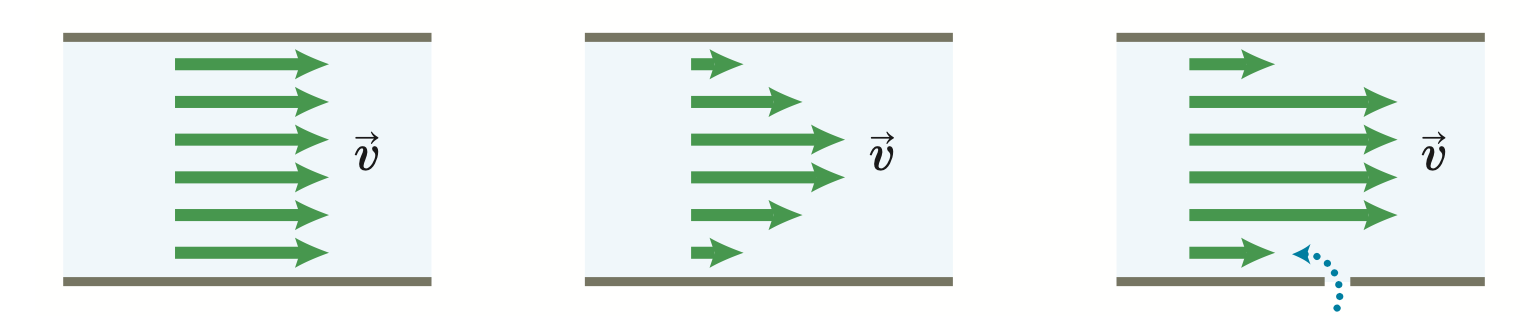
A viscosidade é uma resistência ao fluxo.

Um fluido não viscoso é o mesmo que presumir que não existe atrito.

VEJA AQUI FLUIDO NÃO NEWTONIANO

ou AQUI

(ideal)

(real)

Hidrodinâmica: fluidos em movimento.

Viscoso x Não viscoso e Aerodinâmica

Quando o fluido passa na região onde há um objeto estacionário o regime laminar ou turbulento depende da velocidade e da viscosidade do fluido e da forma do objeto.

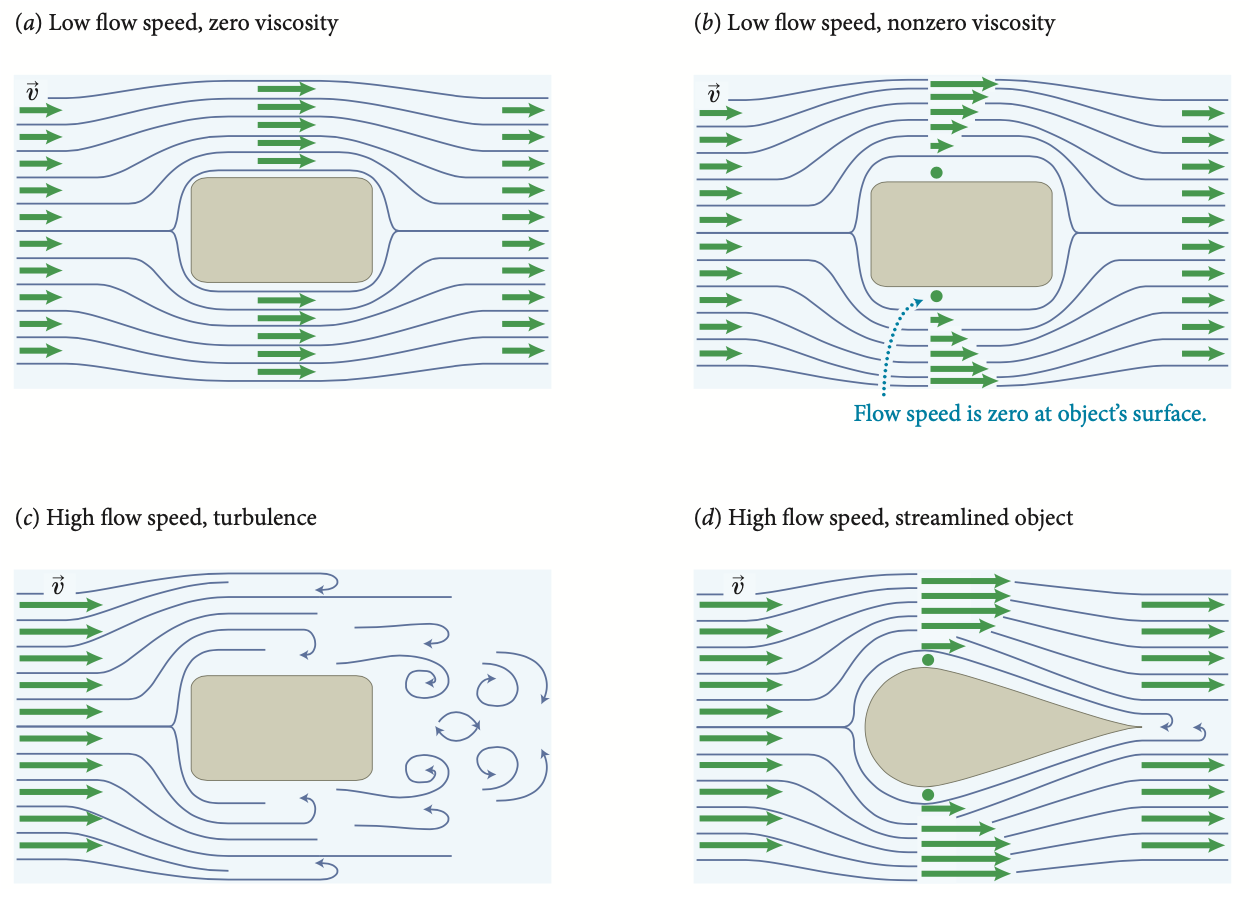
Velocidade baixa e sem viscosidade

Velocidade baixa e com viscosidade

Velocidade alta e com turbulência

Velocidade alta e sem turbulência

Fonte: Eric Mazur

AERODINÂMICA diminui a turbulência, mesmo com viscosidade.