Aula 15

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 14 - Mecânica dos Fluidos

Seções: 14.6.

Distinguir um fluido laminar de um fluido turbulento, e como a velocidade do escoamento em um tubo depende do tamanho desse tubo.

Reconhecer o perfil de velocidades no escoamento de fluidos viscosos e o conceito de camada limite.

Obter a equação de Pouiseuille.

Calcular o número de Reynolds.

Fluidos reais possuem viscosidade (água, sangue, óleo, ...). A velocidade é máxima no centro e quase nula nas paredes. O fluido pode ser decomposto em camadas cilíndricas, concêntricas e telescópica:

v=\frac{\Delta p}{4\eta L}(a^2-r^2)

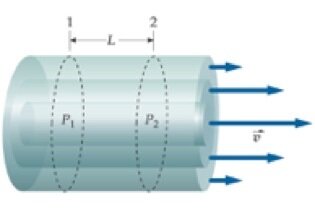
Obtemos o perfil de velocidades para o fluido:

Escoamento de fluidos viscosos. A Lei de Hagen-Poiseuille.

Fonte: Bauer

No regime estacionário existe uma diferença de pressão nas extremidades do tubo cilíndrico. A força de contato ainda promove um cisalhamento sobre a superfície lateral:

\frac{T_{\|}}{A}=\frac{(p_1-p_2)\pi r^2}{2\pi r L}

\frac{T_{\|}}{A}=\frac{(p_1-p_2) r}{2 L}

\frac{T_{\|}}{A} =\eta \frac{dv}{dz}

Aplicando a lei de Newton da viscosidade:

\Rightarrow

p_1

p_2

\vec v

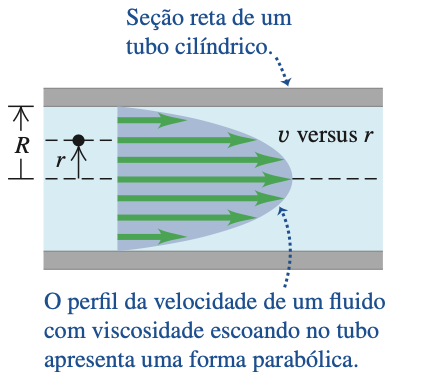
Fonte: Sears

Hidrodinâmica: fluidos em movimento.

A vazão do fluido através da secção reta do tubo cilíndrico é:

I_V = \int_s \vec v\cdot d\vec A

I_V=\frac{\Delta p}{L}\frac{\pi a^4}{8\eta}

Escoamento de fluidos viscosos. A Lei de Hagen-Poiseuille.

Para manter o fluxo sanguíneo numa artéria obstruída (\(a\rightarrow 0\)) a pressão sanguínea aumenta para manter a mesma vazão.

Fonte: https://youtu.be/WG-YCpAGgQQ

A vazão é proporcional à queda de pressão por unidade de comprimento, inversamente proporcional ao coeficiente de viscosidade e varia com a quarta potência do raio do tubo.

Esta é a lei de Hagen-Poiseuille, obtida por ambos entre 1839 e 1846 (Poiseuille, era médico, estava investigando o escoamento do sangue através de um capilar).

Hidrodinâmica: fluidos em movimento.

A resistência R ao fluxo laminar de um fluido incompressível com viscosidade 𝜂 através de um tubo horizontal de raio uniforme r e comprimento L, é dado por

Escoamento de fluidos viscosos. A Lei de Hagen-Poiseuille.

I_V=\frac{\Delta p}{R}

\Rightarrow

R = \frac{8\eta L}{\pi a^4}

A resistência é diretamente proporcional à viscosidade do fluido 𝜂 e o comprimento L do tubo.

Quanto maior a resistência, menor o fluxo ou a vazão para uma dada variação de pressão.

Quanto maior o raio (a), maior o fluxo (se todos os outros fatores permanecem os mesmos).

Qualquer mudança no raio de um tubo tem um efeito muito grande na resistência. Por exemplo, dobrar o raio de um tubo diminui a resistência por um fator de \(2^4 = 16\).

Hidrodinâmica: fluidos em movimento.

Escoamento de fluidos viscosos. Número de Reynolds.

Um indicador chamado número de Reynolds (\(N_R\)) pode revelar se o fluxo é laminar ou turbulento. Para escoamento em um tubo de diâmetro uniforme, o número de Reynolds é definido como:

N_R = \frac{2r\rho v}{\eta}

onde 𝜌 é a densidade do fluido, \(v\) sua velocidade, \(\eta\) sua viscosidade, e \(r\) é o raio do tubo.

O número de Reynolds é uma quantidade adimensional.

Regime laminar:

Regime turbulento:

Regime Instável:

N_R <2000

N_R >3000

2000< N_R < 3000

Fonte: https://youtu.be/uGU5Zff1DXQ

caótico

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Efeito Magnus.

Uma bola lançada com efeito mostra um desvio lateral em sua trajetória.

O plano da curvatura é determinado pela direção do eixo de giro da bola

O ar adjacente à bola tende a acompanhar o movimento da bola.

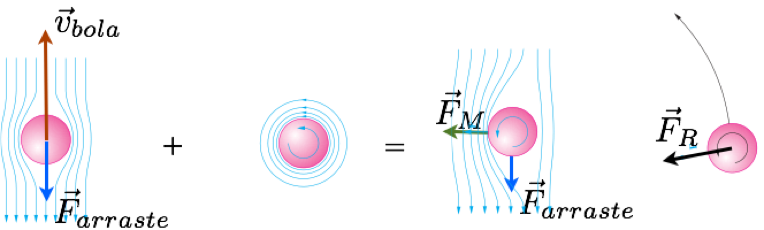
Translada

Rotaciona

Composto

v_E>v_D

p_E< p_D

A força \(\vec F_M\) tem a orientação da diminuição da pressão.

Fonte: Alaor Chaves

Hidrodinâmica: fluidos em movimento.

A equação de Bernoulli. Efeito Magnus.

Aplicando um pouco de álgebra vetorial é possível calcular a força do efeito Magnus:

\vec\nabla p=-\vec f_M

\vec f_M = c(\vec\omega \times \vec v)

\vec f_M = -c\omega v\hat i

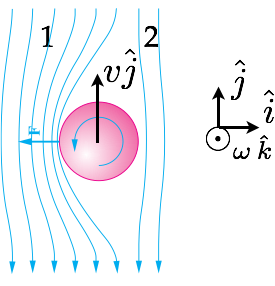
Fonte: Alaor Chaves

Fonte: https://www.youtube.com/embed/vnB_4Jtfy6A?enablejsapi=1

Questão 1

Um sistema de ar condicionado está sendo projetado para fornecer ar a uma pressão manométrica de 0,054 Pa a uma temperatura de 20°C.

O ar é enviado através de um condutor cilíndrico e isolado com diâmetro de 18,00 cm. O conduto tem 20 metros de comprimento e está aberto para uma sala à pressão atmosférica de 101,30 kPa. A sala tem 12 metros de comprimento, 6 metros de largura e 3 metros de altura.

(a) Qual é a taxa de fluxo de volume através do tubo, assumindo o fluxo laminar?

(b) Estime o tempo necessário para substituir completamente o ar da sala.

Questão 2

Na questão , descobrimos que a vazão volumétrica de um sistema de ar condicionado é \(I_V=3,84\times 10^{−3}\) m^3/s. Este cálculo assumiu o fluxo laminar. (a) Essa foi uma boa suposição? (b) Com que velocidade o escoamento se tornaria turbulento?

Questão 3

Um avião está se movendo pelo ar a velocidade v = 200 m/s. As linhas de fluxo logo acima da asa estão com- primidas 80% de sua área original e as sob a asa não estão comprimidas.

a) Determine a velocidade do ar acima da asa.

b) Encontre a diferença de pressão entre o ar acima da asa, P, e o ar sob a asa, P’.

c) Encontre a força resultante para cima em ambas as asas devido à diferença de pressão, se a área da asa é 40 m^2 e a densidade do ar é de 1,3 kg/m^3.

Hidrodinâmica: fluidos em movimento.

Circulação dos fluidos.

A circulação caracteriza o tipo do escoamento do fluido em rotacional ou irrotacional.

\vec r

\vec v

\odot

\vec \omega

Fonte: https://fr.depositphotos.com

C = \oint_C\vec v\cdot d\vec l

circulação

velocidade do fluido

elemento de linha

caminho fechado

Caso o fluido gire como um corpo rígido com uma rapidez angular \(\omega\), a velocidade tangencial num ponto na periferia do fluido a uma distância \(r\) do centro é:

\vec v = \omega r \hat t

O elemento de linha (trajetória) do fluido:

d\vec l = rd\theta \hat t

A circulação no caminho fechado circular:

C=2\pi r v

\vec v = v \hat t

\Rightarrow

C=2\pi \omega r^2

A circulação aumenta com \(r^2\)

A velocidade aumenta com o aumento de \(r\)

Hidrodinâmica: fluidos em movimento.

Circulação dos fluidos.

A circulação caracteriza o tipo do escoamento do fluido em rotacional ou irrotacional.

\vec r

\vec v

\odot

\vec \omega

Fonte: https://biodynamizer.com/

Supondo que para cada linha de corrente a circulação seja constante, mas que a velocidade varia com o raio da circulação:

A equação de Bernoulli para este redemoinho:

A equação para a superfície livre do redemoinho:

C=2\pi r v

\Rightarrow

v=\frac{C}{2\pi r}

A velocidade aumenta com a diminuição de \(r\)

z+\frac{v^2}{2g}=\text{constante}

z+\frac{C^2}{8\pi^2 g r^2}=\text{constante}

\Rightarrow

z=A-\frac{B}{r^2}

z+\frac{C^2}{8\pi^2 g r^2}=\text{constante}

O líquido ocupa a região externa do funil centrado no eixo, de modo que a singularidade em r = 0 é excluída do campo de escoamento (não há fluido).

Hidrodinâmica: fluidos em movimento.

Escoamento rotacional e irrotacional

Escoamento rotacional. Uma partícula do fluido gira ao mesmo tempo que é transportado pelo movimento.

Escoamento irrotacional. Uma partícula do fluido não gira ao mesmo tempo que é transportado pelo movimento.

Se a circulação por unidade de área no entorno de cada ponto se anula numa dada região, o escoamento é dito irrotacional. Caso contrário é dito rotacional.

\frac{C}{A}=0

\frac{C}{A}=2\pi

Motivação

Fonte: https://www.youtube.com/embed/vnB_4Jtfy6A?enablejsapi=1

A trajetória de uma bola curva é realmente curva? A resposta é sim, e o motivo é a turbulência. Em virtude das elevadas velocidades normalmente envolvidas (cerca de 35 m/s, ou 125 km/h), existe uma região de escoamento turbulento atrás da bola. A orientação da rotação da bola fará ela se curvar à esquerda ou à direita.

Um fluido possui movimento relativo devido à tensão tangencial, pois não suporta tal força.

O cisalhamento (força tangencial / área) é uma grandeza escalar sempre positiva.

t=\frac{dT_{\|}}{dA}

Grandeza

Dimensão

Unidade: S.I.

\frac{[F]}{[L]^2}

\frac{\text{N}}{\text{m}^2}=1\text{ Pa } (\text{pascal})

Fonte: https://www.youtube.com/embed/qF8UT60bkcM?enablejsapi=1

Escoamento de fluidos viscosos. Viscosidade.

Hidrodinâmica: fluidos em movimento.

A velocidade varia linearmente com a altura \(z\).

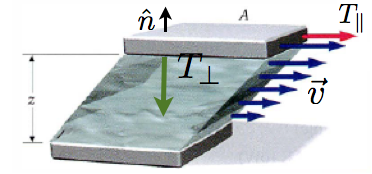
Fonte: Tipler

v(z)=\frac{v_0}{h}z

É um fato experimental que um fluido real em contato com um sólido permanece em repouso em relação à superfície de contato.

\frac{T_{\|}}{A} =\eta \frac{v_0}{h}

À medida que o fluido se afasta da placa superior a velocidade diminui.

\vec v_0

O escoamento é laminar porque o fluido se desloca em camadas planas paralelas que deslizam uma sobre as outras.

Este movimento é descrito pela lei de Newton da viscosidade:

\frac{T_{\|}}{A} =\eta \frac{dv}{dz}

A viscosidade (\(\eta\)) é uma medida do atrito interno entre estas camadas para uma dada temperatura e pressão. O cisalhamento é:

t=\eta \frac{dv}{dz}

\Rightarrow

Escoamento de fluidos viscosos. Viscosidade.

Hidrodinâmica: fluidos em movimento.

Define-se por viscosidade, a grandeza:

Grandeza

Dimensão

Unidade: S.I.

\eta =\frac{h}{v_0}\frac{F}{A}

\frac{[F]}{[L]^2}\text{[T]}

\frac{[\text{N}]}{[\text{m}]^2}[\text{s}]\equiv \text{Pa.s}

No sistema cgs é o Poise (P).

1 poise = 0,1 Pa . s

Para os líquidos a viscosidade decresce com o aumento da temperatura.

Muito viscoso = Dureza

Escoamento de fluidos viscosos. Viscosidade.

Para os gases a viscosidade cresce com o aumento da temperatura.