Aula 19

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 19 - A primeira lei da termodinâmica

Seções: 19.6, 19.7, 19.8

Verificar que a energia interna de um gás ideal a menos de algumas constantes é função somente da temperatura.

Os calores específicos de um gás ideal a partir da primeira lei da termodinâmica.

Estudar os processos termodinâmicos em um gás ideal:

Isocórico

Isobárico

Isotérmico

Adiabático

Motivação

Expansão adiabática

Compressão adiabática

Reduzindo a troca de calor em processos rápidos o processo é chamado de adiabático.

Quão rápido?

A energia interna

Como alterar o estado termodinâmico inicial de um gás ideal a um estado termodinâmico final?

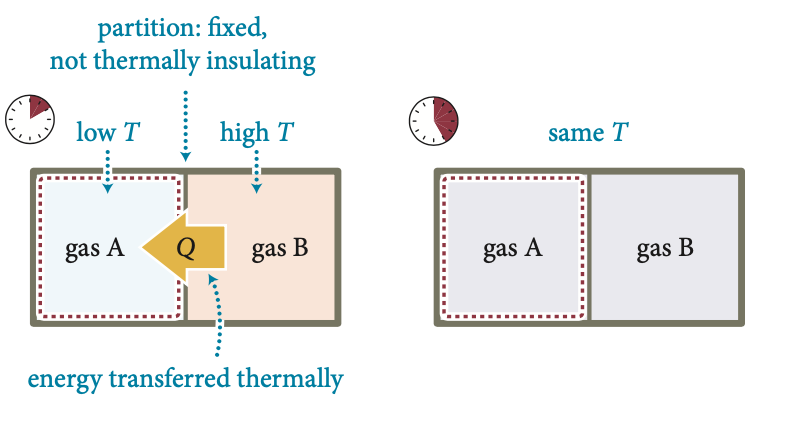
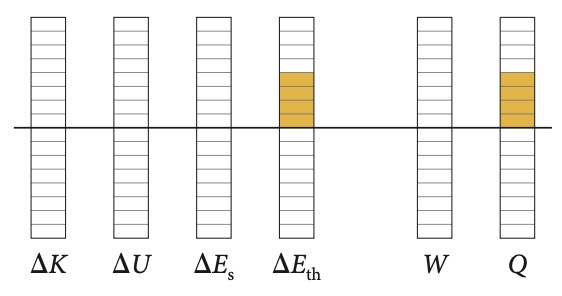
Parede fixa e diatérmica

Energia transferida termicamente

T_{baixa}

T_{alta}

T_{equilíbrio}

Calor

\Delta U = Q-W_{gas}

\Delta U = Q

\Delta E_p

\Delta U

Fonte: Eric Mazur

Trabalho adiabático

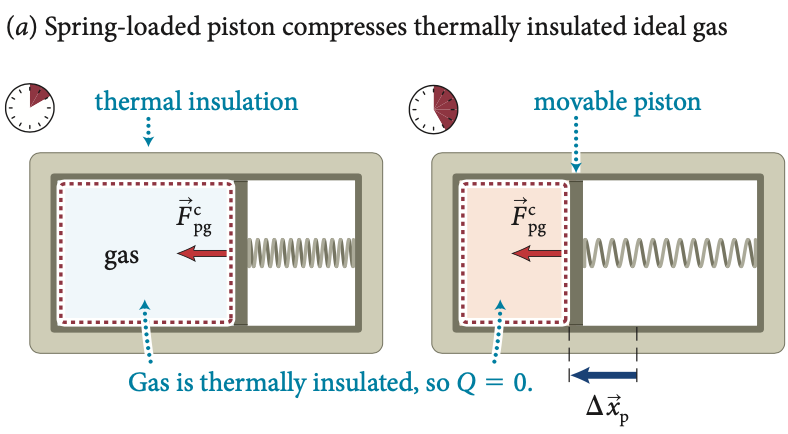
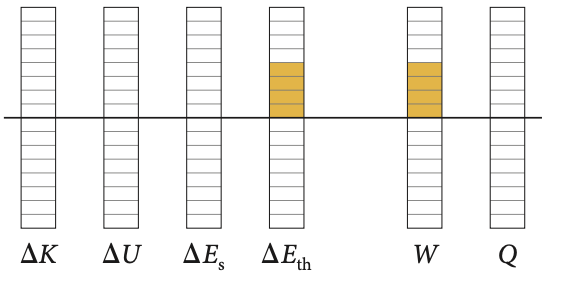
Parede fixa e adiabática

Pistão móvel e adiabático

Fonte: Eric Mazur

Gás termicamente isolado

\Delta U = Q+W_{pistão}

\Delta U = W_{pistão}

\Delta U

\Delta E_p

W_{pistão}=-W_{gas}

A energia interna

Para processos envolvendo variações infinitesimais, a primeira lei da termodinâmica é:

dU=\delta Q -\delta W_{gas}

Para processos quase-estáticos, as variáveis termodinâmicas são bem definidas e

\delta W_{gas} = PdV

A primeira lei da termodinâmica fica

dU=\delta Q -PdV

A energia interna, em geral, é uma função das variáveis termodinâmicas:

U=U(T,V)

U=U(T,P)

U=U(P,V)

Portanto, é uma função de estado. Mas o calor e o trabalho não são funções de estado.

A energia interna

A energia interna \(U\) de um gás ideal depende somente de sua temperatura \(T\), e não do volume ou da pressão.

U_{\text{gás ideal}}=U(T)

Um gás ideal deve satisfazer as equações:

PV=nRT

Para uma dada variação de temperatura, a variação da energia interna não depende do processo.

Como é a função \(U(T)\)?

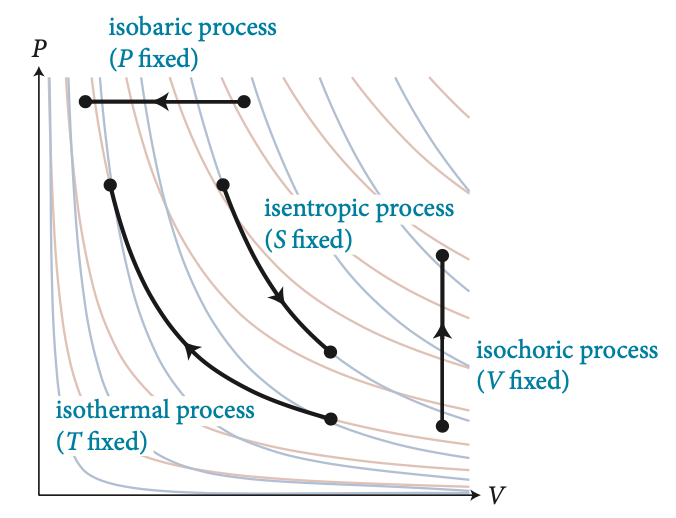
Processos isobáricos

Processos isocóricos

Processos adibáticos

Processos isotérmicos

Fonte: Mazur

Revendo as capacidades térmicas.

C_P=C_V+nR

C_V=\frac{d}{2}nR

C_P=\left(\frac{d}{2}+1\right)nR

d=3\,,\text{monoatômico}

d=5\,,\text{diatômico}

d=7\,,\text{poliatômico}

C_P=C_V

C_P>C_V

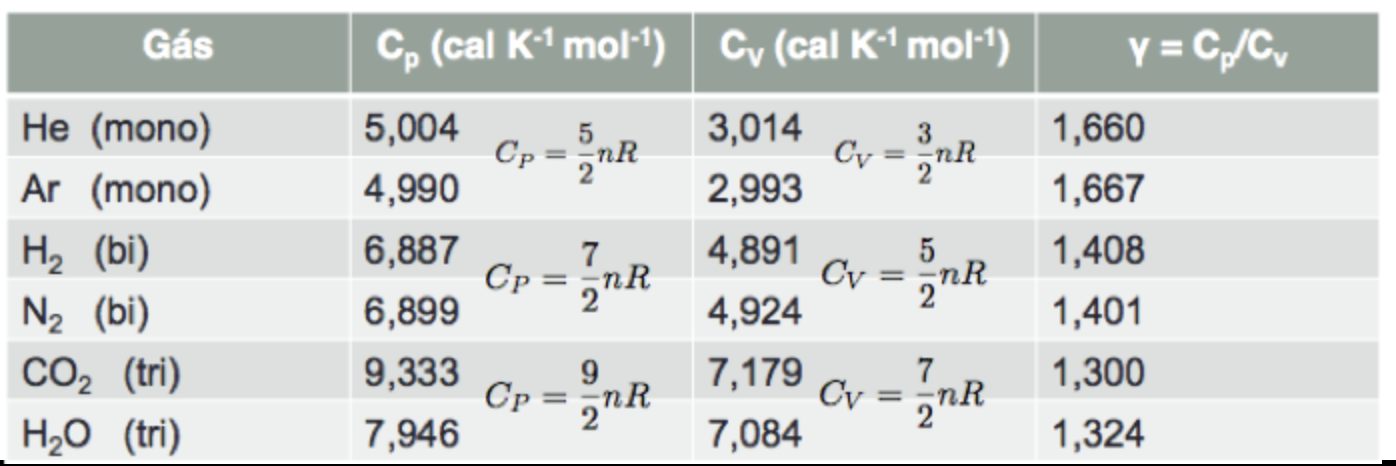
O índice adiabático é definido por:

\gamma = \frac{C_P}{C_V}=\frac{\frac{d}{2}+1}{\frac{d}{2}}

\gamma =1+\frac{2}{d}

Para um gás ideal, a capacidade térmica à pressão constante é maior do que a capacidade térmica à volume constante:

\Rightarrow

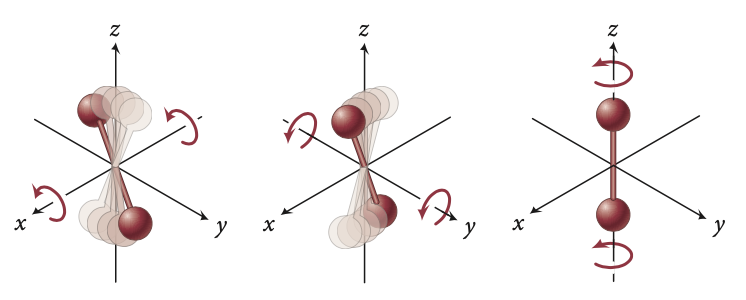
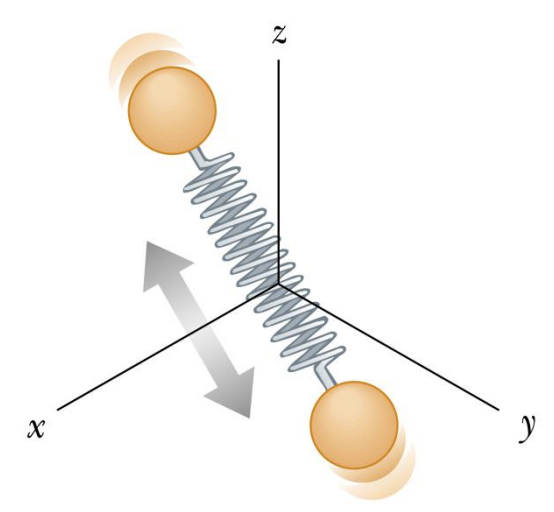
Translada nas três direções do espaço.

Translada e tem mais duas rotações: d = 3+2

Translada, rotaciona e vibra contraindo e expandindo: d = 3 + 2 + 2.

A energia interna nos processos isocóricos

Partindo da expressão geral:

dU = \left( \frac{\partial U}{\partial T} \right)_VdT

U=U(T)

\Rightarrow

E a partir da primeira lei da termodinâmica:

d U = \delta Q - PdV

No processo isocórico \(dV=0\) e não há trabalho, \(PdV=0\):

\delta Q = \left( \frac{\partial U}{\partial T} \right)_VdT

\left(\frac{\delta Q_V}{dT} \right)= \left( \frac{\partial U}{\partial T} \right)_V

\Rightarrow

Capacidade térmica a volume constante

\Rightarrow

\delta Q = dU

dU=C_VdT

\delta Q=C_VdT

A energia interna nos processos isocóricos

No processo isocórico o volume é constante. O trabalho é nulo.

A primeira lei da termodinâmica:

d U = \delta Q - PdV

O processo de transferência de energia se dá via calor. O trabalho realizado pelo gás é nulo porque o volume é constante.

\delta Q = dU= C_VdT

d U = \delta Q

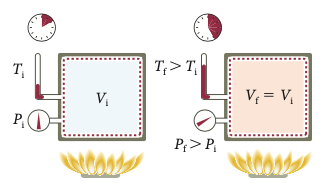
Como o volume é constante a pressão varia de forma direta com a temperatura.

Fonte: Mazur

\frac{P_iV_i}{T_i} = \frac{P_fV_f}{T_f}

\frac{P_i}{T_i} = \frac{P_f}{T_f}

{P_f} = \frac{P_i}{T_i}T_f

{P_f} = \frac{nR}{V}T_f

\Rightarrow

A energia interna nos processos isocóricos

A energia interna de um gás ideal é função apenas da temperatura.

d U = C_VdT

\Delta U = \int_{T_i}^{T_f}C_VdT

\Delta U = \frac{d}{2}nR(T_f-T_i)

\Delta U = \frac{d}{2}(P_fV_f-P_iV_i)

PV=nRT

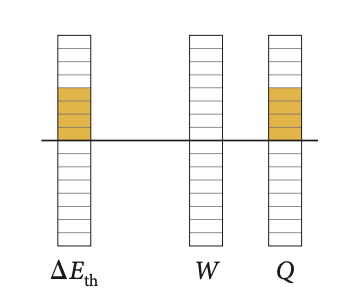
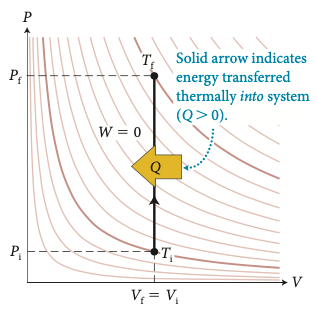
A seta indica energia transferida termicamente na forma de calor:

\(Q>0\)

{P} = \frac{nR}{V}T

{P} = cnt.T

Para uma variação finita:

Fonte: Mazur

Q= \frac{d}{2}(P_fV_f-P_iV_i)

A quantidade de calor é igual à variação da energia interna:

A quantidade de calor a volume constante aumenta a energia interna do sistema.

A energia interna nos processos isotérmicos

Partindo da expressão geral:

U=U(T)

E a partir da primeira lei da termodinâmcia:

d U = \delta Q - PdV

No processo isotérmico \(dT=0\) e sabemos que a energia interna depende da temperatura e não depende do volume. Portanto:

\delta Q = P\,dV

\delta Q=PdV

\delta W=PdV

\Rightarrow

\delta Q =\delta W

\Rightarrow

Calor trocado as custas de trabalho.

\delta Q_T = \delta W

A energia interna nos processos isotérmicos

No processo isotérmico a temperatura é constante. A energia interna é constante.

A primeira lei da termodinâmica:

d U = \delta Q - PdV

O processo de transferência de energia se dá via calor e o trabalho realizado pelo gás e a variação da energia interna é nula.

\delta Q = PdV

0 = \delta Q-PdV

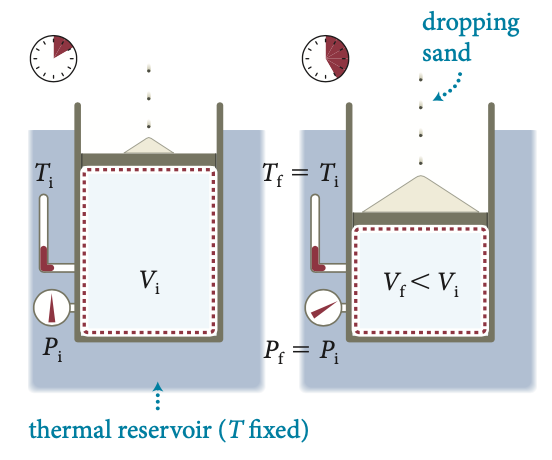
Reservatório térmico (\(T\) é fixo)

derramando areia

P_f

>P_i

Fonte: Mazur

Como a temperatura é constante, a pressão varia de forma inversa ao volume.

\frac{P_iV_i}{T_i} = \frac{P_fV_f}{T_f}

{P_iV_i} = {P_fV_f}

P_f=\frac{nRT}{V_f}

P_f=P_i\frac{V_i}{V_f}

\Rightarrow

A energia interna nos processos isotérmicos

\Delta U = \frac{d}{2}nR(T_f-T_i)

\Delta U =0

PV=nRT

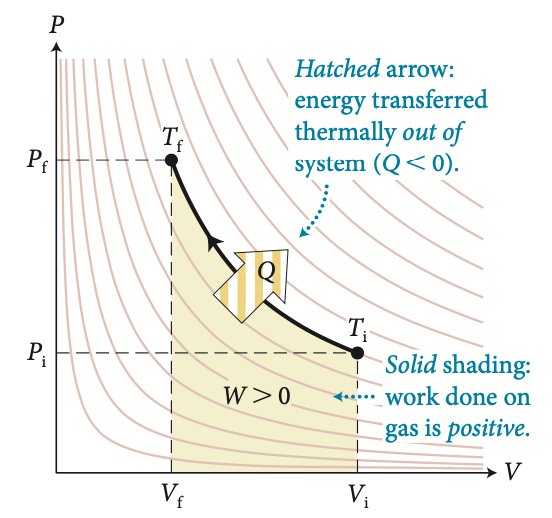
A energia é transferida termicamente na forma de calor

(\(Q<0\)).

O trabalho feito pelo gás é negativo (\(W<0\))

W<0

d U = \delta Q - PdV

P=\frac{nRT}{V}

P=\frac{cnt}{V}

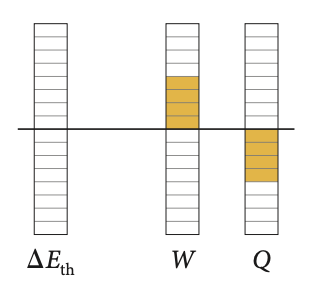
A energia interna de um gás ideal é função apenas da temperatura.

Para uma variação finita:

A quantidade de calor é igual ao trabalho:

Q =W=\int PdV

Q =W=\int_{V_i}^{V_f} \frac{nRT}{V}dV

Q =W=nRT \ln \left( \frac{V_f}{V_i} \right)=PV\ln\left( \frac{V_f}{V_i} \right)

Fonte: Mazur

A energia interna nos processos isobáricos

Partindo da expressão geral:

dU = \left( \frac{\partial U}{\partial T} \right)_PdT

U=U(T)

\Rightarrow

E a partir da primeira lei da termodinâmica:

d U = \delta Q - PdV

\Rightarrow

\delta Q = dU +PdV

Obtemos:

\delta Q = \left[ \left( \frac{\partial U}{\partial T} \right)_P + P\left( \frac{\partial V}{\partial T} \right)_P \right]dT

\left(\frac{\delta Q_P}{dT} \right)= \left( \frac{\partial U}{\partial T} \right)_P + P\left( \frac{\partial V}{\partial T} \right)_P

Capacidade térmica à pressão constante

\Rightarrow

C_P= \left( \frac{\partial H}{\partial T} \right)_P

Entalpia: \(H=U+PV\)

\delta Q=C_PdT

dH=C_PdT

\Rightarrow

\delta Q_P =dH

A energia interna nos processos isobáricos

No processo isobárico a pressão é constante. Há calor e trabalho.

A primeira lei da termodinâmica:

d U = \delta Q - PdV

C_VdT = C_PdT-nRdT

C_P = C_V+nR

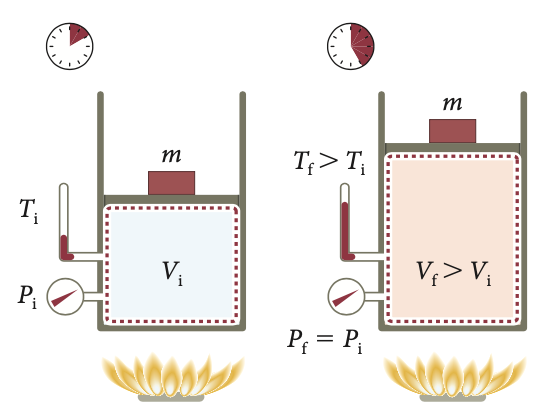
O processo de transferência de energia se dá via trabalho e calor à pressão constante.

Como a pressão é constante o volume varia de forma direta com a temperatura.

\frac{P_iV_i}{T_i} = \frac{P_fV_f}{T_f}

\frac{V_i}{T_i} = \frac{V_f}{T_f}

{V_f} = \frac{V_i}{T_i}T_f

{V_f} = \frac{nR}{P}T_f

\Rightarrow

Fonte: Mazur

A energia interna nos processos isobáricos

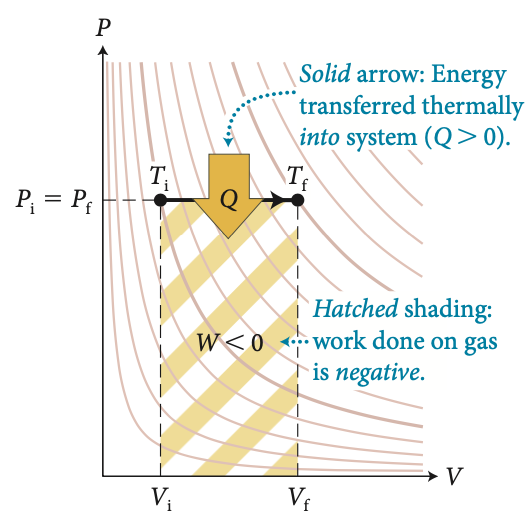
A seta indica energia transferida termicamente na forma de calor:

\(Q>0\)

O trabalho feito pelo gás é positivo

\(W>0\)

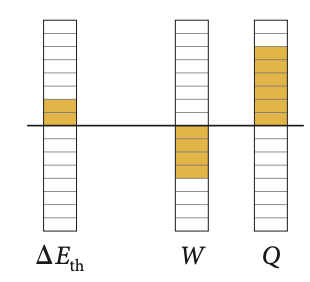
\Delta U = \frac{d}{2}nR(T_f-T_i)

W>0

PV=nRT

{V} = \frac{nR}{P}T

{V} = cnt.T

A energia interna de um gás ideal é função apenas da temperatura.

Para uma variação finita:

d U = \delta Q -\delta W

dU= C_VdT

\delta Q = C_PdT

\delta W= PdV

A energia interna varia as custas de trabalho e calor:

Q = \left(\frac{d}{2}+1\right)nR(T_f-T_i)

\Rightarrow

W= P(V_f-V_i)

\Rightarrow

Fonte: Mazur

A energia interna nos processos adiabáticos

Partindo da expressão geral:

U=U(T)

E a partir da primeira lei da termodinâmcia:

d U = \delta Q - PdV

\Rightarrow

\delta Q = dU +PdV

No processo adiabático \(\delta Q=0\) e sabemos que a energia interna depende da temperatura e não depende do volume. Portanto:

\delta Q = \left( \frac{\partial U}{\partial T} \right)_VdT +P dV

0=C_VdT+PdV

dU=-PdV

\delta W=PdV

\Rightarrow

dU = -\delta W

\Rightarrow

Energia interna varia as custas de trabalho.

dU = -\delta W

dU = \left( \frac{\partial U}{\partial T} \right)_PdT

\Rightarrow

A energia interna nos processos adiabáticos

No processo adiabático não há troca de calor.

A primeira lei da termodinâmica:

d U = \delta Q - PdV

dU = -PdV

dU =-\delta W

dU = C_VdT

PV=nRT

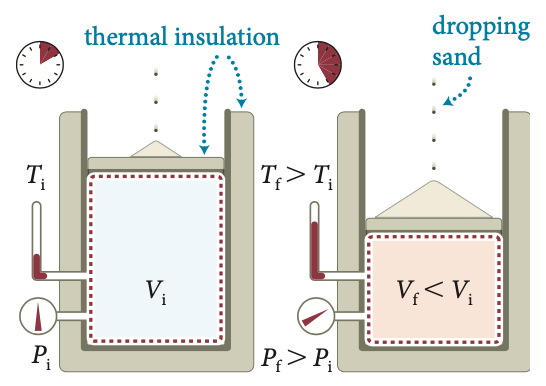
Paredes adiabáticas

Queda de areia

Fonte: Mazur

\frac{dT}{T}= - (\gamma-1)\frac{dV}{V}

Para um processo Entre dois estados inicial e final:

T_fV_f^{\gamma-1} = T_iV_i^{\gamma-1}

P_fV_f^{\gamma} = P_iV_i^{\gamma}

C_VdT= - \frac{nRT}{V}dV

C_V\frac{dT}{T}= - (C_P-C_V)\frac{dV}{V}

O processo de transferência de energia se dá via trabalho adiabático.

C_VdT= - PdV

A energia interna nos processos adibáticos

PV=nRT

W=-\Delta U

P_f=P_i\left(\frac{V_i}{V_f}\right)^{\gamma}

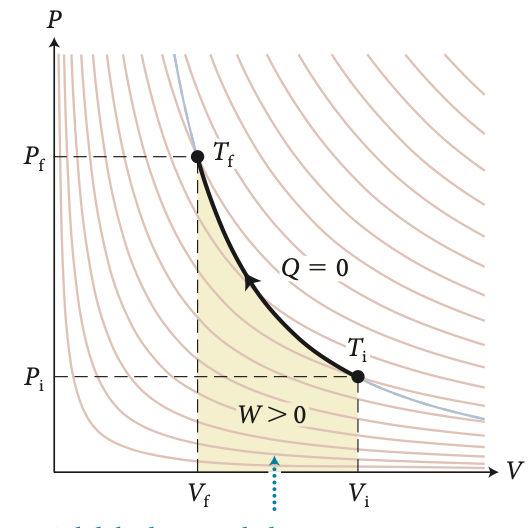
Na compressão adiabática há um aumento da temperatura as custas de trabalho negativo.

W<0

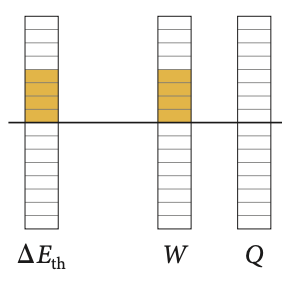
Entre dois estados inicial e final:

W_{i\rightarrow f} = -C_V(T_f-T_i)

W_{i\rightarrow f} = -C_V\left(\frac{P_fV_f}{nR}-\frac{P_iV_i}{nR}\right)

W_{i\rightarrow f} = -\frac{C_V}{nR}\left({P_fV_f}-{P_iV_i}\right)

W_{i\rightarrow f} = -\frac{C_V}{C_P-C_V}\left({P_fV_f}-{P_iV_i}\right)

W_{i\rightarrow f} = -\frac{1}{\gamma-1}\left({P_fV_f}-{P_iV_i}\right)

A energia interna de um gás ideal é função apenas da temperatura.

O trabalho adiabático é função dos estados inicial e final.

A energia interna nos processos adibáticos

Na expansão, o trabalho realizado pelo gás é positivo e isto diminui a energia interna. Na compressão, o trabalho realizado pelo gás é negativo, mas a energia interna aumenta.

O efeito é uma queda de temperatura na expansão e um aumento da temperatura na compressão.

O trabalho adiabático depende somente dos estados final e inicial.

\Delta U =- W_{i\rightarrow f}

W_{i\rightarrow f} = -C_V(T_f-T_i)

W_{i\rightarrow f} = -\frac{1}{\gamma-1}\left({P_fV_f}-{P_iV_i}\right)

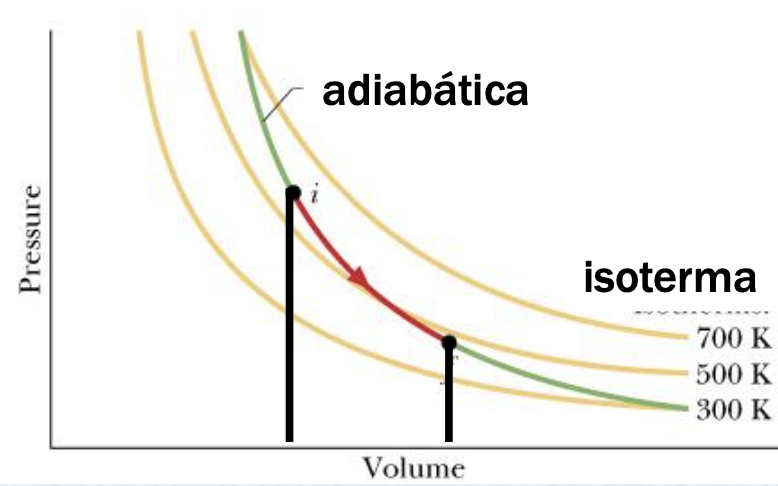
Para uma mesma variação de volume:

Uma expansão adiabática tem uma pressão final menor do que uma expansão isotérmica.

A temperatura diminui durante a expansão adiabática.

Questão 1

Um gás não-ideal possui uma equação de estado da forma

(P − P_0)V = nRT.

Dois moles deste gás são submetidos a uma expansão isotérmica a T=287,7 K, aumentando o volume do gás de V_i=10, 0 L para V_f=50, 0 L. Qual o trabalho realizado pelo gás no processo?

(Observações: R = 0, 082(atm.L)/(mol.K) e P_0 =0,20 atm).

Questão 2

Um litro de oxigênio à temperatura de 27 oC e a uma pressão de 10 atm se expande adiabaticamente até quintuplicar de volume. Quais são a pressão e a temperatura finais? Calcule o trabalho adiabático e o trabalho isotérmico.

Questão 3

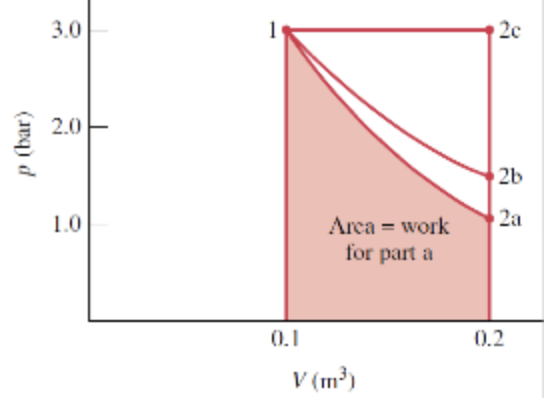
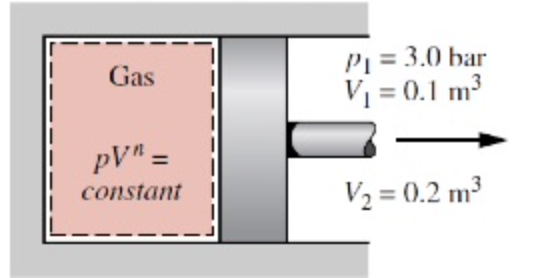
Um gás em uma montagem pistão-cilindro é submetido a um processo de expansão para o qual a relação entre a pressão e o volume é dada por

PV^n=constante

A pressão inicial é 3 x 10^5 N/m^2, o volume inicial é 0,1 m^3 e o volume final é 0,2 m^3. Determine o trabalho para o processo, em kJ, se:

a) n = 1,5

b) n 1,0

c) n = 0

Questão 4

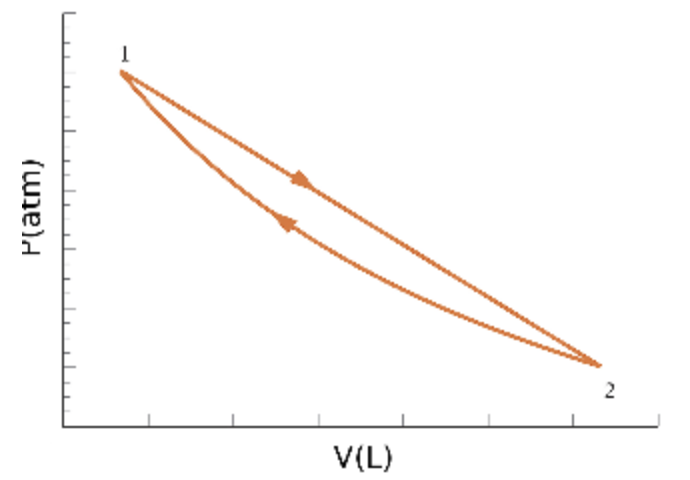
Uma amostra de 1,00 mol de um gás diatômico ideal se expande. Esta expansão é representada pela linha reta de 1 a 2 no diagrama PV. Depois, o gás é comprimido isotermicamente. Esta compressão é representada pela linha curva de 2 a 1 no mesmo diagrama. Calcule o trabalho total realizado no ciclo.

Dados: P_1 = 2,00 atm; V_1 = 11,5 L; P_2 = 1,00 atm. Use R = 0,082 amt.L/(mol.K).

Questão 5

Uma lata de tinta spray, selada e praticamente vazia, ainda contém uma quantidade residual do propelente: 0,020 mol de gás nitrogênio. A etiqueta na lata alerta claramente: “Não incinerar”. (a) Explique este alerta e desenhe um diagrama PV para o gás no caso de a lata ser submetida a uma temperatura alta. (b) Você está encarregado de testar a lata. O fabricante alega que ela pode suportar uma pressão interna de gás de 6,00 atm antes de explodir. A lata está, inicialmente, nas condições normais de temperatura e pressão em seu laboratório. Você inicia o aquecimento da lata uniformemente, usando um aquecedor com uma potência de saída de 200 W. A lada e o aquecedor estão em um forno isolado e você pode supor que 1,0 % do calor liberado pelo aquecedor seja absorvido pelo gás na lata. Quanto tempo você espera que o aquecedor permaneça aceso antes de a lata explodir?

Questão 6

A capacidade térmica a volume constante de certa quantidade de gás monoatômico é 49,8 J/K. (a) Determine o número de moles do gás. (b) Qual é a energia interna do gás a T = 300 K? (c) Qual é a sua capacidade térmica à pressão constante?

Dado: R =8,314 J/(mol.K)

Questão 7

Neste problema, 1,00 mol de um gás ideal diatômico é aquecido, a volume constante, de 300 K a 600 K. (a) Determine o aumento da energia interna do gás, o trabalho realizado pelo gás e o calor por ele absorvido. (b) Determine as mesmas quantidades para quando o gás é aquecido de 300 K a 600 K à pressão constante. Use a primeira lei da termodinâmica e seus resultados da parte (a) para calcular o trabalho realizado pelo gás. (c) Calcule novamente o trabalho na parte (b), agora integrando a equação dW = PdV (trabalho do gás).

Questão 8

Uma amostra de 0,500 mol de um gás monoatômico ideal, a 400 kPa e 300 K, expande-se quase-estaticamente até que sua pressão diminua para 160 kPa. Determine a temperatura e o volume finais do gás, o trabalho realizado por ele e o calor que ele absorve, se a expansão é (a) isotérmica e (b) adiabática.

Questão 9

Uma amostra de 0,500 mol de gás hélio expande-se adiabaticamente e quase-estaticamente, de uma pressão inicial de 5,00 atm e uma temperatura de 500 K para uma pressão final de 1,00 atm. Determine (a) a temperatura final do gás, (b) o volume final do gás, (c) o trabalho realizado pelo gás e (d) a variação da energia interna do gás.

Questão 10

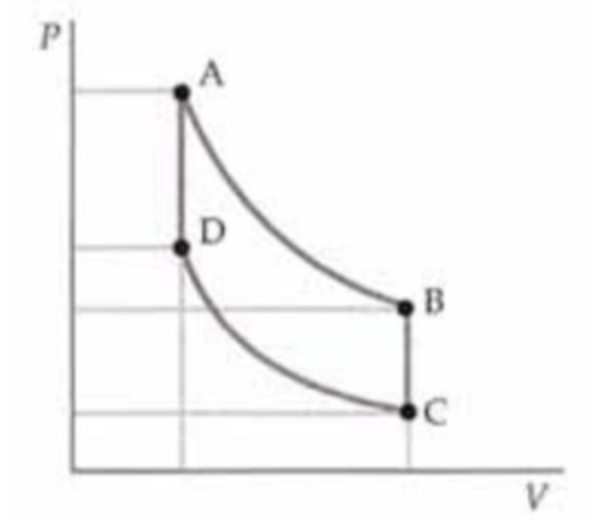
No ponto D da figura, a pressão e a temperatura de 2,00 mols de um gás monoatômico ideal são 2,00 atm e 360 K, respectivamente. O volume do gás no ponto B do diagrama PV é igual a três vezes o volume no ponto D e su a pressão é o dobro da pressão no ponto C. Os caminhos AB e CD representam processos isotérmicos. O gás é conduzido através de um ciclo completo ao longo do caminho DABCD. Determine o trabalho realizado pelo gás e o calor do processo, em cada etapa do ciclo.

A energia interna

Experimentalmente, verifica-se que em um processo de expansão livre, um gás ideal ao expandir:

A pressão e volume do gás variam na expansão livre:

Fonte: https://demonstrations.wolfram.com

Não transfere energia através da fronteira na forma de trabalho:

\delta W = 0

Não transfere energia através da fronteira na forma de calor:

\delta Q = 0

Não altera a temperatura da vizinhança:

Logo, a variação da energia interna é nula:

dU=0

T_f = T_i

\Rightarrow dT= 0

P_f < P_i

\Rightarrow dP< 0

V_f > V_i

\Rightarrow dV> 0

dU=\delta Q -\delta W_{gas}

A energia interna

Seja a energia interna como função da temperatura e pressão:

dU = \left( \frac{\partial U}{\partial T} \right)_PdT + \left( \frac{\partial U}{\partial P} \right)_TdP

U=U(T,P)

A partir das observações experimentais da expansão livre de um gás ideal:

Para uma variação infinitesimal da temperatura e pressão:

\left( \frac{\partial U}{\partial T} \right)_{P=P_0}

\left( \frac{\partial U}{\partial P} \right)_{T=T_0}

P_0

T_0

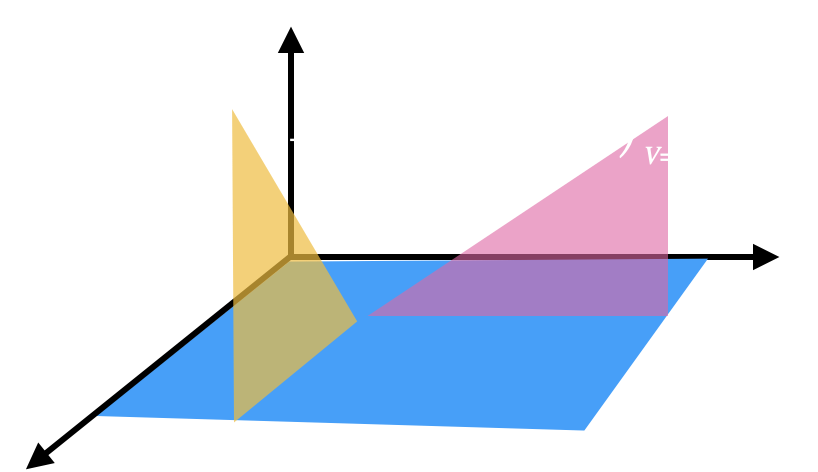
O resultado mostra que a energia interna de um gás ideal não depende da pressão e depende da temperatura.

dT = 0\qquad \Rightarrow

\left( \frac{\partial U}{\partial T} \right)_P\neq 0

\(U\) não é função de \(T\).

Para que \(dU=0\), as condições são:

dP\neq 0\qquad \Rightarrow

\left( \frac{\partial U}{\partial P} \right)_T=0

\(U\) não é função de \(P\).

dU=0\,,\qquad\delta Q=0\,,\qquad \delta W=0\,,\qquad dT = 0\,,\qquad dP\neq 0\,,\qquad dV \neq 0

A energia interna

Seja a energia interna como função da temperatura e pressão:

dU = \left( \frac{\partial U}{\partial T} \right)_VdT + \left( \frac{\partial U}{\partial V} \right)_TdV

U=U(T,V)

A partir das observações experimentais da expansão livre de um gás ideal:

Para uma variação infinitesimal da temperatura e pressão:

\left( \frac{\partial U}{\partial T} \right)_{P=P_0}

\left( \frac{\partial U}{\partial V} \right)_{T=T_0}

V_0

T_0

O resultado mostra que a energia interna de um gás ideal não depende do volume e depende da temperatura.

Para que \(dU=0\), as condições são:

dV\neq 0\qquad \Rightarrow

\left( \frac{\partial U}{\partial V} \right)_T=0

\(U\) não é função de \(V\).

dT = 0\qquad \Rightarrow

\left( \frac{\partial U}{\partial T} \right)_V\neq 0

\(U\) não é função de \(T\).

dU=0\,,\qquad\delta Q=0\,,\qquad \delta W=0\,,\qquad dT = 0\,,\qquad dP\neq 0\,,\qquad dV \neq 0

A energia interna nos processos isocóricos

Partindo da expressão geral:

dU = \left( \frac{\partial U}{\partial T} \right)_VdT + \left( \frac{\partial U}{\partial V} \right)_TdV

U=U(T,V)

\Rightarrow

E a partir da primeira lei da termodinâmcia:

d U = \delta Q - PdV

\Rightarrow

\delta Q = dU +PdV

Obtemos:

\delta Q = \left( \frac{\partial U}{\partial T} \right)_VdT + \left[ \left( \frac{\partial U}{\partial V} \right)_T +P\right]dV

No processo isocórico \(dV=0\) e não há trabalho, \(PdV=0\):

\delta Q_V = \left( \frac{\partial U}{\partial T} \right)_VdT

\left(\frac{\delta Q_V}{dT} \right)= \left( \frac{\partial U}{\partial T} \right)_V

\Rightarrow

Capacidade térmica a volume constante

\Rightarrow

c_V= \left( \frac{\partial U}{\partial T} \right)_V

Energia interna é função apenas de \(T\)

\Rightarrow

\delta Q = dU

dU=C_VdT

\delta Q=C_VdT

0\,,\text{gás ideal}

A energia interna nos processos isotérmicos

Partindo da expressão geral:

dU = \left( \frac{\partial U}{\partial T} \right)_VdT + \left( \frac{\partial U}{\partial V} \right)_TdV

U=U(T,V)

\Rightarrow

E a partir da primeira lei da termodinâmcia:

d U = \delta Q - PdV

\Rightarrow

\delta Q = dU +PdV

Obtemos:

\delta Q = \left( \frac{\partial U}{\partial T} \right)_VdT + \left[ \left( \frac{\partial U}{\partial V} \right)_T +P\right]dV

No processo isotérmico \(dT=0\) e sabemos que a energia interna depende da temperatura e não depende do volume. Portanto:

\delta Q_T = PdV

\delta Q=PdV

\delta W=PdV

\Rightarrow

\delta Q =\delta W

\Rightarrow

Calor trocado as custas de trabalho.

\delta Q_T = \delta W

0\,,\text{gás ideal}

A energia interna nos processos isobáricos

Partindo da expressão geral:

dU = \left( \frac{\partial U}{\partial T} \right)_PdT + \left( \frac{\partial U}{\partial P} \right)_TdP

U=U(T,P)

\Rightarrow

E a partir da primeira lei da termodinâmica:

d U = \delta Q - PdV

\Rightarrow

\delta Q = dU +PdV

Obtemos:

\delta Q = \left[ \left( \frac{\partial U}{\partial T} \right)_P + P\left( \frac{\partial V}{\partial T} \right)_P \right]dT + \left[ \left( \frac{\partial U}{\partial P} \right)_T +P \left( \frac{\partial V}{\partial P} \right)_T \right]dP

No processo isobárico \(dP=0\):

\delta Q_P = \left[\left( \frac{\partial U}{\partial T} \right)_P + P\left( \frac{\partial V}{\partial T} \right)_P\right]dT

\left(\frac{\delta Q_P}{dT} \right)= \left( \frac{\partial U}{\partial T} \right)_P + P\left( \frac{\partial V}{\partial T} \right)_P

\Rightarrow

Capacidade térmica à pressão constante

\Rightarrow

C_P= \left( \frac{\partial H}{\partial T} \right)_P

Entalpia: \(H=U+PV\)

\delta Q=C_PdT

dH=C_PdT

\Rightarrow

\delta Q_P =dH

0\,,\text{gás ideal}

A energia interna nos processos adiabáticos

Partindo da expressão geral:

dU = \left( \frac{\partial U}{\partial T} \right)_VdT + \left( \frac{\partial U}{\partial V} \right)_TdV

U=U(T,V)

\Rightarrow

E a partir da primeira lei da termodinâmcia:

d U = \delta Q - PdV

\Rightarrow

\delta Q = dU +PdV

Obtemos:

\delta Q = \left( \frac{\partial U}{\partial T} \right)_VdT + \left[ \left( \frac{\partial U}{\partial V} \right)_T +P\right]dV

No processo adiabático \(\delta Q=0\) e sabemos que a energia interna depende da temperatura e não depende do volume. Portanto:

C_VdT+PdV=0

dU=-PdV

\delta W=PdV

\Rightarrow

dU = -\delta W

\Rightarrow

Energia interna varia as custas de trabalho.

dU = -\delta W

Entalpia. O experimento de Joule-Thomson.

Nos refrigeradores, o gás (substância de trabalho) deve em algum momento diminuir a temperatura para que o gás entre no refrigerador a uma temperatura menor do que a do seu interior.

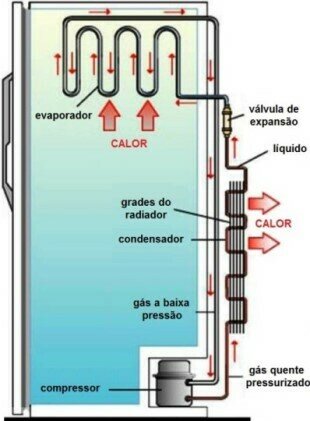
A válvula de expansão controla a entrada do líquido no evaporador, que tem sua pressão diminuída, permitindo assim sua vaporização. Como esse é um processo endotérmico, a temperatura dos arredores diminui para cerca de -19ºC

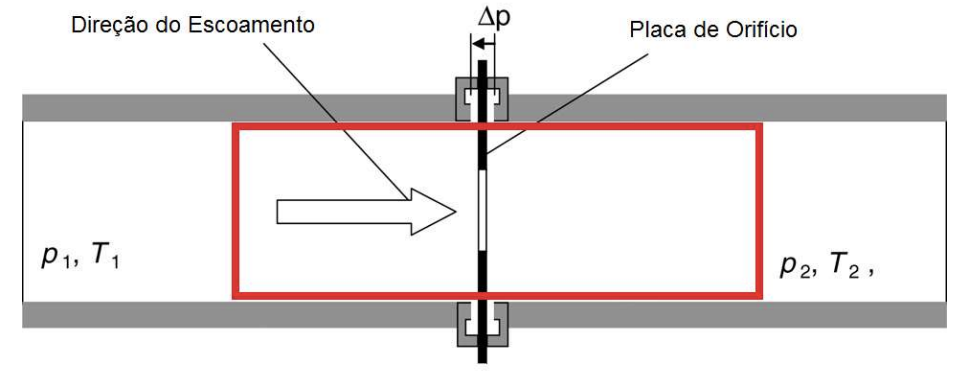
Fonte: https://www.omundodaquimica.com.br/curiosidade

Fonte: http://repositorio.utfpr.edu.br

A pressão e temperatura variam. Verifica-se experimentalmente:

P_1>P_2

T_1>T_2

Entalpia. O experimento de Joule-Thomson.

Sejam dois gases separados por um tampão poroso. O gás da esquerda ao expandir não transfere energia através da fronteira na forma de calor, \(Q=0\).

0=\Delta U +W_{total}

0=U_2-U_1+(P_2V_2-P_1V_1)

U_2+P_2V_2=U_1+P_1V_1

\Rightarrow H_2=H_1

A entalpia \(H=U+PV\) é uma quantidade conservada (isoentálpico).

\Rightarrow \Delta H = 0

P_1>P_2

T_1>T_2

O fluido ao passar por um estrangulamento ou tampão poroso fica sujeito ao processo termodinâmico:

Entalpia. O experimento de Joule-Thomson.

Para processos onde a entalpia seja constante:

A entalpia é função de estado: \(H = H(P,T)\).

dH=\left( \frac{\partial H}{\partial T} \right)_PdT + \left( \frac{\partial H}{\partial P} \right)_TdP

-\left( \frac{\partial H}{\partial P} \right)_TdP = \left( \frac{\partial H}{\partial T} \right)_PdT

-\left( \frac{\partial H}{\partial P} \right)_TdP = C_PdT

-\left( \frac{\partial H}{\partial P} \right)_T = C_P\left( \frac{\partial T}{\partial P} \right)_H

-\left( \frac{\partial H}{\partial P} \right)_T = C_P\mu_{J-T}

O coeficiente de Joule-Thomson:

\mu_{J-T}=\left( \frac{\partial T}{\partial P} \right)_H

\Rightarrow T_2 = T_1+\mu_{JT}(P_2-P_1)

Para \(\mu_{J-T} = 0 \Rightarrow T_2 = T_1\).

Para \(\mu_{J-T} < 0 \Rightarrow T_2 < T_1\).

Para \(\mu_{J-T} > 0 \Rightarrow T_2 >T_1\).

Fonte: https://www.wolframcloud.com/obj/9c447657-cc8e-4904-83ba-ecdd68fb7340

Qual gás diminui de temperatura em um processo de Joule-Thomson?