Aula 21

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 20 - A segunda lei da termodinâmica

Seções: 20.1, 20.2, 20.4, 20.5

Diferenciar processos reversíveis dos processos irreversíveis.

Explicar o princípio do aumento da entropia.

Relacionar a entropia aos processos reversíveis, irreversíveis e impossíveis.

Definir o conceito de entropia.

Calcular a variação da entropia das máquinas térmicas.

Calcular a eficiência das máquinas térmicas.

Motivação

Os estudos iniciais da termodinâmica foram motivados pelo desejo de descobrir os princípios que governavam máquinas térmicas, de forma que pudessem projetar outras mais eficientes e potentes.

Fonte: https://youtu.be/DGEb7nKm9SI

Fonte: https://youtu.be/YqL9tsDtMqc

Fonte: https://youtu.be/73txXT21aZU

Fonte: https://youtu.be/VdW1DFyq-2k

Em um ciclo a energia é conservada (∆U = 0), mas a eficiência da máquina é limitada porque W/Q < 1.

Não se trata de uma questão da tecnologia, mas uma imposição da natureza.

Motivação

Ninguém sabe o que é entropia, de modo que você sempre terá a vantagem em um debate.

(conselho de J. von Neumann a C. Shannon)

Todo matemático sabe que é impossível entender um curso elementar de termodinâmica.

(V. I. Arnold)

A culpa é da entropia. Será?

Processos reversível e irreversível

A primeira lei da termodinâmica:

\Delta U = Q_{total}-W_{total}

se aplicada ao Universo que não possui vizinhança requer:

Q_{total}=W_{total} = 0

\Rightarrow

\Delta U =0

Portanto, a energia do universo é constante:

U_f=U_i=constante

Se a energia do universo se conserva por que devemos economizá-la?

Processos reversível e irreversível

A primeira lei da termodinâmica:

se aplicada a um sistema num certo sentido ou sequência temporal, conservando a energia em cada instante, mas que pode ocorrer no sentido inverso:

Nem toda energia está disponível num processo cíclico.

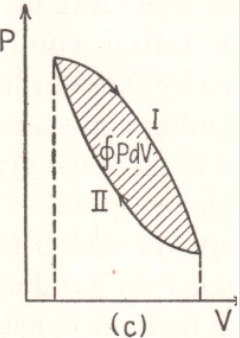
Fonte: Sears & Zemansky

Portanto, a energia do sistema também é constante:

U_f=U_i=constante

\Delta U = Q_{total}-W_{total}

Q_{total}=W_{total} = 0

\Rightarrow

\Delta U =0

Processos reversível e irreversível

O primeiro princípio da termodinâmica não introduz quaisquer limitações na possibilidade de transformar energia de uma forma noutra.

Q\leftrightarrow W

A primeira lei da termodinâmica atesta que é sempre possível transformar trabalho em calor ou calor em trabalho desde que a quantidade de calor seja igual à quantidade de trabalho.

Isto significa que não existe a possibilidade de construir um perpetuum mobile de primeira espécie (criar energia).

Fonte: https://youtu.be/DwOblAnQnh4

Q=W

\Rightarrow

\Delta U =0

(Enrico Fermi)

U_f=U_i=constante

Processos reversível e irreversível

A reserva de energia térmica contida no solo, oceanos e na atmosfera é praticamente ilimitada. Mas é improvável transformar a energia térmica completamente em trabalho.

Não existe a possibilidade de construir um perpetuum mobile da segunda espécie (converter 100% de calor em trabalho).

(Enrico Fermi)

Transformar trabalho em 100% de calor. Sim. É possível.

Transformar calor em 100% de trabalho. Não. Não é possível.

Processos reversível e irreversível

Um reservatório térmico a uma temperatura \(T\) é capaz de transformar calor em trabalho.

Expansão isotérmica. Transformação não cíclica.

Contudo, a transformação de calor em trabalho não é o único resultado final do processo.

No fim do processo, o gás ocupa um volume maior e uma pressão menor do que no princípio.

Não houve um único efeito neste processo. A pressão e volume mudaram!

Q\rightarrow W

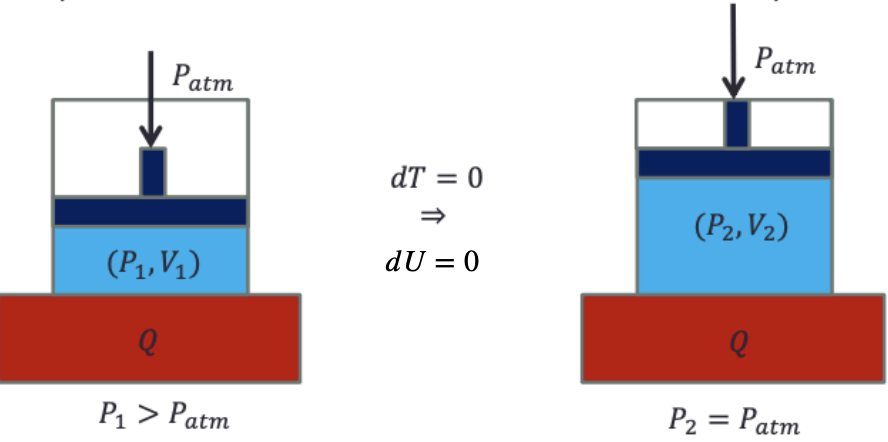
em qualquer processo isotérmico.

A primeira lei é um princípio de conservação da energia.

Q_{1\rightarrow 2} = W_{1\rightarrow 2}

\Rightarrow \Delta U = 0

reservatórios térmicos

Processos reversível e irreversível

Um reservatório térmico a uma temperatura \(T\) é capaz de transformar trabalho em calor.

Expansão e compressão isotérmicas. Transformação cíclica.

Na tentativa de retornar ao estado inicial, num ciclo, algo mudou no processo.

Veremos que em um ciclo, há uma degradação da energia útil (energia que deixou de realizar trabalho), mas a energia ainda é conservada!

Não houve um único efeito neste ciclo. O reservatório térmico precisou ser trocado.

Q\rightarrow W

W\rightarrow Q

dT=0

dU=0

\Rightarrow

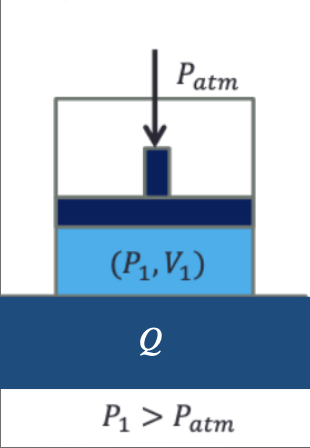
em qualquer processo cíclico.

A primeira lei é um princípio de conservação da energia.

W_{ciclo} = Q_{ciclo}

\Rightarrow \Delta U = 0

Qualquer processo cíclico que resulte apenas na transferência de energia entre dois reservatórios de calor de diferentes temperaturas é um processo irreversível.

Os reservatórios de calor mantêm a temperatura constante, pois há uma transição de fase latente: \(Q = mL\).

Reservatórios de trabalho mantém a pressão constante ao executar trabalho.

Máquina térmica

Processos reversível e irreversível

Qualquer processo cíclico que resulte apenas na transferência de energia entre um reservatório de trabalho e um outro de calor é um processo irreversível.

Processo irreversíveis ocorrem em apenas um único sentido.

O gás é o sistema. Os reservatórios de calor e trabalho são a vizinhança.

Processos reversível e irreversível

Uma vez que dissipações e estados de não equilíbrio estão presentes em todos os processos reais, segue que todos os processos naturais são ditos irreversíveis.

Há irreversibilidade quando:

As condições de equilíbrio mecânico, térmico ou químico não são satisfeitos.

Efeitos dissipativos como atrito, viscosidade, inelasticidade, resistência elétrica e histerese magnética estão presentes.

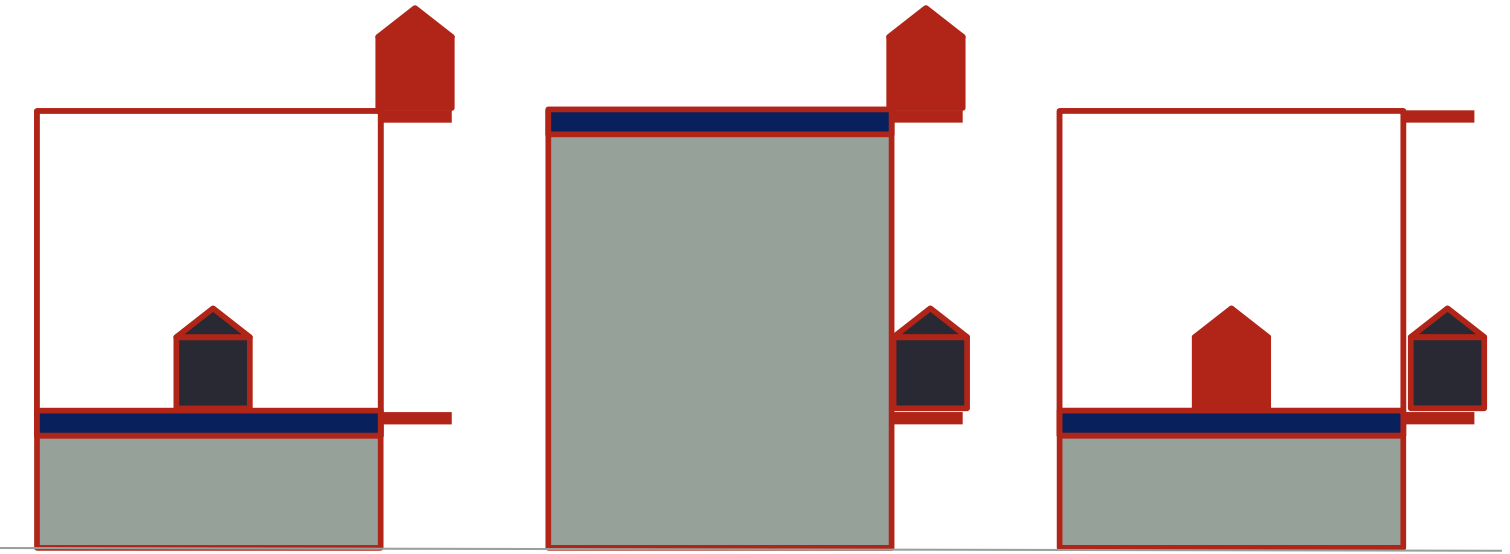
O sistema (gás) retornou ao estado inicial, mas não a sua vizinhança (pesos).

Houve uma alteração no Universo (Sistema+Vizinhança).

Problema: Reduziu-se a capacidade de se realizar trabalho.

O sistema (gás) é reversível.

A vizinhança (pesos) é irreversível.

Processos reversível e irreversível

Um processo reversível é aquele que é realizado de tal forma que, ao final do processo, tanto o sistema quanto a vizinhança local podem ser restaurados aos seus estados iniciais sem produzir nenhuma mudança no resto do universo.

Com muito boa aproximação há reversibilidade quando:

Os processos são quase-estáticos;

Não há efeitos dissipativos.

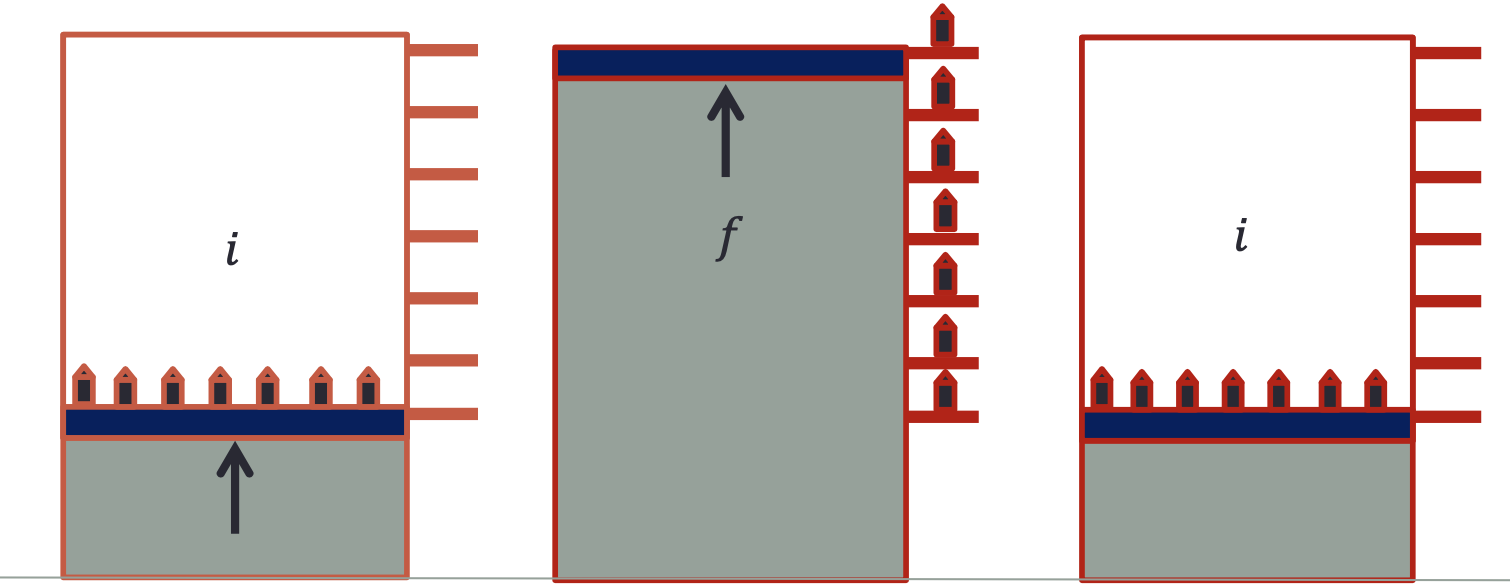
O sistema (gás) e a vizinhança (pesos) retornaram ao estado inicial.

Não houve uma alteração no Universo (Sistema+Vizinhança).

Problema: O processo precisa de muitas etapas (\(N\rightarrow \infty\)) e torna-se lento (\(t\rightarrow \infty\)).

É possível que o peso se mova sozinho?

Processos reversível e irreversível

Processos reversíveis:

Ocorrem em um universo em constante equilíbrio (ideal).

Processos irreversíveis:

Ocorrem em um universo que evolui de maneira a “degradar-se” (real).

O calor não é convertido totalmente em trabalho útil num processo cíclico.

EXEMPLO:

Nem toda energia está disponível como trabalho útil num processo cíclico!

A energia é conservada, mas não é eficientemente aproveitada.

1^a\text{ Lei}

2^a\text{ Lei}

Entropia. A segunda lei da termodinâmica.

Como calor é apenas a diferença entre o trabalho adiabático e o trabalho total:

\Delta U = -W_{adiab ático}

\Delta U =Q-W_{total}

-W_{adiabático}=Q-W_{total}

Q=W_{total}-W_{adiabático}

\Rightarrow

Seja qual for o tipo de trabalho, ele pode ser escrito como o produto de uma variável intensiva (pressão) pela variação de uma variável extensiva (volume):

W=P\Delta V

O outro processo de troca de energia, o calor, pode ser escrito como o produto de uma variável intensiva (temperatura) pela variação de uma variável extensiva (entropia):

Q=T\Delta S

\Rightarrow \quad\Delta S=\frac{Q}{T}

A unidade da entropia \(S\) é o joule/kelvin (J/K).

Entropia. A segunda lei da termodinâmica.

O princípio do aumento da entropia atesta que para qualquer processo, a entropia do universo nunca diminui.

Em qualquer transformação de um sistema isolado, a variação da entropia do universo é não negativa:

\Delta S_{universo} \geq 0

\Delta S_{universo} =0

\Delta S_{universo} >0

\Delta S_{universo} <0

REVERSÍVEL

IRREVERSÍVEL

IMPOSSIVEL

S_f = S_i

S_f > S_i

S_f < S_i

\Delta S_u=\frac{Q}{T} \geq 0

Sistemas reais.

Sistemas idealizados.

Sistema miraculosos.

Entropia. A segunda lei da termodinâmica.

Nas trocas de energia realizadas via troca de trabalho mecânico, adiabaticamente (\(Q=0\)), podemos afirmar que:

\Delta S_{universo} =0

S_{universo,f} = S_{universo,i}

É um processo reversível (idealizado).

Nas trocas de energia realizadas via troca de calor, isotermicamente, podemos afirmar que:

\Delta S_{universo} =+\frac{Q}{T} > 0

É um processo irreversível (real).

S_{universo,f} = S_{universo,i}+\frac{Q}{T}>0

A entropia é constante.

A entropia sempre aumenta.

Entropia. A segunda lei da termodinâmica.

Quando 1500 J de calor flui devido ao sistema A à 500 K e outro sistema B à 300 K:

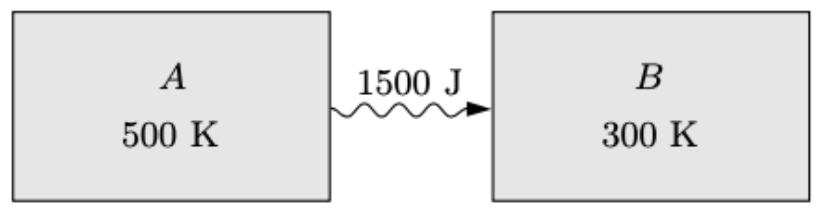
Se A e B são reservatórios térmicos (suas temperaturas não variam) no processo:

A entropia não pode ser destruída, mas pode ser criada.

A entropia é criada quando há fluxo de calor entre objetos com temperaturas diferentes.

\Delta S_A = -\frac{1500\text{ J}}{500\text{ K}} = -3\text{ J/K}

A variação é negativa. Perde pouca entropia quanto \(T\) é alto.

\Delta S_B = +\frac{1500\text{ J}}{300\text{ K}} = +5\text{ J/K}

A variação é positiva. Ganha muita entropia quanto \(T\) é baixo.

\Delta S_u = +2\text{ J/K} >0

A entropia do universo aumentou.

Vizinhança

Sistema

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica: Enunciado de Clausius (espontâneo).

É impossível um processo cujo único resultado líquido seja retirar energia de um reservatório de calor e entregar a mesma quantidade de energia a um outro reservatório de calor à temperatura mais alta.

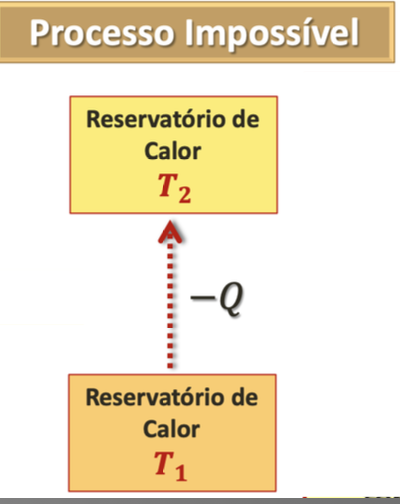
cujo único resultado líquido \(\rightarrow\) algo a mais deve ocorrer, num ciclo.

T_2>T_1

Cortesia: Prof. Tarciro Nortarson

Vizinhança

Sistema

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica: Enunciado de Clausius (espontâneo).

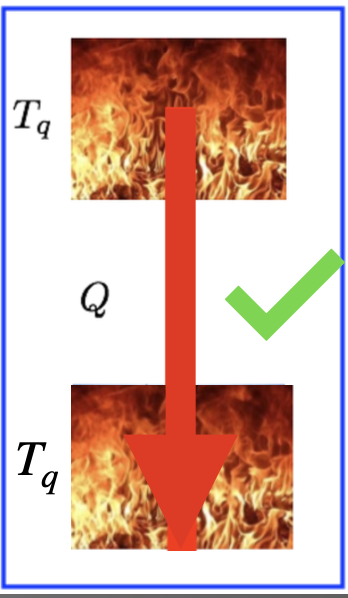
Reservatório de calor a temperaturas iguais:

A partir da primeira lei:

\Delta U_u =\Delta U_{1}+\Delta U_2 = 0

\Delta U_{1}=-Q

\Delta U_{2}=+Q

A partir da segunda lei:

\Delta S_1 = -\frac{Q}{T_1}

\Delta S_2 = +\frac{Q}{T_2}

\Delta S_u=\Delta S_{1}+\Delta S_2 = \left( -\frac{Q}{T_q} +\frac{Q}{T_q} \right)=0

O processo é reversível. O processo pode ocorrer, pois \(\Delta S_u = 0\). Não viola Clausius.

Diminui pouco

Aumenta pouco

T_1=T_2=T_q

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica: Enunciado de Clausius (espontâneo).

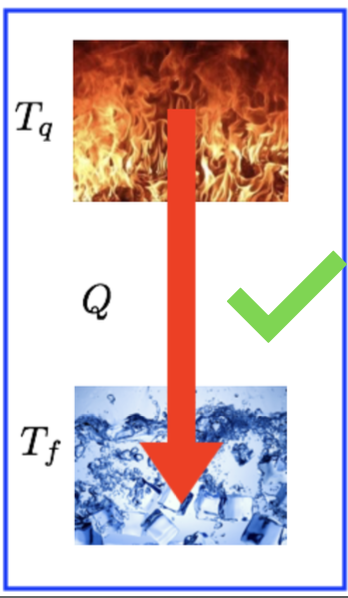
Reservatório de calor a temperaturas diferentes:

A partir da primeira lei:

\Delta U_u =\Delta U_{q}+\Delta U_f = 0

\Delta U_{q}=-Q

\Delta U_{f}=+Q

A partir da segunda lei:

\Delta S_q = -\frac{Q}{T_q}

\Delta S_f = +\frac{Q}{T_f}

\Delta S_u=\Delta S_{f}+\Delta S_q = \left( \frac{Q}{T_f}- \frac{Q}{T_q} \right)>0

O processo é irreversível. O processo pode ocorrer, pois \(\Delta S_u > 0\). Não viola Clausius.

Aumenta muito

Diminui pouco

T_q>T_f

\Delta S_u=0,098{\text{ J/K}}

0,366\text{ J/K}

0,268\text{ J/K}

T_q=373,15\text{ K}

T_f=273,15\text{ K}

Q=100\text{ J}

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica: Enunciado de Clausius (não espontâneo).

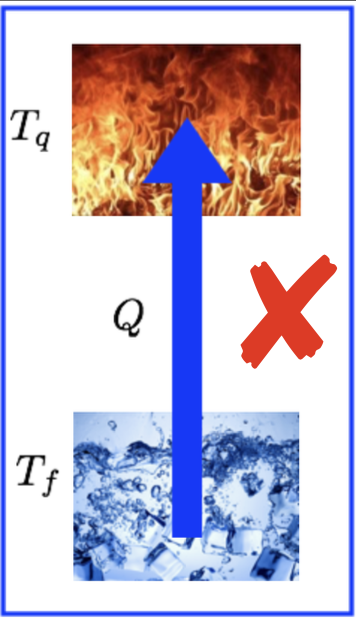
Reservatório de calor a temperaturas diferentes:

A partir da primeira lei:

\Delta U_u =\Delta U_{q}+\Delta U_f = 0

\Delta U_{q}=+Q

\Delta U_{f}=-Q

A partir da segunda lei:

\Delta S_q = +\frac{Q}{T_q}

\Delta S_f = -\frac{Q}{T_f}

\Delta S_u=\Delta S_{q}+\Delta S_f = \left( \frac{Q}{T_q}- \frac{Q}{T_f} \right)<0

O processo é impossível. O processo não pode ocorrer, pois \(\Delta S_u < 0\). Viola Clausius.

Aumenta pouco

Diminui muito

O que fazer para não violar Clausius?

T_q > T_f

\Delta S_u=-0,098{\text{ J/K}}

0,366\text{ J/K}

0,268\text{ J/K}

T_q=373,15\text{ K}

T_f=273,15\text{ K}

Q=100\text{ J}

A experiência mostra que se dois reservatórios de calor, a temperaturas diferentes, estão em contato térmico, a energia será transferida espontaneamente sempre do reservatório à maior temperatura para o reservatório à menor temperatura.

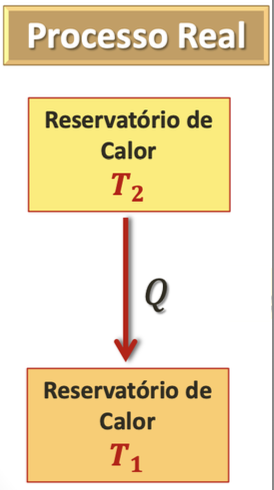
Cortesia: Prof. Tarciro Nortarson

Os reservatórios de calor (vizinhança) são fontes inesgotáveis de energia.

Na ausência de trabalho, a temperatura indica o sentido do fluxo de calor. O enunciado de Clausius explica esse sentido e espontaneidade.

Nos reservatórios térmicos as trocas de calor são realizadas isotermicamente.

T_2 > T_1

Os processos observados na escala macroscópica tendem a ocorrer num só sentido, ou seja, são irreversíveis.

Fonte: http://175mg.blogspot.com/2014/02/blog-post.html

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica: Enunciado de Kelvin (Eficiência).

É impossível um processo cujo único resultado líquido seja retirar energia de um reservatório de calor e entregar a mesma quantidade de energia a um reservatório de trabalho.

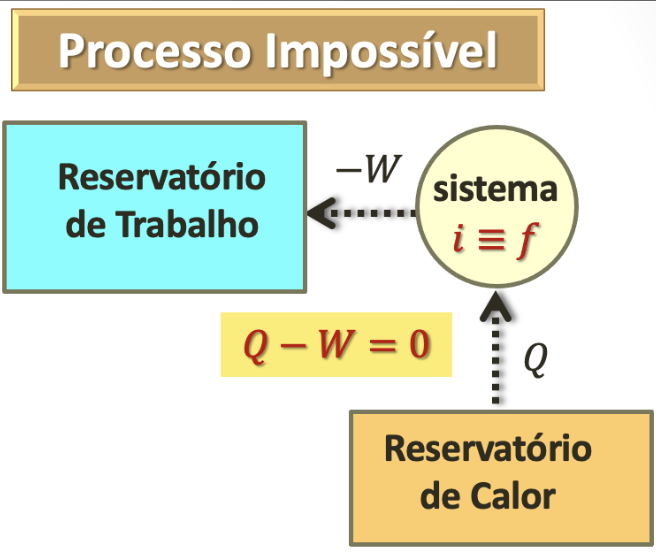
cujo único resultado líquido \(\rightarrow\) algo a mais deve ocorrer, num ciclo.

Cortesia: Prof. Tarciro Nortarson

Entropia. A segunda lei da termodinâmica.

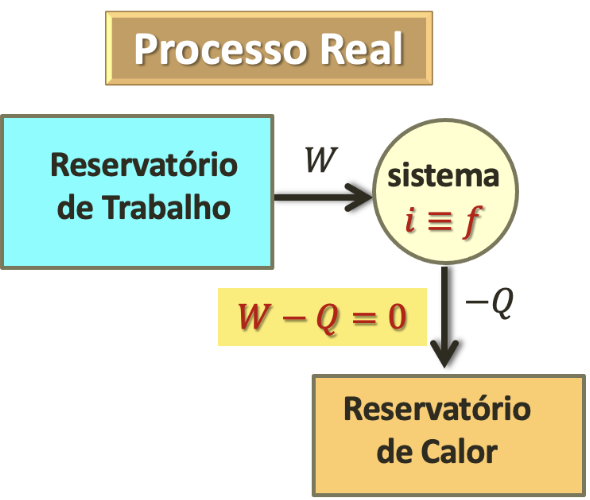
Reservatórios de trabalho e calor.

A partir da primeira lei:

\Delta U_u =\Delta U_s+\Delta U_{t}+\Delta U_c = 0

\Delta U_{t}=-W

\Delta U_{c}=+Q

A partir da segunda lei:

\Delta S_t = 0

\Delta S_c = +\frac{Q}{T}

\Delta S_u=\Delta S_s+\Delta S_{t}+\Delta S_c = \left( 0 +0+ \frac{Q}{T} \right)>0

O processo é irreversível. O processo pode ocorrer, pois \(\Delta S_u > 0\). Não viola Kelvin.

\Delta U_{s}=+W-Q

\Delta S_s = 0

Segunda Lei da Termodinâmica: Enunciado de Kelvin (Eficiência).

Entropia. A segunda lei da termodinâmica.

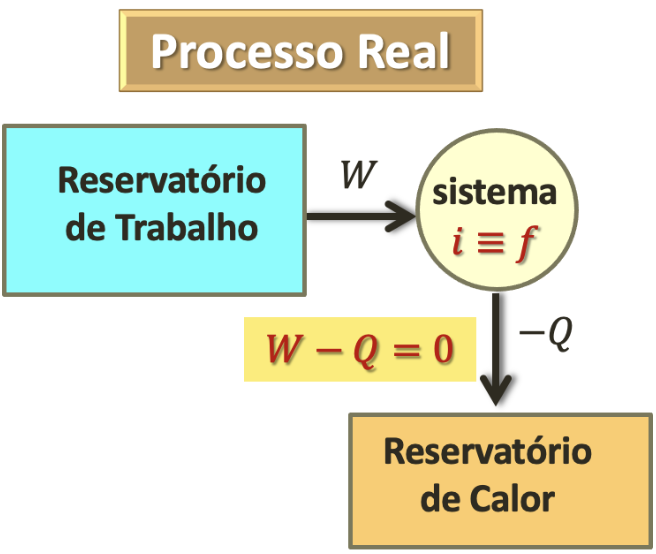
Reservatórios de trabalho e calor

A partir da primeira lei:

\Delta U_u =\Delta U_s+\Delta U_{t}+\Delta U_c = 0

\Delta U_{t}=+W

\Delta U_{c}=-Q

A partir da segunda lei:

\Delta S_t = 0

\Delta S_c = -\frac{Q}{T}

\Delta S_u=\Delta S_s+\Delta S_{t}+\Delta S_c = \left( 0 +0- \frac{Q}{T} \right)<0

O processo é impossível. O processo não pode ocorrer, pois \(\Delta S_u < 0\). Viola Kelvin.

\Delta U_{s}=-W+Q

\Delta S_s = 0

Segunda Lei da Termodinâmica: Enunciado de Kelvin (Eficiência).

O que fazer para não violar Kelvin?

A experiência mostra que uma transferência de uma igual quantidade de energia de um reservatório de trabalho para um reservatório de calor se dá em apenas uma direção.

Cortesia: Prof. Tarciro Nortarson

W\rightarrow Q

Q\rightarrow W

Quando há trabalho envolvido o sentido permitido no processo não é dado mais pela temperatura.

Os reservatórios de trabalho (vizinhança) são fontes inesgotáveis de energia.

Nos reservatórios de trabalho as trocas de trabalho são realizadas isobaricamente.

Os processos observados na escala macroscópica tendem a ocorrer num só sentido, ou seja, são irreversíveis.

É improvável que o vazo
"se desquebre".

Entropia. A segunda lei da termodinâmica.

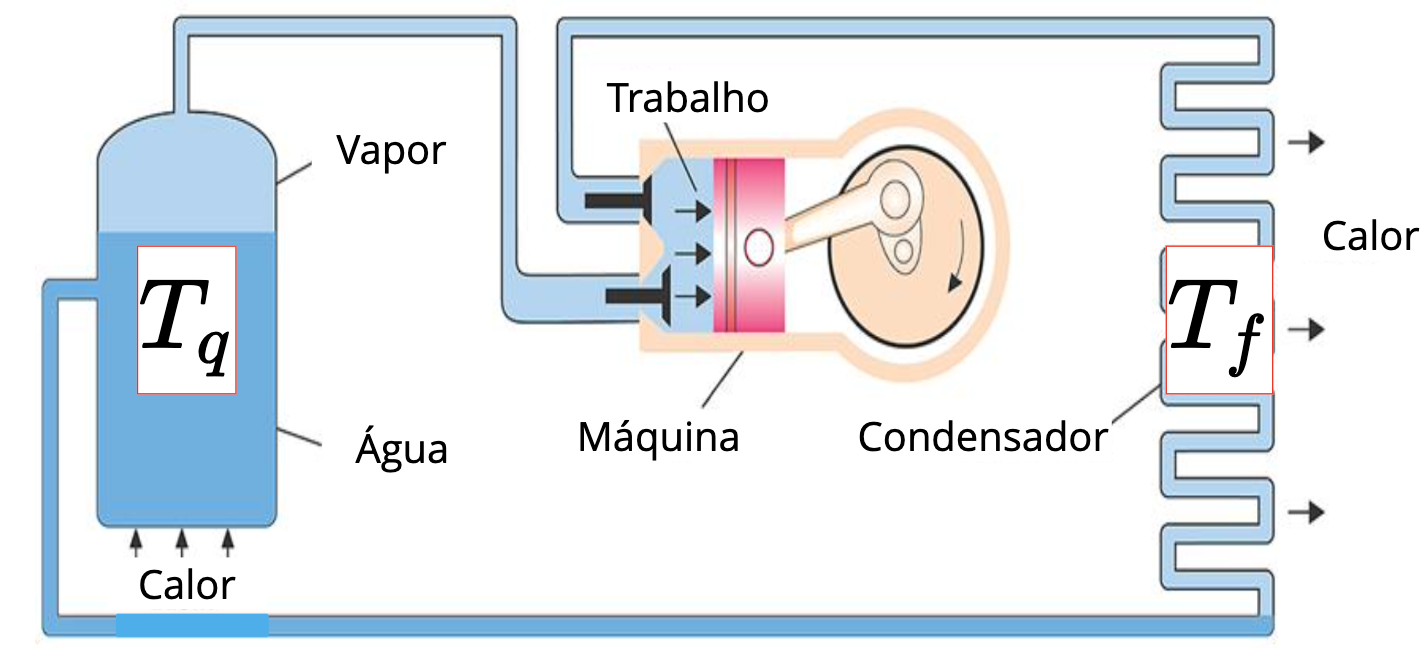
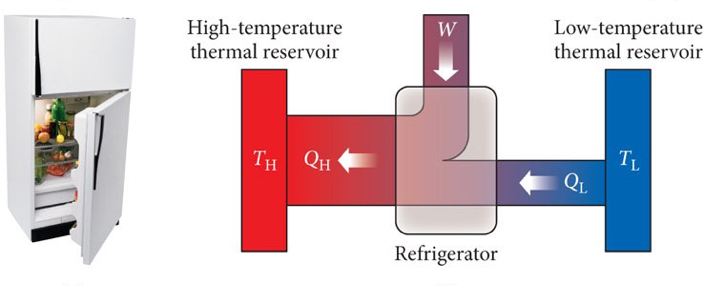
Segunda Lei da Termodinâmica. Máquinas térmicas e refrigeradores.

CLAUSIUS. É impossível realizar um processo cujo único efeito seja transferir calor de um corpo mais frio para um corpo mais quente.

KELVIN. É impossível realizar um processo cujo único efeito seja remover calor de um reservatório térmico e produzir uma quantidade equivalente de trabalho.

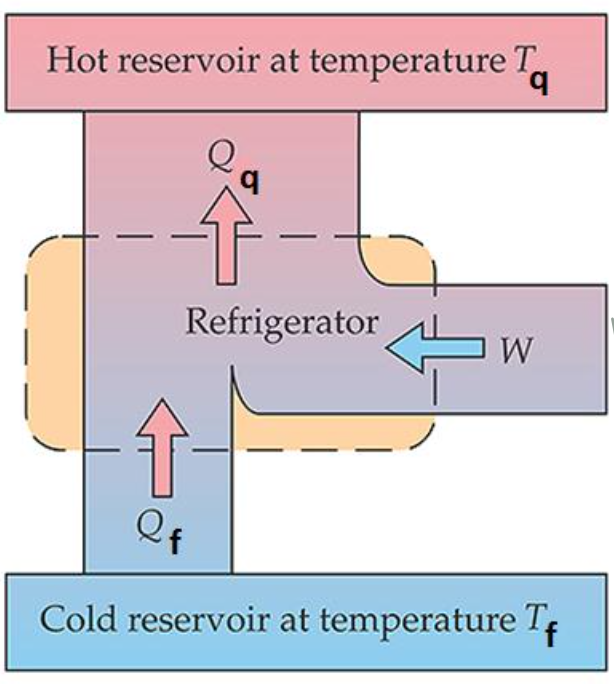
Reservatório quente a temperatura \(T_q\)

Reservatório frio a temperatura \(T_f\)

Q_q

Q_f

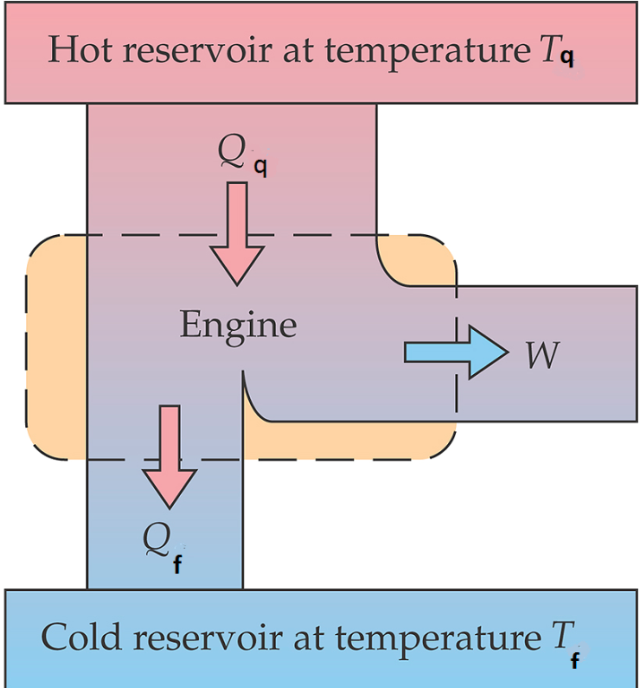
Reservatório quente a temperatura \(T_q\)

Reservatório frio a temperatura \(T_f\)

Q_f

Q_q

Reservatório quente a temperatura \(T_q\)

Reservatório frio a temperatura \(T_f\)

Q_f

Q_q

Reservatório quente a temperatura \(T_q\)

Q_q

Fonte: adaptado de Bauer

Fonte: adaptado de Bauer

Fonte: adaptado de Bauer

Fonte: adaptado de Bauer

Vizinhança

Sistema

Vizinhança

Sistema

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica. Máquinas térmicas. Kelvin.

Reservatório quente a temperatura \(T_q\)

Reservatório firo a temperatura \(T_f\)

Q_f

Q_q

\Delta S_m=0

\Delta S_q=-\frac{Q_q}{T_q}

\Delta S_f=+\frac{Q_f}{T_f}

\Delta S_u=\Delta S_m + \Delta S_f + \Delta S_q\geq 0

\Delta S_u=0 +\frac{Q_f}{T_f} - \frac{Q_q}{T_q}\geq 0

\Delta S_u=\frac{Q_f}{T_f} - \frac{Q_q}{T_q}\geq0

A máquina é reversível

Observe que \(Q_q > W\), pois existe \(Q_f\).

A variação da entropia sobre os trocadores de energia:

Aplicando a segunda lei:

Aumenta muito

Diminui pouco

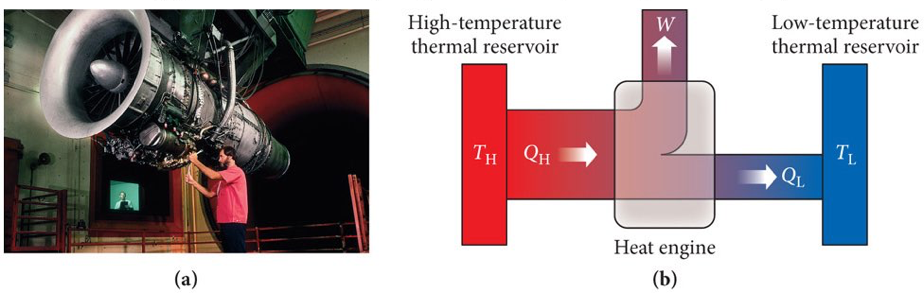
Fonte: Bauer

Fonte: adaptado de Bauer

|Q_q| = W+|Q_f|

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica. Máquinas térmicas. Kelvin.

Em relação à máquina térmica:

Reservatório quente a temperatura \(T_q\)

Reservatório firo a temperatura \(T_f\)

Q_f

Q_q

\Delta S_u=\frac{Q_f}{T_f} - \frac{Q_q}{T_q} \geq 0

O processo será irreversível se:

\Delta S_u > 0

\frac{Q_f}{T_f} > \frac{Q_q}{T_q}

\Delta S_f > \Delta S_q

Aumenta muito

Diminui pouco

O processo será reversível se:

\Delta S_u = 0

\frac{Q_f}{T_f} = \frac{Q_q}{T_q}

\Delta S_f = \Delta S_q

Para uma mesma quantidade de calor, o processo irreversível implica que: \(T_q > T_f\).

Para uma mesma quantidade de calor, o processo reversível implica que: \(T_q = T_f\).

\frac{Q_f}{T_f} > \frac{Q_q}{T_q}

Fonte: adaptado de Bauer

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica. Máquinas térmicas. Kelvin.

Define-se como eficiência de uma máquina térmica, a razão:

Reservatório quente a temperatura \(T_q\)

Reservatório firo a temperatura \(T_f\)

Q_f

Q_q

\varepsilon_M = \frac{W_t}{Q_q}

\varepsilon_M = \frac{Q_q-Q_f}{Q_q}

\varepsilon_M = 1-\frac{Q_f}{Q_q}

No processo irreversível:

\frac{Q_f}{T_f} > \frac{Q_q}{T_q}

\Delta S_u > 0

\frac{Q_f}{Q_q} > \frac{T_f}{T_q}

\varepsilon_{M,I} < 1-\frac{T_f}{T_q}

No processo reversível:

\frac{Q_f}{T_f} = \frac{Q_q}{T_q}

\Delta S_u = 0

\frac{Q_f}{Q_q} = \frac{T_f}{T_q}

\varepsilon_{M,R} = 1-\frac{T_f}{T_q}

\Rightarrow

A eficiência de uma máquina térmica irreversível é menor do que a eficiência de uma máquina reversível.

Simulador: https://www.geogebra.org/m/tb78mjtq

Fonte: adaptado de Bauer

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica. Refrigeradores. Clausius.

\Delta S_m=0

\Delta S_q=+\frac{Q_q}{T_q}

\Delta S_f=-\frac{Q_f}{T_f}

\Delta S_u=\Delta S_m + \Delta S_f + \Delta S_q\geq 0

\Delta S_u=0 +\frac{Q_q}{T_q} - \frac{Q_f}{T_f}\geq 0

\Delta S_u=\frac{Q_q}{T_q} - \frac{Q_f}{T_f}\geq0

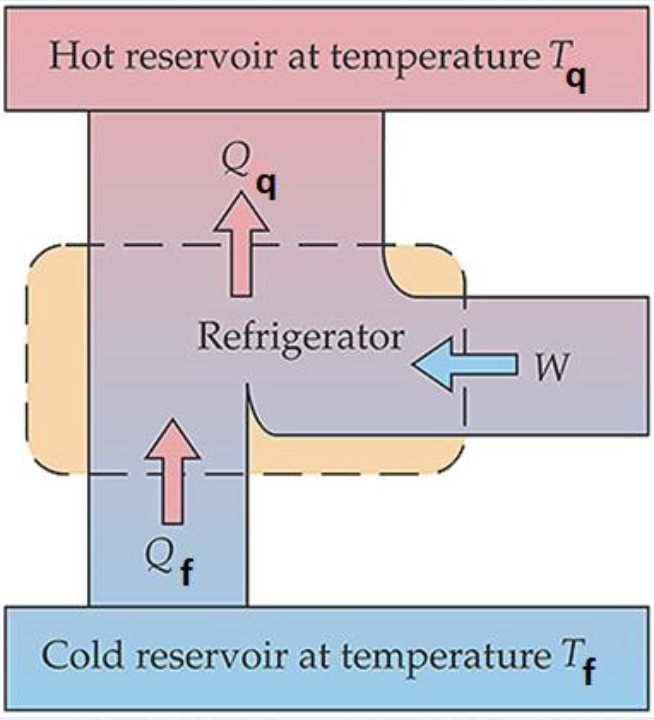
Reservatório quente a temperatura \(T_q\)

Reservatório firo a temperatura \(T_f\)

Q_f

Q_q

A variação da entropia sobre os trocadores de energia:

Aplicando a segunda lei:

A máquina é reversível

Aumenta muito

Diminui pouco

Fonte: Bauer

Fonte: adaptado de Bauer

Observe que \(Q_q > W\), pois existe \(Q_f\).

|Q_q|=W+|Q_f|

Entropia. A segunda lei da termodinâmica.

Segunda Lei da Termodinâmica. Refrigeradores. Clausius.

Em relação ao refrigerador:

\Delta S_u=\frac{Q_q}{T_q} - \frac{Q_f}{T_f} \geq 0

O processo será irreversível se:

\Delta S_u > 0

\frac{Q_q}{T_q} > \frac{Q_f}{T_f}

\Delta S_q > \Delta S_f

Aumenta muito

Diminui pouco

O processo será reversível se:

\Delta S_u = 0

\frac{Q_q}{T_q} = \frac{Q_f}{T_f}

\Delta S_f = \Delta S_q

No processo irreversível ainda é necessário que \(T_q / T_f \geq 1\); logo \(Q_q>Q_f\).

Para uma mesma quantidade de calor, o processo reversível implica que: \(T_q = T_f\).

Reservatório quente a temperatura \(T_q\)

Reservatório firo a temperatura \(T_f\)

Q_f

Q_q

Fonte: adaptado de Bauer

Entropia. A segunda lei da termodinâmica.

Define-se como coeficiente de desempenho do refrigerador, a razão:

CD = \frac{Q_f}{W_t}

CD = \frac{Q_f}{Q_q-Q_f}

\Rightarrow

Segunda Lei da Termodinâmica. Refrigeradores. Clausius.

CD_M = \frac{1}{Q_q/Q_f-1}

\frac{Q_q}{T_q} > \frac{Q_f}{T_f}

\Delta S_u > 0

\frac{Q_q}{Q_f} > \frac{T_q}{T_f}

\Rightarrow

Reservatório quente a temperatura \(T_q\)

Reservatório firo a temperatura \(T_f\)

Q_f

Q_q

CD_{M,I} < \frac{1}{T_q/T_f-1}

No processo irreversível:

No processo reversível:

\frac{Q_q}{T_q} = \frac{Q_f}{T_f}

\Delta S_u = 0

\frac{Q_q}{Q_f} = \frac{T_q}{T_f}

\Rightarrow

O coeficiente de desempenho de um refrigerador irreversível é menor do que a eficiência de um refrigerador reversível.

CD_{M,R} = \frac{1}{T_q/T_f-1}

Fonte: adaptado de Bauer

Entropia. A segunda lei da termodinâmica.

O ciclo termodinâmico é analisado em um diagrama de Clapeyron (Diagrama PV).

Segunda Lei da Termodinâmica. Indisponibilidade da energia.

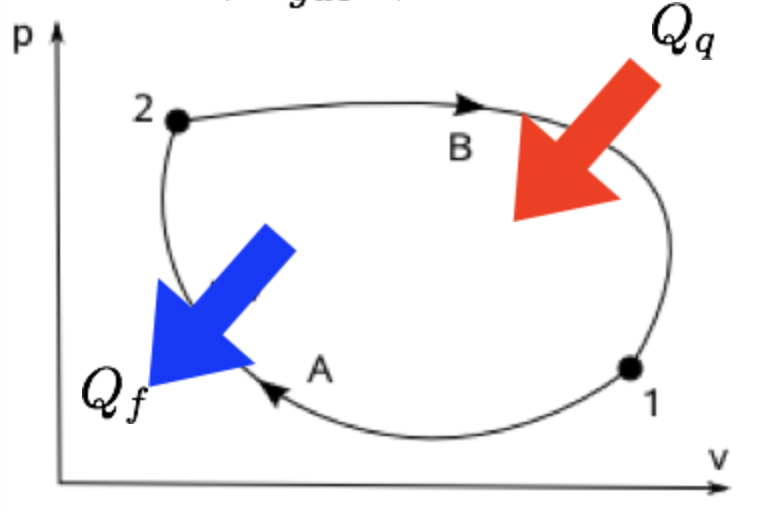
A primeira lei:

\Delta U = Q-W

\Delta U = 0

Em um ciclo:

Q_t=W_t

Q_q-Q_f=W_{útil}

A eficiência é:

\varepsilon = \frac{W_{util}}{Q_q}

\varepsilon = 1-\frac{Q_f}{Q_q}

Quanto maior o trabalho executado para uma dada quantidade de calor que entra na máquina térmica maior será a eficiência.

Quanto menor a quantidade de calor que deixa a máquina térmica maior será a eficiência.

A eficiência nunca será 100% porque alguma quantidade de calor deve ser rejeitada para o reservatório frio, em um ciclo. Isto é, \(Q_f\) não pode ser zero!

W_{útil} =\varepsilon Q_q

Entropia. A segunda lei da termodinâmica.

Os enunciados de Kelvin e Clausius impõem limites de eficiência/desempenho às respectivas máquinas.

Qual é a máxima eficiência e desempenho que pode ser obtida por uma máquina operando entre dois reservatórios à temperaturas diferentes?

A eficiência e desempenho somente depende das fontes térmicas, logo das suas temperaturas absolutas.

Segunda Lei da Termodinâmica. Indisponibilidade da energia.

A eficiência e desempenho máximos são aquelas de um processo reversível operando entre duas fontes de calor.

\frac{Q_f}{Q_q} = \frac{T_f}{T_q}

\varepsilon_{rev} = 1-\frac{T_f}{T_q}

\varepsilon=\frac{W_{útil}}{Q_q}=1-\frac{Q_f}{Q_q}

Processo reversível

Eficiência de qualquer processo

Eficiência máxima

Entropia. A segunda lei da termodinâmica.

W_{indisponível}=W_{reversível}-W_{real}

W_{reversível}>W_{real}

Segunda Lei da Termodinâmica. Indisponibilidade da energia.

O trabalho indisponível ou a energia que foi degradada.

W_{indisponível}=\varepsilon_{rev}Q_q-\varepsilon Q_q

W_{indisponível}=(\varepsilon_{rev}-\varepsilon) Q_q

W_{indisponível}= \left( 1-\frac{T_f}{T_q}-1+ \frac{Q_f}{Q_q} \right) Q_q

W_{indisponível}=T_f \left( \frac{Q_f}{T_f}- \frac{Q_q}{T_q} \right)

W_{indisponível}=T_f \Delta S_u

É uma medida da qualidade da energia. Dado dois sistemas com mesma energia, um com a menor variação de entropia tem maior qualidade de energia.

Reservatório quente a temperatura \(T_q\)

Reservatório firo a temperatura \(T_f\)

Q_f

Q_q

Entropia. A segunda lei da termodinâmica.

Indisponibilidade da energia.

Num processo irreversível a energia é conservada, mas a energia torna-se indisponível para a realização de trabalho útil e é degrada (é perdida no sentido de indisponível).

Durante um processo irreversível, uma quantidade de energia igual à \(T_f\Delta S_u\) torna-se indisponível para a realização de trabalho, onde \(T_f\) é a temperatura do reservatório “mais frio” possível.

W_{indisponível}=T_f\Delta S_{unvierso}

A entropia está associada à ineficiência de uma máquina.

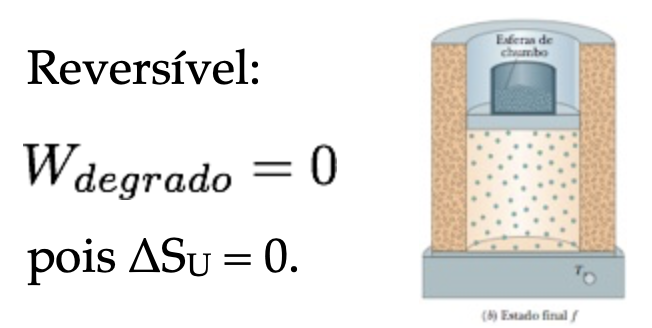
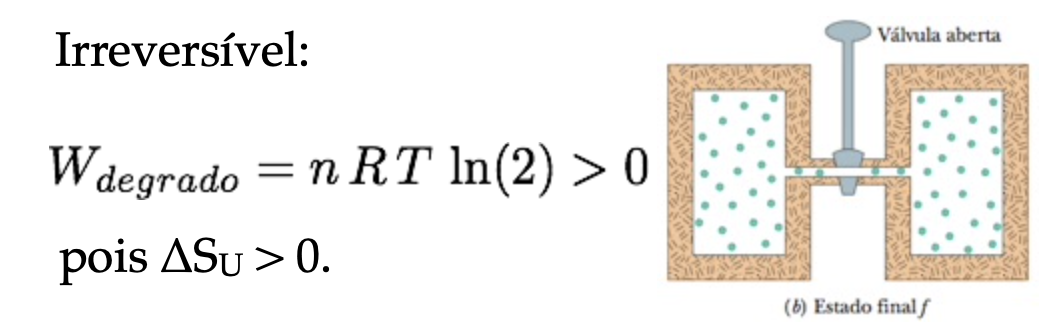
Fonte: Halliday & Resnick

Fonte: Halliday & Resnick

Questão 1

Um refrigerador retira 500 J de calor de um reservatório frio e libera 800 J para um reservatório quente. Suponha falso o enunciado para máquinas térmicas e mostre como uma máquina perfeita, trabalhando acoplada com este refrigerador, pode violar o enunciado para refrigeradores da segunda lei da termodinâmica.

Questão 2

Uma máquina reversível, trabalhando entre dois reservatórios a temperaturas Tq e Tf, tem um rendimento de 30%. Trabalhando como uma máquina térmica, ela libera 140 J de calor para o reservatório frio, a cada ciclo. Uma segunda máquina, trabalhando entre os mesmos dois reservatórios, também libera 140 J para o reservatório frio, a cada ciclo. Mostre que, se a segunda máquina tem um rendimento maior do que 30%, as duas máquinas, trabalhando acopladas, violam o enunciado da segunda lei da termodinâmica para máquinas térmicas. T19-43-ed.6

Questão 3

Uma bomba de calor com coeficiente de desempenho de 3,500 é usada para aquecer uma residência que perde 75000 BTU/hora em um dia frio. Suponha que o custo de eletricidade seja de 10,00 centavos por quilowatt-hora. Qual o custo para aquecer a casa por um dia?

DADOS:

1 BTU = 1055 J

1 BTU/hora = 0,2932 J/s

1 KWh = (1000) x (1 J/s) x (3600 s) = 3,6 x 10^7 J

Questão 4

Se 200 J de calor são liberados por um reservatório a 373K e 152 J são absorvidos por um segundo reservatório a 273K, quanta capacidade de trabalho é “perdida” neste processo ?

Questão 5

Um carro com motor de combustão interna movido a gasolina trafega com velocidade de 26,8 m/s em uma estrada plana e usa gasolina a uma taxa de 6,92 L / 100 km. O conteúdo energético da gasolina é 34,8 MJ/L. Se o motor tem eficiência de 20,0%, quanta potência é fornecida para manter o carro se movendo com velocidade constante?

Questão 6

Suponha que tenhamos 250 kg de água a uma temperatura de 0,00 oC. Queremos congelar essa água colocando-se em um refrigerador que opera em um ambiente com temperatura de 22,0 oC. A temperatura dentro do refrigerador é mantida a -5,00 oC. Qual é a quantidade mínima de energia elétrica que deve ser fornecida ao refrigerador para congelar a água?

Questão 7

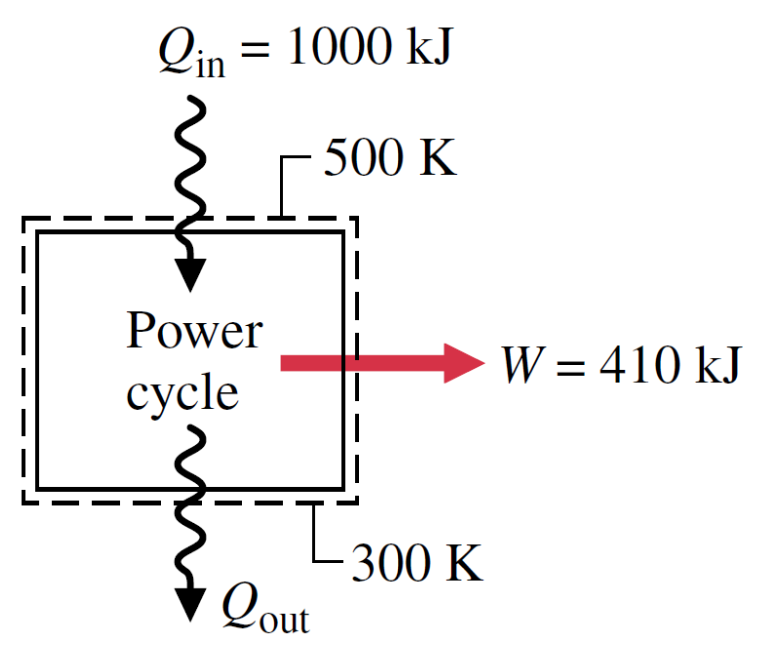
Um inventor declara ter desenvolvido um ciclo de potência capaz de fornecer um trabalho líquido de saída de 410 kJ para uma entrada de energia por transferência de calor de 1000 kJ. O sistema percorrendo o ciclo recebe a transferência de calor de gases à temperatura de 500K e descarrega energia por transferência de calor para a atmosfera a 300K. Avalie esta afirmação.

Questão 8

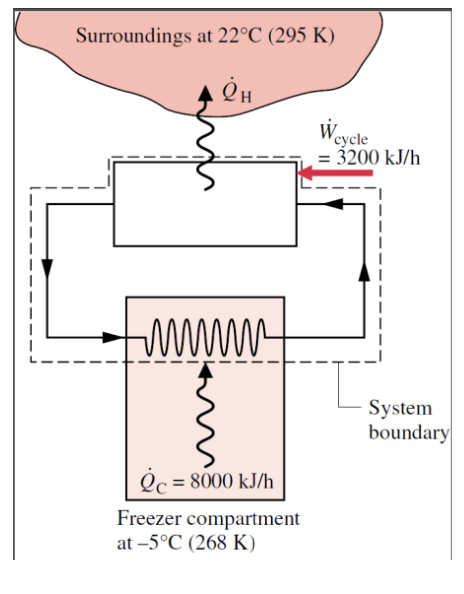
Através da circulação em regime permanente de um refrigerante a uma baixa temperatura através de passagens nas paredes do compartimento do congelador, um refrigerante mantém o compartimento do congelador a -5 oC quando o ar ambiente encontra-se a 22 oC. A taxa de transferência de calor do compartimento congelador para o refrigerante é de 8000 kJ/h e a potência de entrada necessária para operar o refrigerador é de 3200 kJ/h; Determine o CD do refrigerador e compare com o CD de um ciclo de refrigeração reversível operando entre os mesmos reservatórios.

Questão 9

Um gás diatômico ideal segue o ciclo mostrado na figura. A temperatura do estado 1 é 200 K. Determine (a) as temperaturas dos outros três estados numerados do ciclo; (b) o rendimento do ciclo; (c) o rendimento de uma máquina reversível se ela operasse entre o reservatório mais quente e o mais frio.

Fonte: Halliday