Aula 22

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 20 -

Seções: 20.3, 20.6.

Analisar o ciclo de Carnot.

Reconhecer o ciclo de Carnot como uma máquina reversível.

Calcular a eficiência de um ciclo de Carnot.

Estudar os modelos dos motores de combustão interna.

Motivação

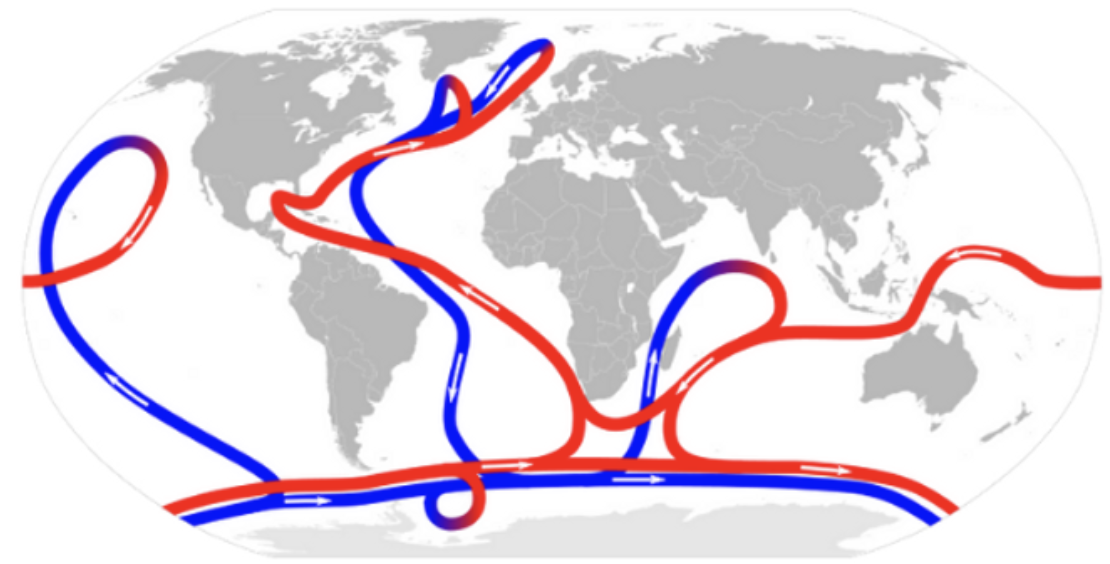
Ilustração da circulação superficial oceânica global. As setas azuis representam correntes frias, as vermelhas são as correntes quentes e as regiões roxas são as áreas de encontro de correntes frias e quentes. Fonte: Miraceti/Wikimedia Commons - https://www.bioicos.org.br/post/correntes-maritimas-circulacao-oceanica

As correntes quentes Equatorial do Norte e Equatorial do Sul. Elas atravessam o oceano Atlântico, passando da África para a América, trazendo grandes massas de água com 25 ºC.

No Brasil, as correntes transportam em média 14 milhões de metros cúbicos por segundo.

Os oceanos operam como máquinas térmicas.

Ocorrendo um equilíbrio térmico dos oceanos não haverá mais as correntes equatoriais!

O ciclo de Carnot

Problema

Dadas uma fonte quente e uma fonte fria, qual é o máximo rendimento que se pode obter de um motor térmico (ou refrigerador) operando entre essas duas fontes?

Máquina Sadi Carnot (1796-1832).

Deve ser uma máquina que opera reversivelmente entre duas fontes.

Com trocas de calor realizadas isotermicamente (reservatórios térmicos).

Com variações de temperatura que ocorrem adiabaticamente (com trabalho e sem calor).

Quase-estático

Sem efeitos dissipativos

Opera ao contrário!

De acordo com a segunda lei, nenhuma máquina térmica pode ter 100% de eficiência.

Máquina hipotética ideal

Para a eficiência máxima de uma máquina térmica, portanto, devemos evitar todo processo irreversível.

O fluxo de calor em uma queda de temperatura finita é um processo irreversível.

Não pode ocorrer nenhuma transferência de calor entre a máquina e qualquer reservatório, porque essa transferência de calor não poderia ser reversível.

O ciclo de Carnot

A máquina de Carnot opera entre apenas 2 reservatórios térmicos: um quente e outro frio.

Máquina de Carnot

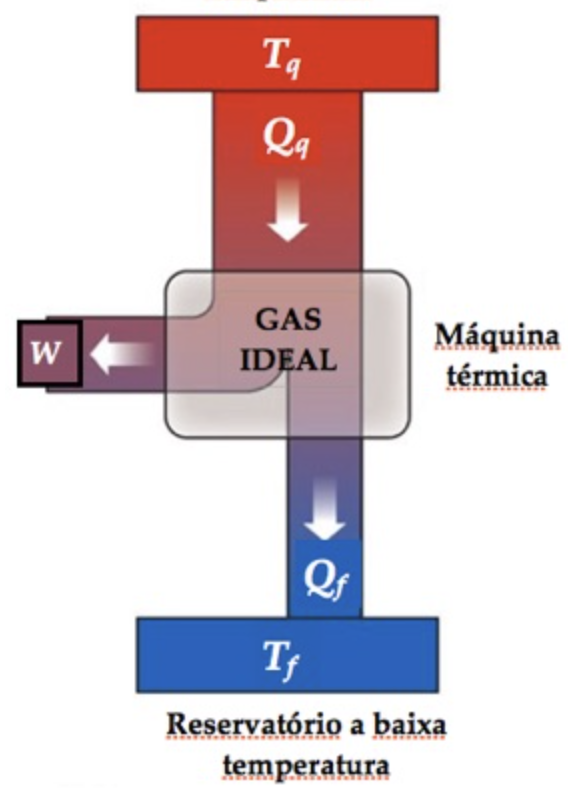
O ciclo de Carnot tem 4 processos alternados: expansão isotérmica, expansão adiabática, compressão isotérmica e compressão adiabática.

Fonte: Bauer

Fonte: https://mundoeducacao.uol.com.br

Fonte: Tipler

Q_{liq}=Q_q-Q_f

W_{util}=Q_{liq}

\Rightarrow \Delta U_{ciclo} = 0

W_{util}

A troca de calor na fonte quente se dá reversivelmente as custas de trabalho, pois não há diferença finita de temperatura

A temperatura precisa diminuir, mas sem que exista troca de calor. Isto se dá as custas de trabalho adiabático.

A troca de calor na fonte fria se dá reversivelmente as custas de trabalho, pois não há diferença finita de temperatura.

A temperatura precisa aumentar, mas sem que exista troca de calor. Isto se dá as custas de trabalho adiabático.

isoterma

adiabática

isoterma

adiabática

O ciclo de Carnot

Máquina e o ciclo de Carnot

Fonte: https://www.geogebra.org/m/th4mjnfc

Nos processos isotérmicos há transferência de calor porque há trabalho isotérmico.

Nos processos adiabático há queda de temperatura devido ao trabalho adiabático.

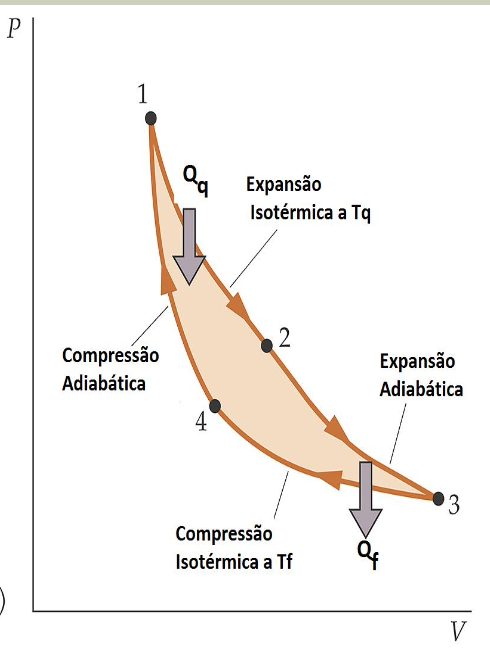
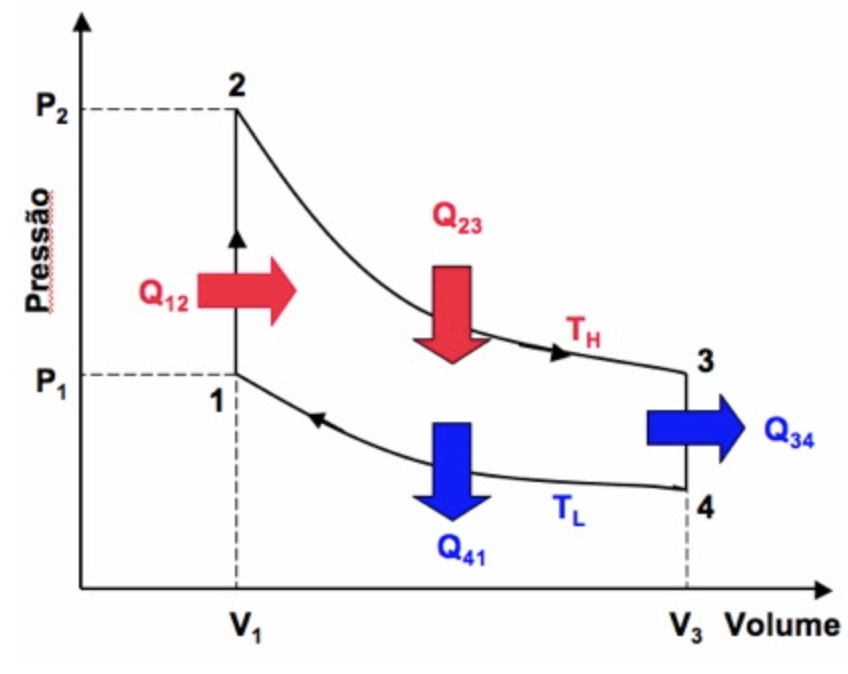
AB: Expansão isotérmica (\(Q_q\))

\Delta U_{AB}=0

Q_{AB}=W_{AB}=nRT_q\ln\left( \frac{V_B}{V_A} \right)>0

BC: Expansão adiabática

Q_{BC}=0

\Delta U_{BC}=\frac{1}{\gamma-1}(P_CV_C-P_BV_B)<0

CD: Compressão isotérmica (\(Q_f\))

\Delta U_{CD}=0

Q_{CD}=W_{CD}=nRT_f\ln\left( \frac{V_D}{V_C} \right)<0

DA: Compressão adiabática

Q_{DA}=0

\Delta U_{DA}=\frac{1}{\gamma-1}(P_AV_A-P_DV_D)>0

O ciclo de Carnot

Máquina e o ciclo de Carnot

Fonte: https://www.geogebra.org/m/th4mjnfc

\Rightarrow

\frac{|Q_{f}|}{|Q_q|}=\frac{T_f}{T_q}

\frac{Q_{f}}{Q_q}=-\frac{T_f}{T_q}

Combinando os dois resultados

Nos processos adiabáticos

\frac{T_q}{T_f}=\left( \frac{V_C}{V_B} \right)^{\gamma-1}

\frac{T_q}{T_f}=\left( \frac{V_D}{V_A} \right)^{\gamma-1}

\left( \frac{V_C}{V_B} \right)= \left( \frac{V_D}{V_A} \right)

\left( \frac{V_B}{V_A} \right)= \left( \frac{V_C}{V_D} \right)

Nos processos isotérmicos

Q_{q}=+nRT_q\ln\left( \frac{V_B}{V_A} \right)>0

Q_{f}=-nRT_f\ln\left( \frac{V_C}{V_D} \right)<0

\frac{Q_{f}}{Q_q}=-\frac{T_f}{T_q}\frac{\ln(V_C/V_D)}{\ln(V_B/V_A)}

A eficiência de Carnot

\varepsilon = 1 -\frac{|Q_f|}{|Q_q|}

\varepsilon = 1 -\frac{T_f}{T_q}

\Rightarrow

O ciclo de Carnot

A eficiência de Carnot

\varepsilon = 1 -\frac{T_f}{T_q}

A eficiência do ciclo de Carnot com gases ideais independe das características do gás e depende apenas das temperaturas dos reservatórios térmicos usados.

Como opera em um ciclo a temperatura do reservatório frio não pode ser nula. Caso contrário teríamos uma máquina miraculosa com 100% de eficiência.

O rendimento de Carnot fornece um limite superior para os rendimentos de uma máquina térmica operando entre dois reservatórios térmicos.

Um reservatório no zero absoluto implica todo calor convertido em trabalho. Uma eficiência de 100% é uma prática impossível.

T_q = 373 \text{ K} \, \qquad{e}\qquad T_f = 273 \text{ K}

\Rightarrow \varepsilon = 0,27

T_q = 173 \text{ K} \, \qquad{e}\qquad T_f = 73 \text{ K}

\Rightarrow \varepsilon = 0,58

O ciclo de Carnot

A eficiência de Carnot. Diagrama TS

No diagrama TS, para um gás ideal como sistema temos que:

A\rightarrow B: Q_{1R}=+T_1\Delta S

B\rightarrow C: \Delta S=0

C\rightarrow D: Q_{2R}=-T_2\Delta S

D\rightarrow A: \Delta S=0

No ciclo:

W_{util}=Q_{liq}=(T_1-T_2)\Delta S

Q_2

Q_1

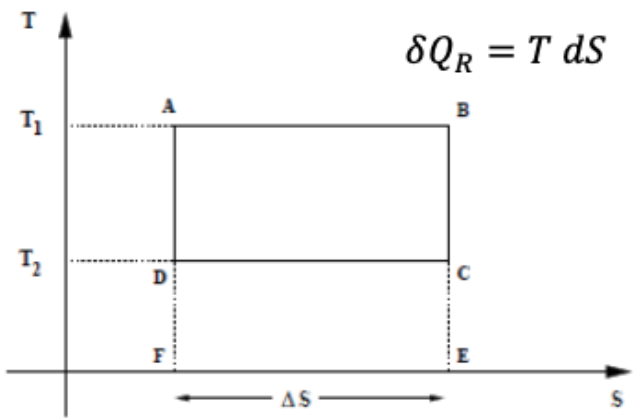
Podemos verificar que a máquina de Carnot é reversível.

A\rightarrow B:S_{B}=S_A+\frac{Q_{1R}}{T_1}

B\rightarrow C:S_{C}=S_B

C\rightarrow D:S_{D}=S_C-\frac{Q_{2R}}{T_2}

D\rightarrow A:S_{A}=S_D

\rightarrow S_{A}=S_B-\frac{Q_{2R}}{T_2}

\rightarrow S_{B}=S_A+\frac{Q_{1R}}{T_1}

No ciclo:

\frac{Q_{1R}}{T_1}= \frac{Q_{2R}}{T_2}

O ciclo de Carnot

A eficiência de Carnot. Diagrama TS

No diagrama TS, para um gás ideal como sistema temos que:

W_{util}=(T_1-T_2)\Delta S \equiv \text{área}_{ABCDA}

No ciclo:

\varepsilon=\frac{W_u}{Q_q}

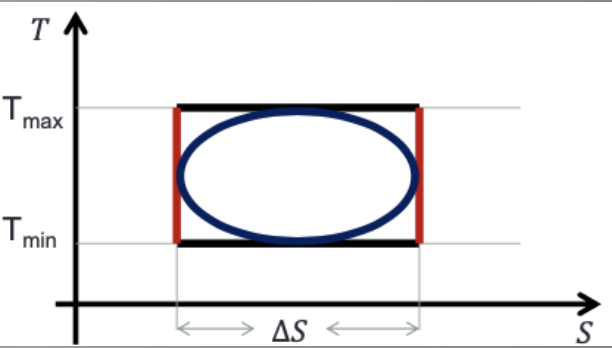
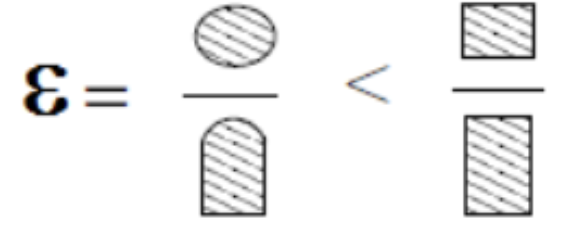
O ciclo de Carnot

A máquina reversível de Carnot

Suponha que a máquina de Carnot (R) seja menos eficiente que uma máquina (I), mas que ambas executem o mesmo trabalho.

Suponha que:

\varepsilon_I > \varepsilon_R

\frac{W}{Q'_q}> \frac{W}{Q_q}

\Rightarrow

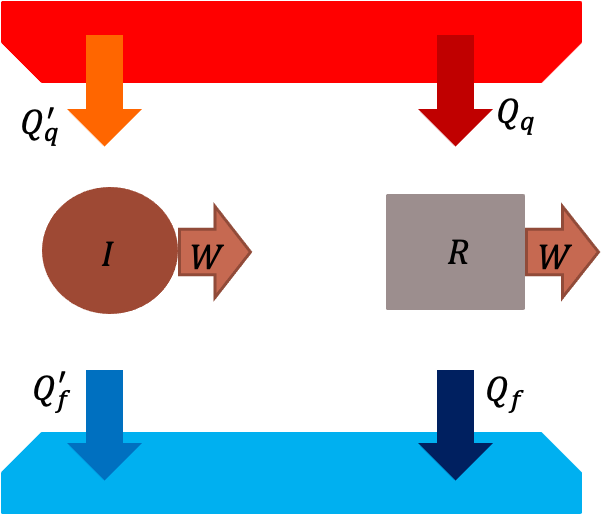
Esta máquina é possível?

Quais as consequências de \(Q_q > Q'_{q}\)?

100 J

120 J

80 J

20 J

40 J

0,67

0,80

O trabalho é o mesmo. Assim, a relação a seguir deve ser satisfeita:

Q_q > Q'_q

120 J

100 J

O ciclo de Carnot

A máquina reversível de Carnot

A máquina de Carnot é reversível. Daí, operando no sentido contrário da máquina térmica, temos o refrigerador de Carnot.

O calor líquido cedido pelo reservatório quente é igual ao calor líquido recebido pelo reservatório frio sem qualquer trabalho realizado, \(W_{util} = Q_{liq,q}-Q_{liq,f} = 0\).

W_I=W_R

Q'_q - Q' _f= Q_q - Q_f

Q'_q - Q_q= Q'_f - Q_f

Q_{liq,q}= Q_{liq,f}

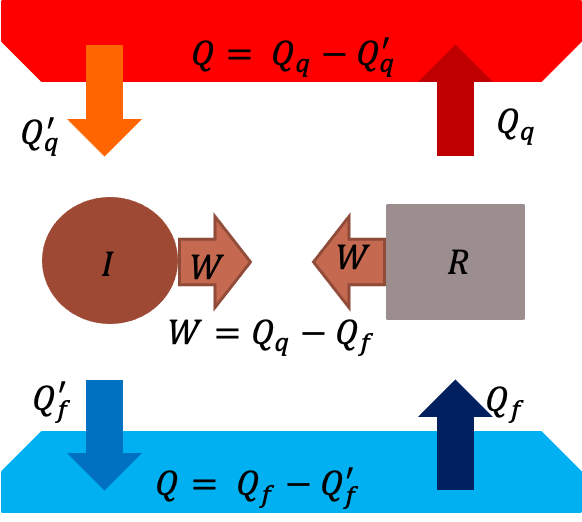
Há uma violação da 2a. Lei da Termodinâmica (enunciado de Clausius). Daí,

\Rightarrow

100 J

120 J

80 J

20 J

40 J

\Rightarrow Q_{liq,I}=Q_{liq,R}

80 J

20 J

\varepsilon_I > \varepsilon_R

\varepsilon_I < \varepsilon_R

O ciclo de Carnot

O teorema e os colorarios de Carnot

O teorema de Carnot

Nenhuma máquina térmica operando entre dois reservatório térmicos pode ser mais eficiente do que uma máquina de Carnot que opera entre os dois reservatórios térmicos.

Os colorários de Carnot

Todas as máquinas de Carnot operando entre os mesmos dois reservatórios térmicos têm a mesma eficiência.

A natureza da substância de trabalho não influencia a eficiência da máquina de Carnot.

A máquina de Carnot depende apenas das temperaturas das fontes de calor.

O ciclo de Carnot

Resumo

Dada duas fontes uma a alta temperatura e a outra a baixa temperatura:

A eficiência máxima é a eficiência de uma máquina de Carnot;

Se uma máquina operando entre as duas mesmas fontes apresenta uma eficiência igual a eficiência de Carnot ela é uma máquina reversível;

Se uma máquina operando entre as duas mesmas fontes apresenta uma eficiência menor que a eficiência de Carnot ela é uma máquina irreversível.

O TEOREMA DE CARNOT se aplica a uma máquina que opera entre DUAS FONTES DE ENERGIA.

Qualquer outra máquina que opere entre estas DUAS FONTES será reversível, irreversível ou impossível.

Máquinas que operam entre mais que duas fontes não se enquadram no Teorema de Carnot.

Motores de combustão à gás

O motor Otto com ciclo Otto à ar padrão por centelha.

O motor Otto é um motor de combustão de 4 tempos.

Fonte: https://youtube.com/shorts/cYmCuT5gBwo?feature=share

Admissão.

Compressão.

Combustão.

Exaustão.

Fonte: Moran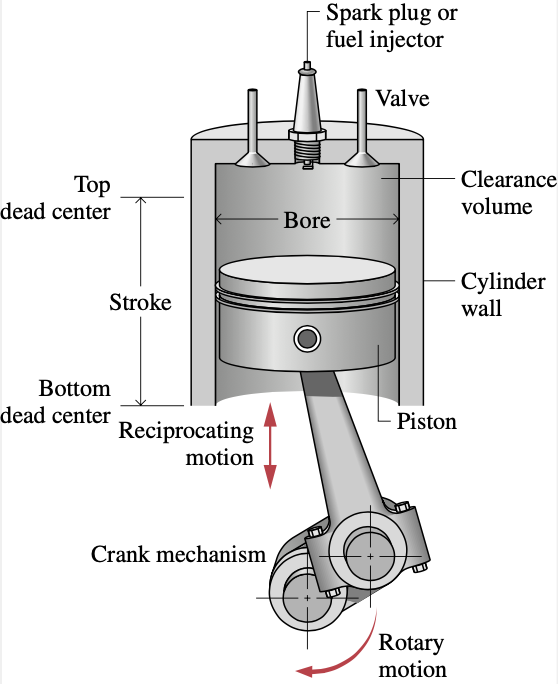

Ponto morto superior

Ponto morto inferior

Curso

Calibre

Válvula

Vela de ignição

Volume morto

Parede do cilindro

Pistão

Movimento de rotação

Mecanismo de manivela

Movimento alternado

O fluido de trabalho é o ar mais combustível.

Motores de combustão à gás

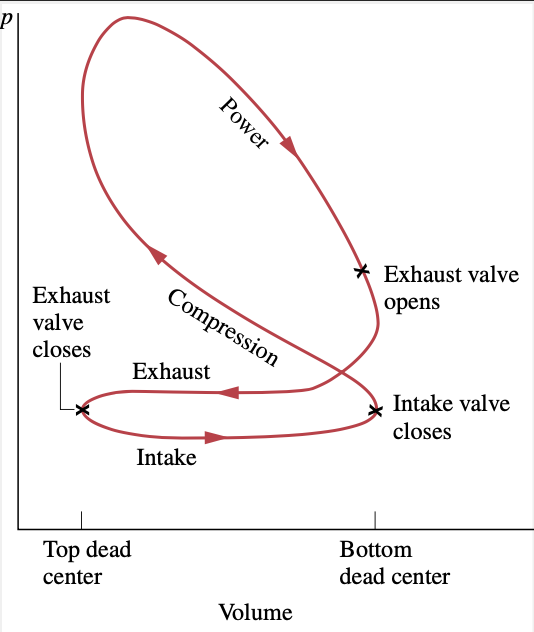
admissão

exaustão

Válvula de admissão fecha

Válvula de exaustão abre

potência

compressão

Válvula de exaustão fecha

ponto morto superior (V)

ponto morto inferior (rV)

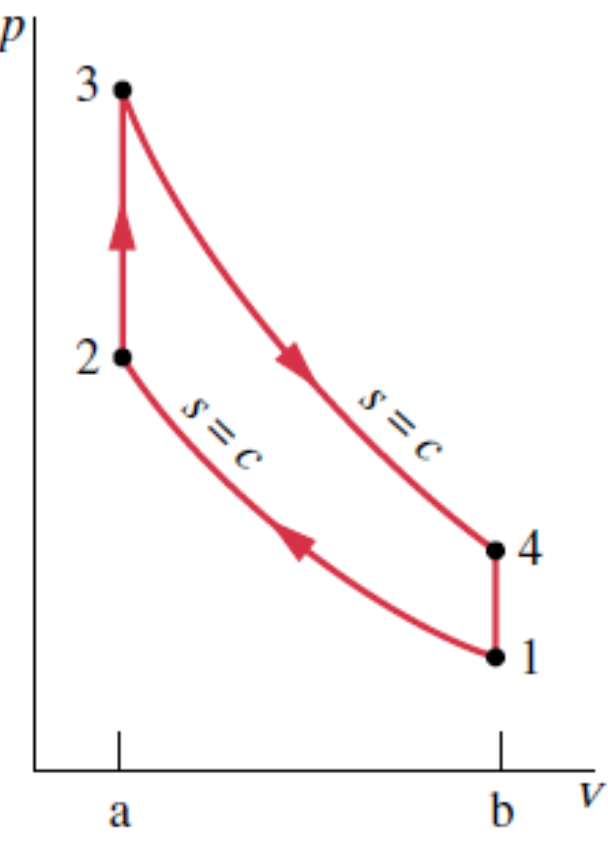
1-2: Compressão adiabática.

2-3: Aquecimento isocórico.

3-4: Expansão adiabática (potência).

4-1: Resfriamento isovolumétrico.

ignição

admissão

fim da combustão

Q_q

Q_f

explosão

exaustão

V_a=V

V_b=rV

O motor Otto com ciclo Otto à ar padrão por centelha.

Motores de combustão à gás

O motor Otto com ciclo Otto à ar padrão.

2-3: Aquecimento isocórico.

3-4: Expansão adiabática.

4-1: Resfriamento isovolumétrico.

Q_q

Q_f

1-2: Compressão adiabática.

Q=0\quad :\quad \Delta U =-W_{adiab}

\Delta U = C_V(T_2-T_1)>0

T_1V_1^{\gamma-1}= T_2V_2^{\gamma-1}

W=0\quad :\quad \Delta U =Q_q

Q_q= C_V(T_3-T_2)>0

Q=0\quad :\quad \Delta U =-W_{adiab}

\Delta U = C_V(T_4-T_3)<0

T_4V_4^{\gamma-1}= T_3V_3^{\gamma-1}

W=0\quad :\quad \Delta U =Q_f

Q_f = C_V(T_4-T_1)<0

V_a=V

V_b=rV

Motores de combustão à gás

O motor Otto com ciclo Otto à ar padrão.

Dos processos isocóricos obtemos a eficiência em função das temperaturas:

\varepsilon=1-\frac{Q_f}{Q_q}

Q_q

Q_f

\varepsilon=1-\frac{T_4-T_1}{T_3-T_2}

(T_4-T_1)V_b^{\gamma-1}= (T_3-T_2)V_a^{\gamma-1}

\frac{(T_4-T_1)}{ (T_3-T_2)}=\left(\frac{V_a}{V_b}\right)^{\gamma-1}

V_4=V_1

V_3=V_2

V_a=V

V_b=rV

Dos processos adiabáticos obtemos uma relação entre as variações de temperatura e a razão dos volumes na compressão:

T_1V_1^{\gamma-1}= T_2V_2^{\gamma-1}

T_4V_4^{\gamma-1}= T_3V_3^{\gamma-1}

\varepsilon=1-\left(\frac{V_a}{V_b}\right)^{\gamma-1}

A eficiência em função da taxa de compressão, \(r=V_1/V_2\):

\varepsilon=1-\left(\frac{1}{r}\right)^{\gamma-1}

Veja que há 4 reservatórios. Não é uma máquina de Carnot.

Motores de combustão à gás

O motor Otto com ciclo Otto à ar padrão.

Os reservatórios quente e frio são modelados como diversos reservatórios auxilares que permitem trocas de calor isotermicamente.

\varepsilon=1-\left(\frac{1}{r}\right)^{\gamma-1}

Diferente do Ciclco de Carnot, a eficiência do Ciclo Otto depende da natureza do sistema (substância de trabalho). Para gases ideais, a dependência se dará através da constante adiabática. Para ɣ = 1,4 e uma razão de compressão r = 8 (compressão máxima para evitar pré-ignição), obtém-se ϵ = 0,56.

A octanagem da gasolina impede a pré-ignição. A gasolina premium tem octanagem que permite uma taxa de compressão entre r = 10 e r = 13.

Os rendimentos reais são da ordem de ϵ = 0,34.

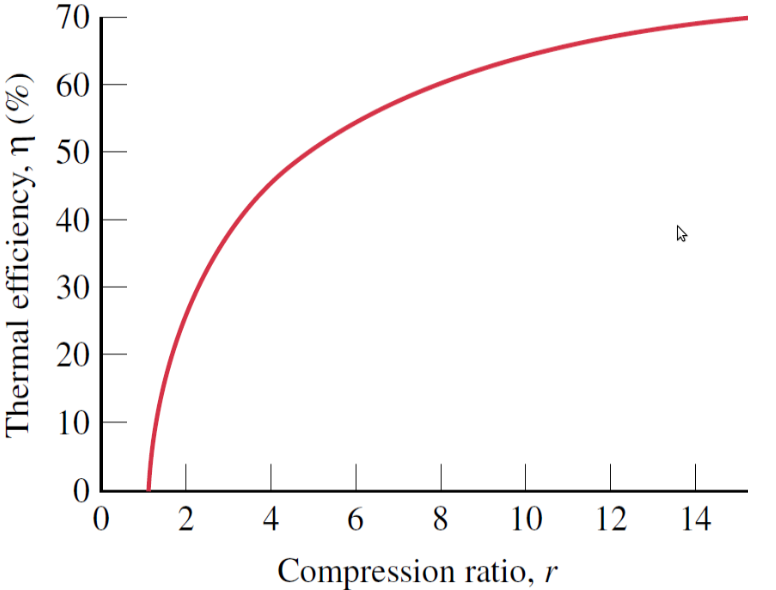
Motores de combustão à gás

O motor Otto com ciclo Otto à ar padrão.

É uma máquina reversível, mas opera entre mais que duas fontes de calor.

O ciclo Otto é realizado entre dois reservatórios, os calores são transferidos nos dois processos isocóricos devem envolver diferenças finitas de temperatura, e, portanto, não deve ser reversível.

Se o ciclo Otto for realizado reversivelmente, ele requer uma série de reservatórios, não meramente dois reservatórios à temperaturas diferentes.

Supondo uma série de reservatórios térmicos, os ciclos Otto e Diesel podem ser tomados como reversíveis!

Você é capaz de mostrar que a variação da entropia é nula para esta máquina?

Motores de combustão à gás

O motor Diesel com ciclo Diesel idealizado por compressão

a-b: Compressão adiabática.

b-c: Expansão isobárica

c-d: Expansão adiabática.

d-a: Resfriamento isocórico.

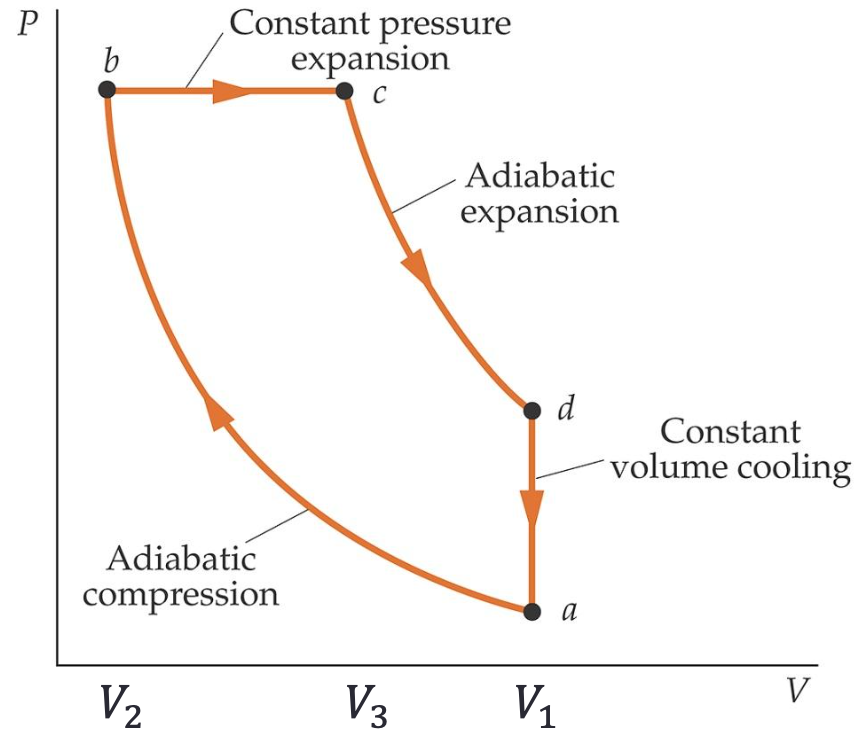
Expansão isobárica

Expansão adiabática

Resfriamento isocórico

Compressão adiabática

Q_q

Q_f

Q=0\quad :\quad \Delta U =-W

\Delta U = C_V(T_b-T_a)>0

T_aV_a^{\gamma-1}= T_bV_s^{\gamma-1}

\Delta U = Q_P-W

Q_q=C_P(T_c-T_b)

Q=0\quad :\quad \Delta U =-W

\Delta U = C_V(T_d-T_c)<0

T_dV_1^{\gamma-1}= T_cV_3^{\gamma-1}

W=0\quad :\quad \Delta U =Q_f

Q_f = C_V(T_d-T_a)<0

ignição

tempo motor

explosão

exaustão

Motores de combustão à gás

O motor Diesel com o ciclo Diesel idealizado

A partir da expansão isobárica e resfriamento isocórico, obtemos a eficiência em função das temperaraturas:

\varepsilon=1-\frac{Q_f}{Q_q}

\varepsilon=1-\frac{C_V}{C_P}\frac{T_d-T_a}{T_c-T_b}

\varepsilon=1-\frac{1}{\gamma}\frac{T_d-T_a}{T_c-T_b}

Veja que há 4 reservatórios. Não é uma máquina de Carnot.

Dos processos adiabáticos obtemos uma relação entre as variações de temperatura e a razão dos volumes na compressão:

T_dV_1^{\gamma-1}= T_cV_3^{\gamma-1}

T_aV_1^{\gamma-1}= T_bV_2^{\gamma-1}

\frac{T_a}{T_b}= \left( \frac{V_2}{V_1} \right)^{\gamma-1}

\frac{T_a}{T_b}= \left( \frac{1}{r} \right)^{\gamma-1}

\frac{T_d}{T_c}= \left( \frac{V_3}{V_1} \right)^{\gamma-1}

\frac{T_d}{T_c}= \left( \frac{1}{r_C} \right)^{\gamma-1}

A razão de corte a razão do volume do cilindro depois e antes do processo de combustão

\varepsilon=1-\frac{1}{r}^{\gamma-1}\left[ \frac{1}{\gamma} \left(\frac{r_C^{\gamma}-1}{r_C-1}\right)\right]

A eficiência em função da taxa de compressão, \(r=V_1/V_2\) e corte \(r_C = V_3/V_2\):

Motores de combustão à gás

O motor Diesel com ciclo Diesel idealizado

\varepsilon=1-\frac{1}{r}^{\gamma-1}\left[ \frac{1}{\gamma} \left(\frac{r_C^{\gamma}-1}{r_C-1}\right)\right]

Na eficiência do ciclo Diesel:

O termo em amarelo é aquele da eficiência de uma máquina Otto. Se \(r_C \rightarrow 1\), obtemos Otto.

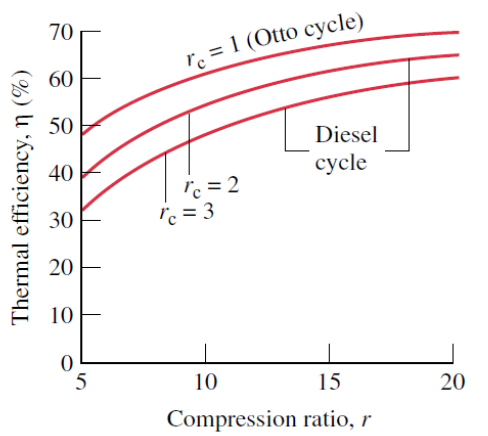
Valores de r em torno de 15 a 20 são normais; com esses valores e com \(\gamma = \) 1,4, a eficiência teórica de um ciclo diesel idealizado é cerca de 0,65 até 0,70.

Para um mesmo fator de compressão \(r\), o ciclo Otto é mais eficiente que o ciclo Diesel.

Como não existe nenhum combustível no cilindro durante a maior parte do tempo de compressão, não pode ocorrer pré-ignição; Para uma mesma eficiência a razão de compressão r pode ser muito maior que a de um motor a gasolina.

Motores de combustão à gás

Outros ciclos

Stirling idealizado

Gerando energia a partir da radiação solar:

https://youtu.be/bwazXoqULKA

https://youtu.be/Ez4_kxfr3Ik

Solução:

https://youtu.be/y2Ck__NZy10

Motores de combustão à gás

Outros ciclos

Brayton idealizado

Solução

https://youtu.be/QUbVQA788oY

Gerando energia a partir de compressores e turbinas.

https://www.youtube.com/live/RJnhKvWsMmo?feature=share

Questão 1

Uma máquina de Carnot retira 3000 J de calor de um reservatório térmico com temperatura T = 500 K e libera calor em um reservatório térmico com temperatura T = 325 K. Quanto trabalho a máquina de Carnot realiza nesse processo?

Questão 2

Uma máquina de Carnot Trabalha entre dois reservatórios de calor como um refrigerador. Durante cada ciclo, 100 J de calor são absorvidos do reservatório frio e 150 J de calor são liberados para o reservatório quente. (a) Qual é o rendimento da máquina de Carnot, quando ela trabalha como uma máquina térmica entre os mesmos dois reservatórios? (b) Mostre que nenhuma outra máquina, trabalhando como um refrigerador entre os mesmos dois reservatórios, pode ter um CD maior que 2,00.

Questão 3

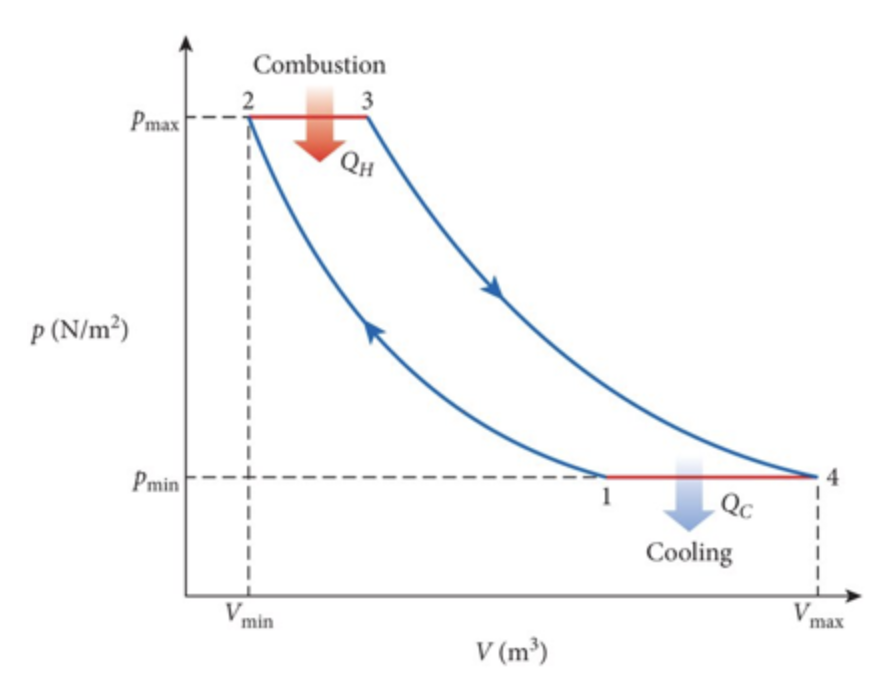
A figura mostra uma máquina de Carnot que trabalha entre as temperaturas T1 = 400 K e T2 = 150 K e alimenta uma refrigerador de Carnot que trabalha entre as temperaturas T3 = 325 K e T4 = 225 K. Qual a razão Q3/Q1?

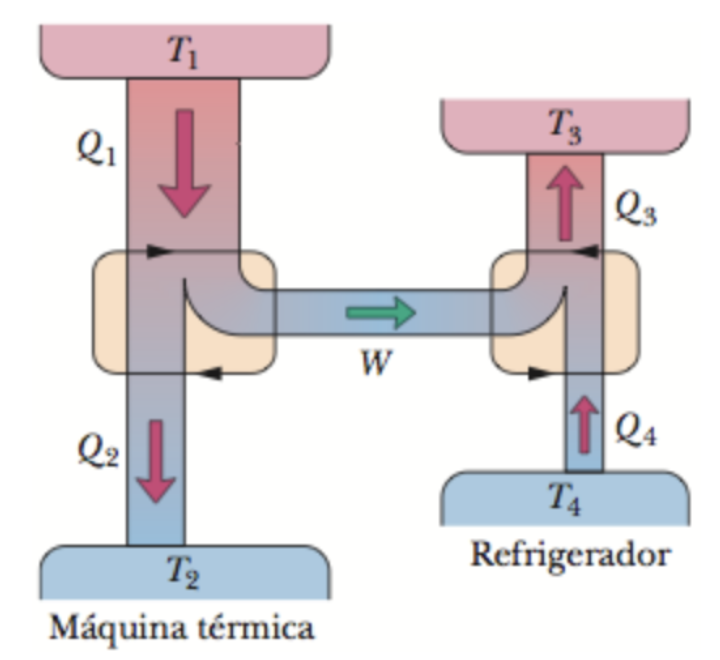
Fonte: Halliday

Questão 4

(a) Uma máquina de Carnot opera entre uma fonte quente a 320 K e uma fonte fria a 260 K. Se a máquina absorve 500 J da fonte quente por ciclo na forma de calor, qual é o trabalho realizado por ciclo? (b) Se a máquina opera como um refrigerador entre as mesmas fontes, que trabalho por ciclo deve ser fornecido para remover 1000 J da fonte fria na forma de calor?