Aula 23

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 20 - A segunda lei da termodinâmica

Seção 20.7

Enunciar o Teorema de Clausius

Verificar que a entropia é uma função do estado termodinâmico.

Verificar a relação entre entropia e equilíbrios térmico e mecânico (omitido).

Calcular a variação da entropia para:

Transformações de um gás ideal.

Expansão livre de um gás ideal.

Transições de fase da água.

Motivação

Fonte: https://youtu.be/krwLTDHzQpc

"Enquanto o paradoxo era minuciosamente estudado por cientistas de todo o mundo, um novo campo de estudos surgiu: a Teoria da Informação". É graças à Teoria da Informação que hoje temos o que podemos chamar de computação moderna.

A entropia de um gás ideal

Para um fluido homogêneo, a entropia S é uma função de estado:

S=S(P,V)
S=S(P,T)
S=S(V,T)

A primeira lei da termodinâmica pode ser reescrita como:

\delta Q=dU-\delta W

Para um processo reversível, podemos usar a definição de entropia:

\delta Q_R=TdS

Assim, podemos combinar as duas leis da termodinâmica, como:

TdS=dU-\delta W

para estudar os processos termodinâmicos já conhecidos!

A entropia de um gás ideal

Nos processos abaixo, um gás homogêneo tem sua temperatura elevada devido ao aumento da pressão (processo isocórico) e depois tem seu volume expandido com diminuição da pressão (processo isotérmico).

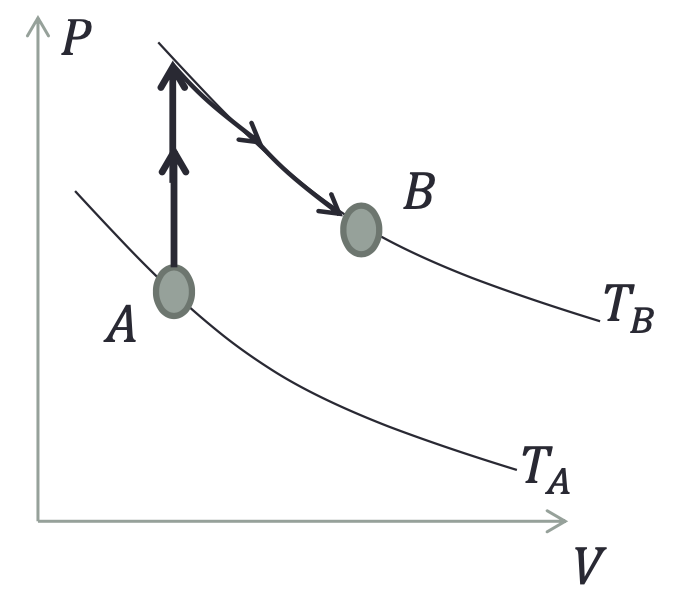
A variação infinitesimal da entropia do gás ideal:

TdS=dU+\delta W
TdS=C_VdT+PdV
dS=C_V\frac{dT}{T}+\frac{P}{T}dV
dS=C_V\frac{dT}{T}+nR\frac{dV}{V}

A variação finita da entropia do gás ideal, vem por integração:

\Delta S_{gas}=C_V\ln\left(\frac{T_B}{T_A}\right)+nR\ln\left(\frac{V_f}{V_i}\right)

Na expansão isotérmica, a entropia do universo é nula. Afinal, o processo é reversível,

\Delta S_u=\Delta S_{gas}+\Delta S_{viz}=0

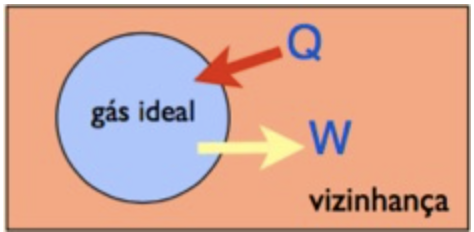
A entropia de um gás ideal

Nos processos isovolumétrico e isotérmico, a variação da entropia de um gás ideal é:

Caso o processo seja apenas uma expansão isotérmica, a variação da entropia do gás ideal aumenta à medida que ele expande e sua pressão diminui ( a entropia aumenta no sentido da diminuição da pressão ):

\Delta S_{gas}=C_V\ln\left(\frac{T_B}{T_A}\right)+nR\ln\left(\frac{V_f}{V_i}\right)
\Delta S_{gas}=+nR\ln\left(\frac{V_f}{V_i}\right)
P_1>P_2
V_1< V_2
P_1< P_2
V_2< V_1

Fonte: Carlos Aguiar (UFRJ)

Q=+nRT\ln\left(\frac{V_f}{V_i}\right)

Caso o processo seja apenas um aquecimento isocórico, a variação da entropia do gás ideal aumenta à medida que a temperatura aumenta (a entropia aumenta devido ao calor fornecido ao gás, elevando a temperatura ):

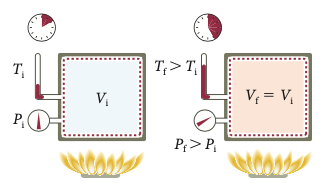
\Delta S_{gas}=+C_V\ln\left(\frac{T_f}{T_i}\right)

Fonte: Eric Mazur

Q=+C_VT\ln\left(\frac{V_f}{V_i}\right)

A entropia de um gás ideal

Nos processos isovolumétrico e isotérmico, a variação da entropia de um gás ideal é:

Utilizando a relação de Mayer (\(C_P=C_V+nR\)), o índice adiabático (\(\gamma = C_P/C_V)\) e as propriedades de logaritimo:

\Delta S_{gas}=C_V\ln\left(\frac{T_B}{T_A}\right)+nR\ln\left(\frac{V_f}{V_i}\right)
\Delta S_{gas}=C_V\ln\left( \frac{P_BV_B^{\gamma}}{P_AV_A^{\gamma}} \right)

Em um processo adiabático:

P_BV_B^{\gamma}= P_AV_A^{\gamma}

A variação de entropia do gás é nula:

\Delta S_{gas}=0

A entropia de um gás ideal

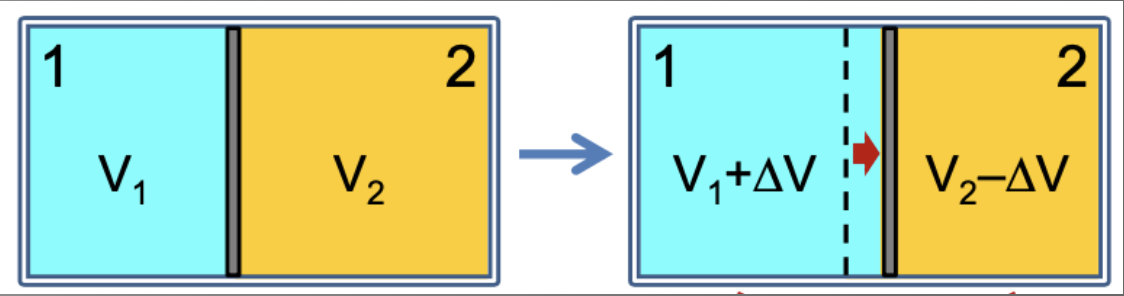
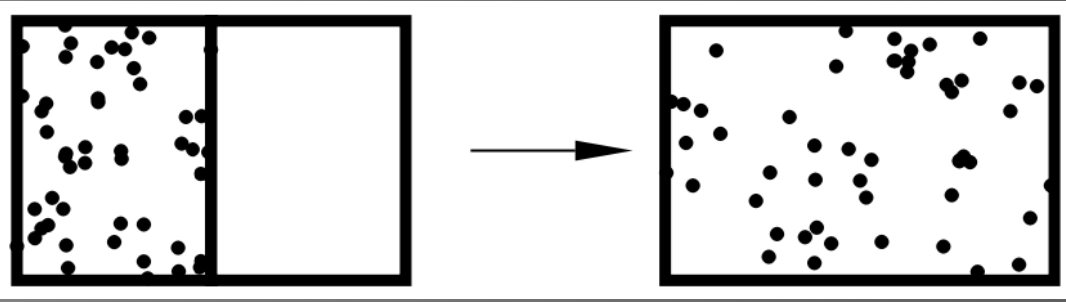
A expansão livre de um gás ideal. É um processo irreversível.

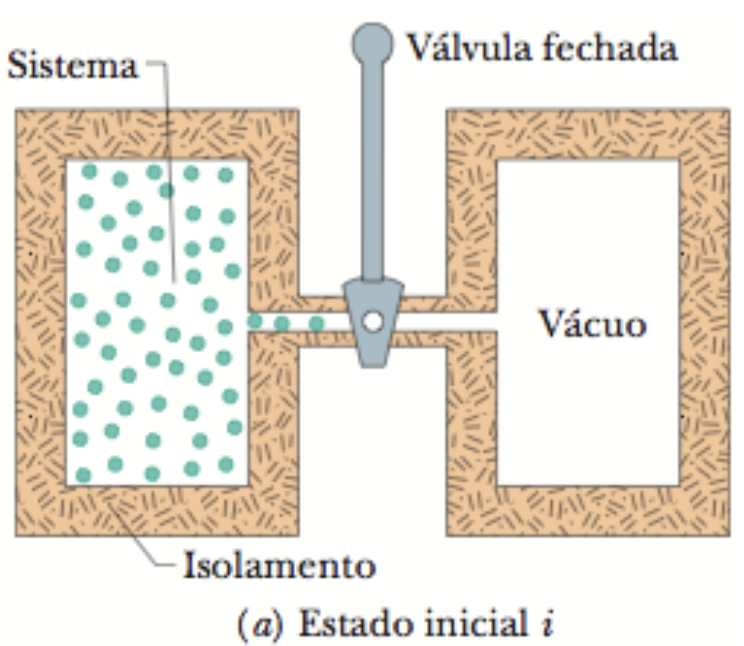
Um gás inicialmente confinado a um lado de um recipiente é permitido se expandir livremente sobre a parte do recipiente que estava inicialmente evacuada.

V_i=V_0\,,\quad T_i=T_0

Os estados inicial e final da expansão livre são iguais aos estados inicial e final de uma expansão isotérmica.

V_i=V_0\,,\quad T_i=T_0
V_f=2V_0\,,\quad T_f=T_0

A expansão livre é irreversível enquanto a expansão isotérmica é reversível.

V_f=2V_0\,,\quad T_f=T_0

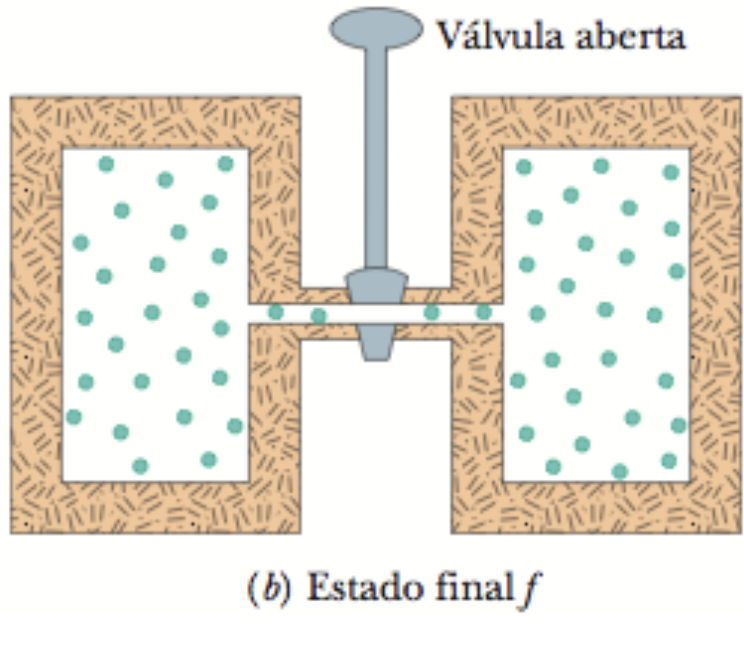
A entropia de um gás ideal

A expansão livre de um gás ideal. É um processo irreversível.

No processo reversível os estados são aqueles de equilíbrio (P,V) são bem definidos. No processo irreversível, não podemos representar o processo entres os estados inicial e final.

Dados um processo irreversível sempre podemos construir um processo reversível que leve aos mesmos estados inicial e final do processo irreversível.

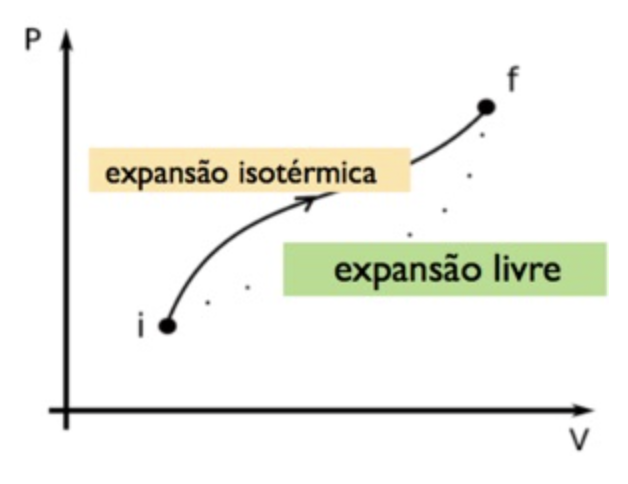
A entropia de um gás ideal

A expansão livre de um gás ideal. É um processo irreversível.

Como os estados inicial e final são aqueles do processo reversível:

\int_R \frac{\delta Q}{T}=S_f-S_i

Nós podemos calcular a variação da entropia do processo irreversível, pois os estados inicial e final são os mesmos:

\int_I \frac{\delta Q}{T}\equiv S_f-S_i

Na expansão livre, aproximamos o processo por um isotérmico:

\Delta S_{gas}=nR\ln\left(\frac{2V_i}{V_i}\right)>0
\Delta S_{gas}=+nR\ln(2)>0

mesmo que na expansão livre \(Q_I = 0\). Este processo é adiabático, mas não é isentrópico!

\Delta S_{viz}=0
\Delta S_{u}=+nR\ln(2)>0

A entropia de um gás ideal

A entropia em processos reais que não são quase-estáticos

Considere o congelamento de 50,0 g de água colocada no congelador de um refrigerador. Suponha as paredes do congelador mantidas a \(-10 ^o\) C. A água, inicialmente líquida a \(0 ^o\) C, é congelada e resfriada até \(-10 ^o\) C.

Um resfriamento lento de uma garrafa no interior de um refrigerador não é uma troca de calor isotérmica: garrafa e congelador estão a temperaturas diferentes.

A entropia total do universo formado pelo refrigerador e água aumenta.

Esse processo é irreversível.

Então, a variação da entropia do universo deve aumentar.

A entropia de um gás ideal

A entropia em processos reais que não são quase-estáticos

Refrigerador:

\Delta S_{refrigerador}=\frac{Q}{T_{reservatório}}

Água:

O processo é isotérmico, pois a temperatura não varia:

\Delta S_{ref}=+63,5\text{ J/K}>0
\Delta S_{refrigerador}=\frac{(50\times 10^{-3})(334\times 10^3)}{263,15\text{ K}}
\Delta S_{agua}=\Delta S_{latente}+\Delta S_{sensível}
\Delta S_{agua}=-\frac{(50 \times 10^{-3})(334\times 10^3)}{273,15}-\int_{263,15}^{273,15}\frac{(50\times 10^{-3})(2,093\times 10^3)dT}{T}
\Delta S_{agua}=-57,2\text{ J/K}<0

O resfriamento não é isotérmico. A água perde calor ao congelar e ao resfriar a diferentes temperaturas.

Universo:

\Delta S_u=\Delta S_{agua}+\Delta S_{refrigerador}
\Delta S_u=6,23\text{ J/K}>0

Processo irreversível.

O teorema de Clausius

Podemos acoplar máquinas térmicas para melhorar a eficiência de trabalho. As máquinas podem ser irreversíveis ou reversíveis.

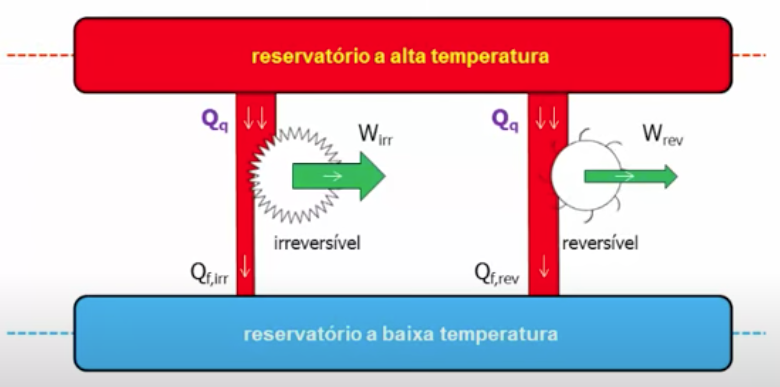
Fonte: Prof. P. Seleghim - https://youtu.be/q6xB_toGWMs

Para a máquina irreversível:

\varepsilon_I=\frac{W_{irrev}}{Q_q}=1-\frac{Q_{f,irrev}}{Q_q}

Para a máquina reversível:

\varepsilon_R=\frac{W_{rev}}{Q_q}=1-\frac{Q_{f,rev}}{Q_q}= 1-\frac{T_{f}}{T_q}

A partir do Teorema de Carnot, as máquinas térmicas reversíveis são mais eficientes.

\varepsilon_R \geq \varepsilon_I
W_{rev} > W_{irrev}
Q_{f,rev} < Q_{f,irrev}
\Rightarrow

O teorema de Clausius

Em máquinas reversíveis um calor \(Q_q\) na temperatura \(T_q\) é “equivalente” a um calor \(Q_f\) na temperatura \(T_f\):

\frac{|Q_q|}{T_q}=\frac{|Q_f|}{T_f}

Pensando num ciclo completo de apenas uma máquina reversível:

\frac{Q_q}{T_q}=-\frac{Q_f}{T_f}
\frac{Q_q}{T_q}+\frac{Q_f}{T_f}=0
\sum_i\frac{Q_i}{T_i}=0
\Rightarrow
\Rightarrow

Para N-máquinas reversíveis operando em um ciclo:

\oint\frac{\delta Q}{T}
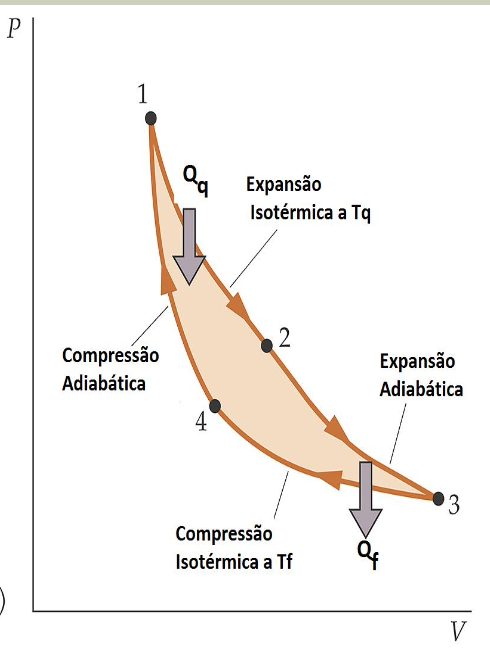
Fonte: Halliday & Resnick
=\int_1^2\frac{\delta Q}{T}+\int_2^3\frac{\delta Q}{T}+\int_3^4\frac{\delta Q}{T}+ \int_4^1\frac{\delta Q}{T}
=\frac{Q_q}{T_q}+0-\frac{Q_f}{T_f}+0
=\frac{Q_q}{T_q}-\frac{Q_f}{T_f}
\oint\frac{\delta Q}{T}
\oint\frac{\delta Q}{T}
\oint\frac{\delta Q}{T}
=0

O teorema de Clausius

Em máquinas irreversíveis um calor \(Q_q\) na temperatura \(T_q\) não é “equivalente” a um calor \(Q_f\) na temperatura \(T_f\):

\frac{|Q_f|}{T_f}\neq\frac{|Q_q|}{T_q}

Levando em conta a convenção de sinais, em um ciclo irreversível:

\sum_I\frac{\delta Q_i}{T_i}<0

Pensando na eficiência de Carnot e de uma máquina irreversível,

\varepsilon_I\leq\varepsilon_R
\Rightarrow
\Rightarrow
\frac{Q_f}{T_f}+\frac{Q_q}{T_q}\leq 0
\Rightarrow
1-\frac{|Q_f|}{|Q_q|}\leq1-\frac{T_f}{T_q}
\frac{|Q_f|}{|Q_q|}\leq\frac{T_f}{T_q}
\frac{|Q_f|}{T_f}\leq \frac{|Q_q|}{T_q}

Para N máquinas irreversíveis:

\oint_I\frac{\delta Q}{T}<\oint_R\frac{\delta Q}{T}
\frac{Q_q}{T_q}-\frac{Q_{f,irrev}}{T_f}< \frac{Q_q}{T_q}-\frac{Q_{f,rev}}{T_f}

Para duas máquinas acopladas:

Q_{f,irrev} > Q_{f,rev}

O teorema de Clausius

A desigualdade de Clausius é equivalente ao princípio do aumento da entropia, pois se

\oint\frac{\delta Q}{T}\leq0

verifica-se que em um sistema isolado, a entropia nunca pode decrescer:

\Delta S_u \geq 0

Para um reservatório térmico e um sistema que evolui de A para B, reversivelmente:

A variação da entropia do sistema (reversível) deve ser maior ou igual à entropia do reservatório térmico.

-\frac{Q_1}{T_{R,1}} -\frac{Q_2}{T_{R,2}}+ \cdots +\Delta S_s\geq 0
\sum_i\frac{Q_i}{T_{R,i}} \leq \Delta S_s
\Rightarrow
\oint \frac{\delta Q}{T} \leq \Delta S_s
\oint \frac{\delta Q}{T}\leq 0

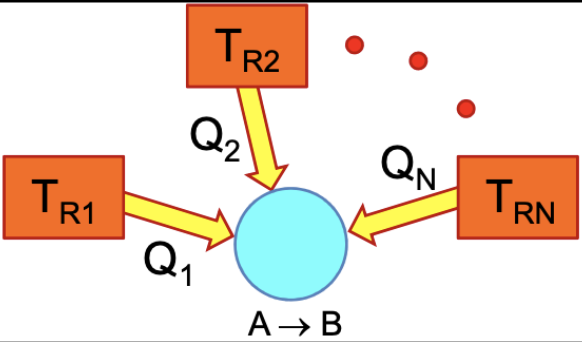
Se o sistema opera num ciclo:

s

O teorema de Clausius

Para um ciclo reversível,

\oint_R\frac{\delta Q}{T}=0

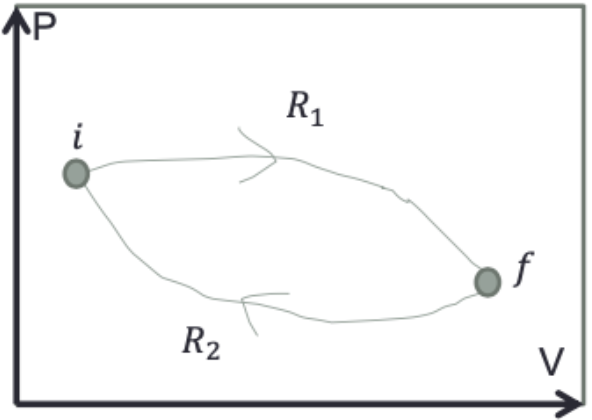
Para os dois caminhos reversíveis da figura:

\left(\int_i^f \frac{\delta Q_{rev}}{T}\right)_{R1} + \left(\int_f^i \frac{\delta Q_{rev}}{T}\right)_{R2}=0
\left(\int_i^f \frac{\delta Q_{rev}}{T}\right)_{R1} = -\left(\int_f^i \frac{\delta Q_{rev}}{T}\right)_{R2}

Mas como R2 é reversível:

-\left(\int_f^i \frac{\delta Q_{rev}}{T}\right)_{R2} = \left(\int_i^f \frac{\delta Q_{rev}}{T}\right)_{R2}
\left(\int_i^f \frac{\delta Q_{rev}}{T}\right)_{R1} = \left(\int_i^f\frac{\delta Q_{rev}}{T}\right)_{R2}

A integral não depende do caminho que conectada os estados. Define-se, então a entropia como

uma função de estado:

S_f-S_i=\int_i^f\frac{\delta Q_{rev}}{T}
\Rightarrow

O teorema de Clausius

Para processos irreversíveis:

\oint_I\frac{\delta Q}{T}<0

Para os dois caminhos da figura:

\left(\int_1^2 \frac{\delta Q}{T}\right)_{I} + \left(\int_2^1 \frac{\delta Q_{rev}}{T}\right)_{R}<0
\left(\int_2^1 \frac{\delta Q_{rev}}{T}\right)_{R} = -\left(\int_1^2 \frac{\delta Q_{rev}}{T}\right)_{R}

Aproveitando a reversibilidade no ciclo completo:

\left(\int_1^2 \frac{\delta Q}{T}\right)_{I} -\Delta S_R<0

A variação da entropia reversível deve ser maior que a integral da entropia irreversível.

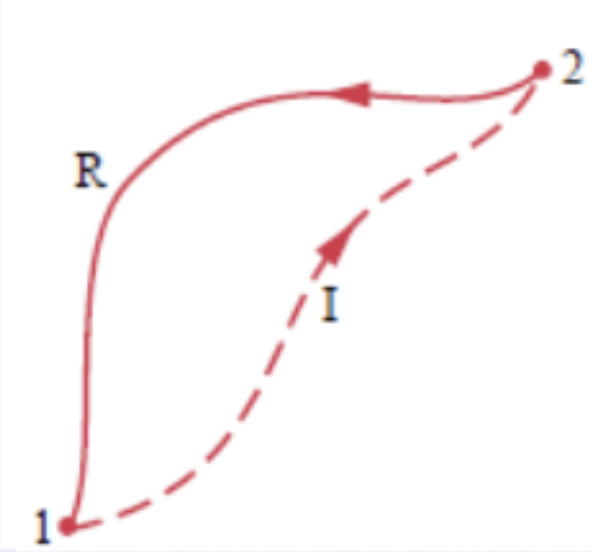
\Delta S_R> \left(\int_i^f\frac{\delta Q}{T}\right)_I
\left(\int_1^2 \frac{\delta Q}{T}\right)_{I} - \left(\int_1^2 \frac{\delta Q_{rev}}{T}\right)_{R}<0

mas no caminho reversível:

O teorema de Clausius

A desigualdade de Clausius

\oint\frac{\delta Q}{T}\leq0
\oint_I\frac{\delta Q}{T}\leq \oint_R\frac{\delta Q}{T}
\int_I\frac{\delta Q}{T} + S_{produzida}= \Delta S_R

Na engenharia:

S_{produzida}
> 0\,\quad irreversível
= 0\,\quad reversível
< 0\,\quad impossível
\{

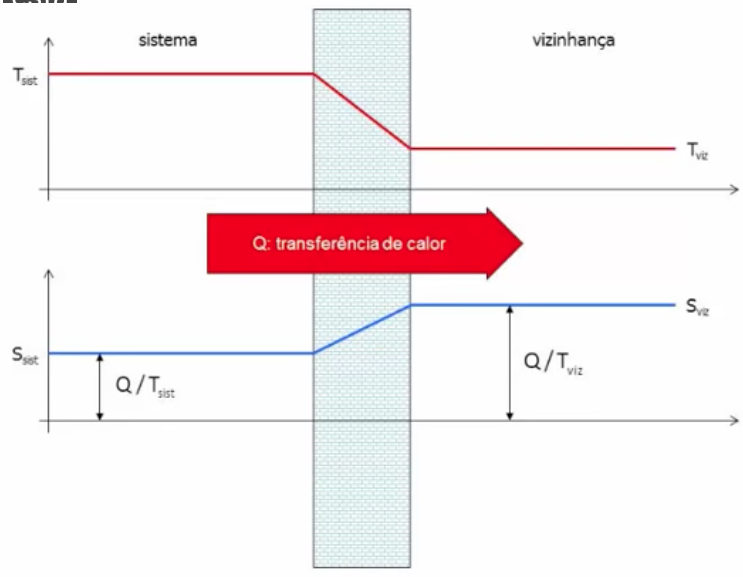
Fonte: Prof. P. Seleghim - https://youtu.be/q6xB_toGWMs

T_q>T_f
Q
\Delta S_q<\Delta S_f

Há um aumento da entropia, pois há uma diferença finita de temperaturas. A entropia produzida é irreversível. A entropia foi produzida pela parede.

A entropia do universo sempre aumenta.

O teorema de Clausius

A desigualdade de Clausius é a forma matemática para a segunda lei da termodinâmica.

\oint\frac{\delta Q}{T}\leq0

a soma deve ser negativa a fim de não violar os enunciados de Clausius/Kelvin.

O limite, para qualquer ciclo irreversível, o processo adiabático é irreversível (não é isentrópico):

\oint\frac{\delta Q}{T}<0
\Delta S_R>\left(\frac{Q}{T}\right)_I
Q_I=0

O limite, para qualquer ciclo reversível, o processo adiabático é reversível (isentrópico):

\oint\frac{\delta Q}{T}=0
\Delta S_R=\frac{Q_{rev}}{T}=0
Q_R=0

O teorema de Clausius

A entropia do universo permanece constante durante processos reversíveis.

A entropia do universo cresce durante processos irreversíveis.

A entropia é uma medida de irreversibilidade.

A entropia indica a direção de evolução de um processo.

A entropia é uma função de estado.

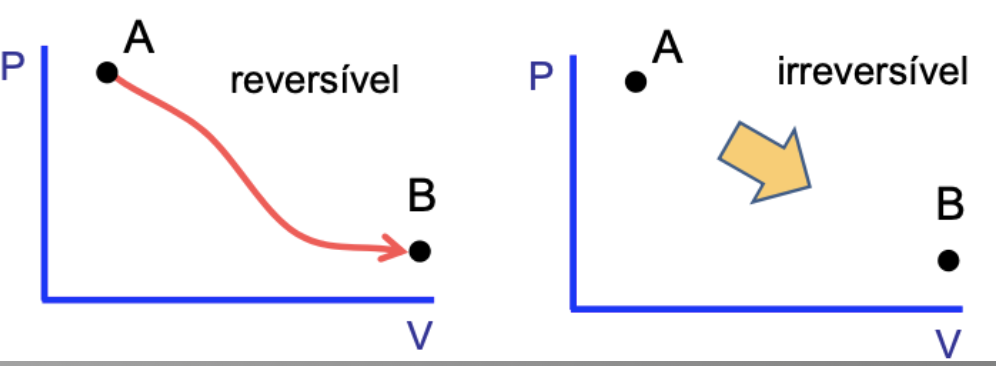
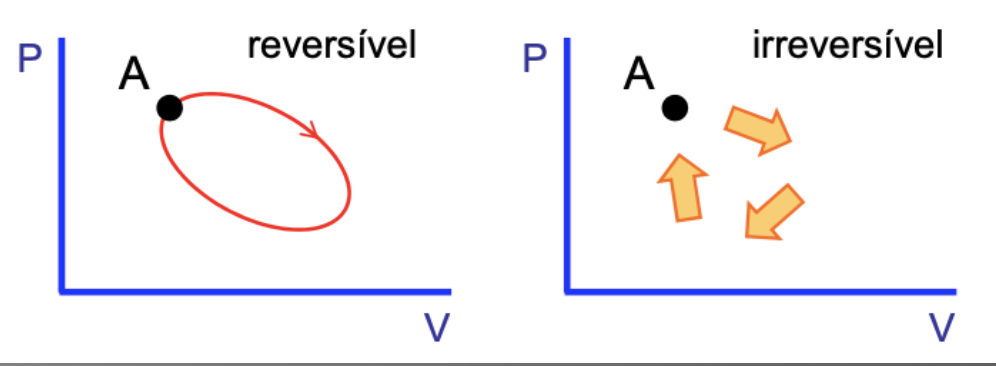
Fonte: Carlos Aguiar (UFRJ)

Fonte: Carlos Aguiar (UFRJ)

A entropia é uma função de estado

Entropia e equilíbrio térmico.

Para um sistema composto dividido por uma parede fixa, impermeável e diatérmica (vínculo interno relaxado), a energia interna é conservada:

U=U_A+U_B=cte.

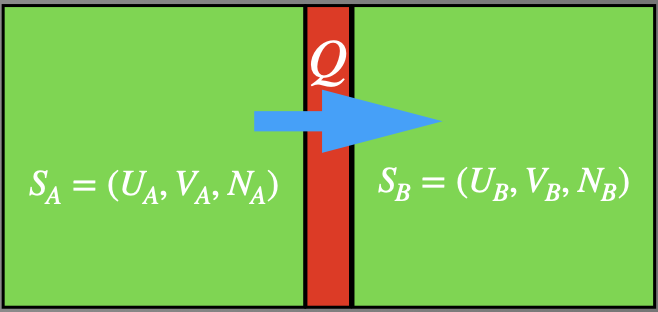
A entropia é maximizada (a entropia sempre aumenta):

S=S_A(U_A,V_A)+S_B(U_B,V_B)
dS=\left( \frac{\partial S_A}{\partial U_A} \right)_{V_A}dU_A+ \left( \frac{\partial S_B}{\partial U_B} \right)_{V_B}dU_B=0

Então, a entropia total:

dU=dU_A+dU_B=0
\left[\left( \frac{\partial S_A}{\partial U_A} \right)_{V_A}- \left( \frac{\partial S_B}{\partial U_B} \right)_{V_B}\right]dU_A=0
\Rightarrow
dU_B=-dU_A
dS=0

A entropia é uma função de estado

Entropia e equilíbrio térmico.

A maximização da entropia leva ao resultado:

\left( \frac{\partial S_A}{\partial U_A} \right)_{V_A}= \left( \frac{\partial S_B}{\partial U_B} \right)_{V_B}

A dimensão dessa grandeza é:

\frac{\text{J/K}}{\text{J}}\equiv \frac{1}{\text{K}}
\frac{\text{energia/temperatura}}{\text{energia}}\equiv \frac{1}{\text{temperatura}}

Conclui-se que a variação da entropia pela variação da energia interna está associada à temperatura:

\left( \frac{\partial S}{\partial U} \right)_{V}=\frac{1}{T}

Do resultado anterior concluímos que no equilíbrio térmico, a entropia é máxima:

\frac{1}{T_A}=\frac{1}{T_B}
T_A=T_B

A entropia é uma função de estado

Entropia e equilíbrio térmico.

Conhecida a função de estado \(S=S(U,V)\),

é a definição termodinâmica da temperatura absoluta.

Para uma mesma variação da energia:

\frac{1}{T}=\left( \frac{\partial S}{\partial U} \right)_{V}

Temperatura alta \(\rightarrow \) pequena variação da entropia.

Temperatura baixa \(\rightarrow \) alta variação da entropia.

\Delta S_u=\Delta S_f +\Delta S_q>0
\Delta S_u=\left[ \frac{1}{T_f}- \frac{1}{T_q} \right]Q>0
\Rightarrow T_q>T_f
\Rightarrow Q>0

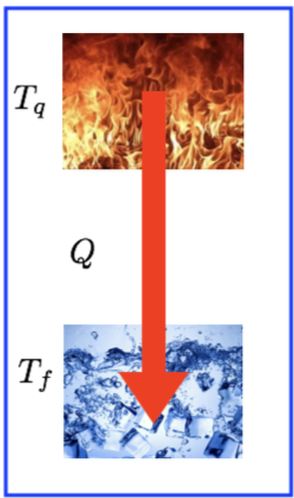
A entropia do universo aumenta. O fluxo de calor se dá no sentido de maior para menor temperatura quando não há trabalho.

A entropia é uma função de estado

Entropia e equilíbrio mecânico.

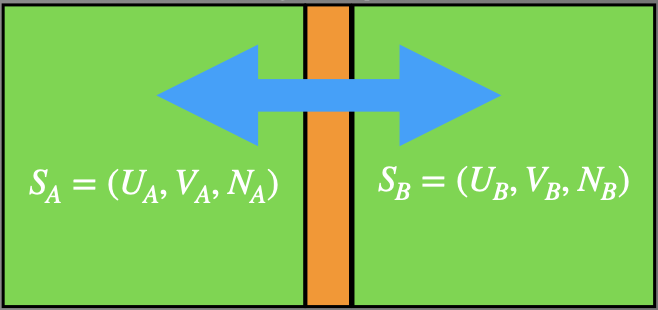
Para um sistema composto dividido por uma parede móvel (vínculo interno relaxado):, impermeável e diatérmico (troca de energia).

U=U_A+U_B=cte.

A entropia é maximizada (a entropia sempre aumenta):

S=S_A(U_A,V_A)+S_B(U_B,V_B)
dS=\left( \frac{\partial S_A}{\partial V_A} \right)_{U_A}dV_A+ \left( \frac{\partial S_B}{\partial V_B} \right)_{U_B}dV_B=0

Então, a entropia total:

dV=dV_A+dV_B=0
\left[\left( \frac{\partial S_A}{\partial V_A} \right)_{U_A}- \left( \frac{\partial S_B}{\partial V_B} \right)_{U_B}\right]dV_A=0
\Rightarrow
dV_B=-dV_A
dS=0

A entropia é uma função de estado

Entropia e equilíbrio mecânico.

A maximização da entropia leva ao resultado:

\left( \frac{\partial S_A}{\partial V_A} \right)_{U_A}= \left( \frac{\partial S_B}{\partial V_B} \right)_{U_B}

A dimensão dessa grandeza é:

\frac{\text{J/K}}{\text{m}^3}\equiv \frac{\text{N.m}^2}{\text{K}}
\frac{\text{energia/temperatura}}{\text{volume}}\equiv \frac{\text{pressão}}{\text{temperatura}}

Conclui-se que a variação da entropia pela variação do volume está associada à pressão e temperatura termodinâmicas:

\left( \frac{\partial S}{\partial U} \right)_{U}=\frac{P}{T}

Do resultado anterior concluímos que no equilíbrio térmico, a maximização da entropia leva ao equillíbrio de pressões (mecânico):

\frac{P_A}{T_A}=\frac{P_B}{T_B}
P_A=P_B|_{T_A=T_B}

A entropia é uma função de estado

Entropia e equilíbrio mecânico.

Conhecida a função de estado \(S=S(U,V)\),

é a definição termodinâmica da pressão absoluta.

Para uma mesma variação do volume e temperatura:

P=T\left( \frac{\partial S}{\partial V} \right)_{U}

Pressão alta \(\rightarrow \) grande variação da entropia.

Pressão baixa \(\rightarrow \) pequena variação da entropia.

\Delta S_u=\Delta S_1 +\Delta S_2>0
\Delta S_u=\left[ \frac{P_1}{T_1}- \frac{P_2}{T_2} \right]\Delta V>0
\Rightarrow P_1>P_2
\Rightarrow \Delta V>0

A entropia aumenta muito na expansão (1) e diminui pouco da compressão (2). O pistão é empurrado no sentido de maior para menor pressão.

Fonte: Carlos Aguiar (UFRJ)

O teorema de Clausius

Existe uma trajetória reversível em “zigzag" entre os dois mesmos estados (\(if\)), consistindo de uma adiabática (\(ia\)) seguida por uma isoterma (\(ab\)) seguida por uma adiabática(\(bf\)) ..., tal que o calor transferido durante a porção isotérmica é o mesmo daquele transferido durante o processo original.

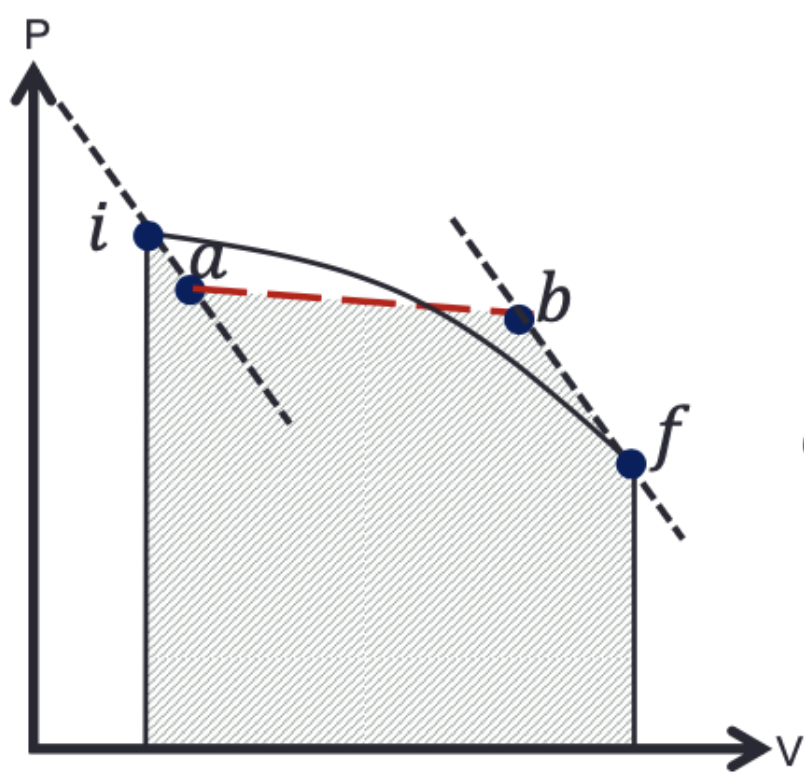
O processo \(i\rightarrow f\) pode ser aproximado com processos intermediários:

i\rightarrow a:\quad\text{adiabático}
a\rightarrow b:\quad\text{isotérmico}
b\rightarrow f:\quad\text{adiabático}

A quantidade de calor líquido é trocado apenas nos trechos isotérmicos:

Q_{if}=Q_{ia}+Q_{ab}+Q_{bf}
Q_{if}=Q_{ab}
0
0

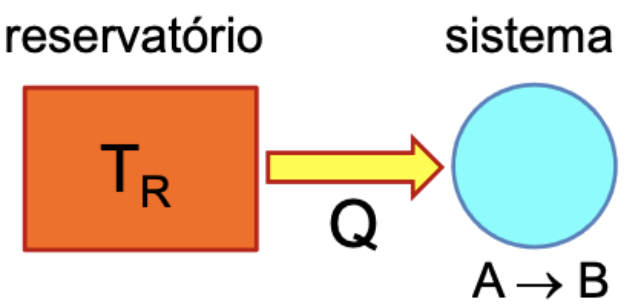
temperatura do reservatório

processo original

isoterma

adiabáticas

O teorema de Clausius

Um ciclo reversível pode ser construído (aproximado) por inúmeras tiras adjacentes (zigzags)

Ao lado, temos apenas um único ciclo contendo os processos intermediários:

A quantidade de calor líquido é trocado apenas nos trechos isotérmicos:

Q_{ciclo}=Q_{isotermas}
W_{ciclo}=Q_{isotermas}

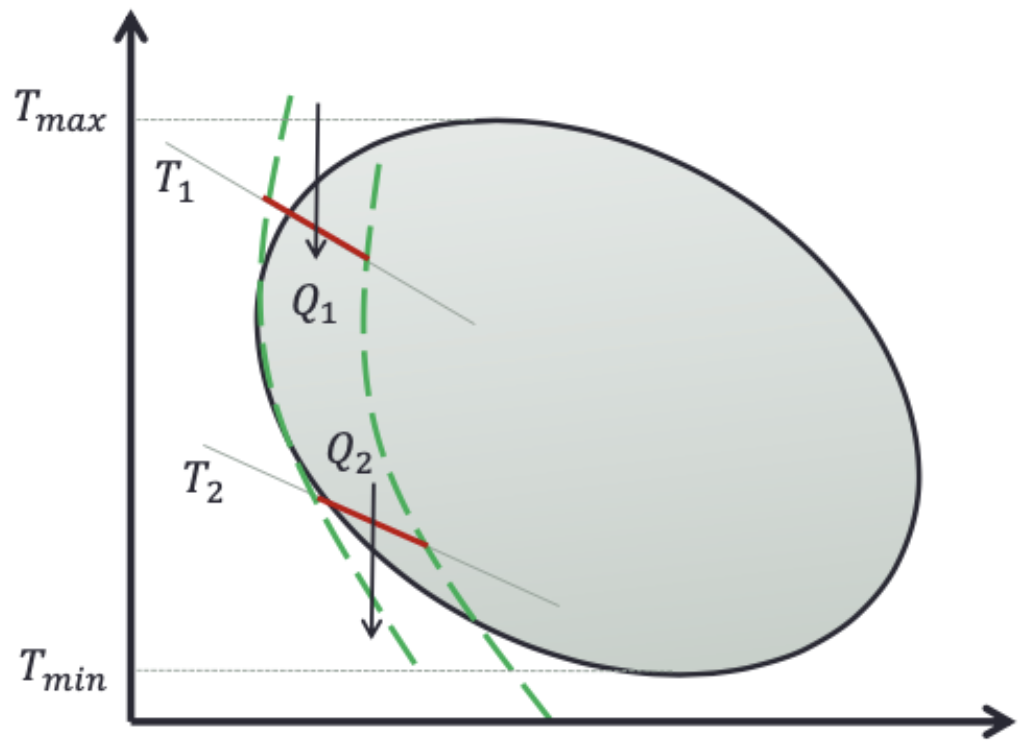
isotermas

adiabáticas

O trabalho líquido, no ciclo, é igual ao calor trocado:

temperatura dos reservatórios

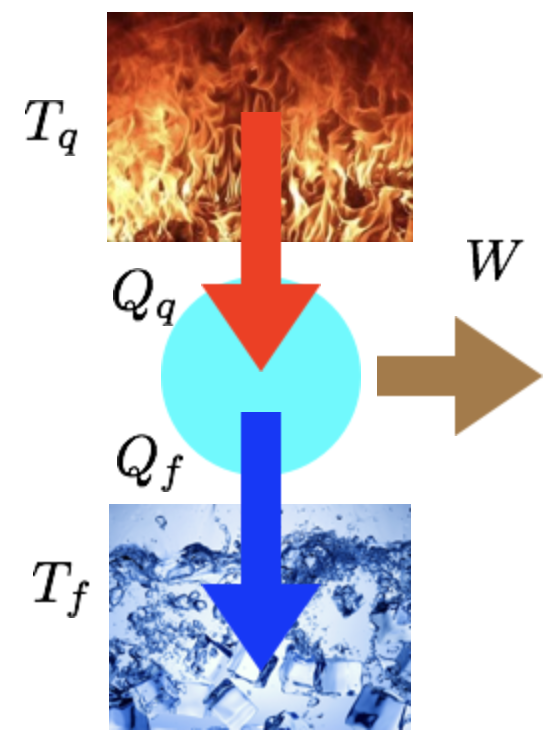
Cada tira representa um ciclo reversível (Carnot):

\frac{|Q_1|}{T_1}=\frac{|Q_2|}{T_2}

O teorema de Clausius

Para um ciclo completo podemos imaginar \(N\) tiras adjacentes, ou máquinas de Carnot.

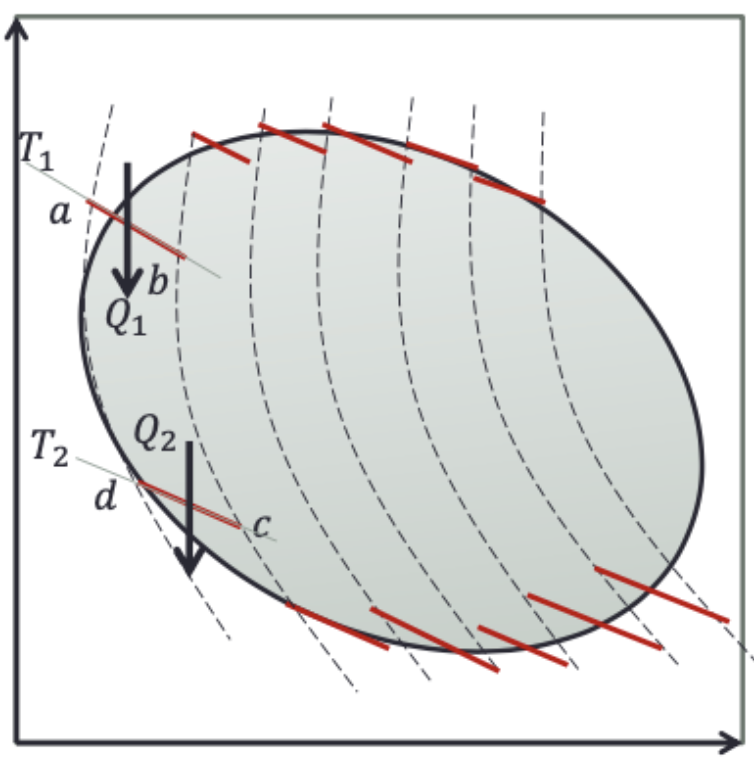
No ciclo abcd (Carnot) utilizando a convenção dos sinais:

\frac{|Q_1|}{T_1}=\frac{|Q_2|}{T_2}
\frac{Q_1}{T_1}=-\frac{Q_2}{T_2}
\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0
\Rightarrow
\Rightarrow

sendo \(T_i\) é a temperatura da fronteira onde há a transferência de energia (calor).

Para todas as tiras finitas do ciclo,  a entropia dos reservatórios:

\sum_i\frac{Q_i}{T_i}=0

Para um número infinito de tiras (reservatórios térmicos com troca de calor isotermicamente):

\oint_R\frac{\delta Q}{T}=0

Questão 1

Suponha que 4,00 mols de um gás ideal sofrem uma expansão reversível isotérmica do volume V1 para o volume V2 = 2,00 V1 a uma temperatura T = 400 K. Determine:

(a) o trabalho realizado pelo gás;

(b) a variação da entropia do gás;

(c) Se a expansão fosse reversível e adiabática em vez de isotérmica, qual seria a variação da entropia do gás?

Questão 2

Determine (a) a energia absorvida na forma de calor e (b) a variação da entropia de um bloco de cobre de 2,00 kg cuja temperatura aumenta reversivelmente de 25,0 oC para 100 oC. O calor específico do cobre é 386 J/(kg.K).

Questão 3

(a) Qual é a variação de entropia de um cubo de gelo de 12,0 g que funde totalmente em um balde de água cuja temperatura está ligeiramente acima do ponto de congelamento da água? (b) Qual é a variação de entropia de uma colher de sopa de água, com uma massa de 5,00 g, que evapora totalmente ao ser colocada em uma placa quente cuja temperatura está ligeiramente acima do ponto de ebulição da água?

Questão 4

Um bloco de cobre de 50,0 g cuja temperatura é 400 K é colocado em uma caixa isolada juntamente com um bloco de chumbo de 100 g cuja temperatura é 200 K. (a) Qual é a temperatura de equilíbrio do sistema dos dois blocos? (b) Qual é a variação da energia interna do sistema do estado inicial para o estado de equilíbrio? (c) Qual é a variação da entropia do sistema?

Questão 5

(a) Para 1,0 mol de um gás monoatômico ideal submetido ao ciclo da figura abaixo, em que V1 = 4,00 V0, qual é o valor de W(P0V0) quando o gás vai do estado "a" ao estado "c" ao longo da trajetória abc? Quanto é o valor de \(\Delta U/(P0V0)\) quando o gás (b) vai de "b" para "c" e (c) descreve um ciclo completo? Quanto é o valor da variação de entropia quando o gás (d) vai de "b" para "c"e (e) descreve um ciclo completo?

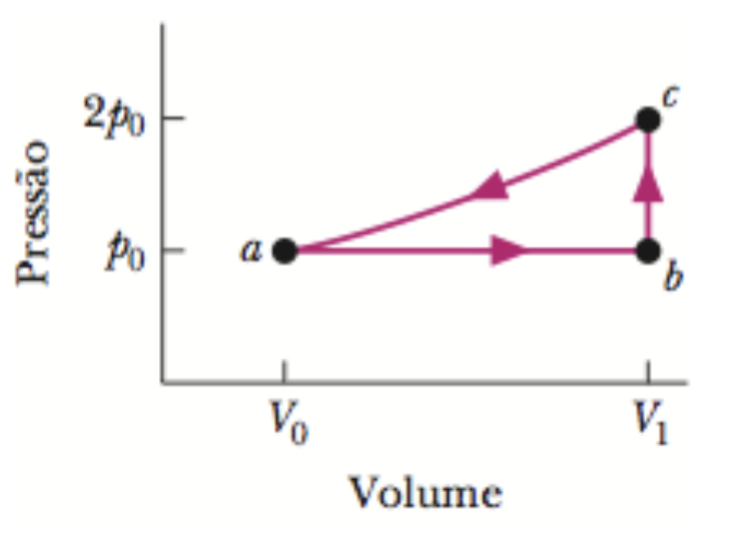
Fonte: Halliday & Resnick

Questão 6

Uma amostra de 2,00 mols de um gás monoatômico ideal é submetida ao processo reversível da figura. A escala do eixo vertical é definida por Ts = 400,0 K e a escala do eixo horizontal é definida por Ss = 20,0 J/K. (a) Qual é a energia absorvida pelo gás na forma de calor? (b) Qual é a variação da energia interna do gás? (c) Qual é o trabalho realizado pelo gás?

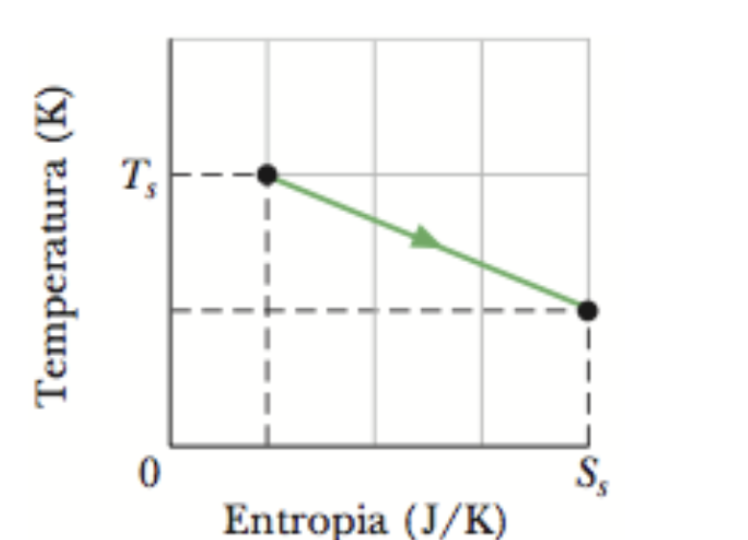
Fonte: Halliday & Resnick

Questão 7

Suponha que 1,0 mol de um gás monoatômico ideal inicialmente ocupando um volume de 10 L e a uma temperatura de 300 K seja aquecido a volume constante até 600 K, liberado para se expandir isotermicamente até a pressão inicial e, finalmente, contraído à pressão constante até os valores iniciais de volume, pressão e temperatura. Durante o ciclo, qual é (a) a energia líquida introduzida ao sistema (o gás) na forma de calor e (b) o trabalho líquido realizado pelo gás? (c) Qual é a eficiência do ciclo?

Questão 8

Cerca de 1,00 mol de um gás ideal, a 300 K, sofre uma expansão livre adiabática de V1 = 12,3 L para V2 = 24,6 L. Ele é, então, comprimido isotermicamente e de maneira reversível de volta ao seu estado original. (a) Qual é a variação da entropia do universo para o ciclo completo? (b) Quanto trabalho é perdido neste ciclo? (c) Mostre que o trabalho perdido é T ∆SU.

Questão 9

(a) Qual, destes dois processos, desperdiça a maior quantidade de trabalho? (1) Um bloco que se move com 0,50 J de energia cinética sendo levado ao respouso pelo atrito cinético, quanto a temperatura ambiente é de 300 K; (2) um reservatório a 400 K liberando 1,00 kJ de calor para um reservatório a 300 K? (b) Qual é a variação da entropia do universo para cada processo?

Made with Slides.com