
Aula 24
Introdução à Física Clássica II
Prof. Ronai Lisbôa
Não compreendeu algo? Algo está esquisito? Comente!
Objetivos
Ao final dessa aula você deve se capaz de:
Bibliografia
Sears & Zemansky - Vol. 2 - 14a. edição.
Capítulo 20 - Segunda lei da termodinâmica
Seção: 20.7
Calcular a entropia a partir de conceitos estatísticos.
Calcular a entropia a partir de conceitos estatísticos.
Diferenciar microestados de macroestados.
Reconhecer a maximização da entropia nos estados de equilíbrio.
Diferenciar ordem x desordem.
Motivação
Fonte: https://youtu.be/qjHfkfIs1Ug
Entropia. Ordem x desordem?
Você já viu um pêndulo imóvel de repente começar a balançar por conta própria?
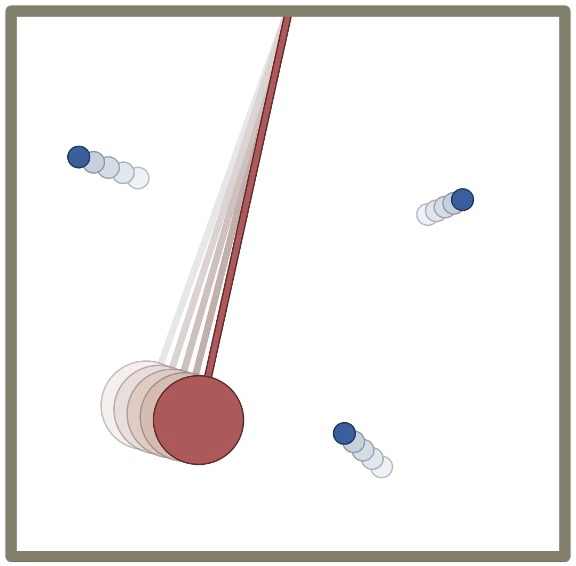
Provavelmente, não!
Por que um pêndulo oscilante sempre desacelera e nunca acelera?
As oscilações ficam menores porque a cada oscilação uma pequena parte da energia mecânica coerente do pêndulo é convertida em energia térmica incoerente.
Quando o pêndulo parou, toda a sua energia mecânica foi dissipada.
Essa energia não se foi. Ela ainda existe, mas não é capaz de fazer mover o pêndulo novamente, pois degradou-se.
Degradou-se em energia térmica incoerente associada ao movimento das moléculas no ar ao redor do pêndulo.
Fonte: Eric MazurEntropia. Ordem x desordem?
A tendência universal para a energia mecânica se dissipar parece estar relacionada à natureza incoerente do movimento de átomos e moléculas na escala atômica.
O oscilador poderia começar a oscilar novamente se as partículas de ar fornecessem a energia cinética. Isso é altamente improvável, pois converter energia térmica (incoerente/aleatório) em trabalho (coerente/ordenado) é improvável nesta escala microscópica.
Oscilador:
N = 1
m = 0,10 kg
v = 0,80 m/s
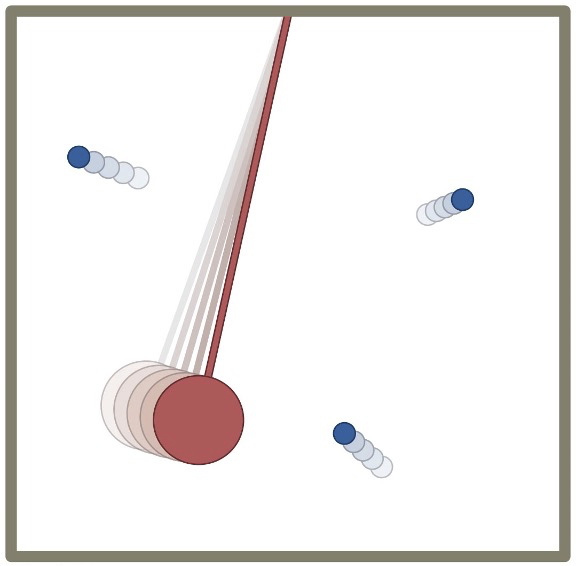
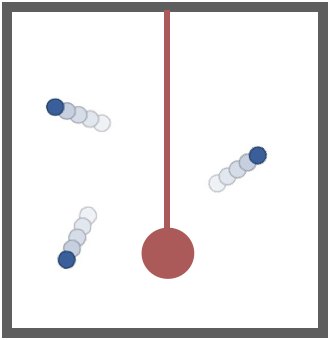
Partículas:
N = \(1,0 \times 10^{23}\)
m = \(4,7\times 10^{-26}\) kg
v = 500 m/s
As energias cinética do oscilador de uma única partícula são:
As energias cinética do oscilador das N partículas são:
Fonte: Eric MazurEntropia. Equipartição da energia.
Precisamos usar uma abordagem muito diferente para conectar o mundo atômico de átomos e moléculas ao mundo macroscópico que descrevemos até agora.
Precisamos usar a teoria da probabilidade para determinar a probabilidade de certos eventos ocorrerem.
As probabilidades favorecem fortemente a desaceleração de um pêndulo em vez de acelerá-lo.
Suponha que oscilador inicialmente em movimento pode compartilhar 6 joules energia com as três partículas dentro da caixa.
Dizemos que há 1 microestado com ZERO energia distribuída nos osciladores.
Macroestado do oscilador
Macroestado das partículas
Na interação, o oscilador pode ceder 1 joule de energia para as partículas.
Mas há 3 modos de distribuir 1 joule de energia entre as três partículas.
Na linguagem da física estatística, nós dizemos que o número de microestados é igual a 3.
Entropia. Equipartição da energia.
Macroestado do oscilador
Macroestado das partículas
Na interação, o oscilador pode ceder 2 joules de energia para as partículas.
Há 6 modos de distribuir 2 joule de energia entre as três partículas.
O número de microestados é igual a 6.
Entropia. Equipartição da energia.
Macroestado do oscilador
Macroestado das partículas
À medida que a quantidade de energia das partículas aumenta, o número de microestados associados a esse macroestado aumenta.
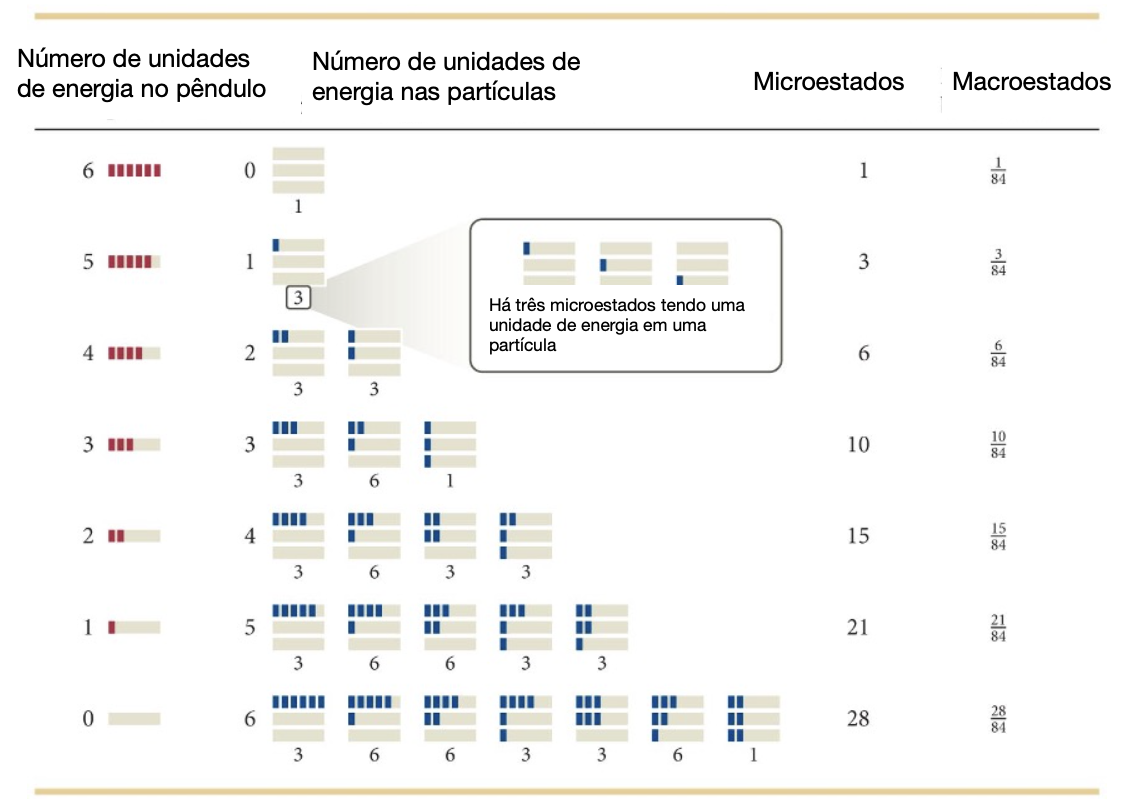
Trata-se de um problema de contagem.
Arranjar \(u=6\text{ J}\) de energia entre \(n=4\) partículas. A multiplicidade de estados é:
Entropia. Equipartição da energia.
Fonte: Eric MazurO macroestado mais provável é:
A distribuição de 0 energia para o oscilador e 6 joules de energia entre as 3 partículas.

A multiplicidade de estados para as partículas:
A multiplicidade de estados para o oscilador:
A multiplicidade de estados para o oscilador e as partículas é o produto (eventos independentes):
A probabilidade deste macroestado é dado pelo microestado:
Entropia. Equipartição da energia.
Fonte: Eric MazurA probabilidade de encontrar toda a energia no pêndulo é menor do que encontrar o pêndulo com alguma energia.
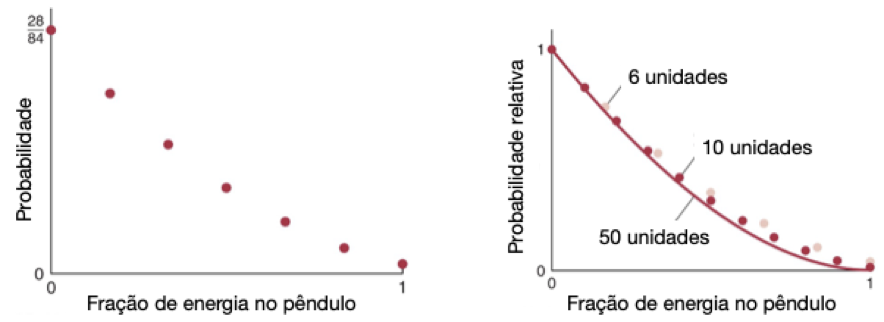
Mesmo assim, a probabilidade relativa do pêndulo conter toda a energia é diferente de zero.
Há uma probabilidade muito pequena, mas diferente de zero, de o pêndulo ganhar toda a sua energia novamente.
Entropia. Equipartição da energia.
Fonte: Eric MazurCada partícula tende a ter a menor quantidade de energia possível.
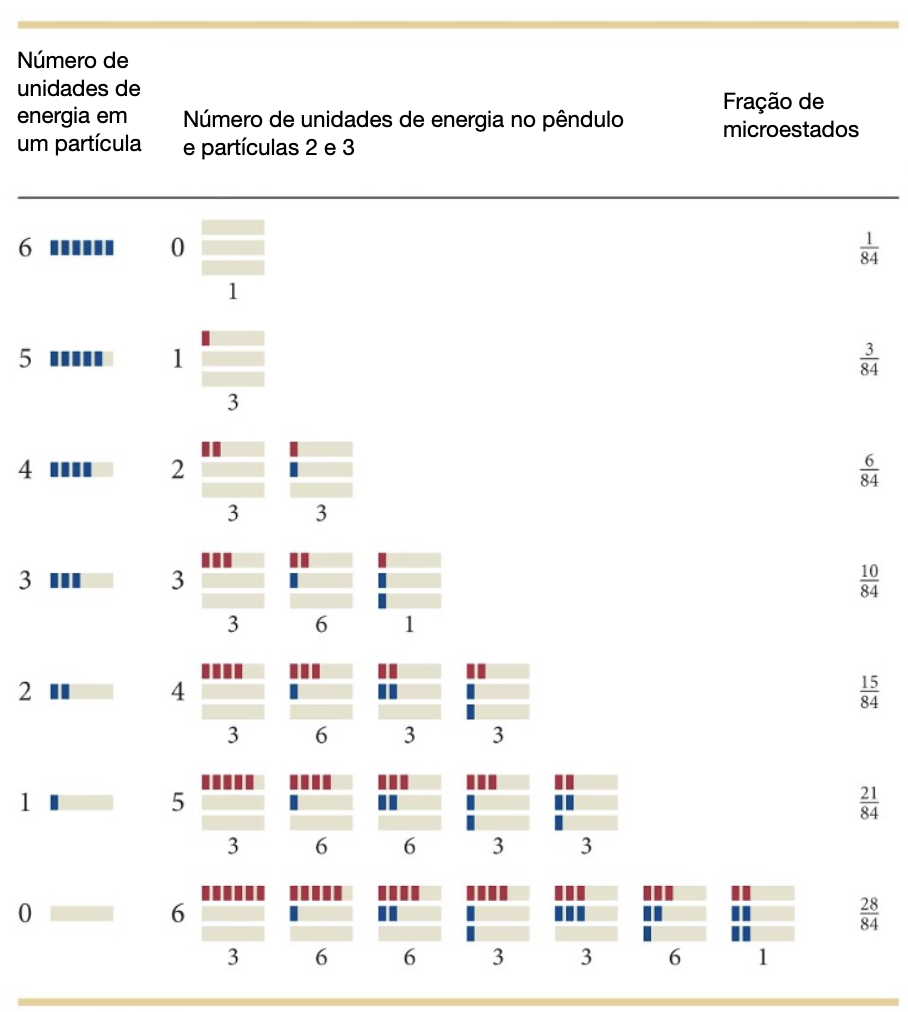
O sistema tende a distribuir essa energia igualmente por todas as partículas.
As chances são maiores de que as partículas tenham pouca ou nenhuma energia.
Entropia. Equipartição da energia.
Cada partícula tende a minimizar sua energia.
A probabilidade de qualquer microestado é 1/84 (porque existem 84 microestados igualmente prováveis).
Em um sistema isolado em equilíbrio térmico, todos os microestados acessíveis são igualmente prováveis.
Fonte: Eric MazurA probabilidade de não encontrar nenhuma energia no pêndulo é a maior.

Ao longo do tempo, a energia média deste microestado é:
Entropia. Equipartição da energia.
Equipartição de energia.
Desde que as interações entre as diferentes partes de um sistema randomizem a distribuição de energia, cada parte do sistema tende a ter uma parcela igual da energia do sistema.
Fonte: Eric MazurAs colisões não apenas randomizam a distribuição de energia em um gás, mas também randomizam as distribuições espaciais.
Entropia. Equipartição do espaço.
Se removermos a partição, o gás se difunde para preencher todo o volume.
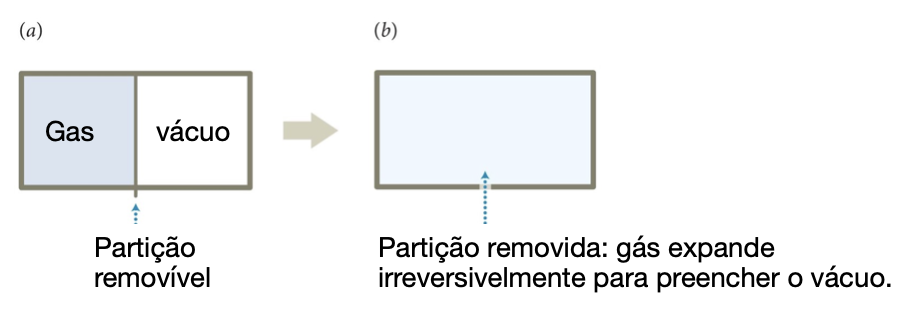
Uma vez que as partículas se expandem para o lado direito do recipiente, elas não se contraem espontaneamente novamente para o lado esquerdo. Isso é muito improvável de ocorrer!
A difusão irreversível se deve ao movimento incoerente das partículas no nível atômico.
As colisões entre as partículas misturam tanto a rapidez das partículas quanto as direções em que elas se movem.
Fonte: Eric MazurEntropia. Equipartição do espaço.
A probabilidade em qualquer instante de encontrar uma partícula em qualquer posição no recipiente é a mesma que em qualquer outra posição ou instante – não há uma posição “preferida” para as partículas.
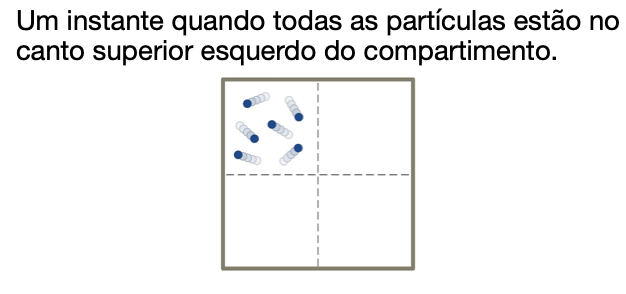
O microestado deste sistema é determinado especificando quantas partículas estão em cada um dos quatro compartimentos.
Temos q = 6 partículas e n = 4 compartimentos.
Isso é análogo ao problema de 6 unidades de energia e 4 partículas.
Fonte: Eric MazurEntropia. Equipartição do espaço.
A probabilidade de não encontrar nenhuma partícula no quadrante superior esquerdo é a maior!
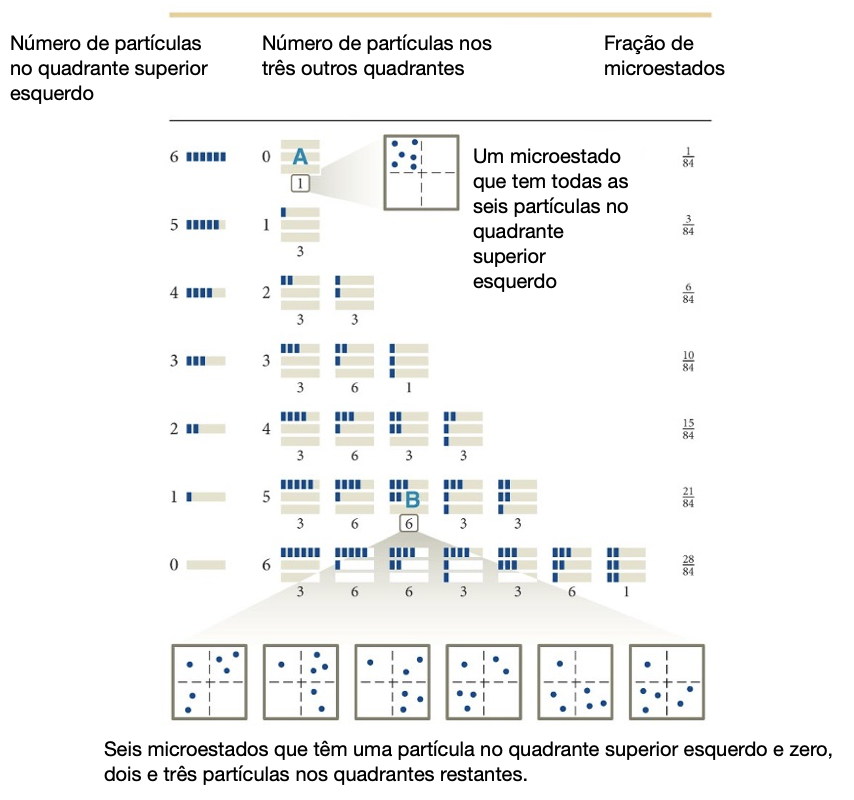
Contudo, ao longo do tempo o número médio de partículas nesse lado é:
Dividindo a caixa em um grande número M de compartimentos iguais e aumentando o número de partículas N. Em média cada compartimento tende a ter sua “parte” N/M das partículas. resultando em uma distribuição uniforme de todas as partículas no espaço.
Equipartição do espaço.
Fonte: Eric MazurEntropia. Evolução para o macroestado mais provável.
Se começarmos com toda a energia do pêndulo, o sistema só pode evoluir gradualmente para o macroestado mais provável.
Supondo que o sistema esteja no microestado \(\Omega = 15\) em que duas unidades de energia estão no pêndulo e ocorre uma colisão, os macroestados acessíveis são os vizinhos a ele: 10 e 21. A probabilidade de cada um desses microestados é dado pela fração de microestados:
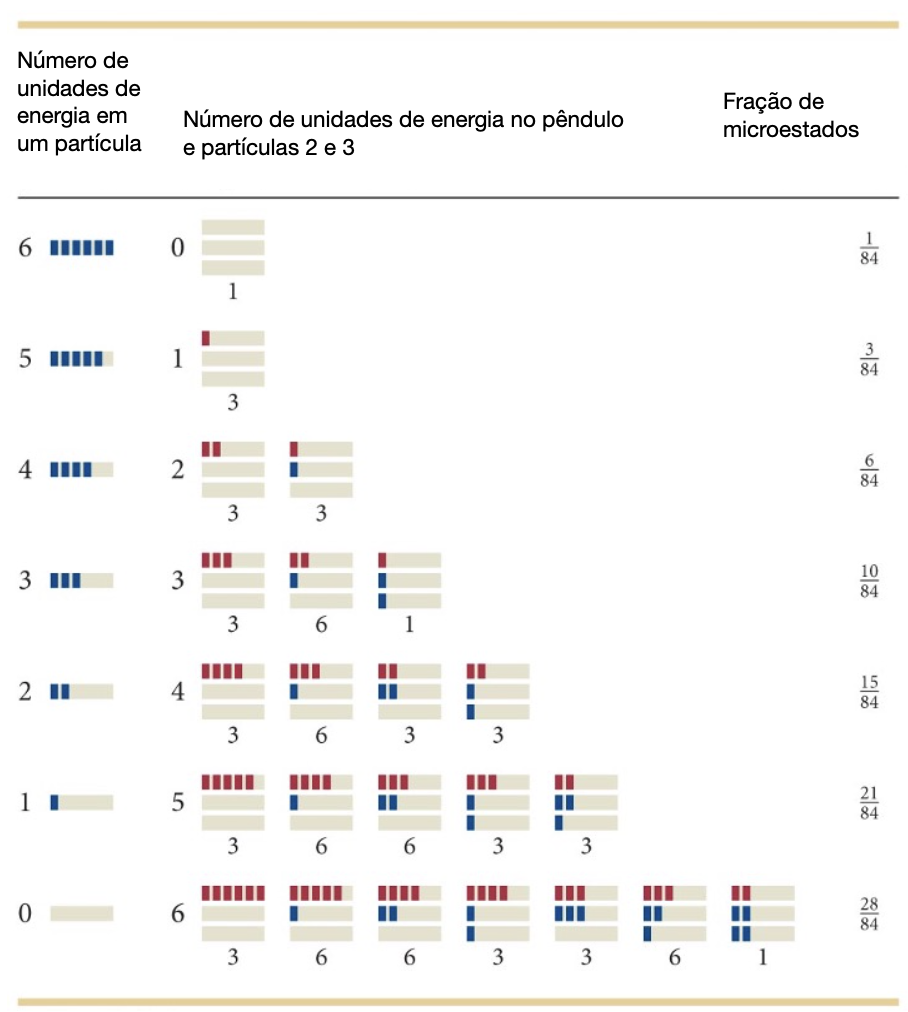
Aumentar: P = 10/46
Permanecer: P = 15/46
Diminuir: P = 21/46
A probabilidade de reduzir a energia no pêndulo é sempre maior que a de aumentar a energia, e assim o sistema evolui gradativamente para macroestados de probabilidade crescente.

Fonte: Eric MazurQuando o sistema está em equilíbrio, o macroestado mais provável é o estado de equilíbrio.
Se o pêndulo e as partículas ocupam temporariamente um macroestado que é menos provável do que o estado de equilíbrio, então quaisquer colisões subsequentes tendem a mover o sistema de volta ao equilíbrio.

Esse fluxo unidirecional de energia do pêndulo para as partículas de gás é a essência da irreversibilidade.
A razão subjacente para a irreversibilidade é estatística: qualquer sistema que esteja em um macroestado de baixa probabilidade tende a evoluir para o macroestado que possui o número máximo de microestados.
Uma vez que o sistema atingiu esse estado de equilíbrio, sua probabilidade de retornar espontaneamente a um macroestado que possui um pequeno número de microestados é infinitamente pequena.
Entropia. Evolução para o macroestado mais provável.
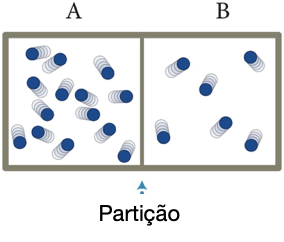
Fonte: Eric MazurA caixa contém 20 partículas e é dividida nos compartimentos A e B.
A caixa contenha 10 unidades de energia.
A divisória é impermeável, adiabática e fixa.
Inicialmente o número de microestados é:
O que aconteceria se trocássemos a divisória por uma divisória que permite trocar apenas energia?
Entropia. Evolução para o macroestado mais provável.
A energia é constante:
O número de partículas é constante:
Fonte: Eric MazurAs 10 unidades de energia serão distribuídas entre as 20 partículas.
Entropia. Evolução para o macroestado mais provável.
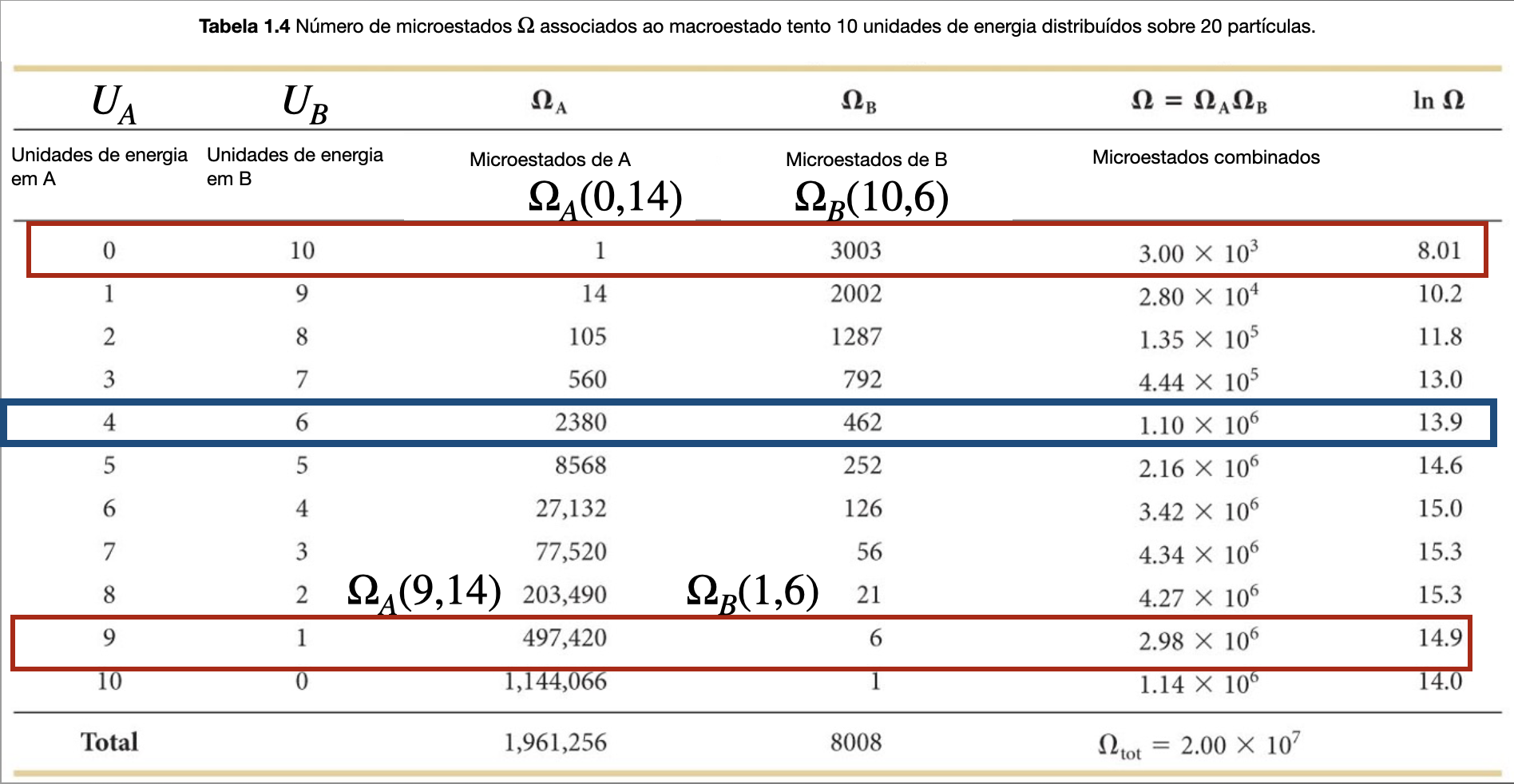
Microestado inicial

Fonte: Eric MazurFonte: Eric MazurÀ medida que o número de unidades de energia no compartimento A aumenta o número de microestados aumenta.
Entropia. Evolução para o macroestado mais provável.
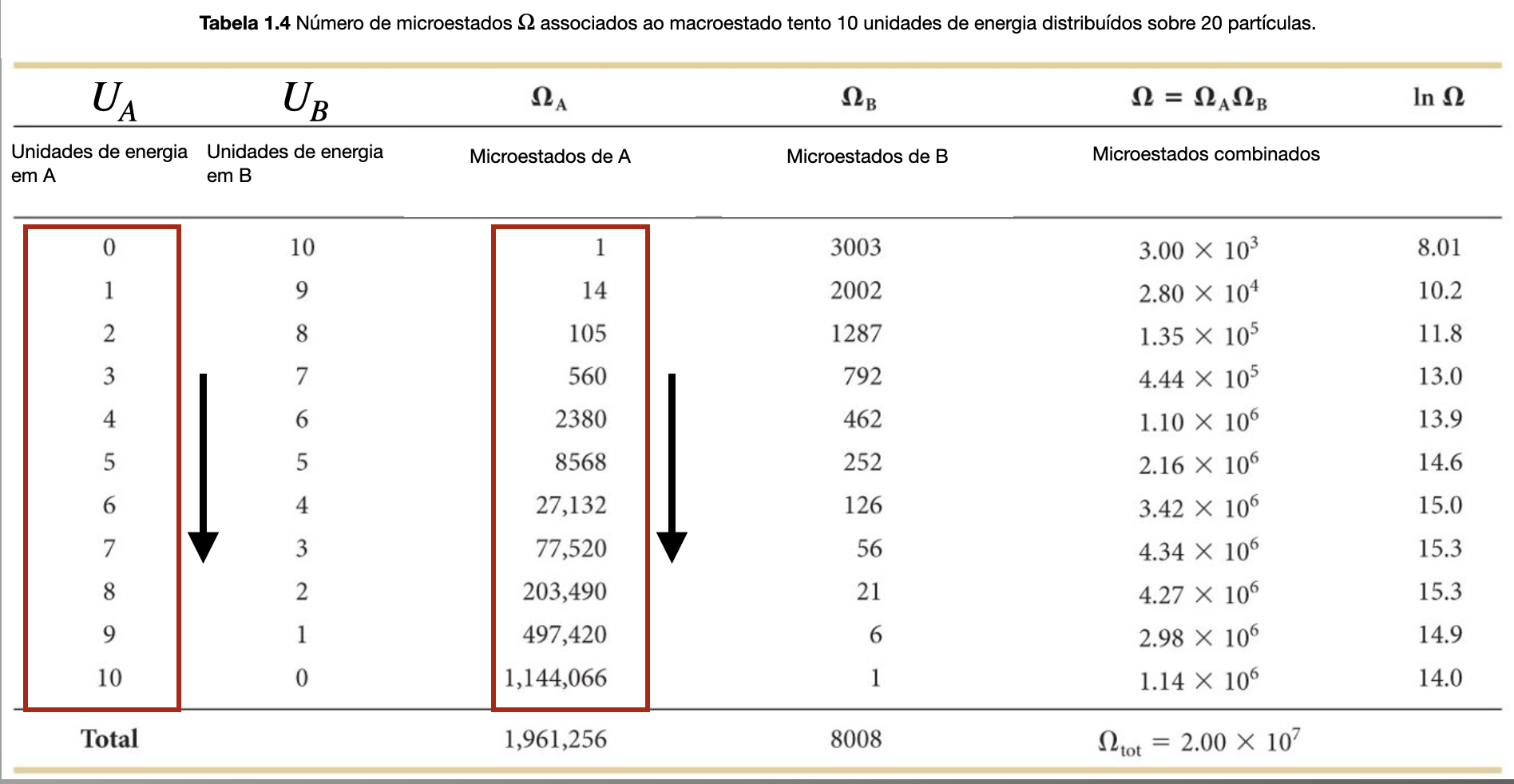
Fonte: Eric MazurÀ medida que o número de unidades de energia no compartimento B diminui o número de microestados diminui.
Entropia. Evolução para o macroestado mais provável.
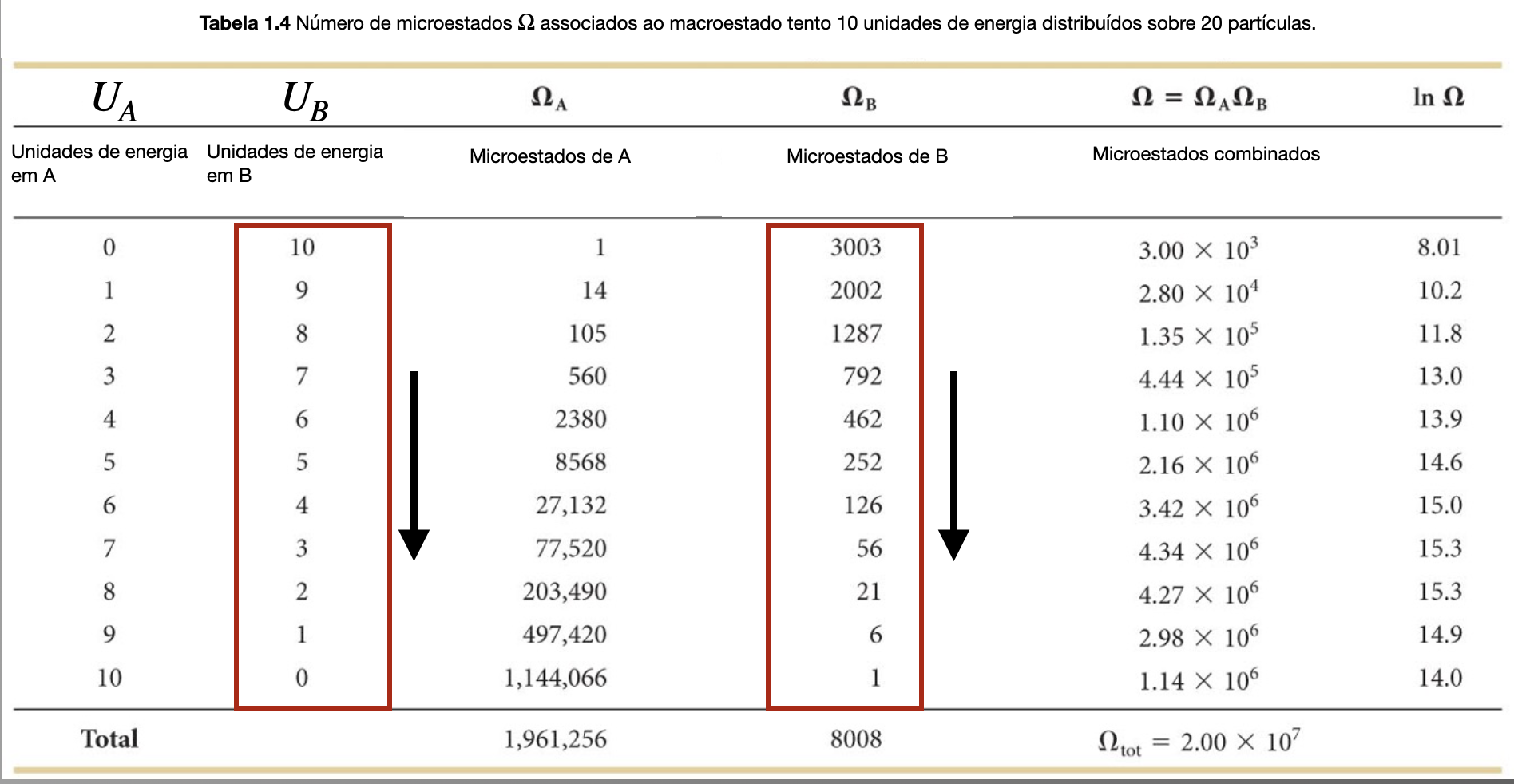
Fonte: Eric MazurO número de microestados em um compartimento diminui à medida que o número de microestados no outro compartimento aumenta.
Entropia. Evolução para o macroestado mais provável.
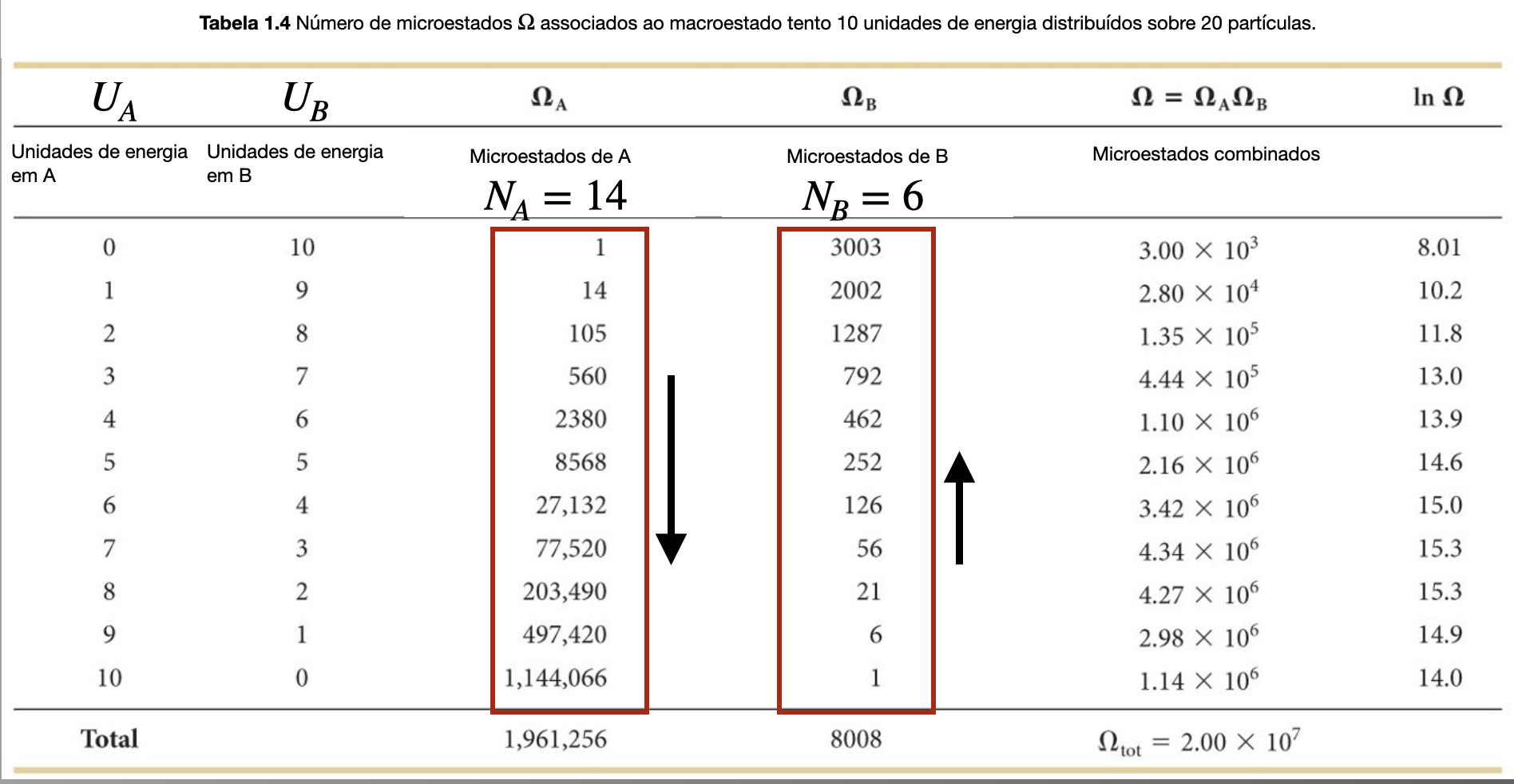
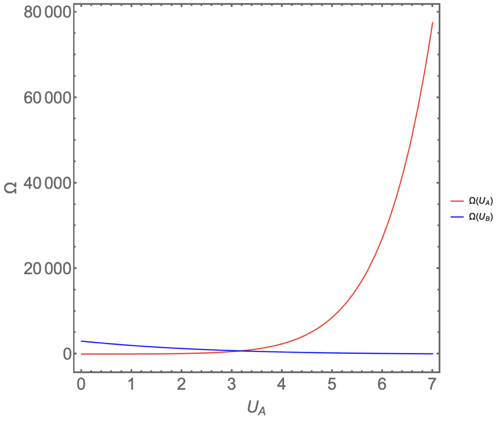
O número de microestados em B diminui, ou seja, B se move em direção a um macroestado de menor probabilidade. Entretanto, a taxa na qual \(\Omega_A\) aumenta é maior do que a taxa na qual \(\Omega_B\) diminui.
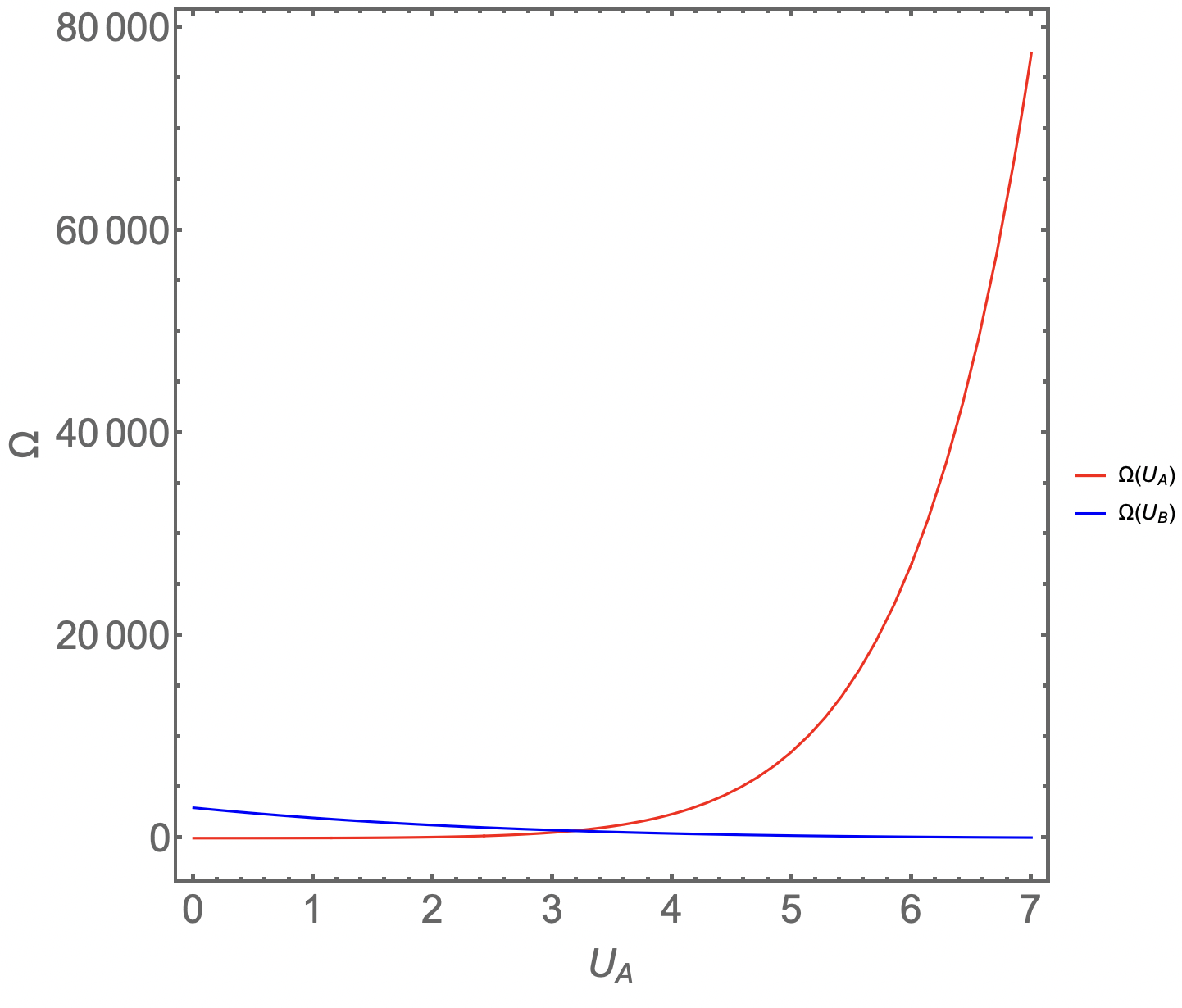
Fonte: Eric MazurO número \(\Omega\) de microestados disponíveis para o sistema é obtido pela multiplicação de \(\Omega_A\) por \(\Omega_B\) , tal que \(\Omega=\Omega_A\Omega_B\).
Entropia. Evolução para o macroestado mais provável.

A probabilidade de cada macroestado é obtida dividindo \(\Omega\), o número de microestados associados a esse macroestado, por \(\Omega_{total}\) :
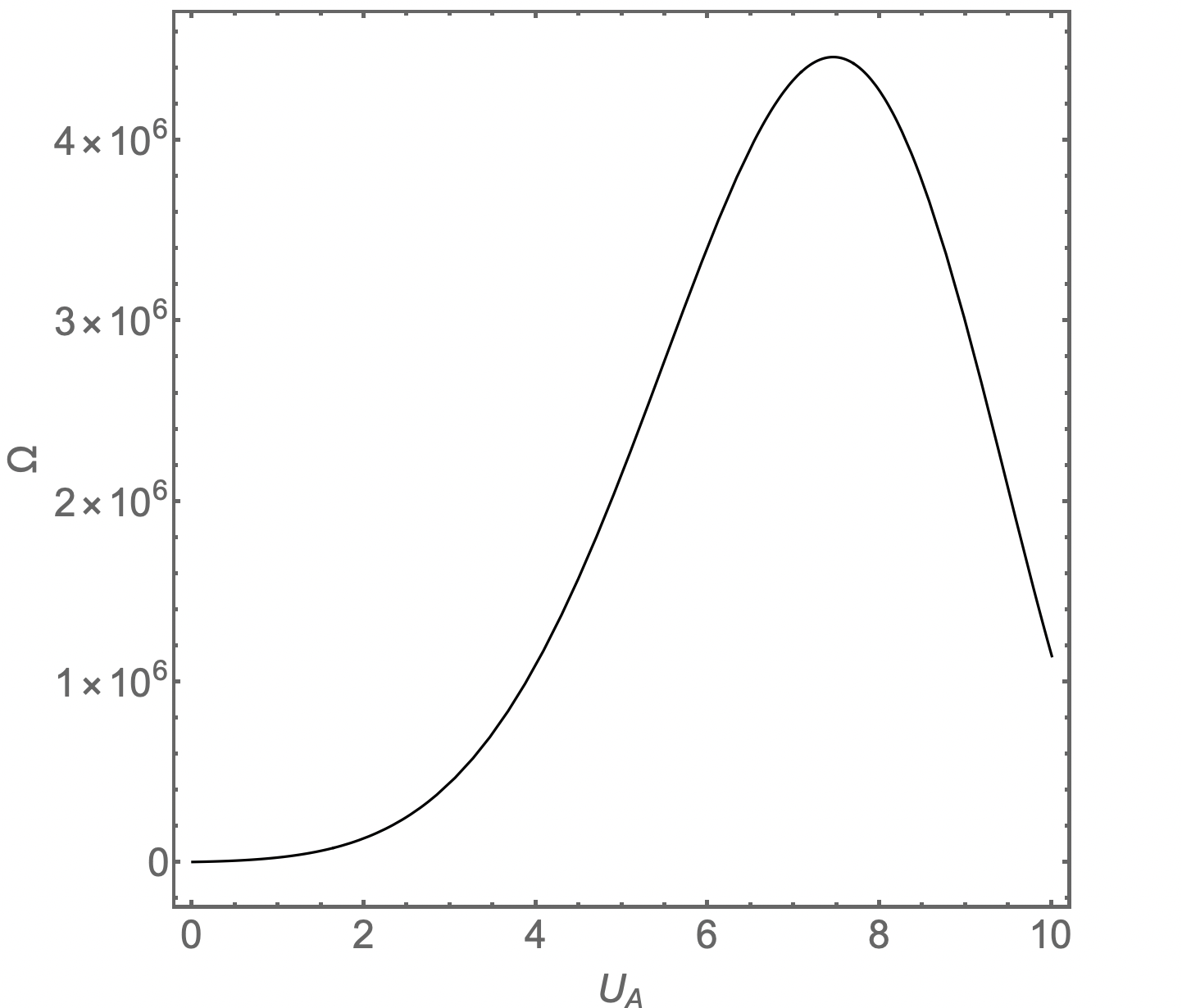
O número de microestados combinados atinge um \(U_A=7\) máximo quando .
Fonte: Eric MazurApós um número muito grande de colisões partícula-partição ter ocorrido, as probabilidades de encontrar o sistema em no macroestado \(U_A = 1\) e no macroestado \(U_A = 7\) são:
Entropia. Evolução para o macroestado mais provável.
Colisões entre as partículas e a partição redistribuem a energia entre as partículas, e ao longo do tempo o sistema evolui em direção ao macroestado mais provável - aquele para em que cada partícula tem sua "parte justa" de energia do sistema.


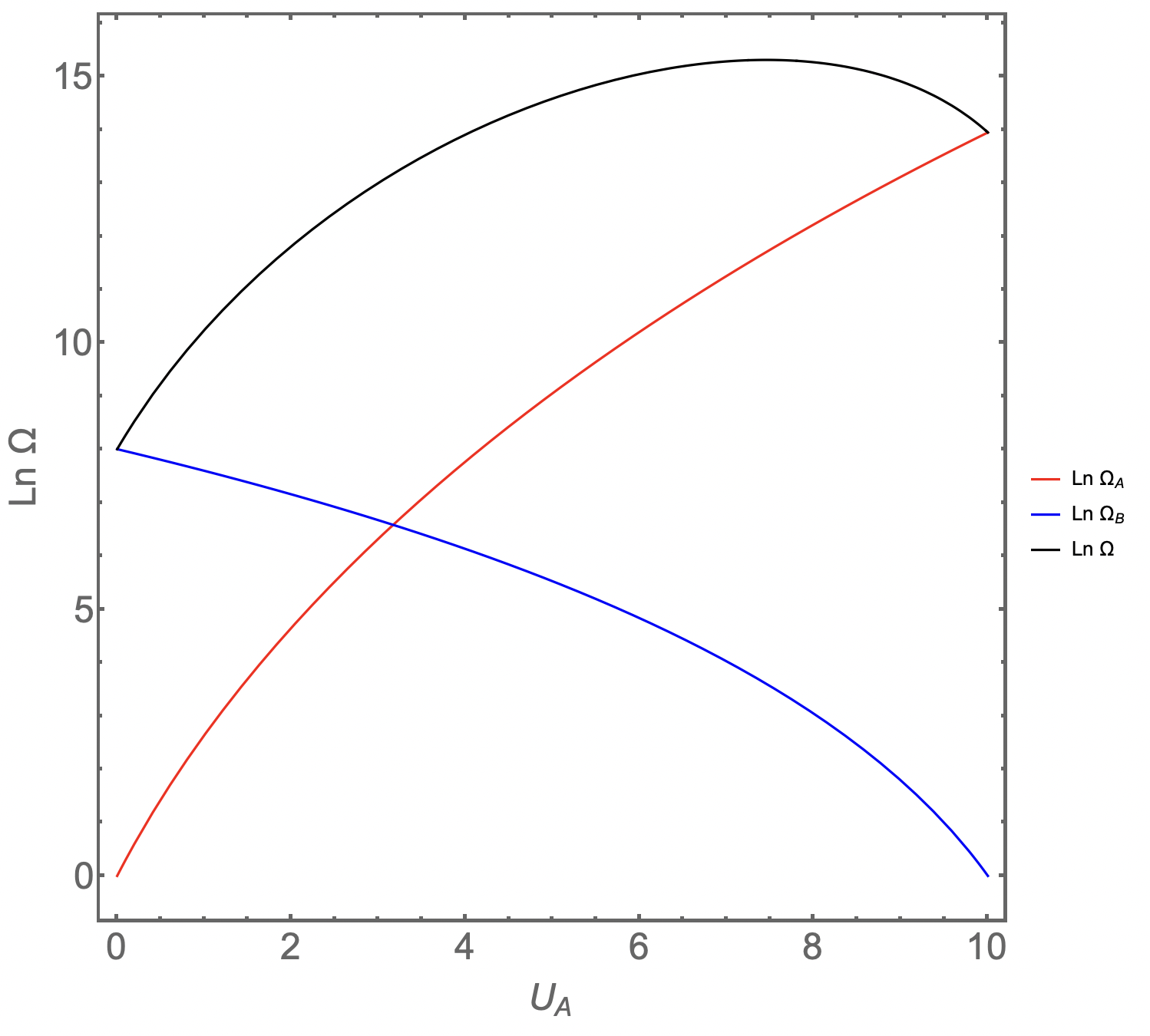
Fonte: Eric MazurComo o número de microestados é muito grande, é mais conveniente trabalhar com o logaritmo natural desse número.
Entropia. Evolução para o macroestado mais provável.
Um sistema isolado sempre evolui de modo a maximizar o número de microestados \(\Omega\). Quando este número atinge um máximo, o sistema está em equilíbrio. Essa é a segunda lei da termodinâmica!

Essa tendência irreversível dos sistemas isolados de maximizar \(\Omega\) é chamada de segunda lei da termodinâmica ou entropia.
O número de microestados espaciais depende de V e N.
Entropia. Equilíbrio térmico de mecânico.
O número de microestados é:
Dividimos o compartimento em M partes iguais:
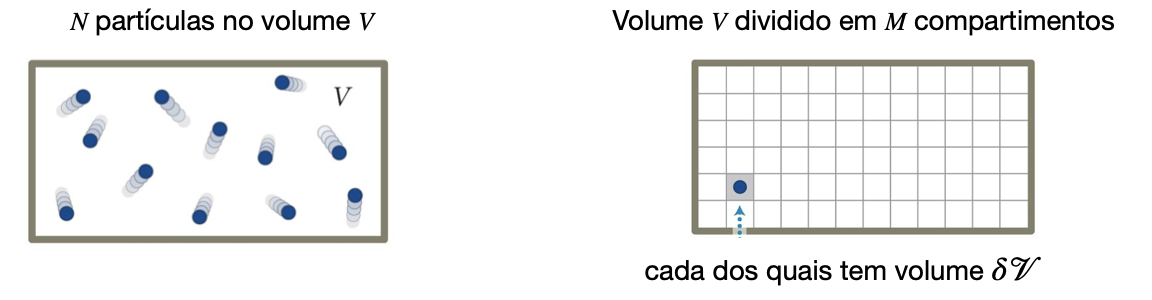
O logaritmo natural do número de microestados é a entropia
Fonte: Eric MazurA entropia é uma quantidade que é uma medida do número de microestados em um sistema. Quanto maior o número de microestados, maior a entropia. A entropia nos permite quantificar o espalhamento de energia ou partículas no espaço.
Entropia. A dependência da entropia com o volume
Para um sistema de N partículas de gás equiparticionadas sobre um volume V, podemos escrever que:
Em geral, estamos preocupados com variações na entropia:
que não depende do tamanho dos compartimentos, \(\delta V\) .
Como a entropia muda quando um sistema de dois gases que interagem evolui para o equilíbrio.
Entropia. A dependência da entropia com o volume
A entropia de um sistema combinado é a soma das entropias dos sistemas individuais.
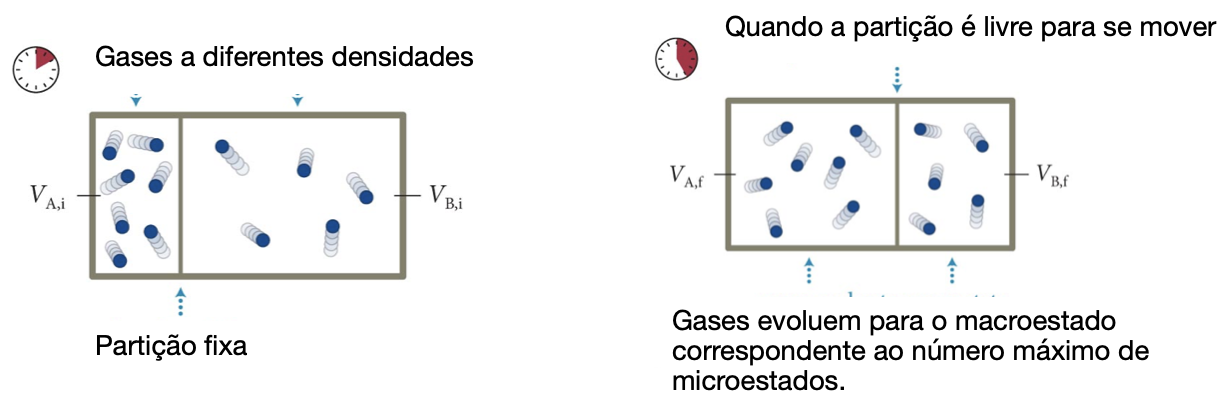
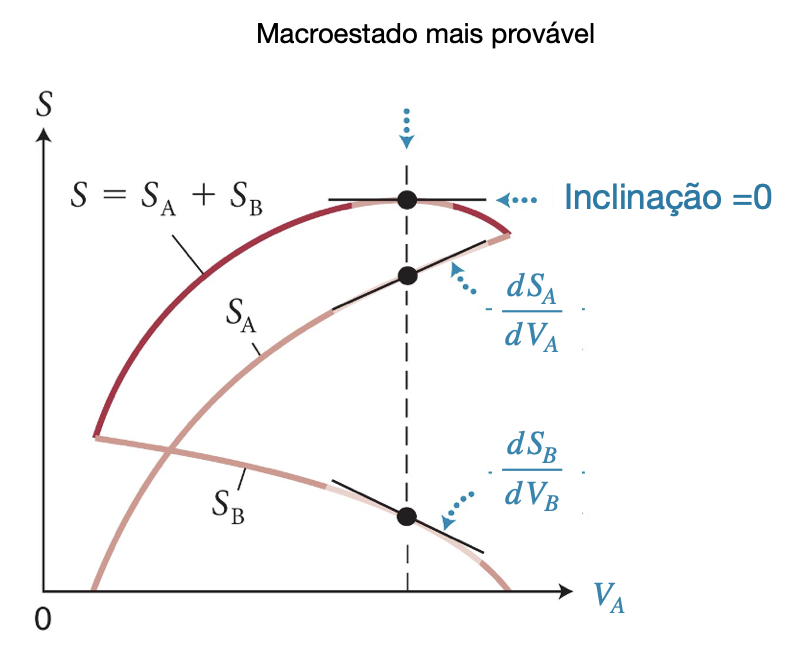
A entropia é máxima no equilíbrio mecânico.
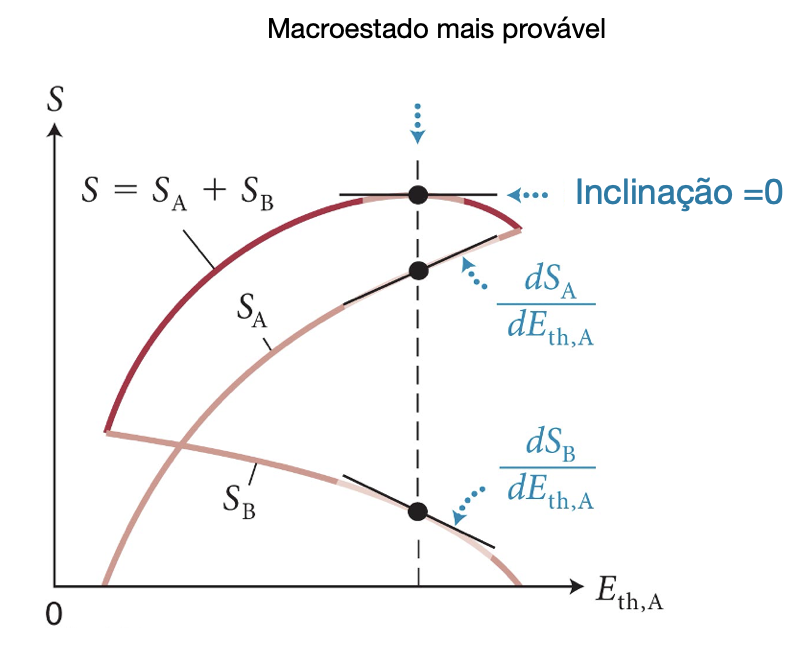
A entropia é máxima no equilíbrio térmico.
Fonte: Eric MazurFonte: Eric MazurFonte: Eric MazurA energia térmica de um gás em termos de sua temperatura é:
Entropia. Gás ideal monoatômico.
A entropia em termos da temperatura:
onde \(S_0\) absorve todos os termos constantes.
A variação da entropia em termos da temperatura:
A entropia em termos do volume:
onde \(S_0\) absorve todos os termos constantes.
A variação da entropia em termos do volume:
Podemos combinar as equações para a entropia para obter uma expressão que nos diga como a entropia depende tanto do volume quanto da temperatura.
Entropia. Gás ideal monoatômico.
Tomando o logaritmo natural desta equação
Devemos substituir os resultados anteriores para entropia do gás ideal monoatômico:
Suponha que eu jogue três moedas. Quantos resultados possíveis existem?
Combinatória

1
3
3
1
8
A combinatória está preocupada com a composição de eventos e não com a sequência de eventos (a ordem não importa).
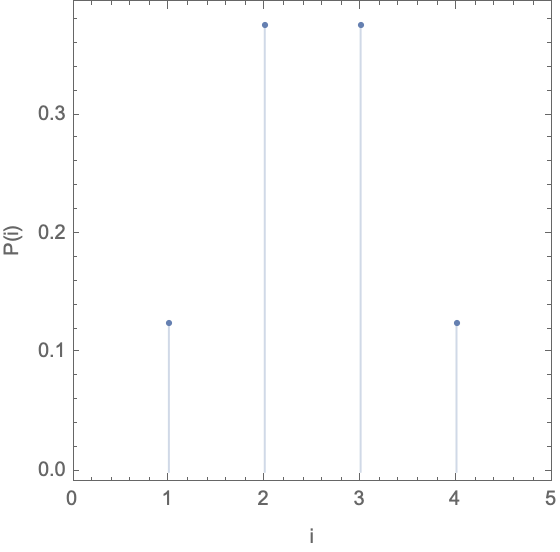
Suponha que eu jogue três moedas. Quantos resultados possíveis existem?
Combinatória

1
3
3
1
8
Macroestado - descrevemos um sistema em termos de suas propriedades de grande escala.
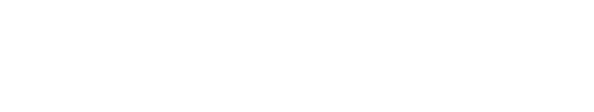
Para um gás o macroestado é descrito por propriedades de grande escala que podem ser medidas prontamente, como temperatura, pressão e volume. O microestado é descrito por propriedades de pequena escala como a posição e momento de cada partícula individual.
Microestado - descrevemos um sistema em termos de suas propriedades de pequena escala.

Há 8 microestados com a mesma probabilidade:
Há 4 macroestados com as distintas probabilidades:
Suponha que eu jogue três moedas. Quantos resultados possíveis existem?
Combinatória

1
3
3
1
8
Multiplicidade - Número de microestados correspondentes a um dado macroestado
A probabilidade de qualquer macroestado particular pode ser escrita:

Combinatória
Precisamos de uma equação para calcular de quantas formas diferentes um conjunto de objetos pode ser arranjado (ordem importa) e combinado (ordem não importa).
Quantas são as possíveis sequências numéricas?
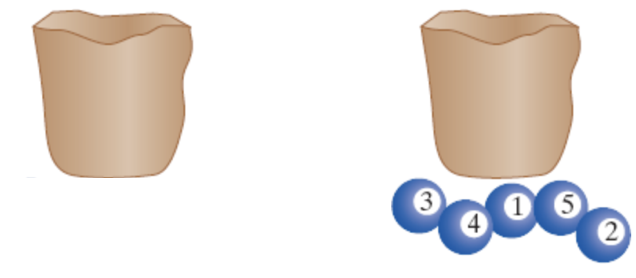
Suponha agora que, das cinco bolas, três são vermelhas (R) e duas são verdes (G), e perguntamos quantos arranjos diferentes das cores são possíveis
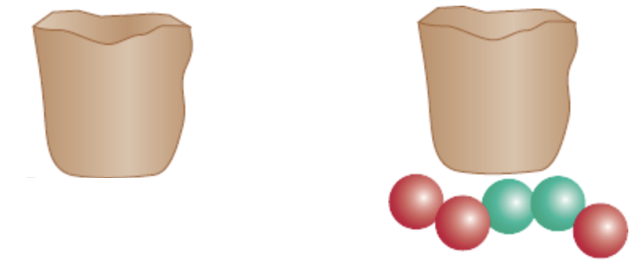
Quantas são as possíveis sequências numéricas?
Fonte: Ruth & ShabayFonte: Ruth & ShabayCombinatória
Em geral, para uma coleção de N objetos com t categorias, dos quais ni objetos indistinguíveis entre si, mas distinguíveis nas outras t-1 categorias, a multiplicidade é
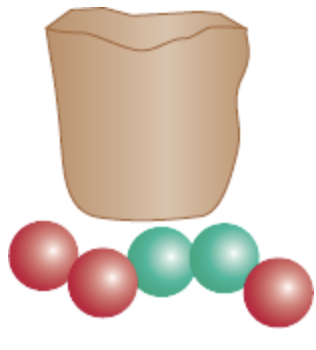
Aqui há t = 2 categorias: R e G.
Na categoria 1 (R): \(n_1=3\) .
Na categoria 2 (G): \(n_2=2\) .
Para sistemas com apenas duas categorias (cima/baixo, direita/esquerda, vermelho/verde, cara/coroa, etc.)
É o número de modos de escolher n objetos de uma categoria a partir de um total de N objetos.
Fonte: Ruth & ShabayCombinatória
Sistemas de dois resultados possíveis e independentes das tentativas anteriores é chamado de processo de Bernoulli.
A probabilidade de Bernoulli é definida como
E é uma distribuição binomial.


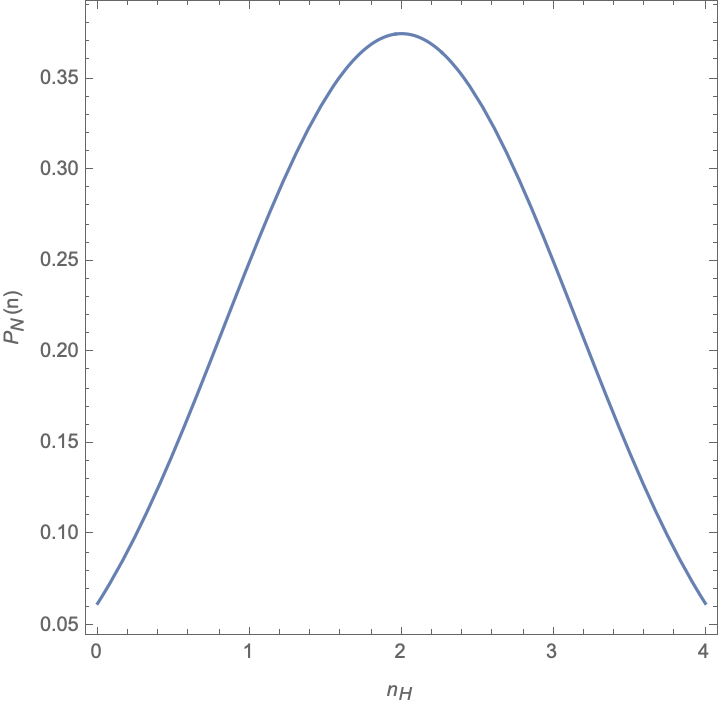
Suponha que você esteja jogando quatro moedas e decida definir o macroestado do sistema após qualquer lançamento como o número de caras lançadas. Quantos (a) macroestados e (b) microestados existem para este sistema? (c) Qual é a probabilidade de sair três caras? (d) Qual é o macroestado mais provável após qualquer lançamento?

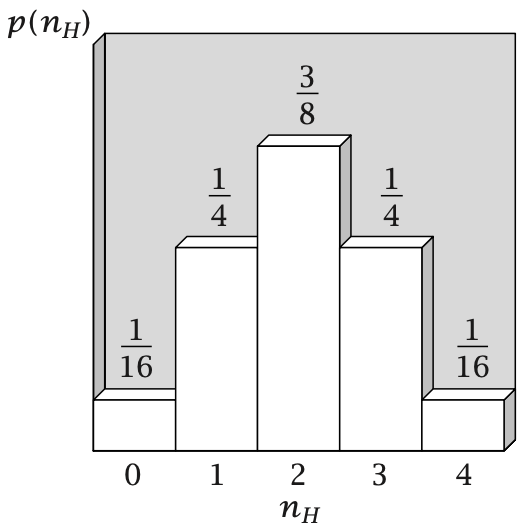

\(\Omega(N,n_H)\) é um máximo quando há \(n_H=2\) caras, (multiplicidade 6).
O macroestado mais provável é para \(n_H=2\).