Prof. Ronai Lisboa
Cozinhando
numericamente uma
Estrela de Nêutrons
Executado
Objetivos
Calcular numericamente a evolução da estrutura de uma estrela de nêutrons.
1
Empregar métodos numéricos para solução de equações diferenciais, como Runge-kutta; integração e diferenciação numéricas, etc.
2
Escrever um código fonte em python.
3
O que nós precisamos fazer...
O que você precisa conhecer para saber fazer uma estrela de nêutrons básica.


O que você vai ganhar?
Noções básicas de relatividade geral
Noções básicas de física nuclear
Noções básicas de computação numérica científica (não web)
O que você não vai ganhar?
Money... porque não tem bolsa



As estrelas de nêutrons
são objetos astrofísicos de grande interesse devido a sua estrutura exótica.
São exóticos porque a matéria tem comportamento diferente sob condições extremas de pressão e temperatura.
A matéria do nosso dia-a-dia (ordinária) tem aumento da temperatura quando a pressão aumenta. Correto?
As estrelas de nêutrons
por outro lado são "densas" e ao mesmo tempo "frias" mesmo a pressões tão elevadas.
Olhe o gráfico ao lado e procure a região em que estão as estrelas de nêutrons.
Viu? Ela está em uma região de baixa temperatura e altas densidades (e potencial químico).
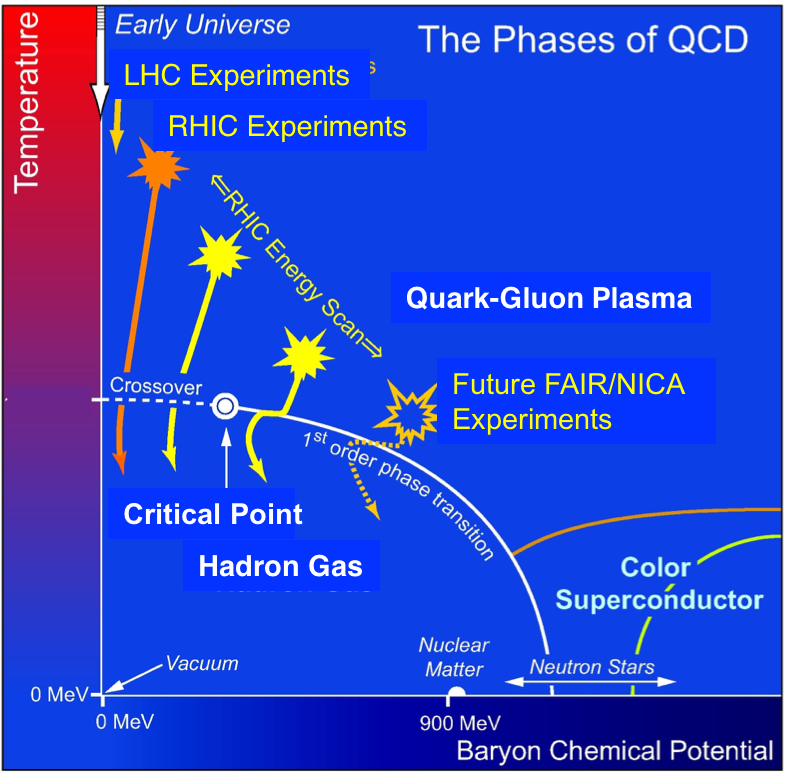
Não sabemos ao certo porque elas são assim... ainda!


Uma forma de compreender melhor as estrelas de nêutrons é investigar a relação entre a massa e o raio destes objetos.
A massa de uma estrela de nêutrons pode ser algo próximo de 2,0 x a massa do Sol, mas ocupando apenas um raio de 11 km.
A arte ao ilustra uma estrela de nêutrons próxima à Berlin/Alemanha.
As estrelas de nêutrons são remanescentes compactos e extremamente densos de explosões de supernovas.
Não se sabe como se comporta a matéria extremamente densa, rica em nêutrons, e é impossível criar tais condições em qualquer laboratório da Terra.
Os físicos propuseram vários modelos (equações de estado), mas não se sabe quais (se houver) desses modelos descrevem corretamente a matéria das estrelas de nêutrons na natureza.
O que é um estrela de nêutrons?
Como posso cozinhar uma estrela?


O que eu devo fazer?
- Encontrar a raiz da função:
Escreva um código em Python para:
sendo:
e
\(m\) é a massa do nêutron e \(c\) é a velocidade da luz no vácuo. Use os valores destas grandezas no Sistema Internacional.
- Calcule a função abaixo utilizando o valor da raiz \(k\) obtida na equação anterior:
Em seguida...
e
- Faça um gráfico da pressão \(p\) em função da energia \(\varepsilon\).
Cuidado com os overflows! A partir dos valores de \((m,c)\) você precisa pensar em um valor adequado para \(p_0\). Para cada valor \(p_0\) você terá raízes distintas. Assim, escolha um intervalo \(p_{min} < p_0 < p_{max}\), calcule as raízes para cada \(p_0\) no intervalo, calcule \(p(k) \text{ e } \varepsilon(k)\).
1
Calcular a raiz da função \(p(k)-p_0=0\)
3
Fazer um gráfico onde o eixo vertical são os valores de \(\varepsilon\) e o eixo horizontal os valores de \(p\) para cada raiz \(k\),
5
Os encontros serão semanais ou quinzenais. O tempo é o estudante que cria à medida que cumprir as metas.
2
Usar o resultado da raiz (\(k\)) na função \(\varepsilon(k)\)
4
Entrar em contato para elaborarmos um Plano de Trabalho para você aprender um pouco de física e computação científica raiz!
Entre em contato via e-mail.
Caso queira fazer uma estrela e tenha obtido êxito
Que e-mail? Por favor, veja no SIGAA.
Estou na sala 41(terceiro andar da ECT) ou nos laboratórios de Física (segundo andar da ECT).