Lisp
"It's 2002, and programming languages
have almost caught up with 1958"
Paul Graham - Revenge of the Nerds
Ronie Uliana
Lambda Calculus*
*não contém cálculo
≈1930
Alan Turing
Alonzo Church
Modelo universal de "computação"
Máquina de Turing
Lambda Calculus
<=equivalentes=>
Máquina de Turing
Lambda Calculus

Menos "charmoso", mais simples
(λa.ab) c = cb
- Uma expressão é:
- Uma letra
- Uma função
- A função substitui a letra
- Só...
Não tem...
- Não tem contas
- Não tem números
- Não tem operadores
- Não tem nada...
Só "variáveis" e funções
Exemplos
(λa.a) x = x
(λab.ba) xz = zx
(λab.b) x = (λb.b)
(λab.ba) (yz) = (λb.b(yz))
x = x
x (λa.b) z = xb
Números com Lambda
- 0 = (λab.b)
- 1 = (λab.a(b))
- 2 = (λab.a(a(b)))
- 3 = (λab.a(a(a(b))))
- ...
Operações aritméticas
- Sucessor = (λabc.b(abc))
- Adição = número sucessor número (1 + 2)
- Multiplicação = (λab.a(bc))
Sucessor: (λabc.b(abc))
(λ abc.b( abc)) (λab.b)
(λbc.b((λ ab. b)bc))
(λbc.b(c))
(λ abc.b( abc)) (λbc.b(c))
(λbc.b((λ bc. b( c))bc))
(λbc.b(b(c)))
- 0 = (λab.b)
- 1 = (λab.a(b))
- 2 = (λab.a(a(b)))
- 3 = (λab.a(a(a(b))))
- ...
Adição: núm suc núm
2 + 3?
(λab.a (a (b ) ) ) (λabc.b(abc)) (λab.a(a(a(b))))
(λb. (λabc.b(abc)) ( (λabc.b(abc)) (b ) ) ) (λab.a(a(a(b))))
(λabc.b(abc)) ( (λabc.b(abc)) ((λab.a(a(a(b)))) ) )
(λabc.b(abc)) ( (λbc.b( (λ ab.a(a(a(b))))bc)) )
(λabc.b(abc)) (λbc.b(b(b(b(c)))))
(λbc.b( (λbc.b(b(b(b(c))))) bc))
(λbc.b(b(b(b(b(c))))))
0 = (λab.b)
1 = (λab.a(b))
2 = (λab.a(a(b)))
3 = (λab.a(a(a(b))))
...
O básico
- Sintaxe
- Prefix notation
- Declarações
Toda a sintaxe do Lisp
em uma linha:
(algo parâmetros ...)
Sério... essa é toda a sintaxe =/
Prefix notation
1 + 2 = (+ 1 2)
1 + 2 + 3 + 4= (+ 1 2 3 4)
1 < 2 = (< 1 2)
x > 1 && x < 3 = (< 1 x 3)
Declarações
- Variáveis:
- x = 1 => (define x 1)
- Funções:
- function tipo_soma(a, b) ... => (define (tipo-soma a b) ...
- tipo_soma(1, 2) => (tipo-soma 1 2)
Homoiconicidade
Código = Dados
Dados = Código
(AST)
AST
Abstract Syntax Tree é com um programa é representado depois do "parsing".
É como o computador sabe o que fazer primeiro.
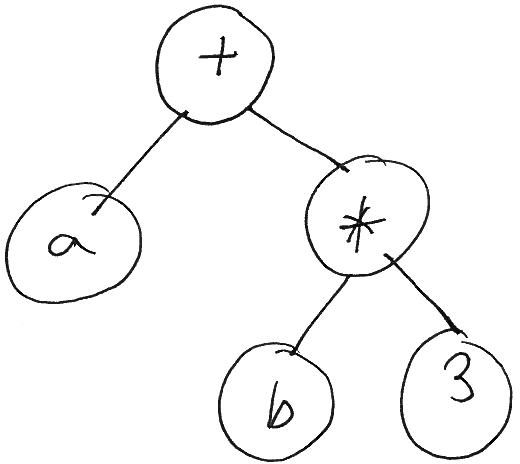
a + b * 3
O código em Lisp é uma AST
(+ a (* b 3))
(raiz nó
(raiz nó nó))
O código é uma lista
Posso manipular listas
Posso manipular o código
#lang racket
(require (for-syntax syntax/parse))
(define-syntax (: stx)
(syntax-parse stx #:datum-literals (+ - * / ^)
[(_ l ... + r ...) #'(+ (: l ...) (: r ...))]
[(_ l ... - r ...) #'(- (: l ...) (: r ...))]
[(_ l ... * r ...) #'(* (: l ...) (: r ...))]
[(_ l ... / r ...) #'(/ (: l ...) (: r ...))]
[(_ l ^ r ...) #'(expt l (: r ...))]
[(_ x) #'x]))
(: 1 + 4 ^ 2)Exemplo de Macro
Lisp evoluiu
(1958) Lisp
(1970) Scheme
(1984) Common Lisp
(1994) Racket
(2007) Clojure




Common Lisp
Lisp "padrão"
- Padrão ANSI
- Extenso (+)
- Comandos arcanos (-)
- CLOS c/ Multimétodos (+)
Racket
Uma linguagem
para criar linguagens
- 1994 (PLT-Scheme)
- 2010 Racket
- Macros (+)
- Design by Contract (+)
- Coleções (-)
Clojure
Um Lisp moderno
(foco em imutabilidade)
- 2007
- Concorrência (+)
- Coleções (+)
- JVM (+)
- Sem tail call optimization (-)
- Macros (-) (no hyg, no readr)
Racket
- Uncharted 2, 2009
- The Last of US, 2013
- ... (não há muito mais)
Clojure
- Datomic, 2012 (Datalog distribuído)
- WallMart, Black Friday 2014
- PuppetLabs, 2014
- NuBank, 2015
- ... (existe muito mais)
Embedded Scheme
- Script-fu, GIMP
- Nyquist, Audacity
- EmacsLisp, Emacs
- AutoLisp, Autocad
- rep, Sawfish
Novos Lisps?
Novos dialetos de Lisp nos últimos 10 anos
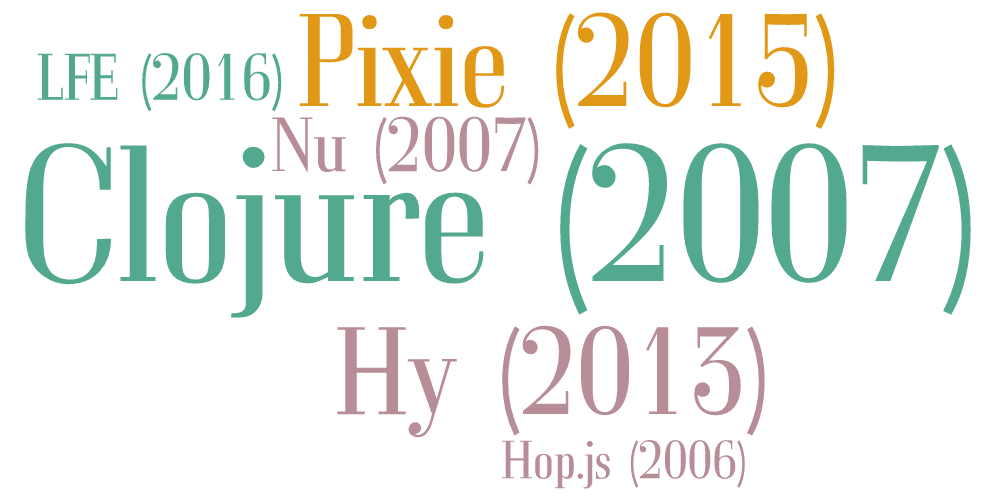
Influência => Macros!
- Elixir
- Julia
- Rust
- ... outros!