Fast Fourier Transform

RUSHAL\ \ VERMA
RUSHAL  VERMARUSHAL\ \ VERMA
\quad 14BCS042
14BCS042\quad 14BCS042
III^{rd}\ \ SEMESTER
IIIrd  SEMESTERIII^{rd}\ \ SEMESTER

Contents

  1. Need of this algorithm
  2. Big Idea
  3. What it does
  4. Wiki Definition
  5. Working of the Algorithm
  6. Mathematical Aspect
  7. Roots of the Unity
  8. Applications
  9. Refrences

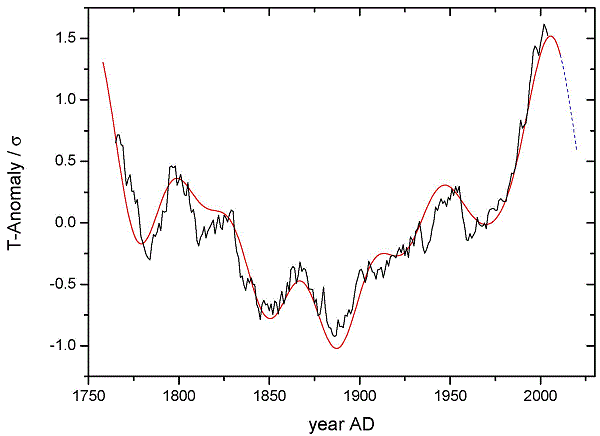
Noisy 

Less Noisy

Big Idea

  • Change representation of Mathematical Objects

  • Some representations have efficiency benefits over other
f(x) = 5 + 2x + x^2
f(x)=5+2x+x2f(x) = 5 + 2x + x^2

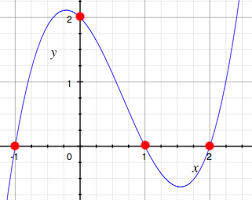
Polynomial of degree 2 denotes 3 numbers which represents the polynomial.

 

 

 

n-1 degree indicates n coefficients

 

if we have n coefficients then we are able to get a n-1 degree polynomials.

 

what it does

Takes input in the form of polynomial

A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
A(x)=a0+a1x+a2x2+...+an−1xn−1A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}

Evaluate it into n points

A(w_0), A(w_1), A(w_2), ... , A(w_n)
A(w0),A(w1),A(w2),...,A(wn)A(w_0), A(w_1), A(w_2), ... , A(w_n)

What the wiki says about it! 

IFFT

FFT

A(x)
A(x)A(x)

Coeffiecients Form

Point-wise Form

N- Points Curve

Degree of n-1 polynomial

FFT

Input:

a_0, a_1, a_2, ... , a_{n-1}
a0,a1,a2,...,an−1a_0, a_1, a_2, ... , a_{n-1}
A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
A(x)=a0+a1x+a2x2+...+an−1xn−1A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}

Output:

n coefficients

Point-Wise Representation
A(w_0), A(w_1), A(w_2), ... , A(w_n)
A(w0),A(w1),A(w2),...,A(wn)A(w_0), A(w_1), A(w_2), ... , A(w_n)
where\ w_1, w_2, .....\ , w_n \ are\ distinct \ points.
where w1,w2,..... ,wn are distinct points.where\ w_1, w_2, .....\ , w_n \ are\ distinct \ points.

Brute force method to evaluate A at n points

A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
A(x)=a0+a1x+a2x2+...+an−1xn−1A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
A(w_0) - \ \theta(n) \ \ operations
A(w0)− θ(n)  operationsA(w_0) - \ \theta(n) \ \ operations
A(w_0),\ ... \ ,\ A(w_n) - \ \theta(n^2) \ \ operations
A(w0), ... , A(wn)− θ(n2)  operationsA(w_0),\ ... \ ,\ A(w_n) - \ \theta(n^2) \ \ operations
We\ seek\ for\ \theta(nlogn)
We seek for θ(nlogn)We\ seek\ for\ \theta(nlogn)

solve the large problem by

 

                       solving smaller problems

                       and combining solutions

T(n)\ =\ 2T(\frac{n}{2}) + \theta(n)
T(n) = 2T(n2)+θ(n)T(n)\ =\ 2T(\frac{n}{2}) + \theta(n)
A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
A(x)=a0+a1x+a2x2+...+an−1xn−1A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
= a_0 \ \ \ \ \ \ + a_2x^2\ \ \ \ \ \ +\ a_{n-2}x^{n-2}
=a0      +a2x2      + an−2xn−2= a_0 \ \ \ \ \ \ + a_2x^2\ \ \ \ \ \ +\ a_{n-2}x^{n-2}
+\ a_1 \ \ \ \ \ \ + a_3x^3\ \ \ \ \ \ \ \ \ +\ \ \ \ \ \ a_{n-1}x^{n-1}
+ a1      +a3x3         +      an−1xn−1+\ a_1 \ \ \ \ \ \ + a_3x^3\ \ \ \ \ \ \ \ \ +\ \ \ \ \ \ a_{n-1}x^{n-1}
A_e(y) = a_0 + a_2y + a_4 y^2 + \ ...\ +a_{n-2}^\frac{n-2}{2}
Ae(y)=a0+a2y+a4y2+ ... +an−2n−22A_e(y) = a_0 + a_2y + a_4 y^2 + \ ...\ +a_{n-2}^\frac{n-2}{2}
A_o(y) = a_1 + a_3y + a_5 y^2 + \ ...\ +a_{n-1}^\frac{n-1}{2}
Ao(y)=a1+a3y+a5y2+ ... +an−1n−12A_o(y) = a_1 + a_3y + a_5 y^2 + \ ...\ +a_{n-1}^\frac{n-1}{2}
A(x) = A_e(x^2) + xA_o(x^2)
A(x)=Ae(x2)+xAo(x2)A(x) = A_e(x^2) + xA_o(x^2)
FFT(f[i,\ .....\ ,\ n])
FFT(f[i, ..... , n])FFT(f[i,\ .....\ ,\ n])

Evaluates degree n poly on the nth roots of UNITY

E[] = FFT (A_e)
E[]=FFT(Ae)E[] = FFT (A_e)
O[] = FFT (A_o)
O[]=FFT(Ao) O[] = FFT (A_o)
returns\ A[w_0\ ...\ w_n]\ using\ the\ equation
returns A[w0 ... wn] using the equationreturns\ A[w_0\ ...\ w_n]\ using\ the\ equation
A(w_i) = A_e(w_i^2) + w_iA_o(w_i^2)
A(wi)=Ae(wi2)+wiAo(wi2)A(w_i) = A_e(w_i^2) + w_iA_o(w_i^2)

Last Remaining Issue:

w_i\ =\ \ ?
wi =  ?w_i\ =\ \ ?

Roots of UNITY

x^n = 1
xn=1x^n = 1

should have n no of solution and we need to find them.

e^{2\pi i} \ = \ 1
e2πi = 1e^{2\pi i} \ = \ 1

consider                 for j = 0,1,2,3, ...., n-1

e^{{2\pi ij/n}{}} \
e2πij/n e^{{2\pi ij/n}{}} \
[e^{2\pi i j/n}]^n = [e^{(2\pi i /n)\ . j}]^n = [e^{2\pi i}]^j = 1^j = 1
[e2πij/n]n=[e(2πi/n) .j]n=[e2πi]j=1j=1[e^{2\pi i j/n}]^n = [e^{(2\pi i /n)\ . j}]^n = [e^{2\pi i}]^j = 1^j = 1
[e^{2\pi i j/n}] = w_{j,n} \ is \ a \ n^{th} \ root\ of\ unity
[e2πij/n]=wj,n is a nth root of unity[e^{2\pi i j/n}] = w_{j,n} \ is \ a \ n^{th} \ root\ of\ unity
[e^{2\pi i j/n}] = \cos (2\pi i j/n) + i \sin (2\pi i j/n)
[e2πij/n]=cos(2πij/n)+isin(2πij/n)[e^{2\pi i j/n}] = \cos (2\pi i j/n) + i \sin (2\pi i j/n)
w_{0,n}\ , w_{1,n}\ ,w_{2,n}\ w_{3,n}\ ......\ w_{n-1,n}
w0,n ,w1,n ,w2,n w3,n ...... wn−1,nw_{0,n}\ , w_{1,n}\ ,w_{2,n}\ w_{3,n}\ ......\ w_{n-1,n}
w_{1,8}\ =\ e^{2\pi i(1/8)}
w1,8 = e2πi(1/8)w_{1,8}\ =\ e^{2\pi i(1/8)}
\ = cos({2\pi i(1/8)}) + isin({2\pi i(1/8)})
 =cos(2πi(1/8))+isin(2πi(1/8))\ = cos({2\pi i(1/8)}) + isin({2\pi i(1/8)})
\frac{1}{\sqrt2}
12\frac{1}{\sqrt2}
i\frac{1}{\sqrt2}
i12i\frac{1}{\sqrt2}
+
++
=
==

Squaring the nth roots of the unity

\large{x^n}\ =\ 1
xn = 1\large{x^n}\ =\ 1
\large{x^{n/2}}\ =\ 1
xn/2 = 1\large{x^{n/2}}\ =\ 1

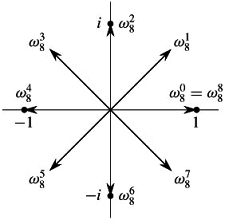
Produce the set of n/2 roots of the unity

Fact: 

squaring the nth roots of the unity 

results in n/2th roots of the unity

Evaluate at a root of the unity

A(x) = A_e(x^2) + xA_o(x^2)
A(x)=Ae(x2)+xAo(x2)A(x) = A_e(x^2) + xA_o(x^2)
A(w_{i,n}) = A_e(w_{i,n}^2) + w_{i,n}A_o(w_{i,n}^2)
A(wi,n)=Ae(wi,n2)+wi,nAo(wi,n2)A(w_{i,n}) = A_e(w_{i,n}^2) + w_{i,n}A_o(w_{i,n}^2)

nth root of the unity

n/2th root of the unity

n/2th root of the unity

FFT(f= a[i,..,n])
FFT(f=a[i,..,n])FFT(f= a[i,..,n])
E[...] \leftarrow \ FFT(A_e)\quad \quad//eval\ A_e\ on\ n/2\ roots\ of\ the\ unity.
E[...]← FFT(Ae)//eval Ae on n/2 roots of the unity.E[...] \leftarrow \ FFT(A_e)\quad \quad//eval\ A_e\ on\ n/2\ roots\ of\ the\ unity.
O[...] \leftarrow \ FFT(A_o)\quad \quad //eval\ A_o\ on\ n/2\ roots\ of\ the\ unity.
O[...]← FFT(Ao)//eval Ao on n/2 roots of the unity.O[...] \leftarrow \ FFT(A_o)\quad \quad //eval\ A_o\ on\ n/2\ roots\ of\ the\ unity.

combine results using the equation:

A(w_{i,n}) = A_e(w_{i,n}^2) + w_{i,n}A_o(w_{i,n}^2)
A(wi,n)=Ae(wi,n2)+wi,nAo(wi,n2)A(w_{i,n}) = A_e(w_{i,n}^2) + w_{i,n}A_o(w_{i,n}^2)

returns n points. 

Applications

Multiply two numbers in nlogn time.

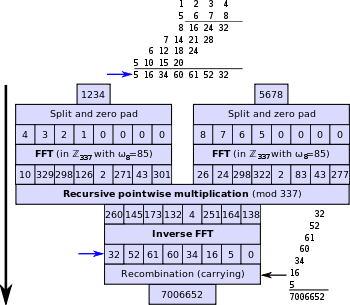
Schönhage–Strassen Algorithm

O(n\ log n\ log log \ n)
O(n logn loglog n)O(n\ log n\ log log \ n)

Faster than Karatsuba Multiplication Algorithm

Refrences

  1. CS 4102-https://www.cs.virginia.edu/~shelat/4102/
  2. https://www.youtube.com/watch?v=2V7XT_iiRRw
  3. http://www.cs.cmu.edu/afs/cs/academic/class/15451-s10/www/lectures/lect0423.txt
  4. https://en.wikipedia.org/wiki/Sch%C3%B6nhage%E2%80%93Stras
sen_algorithm
  5. https://en.wikipedia.org/wiki/Fast_Fourier_transform

THANK YOU

Made with Slides.com