Dexterous Manipulation with Diffusion Policies

Towards Foundations Models for Control(?)

Russ Tedrake

November 3, 2023

​"What's still hard for AI" by Kai-Fu Lee:

  • Manual dexterity

  • Social intelligence (empathy/compassion)

"Dexterous Manipulation" Team

(founded in 2016)

For the next challenge:

Good control when we don't have useful models?

For the next challenge:

Good control when we don't have useful models?

  • Rules out:
    • (Multibody) Simulation
    • Simulation-based reinforcement learning (RL)
    • State estimation / model-based control
  • My top choices:
    • Learn a dynamics model
    • Behavior cloning (imitation learning)

"And then … BC methods started to get good. Really good. So good that our best manipulation system today mostly uses BC ..."

Senior Director of Robotics at Google DeepMind

Levine*, Finn*, Darrel, Abbeel, JMLR 2016 

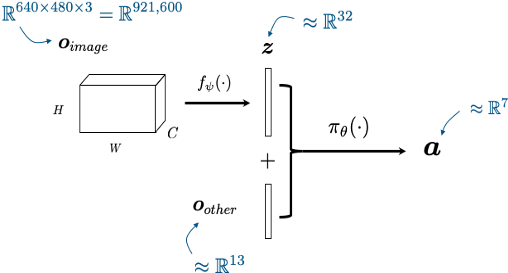
Visuomotor policies

perception network

(often pre-trained)

policy network

other robot sensors

learned state representation

actions

x history

I was forced to reflect on my core beliefs...

  • The value of using RGB (at control rates) as a sensor is undeniable.  I must not ignore this going forward.
     
  • I don't love imitation learning (decision making \(\gg\) mimcry), but it's an awfully clever way to explore the space of policy representations
    • Don't need a model
    • Don't need an explicit state representation
      • (Not even to specify the objective!)

We've been exploring, and seem to have found something...

From yesterday...

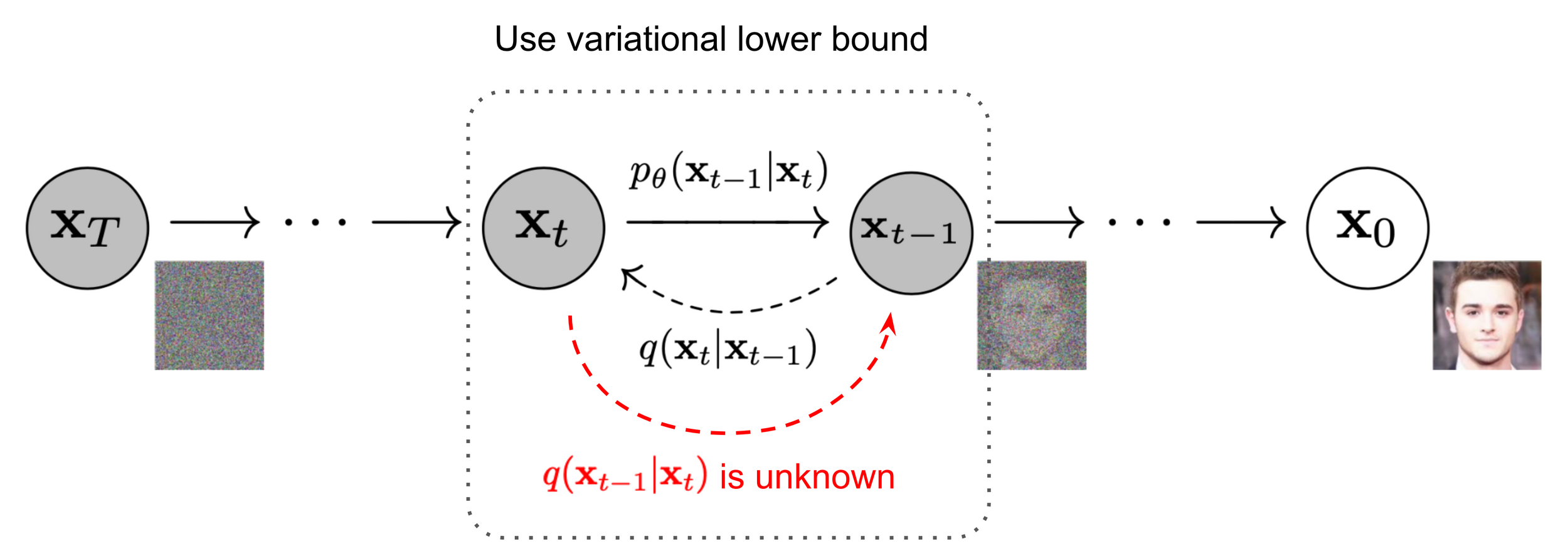
Denoising diffusion models (generative AI)

Image source: Ho et al. 2020 

Denoiser can be conditioned on additional inputs, \(u\): \(p_\theta(x_{t-1} | x_t, u) \)

A derministic interpretation (manifold hypothesis)

Denoising approximates the projection onto the data manifold;

approximating the gradient of the distance to the manifold

Representing dynamic output feedback

..., u_{-1}, u_0, u_1, ...
..., y_{-1}, y_0, y_1, ...

input

output

Control Policy
(as a dynamical system)

"Diffusion Policy" is an auto-regressive (ARX) model with forecasting

\begin{aligned} [y_{n+1}, ..., y_{n+P}] = f_\theta(&u_n, ..., u_{n-H} \\ &y_n, ..., y_{n-H} )\end{aligned}

\(H\) is the length of the history,

\(P\) is the length of the prediction

Conditional denoiser produces the forecast, conditional on the history

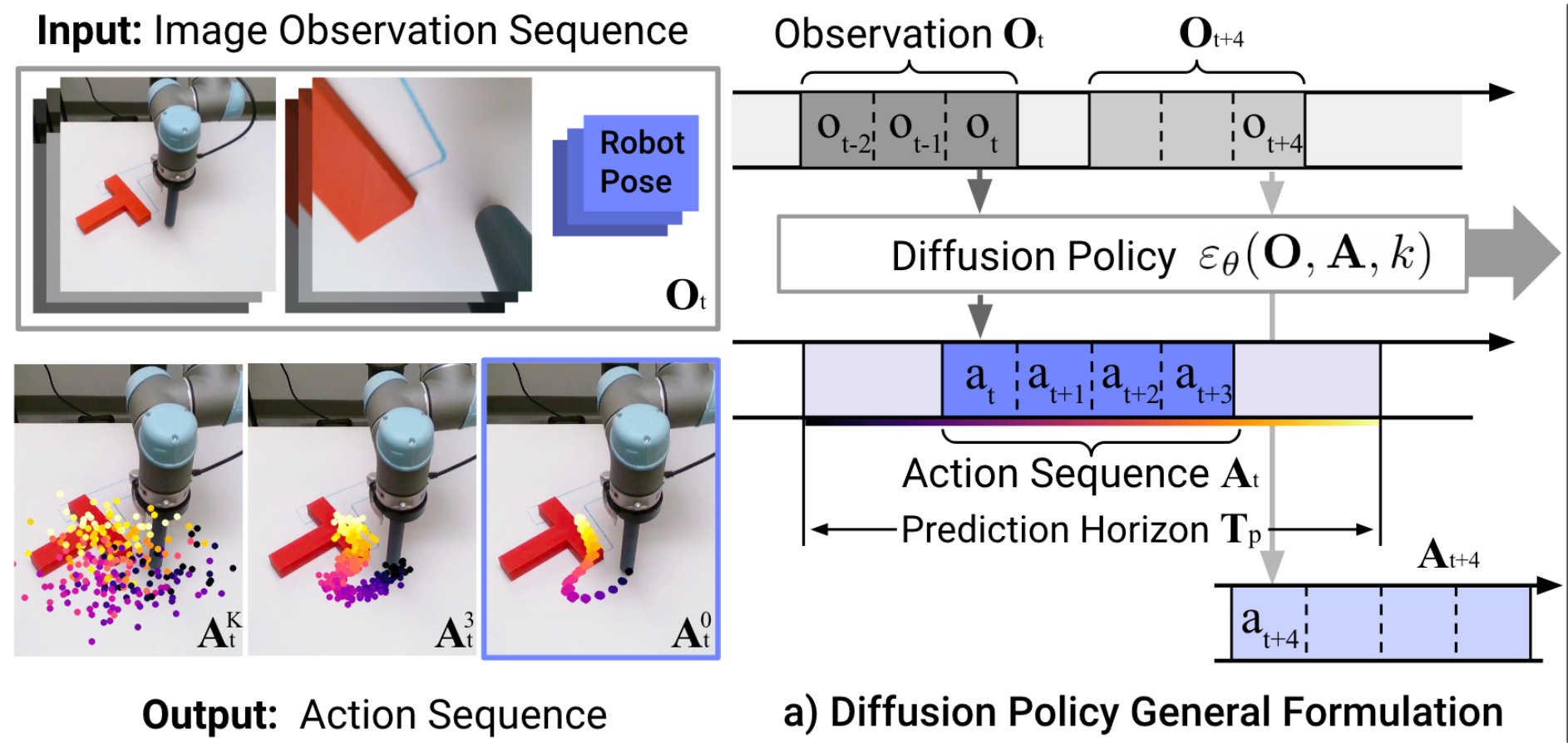
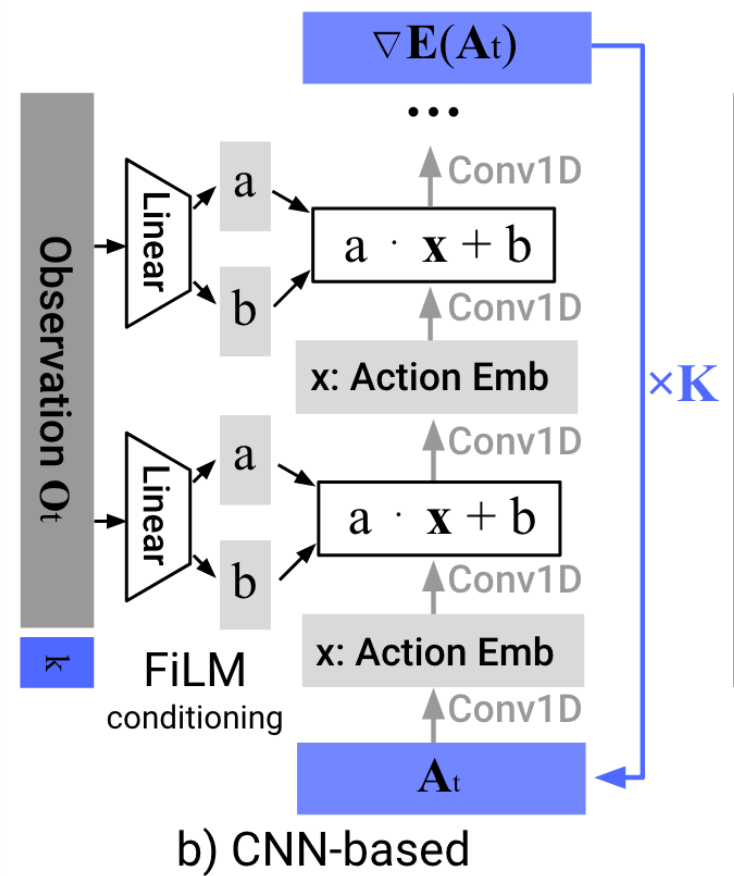
Image backbone: ResNet-18 (pretrained on ImageNet)
Total: 110M-150M Parameters
Training Time: 3-6 GPU Days ($150-$300)

Learns a distribution (score function) over actions

e.g. to deal with "multi-modal demonstrations"

Andy Zeng's MIT CSL Seminar, April 4, 2022

Andy's slides.com presentation

Why (Denoising) Diffusion Models?

  • High capacity + great performance
  • Small number of demonstrations (typically ~50)
  • Multi-modal (non-expert) demonstrations
  • Training stability and consistency
    • no hyper-parameter tuning
  • Generates high-dimension continuous outputs
    • vs categorical distributions (e.g. RT-1, RT-2)
    • Action-chunking transformers (ACT)
  • Solid mathematical foundations (score functions)
  • Reduces nicely to the simple cases (e.g. LQG / Youla)

Enabling technologies

Haptic Teleop Interface

Excellent system identification / robot control

Visuotactile sensing

with TRI's Soft Bubble Gripper

Open source:

https://punyo.tech/

Scaling Up

  • I've discussed training one skill
  • Wanted: few shot generalization to new skills
    • multitask, language-conditioned policies
    • connects beautifully to internet-scale data

 

  • Big Questions:
    • How do we feed the data flywheel?
    • What are the scaling laws?

 

  • I don't see any immediate ceiling

Discussion

I do think there is something deep happening here...

  • Manipulation should be easy (from a controls perspective)
  • probably low dimensional?? (manifold hypothesis)
  • memorization can go a long way

If we really understand this, can we do the same via principles from a model?  Or will control go the way of computer vision and language?

Discussion

What if I did have a good model? (and well-specified objective)

  • Core challenges:
    • Control from pixels
    • Control through contact
    • Optimizing rich robustness objective
  • The most effective approach today:
    • RL on privileged information + teacher-student

Deep RL + Teacher-Student

Lee et al., Learning quadrupedal locomotion over challenging terrain, Science Robotics, 2020

Deep RL + Teacher-student (Tao Chen, MIT at TRI)

Understanding RL for control through contact

  • Core challenges:
    • Control from pixels
    • Control through contact
    • Optimizing rich robustness objective

Do Differentiable Simulators Give Better Policy Gradients?

H. J. Terry Suh and Max Simchowitz and Kaiqing Zhang and Russ Tedrake

ICML 2022

Available at: https://arxiv.org/abs/2202.00817

The view from hybrid dynamics

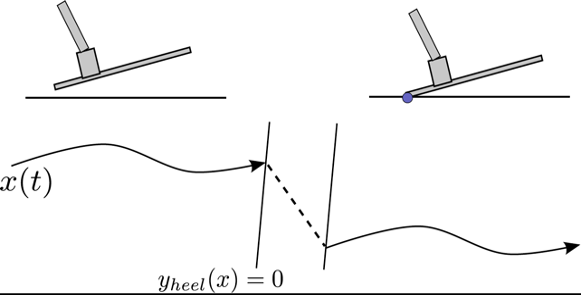
Continuity of solutions w.r.t parameters

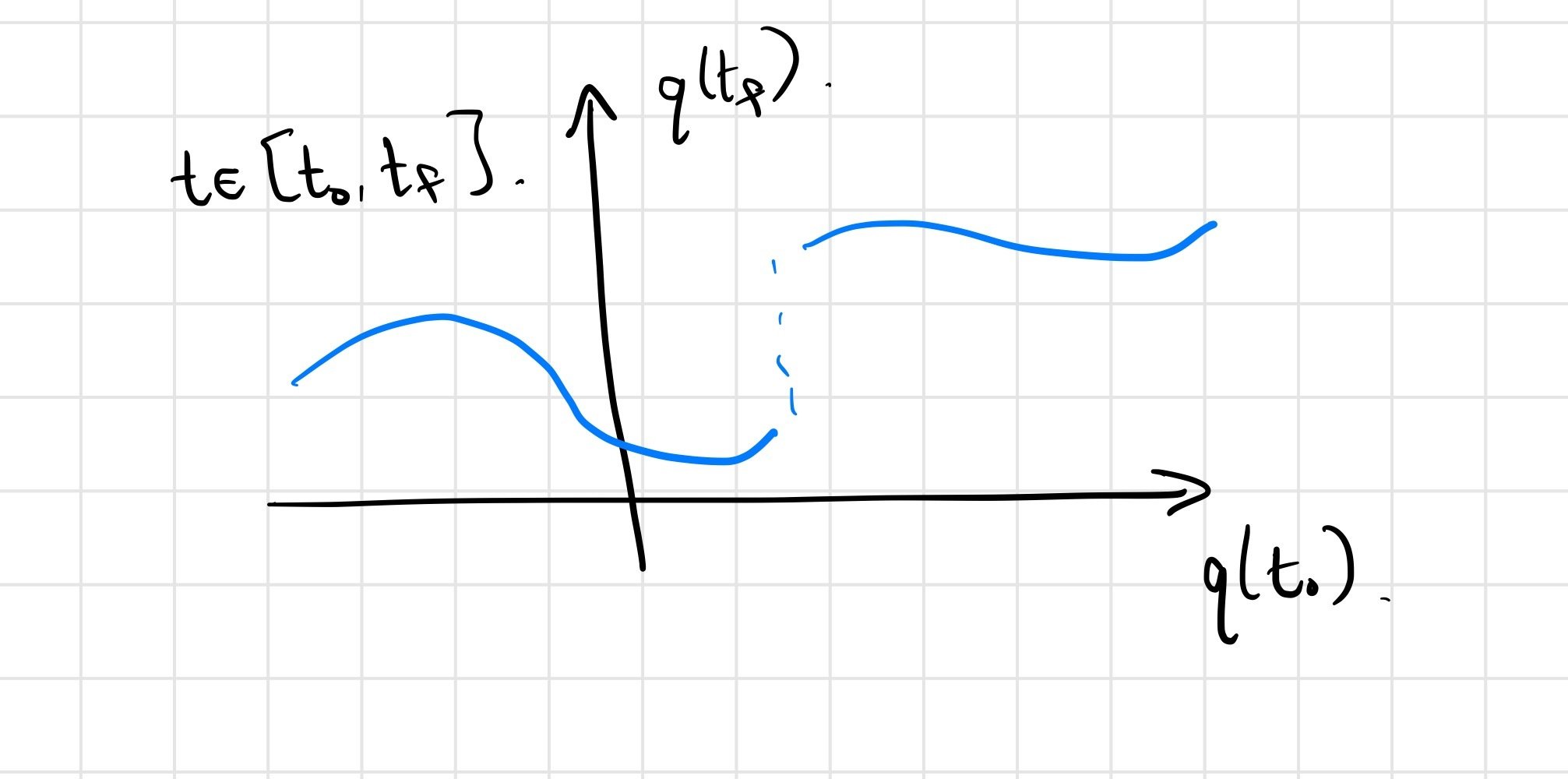
A key question for the success of gradient-based optimization

Use initial conditions here as a surrogate for dependence on policy parameters, etc.; final conditions as surrogate for reward.

Continuity of solutions w.r.t parameters

For the mathematical model... (ignoring numerical issues)

we do expect \(q(t_f) = F\left(q(t_0)\right)\) to be continuous.

  • Contact time, pre-/post-contact pos/vel all vary continuously.
  • Simulators will have artifacts from making discrete-time approximations; these can be made small (but often aren't)

point contact on half-plane

Continuity of solutions w.r.t parameters

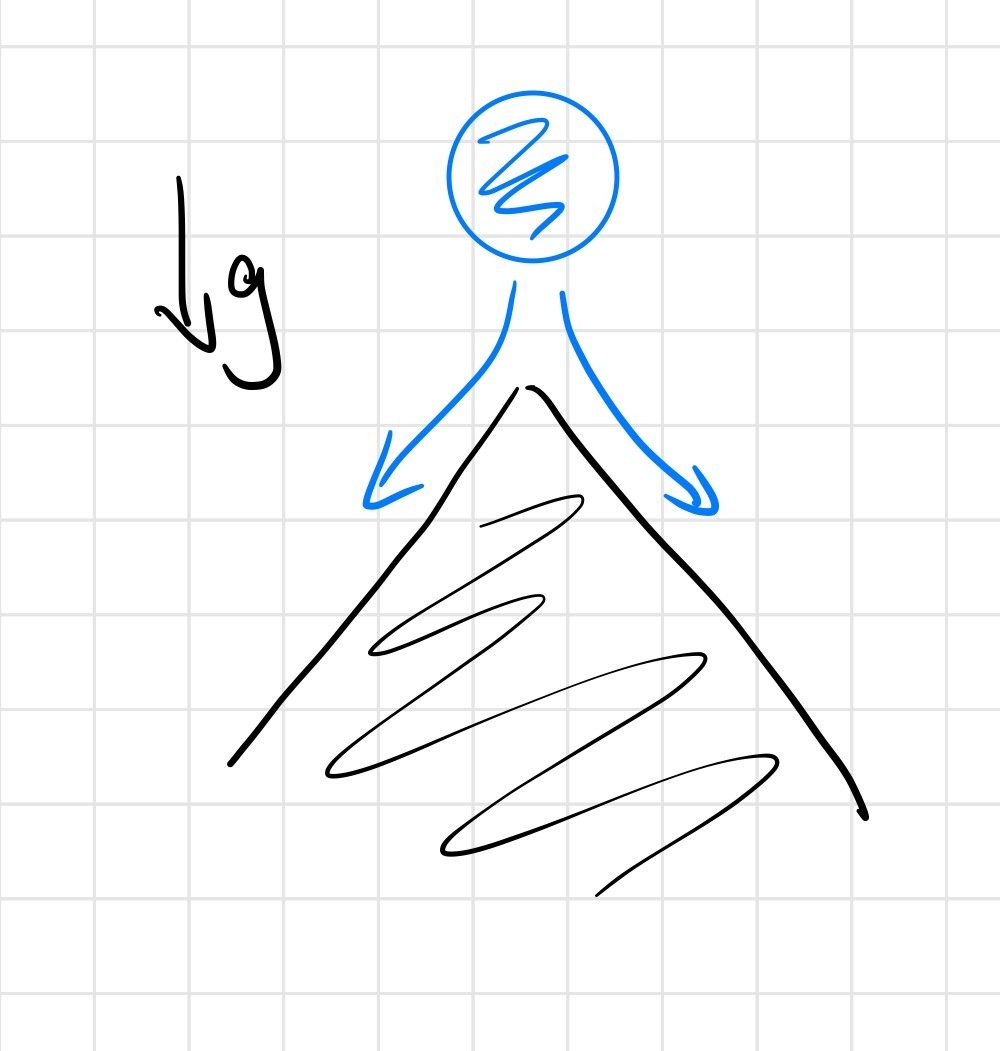
We have "real" discontinuities at the corner cases

 

 

 

 

  • making contact w/ a different face
  • transitions to/from contact and no contact

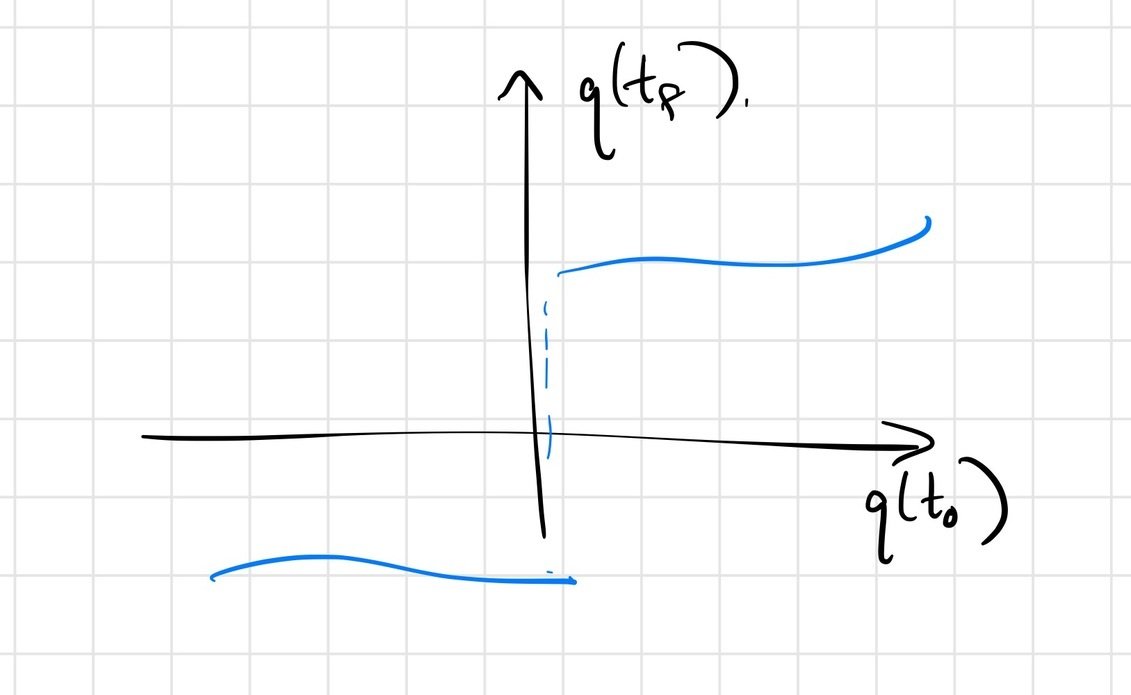
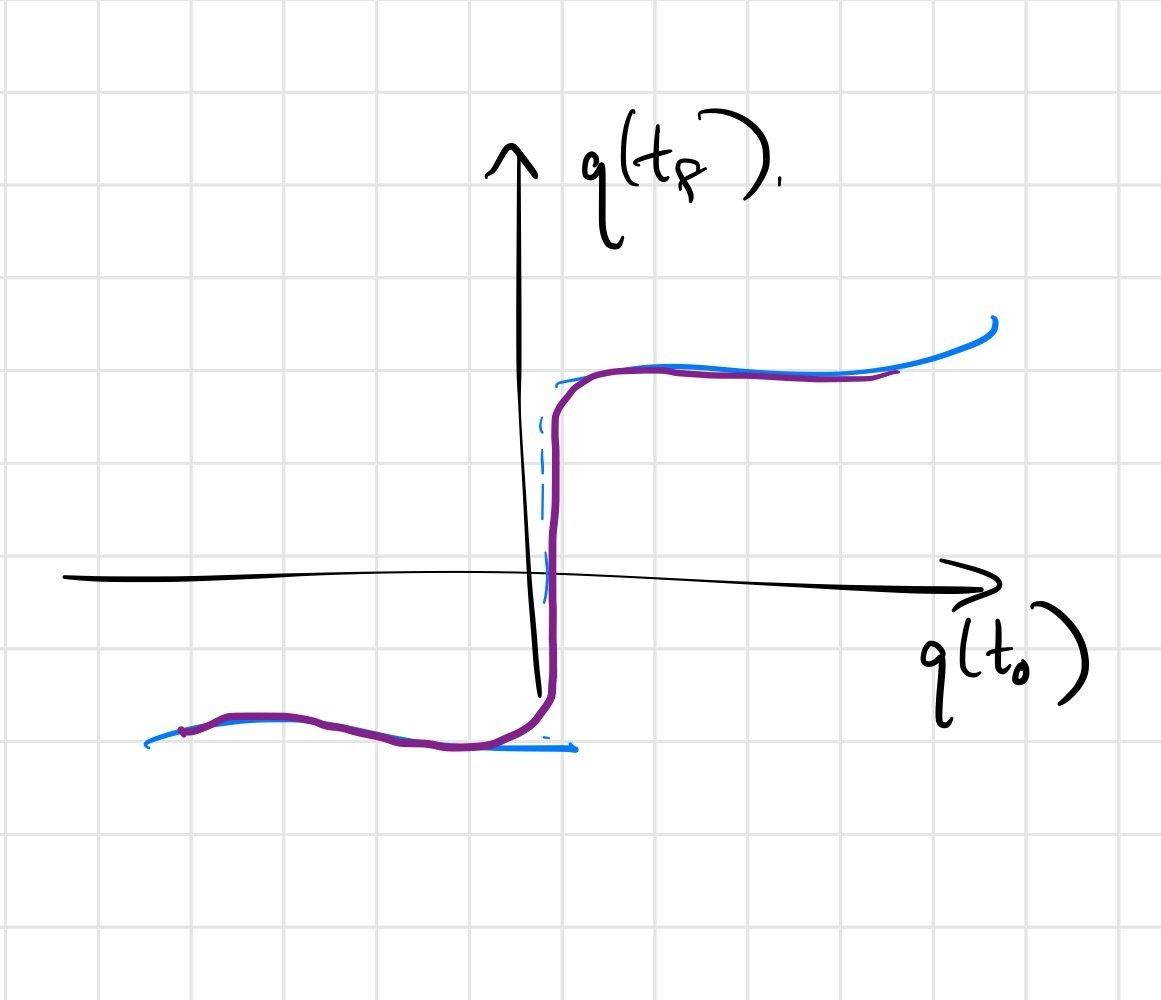
Soft/compliant contact can replace discontinuities with stiff approximations

Non-smooth optimization

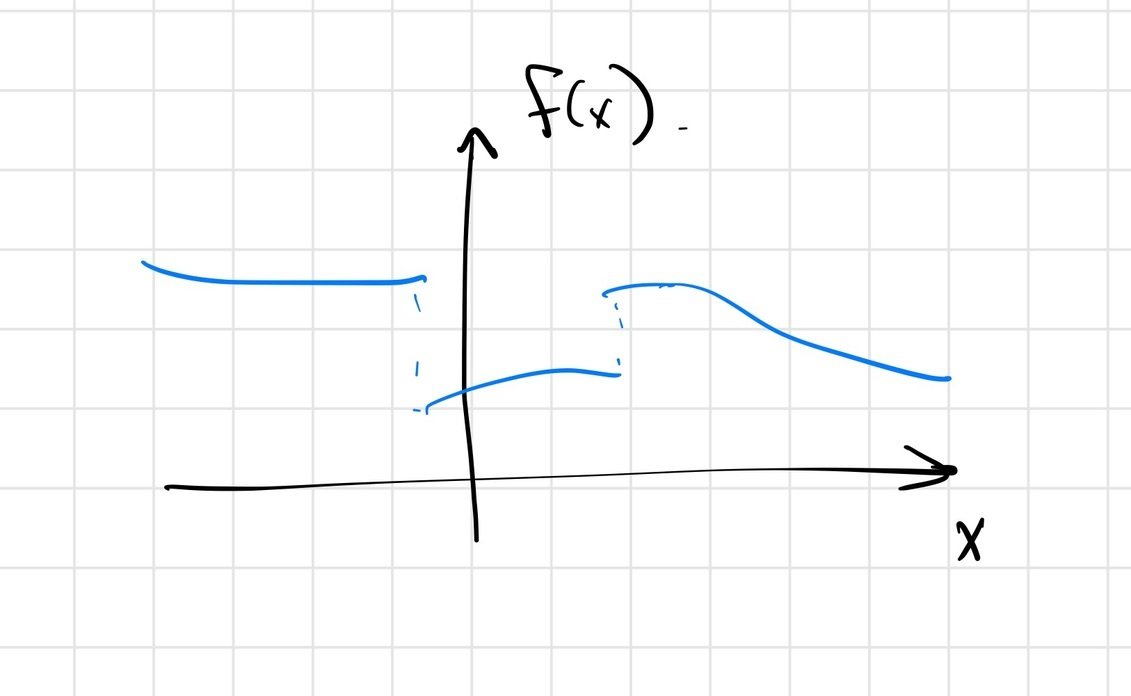
\[ \min_x f(x) \]

For gradient descent, discontinuities / non-smoothness can

  • introduce local minima
  • destroy convergence (e.g. \(l_1\)-minimization)

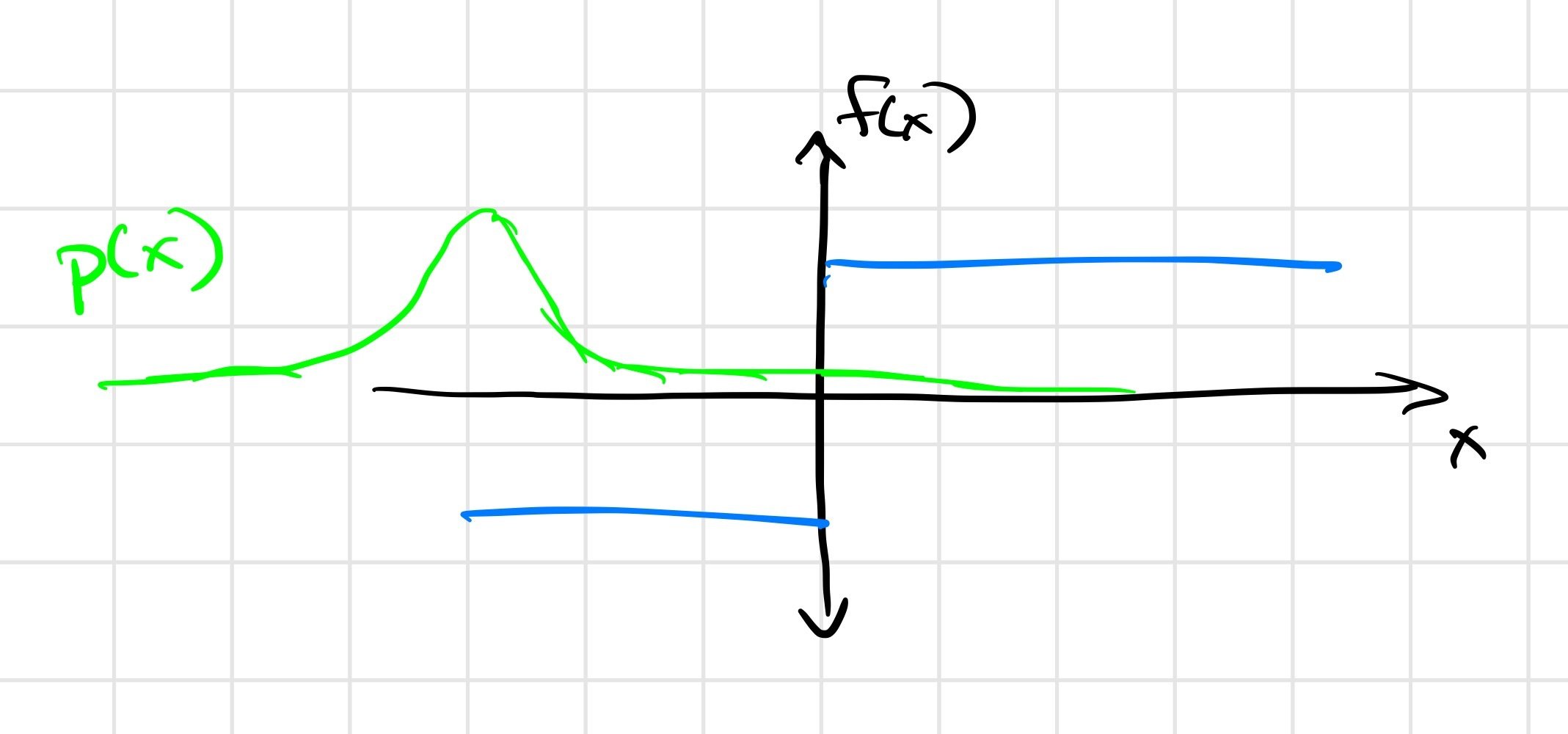
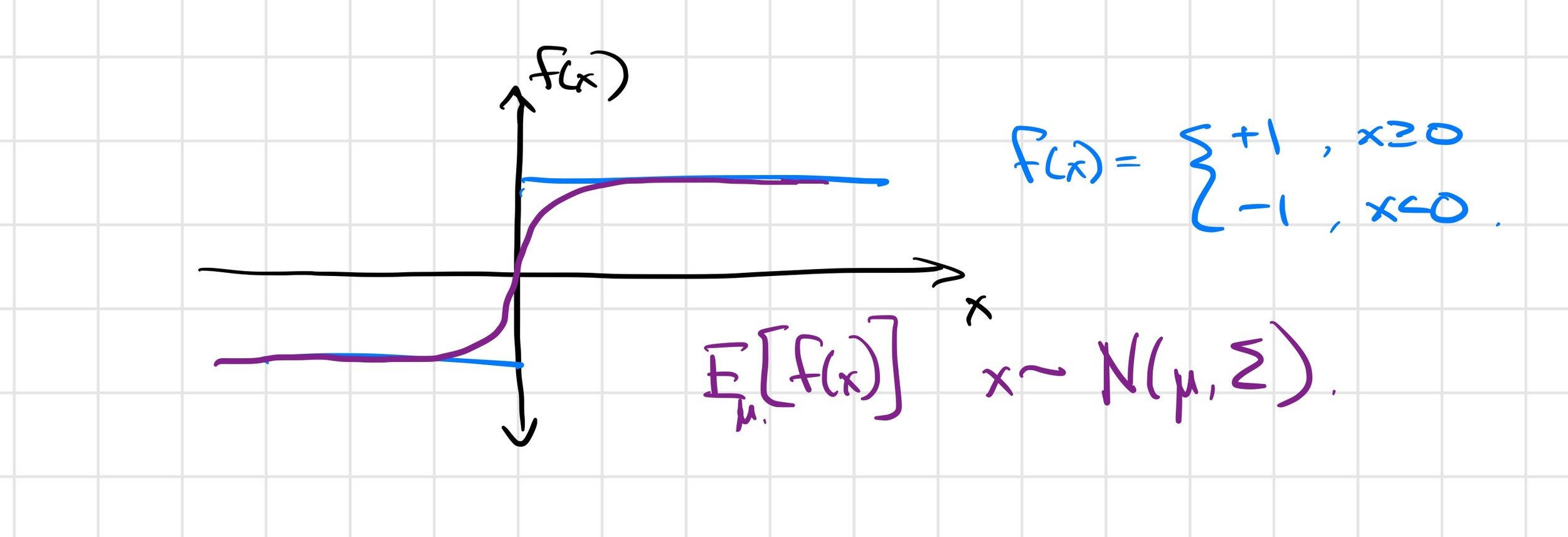
Smoothing discontinuous objectives

  • A natural idea: can we smooth the objective?

 

  • Probabilistic formulation, for small \(\Sigma\): \[ \min_x f(x) \approx \min_\mu E \left[ f(x) \right], x \sim \mathcal{N}(\mu, \Sigma) \]

 

  • A low-pass filter in parameter space with a Gaussian kernel.

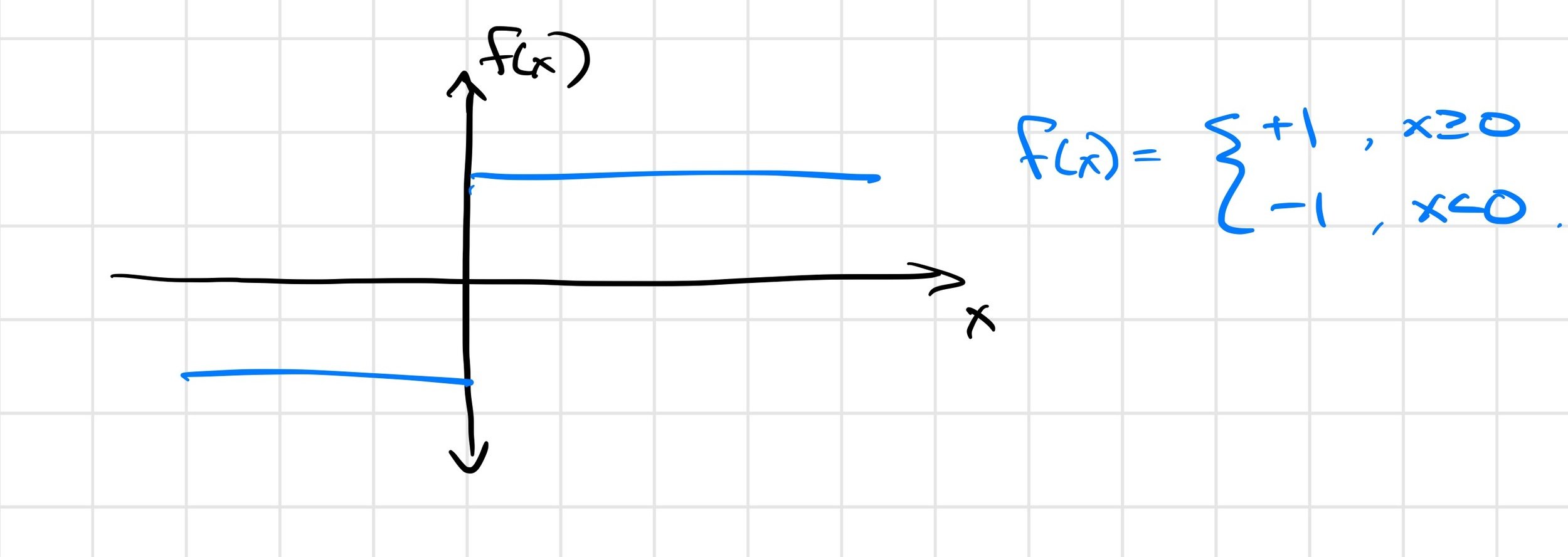
Example: The Heaviside function

  • Smooth local minima
  • Alleviate flat regions
  • Encode robustness

Smoothing with stochasticity

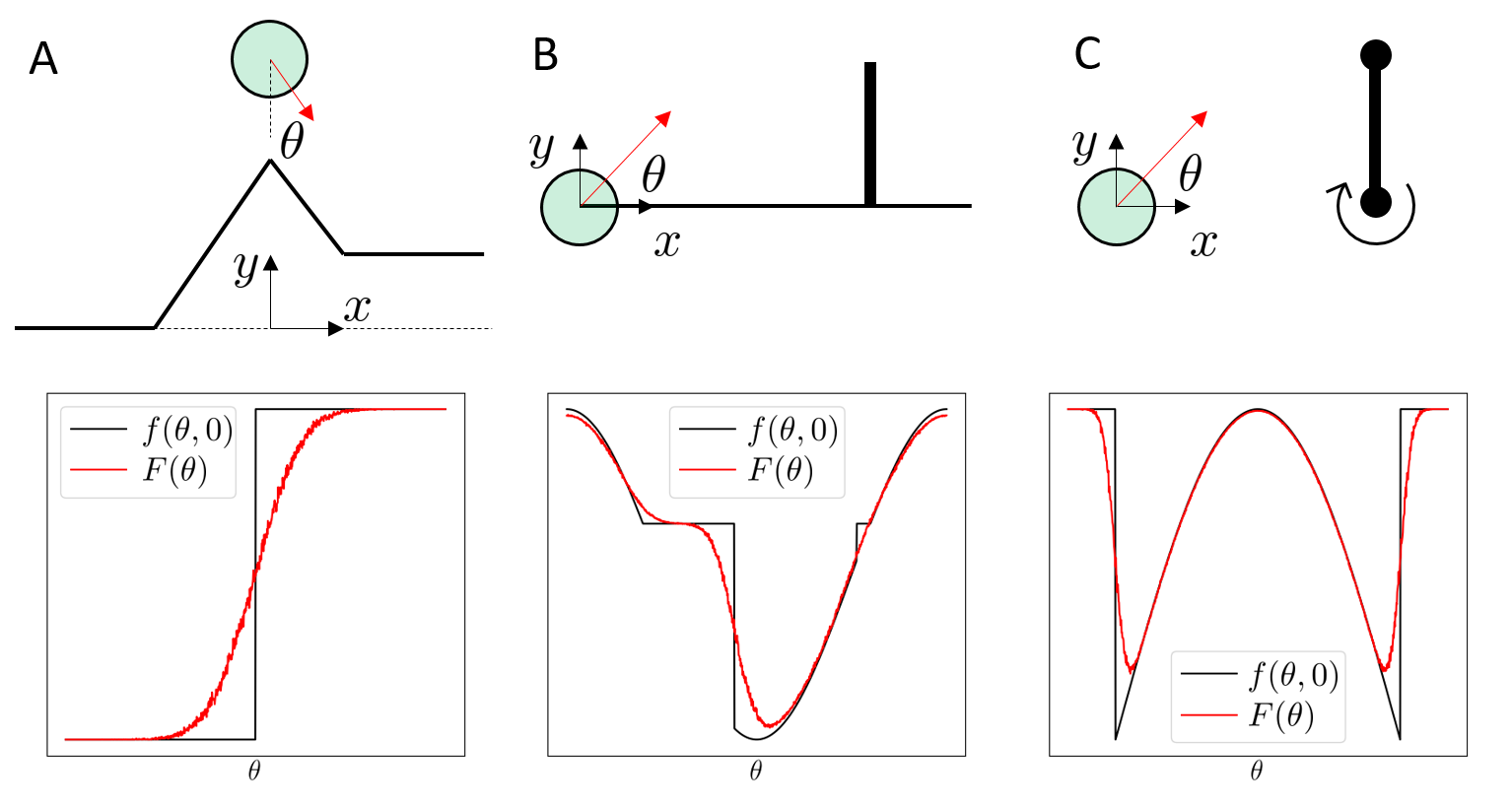
\begin{gathered} \min_\theta f(\theta) \end{gathered}
\begin{gathered} \min_\theta E_w\left[ f(\theta, w) \right] \\ w \sim N(0, \Sigma) \end{gathered}

vs

Smoothing with stochasticity for Multibody Contact

Relationship to RL Policy Gradient / CMA / MPPI

In reinforcement learning (RL) and "deep" model-predictive control, we add stochasticity via

  • Stochastic policies
  • Random initial conditions
  • "Domain randomization"

then optimize a stochastic optimal control objective (e.g. maximize expected reward)

 

These can all smooth the optimization landscape.

What about discrete decisions?

 

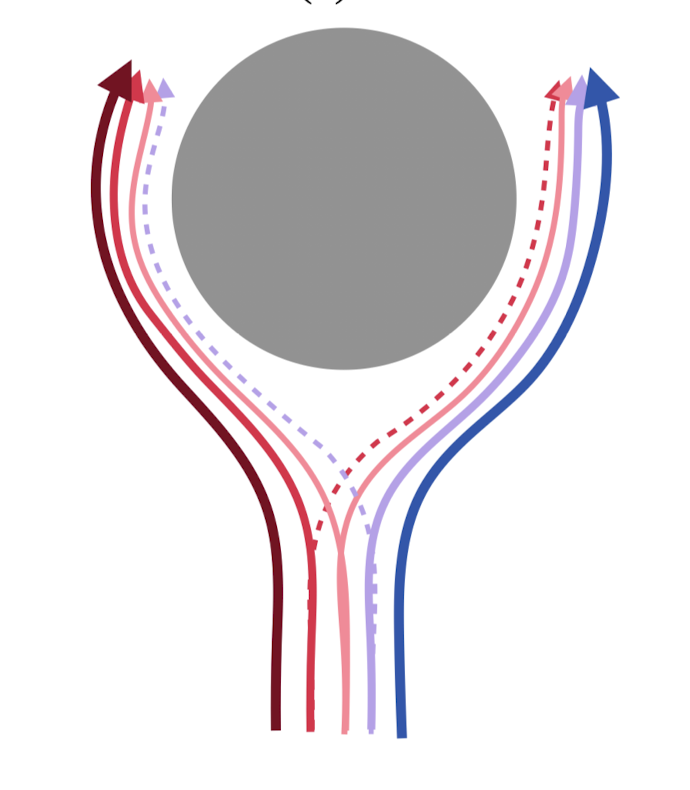
Graphs of Convex Sets (GCS)

(discrete + continuous planning and control)

Graphs of Convex Sets

 

  • For each \(i \in V:\)
    • Compact convex set \(X_i \subset \R^d\)
    • A point \(x_i \in X_i \) 
  • Edge length given by a convex function \[ \ell(x_i, x_j) \]

Note: The blue regions are not obstacles.

Graphs of Convex Sets

Mixed-integer formulation with a very tight convex relaxation

  • Efficient branch and bound, or
  • In practice we only solve the convex relaxation and round

Main idea: Multiply constraints + Perspective function machinery

Motion Planning around Obstacles with Convex Optimization.

Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.

Available at: https://arxiv.org/abs/2205.04422​

Accepted for publication in Science Robotics

A new approach to motion planning

Claims:

  • Find better plans faster than sampling-based planners
  • Avoid local minima from trajectory optimization
  • Can guarantee paths are collision-free
  • Naturally handles dynamic limits/constraints
  • Scales to big problems (e.g. multiple arms)

Default playback at .25x

Adoption

Dave Johnson (CEO): "wow -- GCS (left) is a LOT better! ... This is a pretty special upgrade which is going to become the gold standard for motion planning."

GCS Beyond collision-free motion planning

  • Planning through contact.
  • Task and Motion Planning / Multi-modal motion planning.
    • GCS \(\gg\) shortest path problems (permutahedron, etc).

 

  • Also deep connections to RL.
    • Machinery that connects results from tabular RL and continuous RL (e.g. linear function approximators)

Planar pushing (Push T)

More general manipulation

Summary

  • Dexterous manipulation is still unsolved, but progress is fast
  • Visuomotor diffusion policies
    • one skill with ~50 demonstrations
    • multi-skill \(\Rightarrow\) foundation model
  • We still need deeper (rigorous) understanding
    • Randomized smoothing
    • Graphs of convex sets (GCS)
  • Much of our code is open-source:

 

pip install drake
sudo apt install drake

drake.mit.edu

Online classes (videos + lecture notes + code)

http://manipulation.mit.edu

http://underactuated.mit.edu

drake.mit.edu