動態規劃

Dynamic Programming, DP

作者：sa072686 (sa072686@gmail.com)

核心概念

大問題轉成「同性質」小問題計算
- 透過「狀態」定義問題
- 透過「轉移」定義如何轉化為小問題
重複的子問題不計算第二遍
- 「建表」儲存已計算過狀態的答案

實作方法

Top-down：利用遞迴由上而下求解
Bottom-up：從起始狀態由下而上層層遞推

計數問題範例

符合條件有幾種不同情形、幾種走法、…

爬樓梯問題
～Origin～

從第 0 階開始往上爬，每次只能往上爬 1 或 2 階
求有多少種不同走法可以爬上第 n 階？

爬樓梯問題
～Origin～

n = 5 時的答案為 8

11111
1112
1121
1211
2111
122
212
221

觀察

窮舉「最後一步」的所有可能
- 如果爬 1 階抵達第 n 階
- 設最後一步前在第 x 階
- 解一次方程

\begin{aligned} x + 1 = n\\ \rightarrow x = n - 1 \end{aligned}

可知：抵達第 x = n-1 階後，再爬 1 階就到第 n 階

設抵達第 n-1 階有 100 種方法
每種各能提供 1 種抵達第 n 階的走法 → 總共 100x1 種

觀察

窮舉「最後一步」的所有可能
- 如果爬 2 階抵達第 n 階
- 設最後一步前在第 x 階
- 解一次方程

\begin{aligned} x + 2 = n\\ \rightarrow x = n - 2 \end{aligned}

可知：抵達第 x = n-2 階後，再爬 2 階就到第 n 階

設抵達第 n-2 階有 50 種方法
每種各能提供 1 種抵達第 n 階的走法 → 總共 50x1 種

爬樓梯問題
～Origin～

n = 5 時的答案為 8

11111
1112
1121
1211
2111
122
212
221

★最後一步爬 1 階

★最後一步爬 2 階

觀察

？？ 1

最後一步

抵達第 n-1 階的任何方法

抵達第 n 階

的一種方法

結論

抵達第 n 階方法：
- 抵達第 n-1 階的任一種方法 + 爬 1 階
- 抵達第 n-2 階的任一種方法 + 爬 2 階
→ 抵達第 n 階方法數 = 抵達第 n-1 階方法數 x 1

+ 抵達第 n-2 階方法數 x 1

設函數 f( i ) = 抵達第 i 階的方法數

f(i) = f(i-1)\times1 + f(i-2)\times 1

正確性

涵蓋所有可能的「最後一步」
- → 不會漏算
f( i-1 ) 由來的方法與 f( i-2 ) 在「最後一步」必定相異
- → 不會多算
不會漏算 + 不會多算 → 只能剛剛好是答案
- x <= ans && x >= ans
- → x == ans

最佳化問題範例

達成目標所有方法中最佳花費、最小步驟、…

爬樓梯問題
～改～

從第 0 階開始往上爬，每次只能往上爬 1 或 2 階
站上第 i 階需支付 c[ i ] 的過路費
求最少付多少錢才能爬上第 n 階？

觀察

同樣窮舉最後一步，會有兩種情形
- 從 n-1 階爬 1 階抵達
- 從 n-2 階爬 2 階抵達
以上兩種的額外花費同樣是第 n 階的 c[ n ]
- 設抵達 n-1 階要花 50 元
- 設抵達 n-2 階要花 30 元
- 50 + c[ n ] > 30 + c[ n ]
- 故這兩種之中，花費較小的較佳

結論

抵達第 n 階的最小花費為以下兩種取較小者
- 抵達第 n-1 階的最小花費 + c[ n ]
- 抵達第 n-2 階的最小花費 + c[ n ]
設函數 f( i ) = 抵達第 i 階的最小花費

f(i) = min(f(i-1), f(i-2)) + c[i]

正確性

證明取「當前最佳」必保證「未來最佳」
- 設走法 A 走到第 i 階時，花費 x 元
- 設走法 B 走到第 i 階時，花費 y 元
- 設 y > x 故走法 B 目前為比 A 更差的方法
- 設走法 B 可得到最佳解，最終總花費 c 元
  - 從第 i 階開始，路上花了 c-y 元
- 讓走法 A 從第 i 階開始，照抄 B 的走法
  - 應該會跟 B 一樣花 c-y 元，總花費 x+(c-y)
- 由定義 x < y 可推得

x < y \rightarrow x+(c-y) < y+(c-y) = c

故 c 不是最佳解，得證「若當前不是最佳，未來也必不是」

小結

切尾巴大法（適用大半問題，但不是所有）
- 窮舉最後一步（或最後一個單位）
- 拔掉看看會不會是個同性質子問題
  - 如果很像但不全相同，可以試著微調
- 看看能否以子問題答案來表達原問題答案
- 如果可以，先定義「狀態」
  - 用一些參數把問題和答案描述成函數
  - 例如 f( i ) = 爬上第 i 階的方法數
- 再定義「轉移」
  - 如何將「原問題」的答案描述為「子問題」的答案
  - 例如第 i 階方法數為第 i-1 階方法數加上第 i-2 階方法數
  - 寫成 f( i ) = f( i-1 )x1 + f( i-2 )x1

複雜度估計

重複問題不計算，故與一般遞迴不全相同

子問題不二算

所有子問題只被計算一遍
之後都是 O(1) 查表回答

總計算量

狀態數量 x 每個狀態所需計算量
= 狀態數 x 轉移計算量

例：爬樓梯問題

狀態量 n x 轉移 2
= 2n
= O(n)

如何實作

以及重複子問題的嚴重性

一般遞迴做法

int stair( int n )
{
	if (n <= 1)
		return 1;
	return stair( n-1 ) + stair( n-2 );
}

※ stair 可自由替換成好理解的名字

滿滿的重複計算

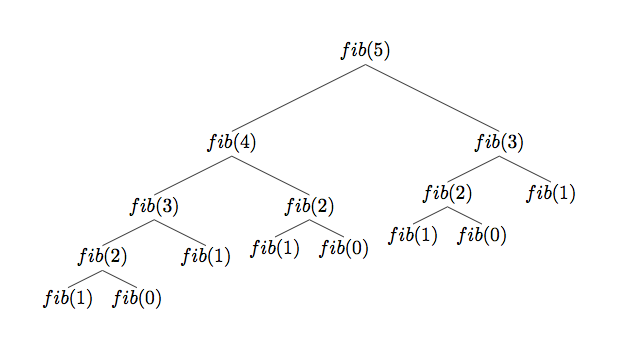
f( 5 ) 算 1 萬遍一樣是 8 種走法

那你算那麼多遍幹嘛
每次重算還要往下重算 f( 4 ) 和 f( 3 )
- f( 4 ) 還得往下重算 f( 3 ) 和 f( 2 ) ...

裏．爬樓梯問題

求 f( i ) 要幾次 func call
- 呼叫 f( i ) 本身花 1 次 func call
- f( i ) 需要先遞迴計算 f( i-1 ) 和 f( i-2 )
  - 所以加上 f( i-1 ) 和 f( i-2 ) 的 func call 次數
- 設 g( i ) = 計算 f( i ) 所需 func call 次數
- 由上可知需要 1 次，加上 f( i-1 ) 和 f( i-2 ) 的次數
  - 可以用 g( i-1 ) 和 g( i-2 ) 來表達

g(i) = 1 + g(i-1) + g(i-2)

※ 和 f() 成長一樣快，常數更大

如果你建表記錄，重複直接查表

直接查表 O(1)

計算量

每個狀態只計算 1 次，之後都是 O(1) 查表直接回答
共計 n 個狀態
每個狀態需要 2 次 func call 來計算
只要 2n 即 O( n ) 的計算量
- 對照組：g() 大約是 O( 2^n ) 等級
如果每個狀態需要 n 次或更多次計算…？
- 現在每個狀態才固定 2 次

如何建表查表

int stair( int n )
{
	if (used[n])
		return dp[n];
	used[n] = true;
	if (n <= 1)
		dp[n] = 1;
	else
		dp[n] = stair( n-1 ) + stair( n-2 );
	return dp[n];
}

DP

☆Top-down★

純遞迴不記錄

int stair( int n )
{
	if (n <= 1)
		return 1;
	return stair( n-1 ) + stair( n-2 );
}

int stair( int n )
{
	if (used[n])
		return dp[n];
	used[n] = true;
	if (n <= 1)
		dp[n] = 1;
	else
		dp[n] = stair( n-1 ) + stair( n-2 );
	return dp[n];
}

※ code 和前面相同，純對照用

DP ～Bottom-up～

dp[0] = 1;
dp[1] = 1;
for (i=2; i<=n; i++)
	dp[i] = dp[ i-1 ] + dp[ i-2 ];

Top-down

相對直覺（因人而異）
常數較大（function call 比較貴）
風險較高（有可能 stack-overflow）
有機會可以不計算非必要的子問題
適用幾乎所有題目

Bottom-up

相對不直覺（因人而異）
常數較小
風險較低
必須計算所有子問題（無法事先知道必不必要）
適用絕大多數題目，但相對 Top-down 少一些

※ 兩種都要最低限度會寫會用，才有資格偏食

（個人強烈推薦 Bottom-up 但絕不能只練一種）

狀態壓縮

DP 節省的計算量從何而來？

DP 透過狀態進行壓縮來加速

刻意省略部份描述去除差異，將不同方法視為相同狀態
- 像是「各位同學」這說法去除了外貌個性技能等差異
- 像 f( 5 ) 將所有「踏上第 5 階」的 8 種不同走法，去掉差異後，壓縮成「8」這單一的數字
- 只要這 8 種都符合「踏上第 5 階」這個敘述
向後擴展時，這 8 種不同的走法，只需要總共 1 次計算
- 大家都爬 1 階走到第 6 階
- 大家都爬 2 階走到第 7 階

壓縮的前提

符合同個敘述的不同方法，未來發展必須完全相同
例如爬上第 5 階的 8 種方法，任取兩種 A 和 B
- 它們爬上任何第 i>5 階，能採取的方法完全相同
- A 能用的走法，B 就能用；B 能用的走法，A 就能用
- 任取 2 個都符合這條件時，這群人就能壓縮在一起
反例：以 g( i ) = 往上爬 i 次的方法數
- 同樣是 g( 1 ) 有的在第 1 階，有的在第 2 階
- 這些方法爬上第 3 階能用的走法不完全相同
- 但你已去掉差異，因此不能分辨
- 這樣壓縮就是錯的，所以這狀態不行

從壓縮來思考

對於較複雜的 DP 問題，有時是從「哪些情況在怎樣的狀態下可以壓縮、合併」出發思考
也就是說，找到某些情況未來完全相同時，去湊看能合併他們的狀態，再對這狀態找轉移
- 用這樣去判斷一題是不是 DP 以及如何 DP

最佳化問題的額外壓縮條件

最佳化問題則是把「當前最佳」以外的方法全部扔掉
- 壓縮成只保留當前最佳解，所以只看 1 組就好
必須證明「當前最佳」必定是「未來最佳」
- 可參考最佳化問題那邊的證明方式
  - 其實證明本身用上了前述的「同狀態時未來發展必須相同」的性質
- 如果不滿足這點，扔掉「當前最佳」以外的方法時，可能會把未來最佳給扔了

爬樓梯問題．改二

從第 0 階開始往上爬，每次只能往上爬 1 或 2 階
站上第 i 階需支付 c[ i ] 的過路費
你姊會幫你出掉「總過路費」個位數零頭以外的部份
求「你自己」最少付多少錢才能爬上第 n 階？
- 你姊幫付的不算
- 總過路費 87 元比總過路費 19 元更好
  - 因為前者你只付 7 元，後者必須付 9 元

壓縮時扔掉最佳解的例子

如果走到第 i 階時有兩種走法 A 和 B
A 要付零頭 6 元
B 要付零頭 3 元
請問 A 和 B 哪個更好？
- B 當前更好，但如果未來零頭是 5
- A 變成 6+5=11 付 1 元
- B 變成 3+5=8 付 8 元
- 未來 A 可能更好
不管丟掉 A 或丟掉 B 都可能丟掉最佳解
- 當前最佳 != 未來最佳

解決方法

換個狀態
搞不好這題根本不適合 DP，換個做法
使用下個部份要講的技巧：增維

增維

修改狀態來拆散不該被壓縮在一起的方法們

其實還有降維

反過來拔掉區分了也沒有意義的狀態描述，不過…

如何增維

對狀態追加描述，區分本不該被壓縮合併的方法們
以《爬樓梯問題．改二》為例
- 不同零頭間沒有絕對優劣，未來發展也不同
  - 不該被壓縮在一起，目前較差的會被丟掉
- 追加描述「當前零頭」拆開它們
  - 但零頭一樣就沒差別了，只需記錄可不可能
修改後為 f(i, j) = 爬上第 i 階時總過路費零頭 j 是否可能
- 設 k 為加上 c[ i ] 零頭後，零頭部份剛好是 j 的數
  - 0 <= k <= 9
- f(i, j) = f(i-1, k) || f(i-2, k)

真．爬樓梯問題

從第 0 階開始往上爬，每次只能往上爬 1、2 或 3 階
不得連續爬相同階數
- 可以 1、2、1 交替，不能 1、1 連續相同階數
求有多少種不同走法可以爬上第 n 階？

觀察

上一步爬幾階，會影響未來發展
若將上一步爬的階數不同的方法壓縮在一起，會無法區別
應該對上一步爬幾階來增維，區分上一步階數不同的情況

各位可以試著增維看看

答案在下一面，此頁防雷

對上一步階數增維

設 f(i, j) = 抵達第 i 階且最後一步爬 j 階的方法數

f(i, j) = sum(f(i-j, k))\\ for\ k = [1, 3], k \neq j

CSES 1635

給 n 種硬幣面額，求湊出 k 的方法數

2 + 5 和 5 + 2 算不同方法

思考方向

考慮總和為 k 時，面額若有 {2, 3, 5}

最後使用 2 時，剩下為 k-2
最後使用 3 時，剩下為 k-3
最後使用 5 時，剩下為 k-5
則 k-2, k-3, k-5 每種做法
各可以提供 1 種方式達成總和 k

由於順序不同視作不同
其實等價於爬樓梯問題

狀態與轉移

設狀態 dp(i) 為總和 i 之方法數

dp(i) = \sum_{k=1}^{n} dp(i-C_k)

Ck 為第 k 種面額

CSES 1638

給地圖，有障礙物
每步只能往右或往下
求從左上走到右下的方法數

思考方向

每步往下或往右
故每格必從上或左兩方向過來
抵達左、上兩格的每種走法
都能提供 1 種走法

狀態與轉移

設 dp(i, j) 為抵達座標 (i, j) 之方法數

dp(i, j) = dp(i-1, j) + dp(i, j-1)

TOJ 540

給 n 個路段用 3 種不同跑法所需時間
每種跑法至少要跑 1 段路
每段路必須使用相同跑法跑完
從跑法 i 只能切換至跑法 i+1
求最小所需時間

思考方向

目前所在路段影響接下來要跑多少
目前跑法影響下一段路能用哪些跑法
因此這些影響未來發展的必須增維

考慮第 i 段路以第 k 種跑法跑完
那麼它第 i-1 段必是用 k or k-1 種跑法跑完
從所有符合的情況選最佳
即為當前最佳

狀態與轉移

設 dp(i, j) 為用第 j 種跑法跑完路段 1~i
所需最小時間

dp(i, j) = \min\begin{cases}dp(i-1, j)\\dp(i-1, j-1)\end{cases} + T_{i,j}

其中 Ti,j 為第 i 路段以 j 跑法跑完的時間

AtCoder dp_c

在 n 天每天從 3 種活動選 1 執行
給每一天每種活動的快樂值
不能連續 2 天進行同種活動

求這 n 天最大快樂值總和

思考方向

今天是第幾天影響每種活動快樂值和天數
今天的活動影響明天能做的事
以上皆影響未來發展

考慮今天做第 j 種活動
那麼前一天必須做 (j+1)%3, (j+2)%3 種活動
使活動不連續
從不連續中取最佳幸福值
為當前最佳

狀態與轉移

設 dp(i, j) 為到第 i 天為止
最後一天進行第 j 種活動
的最大幸福值

dp(i, j) = \max\begin{cases}dp(i-1, (j+1)\%3)\\dp(i-1, (j+2)\%3)\end{cases} + H_{i,j}

Hi,j 為第 i 天做 j 活動的幸福值

UVa 10036

給 n 數，每數可選要加或減
求最終算出的值為 k 的倍數

n <= 10000

k <= 100

思考方向

考慮最終為 k 倍數
設最後一數為 5
則前面總和需為 k*x - 5 或 k*x + 5

也就是說，設前一步總和為 s，則
(s + 5) % k == 0
(s - 5) % k == 0
至少其中之一必須可達成

故子問題須湊出 %k 下
特定餘數能否達成

狀態與轉移

設 dp(i, j) 為到第 i 數時
總和 % k 為 j 是否可能達成

dp(i, j) = OR\begin{cases}dp(i-1, (j-A_i)\%k)\\dp(i-1, (j+A_i)\%k)\end{cases}

Kattis hammingellipses

給長度 n 兩序列 A, B
每元素由 0 到 k-1 構成

定義 H(i, j) 為兩序列 i, j
有多少個位置的元素值不同

給整數 d
求存在多少種相異序列 C
C 每元素由 0 到 k-1 構成
且滿足 H(A, C) + H(B, C) = d

思考方向

考慮 C[n] 的所有情況

若 A[n] == B[n] 時
- 若 C[n] == A[n] 則距離不變
- 若 C[n] != A[n] 則距離總和 + 2
若 A[n] != B[n] 時
- 若 C[n] == A[n] 則距離 + 1
- 若 C[n] == B[n] 則距離 + 1
- 若都不相等，則距離總和 + 2

距離和必須為 d
故視 C[n] 前 n-1 個字可能距離必須為
d, d-1, d-2 其中一種

狀態與轉移

設 dp(i, j) 為 C[1] 到 C[i] 這段
和 A,B 距離總和為 j 的方法數

dp(i, j) = \begin{cases} sum\begin{cases}dp(i-1, j)\\dp(i-1, j-2)\times(k-1)\end{cases} if A_i=B_i\\ sum\begin{cases}dp(i-1, j-1)\times2\\dp(i-1, j-2)\times(k-2)\end{cases} if A_i\neq B_i \end{cases}

回溯解

記錄每種狀態從誰轉移而來
由終點狀態逆推即可

AtCoder typical90_bd

n 天每天買 A,B 福袋其中一種
給每天的 A,B 福袋價格
求總花費恰為 S 元的買法

思考方向

每天買什麼不影響，只有總價格影響未來

第 n 天總和恰為 S 元
表示第 n-1 天必須達成

S - A[n]
S - B[n]

其中一種金額

狀態與轉移

設 dp(i, j) 為到第 i 天買了總和 j 元
是否可能達成

dp(i, j) = OR\begin{cases}dp(i-1, j-A_i)\\dp(i-1, j-B_i) \end{cases}

回溯解

記錄 F(i, j) = A or B
若 dp(i-1, j-Ai) 可達成則記 A
若 dp(i-1, j-Bi) 可達成則記 B

若皆可達成，則視題目要求決定記誰
最後從終點狀態照 F 的記錄回推即可

若終點 F(n, S) 為 A
則下一步回頭查 F(n-1, S-A[n])
否則回頭查 F(n-1, S-B[n])
依此類推，遞迴解決

最小字典序回溯解

由於終點回推時是先推得最後一步
同時是字典序中最不重要的一步

故字典序時可倒序計算
將原終點當起點，原起點當終點
回推時的最後一步
即為原第一步

優化

大原則：轉移可能可壓，狀態數則不行
故多種可行狀態時
狀態數越少，可能性越大

AtCoder dp_m

有 n 個小孩，第 i 小孩要發 0~Ai 顆糖
你有 K 糖要發完，求滿足條件有幾種發法？

n <= 100
K <= 10000

思考方向

考慮發完 K 糖時
第 n 個小孩可能取得 0 到 A[n] 顆

也就是說，前 n-1 小孩發掉的糖數
必須為 K-0 到 K-A[n]
所以糖數重要，找到子問題描述

狀態與轉移

設 dp(i, j) 為到第 i 小孩
發掉恰 j 糖的方法數

dp(i, j) = \sum_{k=0}^{A_i}dp(i-1, j-k)

狀態數 n * k
轉移 k
最差 100 x 10000^2 = 10^10 …

改進

dp(i, j) = \sum_{k=0}^{A_i}dp(i-1, j-k)

考慮 dp(i, j) 計算上需要
dp(i-1, j)
dp(i-1, j-1)
dp(i-1, j-2)
…
可視為 dp[i-1] 裡的區間和

改進

dp(i, j) = \sum_{k=0}^{A_i}dp(i-1, j-k)

設 pfx(i, j) 為 dp(i, 0) + ... + dp(i, j)

pfx(i, j) = pfx(i, j-1) + dp(i, j)

改進

dp(i, j) = \sum_{k=0}^{A_i}dp(i-1, j-k)

pfx(i, j) = pfx(i, j-1) + dp(i, j)

綜合以上，整理遞迴式為

dp(i, j) = pfx(i-1, j) - pfx(i-1, j-A_i-1)

則 dp, pfx 轉移均為 O(1)
複雜度 O(nk)
最差為 100 x 10000 = 10^6 合理

UVa 10721

給 n, x, y
求長度 n 的 0/1 序列滿足
連續的 0/1 數量不超過 x
連續相同的區段數恰為 y

思考方向

考慮第 n 元素可為 0 或 1
區段數必須恰為 y
故

若第 n-1 元素與 n 相異
則區段數增加 1
前面必須恰為 y-1 段

若第 n-1 元素與 n 相同
則屬同一區段，連續相同字數 + 1

故子問題必須同時注意區段數和連續相同數

狀態與轉移

設 dp(i, j, k) 為長度 i 時
區段數恰為 j 最後一段連續字數 k
的方法數

dp(i, j, k) = \begin{cases} \sum_{t=1}^{x}dp(i-1, j-1, t)&, if(k = 1)\\ dp(i-1, j, k-1)&, else \end{cases}

改進

考慮最後一個區段，而非最後一個元素
則窮舉最後區段字數為 t = 1 到 x
前面的 n-t 元素則需湊足 y-1 區段

狀態與轉移

設 dp(i, j) 為長度 i 區段數恰為 j 的方法數

dp(i, j) = \sum_{k=1}^{x}dp(i-k, j-1)

由於 k 連續，故 i - k 連續
可套用前綴和將轉移壓至 O(1)

動態規劃

核心概念

實作方法

計數問題範例

爬樓梯問題 ～Origin～

爬樓梯問題 ～Origin～

觀察

觀察

爬樓梯問題 ～Origin～

觀察

結論

正確性

最佳化問題範例

爬樓梯問題 ～改～

觀察

結論

正確性

小結

複雜度估計

子問題不二算

總計算量

例：爬樓梯問題

如何實作

以及重複子問題的嚴重性

一般遞迴做法

滿滿的重複計算

f( 5 ) 算 1 萬遍一樣是 8 種走法

裏．爬樓梯問題

如果你建表記錄，重複直接查表

計算量

如何建表查表

DP

純遞迴不記錄

DP ～Bottom-up～

Top-down

Bottom-up

狀態壓縮

DP 透過狀態進行壓縮來加速

壓縮的前提

從壓縮來思考

最佳化問題的額外壓縮條件

爬樓梯問題．改二

壓縮時扔掉最佳解的例子

解決方法

增維

其實還有降維

如何增維

真．爬樓梯問題

觀察

各位可以試著增維看看

對上一步階數增維

CSES 1635

思考方向

狀態與轉移

CSES 1638

思考方向

狀態與轉移

TOJ 540

思考方向

狀態與轉移

AtCoder dp_c

思考方向

狀態與轉移

UVa 10036

思考方向

狀態與轉移

Kattis hammingellipses

思考方向

狀態與轉移

回溯解

AtCoder typical90_bd

思考方向

狀態與轉移

回溯解

最小字典序回溯解

優化

AtCoder dp_m

思考方向

狀態與轉移

改進

爬樓梯問題
～Origin～

爬樓梯問題
～Origin～

爬樓梯問題
～Origin～

爬樓梯問題
～改～