INTRO TO
GENERALIZED LINEAR MIXED MODELING
Outline
LINEAR MODELS
-
Equation: Y = Xβ + ε
-
Assumptions:
-
Linearity
-
Homoscedasticity
-
Normal residuals
-
Independent observations
-
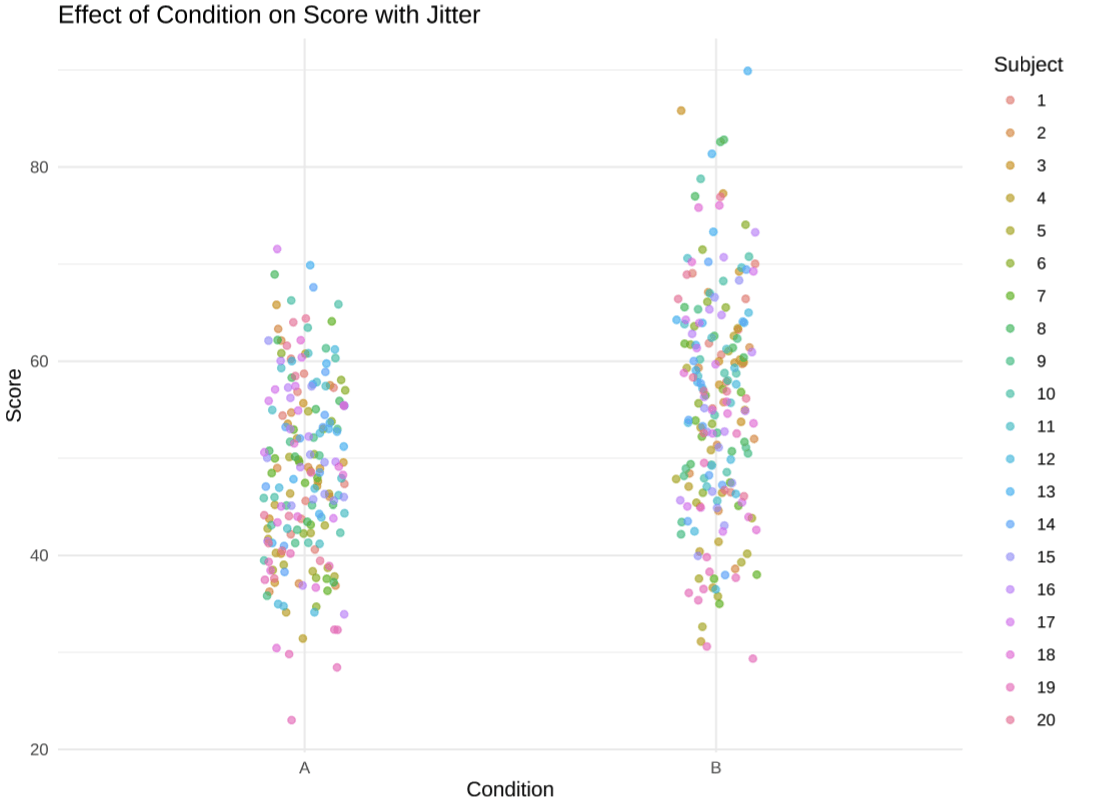
LINEAR MODELS
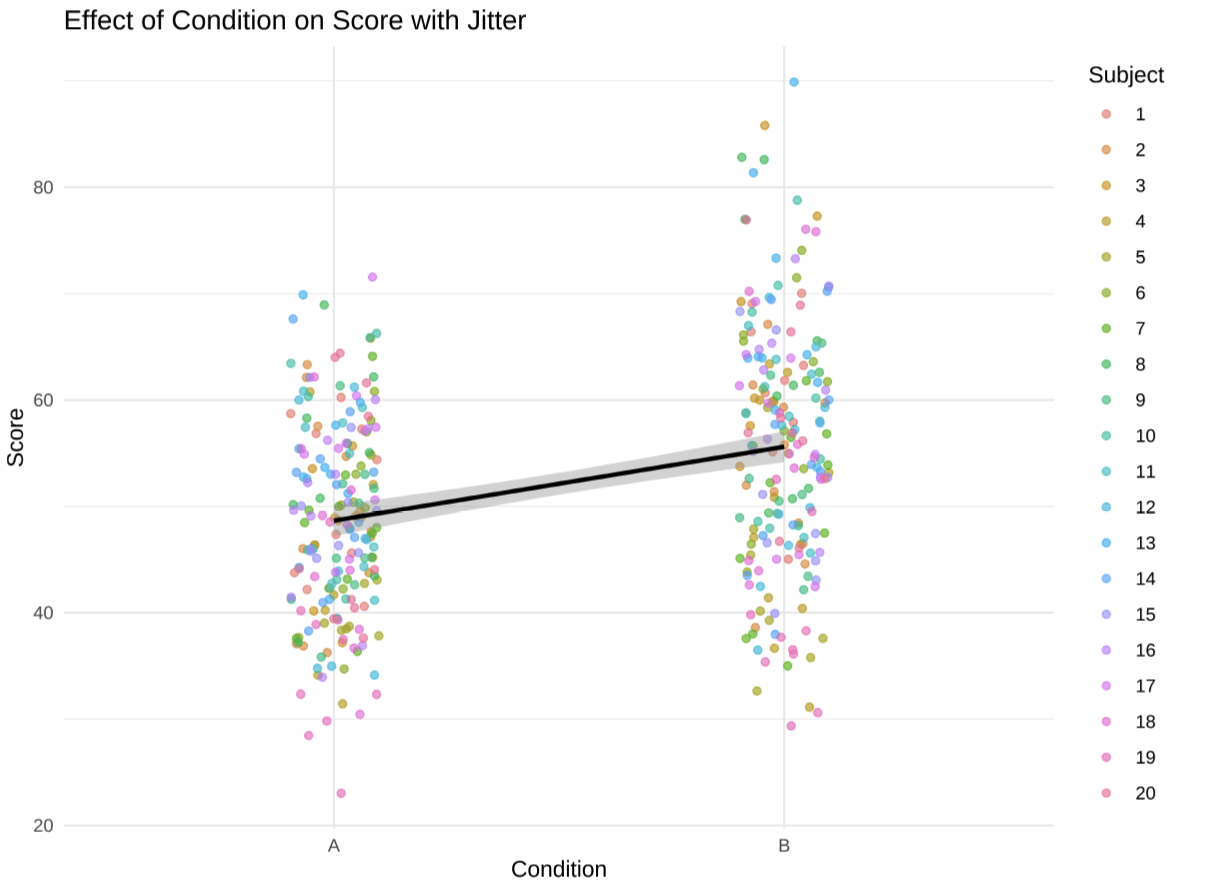
LINEAR MODELS
No handling of:
-
Correlated data (e.g., repeated measures)
-
Hierarchical structure
-
Non-normal data (e.g., binary, count)

LINEAR MODELS
No handling of:
-
Correlated data (e.g., repeated measures)
-
Hierarchical structure
-
Non-normal data (e.g., binary, count)

GENERALIZED LINEAR MODELS
Equation: g(E[Y])=Xβg(\mathbb{E}[Y]) = X\betag(E[Y])=Xβ
- Key: Link function ggg
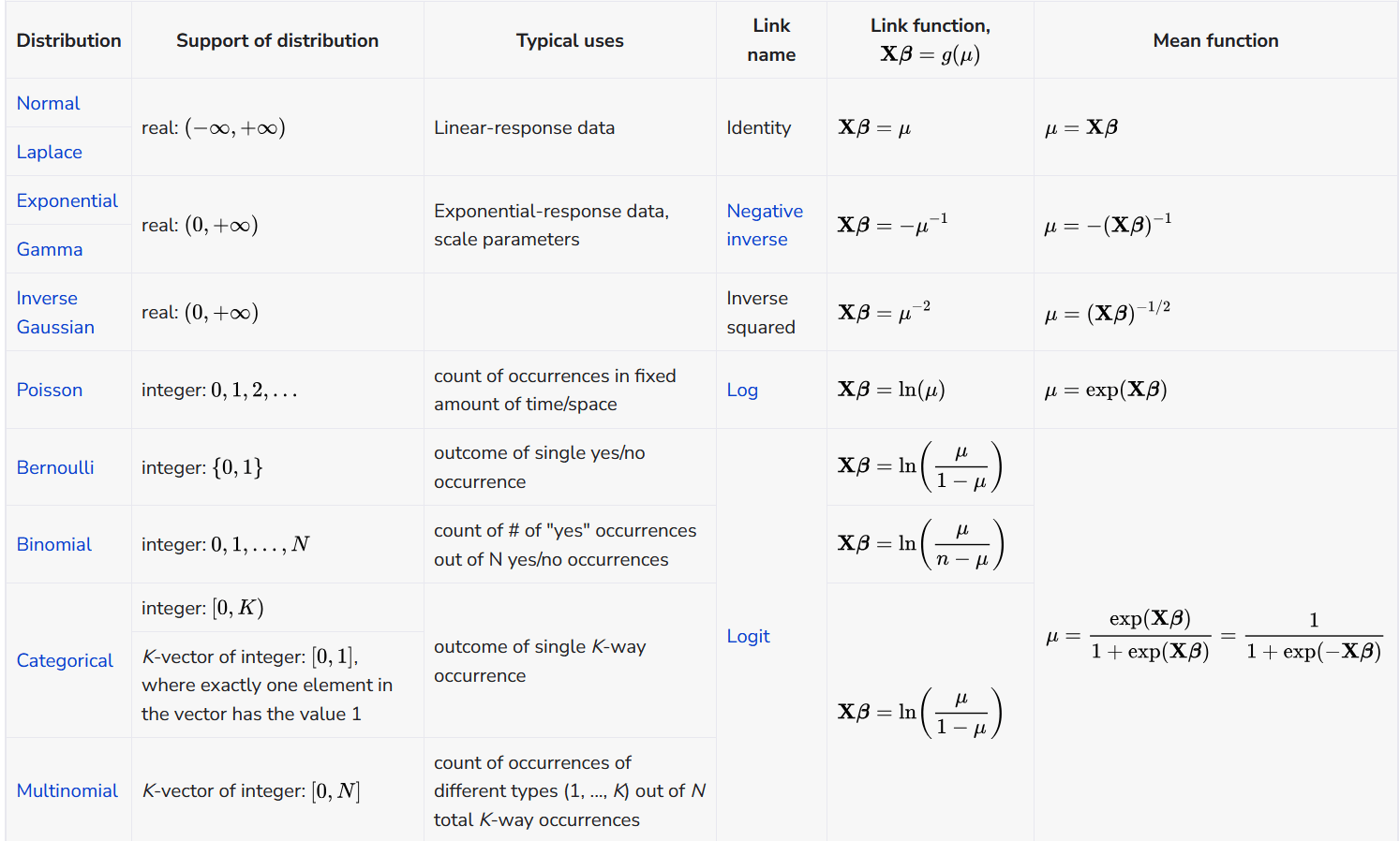
Link function matters!
LINEAR MIXED MODELS
- Old Equation: Y = Xβ + ε
- Equation: Y=Xβ+Zb+εY = X\beta + Zb + \varepsilonY=Xβ+Zb
-
New term: ZbZbZb = random effects
- Clustering
- Repeated Measures

LINEAR MIXED MODELS
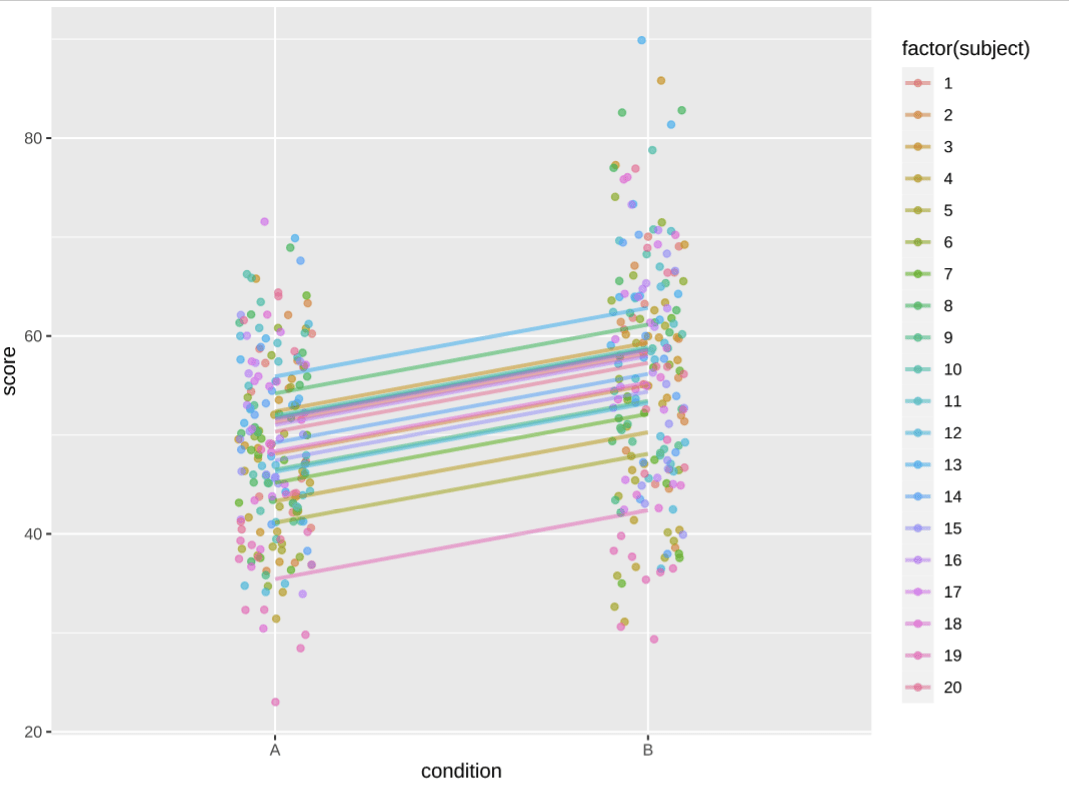

LINEAR MIXED MODELS


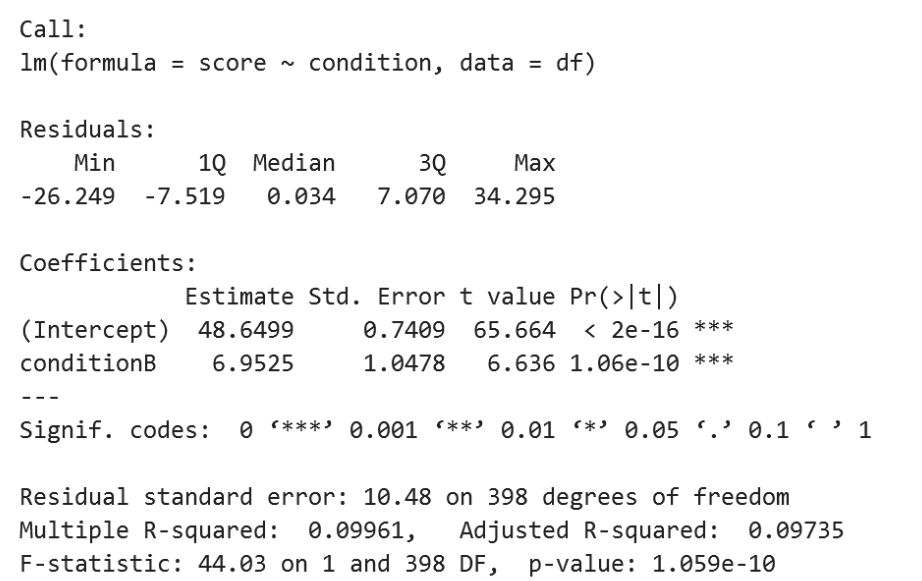
LM Report
LMM Report
LINEAR MIXED MODELS


LM Report
LMM Report
GENERALIZED LINEAR MIXED MODELS
Equation: g(E[Y])=Xβg(\mathbb{E}[Y]) = X\betag(E[Y])=Xβ +Zb
ZbZbZb = random effects
- Key: Link function ggg
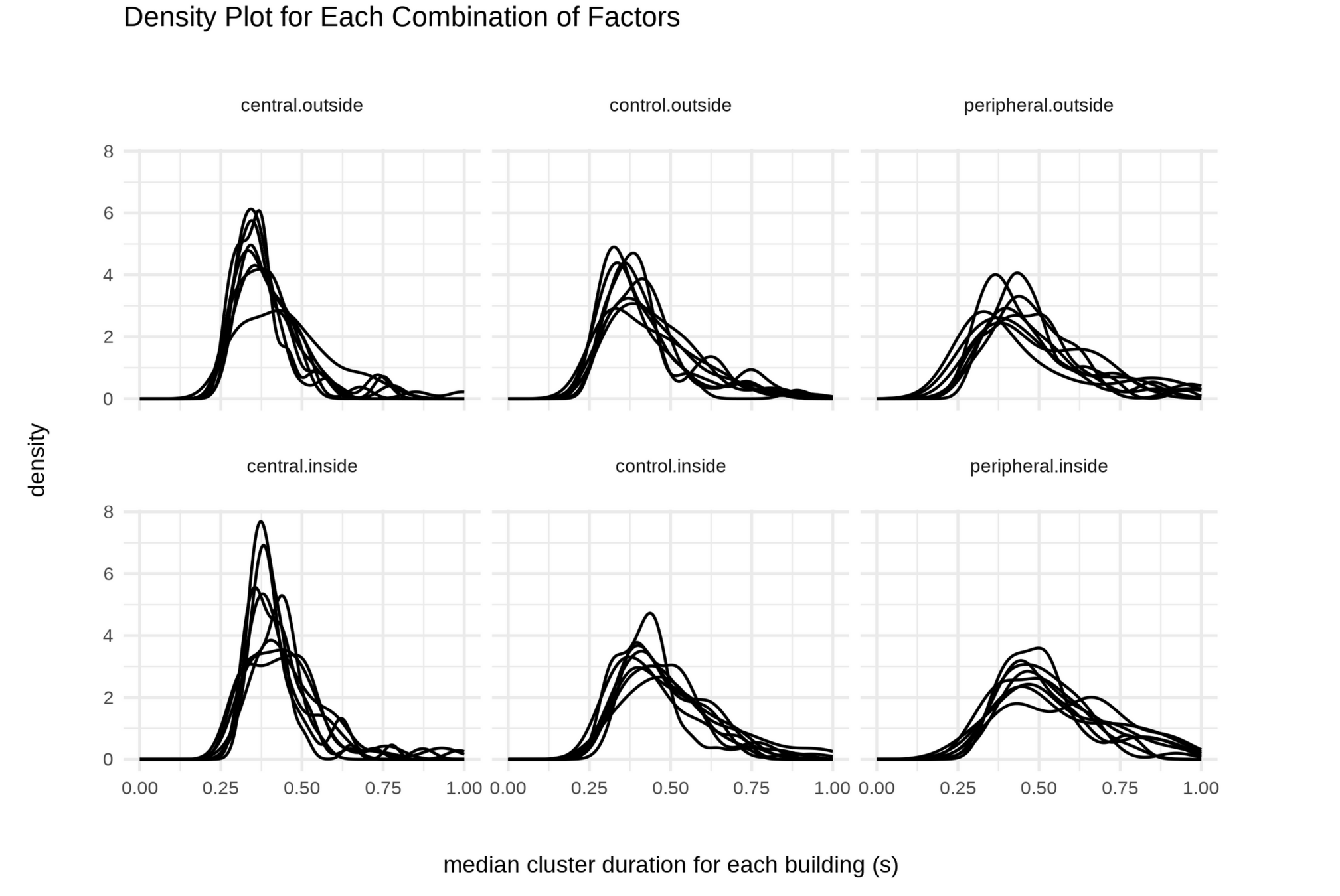
GENERALIZED LINEAR MIXED MODELS


GENERALIZED LINEAR MIXED MODELS


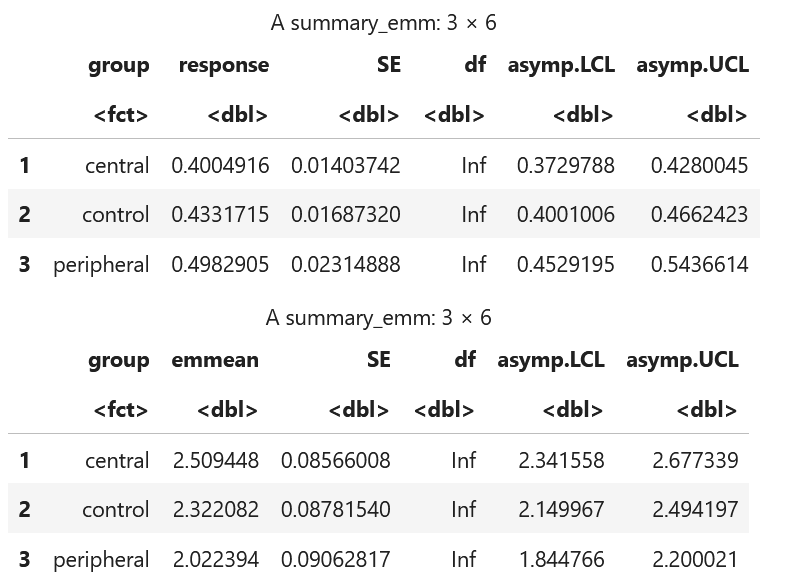
Equation: g(E[Y])=Xβg(\mathbb{E}[Y]) = X\betag(E[Y])=Xβ +Zb
ZbZbZb = random effects
- Key: Link function ggg
GENERALIZED LINEAR MIXED MODELS



Equation: g(E[Y])=Xβg(\mathbb{E}[Y]) = X\betag(E[Y])=Xβ +Zb
ZbZbZb = random effects
- Key: Link function ggg

SUMMARY
