IS DTC MBL+Kick?
Background:
Vanilla Model of DTC:
One creates a disorder or in principle any area law phase which gives rise to a glassy order.
One adds kick to the glassy order. Correlators involving local operators and in the correct basis exhibits explicit TTSB
DTC Phase diagram
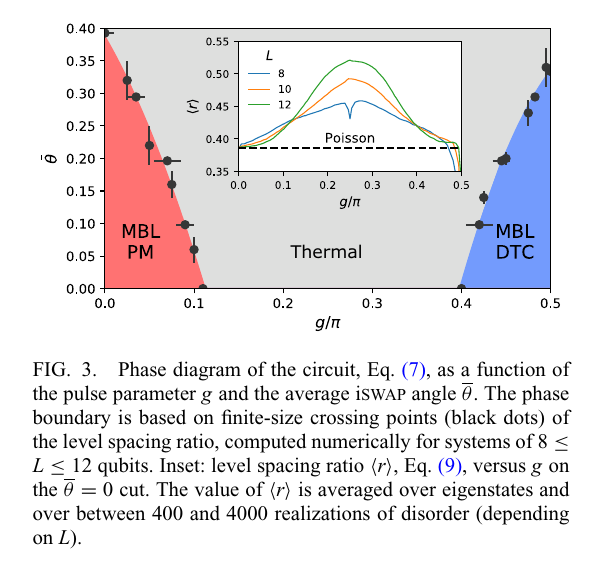
This diagram is basically a ETH-MBL phase diagram. Does the kick survive all the way to the MBL criticiality? Does it survive more?
Other measures of DTC: DFFT
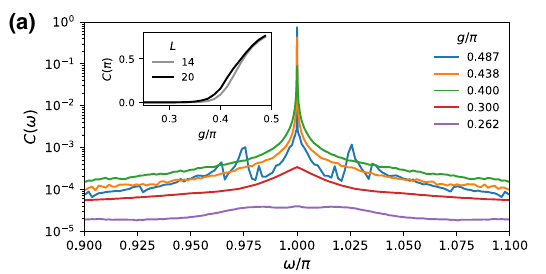

Behaviour of the temporal correlator
Perfect MBL (without disorder avergaing)
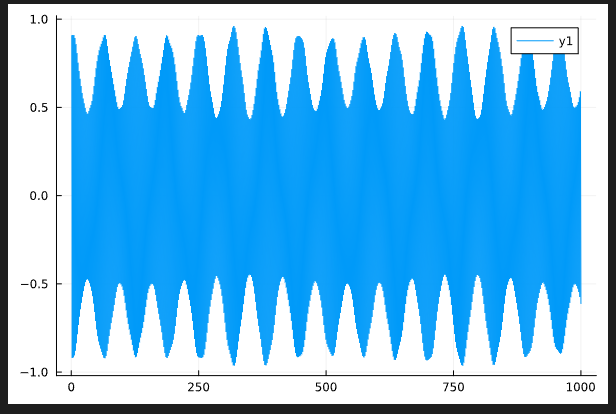
Behaviour of the temporal correlator
MBL:finite detuning (without disorder avergaing)
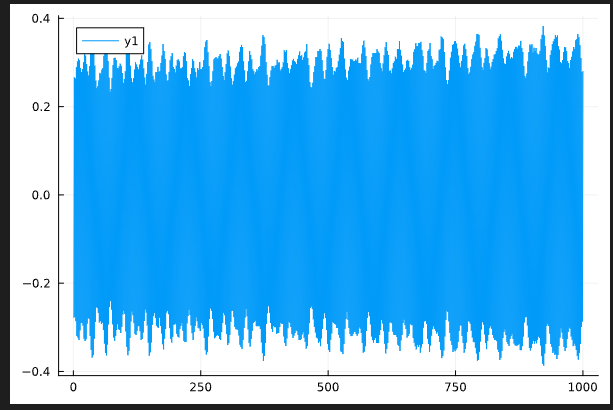
Behaviour of the temporal correlator
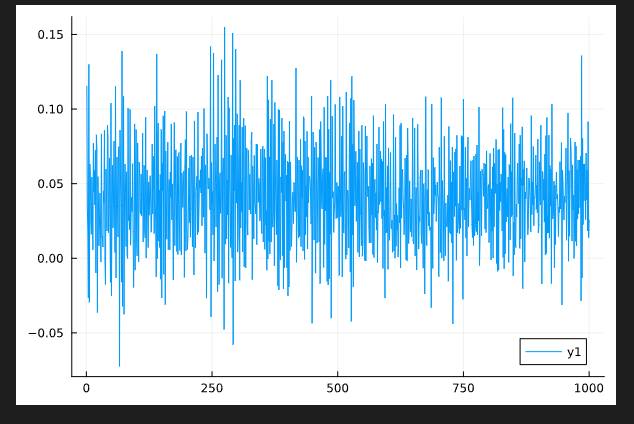
Thermal (without disorder avergaing)
Corresponding FFTs
Perfect MBL (without disorder avergaing)
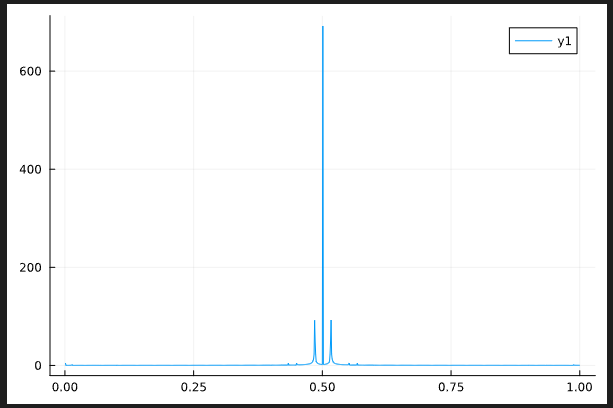
Behaviour of the temporal correlator
MBL:finite detuning (without disorder avergaing)
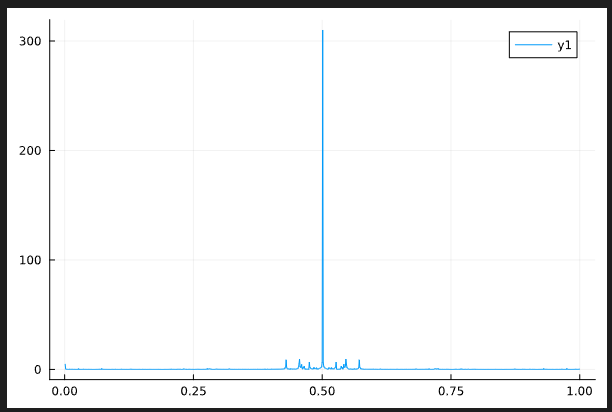
Behaviour of the temporal correlator
Thermal (without disorder avergaing)
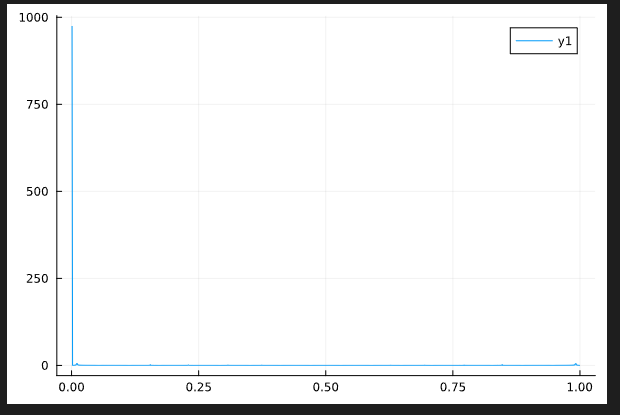
Behaviour of the temporal correlator
This line is probably an artifact

Phase space computation
(without disorder avergaing)
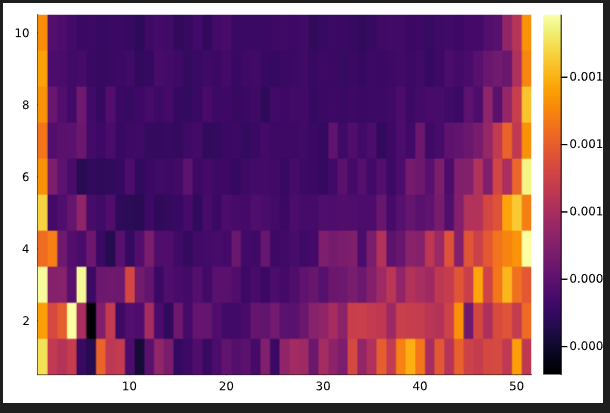
Behaviour of the temporal correlator
Perfect MBL (disorder averged 1202 ensembles)
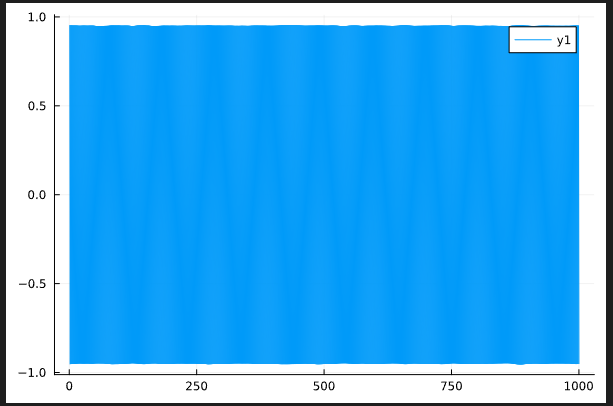
Behaviour of the temporal correlator
MBL:finite detuning (without disorder avergaing)
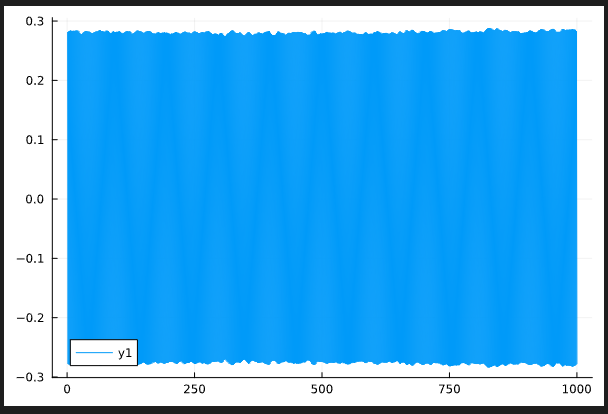
Behaviour of the temporal correlator
Thermal (without disorder avergaing)
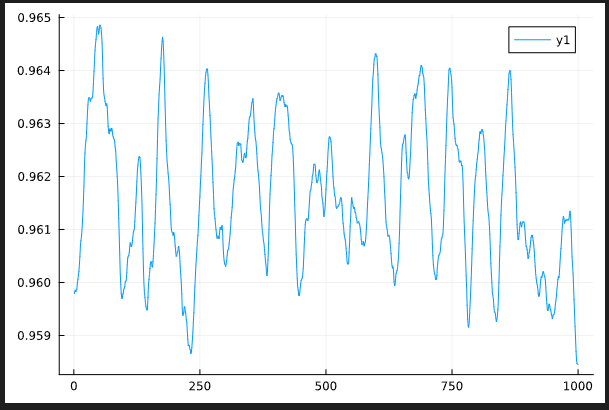
Corresponding FFTs
Perfect MBL (without disorder avergaing)
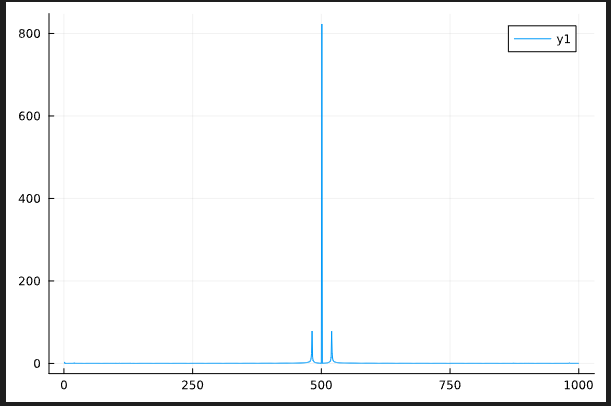
Behaviour of the temporal correlator
MBL:finite detuning (without disorder avergaing)
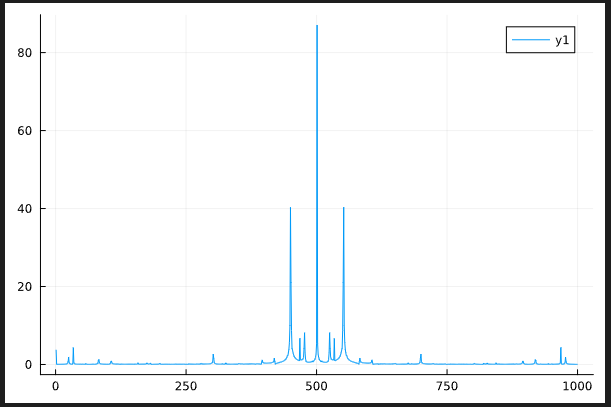
Behaviour of the temporal correlator
Thermal (without disorder avergaing)
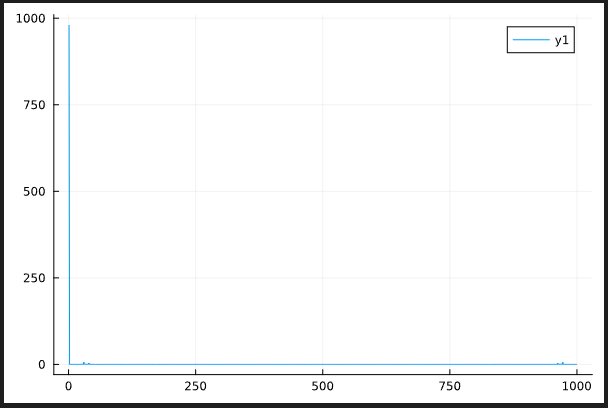
Phase space computation
(without disorder avergaing)

Some things to ponder:
1. Other signatures of DTC? (Vedika mentions a bit more)
what about <n|Z|m>.
2. Is MBL really neccesary for DTC?
3. Does the kick stabilises MBL? (even in vedika's case the diagram is not symmetric)
4. Interpretations; Motivation: Quantum Zeno