Sagnik Ghosh •Uni Bonn •Jelena Klinovaja •July 11, 2023
Discrete Time Crystals
In NISQ ERA
Model : Ippoliti PRXQuantum030346.2021
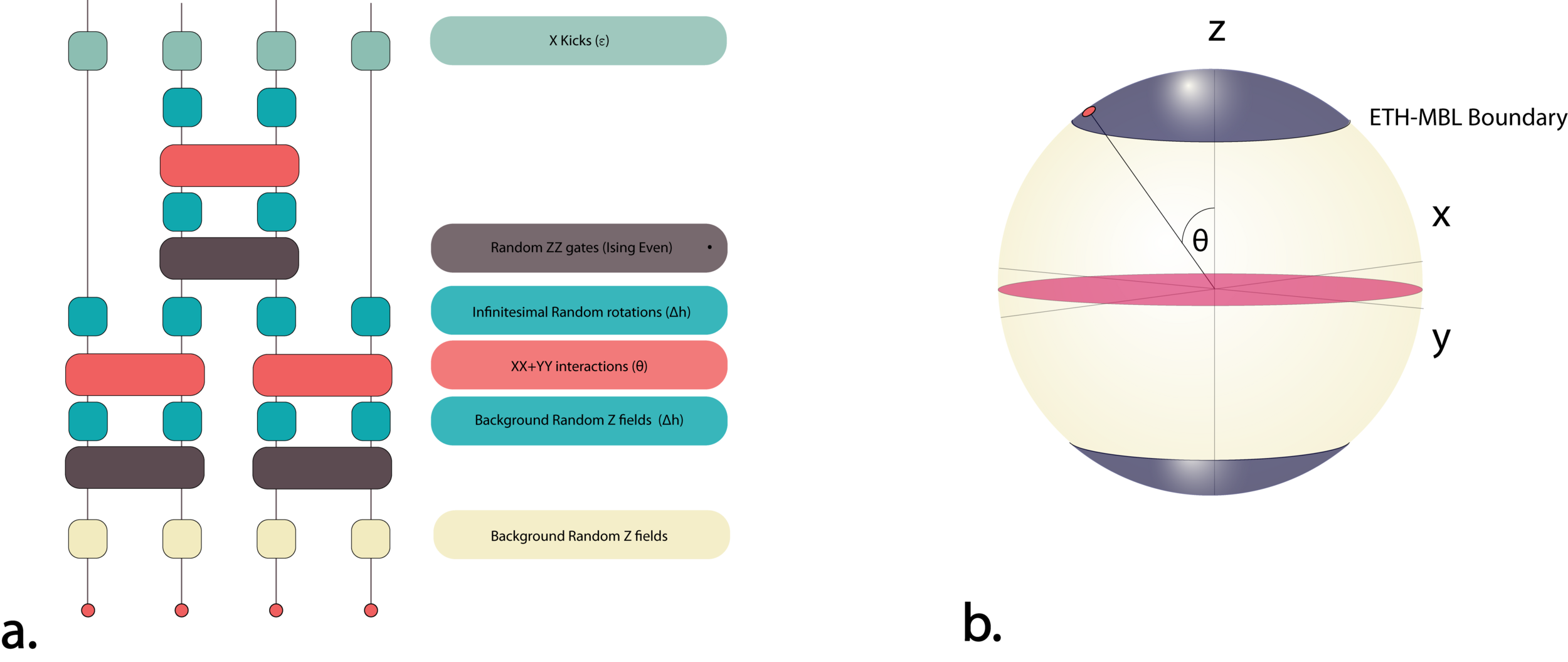
X kicks
Random ZZ gates (Ising Even)
XX+YY Interactions (\theta)
Background Z fields
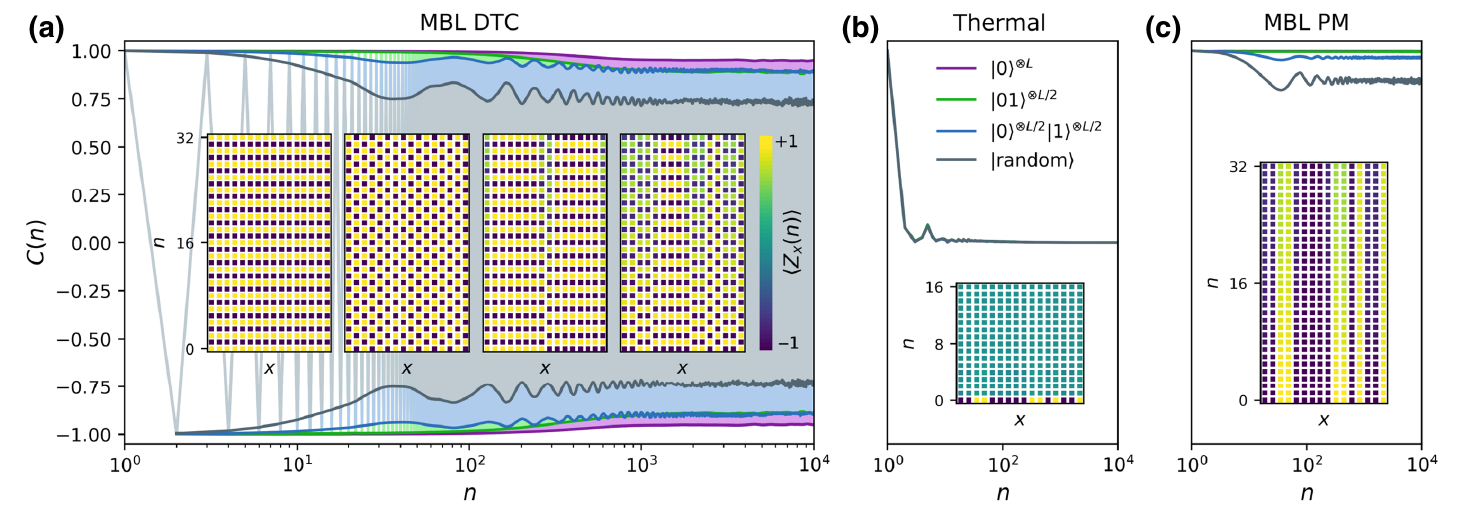
Features of DTC: (Ippoliti PRXQuantum030346.2021)
Dynamical
Signatures:
Eigenstate
Signatures:
Geometry:


DTC in chip
Is DTC really MBL+Kick
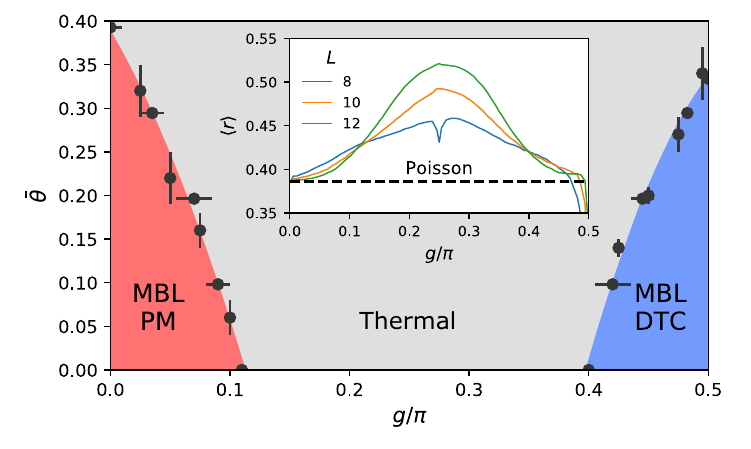
Recall the g. \theta phase diagram has no information on the DTCness. But one can cook up another order parameter namely the height of the envelope of the time series.
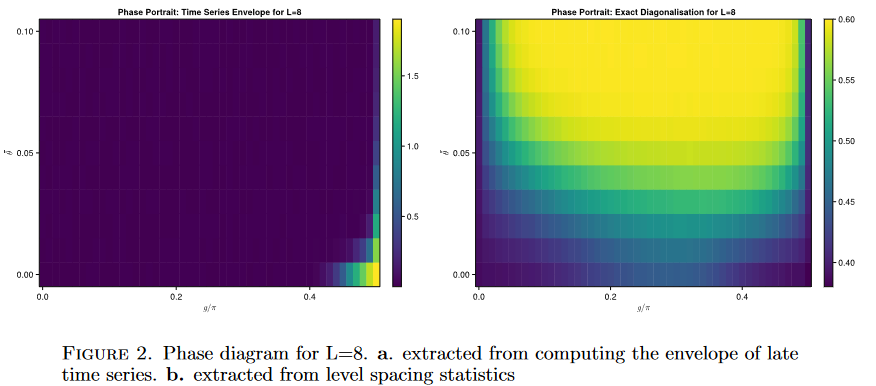
Does not look the same.
The system undergoes the ETH-MBL transitions twice. Once from the Paramegnetic side, once from the DTC side. Are they similar?
Assymetry in transitions:

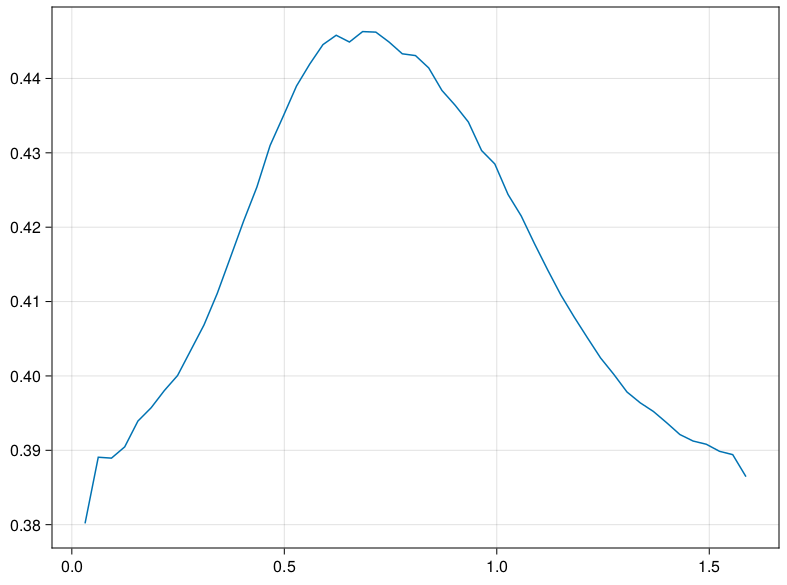
Turns out no.
Different co-efficents. Different Universility classes
Eigenstate signatures of time-translational symmetry?
A Krylov Space Technique

Polynomial filtering diagonalisation

David Luitz
More by Leo (with his own plots)
Polynomial filtering diagonalisation
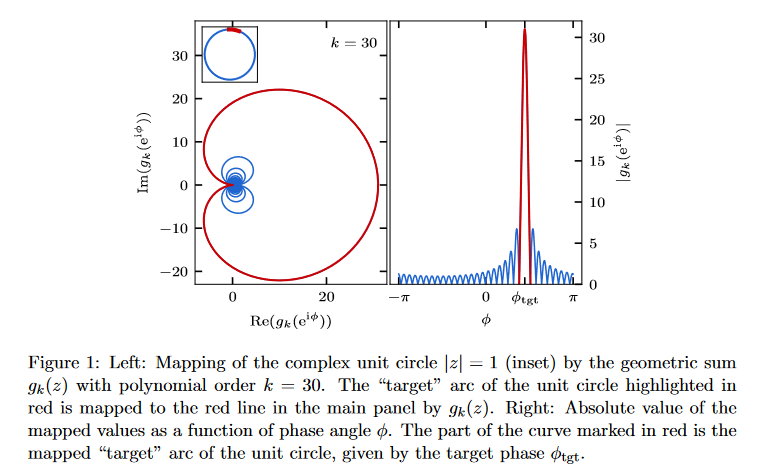
Vanilla Model: Robustness of periods and levels
We can play this game in 3 levels too. Consider a spin-1 chain instead. The relevant kick is one that permutes 0->1, 1->2, 2->1.
Again MBL (of correct symmetry) is needed to escape heating up till infinite temperature.
A Spin-1 DTC
This kick is similar to the RX(4\pi/3).
One can show this kick is unique for a given level. So the only (1-body) kicks that work in three level are all similar to RX(4\pi/3)
So: Underlying Hilbert space dimensions seems to be mapped to the periodicity one can achieve.
But one can reduce a spin 1 chain to a chain of two qubits. (with one extra dimension of patching)
A Spin-1 DTC
Note that now we have 4 body gates (for the disoder) and the rotations are two body gates. These 4 body gates can be reduced to 6 CNOTS and few rotations. So efficient.
Turns out if one uses the original spin-1/2 brickwall and the reduced three level kick, one still has a stable DTC. (note this brickwall does not have correct symmetry conditions).
Why is this stable?
I called dibs on these:
Scaling things up! Can we pin point the universality classes?

Mechanism of TTSB. Classification of criticalities in Floquet TTSB. Is TTSB geometry sensitive?
How DTC changes MBL? New symmetry sectors? Different dynamical rules?
<List to be updated as we go. stay tuned...>
Back to Basics
What are Time Crystals?
Defined using symmetry. Consider Hamiltonian Dynamics. (continuous time transnational symmetry).
But operator dynamics shows distinct (and sufficiently robust) periods (against perturbation, de-phasing).
Discrete Time Crystals
Play the same game in Floquet.
Definition: Floquet Time Crystals
Consider a quantum system (tunable using some parameters) that has period T.
The system is said to undergo a spontaneous time transnational symmetry breaking if the correlators of the system exhibits dynamics with a period nT n \in \mathcal{N}, for an extended range of the tunable parameters.
Classical, Equilibrium systems disallow. No free lunch. [Watanabe et. al.]