Time Crystals without disorder
Sagnik Ghosh 05.06.2024
Recipe for Time Crystals
- Needs non-adiabatic driving (residual correlations)
2. Escape featureless infinite temperature states
Recipe for Time Crystals
Generic (interacting) systems heats up to infinite temp states
Recipe 1: Use disorder to escape ergodicity
Recipe 2: Systems with tilted potential also results in localisation.
Can we use it for creating Time Crystals?
For interacting systems it is a bit more involved as for any finite size system with reflection symmetry does not remain localised. But in thermodynamic limit it is not a problem and does show time crystalline signatures.
Model
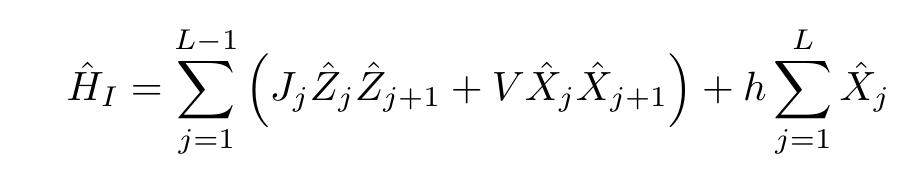
J is sampled from a constant tilt:
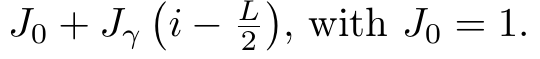
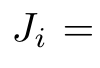
For, V, h, theta zero the system is diagonal in computational basis. And ZZ correaltions are trivial.
System is periodically kicked by,
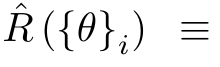
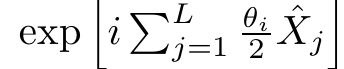
At this special point, Eigenstates of H is degenerate and a state and its parity flip has the same eigenvalue.
Z anti comutes with P, so one can cook up cat states
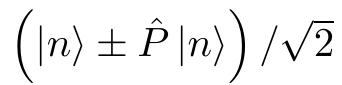
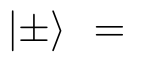
that has the property
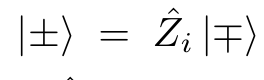
One has to ensure that they remain degenerate under external perturbation.
For any finite L a local perturbation will couple them
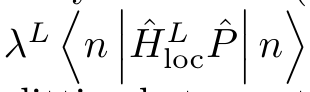
This will result in exponential splitting between the states
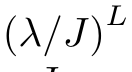
For uniform J the condition of DTC is
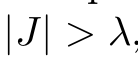
For other potentials, the system remains quasi degenerate as long as there is a region
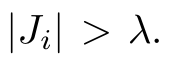
That grows with system size, which is guaranteed for linear potential
Localisation is in these potential is previously established
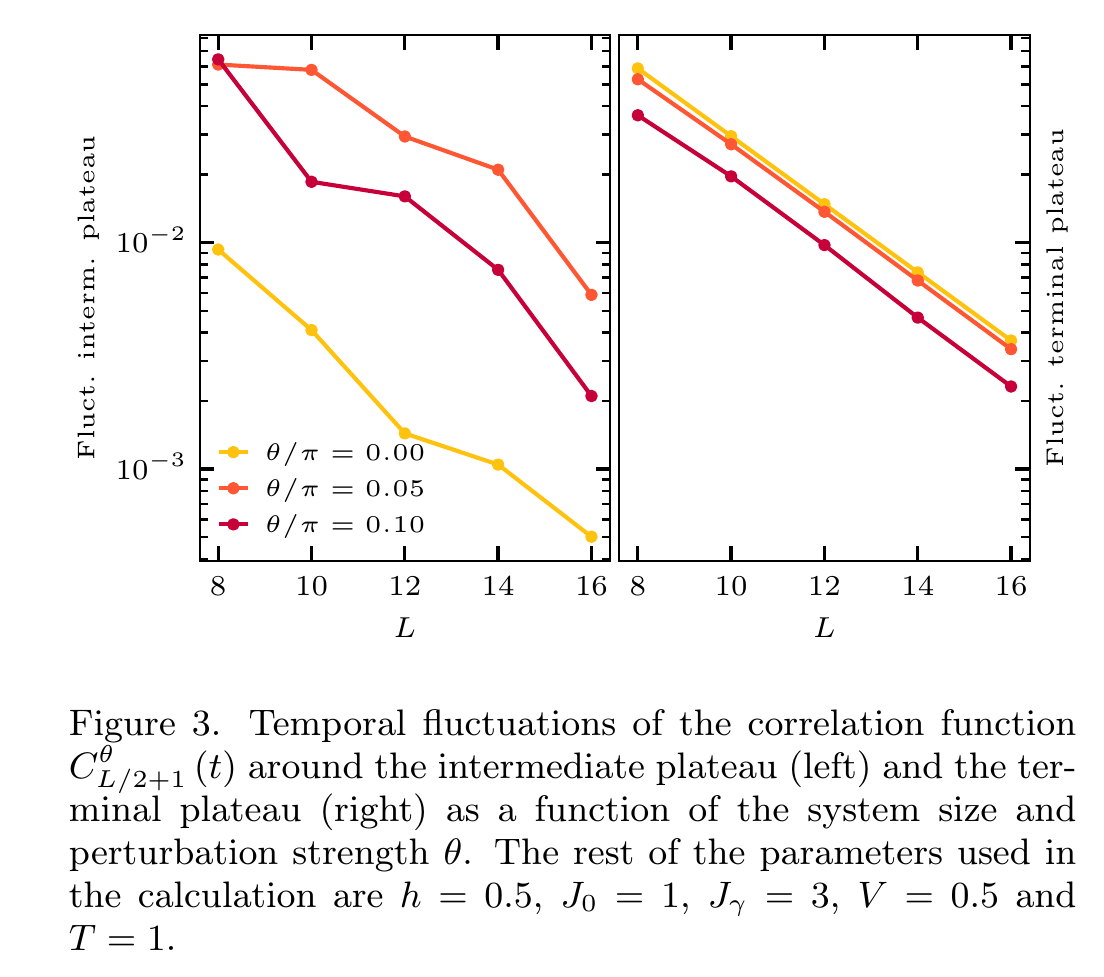
Signature of DTC
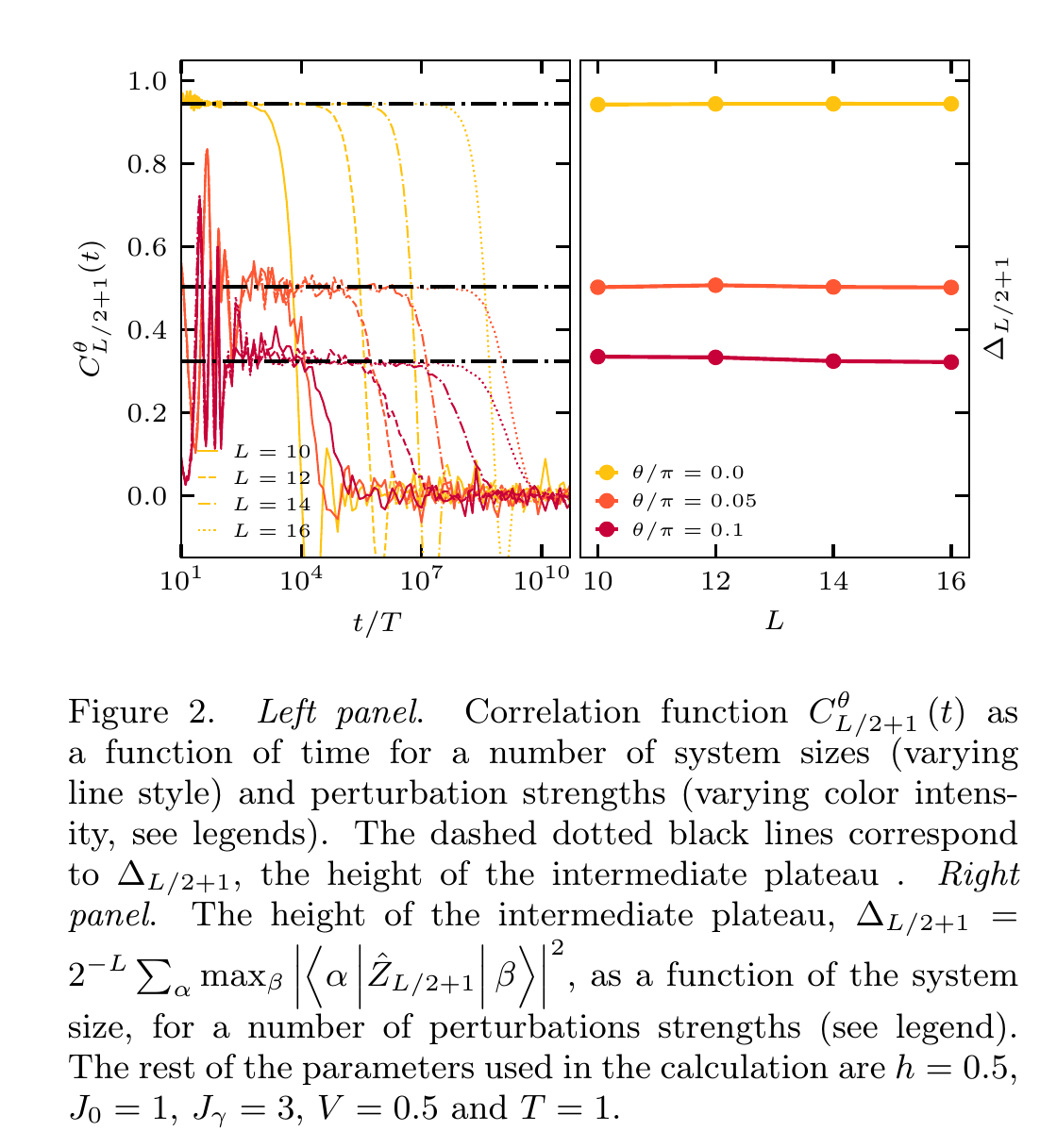
Fluctuations around final plateau