CMSC389O TA Interview

Topic: Largest Rectangle in Histogram

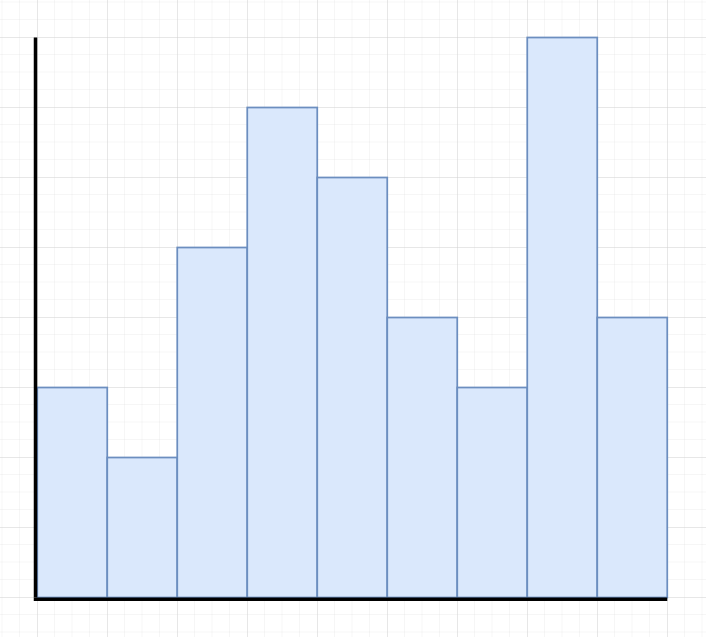
Suppose we want to find the largest rectangle

The rectangle would be the largest

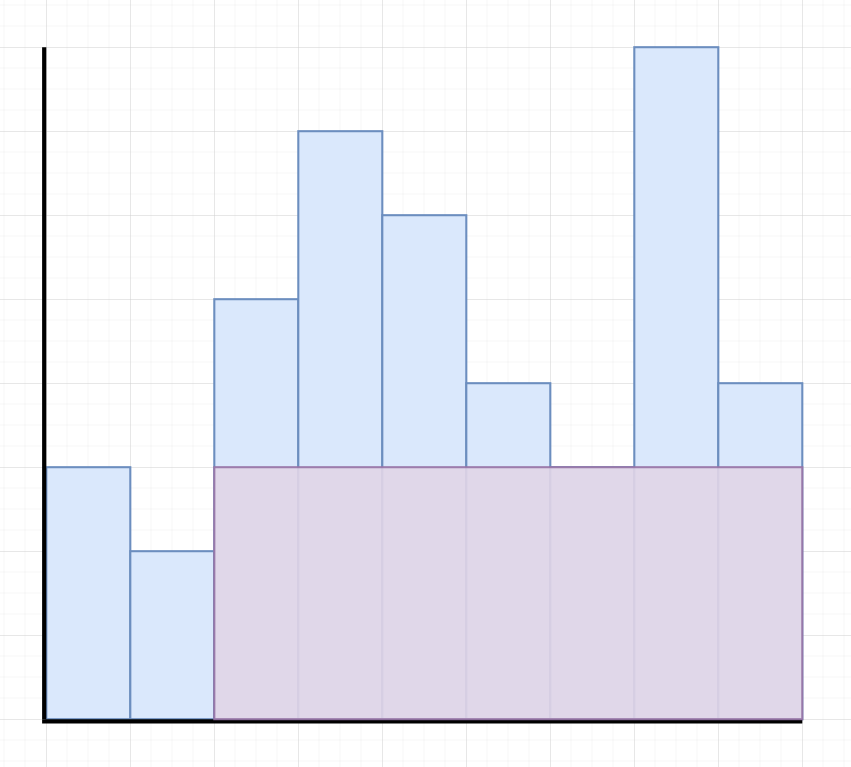
How to find the largest rectangle?

Consider Iterating over all intervals!

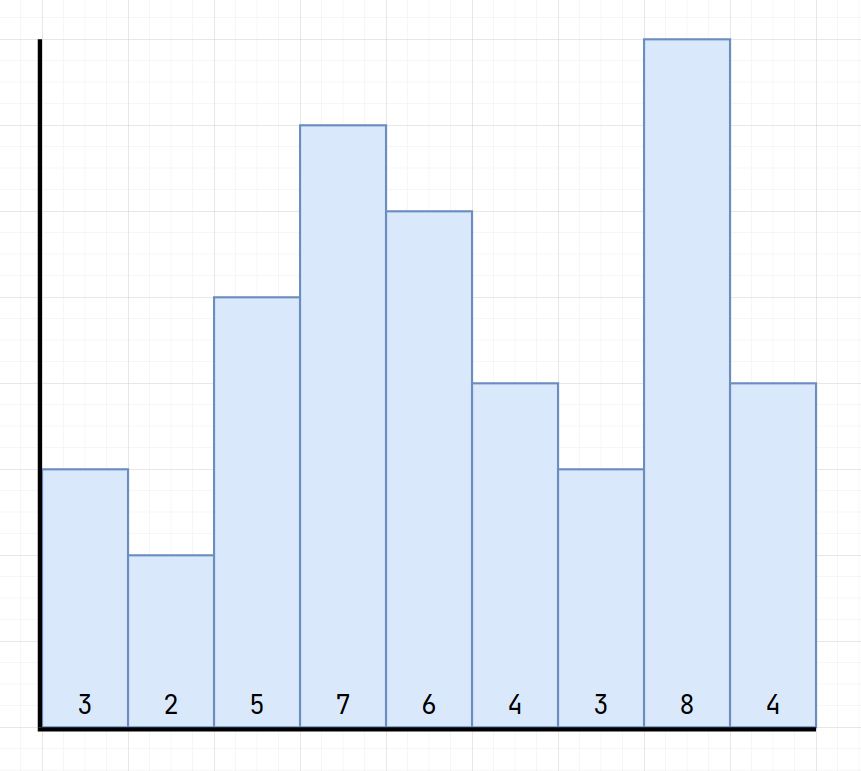
// Assume that the heights are stored in h[]
for(int l = 1; l <= n; l++){
    for(int r = l; r <= n; r++){
    	//What to do here?
    }
}

Consider the interval $[l,r]$, what is the answer?

// Assume that the heights are stored in h[]
int maximumArea = 0;
for(int l = 1; l <= n; l++){
    for(int r = l; r <= n; r++){
    	//What to do here?
    }
}

Consider the interval $[l,r]$, what is the answer?

1. Keep the answer in a variable!

// Assume that the heights are stored in h[]
int maxArea = 0;
for(int l = 1; l <= n; l++){
    int minH = h[l];
    for(int r = l; r <= n; r++){
        minH = min(minH ,h[r]);
    }
}

Consider the interval $[l,r]$, what is the answer?

1. Keep the answer in a variable!

2. Keep track of $\text{minHeight}$

// Assume that the heights are stored in h[]
int maxArea = 0;
for(int l = 1; l <= n; l++){
    int minH = h[l];
    for(int r = l; r <= n; r++){
        minH = min(minH ,h[r]);
        maxArea = max(maxArea, minh*(r-l+1));
    }
}

Consider the interval $[l,r]$, what is the answer?

1. Keep the answer in a variable!

2. Keep track of $\text{minHeight}$

3. Area is $\text{minHeight} \times (r-l+1)$

// Assume that the heights are stored in h[]
int maxArea = 0;
for(int l = 1; l <= n; l++){
    int minH = h[l];
    for(int r = l; r <= n; r++){
        minH = min(minH ,h[r]);
        maxArea = max(maxArea, minh*(r-l+1));
    }
}

Consider the interval $[l,r]$, what is the answer?

1. Keep the answer in a variable!

2. Keep track of $\text{minHeight}$

3. Area is $\text{minHeight} \times (r-l+1)$

4. We are done!

What was the time complexity?

$$O(n^2)$$

What was the time complexity?

$$O(n^2)$$

Too slow!

How can we do better?

Recall what we did to find the answer!

How can we do better?

Recall what we did to find the answer!

$$\min_{(l,r) \in I}\{\min(h_l,\cdots,h_r)(r-l+1)\}$$

What if we check the cases where each bar is minimum?

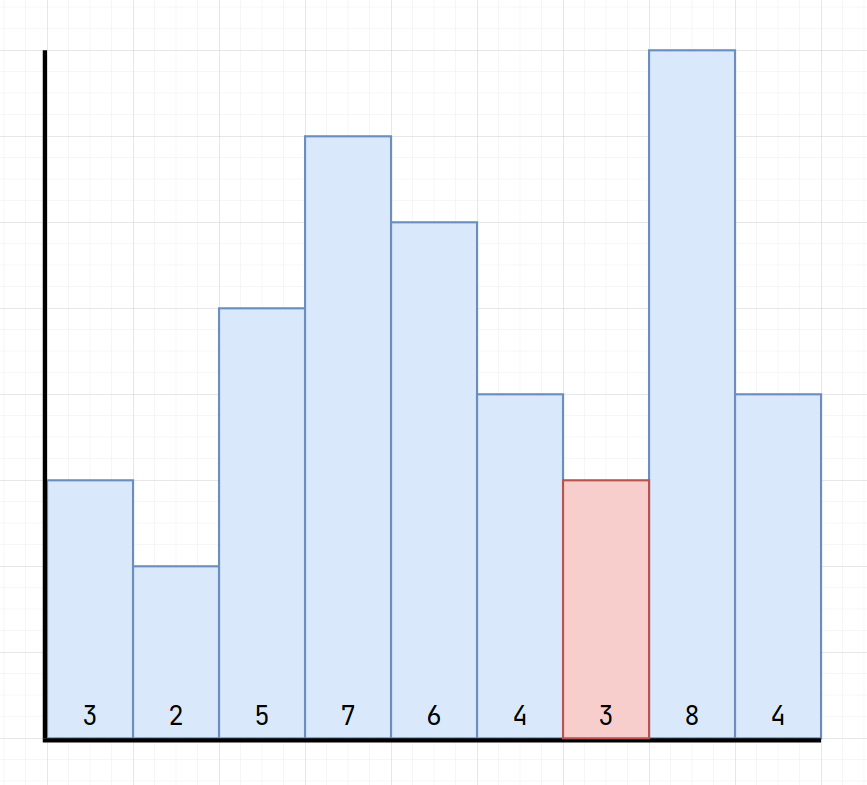
What if we check the cases where each bar is minimum?

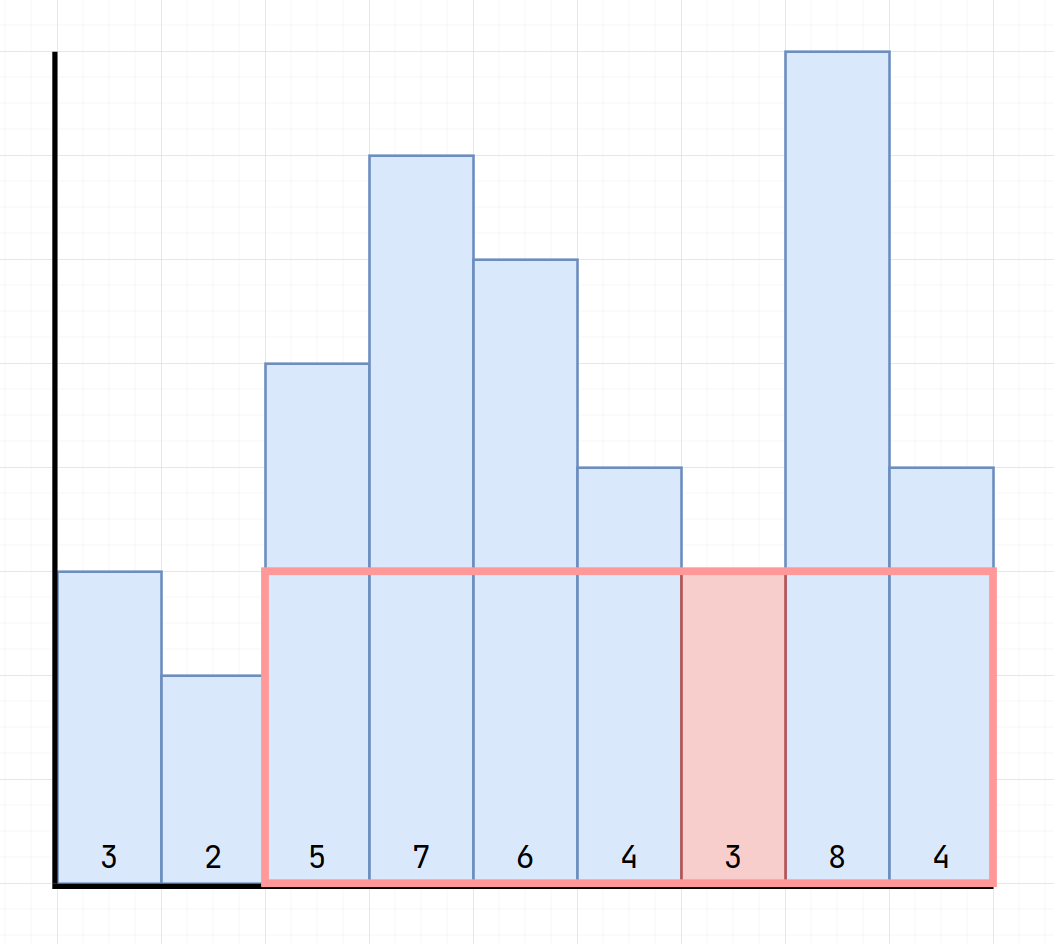
What about changing the formula to

$$\min_{1 \le i \le n}(h[i] \times (r[i]-l[i]+1))$$

$l[i]$ is the next element to the "first element on left lower than $i$"

$r[i]$ is the prev element to the "first element on right lower than $i$"

Recall Stack from CMSC132!

1. Last in First Out

2. Push a element on Top

3. Access the element on Top of the stack

To find the first element to the left less than $i$

We want to store the possible candidates in the stack

We want the top of the stack to be the index we want to find!

Therefore, let the top of the stack be $j$

if $h[j] \ge h[i]$ then we pop the value from stack

Stack

POP!

Stack

POP!

Stack

POP!

Stack

POP!

Stack

POP!

Stack

POP!

Stack

Now we know how to find $l[i]$!
Let's write it into code!

stack<int> st; // Stores possible candidates

for(int i = 1; i <= n; i++){
    if(!st.empty() && h[st.top()] > h[i]){
        st.pop();
    }
    l[i] = (st.empty() ? 1 : st.top()+1);
    st.push(i)
}

The code to find $l[i]$!

stack<int> st; // Stores possible candidates

for(int i = 1; i <= n; i++){
    if(!st.empty() && h[st.top()] > h[i]){
        st.pop();
    }
    l[i] = (st.empty() ? 1 : st.top()+1);
    st.push(i)
}

while(!st.empty()) st.clear();

for(int i = n; i >= 1; i--){
    if(!st.empty() && h[st.top()] > h[i]){
        st.pop();
    }
    r[i] = (st.empty() ? n : st.top()-1);
    st.push(i)
}

Do this again for $r[i]$

Now we have everything to solve the problem

let's write the main part of the code!

Now we have everything to solve the problem

let's write the main part of the code!

int maxArea = 0;
for(int i = 1; i <= n; i++){
    maxArea = max(h[i] * (r[i] - l[i] + 1));
}

The code now runs in $O(n)$!

We often call this method the

Monotonic Stack Method