{flow}
UMD Competitive Programming Club
Sam
Network Flow
# What's Flow
-
A graph consisting of a source \(s\) and sink \(t\) where the edges has non-negative capacity \(c(e)\).
-
A flow on an edge is a value \(f(e)\) that does not exceed the value \(c(e)\). \((f(e) \le c(e), \ \forall e \in E\)
-
For all vertex \(v \in V\), the sum of incoming flow is eaual to outgoing flow.
Network Flow
# What's Flow
-
An easier way of viewing network flow is by using water that came out from the source, goes through pipes, and end up in the sink.

{max flow}
We want to find "Maximum Flow" of a network
Maximum FLow
# MAX FLOW
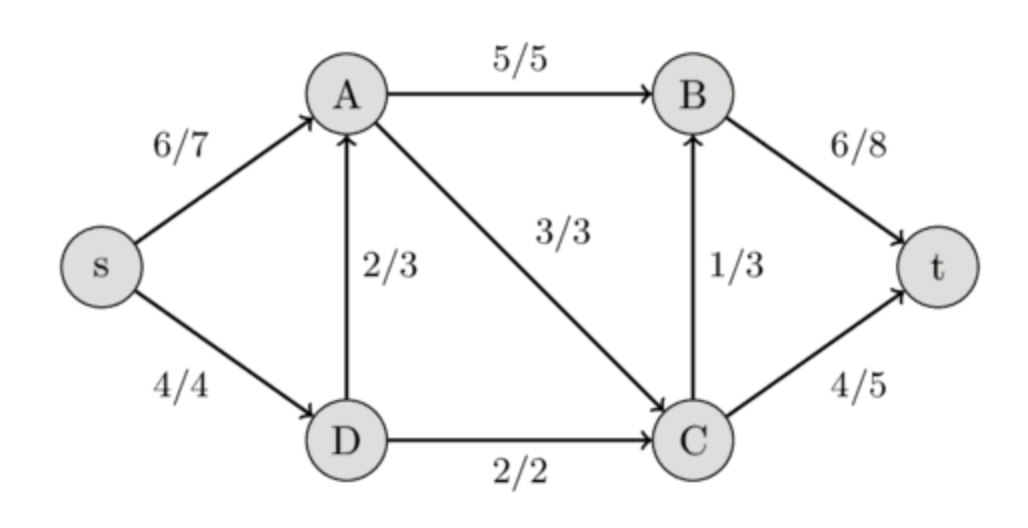
- We want to find the maximum amount of flow that can flow through the network
- In the following image, the answer is \(10\)
How to find flow?
# MAX FLOW
- Residual graph
- Algorithms:
- Ford-Fulkerson: A concept, basically check if there exists an Augmenting Path, then flow through it. \(O((V+E)f)\) where \(f\) is max flow.
- Edmond-Karps: Use BFS to do Ford-Fulkerson \(O(E^2V)\)
- Dinic: A smarter way with DFS/BFS. \(O(V^2E)\)
- Dinic is \(O(E\sqrt{V})\) with bipartite graphs.
- Flow algorihms usually run a lot faster than theoretical complexity: \(O(flow)\) as said by taiwanese CPers
{problems}
Let's apply them on problems
# PROBLEMS
Minimum Path Cover of a DAG
Uva - Collectors Problem
{min cut}
Max flow = Min cut
Minimum Cut
# MIN CUT
- It turns out that for any flow network, we have max flow = min cut.
- We can use this to model even more problems!
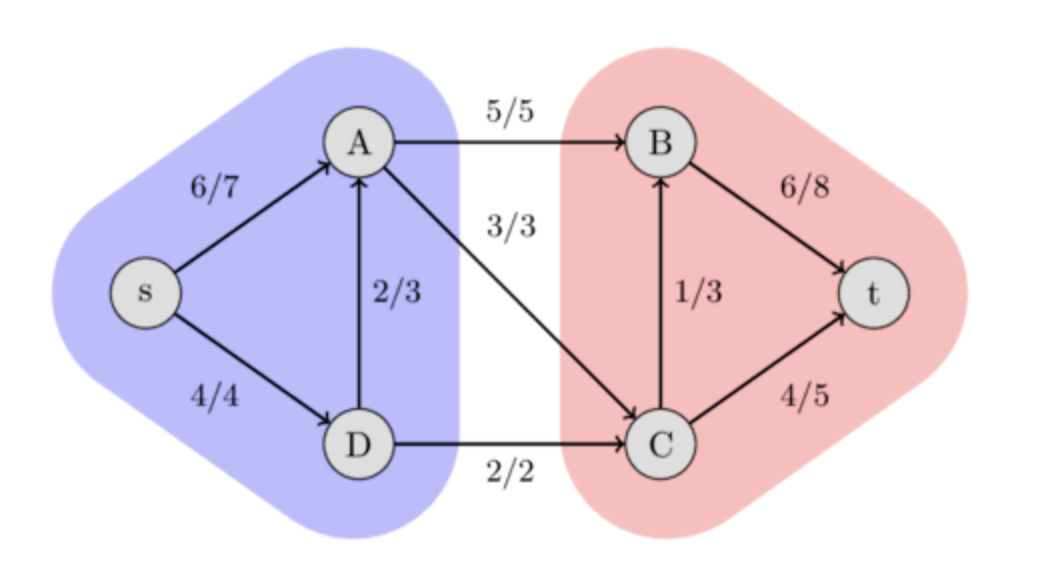
Minimum Cut
# MIN CUT
Codeforces 1473F - Strange Set
Codeforces - Best Subsequences
{MCMF}
Min Cost Max Flow!
Min Cost Max Flow
# MCMF
Codeforces - Armchair